A novel code system for revealing sources of students' difficulties with stoichiometry

Abstract

A coding scheme is presented and used to evaluate solutions of seventeen students working on twenty five stoichiometry problems in a think-aloud protocol. The stoichiometry problems are evaluated as a series of sub-problems (e.g., empirical formulas, mass percent, or balancing chemical equations), and the coding scheme was used to categorize each sub-problem solution as successful, neutral, or unsuccessful, with more detailed codes comprising the neutral and unsuccessful categories, for a total of eight codes. A relatively high frequency of neutral results was found in which students simply did not realize when or how to approach a sub-problem. A lack of conceptual understanding of the mole concept appears to be closely related to students skipping crucial steps in stoichiometry problems, especially the sub-problems stoichiometric ratio and mole concept. Students' failures were also observed to be due to a lack of basic knowledge, such as the names of chemical compounds. The application of the new code system was shown to reveal difficulties that might have otherwise been missed by an analysis that focused on end results only.

---

Introduction

It has been observed that problem solving is “what you do when you don't know what to do” (Frank et al., 1987). In general chemistry education, the quintessence of problem solving is stoichiometry in all its various forms. Introduced in 1843 in Germany and 1859 in the United States of America, stoichiometry was introduced to supplement a perceived lack of numerical problems in the textbooks of the day (Jensen, 2003). It has been a thorn in the side of students and teachers alike since its introduction; students struggling to learn the subject and teachers struggling to better teach the subject.

As a result, there have been many studies looking at how best to teach stoichiometry, a fraction of which will be highlighted here. Most of the studies on student success in stoichiometry focus on the end result – whether or not students got the right answer on a stoichiometry problem – and lack a coherent method to analyse weaknesses in problem solving or stoichiometry (Nurrenbern and Pickering, 1987; Astudillo and Niaz, 1996; Gauchon and Meheut, 2007). Nurrenbern and Pickering (1987), studying students in general chemistry courses at two large, mid-western colleges, looked at the differences between student conceptual learning in stoichiometry and their ability at problem solving. Exams were used and included a variety of stoichiometry questions, some that were algorithmic in their format and some that were conceptual in nature. Though students could algorithmically solve problems, it was determined that this did not necessarily show conceptual understanding on the part of the students. The authors concluded that “teaching students to solve chemistry problems is not equivalent to teaching them about the nature of matter”.

In a general chemistry course for first-year students in a Venezuelan university, students were given multiple small tests, and were asked to write down justifications for their answers, which were then graded (on a scale of 0–10) by the researchers (Astudillo and Niaz, 1996). It was found that students performed better on stoichiometric problems when they viewed matter in terms of moles (mole concept), rather than mass. It was also observed that student misconceptions were an attempt to simplify the problem, thereby avoiding difficulties by creating easier alternative mental constructs. Those easier mental constructs, in the context of limiting reagent (LR), were investigated in a study of 10th grade French students (Gauchon and Meheut, 2007). The students in the study had difficulty in understanding what chemicals should be present at the end of a reaction and held two conflicting preconceptions: both reactants will be used up regardless of the proportions, and only one reactant will be used up, depending on whether or not the phases of the reactants were the same. Unfortunately, teaching had little effect on the students' preconceptions.

Since stoichiometry is a large subject with many sub-topics, some researchers have chosen to separate their analysis by dividing the students based on their learning strategies (BouJaoude and Barakat, 2003), or by dividing based on the various sub-topics (Huddle and Pillay, 1996). In an 11th grade science course taught in English in Lebanon, BouJaoude and Barakat (2003) determined that conceptual understanding was correlated with success at problem solving, though causality was not established. Their method classified students by their learning method (i.e., rote learning approach, intermediate learning approach, or meaningful learning approach) and their conceptual understanding (i.e., none, partial, or full), and found that conceptual thinkers solved problems in fewer steps. Unfortunately, their method could not determine a pattern in the students' incorrect strategies. Part of the difficulty, as suggested by Huddle and Pillay (1996), is that students' ability to understand problems on the conceptual level may still be developing in first-year college students. Their study, performed with college students in Johannesburg, South Africa, also found that misconceptions of stoichiometry can be hard to dislodge. The authors looked at sub-problems inside stoichiometry problems to determine more specific misconceptions, though their informal approach made it difficult to generalize beyond their specific stoichiometry problems. In general, it has been shown that student success in problem solving is related to their working memory capacity (Johnstone and El-Banna, 1989). When a student's working memory capacity is exceeded, performance was shown to decrease significantly (Johnstone et al., 1993).

Knowledge space theory (KST) is a more complex way of looking at conceptual understanding. Arasasingham et al. (2004) used KST to build a statistical model that described a finite number of “knowledge states” that represent cognitive development in stoichiometry. It does produce a reproducible model, but cannot look at individual student sub-problems, rather it must look at student knowledge as a whole. This was done using an eight-question test with 731 science and engineering majors at UC-Irvine. The goal was to assess how students connected the micro, macro, and symbolic representations of stoichiometry. The authors determined that students (i.e., non-expert thinkers) generally proceed from symbolic understanding, to numerical understanding, to visualization at the molecular level. In general, they found that students do not have particulate understanding and cannot visualize the molecular level.

One method suggested for improving students' performance in stoichiometry is the creation of mole ratio flow charts (Wagner, 2001). These flow charts, which Wagner asked his students to create themselves before combining them into a master chart for the entire class, did not show significant statistical differences in student performance over the use of the more traditional dimensional analysis. The flow charts were, however, preferred by the students. Similarly, a method encouraging students to write about their understanding of stoichiometry to fellow students in lower grades (“write-to-learn”) failed to show quantitative differences in student performance, though qualitative analysis showed that students were improving in their conceptual understanding of stoichiometry (Hand et al., 2007).

Many other methods have been suggested and published for improving students' understanding of stoichiometry. These suggestions generally lack research that attests to their efficacy, though usually report improved student performance, which can itself be important (Bauer, 2008). Krieger (1997) has suggested the creation of a flow chart based on The Three Stooges, Witzel (2002) suggested teaching stoichiometry using LEGO blocks, and Haim et al. (2003) suggest visualizing stoichiometry by the creation of hamburgers. Flow charts are also suggested for visualizing how amounts of substances are represented (Ault, 2001), and for stoichiometry in chemical engineering (Felder, 1990). Whether these methods improve students' conceptual understanding of stoichiometry or their ability to solve complex problems is not known. A general model that could study and compare their effectiveness is introduced below.

Method

Sub-problems

Due to the importance of and its prevalence in general chemistry education, stoichiometry was chosen as the topic to be analysed in this study. Stoichiometry is a subject with many sub-topics, and thus was an ideal subject for the application of the new research model described herein. As the model looks at sub-problems within a larger problem, stoichiometry was broken down into ten sub-problems: writing chemical equations (WEQ), balancing chemical equations (BEQ), mass percent (MP), empirical formulae (EF), molecular formulae (MF), percent yield (PY), limiting reagent (LR), mole concept (MC), conservation of mass (CM), and stoichiometric ratio (SR). While all of these concepts are familiar to any chemistry instructor, the term mole concept may not be specific enough. For our classification, mole concept is finding the number of moles using either the number of particles or the mass of the substance, or calculating the mass or number of particles of the substance using the number of moles. The abbreviations for the sub-problems can be seen in Table 3.

Subjects and research protocol

The student cohort who participated as subjects in this study was recruited from a regional, primarily undergraduate, Midwestern university in the United States of America. In all, 18 subjects volunteered for the study and 17 of those students completed the study and were included in the final research. All students were registered for a second semester general chemistry class in spring 2006 when recruited for the study. The authors were not instructors for any of the subjects at the time of the research.

The protocol used to determine how students were approaching the various stoichiometry problems was the “think-aloud” protocol. During this protocol, the students were asked to solve a series of stoichiometry problems and to vocalize their thought process during the task. The researcher sat with the student and occasionally asked questions to clarify what the student was thinking at that time. The researchers were also allowed to give some hints when the students were clearly unable to proceed without additional information. Additional information on the protocol, as used for this study, was described previously by Gulacar and Fynewever (2010). The mole concept achievement test (MC-AT) was administered to each student to determine their initial familiarity with the mole concept (Gower, 1977; Griffiths et al., 1983).

Mapping students' failures and successes

Previously, Gulacar and Fynewever (2010) introduced a new method for studying the difficulties students have with multi-step stoichiometry problems. The method was a modification of a model introduced by Johnstone and El-Banna to predict student difficulty by accounting for complexity in solving a problem; a model that was modified by Tsaparlis to account for the differing difficulty in various problem steps (Johnstone and El-Banna, 1986, 1989; Tsaparlis, 1998). The new modification introduced by Gulacar and Fynewever focuses on the sub-problems that a given problem is comprised of and evaluates student difficulty with each sub-problem at a much finer level than the previous models. What is lost in predictive power (i.e., this new model analyses in a post-hoc fashion only) is gained in more specific knowledge about what difficulties students are encountering in solving a particular problem.

The codes described here were developed initially while analysing the data from the think-aloud protocol described in the study above. In analysing the data (i.e., student work, transcripts, video), it was noted that the mistakes of the students were nuanced. These various mistakes were categorised, which resulted in the codes described here. The codes were further revised by the first author through discussions with his colleagues. The resulting codes were shared with the last author who used them to code the same problems. Cohen's kappa was calculated to determine that the application of the codes was consistent (see below).

The goal of this paper is to introduce this new set of codes used to study student difficulties in solving multi-step problems and apply these codes to the sub-problems of stoichiometry. To do this, the data from Gulacar and Fynewever will be revisited in order to focus specifically on the details of the coding scheme and to subsequently draw new, more detailed conclusions that were previously unrealized. Previous research has shown that students have difficulties with multi-step problems, but only focused on whether a sub-problem was correct or incorrect, without concern for the manner in which the sub-problem was incorrect (Ayres and Sweller, 1990; Huddle and Pillay, 1996). To attain this greater level of specificity, the complete set of codes, categorized into three groups, is described. These codes are then applied to the pre-determined sub-problems that comprise each problem analysed. A summary of the codes and their abbreviations can be seen in Table 1; the totals of each code group in Table 2; application of the codes is described in Fig. 1.

Table 1 Abbreviations and brief descriptions of codes

S	Successful	Sub-problem correct
NR	Not required	Found alternate method
DD	Did not know to do	Sub-problem skipped
DSE	Did something else	Work unrelated to problem
CD	Could not do	Right concept; no work
UG	Unsuccessful – guessed	Guessed
URH	Unsuccessful – received hint	Hint given to student
UDI	Unsuccessful – did incorrectly	Incorrect solution

---

Table 2 Total number of codes applied^a

	Total	WEQ	BEQ	MP	EF	MF	PY	LR	MC	SR	CM
a Shows the number of times students were successful (group I), unsuccessful (group III), or had some other difficulty with solving a sub-problem (group II). Abbreviations for the chemistry topics shown are referenced in Table 3.
Group I (successful)	1340	81	166	102	23	15	52	20	602	240	39
Group II (neutral)	382	7	3	18	7	0	20	9	176	130	12
Group III (unsuccessful)	250	99	18	16	21	2	13	5	38	38	0

---

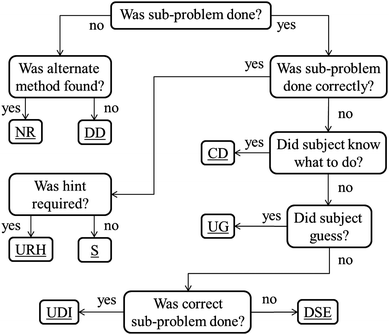Fig. 1 Decision tree for assigning codes.

Group I (successful)

Successful (S). The code “S” was assigned to a sub-problem when the calculation for that piece was done correctly or when the subject remembered a needed piece of information correctly. This was only applied if the student achieved the success on their own, without the use of hints. For S, the following must be true:

• The sub-problem is required for proper solution and was solved correctly.

Group II (neutral)

Not Required (NR). The code “NR” was assigned to a sub-problem when the student solved the problem using a different method than the one expected by the investigator. Since each sub-problem in a student's solution method was given a code to evaluate a student's progress through the problem, the NR code was necessary in order to compare students' methods. NR represents an alternate, correct method that would otherwise create inconsistencies in the coding methodology if the code was not applied. This was only applied if solving the sub-problem was not necessary in the student's method. For NR, the following must be true:

• The expected sub-problem was not solved by the student.

• The student's method was determined to be an alternate, valid method of solving the problem.

Example: Methane and ethane are the two simplest hydrocarbons. What is the mass % of C in a mixture that is 40% methane and 60% ethane by mass (Silberberg, 2006)?

In solving the above problem, a student was expected to calculate the moles and grams of carbon in the mixture. However, a student could alternately choose to calculate mass percent in each compound first, skipping the explicit calculations above, which necessitated the application of the NR code.

Did not know to do (DD). The code “DD” was assigned to sub-problems when students did not know that a specific calculation or specific step was required for proper completion and this step was left blank (i.e., not attempted at all). For DD, the following must be true:

• The sub-problem is required for proper solution (could not use NR).

• The sub-problem was left blank (no work attempted).

Example: Hydrocarbon mixtures are used as fuels. How many grams of CO₂ (g) are produced by the combustion of 200 g of a mixture that is 25% CH₄ and 75% C₃H₈ by mass (Silberberg, 2006)?

In order to solve this problem, a student first needs to write and balance the chemical equations. Students were observed skipping these steps, however, and trying to solve the problem without properly balanced chemical equations. As a result, DD was applied to both the sub-problems of writing chemical equations and balancing chemical equations .

Did something else (DSE). The code “DSE” was assigned to a sub-problem when the student did not do a required calculation for that sub-problem and did something else (correctly or incorrectly) instead. For DSE to apply, all of the following must be true (see below for descriptions of codes CD and UDI):

• The sub-problem is required for proper solution (could not use NR).

• The sub-problem was not left blank (could not use DD or CD).

• Something altogether different was attempted instead of the correct sub-problem (could not use UDI or S).

Example: a chemical engineer studied the reaction:

N₂O₄ (l) + 2N₂H₄ (l) → 3N₂ (g) + 4 H₂O (g)

The chemical engineer measured a less-than-expected yield of N₂ and discovered that the following side reaction occurs:

2N₂O₄ (l) + N₂H₄ (l) → 6NO (g) + 2H₂O (g)

In one experiment, 10.0 g of NO formed when 100.0 g of each reactant was used. What is the highest percent yield of N₂ that can be expected (Silberberg, 2006)?

In order to find the actual mass of N₂, subjects needed to find the actual mass of N₂O₄, its number of moles (mole concept), the number of moles of N₂ (stoichiometric ratio), and the mass of N₂ (mole concept), respectively. The last sub-problem was classified as mole concept, but some students just subtracted 10 from the theoretical yield of N₂, which was not related to mole concept or any other sub-problem. For this reason, the code DSE was applied.

The reason DSE was assigned in preference to NR (not required) was due to the logic underlying the students' solutions for this problem. When their solutions were investigated, it appeared that the sub-problem to which DSE was assigned was necessary for the students' solutions. Therefore, NR could not be used.

Likewise, DD was assigned only when the student did not do anything for that sub-problem and could not be applied in this case. In the cases where the DSE code was assigned, the students had always attempted to supply an answer, a calculation, or some required information. DSE was originally created to differentiate between the cases where an answer was provided but it was not relevant to any of the sub-problems (DSE) and the cases where the subject did not put anything for that sub-problem (DD).

S (successful) or UDI (unsuccessful–did incorrectly) could not be applied, either, as the presented work was not relevant to one of the sub-problems. For example, subtracting 10 from the theoretical mass is just a mathematical calculation that is not relevant to either mole concept or any of the other sub-problems. Therefore, neither S nor UDI were used as the calculation was not of interest. Designating UDI would falsely indicate that the student attempted the correct sub-problem and made a mistake. However, with DSE, the student did not attempt the sub-problem at all (even though they did not leave it blank). It does not matter if the student's calculation was done correctly or incorrectly.

Group III (unsuccessful)

Unsuccessful–did incorrectly (UDI). The code “UDI” was assigned to any sub-problem that a student performed incorrectly. For UDI, the following must be true:

• The sub-problem is required for proper solution (could not use NR).

• The sub-problem was not left blank (could not use DD or CD).

• The correct sub-problem was attempted but done incorrectly.

Example: Balance the following reaction (Silberberg, 2006):

CaCO₃ (s) + HNO₃ (l) → Ca(NO₃)₂ (aq) + CO₂ (g) + H₂O (l)

Student's incorrect answer:

CaCO₃ (s) + 2HNO₃ (l) → Ca(NO₃)₂ (aq) + 3CO₂ (g) + H₂O (l)

As can be seen, though the student attempted to balance the chemical equation, they simply did not come up with the correct answer to this sub-problem.

Unsuccessful–received hint (URH). The code “URH” was assigned to any sub-problem for which a student received a hint regarding one of the main sub-problems. This code was only applied when students were able to then use the hint to find the correct answer for a piece. If the answer was incorrect or the students did not do anything, the appropriate codes, either UDI or DD, were used. For URH, the following must be true:

• A hint was given to the student.

• The sub-problem was answered correctly (could not use DD or UDI).

Unsuccessful–guessed (UG). The code “UG” was assigned to any sub-problem where a student just guessed at an answer without attempting any necessary calculations or operations. Regardless of whether their guess was correct or incorrect, the fact that they simply guessed means they were unsuccessful. For UG, the following must be true:

• The sub-problem is required for proper solution.

• Evidence shows that the student guessed; no reasoning is given by the student for their answer.

Could not do (CD). The code “CD” was assigned to any sub-problem when the student knew what they needed to do, but could not do it or remember how to complete it (evidence for this was found in the transcripts). It does not matter if the student knows the reasoning behind the sub-problem they need to perform. They might not remember the name of the sub-problem, but they are aware of it and cannot figure out how to do it. For a CD code to be given, the student must leave the piece blank, otherwise UDI or DSE would have applied. For CD, the following must be true:

• The sub-problem is required for proper solution (could not use NR).

• The sub-problem was left blank.

• The student gives some other indication of the correct path (e.g. verbally) but cannot begin the sub-problem.

Reliability of coding

Since the assignment of the above codes is the key to the application of this research method, consistent application of the codes is essential and must be checked statistically. For determining how well two researchers are applying codes beyond what is expected by probability, it is suggested that Cohen's kappa coefficient be calculated to determine inter-rater reliability (Fleiss et al., 1969).

To that end, two researchers separately analysed all 17 students' solutions for six questions (chosen randomly) and included a total of 17 sub-problems. In total, 289 sub-problems were analysed (17 × 17). After coding the sub-problems separately, the codes were categorized under three groups based on their meanings and their functions in the calculations of the success rates:

• Group I – successful codes: S

• Group II – neutral codes: NR, DD, and DSE

• Group III – unsuccessful codes: UDI, UG, URH, and CD

Following the coding and grouping, the inter-reliability test found Cohen's kappa coefficient to be κ = 0.82, which was determined to be of sufficiently high value for data validity.

Assigning the codes

Assigning the codes was done according to the logic outlined in the decision tree (Fig. 1). All of the questions in the tree are yes or no questions. For visual clarity, the decision questions were simplified; the full questions are as follows:

• “Was the sub-problem done?” Was the sub-problem expected by the examiner done by the subject?

• “Was an alternate method found?” Was an alternate method to the expected sub-problem found and used by the subject or was a required step skipped?

• “Was the sub-problem done correctly?” Was the expected sub-problem calculated correctly?

• “Was a hint required?” Was a hint needed (and given) for correctly doing the sub-problem?

• “Did the subject know what to do?” Did the subject know what sub-problem was required but could not remember how to perform that step?

• “Did the subject guess?” Did the subject guess at the answer, rather than attempt a calculation?

• “Was the correct sub-problem done?” Did the subject attempt the correct sub-problem, as needed for later success?

Post-test calculations

To analyse students' difficulties, the codes applied above were tallied for each stoichiometry sub-problem and for each group. The results can be seen in Table 2. The success rate for each sub-problem was calculated as the “Attempt Success Rate” (ASR). ASR was calculated by dividing the number of successful attempts (group I) by the sum of the successful attempts (group I) and unsuccessful attempts (group III); group II classifications were not included in the ASR. Note that this success rate is calculated based only on attempts, and as such it excludes those instances where the students were neither unsuccessful nor successful because they simply did not do a certain piece (DD, DSE, or NR). The ASR for each sub-problem can be seen in Table 3, and is not the same calculation used by Gulacar and Fynewever (2010).

Table 3 Attempt success rate (ASR) and complete success rate (CSR) for each sub-problem in solving stoichiometry problems

	ASR (%)	CSR (%)
Writing chemical equation (WEQ)	45	43
Empirical formulae (EF)	52	45
Percent yield (PY)	80	63
Limiting reagent (LR)	80	59
Stoichiometric ratio (SR)	86	66
Mass percent (MP)	86	77
Molecular formulae (MF)	88	88
Balancing chemical equations (BEQ)	90	89
Mole concept (MC)	94	77
Conservation of mass (CM)	100	77

---

In that previous paper, the variable reported as “average success rate” only included NR as a neutral code. It was later determined that DD and DSE could not be considered unsuccessful as the students did not do the sub-problem at all, and could not be classified accurately as successful or unsuccessful. It was recognised, however, that failing to do a sub-problem was an error, so the previous calculation was reclassified as “Complete Success Rate” (CSR). CSR divides the number of successful attempts (group I) by the sum of all codes (group I, II, and II) except for NR. The results can be seen in Table 3.

To determine if there was a significant difference between the various categories of sub-problems, SPSS 20 was used to calculate Pearson's χ² (chi squared). The differences between sub-problems was determined to be significant, χ²(16) = 462, p < .001. Monte Carlo simulations (two-sided) found the probability that the difference observed occurred at random (i.e., false positive; Type I error) was less than .001 for all scenarios. Three cells (11%) had an expected value of less than 5; due to the large size of the table, this result was considered acceptable (Field, 2009). Spearman's rho (r_s) was calculated via SPSS 20 to determine correlations between students' performance on the mole concept achievement test (MC-AT) and the frequency of various codes.

Results and discussion

Overall, the student cohort had a strong grasp of many of the components, or sub-problems, of stoichiometry. Of the ten sub-problems that were monitored, eight of them had student attempt success rates of 80% or higher; other than LR and PY, the other six sub-problems had an attempt success rate of greater than 85% (Table 3). The strongest sub-problems were measured to be MF, BEQ and MC. The students were least successful with WEQ and EF.

To determine the success of students with individual sub-problems, it is important to consider the typical mistakes that students make for each type of sub-problem. While it is satisfying for an instructor to see a student solve a problem correctly, this generally reveals less about a student than when they solve a problem incorrectly. As such, there is little to say about sub-problems that had high ASR and low counts in the neutral (group II) categories as well, except that S correlated strongly (r_s = 0.791, p < .001; Table 4) with success on the MC-AT. Rather, analysis below will focus first on group II, the “neutral” category, and then on group III, the unsuccessful category.

Table 4 Correlations between students' scores on the MC-AT and the frequency of codes received

	N = 17	Correlation coefficient^a	Sig. (2-tailed)
a Correlations were calculated using Spearman's rho; correlations significant at the 95% confidence level or higher are in bold; non-signficant correlations are in italics.
Group I	S	.791	.000
Group II	NR	.396	.116
	DD	−.781	.000
	DSE	−.674	.003
Group III	CD	.336	.187
	UDI	−.655	.004
	URH	.240	.353
	UG	−.487	.047

---

Group II (neutral)

Group II, made up of the codes DD, DSE and NR, was generally an indication that students were looking for a path to solve the problem. In some cases, students found an alternate path that led to success (NR). In others, students did not have a clear idea of how to proceed and either skipped a key step (DD) or took a direction that was not helpful to the solution of the problem (DSE).

Conceptually, DSE and DD are very similar. DSE, as an assigned code, was quite rare in the sampled student population. Only 32 of the 1972 codes assigned were DSE, and 21 of those were for the mole concept (MC), with five assigned to the sub-problem SR and six to PY (see Table 5). In contrast, the most common code applied, other than S, was DD, and the code was applied 125 times to MC and 82 times to SR. Both MC and SR had high student attempt success rates (Table 3) and the portion of unsuccessful codes (group III) applied to each sub-program were less than 10% of the codes in each case. The group II codes, and DSE and DD in particular, show that, while students were generally proficient at these sub-problems, what they lacked was an ability to account for these steps in solving a larger problem.

Table 5 Sum of codes^a assigned

a Sorted into groups I, II, and III.
I	Successful	S	1340
II	Not required	NR	80
	Did no know to do	DD	270
	Did something else	DSE	32
III	Unsuccessful – did incorrectly	UDI	149
	Unsuccessful – received hint	URH	78
	Unsuccessful – guessed	UG	9
	Could not do	CD	14

---

The same was true of limiting reagent sub-problems (LR). One-quarter of the codes assigned to LR were in group II, and all of those codes were DD. LR had a student attempt success rate of 80%, which suggests that, like MC and SR, students understood how to do the appropriate calculations for the sub-problem. The difficulty they had, however, was in remembering to use the LR concept at all. When the students skipped this sub-problem, they often struggled with handling the given amounts of the reactants and determining which reactant to use in solving the overall problem. Because several students did not consider and determine the LR before doing the rest of the problem, DD was assigned nine times. This number might have been higher had students not been reminded to consider determining the limiting reagent in the first of two questions relating to LR. Most students proceeded to determine (correctly or incorrectly) the limiting reagent for the first problem, but did not attempt to calculate the LR in the second problem. (URH, was not assigned because reminding students to consider the LR was not a hint about how to do the LR sub-problem.)

In the cases of mole concept, stoichiometric ratio, and limiting reagent, the sub-problem was usually not the goal in the solutions but more like a tool to reach the goal. As students did not always see their goals clearly, they could not always see the necessity of using the MC, SR, or LR sub-problems. Sometimes these students were successful in finding a way around their lack of knowledge (NR), but mostly they did not know they were missing a step in the solution, and therefore received DD or DSE.

When the number of times a student received DD was compared with that student's score on the MC-AT, a significant, negative correlation was observed (Table 4). This correlation, significant at the 99.9% confidence level, accounted for approximately 60% of the total observed variance. Though causation cannot be proven, this is strong evidence that students who were failing to include the MC and SR sub-problems in their attempt to solve the stoichiometry problems were likely doing so because they did not have a strong grasp of the mole concept. According to BouJaoude and Barakat (2003), it is expected that a lack of conceptual understanding leads to failure at stoichiometry. This correlation shows that a lack of conceptual understanding likely means that students will skip over the appropriate sub-problem or try to substitute some concept that they do understand (DSE). There was no significant correlation between the number of NR codes and a student's score on the MC-AT. While the alternate solutions represented by NR did allow students to correctly solve the stoichiometry problems, the use of those alternate routes does not appear to be related to a student's understanding of the mole concept.

Group III (unsuccessful)

Group III is comprised of four codes, UDI, URH, UG and CD. In all of these cases, students failed to do some sub-problem without assistance from the interviewer. The difficulties seen in this category related to some lack of basic knowledge, usually something that needed to be memorized by the student or a misconception about how to calculate a given step. The sub-problems where students were most unsuccessful (low attempt success rate; Table 3) were WEQ and EF.

In all, UG and CD were very rare and only occurred nine and fourteen times respectively, out of a possible 1972 (Table 5). When students guessed, they offered no attempt at calculation or reasoning out their answer, and so even coincidentally correct answers were considered unsuccessful. CD only applied to problems where students knew which step was to be performed but could not perform that step. As was suggested in the group II analysis, students generally knew how to perform sub-problems in isolation and frequently had difficulties in remembering to include various sub-problems (resulting in codes from group II). As evidenced by the low occurrence of CD, students rarely knew a sub-problem was needed without knowing how it should be calculated. Students similarly did not bother to guess at answers, instead tried to work it out, if incorrectly.

The only sub-problem in which students were given hints was WEQ. In all, students received a hint 78 times (URH), accounting for 78% of the unsuccessful WEQ codes. Student success dramatically improved when they were given hints; most hints were about chemical nomenclature, atomic symbols, or ion charges. This is the sort of knowledge that mostly requires students to memorize a set of facts for later recall. The need for this sort of basic instruction was mentioned previously by Gulacar and Fynewever (2010). It is likely that students would have improved their performance after hints about other sub-topics, but such hints were not the focus of the study. Hints were given in WEQ because, without the hints, the students would not have been able to complete most of the study.

The think-aloud protocol was used to collect the data used to justify the classification of each student's activities by the new codes and provided information on just what type of difficulties each student was experiencing with the material. For all cases where the student tried and failed to get a correct answer on a specific sub-problem, the code UDI was assigned. In a sense, this is a catch-all for all of the various other reasons that students were unsuccessful; reasons that could not be classified into the other categories. As a result, this was the second most frequent code (apart from “successful”). While a detailed breakdown of these reasons will be discussed in another paper, a short summary of some of the findings will follow here, starting with the sub-problems that students found the most difficult.

In writing chemical equations, students had difficulty writing formulae for compounds in which an element was implicit (i.e., hydrogen is implicit in nitric acid; oxygen is implicit in combustion reactions). Students also found naming compounds with elements that possess a variety of possible oxidation states difficult. For EF and MF, students had difficulty remembering the meaning of empirical and molecular formula and in differentiating the formulae from each other. Students also used incorrect methods to find the empirical formulae, such as using the mass of the elements instead of using the number of moles. A review of the transcripts from the think-aloud protocols revealed that the difficulties with PY were a mixture of mathematical (students were unable to use the PY formula) and memorization (students had difficulty in remembering the PY formula). There was also frequent confusion between the percent error and percent yield.

Though students were generally successful with MC and SR, the errors observed in these two sub-problems were very similar. In both SR and MC, students had difficulty using the subscripts in a molecular formula; students had a similar difficulty in the proper meaning of the coefficients in chemical equations when determining the SR. Although those mistakes were not very common, they still warranted a mention because there is possibility of seeing them more often in a larger population.

Conclusions

As outlined in this paper, a new, comprehensive method for investigating multi-step problems and the difficulties students encounter while solving these problems has been developed. Based on a series of codes assigned by review of transcripts taken during a “think-aloud” protocol, the method looks at the way in which a student succeeds or fails at each step, or sub-problem, in the solution of a multi-step problem. Eight total codes were described; grouped into three larger groups: successful, neutral, and unsuccessful.

The codes were used here to analyse student success and failure in the process of stoichiometry problems, and revealed two major difficulties students were encountering with stoichiometry problems: a lack of knowledge as to the proper order of sub-problems for successful completion, and a lack of basic memorized information needed to perform the chemistry problems. The method of analysis (i.e., application of the codes) does not, however, apply solely to stoichiometry, or even chemistry. This method can be applied to any multi-step problem to help identify sources of student confusion. Of course, the sub-problems (Table 3) would be different for different analyses.

Student failures in stoichiometry (group III) were primarily attributed to knowledge that required a certain amount of memorization on the part of students. Lack of proper preparation prevented success. In the analysis of student difficulties in stoichiometry, it was noticed that there was, in the student cohort measured, a lack of knowledge considered fundamental to understanding chemistry, such as chemical names and ionic charges. While names of specific chemicals may not be necessary to the understanding of chemistry (e.g., a student may know HNO₃ and its reactivity without knowing the name nitric acid), knowing the expected charges of various ions is necessary for understanding the possible reactions. Indeed, more successful students have been shown to use more symbolic representation than their less successful counterparts (Bodner and Domin, 1995). The ACS Society Committee on Education (2012) does not provide an opinion on whether or not memorizing chemical names is essential to chemical education, and it has been argued that a fundamental change in the teaching of general chemistry courses may be in order (Cooper, 2010). Whether teaching topics best learnt by rote is of importance to a general chemistry course is left to the course instructor. Thus, the relative importance of the group III and group II codes will differ, depending on the instructor's focus. Rote memorization of formulae was also noticed by Powell (2013) when studying multi-step algebra problems in Fredonia, New York. Though most of the errors were noted with eighth grade students, some of that reliance on memorized formulae was evident in college students, as well.

More conceptually, however, the students in the study lacked the ability to properly plan how to solve a multi-step problem like a stoichiometry problem. The top two codes applied, other than “successful,” were both from the group II category: DD and NR. These codes indicated that many students were struggling to form a roadmap for completing the problems. In some cases, students were able to generate a roadmap that, while novel to the authors, did successfully solve the given stoichiometry problem (NR). This may be part of the “stage effect,” a tendency for students to find intermediate sub-problems more difficult than the final sub-problems that constitute the “goal” of the problem (Ayres and Sweller, 1990). The failure of students to properly plan out a multi-step problem may also be due to fewer meaningful mental connections between chemistry concepts. Generally speaking, novices have less interconnected mental maps than do experts (Bédard and Chi, 1992).

The use of these alternate solutions was not correlated with a student's understanding of the mole concept (as measured by the MC-AT), unlike the successful (S) codes. These students may have begun to move beyond rote learning to reasoning out their own strategies, but, for this cohort of students, the reason appears to have been unrelated to chemistry knowledge. This suggests that the appearance of DD and NR are more likely due to a cognitive overload, which caused the students to forget steps or lose their direction (Ayres and Sweller, 1990; Sweller, 1994). This effect has been noted before; success in stoichiometry problems is positively correlated with memory capacity (Overton and Potter, 2008, 2011). The larger a student's memory capacity, the less likely they are to experience cognitive overload. The application of NR occurred less frequently than did DD, where students simply skipped over some crucial step in solving the problem because they did not know it was even necessary. This happened most frequently with students skipping over the mole concept or stoichiometric ratio, and would be consistent with difficulties due to cognitive overload.

Unfortunately, the solution to students' lack of planning skills was not part of the study design. It may be that these students would benefit from a different teaching method, such as mole concept flow charts (Krieger, 1997; Wagner, 2001). This is but one of the limitations of this study. As the student sample was small, only seventeen students, the results of the study cannot be generalized to all college-age students. Furthermore, as all of the students were taken from one class and were instructed in the exact same manner, the difficulties uncovered may be symptomatic of the teaching method rather than the students. The students in this cohort may also have had an atypical grasp on the concepts of stoichiometry, and another cohort may show very different results, either much better or much worse.

Notes and references

1. ACS Society Committee on Education, (2012), ACS Guidelines and Recommendations for the Teaching of High School Chemistry, Washington, D.C.: American Chemical Society, 2012.
2. Arasasingham R. D., Taagepera M., Potter F. and Lonjers S., (2004), Using knowledge space theory to assess student understanding of stoichiometry. J. Chem. Educ., 81(10), 1517–1523.
3. Astudillo L. and Niaz M., (1996), Reasoning strategies used by students to solve stoichiometry problems and its relationship to alternative conceptions, prior knowledge, and cognitive variables, J. Sci. Educ. Technol., 5(2), 131–140.
4. Ault A., (2001), How to Say How Much: Amounts and Stoichiometry, J. Chem. Educ., 78(10), 1347.
5. Ayres P. and Sweller J., (1990), Locus of Difficulty in Multistage Mathematics Problems, Am. J. Psychol., 103(2), 167–193.
6. Bauer C. F., (2008), Attitude toward Chemistry: A Semantic Differential Instrument for Assessing Curriculum Impacts, J. Chem. Educ., 85(10), 1440–1445.
7. Bédard J. and Chi M. T. H., (1992), Expertise, Curr. Dir. Psychol. Sci., 1(4), 135–139.
8. Bodner G. and Domin D., (1995), The role of representations in problem solving in chemistry, in D. R. Lavoie (ed.), Toward a Cognitive-Science Perspective for Scientific Problem Solving. NARST Monograph, Number Six, Columbus, OH: NARST, vol. 6, pp. 245–263.
9. BouJaoude S. and Barakat H., (2003), Students' problem solving strategies in stoichiometry and their relationships to conceptual understanding and learning approaches, Electron. J. Sci. Educ., 7(3), 1–42.
10. Cooper M., (2010), The Case for Reform of the Undergraduate General Chemistry Curriculum, J. Chem. Educ., 87(3), 231–232.
11. Felder R. M., (1990), Stoichiometry without tears, Chem. Eng. Educ., 24(4), 188–196.
12. Field A., (2009), Discovering Statistics using SPSS, London, England: Sage.
13. Fleiss J. L., Cohen J. and Everitt B. S., (1969), Large sample standard errors of kappa and weighted kappa, Psychol. Bull., 72(5), 323–327.
14. Frank D. V., Baker C. A. and Herron J. D., (1987), Should students always use algorithms to solve problems? J. Chem. Educ., 64(6), 514.
15. Gauchon L. and Meheut M., (2007), Learning about stoichiometry: from students' preconceptions to the concept of limiting reactant, Chem. Educ. Res. Pract., 8(4), 362–375.
16. Gower D. M., (1977), Hierarchies Among the Concepts Which Underlie the Mole, Sch. Sci. Rev., 59(207), 285–299.
17. Griffiths A. K., Kass H. and Cornish A. G., (1983), Validation of a learning hierarchy for the mole concept, J. Res. Sci. Teach., 20(7), 639–654.
18. Gulacar O. and Fynewever H., (2010), A Research Methodology for Studying What Makes Some Problems Difficult to Solve, Int. J. Sci. Educ., 32(16), 2167–2184.
19. Haim L., Cortón E., Kocmur S. and Galagovsky L., (2003), Learning Stoichiometry with Hamburger Sandwiches, J. Chem. Educ., 80(9), 1021–1022.
20. Hand B., Yang O.-M. and Bruxvoort C., (2007), Using Writing-to-Learn Science Strategies to Improve Year 11 Students' Understandings of Stoichiometry, Int. J. Sci. Math. Educ., 5(1), 125–143.
21. Huddle P. A. and Pillay A. E., (1996), An In-Depth Study of Misconceptions in Stoichiometry and Chemical Equilibrium at a South African University, J. Res. Sci. Teach., 33(1), 65–77.
22. Jensen W. B., (2003), The Origin of Stoichiometry Problems, J. Chem. Educ., 80(11), 1248.
23. Johnstone A. H. and El-Banna H., (1986), Capacities, demands and processes – a predictive model for science education, Educ. Chem., 23(5), 80–84.
24. Johnstone A. H. and El-Banna H., (1989), Understanding learning difficulties – a predictive research model, Stud. High. Educ., 14(2), 159–168.
25. Johnstone A. H., Hogg W. R. and Ziane M., (1993), A working memory model applied to physics problem solving, Int. J. Sci. Educ., 15, 663–672.
26. Krieger C. R., (1997), Stoogiometry: A Cognitive Approach to Teaching Stoichiometry, J. Chem. Educ., 74(3), 306–309.
27. Nurrenbern S. C. and Pickering M., (1987), Concept Learning versus Problem Solving: Is There a Difference? J. Chem. Educ., 64(6), 508–510.
28. Overton T. L. and Potter N. M., (2008), Solving open-ended problems, and the influence of cognitive factors on student success, Chem. Educ. Res. Pract., 9(1), 65–69.
29. Overton T. L. and Potter N. M., (2011), Investigating students' success in solving and attitudes towards context-rich open-ended problems in chemistry, Chem. Educ. Res. Pract., 12(3), 294–302.
30. Powell A. N., (2013), A study of middle school and college students' misconceptions about solving multi-step linear equations. Masters Thesis, State University of New York at Fredonia, Fredonia, NY. Retrieved from http://hdl.handle.net/1951/58371.
31. Silberberg M. S., (2006), Chemistry: The molecular nature of matter and change, 4th edn, New York: McGraw-Hill.
32. Sweller J., (1994), Cognitive load theory, learning difficulty, and instructional design, Learn. Instr., 4(4), 295–312.
33. Tsaparlis G., (1998), Dimensional analysis and predictive models in problem solving, Int. J. Sci. Educ., 20, 335–350.
34. Wagner E. P., (2001), A Study Comparing the Efficacy of a Mole Ratio Flow Chart to Dimensional Analysis for Teaching Reaction Stoichiometry, Sch. Sci. Math., 101(1), 10–22.
35. Witzel J. E., (2002), Lego Stoichiometry, J. Chem. Educ., 79(3), 352A–352B.

---