A pathway to diphosphorus from the dissociation of photoexcited tetraphosphorus

Abstract

We report a computational study of an energetically favorable pathway for the excited-state dissociation of a tetrahedral P₄ molecule into two P₂ molecules via the simultaneous breaking of four chemical bonds along a highly symmetric (D_2d) reaction pathway. Along this pathway, a degeneracy occurs between the first excited state of P₄ and the ground state of 2P₂ at a lower total energy (ca. 4.7 eV) than the initial state, indicating that the initial photoexcitation provides sufficient energy for the dissociation without significant kinetic barriers. We also found that sequential dissociation of the four P–P bonds exhibits larger activation barriers thus making this a less viable dissociation pathway. Our computational investigation uncovers complicated photochemistry in elemental phosphorus, and suggests a likely mechanism for the environmentally friendly inclusion of phosphorus atoms into organic molecules.

---

1. Introduction

The idea of “cracking” P₄ into two P₂ molecules in order to take advantage of the high reactivity of the π bonds in the latter is attractive,¹ but this process is not conveniently accessed thermally as very high temperatures (ca. 1100 K) are needed to break down the tetrahedral P₄ molecule.² On the other hand there have been indications since at least 1937 that UV irradiation of white phosphorus, a process that converts it into a red form, may initially bring about P₂ generation.³ In one report on the P₄ co-photolysis with metal carbonyl complexes, Dahl et al. mention that “P₄ in solution photolyzes readily to P₂ at ambient temperatures”.⁴ Co-photolysis of P₄ with metal carbonyl complexes with formation of metal-phosphorus products has been reported in a few other cases,⁵ but only recently, Tofan and Cummins demonstrated the inclusion of diphosphorus moieties into organic molecules is afforded directly from the irradiation of mixtures of P₄ and 1,3-dienes.⁶ The major organophosphorus products are cyclic compounds with a single P₂ unit shared between the two fused six-membered rings. This reaction was proposed to occur through Diels–Alder additions of 1,3-diene molecules to photo-generated P₂ units (Scheme 1).⁶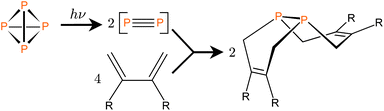

Scheme 1 One-step synthesis of diphosphanes with the proposed involvement of P₂ as a reaction intermediate.⁶

Here we report a theoretical investigation of the photolysis mechanism of P₄. In this reaction, the starting point was an electronically excited state of a single P₄ molecule and the endpoint was the ground state of two P₂ molecules. We knew that this pathway must proceed through the dissociation of four chemical bonds and may involve a change in the electronic state. From a theoretical perspective, the problem is highly interesting in that the P₄ is a small enough system to be treatable using highly accurate multi-reference quantum chemistry methods, yet the task of elucidating a low-energy pathway for photolysis involves a nontrivial exploration of the multidimensional potential energy surface (PES). In terms of experimental chemistry, an understanding of the P₄ photolysis mechanism could lead to improved specificity and reaction yields for this type of photochemistry and increase the viability of this pathway as an environmentally friendly method for the incorporation of phosphorus atoms into organic molecules.⁷

In our explorations of the excited state PES, we found a surprising pathway for the direct dissociation of excited P₄ into 2P₂ that involves the simultaneous breaking of four P–P bonds. This pathway is easily visualized by placing the four phosphorus atoms on the corners of a cube such that no two atoms share a cube edge; the dissociation coordinate is equivalent to moving the top and bottom faces of the cube away from one another while contracting the P–P bonds in each diatomic subunit (Fig. 1), from 2.1994(3) Å in P₄,⁷ to 1.8934 Å in P₂.⁸ This result is counterintuitive because large reaction barriers would be expected for the simultaneous breaking of four chemical bonds. In this situation, we do not encounter any significant barriers because a state crossing exists along the dissociation coordinate in which the first excited state of P₄ becomes degenerate with the ground state of 2P₂. The state crossing occurs at a lower energy than the P₄ excitation energy, so the photon energy is sufficient to carry out the dissociation.

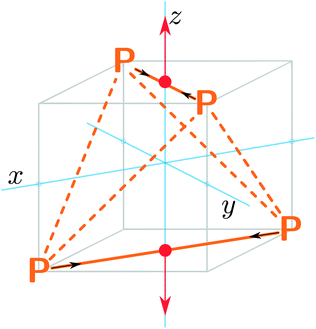Fig. 1 Dissociation of the P₄ tetrahedron into two P₂ units with simultaneous breaking of four P–P bonds occurs through a D_2d-symmetric pathway.

Although the precise mechanism of P₄ → 2P₂ photolysis contains interesting open questions, much is known about the molecules at the two endpoints of the reaction; here we briefly summarize the most important experimentally known properties and the corresponding theoretical calculations. Experimentally, the thermochemistry of the photolysis reaction is known. The reaction enthalpy for P₄ → 2P₂ is experimentally measured to be +53.8 ± 0.7 kcal mol⁻¹;⁹ dissociation occurs spontaneously at 1100 K as the reaction becomes entropically driven.² In terms of photochemistry, P₄ is experimentally known to possess two low-lying excitations at 5.1 eV and 5.9 eV with more strongly absorbing manifolds of excitations above 7 eV.^10–12 The low-lying excitations are interpreted as being HOMO–LUMO in character, although there are symmetry-imposed restrictions on the allowed transitions. Theoretically, the reaction enthalpy of P₄ → 2P₂ can be computed to within 1 kcal mol⁻¹ of the experimental measurement; such an accurate estimation requires a treatment of dynamic electron correlation at the coupled cluster singles, doubles, and nonperturbative triples (CCSD(T)) level of theory using a nearly complete basis set.¹³ The UV absorption spectra of tetrahedral P₄ and P₂ have also been computed using the configuration interaction singles (CIS), random phase approximation (RPA) and equation-of-motion coupled cluster singles and doubles (EOM-CCSD) theoretical methods to within 0.5 eV (≈10 kcal mol⁻¹) of the experimental measurement.¹⁴

2. Theory and computational methods

Our calculations are performed on gas-phase phosphorus clusters in the absence of a solvating environment. There are a number of theoretical studies on phosphorus clusters in the literature, but most of them have focused on equilibrium configurations of the ground electronic state. For example, Häser and Ahlrichs have investigated the equilibrium geometries and energies of many phosphorus clusters sometimes containing up to thirty atoms.^14–16 These studies were carried out using methods including Hartree–Fock, density functional theory (DFT), second-order Moller–Plesset perturbation theory (MP2), and CCSD. We refer to these as single-reference electronic structure methods because they are based upon the assumption that the ground-state wavefunction is mostly described by a single electron configuration or Slater determinant, which is then used as a reference state for the calculations of electron correlation effects. Single-reference methods for the calculation of excited state energies include CIS, RPA, time-dependent density functional theory (TDDFT), and EOM-CCSD.

The ground state of tetrahedral P₄ and P₂ are both closed-shell configurations with singlet spin multiplicity, and thus they are qualitatively well described by single Slater determinants. However, in general there is no reason to expect that the electronic state should stay the same throughout the entire dissociation pathway. Furthermore, the ground state of reaction intermediates may have multi-reference character (also known as static correlation); this means that the wavefunction cannot be described by a single Slater determinant. Multi-reference wavefunctions often appear in geometries where chemical bonds are broken and the system contains multiple radicals, and in these situations single-reference methods may be qualitatively incorrect. One would thus expect single-reference methods to perform well at the endpoints of the pathway but give unreasonable answers in the middle; this is indeed what we found in early exploratory calculations.

For this reason, we turn to complete active space self-consistent field (CASSCF), which is a method capable of describing static correlation; in CASSCF, the wavefunction is a linear combination of several Slater determinants, each of which represents a distinct electron configuration or orbital occupation. A CASSCF calculation is specified by choosing the number of active electrons and the number of active orbitals, and the wavefunction includes all configurations that can be constructed from placing the active electrons into the active orbitals.¹⁷ For example, in a CASSCF(2,3) calculation, there are two active electrons in three active orbitals, giving rise to six possible electron configurations, all of which are included in the wavefunction. The reliability of CASSCF calculations depends heavily on a good choice of the number of active electrons and the size of the active space.

In order to obtain quantitative accuracy, a calculation also needs to include dynamic correlation, which in the CASSCF picture corresponds to minuscule contributions to the energy from the electron configurations not considered in the wavefunction. Since the wavefunction does not contain sizable contributions from these configurations, they are not treated explicitly and instead are included using perturbation theory. Therefore, we expect that methods like CASSCF with second and third order corrections from Rayleigh–Schrödinger perturbation theory (RSPT2 and RSPT3) would provide quantitative accuracy for intermediate states on the pathway.

The CASSCF calculations took the symmetry of the geometries into account; orbitals were classified into the four irreducible representations of the D₂ point group (A, B₁, B₂, B₃). Along the entire dissociation pathway, the orbital occupations corresponding to the four representations was (9,7,7,7). The closed-shell orbitals were chosen to be (7,7,7,7) and the active space was chosen to be (3,2,2,2), because these frontier orbitals were well-separated from the occupied and virtual manifolds above and below for the entire dissociation process. The number of electronic states computed were (3,2,2,2) and state-averaging was performed within each representation. This makes the level of theory CASSCF(4,9)-RSPT3.

We verified our choice of active space with a CASSCF(12,13) calculation, where the active space includes all bonding electrons but is too large for applying accurate dynamic correlation treatments; here the closed-shell orbitals was (6,6,6,6) and the active space was (4,3,3,3). In both the (4,9) active space and the (12,13) active space, the CI vector describing the ground state and the orderings of the excited states stayed the same (ESI, Fig. S1 and S2†), providing verification that the (4,9) active space is a qualitatively correct description. We found that RSPT3 provided similar answers to RSPT2 but gave better agreement with the excitation energies in the tetrahedral geometry (ESI, Fig. S3†); this agreed with our intuition that RSPT3 should provide an improved treatment of dynamic correlation.

All calculations were performed with gas-phase structures using aug-cc-pVTZ basis sets and the MOLPRO software package.¹⁸

3. Results and discussion

Sequential dissociation coordinate.

In our initial explorations, we optimized the geometry of P₄ in the first excited state. This caused the tetrahedral molecule to rearrange into a C_2v-symmetric structure (Scheme 2, top middle) in which one of the P–P bonds was broken. From this geometry, an electronic relaxation to the ground state leads straight back to tetrahedral P₄. The system is highly unlikely to follow minimum energy paths, however, since it possesses a large kinetic energy from the initial excitation; this motivated us to explore other potential pathways. We found another exothermic rearrangement leading to a D_2d-symmetric minimum (Scheme 2, top right) with a low activation barrier of ≈0.5 eV in which one more P–P bond was broken. However, further bond dissociation involved much greater activation barriers of approximately ≈1.4 eV; here the system proceeds through a C₂-symmetric transition state. Thus, a dissociation pathway passing through the molecular geometry critical points involving the sequential breaking of P–P bonds is possible, though it may require the system to possess large amounts of kinetic energy for crossing over the large activation barriers.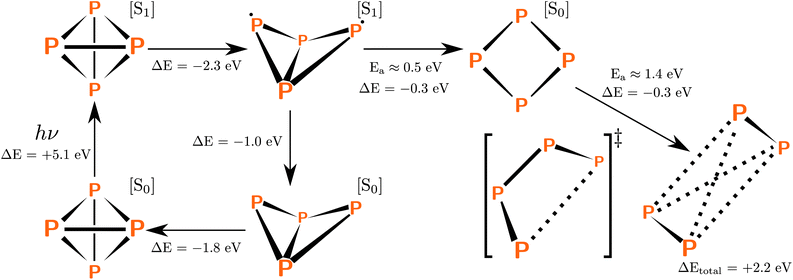

Scheme 2 Molecular geometry critical points in the sequential dissociation pathway. The bottom left is the ground state of P₄ and the far right is the ground state of 2P₂. P₄ enters the excited state after absorbing a photon, and a geometry optimization on the excited state surface leads to the C_2v-symmetric geometry (top middle). From here, relaxation to the ground state leads back to tetrahedral P₄, but rearrangement into a D_2d-symmetric minimum is also possible (top right). Dissociation of the D_2d-symmetric geometry into two 2P₂ molecules occurs with a significant activation barrier of ≈1.4 eV.

Direct dissociation coordinate.

With the results of the previous exploration in mind, we reasoned that excited-state P₄ is likely to follow a highly ballistic trajectory without passing through the molecular geometry critical points.¹⁹ This motivated us to study a direct dissociation coordinate in which the opposite edges of the P₄ tetrahedron were pulled apart linearly, involving the simultaneous breaking of four P–P bonds (Fig. 1). To our surprise we found that the energy along this coordinate was almost entirely downhill, with the exception of a very small barrier (0.1 eV) in the neighborhood of a state crossing.

To generate the direct dissociation coordinate, we first optimized both the P₄ and P₂ structures at the MP2/aug-cc-pVTZ level. The dissociated geometry was built from placing two optimized P₂ molecules 5 Å apart on the z-axis, with one P₂ molecule placed symmetrically on the x-axis and the other on the y-axis. For comparison, the distance between the two P₂ units within the optimized P₄ molecule was found to be 1.56 Å. Fifty intermediate frames were generated by linearly interpolating from P₄ to 2P₂, corresponding to a 0.070 Å increase per frame in the distance between the two units.

Calculations were carried out for each point on the dissociation trajectory. At frame 0 (the tetrahedral geometry, z-axis separation = 1.56 Å), there are two threefold-degenerate excited states between 5 eV and 6 eV corresponding to the experimental optical excitation between the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO). As the dissociation proceeds, the degeneracy is lifted and the excited states in the B₁ and B₂ representations increase monotonically in energy (Fig. 2 depicts the A and B₃ states, but not the B₁ and B₂ since these increase monotonically). The energy of the lowest B₃ state decreases slightly until a minimum of 4.2 eV is reached at frame 5 (dimer separation = 1.90 Å), corresponding to an excimer-like geometry.²⁰

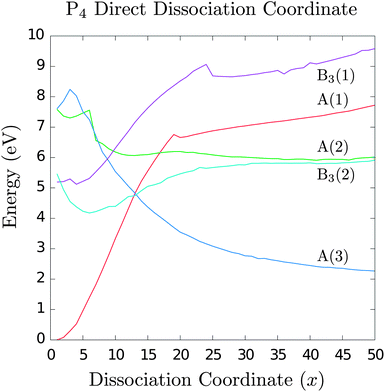Fig. 2 Energies of P₄ electronic states along the direct dissociation coordinate. The experimental excitation corresponds to state B₃(1) or B₃(2). Note the appearance of a minimum in state B₃(2) at x = 5, which we show later to be a saddle point on the many-dimensional potential surface. There is a near threefold degeneracy at x = 12 where the system may cross into the A(3) state; this corresponds to the ground state of two closed-shell P₂ molecules. At dissociation, we recover the experimental P₄ → 2P₂ reaction enthalpy (compare asymptotic value of A(3) to starting value of A(1)).

As we proceed along this coordinate, there is a degeneracy around 4.7 eV at frame 12 (z-axis separation = 2.50 Å) where the lowest B₃ state intersects with the A(1) and A(3) states. It is unclear whether this is a true threefold degeneracy or three close intersections of twofold degeneracies. The most interesting result is that the A(3) electronic state corresponds to the ground state configuration of a P₂ dimer, and the degeneracy occurs at a lower energy with respect to the initial excitation. Thus, this provides a possible pathway for the direct dissociation of photoexcited P₄ into two P₂ molecules. We note that at this degeneracy it is also possible to cross back to the ground state surface; this is expected to lead back to the tetrahedral geometry of ground state P₄.

At the end of the trajectory, the geometry approaches that of two well-separated P₂ molecules. The A(3) state becomes the ground state at the dissociation limit and is dominated by a single determinant of coefficient 0.94. The next highest states (A(1) and A(2)) become essentially degenerate excitations of single P₂ dimers with a small exchange splitting. The excitation energy of approximately 3.8 eV is in good agreement with experimental absorption spectra of P₂.²¹

The photochemistry along this pathway can be understood by examining the frontier orbitals (as shown in Fig. 3). At the tetrahedral P₄ geometry, the HOMO shows bonding character across four edges of the tetrahedron and antibonding character across two edges, while the LUMO has complementary character with antibonding character across four edges and bonding character across two. Our intuition is that the direct dissociation coordinate involves an electronic state where two electrons from the HOMO are promoted into the LUMO, and this electronic state would correspond to the ground state of 2P₂ at dissociation. This intuition is supported by examining the CI vector and MOs across the pathway.

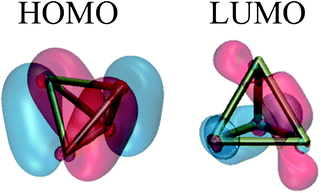Fig. 3 Highest occupied and lowest unoccupied molecular orbitals of P₄. In the tetrahedral geometry, these orbitals are twofold and threefold degenerate, respectively. Note the bonding character of the HOMO and LUMO; the HOMO has bonding character across four edges of the tetrahedron and antibonding character across two edges, and vice versa for the LUMO. Qualitatively, P₄ dissociation involves the transfer of two electrons from the HOMO into the LUMO, which breaks four P–P bonds and increases the bond order of the other two.

Since the potential surface for P₄ dissociation is a many-dimensional hypersurface, we decided to scan the potential surface in other dimensions orthogonal to the direct dissociation coordinate. We computed two-dimensional energy profiles of the ground state and lowest two excited states along the dissociation coordinate and two orthogonal deformation coordinates and plotted the results (Fig. 4 and 5). From the plots, we can see that the excimer-like geometry found in the one-dimensional profile is really a saddle point, and the true minima involve deformations in other coordinates (this is hardly surprising because our geometry optimizations led to the C_2v-symmetric structure). However, the potential surface of the first excited state is smooth and mostly flat compared to the other two surfaces, lending some credence to our hypothesis that excited-state P₄ may follow a highly ballistic trajectory.

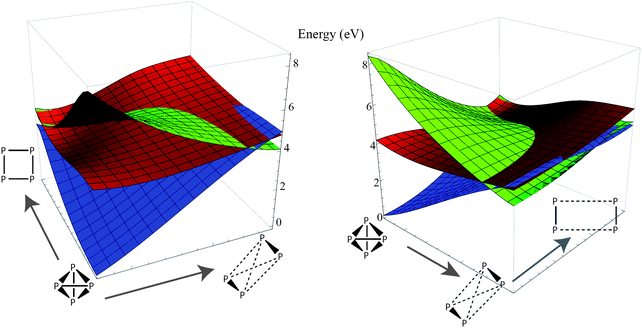Fig. 4 Two perspectives of a two-dimensional energy plot of the ground state (blue) and two lowest excited states (red, green). The coordinate to the right is the dissociation coordinate (3 ≤ x ≤ 15 in Fig. 2), and the orthogonal coordinate is a torsion about the dissociation vector (the range is roughly π/4). The coordinates in this plot have D₂ symmetry. Note that the lowest excited state surface is relatively flat compared to the ground state, and there is a shallow minimum along the twisting coordinate.

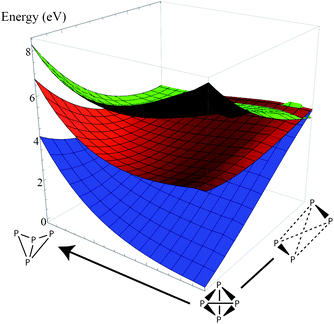Fig. 5 Two-dimensional energy plot of the ground state (blue) and two lowest excited states (red, green). The coordinate to the right is the dissociation coordinate (3 ≤ x ≤ 15 in Fig. 2), and the orthogonal coordinate is a torsion about the vector orthogonal to the dissociation vector and the P–P bond (the range is roughly π/4). The coordinates in this plot have C₂ symmetry. Note that the lowest excited state surface is relatively flat compared to the ground state, and there is a shallow basin in the middle of the surface that is not visible in the one-dimensional dissociation plot.

4. Conclusions

Our calculations of the excited-state potential surface of P₄ show that it may be possible to dissociate P₄ into 2P₂ by the simultaneous breaking of four P–P bonds with the energy provided by UV irradiation. While there exist many pathways that lead back to the tetrahedral geometry, this does not rule out the possibility that a small population of molecules in the excited state may proceed along or near the direct dissociation pathway to generate small amounts of P₂ in the reaction mixture. Qualitatively this is in agreement with the observations of Tofan and Cummins, in which a portion of the P₄ reactant was recovered from the reaction mixture after twelve hours of UV illumination.⁶

While our study suggests a possible pathway for the photolysis of P₄ into 2P₂, a firmer conclusion regarding the actual dissociation mechanism would necessitate further study using non-adiabatic molecular dynamics to explore the potential energy surfaces properly.²² Further studies of this nature may also shed light on other aspects of the photochemistry, such as the expected quantum yield for the photolytic reaction.

Acknowledgements

This work was funded by ENI S.p.A. as part of the Solar Frontiers Research Program. This material is based upon work supported by the National Science Foundation under Grant CHE-6923295 (T. V. V.) and CHE-1111357 (C. C. C.).

References

1. N. A. Piro, J. S. Figueroa, J. T. McKellar and C. C. Cummins, Science, 2006, 313, 1276–1279.
2. (a) D. P. Stevenson and D. M. Yost, J. Chem. Phys., 1941, 9, 403–408; (b) H. Bock and H. Müller, Inorg. Chem., 1984, 23, 4365–4368; (c) O. J. Scherer, Angew. Chem., Int. Ed., 2000, 39, 1029–1030.
3. G. Rathenau, Physica, 1937, 4, 503–514.
4. M. E. Barr, S. K. Smith, B. Spencer and L. F. Dahl, Organometallics, 1991, 10, 3983–3991.
5. (a) O. J. Scherer, J. Vondung and G. Wolmershuser, Angew. Chem., Int. Ed., 1989, 28, 1355–1357; (b) M. E. Barr and L. F. Dahl, Organometallics, 1991, 10, 3991–3996; (c) O. J. Scherer, G. Berg and G. Wolmershäuser, Chem. Ber., 1996, 129, 53–58; (d) M. Scheer and U. Becker, Chem. Ber., 1996, 129, 1307–1310; (e) O. J. Scherer, T. Vömecke and G. Wolmershäuser, Eur. J. Inorg. Chem., 1999, 1999, 945–949.
6. D. Tofan and C. C. Cummins, Angew. Chem., Int. Ed., 2010, 49, 7516–7518.
7. (a) B. M. Cossairt, C. C. Cummins, A. R. Head, D. L. Lichtenberger, R. J. F. Berger, S. A. Hayes, N. W. Mitzel and G. Wu, J. Am. Chem. Soc., 2010, 132, 8459–8465; (b) M. Scheer, G. Balzs and A. Seitz, Chem. Rev., 2010, 110, 4236–4256; (c) M. Caporali, L. Gonsalvi, A. Rossin and M. Peruzzini, Chem. Rev., 2010, 110, 4178–4235.
8. G. Herzberg and K. Huber, Molecular spectra and molecular structure, Van Nostrand, 1979, pp. 518–521.
9. CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, 91st edn, 2010–2011, http://www.hbcpnetbase.com/.
10. R. R. Hart, M. B. Robin and N. A. Kuebler, J. Chem. Phys., 1965, 42, 3631–3638.
11. C. R. Brundle, H. Basch, N. A. Kuebler and M. B. Robin, Inorg. Chem., 1972, 11, 20–25.
12. M. E. Boyle, B. E. Williamson, P. N. Schatz, J. P. Marks and P. A. Snyder, Chem. Phys. Lett., 1986, 125, 349–354.
13. A. Karton and J. M. L. Martin, Mol. Phys., 2007, 105, 2499–2505.
14. M. Häser and O. Treutler, J. Chem. Phys., 1995, 102, 3703–3711.
15. R. Ahlrichs, S. Brode and C. Ehrhardt, J. Am. Chem. Soc., 1985, 107, 7260–7264.
16. M. Häser, U. Schneider and R. Ahlrichs, J. Am. Chem. Soc., 1992, 114, 9551–9559.
17. K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
18. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2010.1, a package of ab initio programs, 2010, http://www.molpro.net.
19. B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89.
20. S. A. Jenekhe and J. A. Osaheni, Science, 1994, 265, 765–768.
21. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Vol. IV in Constants of Diatomic Molecules, Von Nostrand, New York, 1979.
22. (a) H. R. Hudock, B. G. Levine, A. L. Thompson, H. Satzger, D. Townsend, N. Gador, S. Ullrich, A. Stolow and T. J. Martinez, J. Phys. Chem. A, 2007, 111, 8500–8508; (b) J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562; (c) M. Ben-Nun, J. Quenneville and T. J. Martinez, J. Phys. Chem. A, 2000, 104, 5161–5175.

---

Footnote

† Electronic supplementary information (ESI) available: MOLPRO input file for the CASSCF calculations and molecular geometries along both dissociation coordinates. See DOI: 10.1039/c3ra43940b

---