 Open Access Article
Open Access ArticleHigh-throughput co-encapsulation of self-ordered cell trains: cell pair interactions in microdroplets†
Todd P. Lagus and Jon F. Edd*
Vanderbilt University, Department of Mechanical Engineering, 2400 Highland Avenue, Nashville, TN 37212, USA. E-mail: jon.f.edd@vanderbilt.edu
First published on 21st August 2013
Abstract
Droplet microfluidics is a booming sub-field of microfluidics that adds the benefits of confinement, including signal accumulation and isolation, to cell analysis. However, controlling the number of cells per droplet has been limited to using Poisson (random) encapsulation for the highest throughputs. The Poisson probability of a droplet containing one and only one cell is limited to 36.8%, and the probability of pairing two distinct cell types in a droplet is limited to 13.5%. Combining droplet microfluidics with inertial microfluidics, we present a device which efficiently co-encapsulates cell pairs in droplets at rates on the order of 6 kHz. We demonstrate particle co-encapsulation where 64% of droplets contained the correct one-to-one pairing, representing a nearly fivefold improvement to Poisson co-encapsulation. We also apply the device to encapsulate two separate strains of Chlamydomonas reinhardtii. C. reinhardtii is a single-cell microalgae with applications as a model organism, recombinant protein source, and potential source of multiple biofuels. After inducing gametogenesis by nitrogen starvation and thermally inducing flagella loss, we co-encapsulate separate mating-type plus (mt+) and mating-type minus (mt−) C. reinhardtii cells in droplets. Here, 29% of droplets contained one and only one cell of each mating type, over a twofold improvement to the Poisson co-encapsulation probability of 13%. Approximately one hour following deflagellation, gametes regained flagellar motility and mating ability within the droplets. The mated zygotes were stored in emulsion form without nutrient replenishment. After 17 days, both zygospores and, remarkably, some unmated gametes remained viable. When the emulsion was broken and plated on full-nutrient agar, zygospore germination, tetrad hatching, and then mitosis followed. In addition to algae, the device has the potential for confined interaction studies for a variety of cell types.
Introduction
Droplet microfluidics provides a platform technology for encapsulation of cells in uniformly-sized (monodisperse) aqueous compartments that are suspended in an immiscible oil carrier fluid. Confinement of cells in droplets facilitates the accumulation of cell secretions which otherwise diffuse widely in bulk cell suspensions. Single-cell encapsulation in droplets has been exploited for amplification of cell surface proteins1,2 and cell lysates,3 testing of high-throughput drug efficacy,4 and detecting growth events,5–7 where high cell density quorum-sensing is quickly achieved by confinement. Advanced materials also allow for cell encapsulation in hydrogel precursor droplets which are then cured and re-suspended into buffer for long-term cell culture8–10 or 3D cell patterning.11Co-flowing,12 T-junction,13 and flow-focusing14 nozzles enable droplet generation at rates which can exceed 10 kHz from a single nozzle. For the flow-focusing nozzle design used here, the oil phase flow pulls an immiscible aqueous flow fluid into a thinning “neck” region. When oil shear stresses, maximized at the nozzle constriction, overcome interfacial tension forces, a droplet breaks from the main aqueous flow (see results in Fig. 4 and 6).15 The process repeats at kHz rates, and the droplet breaks from the main flow at the same neck position each time, thus leading to a near-uniform droplet size. As a result of their high-speed production, droplets are well-suited for high throughput screening using techniques such as fluorescence activated cell sorting (FACS)16 and other microfluidic droplet screening methods.17,18
However, protocols and applications using cell-laden droplets often suffer from the inability to control the number of cells in a droplet.19 In randomly dispersed aqueous cell suspensions, cells are encapsulated according to Poisson statistics. The probability that a droplet contains k cells is therefore given by
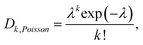 | (1) |
However, both manual22 and passive23–25 methods have been devised to provide more control of number of cells in a droplet. To reduce the number of droplets containing the “incorrect” number of cells, high efficiency encapsulation at kHz rates has been achieved using a combination of droplet microfluidics and inertial microfluidics.24,25 Inertial microfluidics defies the notion that small microfluidic channels preclude inertial effects on finite-sized particles and cells in flow. At sufficiently high mean flow velocity and cell diameter a, cells migrate (due to inertial lift forces) across streamlines to lateral equilibrium positions and form self-ordered trains of equal longitudinal spacing. The flow velocity and cell diameter are non-dimensionalized by the particle Reynolds number Rep (= Rec(a/Dh)2), where the channel Reynolds number Rec = ρUmaxDh/μ, and Umax, Dh, ρ, and μ represent the maximum fluid velocity (assuming no particles), channel hydraulic diameter, fluid density, and fluid dynamic viscosity, respectively. Higher Rep values increase the quality of focusing and ordering and decrease the required channel length, which scales as 1/Rep.26
To achieve controlled encapsulation, ordering channels are placed upstream of a droplet-generating nozzle. The droplet generation frequency is tuned to match the frequency at which the self-ordered cells arrive at the nozzle by adjusting the aqueous and oil flow rates. In straight ordering channels, single-cell encapsulation efficiency Dk=1 (the fraction of droplets containing one and only cell or particle) has been demonstrated at 80% for 10 μm particles24,25 and 60% for human HL60 cells with 90% cell viability.24 Another study27 achieved ordered encapsulation using curved channels, which induced secondary Dean flows that pushed cells to one side of the ordering channel. That study achieved 80% encapsulation efficiency of HL60 cells, 92% of which maintained their membrane integrity. Recently, ordered co-encapsulation of two and only two microparticles per droplet was demonstrated using a straight ordering channel.25 In that study, decreasing the oil flow (continuous phase) rate reduced the droplet generation frequency, independent of ordering, such that approximately two particles arrived at the nozzle for each droplet formed (λ = 1.8). As a result, 71.5% of droplets contained two and only two particles as opposed to a predicted Dk=2,Poisson = 26.7% using eqn (1).
Ordered co-encapsulation in previous work was limited to single particle types from the same ordering channel.25 While interactions between like cells are of interest, the ability control the co-encapsulation of multiple cell types (without the need to induce pairwise fusion28,29 of droplets containing one cell of each type) would significantly broaden the utility of co-encapsulation. Previous cell–cell interaction studies have employed continuous flow microfluidic devices to study co-cultured cell migrations when tumor cells were paired with endothelial30 and immune cells.31 More recently, co-culture of distinct cell lines has been performed within droplets.32,33 One study32 used Poisson co-encapsulation of separate blood progenitor cell lines in agarose gel microspheres and re-suspended them in buffer to demonstrate sub-population responsiveness to interleukin-3 (IL-3). This study varied the average ratio of human MBA2 cells (secrete IL-3) to M07e cells (require IL-3) and used FACS to assess cell viability over several days. The study was limited to droplet generation rates on the order of 40 Hz, and controlled only the average cell ratios in the droplet samples, not the number of cells in each particular droplet.
To illustrate the need for controlled co-encapsulation, consider the encapsulation of a random mixture of two cell types (A and B) using Poisson statistics. The probability DkA of a droplet containing kA cells of Type A at concentration λA (cells per droplet) is again given by eqn (1). Independently, the probability DkB of a droplet containing kB cells of Type B at an independent concentration λB also follows eqn (1). The Poisson probability for co-encapsulation where a droplet contains kA cells of Type A and kB cells of Type B is then given by the product of the two independent probabilities as
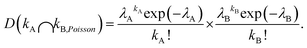 | (2) |
For perfect one-to-one co-encapsulation of two distinct cell types (kA = kB = 1), the Poisson probability is maximized when λA = 1 and λB = 1. Thus, the maximum probability of one-to-one co-encapsulation from a randomly distributed cell suspension is DkA=kB=1,Poisson = 13.5%. For parameters used in typical FACS applications (λA and λB ∼ 0.3), the Poisson probability of obtaining one-to-one co-encapsulation is just 5%. Additionally, 35% of droplets would be empty, 33% would contain just one cell, and 7% would contain more than two cells. For optimal co-encapsulation, one could independently control the number and type of each cell in a droplet while maintaining high throughput.
Note that pairwise fusion of single-cell containing droplets is also possible for creating encapsulated cell pairs. However, methods such as electro-coalescence28 and optical coalescence34 require external interfaces that increase device complexity. Some passive methods such as using channel surface wettability modification35 can also induce coalescence. Importantly, all droplet-merging methods require slowing or even stopping of flow to induce droplet contact and coalescence,36 thereby reducing throughput.
Here, we present a passive co-encapsulation device which combines two ordered cell trains to exceed the Poisson limit. Specifically, two 44 μm wide by 31 μm tall ordering channels, aligned in parallel, convey separate aqueous cell suspensions at sufficiently high Rep to induce ordered trains of equal longitudinal spacing (Fig. 1a). We report results which show significant improvements in co-encapsulation efficiency DkA=kB=1 for both polystyrene microspheres and unicellular algae. C. reinhardtii provides a particularly relevant cell type due to its wide use as a model organism in biology,37 emergence as a source for recombinant proteins,38 and multiple end uses in the biofuel industry (ethanol,39 hydrogen,40 and biodiesel41).42 Most notably, its life cycle is well-suited to droplets; algae undergo sexual production by meiosis. Using separate mating type plus (mt+) mating type minus (mt−) strains, we induced gametogenesis and co-encapsulated gamete pairs in droplets. Following ordered co-encapsulation, we show that cells retained their mating ability. Somewhat remarkably, zygospores and unmated gametes were viable for 17 days in droplets without culture media replenishment. We broke the emulsion on agar to induce zygospore hatching and allow the algae offspring to resume asexual (vegetative) reproduction. The ability to efficiently encapsulate cell pairs, exploit paired cell interactions, and achieve long-term cell survival highlight a remarkable droplet microfluidic tool that may be applied to high-throughput screening and a wide range of cell interaction assays.
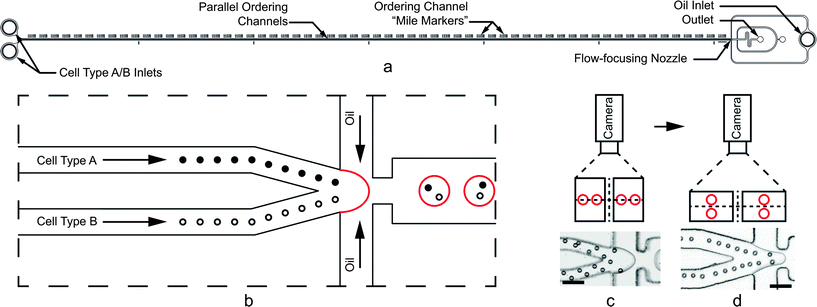 | ||
| Fig. 1 (a) Cell and particle co-encapsulation device. Parallel ordering channels are 6 cm long. (b) Close-up schematic of the flow-focusing nozzle. Cells hydrodynamically order with equal longitudinal spacing in one of two upstream channels. Immiscible oil pulls droplets from the aqueous cell streams such that one cell of each type arrives at the nozzle at the same frequency as droplet formation, thus encapsulating a pair in a single droplet. (c and d) For the high aspect ratio (W < H) arrangement shown in (c), the particles on the inside walls accelerate downstream faster than those on the outside walls, disrupting encapsulation of pairs. Low aspect ratio (W > H) channels shown in (d) provide quadrilateral symmetry so that all particles and cells experience the same velocity profiles, leading to more optimal pairing. The particles in (d) appear to form one collinear train, but closer inspection reveals staggered ordering on the top and bottom surfaces of the channel. Scale bars in (c) and (d) represent 50 μm. | ||
Materials and methods
Device design
Two parallel ordering channels, width W = 44 μm and height H = 31 μm, merge immediately before a flow-focusing nozzle as shown in Fig. 1a and b. For calculating Rec, we used known finite difference solutions43 for rectangular channel flow to obtain Umax/Umean = 2.068 for the aspect ratio α (= W/H) = 0.70. The aqueous channel outlet is 75 μm wide, and the nozzle constriction is 44 μm wide. Importantly, the low aspect ratio (W > H) design, flipped from previous work (where W < H),24,25 avoids unequal acceleration of cells when two high aspect ratio channels merge. To illustrate this motivation, consider the high aspect ratio case shown in Fig. 1c using polystyrene microspheres. When the channels merge, the particles on the inside channel walls experience a velocity mismatch with those on the outer channel walls. The mismatch disrupts the longitudinal spacing between particles and causes inefficient co-encapsulation. In the low aspect ratio case (Fig. 1d), the particles are ordered on the channel centerline (when viewed from the top) and experience a quadrilateral symmetry when two streams merge. Since all particles experience the same velocity profile at the merge, more consistent spacing is maintained.It is important to note that the ordering shown in Fig. 1c and d only appears different due to the camera angle and three-dimensional effects. Because cells tend to order along the short channel dimensions with the strongest velocity gradients, cells appear staggered when viewed from the top of the high aspect ratio channel. The camera schematics in Fig. 1c and d show that when the particles order in staggered trains (on the top and bottom of the low-aspect ratio channel), the ordering only appears different due to the two-dimensional camera view. Additional design considerations regarding ordering and the dripping to jetting transitions are addressed in the Results and discussion section.
Fabrication and materials
Devices were constructed using standard soft lithography procedures.44 Briefly, master molds were fabricated using SU-8 photoresist (Microchem 2050, Newton, MA) patterned by ultraviolet exposure through a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 dpi patterned mylar mask (FineLine Imaging, Colorado Springs, CO). Polydimethyl siloxane (PDMS) elastomer (Dow Corning Sylgard 184, Midland, MI) was mixed at a 10
000 dpi patterned mylar mask (FineLine Imaging, Colorado Springs, CO). Polydimethyl siloxane (PDMS) elastomer (Dow Corning Sylgard 184, Midland, MI) was mixed at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w base to curing agent ratio, poured onto the master mold, de-gassed, and cured overnight at 65 °C. The PDMS devices were then bonded to 3′′ × 1′′ glass microscope slides using a hand-held corona surface treater (Electro-Technic Products BD-20AC, Chicago, IL).45 Devices were baked at 120 °C overnight to return the channel walls to a hydrophobic state.46 To further ensure hydrophobicity, the devices were also injected with Aquapel™ and then purged with air to coat interior channel surfaces.24
1 w/w base to curing agent ratio, poured onto the master mold, de-gassed, and cured overnight at 65 °C. The PDMS devices were then bonded to 3′′ × 1′′ glass microscope slides using a hand-held corona surface treater (Electro-Technic Products BD-20AC, Chicago, IL).45 Devices were baked at 120 °C overnight to return the channel walls to a hydrophobic state.46 To further ensure hydrophobicity, the devices were also injected with Aquapel™ and then purged with air to coat interior channel surfaces.24Experimental setup
Fluorocarbon oil (3M FC-40, Saint Paul, MN), stabilized by a 2.5% w/w PFPE–PEG block copolymer surfactant (RainDance Technologies, Lexington, MA),47 served as the oil carrier fluid for aqueous droplets. Aqueous and oil flow rates were independently controlled using three separate positive displacement syringe pumps (Chemyx Nexus 3000, Stafford, TX). To demonstrate co-encapsulation, 10 μm, monodisperse (coefficient of variation <5%) polystyrene microspheres (Thermo G1000, Waltham, MA) served as cell surrogates for initial experiments. Rather than using density-matched solutions, we exploited the density mismatch between the aqueous fluid and particles (specific gravity = 1.05 for polystyrene microspheres) to control particle concentration via sedimentation within the syringes.25 For both particle and cell co-encapsulation results, the aqueous flow rate was 10 μL min−1 in each ordering channel, and the total oil flow rate was 45 μL min−1.Algal cultures
Microalgae C. reinhardtii (mt−) CC-124 and (mt+) CC-125 strains (Chlamydomonas Resource Center, Saint Paul, MN) were prepared separately in Sueoka's High Salt Media (HSM)48 using an orbital shaker plate (SCILOGEX SK-180-Pro, Berlin, CT) at 160 rpm. Culture temperature and gas composition were maintained at ambient conditions. Cell cycle synchronization was achieved by cycling between 12 hour light and 12 hour dark periods.37 Following centrifugation at 100 g for 20 minutes and aspiration of supernatant, samples were re-suspended in a nitrogen-free variety of Sueoka's High Salt Media and exposed to continuous light for 24 hours to induce gametogenesis.37,49 Immediately prior to experiments, cells were concentrated by centrifugation to working concentrations of approximately 30 × 106 cells per mL, as measured by counting cells within a hemocytometer. Again, we controlled cell concentrations in real time using sedimentation (C. reinhardtii specific gravity ∼ 1.04)50 within the syringes.Reversible algae deflagellation
For initial vegetative algae cell ordering experiments in single channels, cells tended to bounce away from the channel walls and off their hydrodynamic focusing and ordering positions (see Fig. 2a) due to the presence of flagella. However, C. reinhardtii cells are known to excise or resorb their flagella, i.e. “deflagellate”, in response to various environmental stresses such as low pH (ref. 51 and 52) or elevated temperature.53 Deflagellated cells can then quickly regrow the flagella when more favorable conditions return provided the stress was not too damaging. For example, C. reinhardtii gametes deflagellated using pH shock have been shown to regain both flagellar motility and mating capability.51 After 25 minutes removed from the pH shock, the cells regained motility. Between 45 minutes and two hours following deflagellation, the gametes were able to mate.51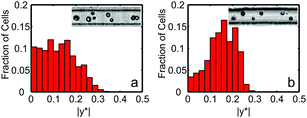 | ||
| Fig. 2 Normalized histograms of vegetative C. reinhardtii cell counts as a function of non-dimensional cross-stream channel position |y*|. (a) Normalized histogram for cells with flagella (N = 164). (b) Normalized histogram for deflagellated cells (N = 113). In both histograms, |y*| = 0 represents the channel centerline, and |y*| = 0.5 represents the channel wall for a 27 μm wide by 52 μm tall single channel. Measurements were taken at the end of the 6 cm long channel. For (b), cells were deflagellated by submerging a 1.5 mL centrifuge tube sample in a 40 °C water bath for 30 minutes. Both the histogram and still images show improvements in focusing and ordering for the deflagellated cells. | ||
To demonstrate the importance of flagella removal on ordering, Fig. 2 shows histograms of cross-sectional focusing position for vegetative UTEX-90 (UTEX, Austin, TX) C. reinhardtii cells with flagella (Fig. 2a) compared to cells without flagella (Fig. 2b). Measurements of cross-sectional position were taken 6 cm from the inlet of a 27 μm wide and 52 μm high ordering channel.24 For the results shown in Fig. 2 and for co-encapsulation experiments, algae were moved to 1.5 mL centrifuge tubes and heated in a constant temperature bath (40 °C) for 30 minutes to induce reversible loss of flagella immediately prior to co-encapsulation experiments.
Droplet visualization
Following co-encapsulation, droplet samples were coupled directly into a customized Dropspot54 array device, shown in Fig. 3. This array allowed for long-term tracking of flagellar mt+ and mt− agglutination (mating) and zygote formation within specific droplets, which were identified by their array coordinates. Arrays were secured to a Petri dish and immersed in a layer of DI water to prevent slow droplet evaporation through the PDMS. A larger emulsion sample was also stored in the dark at room temperature for zygospore maturation. Seventeen days post-encapsulation, 50 μL of emulsion was pipetted onto nitrogen-containing HSM agar along with 2 μL of a droplet destabilizer (RDT 1000, RainDance Technologies) to break the emulsion. The agar plated cells were then exposed to light for 24 hours to trigger zygospore germination and returned to a 12 hour light/12 hour dark cycle to resume vegetative algae growth by mitosis.55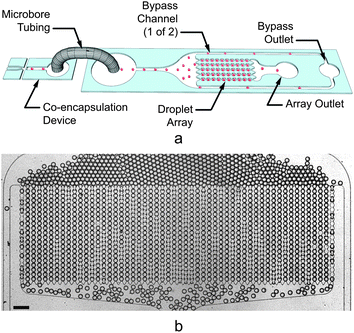 | ||
| Fig. 3 (a) Three-dimensional schematic illustrating the coupling between the co-encapsulation device (left) and customized Dropspot54 array (right). Droplets (represented by the red spheres) generated in the co-encapsulation device are conveyed via tubing to the inlet of a droplet array device. Droplets either flow through the array (to an array outlet tube) or a bypass channel (to a bypass outlet tube). When the array contains the desired numbers of droplets, the array outlet tube is reversibly clamped, immobilizing the droplets in the transparent device. Additional generated droplets may continue to be generated and exit through the bypass outlet, or the flows may be stopped. (b) Still image showing empty droplets filling the 55 μm tall array device used in this study. The array contained 54 columns and 20 rows for a total of 1080 array traps. The trap diameter measured 61 μm with a minimum constriction width of 35 μm between traps in the same column. The scale bar represents 200 μm. | ||
Imaging
Imaging was performed using transmitted brightfield illumination on an inverted microscope (Zeiss Axio Observer, Oberkochen, GER) using a high-speed camera (Vision Phantom V310, Wayne, NJ). Droplet encapsulation videos were acquired at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005 frames per second. A customized MATLAB tracking code56 was utilized to calculate particle and cell spacing and velocities. Particle and cell co-encapsulation statistics were obtained by visually observing high-speed video of the particles and cells during co-encapsulation. Static array videos were acquired intermittently at 100 frames per second. Representative supplemental videos for Fig. 2, 4, 6, and 7 are available online as ESI.†
005 frames per second. A customized MATLAB tracking code56 was utilized to calculate particle and cell spacing and velocities. Particle and cell co-encapsulation statistics were obtained by visually observing high-speed video of the particles and cells during co-encapsulation. Static array videos were acquired intermittently at 100 frames per second. Representative supplemental videos for Fig. 2, 4, 6, and 7 are available online as ESI.†Results and discussion
Co-encapsulation of polystyrene microspheres
Before applying the device to living cells, we co-encapsulated separate streams of 10 μm polystyrene microspheres to demonstrate device operation. The results in Fig. 4a show ordered particle trains at the end of the two channels, which merge at the flow-focusing nozzle. For channel A (top), the longitudinal particle spacing was 24.9 ± 5.3 μm while the particles traveled at an average velocity of 13.6 ± 0.1 cm s−1. For channel B (bottom), the longitudinal particle spacing was 23.7 ± 4.3 μm, and the average velocity was 14.1 ± 0.2 cm s−1. Note that the spacing statistics only include particle distances that are less than 45 μm; particles that were further apart were assumed to be a part of a separate train.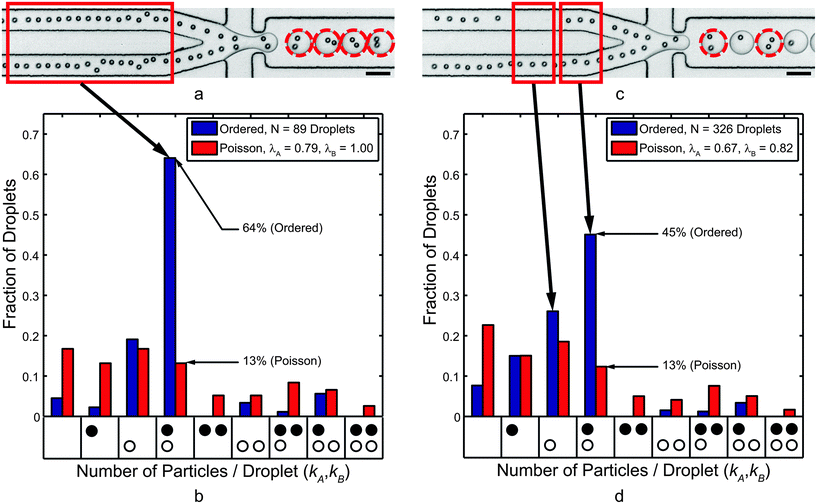 | ||
| Fig. 4 (a) Co-encapsulation of separate 10 μm polystyrene microsphere trains at 5.8 kHz. The dashed circles highlight droplets that contained one particle of Type A (top channel) and one particle of Type B (bottom channel). (b) Histogram showing the normalized frequency of droplets that contained the number of particles indicated by each x-axis bin. The black circles represent Type A particles while the white circles represent Type B particles, and each bin represents a droplet composition. For average particle A and B concentrations of 0.79 and 1.0 per droplet, respectively, there are few gaps in the trains (see red box). (c) When the local particle concentrations drop to 0.67 and 0.82, respectively, gaps in the ordering trains (e.g., see red boxes) emerged. The co-encapsulation efficiency decreased but still significantly outperformed Poisson co-encapsulation. Scale bars in (a) and (c) represent 50 μm. | ||
The combination of particle spacing and velocities imply that the average rate of particle arrival at the flow-focusing nozzle was 5.5 ± 1.2 kHz for channel A and 5.9 ± 1.1 kHz for channel B. Note that the instantaneous frequency depended highly on local longitudinal spacing, which is in part a function of particle concentrations λA and λB.57 The inter-particle spacing was as low as 14 μm for very dense particle suspensions, but less concentrated suspensions led to larger gaps between trains (Fig. 4c). However, because the droplet generation rate (5.8 kHz) was in line with the particle deliver rate to the flow-focusing nozzle, the statistics presented in Fig. 4b show 64% (= DkA=kB=1) of droplets contained the correct contents: a single co-encapsulation pair. Data in Fig. 4b reflects results from two particle trains with relatively few gaps; that is, λA = 0.79 and λB = 1.0. However, the calculated Poisson co-encapsulation efficiency (eqn (2)) is just 13%, so ordered co-encapsulation resulted in a nearly fivefold increase in the number of correctly loaded droplets.
Fig. 4c and subsequent encapsulation statistics in Fig. 4d highlight the importance of maintaining both particle concentrations near unity. Specifically, Fig. 4c shows particle ordering in channels with several gaps between ordered particle trains (λA = 0.67 and λB = 0.82). The train spacing increased due to lower particle concentrations such that the particle frequency at the flow-focusing nozzle dropped to 5.1 ± 1.1 kHz in channel A and 5.4 ± 1.3 kHz for channel B. This led to more empty droplets and droplets containing a single particle of either type. Here, the paired co-encapsulation efficiency fell to DkA=kB=1 = 45%, which is still a nearly fourfold improvement over Poisson co-encapsulation. Interestingly, for the results in Fig. 4c and d, the bottom train had relatively few gaps (λB = 0.82). As a result, the percentage of droplets containing one and only one Type B particle was still 72.6%. This result agrees well with the single-cell encapsulation efficiency values reported in previous studies24,25,27 and supports the eqn (2) assertion that the encapsulation efficiencies of separate streams are independent.
To see a wider range of local particle concentrations, Fig. 5 plots the co-encapsulation efficiency data versus the minimum of the Type A and Type B particle concentrations. Intuitively, the minimum particle concentration of the two streams, min(λA, λB), dictates the maximum attainable co-encapsulation efficiency. For example, the co-encapsulation efficiency when λA = 0 particles/droplet would be zero, no matter the value of λB. When λA = 0.1 particles/droplet, the theoretical maximum co-encapsulation efficiency DkA=kB=1 is also 0.1. We infer that, for λA and λB less than one, the theoretical maximum co-encapsulation efficiency is linearly proportional to the minimum concentration such that DkA=kB=1 = min(λA, λB), reaching a maximum of unity when λA = λB = 1. The data and weighted curve fit illustrate that when the ordered particle concentrations are very low, the likelihood that individual trains, while ordered, reach the nozzle at the same time also becomes similar to Poisson statistics. When the particle concentrations increase towards unity, fewer gaps in the trains leads to better pairing efficiencies.
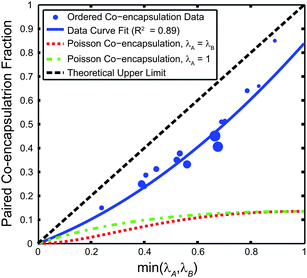 | ||
| Fig. 5 Co-encapsulation efficiency DkA=kB=1 of 10 μm polystyrene microspheres versus min(λA, λB). The theoretical maximum co-encapsulation efficiency is DkA=kB=1 = min(λA, λB). The co-encapsulation data point size is proportional to the N value, where the smallest marker size corresponds to N = 41 droplets, and the largest corresponds to N = 326 droplets. For the weighted (by N) curve fit of the form Ax2 + Bx + C, A = 0.4138, B = 0.4247, and C is constrained to 0. Two different Poisson co-encapsulation distributions (using eqn (2)) are plotted using both λA = λB (a likely design situation) and λA = 1 (where the DkA=kB=1,Poisson is maximized). | ||
While empty droplets and single-cell containing droplets are problematic, they are not as problematic as droplets containing incorrect groupings of multiple cells (0/2, 2/0, 2/1, 1/2, etc.), especially when considering FACS sorting based on fluorescent signal strength. For example, FACS may not be able to discern between a strong signal exhibited by a particularly active cell pair from a strong signal that may be the cumulative result of having multiple cell groups in a droplet. Despite the decrease in efficiency due to the less than optimal particle concentration in Fig. 4a, c and d metric to define the ratio of droplets containing one-to-one co-encapsulation to those containing incorrect groupings (DkA=kB=1/DkA or kB>1) was 7.4, as opposed to 0.4 for the Poisson case. In other words, of all the droplets containing two or more particles, 88% of those contained “correct” pairings while only 28% would have contained correct pairing for the Poisson case. Thus, one could also sort based solely on the number of cells in a droplet (without additional cell labeling) with significantly higher confidence that the droplet contains two separate cell types.
Co-encapsulation of microalgae gametes
Trains of mt− (Type A) and mt+ (Type B) C. reinhardtii cells are shown in the upstream ordering channels of Fig. 6a. Here, cells traveled downstream with an average speed of 16.6 ± 0.5 cm s−1 in channel A (top) and 16.7 ± 1.6 cm s−1 in channel B (bottom). Visually, the cell trains also appear to be less ordered. Here, the longitudinal cell spacing was 25.7 ± 8.8 μm in channel A and 26.8 ± 12.2 μm in channel B. This leads to the immediate observation that cell focusing and ordering quality (uniformity of cell velocity and cell train spacing), was degraded when compared to the case of 10 μm particles. A major factor in this change was a decrease in the particle Reynolds number Rep (as low as 0.16 for 5 μm cells while 0.62 for 10 μm particles). In other words, with cell diameters as low as 5 μm, the decrease in Rep was fourfold for the smallest cells. The average cell diameter (major axis length) was 7.7 ± 1.1 μm (Rep ∼ 0.37) while the average minor axis length was 6.5 ± 1.0 μm. Based on cell spacing (not including train gaps over 45 μm) and velocity, the cells in Fig. 6a reached the nozzle at a frequency of 6.4 ± 2.2 kHz for channel A and 6.2 ± 2.9 kHz for channel B. Droplets, 57 pL on average, were generated at 6.0 kHz.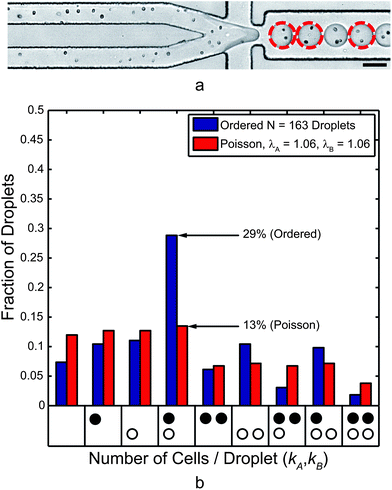 | ||
| Fig. 6 (a) Co-encapsulation of separate mt+ (Type A, top) and mt− (Type B, bottom) C. reinhardtii cell trains at 6.0 kHz. The dashed circles highlight droplets that contained one cell of each mating type. The scale bar represents 50 μm. (b) This histogram presents the normalized frequency of droplets that contained the number of cells indicated by each x-axis bin. The black circles represent mt+ and the white circles represent mt− cells, and each bin represents a droplet composition. While ordering quality and encapsulation efficiency were decreased compared to the 10 μm microsphere case, the paired encapsulation efficiency was over a twofold improvement to Poisson co-encapsulation. | ||
It is critical to note that while Rep can be raised by simply increasing flow rates, droplet generation places conflicting design constraints on these flow rates. The Weber number (We = ρU2Dh/σ) represents the ratio of inertial forces of the aqueous flow to interfacial tension forces. The capillary number (Ca = μU/σ) represents the ratio of viscous forces from the oil flow to interfacial tension forces. Aqueous fluid properties are used for calculating We, and oil phase properties are used for calculating Ca. For both quantities, σ represents the interfacial tension between the immiscible fluids, and all geometrical dependent quantities are taken at the flow-focusing nozzle. For small We and Ca (both ≪ 1), droplets form at the nozzle when the oil flow pulls droplets from the main aqueous flows. As We approaches 1 (higher aqueous flow rates), the aqueous stream begins to “jet” as inertial forces shoot the droplet interface downstream, leading to unstable droplet generation. As Ca approaches 1 (higher oil flow rates), the oil phase tends to pull the aqueous stream into long, thin jets.12 Neither inertial jetting nor capillary jetting is acceptable for controlled encapsulation. For ordered co-encapsulation, adding a second channel roughly doubles the aqueous flow rates at the nozzle. As a result, channel and nozzle geometries must be carefully designed so that the flow rates are sufficient for ordering but small enough to avoid the transition from droplet generation to jetting.
While the ellipsoidal cell size variation and shape are not directly addressed here, some previous studies58,59 have addressed the effect of particle and cell shape on inertial focusing. Note that these studies separated focused streams of particles based on shape and did not address ordering and inter-particle spacing. Additional, flow rates were much higher (40–80 μL min−1) than allowed for low Weber number droplet generation in our device. Our device did induce strong ordering of the ellipsoidal algae cells using the 31 μm × 44 μm device and a thinner 22 μm × 44 μm with flow rates on the order of 15–20 μL min−1 (see ESI Fig. S1†). At the combined flow rates, however, the Weber number was too high, and inertial jetting ensued at the flow-focusing nozzle.
Despite the decreases in longitudinal ordering quality, the co-encapsulation statistics, presented in Fig. 6b, still demonstrate a twofold improvement over the Poisson case for the same cell concentrations. Gametes were paired at an encapsulation efficiency DkA=kB=1 = 29% compared to a Poisson encapsulation efficiency of 13%. Table 1 shows results for additional experiments. As previously noted, the most problematic droplets for FACS sorting are those containing two or more of either cell type. The ratio of droplets containing correct pairings to those containing incorrect groupings (DkA=kB=1/DkA or kB>1) was 0.7 but still higher than 0.4 (the Poisson case). Of all the droplets containing two or more cells, 42% of those were “correctly” paired (DkA=kB=1/DkA+kB≥2) while only 22% would be correctly paired in the Poisson case. To achieve this same DkA=kB=1/DkA or kB>1 = 0.7 ratio in the Poisson case, the values of λA and λB must be 0.29, implying a co-encapsulation efficiency of 4.7% using eqn (2). In that sense, the current data represents a sixfold improvement over Poisson co-encapsulation.
| N | λA | λB | DkA=kB=1,Poisson | DkA=kB=1,data |
|---|---|---|---|---|
| 60 | 0.98 | 0.92 | 13% | 42% |
| 63 | 0.76 | 0.89 | 13% | 32% |
| 80 | 0.81 | 0.73 | 13% | 31% |
| 105 | 0.80 | 1.11 | 13% | 29% |
| 163 | 1.06 | 1.06 | 13% | 29% |
Mating reaction
Under typical culture conditions, C. reinhardtii produces asexually through mitosis. However, the ability of C. reinhardtii to sexually reproduce provides an extremely relevant application for co-encapsulation. When subjected to nitrogen starvation under continuous light exposure, vegetative cells convert to gametes (through either direct conversion or mitosis). Each C. reinhardtii strain is genetically predetermined to form gametes which are either mating-type minus (mt−) or mating-type plus (mt+).37,49 When haploid mt− and mt+ cells meet, agglutination proteins on their flagella initiate adhesion of the cells, gamete activation, and ultimately cell fusion to form a diploid zygote. Upon suspension in nitrogen-containing culture media after at least five days in dormancy, the zygospore will initiate separation into four recombinant haploids, two of which are mt+ and two of which are mt−, but all of which are genetically distinct.37Fig. 7a shows two cases of encapsulated algae in a static droplet array54 containing a pair of cells which had begun mating (left) and another pair where initial agglutination is captured in a time sequence of images (right). Fig. 7d and e show a close-up of flagellar entanglement (agglutination) between two algae gametes in a droplet approximately 30 minutes post-encapsulation and 1 hour following removal from the thermal deflagellation bath. This agglutination time (1 hour post-deflagellation) matches a previous study,51 where resumption of mating capability occurred between 45 minutes and 2 hours for gametes deflagellated using pH shock.
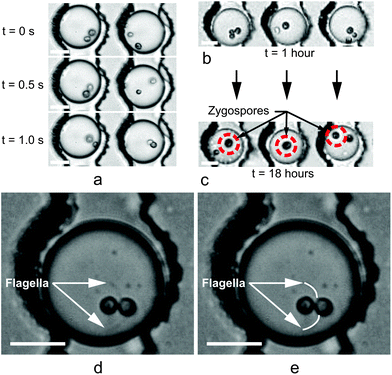 | ||
| Fig. 7 Droplets immobilized using static Dropspot54 arrays for tracking individual C. reinhardtii gamete pairs. (a) Time sequence taken 30 minutes post-encapsulation and 1 hour following removal from the thermal deflagellation bath. In the left droplet, mating had begun prior to the t = 0 s frame (t = 0 selected arbitrarily). In the right droplet, the mt+ and mt− algae cells swam in the droplet but then agglutinated between t = 0.5 s and 1.0 s. (b and c) Successful mating was determined by comparing the number of cells in each droplet one hour post-encapsulation (b) to the number of cells 18 hours post-encapsulation (c). In droplets where mating occurred, the decrease in the number of cells indicated the number of mating reactions that took place. Additionally, mating was further confirmed by the presence of a larger zygote (indicated by the circles in (c)), formed from the fusion of the mt+ and mt− cells. Unmated gametes in (c) remained motile. (d and e) Close-up view of flagellar agglutination. The original image is shown in (d), and visible flagella have been traced in (e) to highlight their presence. Flagella remained in motion as the cells prepared to fuse. Scale bars in (a–d) represent 20 μm. | ||
Zygote formation was deemed successful by comparing the number of cells visible in a droplet shortly after encapsulation to the number of cells 18 hours later (sufficient time to fully mate). Fig. 7b and c show the decrease in the number of algae in each droplet due to gamete fusion and zygote formation. Gametes not involved in a mating reaction remained motile in the droplets shown. Of 341 droplets examined, 179 droplets contained two or more algae cells following encapsulation. Of these 179 droplets, 18% contained zygotes after 18 hours, and 7% contained zygotes originating from a droplet containing one and only one cell of each mating type.
For more rigorous mating statistics, one could stain either the mt+ or mt− mating type to distinguish between the two following encapsulation. However, a fluorescence stain must penetrate a thick cell wall and then cleave within the cell. Initial attempts to stain one C. reinhardtii mating type with fluorescein, fluorescein diacetate, calcein, and calcein AM did not yield adequate fluorescence signals to differentiate between the stained and unstained mating types, even at high stain concentrations. These particular stains are optimized for animal cells, which lack cell walls and are thus easier to penetrate than algae cells. An additional stain (BODIPY 505/515)60 was successful in staining the algal lipid bodies but diffused from the stained cell type into the unstained type too quickly (on the order of seconds) to differentiate between mating types.
Zygospore maturation
The C. reinhardtii mt+ and mt− co-encapsulation emulsion sample was stored in the dark at room temperature for 17 days following encapsulation. Aside from ambient air gas diffusion, no additional nutrients or media were supplied to the droplets or the cells they contained. After 17 days, a number of zygospores were visible, along with smaller, unmated cells. Remarkably, some of these smaller cells appeared motile despite that no additional nutrients or light energy were supplied. Assuming that zygospore germination did not occur in the absence of light and nitrogen, we inferred that these surviving cells were unmated gametes. However, since the original composition of specific droplets in the collected emulsion was unknown (the bulk emulsion was not held in an indexed array), we could not deduce the fraction of gametes that survived in the droplet during this time. Zygospores are adapted to survive long periods of starvation by forming a thick, protective wall, and other long-term survival behaviors have been documented.37 Resting cell spores of Chlamydomonas nivalis,61 have shown the viability after multiple years in dry, frozen storage.37 One study7 used nano-liter scale droplet encapsulation to study Cholorella vulgaris algae growth rates for 33 days. Another growth rate study6 encapsulated C. reinhardtii cells in 270 pL droplets, where cells remained viable in the droplets after 10 days. Still, 17 day gamete survival in 57 pL droplets observed here was surprising. One explanation for the extended survival of some gametes is that the cells fed on their own lipids. Triaglycerol lipids, a potential source for algal biofuel,41 are generated as a stress response when the cells are starved in nitrogen-free media for gametogenesis.Fig. 8a shows three zygospores following agar plating but prior to hatching. Fig. 8b shows the broken zygospores, 24 hours later, with offspring and subsequent mitosis. To further demonstrate viability, Fig. 8c shows a resumption of mitosis of additional cells on agar plates. Since the emulsion contained zygospores and unmated gametes, we could not determine if the cells shown here resulted from single-cell mitosis or zygospore hatching. Still, the ability to survive 17 days in a droplet and resume asexual reproduction for single cells is even more significant.
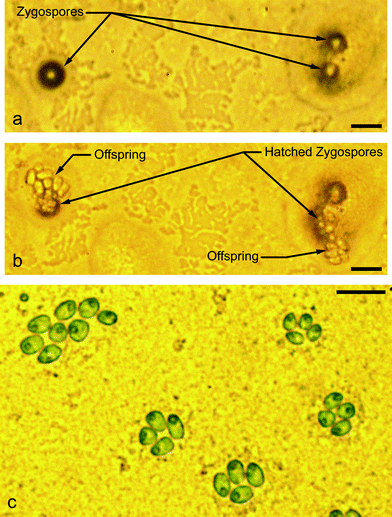 | ||
| Fig. 8 Seventeen days following encapsulation, the emulsion was broken onto High Salt Media (HSM) (complete nutrient media with nitrogen) agar and exposed to light for 24 hours and then returned to 12 hour light/12 hour dark cycles. (a) Three zygospores on HSM agar, three days following plating on agar. (b) The following day, two of the three zygospores had germinated into tetrads and broken out of their zygospore shells. Based on the number of cells shown, the vegetative cell tetrads had also begun asexual reproduction by mitosis. (c) Mitosis on HSM agar, three days following agar plating. Scale bars in (a)–(c) represent 20 μm. | ||
Conclusions
We have described a new device that merges parallel, ordered cell trains at a flow-focusing droplet nozzle. The resulting co-encapsulation statistics showed significant improvement in pairing separate particle and cell types in droplets at multi-kHz rates. This device showed an improvement in one-to-one co-encapsulation of mt+ and mt− C. reinhardtii algae gametes from 13% in the Poisson case to 29% in the ordered co-encapsulation device. Note that using typical dilutions with the same ratio of paired cell droplets to incorrectly grouped cell droplets, the predicted Poisson encapsulation efficiency was on the order of 5%. For larger 10 μm polystyrene microspheres with higher Rep, the improvement in paired co-encapsulation efficiency was fivefold, from 13% in the Poisson case to 64% for ordered co-encapsulation.Moreover, we have demonstrated the long-term survival of algae cells in microdroplets. Following thermal deflagellation, hydrodynamic self-ordering, encapsulation in 57 pL droplets, and flagellar regrowth, mt+ and mt− C. reinhardtii gametes maintained their ability to sexually agglutinate and form a zygote within a droplet. Furthermore, zygospore maturation and gamete survival continued in the extremely confined environment for 17 days, far longer than for animal cells.62 Subsequent agar plating resulted in zygospore hatching and vegetative offspring expansion by mitosis. The long-term survival and ability to resume both sexual and asexual reproduction highlights the remarkable survival ability of C. reinhardtii cells and may set a record for duration of cell survival in sub-100 pL droplets at ambient temperature.
When encapsulating a single algae cell from a single unique line, all cells and resulting asexual offspring are theoretically identical. Droplet confinement could lead to the identification of rare cells due to mutations during mitosis, but these mutations may be slow unless induced. Sexual mating provides unique offspring from each mating event. Completing the zygospore maturation and re-introduction of nitrogen media within the droplet would provide four unique offspring that are isolated from the bulk cell population. From this droplet, new, isolated strains are contained and may be screened for new, useful phenotypes. Following sorting, selected cells could be re-suspended in media for asexual reproduction of the new strain. Exploiting controlled encapsulation of single or multiple cells can accelerate high-throughput screening of microalgae for improved biofuel (or other) desirable traits. More broadly, new avenues are opened for studying the basic biology and applications of cell–cell interactions.
Acknowledgements
We thank Elizabeth Harris (Chlamydomonas Genetics Center, Duke University), David Nobles (UTEX Culture Collection, University of Texas at Austin), and Matt Laudon (Chlamydomonas Resource Center, University of Minnesota, Twin Cities) for their helpful correspondence. We also thank Dylan Losey (Vanderbilt University) for useful discussions and support.References
- H. N. Joensson, M. L. Samuels, E. R. Brouzes, M. Medkova, M. Uhlen, D. R. Link and H. Andersson-Svahn, Angew. Chem., Int. Ed., 2009, 48, 2518–2521 CrossRef CAS PubMed.
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J. C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed.
- P. Kumaresan, C. J. Yang, S. A. Cronier, R. G. Blazej and R. A. Mathies, Anal. Chem., 2008, 80, 3522–3529 CrossRef CAS PubMed.
- J. Q. Boedicker, L. Li, T. R. Kline and R. F. Ismagilov, Lab Chip, 2008, 8, 1265–1272 RSC.
- J. Q. Boedicker, M. E. Vincent and R. F. Ismagilov, Angew. Chem., Int. Ed., 2009, 48, 5908–5911 CrossRef CAS PubMed.
- J. Pan, A. L. Stephenson, E. Kazamia, W. T. Huck, J. S. Dennis, A. G. Smith and C. Abell, Integr. Biol., 2011, 3, 1043–1051 RSC.
- A. Dewan, J. Kim, R. H. McLean, S. A. Vanapalli and M. N. Karim, Biotechnol. Bioeng., 2012, 109, 2987–2996 CrossRef CAS PubMed.
- D. Luo, S. R. Pullela, M. Marquez and Z. Cheng, Biomicrofluidics, 2007, 1, 34102 CrossRef PubMed.
- Y. S. Lin, C. H. Yang, K. Lu, K. S. Huang and Y. Z. Zheng, Electrophoresis, 2011, 32, 3157–3163 CrossRef CAS PubMed.
- T. Rossow, J. A. Heyman, A. J. Ehrlicher, A. Langhoff, D. A. Weitz, R. Haag and S. Seiffert, J. Am. Chem. Soc., 2012, 134, 4983–4989 CrossRef CAS PubMed.
- S. Kobel and M. P. Lutolf, Curr. Opin. Biotechnol., 2011, 22, 690–697 CrossRef CAS PubMed.
- A. Utada, A. Fernandez-Nieves, H. Stone and D. Weitz, Phys. Rev. Lett., 2007, 99, 094502 CrossRef PubMed.
- T. Nisisako, T. Torii and T. Higuchi, Lab Chip, 2002, 2, 24–26 RSC.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364 CrossRef CAS.
- S. Y. Teh, R. Lin, L. H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- Y. J. Eun, A. S. Utada, M. F. Copeland, S. Takeuchi and D. B. Weibel, ACS Chem. Biol., 2011, 6, 260–266 CrossRef CAS PubMed.
- J. C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak, L. Frenz, C. Rick, M. L. Samuels, J. B. Hutchison, J. J. Agresti, D. R. Link, D. A. Weitz and A. D. Griffiths, Lab Chip, 2009, 9, 1850–1858 RSC.
- T. P. Lagus and J. F. Edd, J. Phys. D: Appl. Phys., 2013, 46, 114005 CrossRef.
- J. Hong, A. J. deMello and S. N. Jayasinghe, Biomed. Mater., 2010, 5, 21001 CrossRef PubMed.
- A. L. Givan, Methods Mol. Biol., 2011, 699, 1–29 CAS.
- S. Koster, F. E. Angile, H. Duan, J. J. Agresti, A. Wintner, C. Schmitz, A. C. Rowat, C. A. Merten, D. Pisignano, A. D. Griffiths and D. A. Weitz, Lab Chip, 2008, 8, 1110–1115 RSC.
- M. Y. He, J. S. Edgar, G. D. M. Jeffries, R. M. Lorenz, J. P. Shelby and D. T. Chiu, Anal. Chem., 2005, 77, 1539–1544 CrossRef CAS PubMed.
- M. Chabert and J. L. Viovy, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3191–3196 CrossRef CAS PubMed.
- J. F. Edd, D. Di Carlo, K. J. Humphry, S. Koster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262–1264 RSC.
- T. P. Lagus and J. F. Edd, J. Visualized Exp., 2012, 64, 4096 Search PubMed.
- D. Di Carlo, Lab Chip, 2009, 9, 3038–3046 RSC.
- E. W. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. van den Berg, Lab Chip, 2012, 12, 2881–2887 RSC.
- M. Zagnoni, G. Le Lain and J. M. Cooper, Langmuir, 2010, 26, 14443–14449 CrossRef CAS PubMed.
- C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 RSC.
- Y. Gao, D. Majumdar, B. Jovanovic, C. Shaifer, P. C. Lin, A. Zijlstra, D. J. Webb and D. Li, Biomed. Microdevices, 2011, 13, 539–548 CrossRef CAS PubMed.
- L. Businaro, A. De Ninno, G. Schiavoni, V. Lucarini, G. Ciasca, A. Gerardino, F. Belardelli, L. Gabriele and F. Mattei, Lab Chip, 2013, 13, 229–239 RSC.
- E. Tumarkin, L. Tzadu, E. Csaszar, M. Seo, H. Zhang, A. Lee, R. Peerani, K. Purpura, P. W. Zandstra and E. Kumacheva, Integr. Biol., 2011, 3, 653–662 RSC.
- S. Srigunapalan, I. A. Eydelnant, C. A. Simmons and A. R. Wheeler, Lab Chip, 2012, 12, 369–375 RSC.
- C. N. Baroud, M. R. de Saint Vincent and J. P. Delville, Lab Chip, 2007, 7, 1029–1033 RSC.
- L. M. Fidalgo, C. Abell and W. T. Huck, Lab Chip, 2007, 7, 984–986 RSC.
- R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601 CrossRef PubMed.
- E. H. Harris, The chlamydomonas sourcebook: introduction to chlamydomonas and its laboratory use, Academic Press, San Diego, 2009 Search PubMed.
- S. Rosales-Mendoza, L. M. Paz-Maldonado and R. E. Soria-Guerra, Plant Cell Rep., 2012, 31, 479–494 CrossRef CAS PubMed.
- R. Harun, M. K. Danquah and G. M. Forde, J. Chem. Technol. Biotechnol., 2010, 85, 199–203 CAS.
- S. J. Burgess, B. Tamburic, F. Zemichael, K. Hellgardt and P. J. Nixon, Adv. Appl. Microbiol., 2011, 75, 71–110 CAS.
- S. S. Merchant, J. Kropat, B. Liu, J. Shaw and J. Warakanont, Curr. Opin. Biotechnol., 2012, 23, 352–363 CrossRef CAS PubMed.
- C. S. Jones and S. P. Mayfield, Curr. Opin. Biotechnol., 2012, 23, 346–351 CrossRef CAS PubMed.
- N. M. Natarajan and Lakshmanan, Indian J. Technol., 1972, 10, 435–438 CAS.
- D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, Anal. Chem., 1998, 70, 4974–4984 CrossRef CAS PubMed.
- K. Haubert, T. Drier and D. Beebe, Lab Chip, 2006, 6, 1548–1549 RSC.
- A. C. Hatch, J. S. Fisher, A. R. Tovar, A. T. Hsieh, R. Lin, S. L. Pentoney, D. L. Yang and A. P. Lee, Lab Chip, 2011, 3838–3845 RSC.
- C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angile, C. H. Schmitz, S. Koster, H. Duan, K. J. Humphry, R. A. Scanga, J. S. Johnson, D. Pisignano and D. A. Weitz, Lab Chip, 2008, 8, 1632–1639 RSC.
- N. Sueoka, Proc. Natl. Acad. Sci. U. S. A., 1960, 46, 83–91 CrossRef CAS.
- R. Sager and S. Granick, J. Gen. Physiol., 1954, 37, 729–742 CrossRef CAS PubMed.
- K. Yoshimura, Y. Matsuo and R. Kamiya, Plant Cell Physiol., 2003, 44, 1112–1118 CrossRef CAS PubMed.
- K. M. Solter and A. Gibor, Nature, 1977, 265, 444–445 CrossRef CAS PubMed.
- X. Ai, Q. Liang, M. Luo, K. Zhang, J. Pan and G. Luo, Lab Chip, 2012, 12, 4516–4522 RSC.
- R. A. Lewin, T. H. Lee and L. S. Fang, Symp. Soc. Exp. Biol., 1982, 421–437 CAS.
- C. H. Schmitz, A. C. Rowat, S. Koster and D. A. Weitz, Lab Chip, 2009, 9, 44–49 RSC.
- X. Jiang and D. Stern, J. Visualized Exp., 2009, e1274 Search PubMed.
- J. C. Crocker, track.pro (MATLAB Version), http://physics.georgetown.edu/matlab/, 1999.
- K. J. Humphry, P. M. Kulkarni, D. A. Weitz, J. F. Morris and H. A. Stone, Phys. Fluids, 2010, 22, 081703 CrossRef.
- S. C. Hur, S.-E. Choi, S. Kwon and D. D. Carlo, Appl. Phys. Lett., 2011, 99, 044101 CrossRef.
- M. Masaeli, E. Sollier, H. Amini, W. Mao, K. Camacho, N. Doshi, S. Mitragotri, A. Alexeev and D. Di Carlo, Phys. Rev. X, 2012, 2, 031017 Search PubMed.
- M. S. Cooper, W. R. Hardin, T. W. Petersen and R. A. Cattolico, J. Biosci. Bioeng., 2010, 109, 198–201 CrossRef CAS PubMed.
- J. T. Hardy and H. Curl, Nat. Hist., 1972, 81, 74–78 Search PubMed.
- J. Clausell-Tormos, D. Lieber, J. C. Baret, A. El-Harrak, O. J. Miller, L. Frenz, J. Blouwolff, K. J. Humphry, S. Koster, H. Duan, C. Holtze, D. A. Weitz, A. D. Griffiths and C. A. Merten, Chem. Biol., 2008, 15, 427–437 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra43624a |
| This journal is © The Royal Society of Chemistry 2013 |
