Impact of additives on zirconium oxidation by water: mechanistic insights from first principles

Abstract

Zirconium alloys are widely used as cladding materials employed to contain the fission fuel in nuclear power plants. A limiting factor for fuel longevity is the corrosion property of the zirconium alloys. In the reactor, the main corrodent is water. The oxide forms thermodynamically during hydrogen evolution. Due to the corrosion mechanism, a fraction of the hydrogen is transferred to the alloy. It has long been known that the alloying elements actually control the hydrogen pick-up fraction, HPUF. A mechanism that explains these observations by means of density functional theory calculations is presented and validated. A hydroxylated grain boundary model decorated by various transition metal, TM, ions is employed to study the dependence of the hydrogen evolution reaction, HER, on the choice of TM ion and spin state along the hydride–proton recombination pathway. The efficiency of the system to utilize the overpotential for hydrogen evolution, originating from the overall corrosivity of the alloy, is found to be decisive for the HPUF. A dual origin of the detrimental effects of Co and Ni additives on the HPUF is identified.

---

I. Introduction

Today, fundamental aspects of apparently disparate branches of material science are seen to coalesce, which is due to a unifying atomistic paradigm in conjunction with the prevailing computational technology, as manifested in implementations of density functional theory. Here, this is realised in the analysis of corrosion, where electrochemical interpretive concepts have long since been employed. Thus, corrosion is associated with a redox process where the reduction is said to occur at the cathode, while oxidation takes place at the anode. Sustained corrosion requires media that conduct electrons and ions in order to maintain electroneutrality at both electrodes. Clearly, such a corrosion process is related to the operation of a fuel cell, yet the corresponding technological implications remain to be explored more fully.

The control of electron and ion transport is crucial both for obtaining improved materials for fuel cell applications and for improved corrosion protection; the same materials are often investigated for similar reasons. This is so for ZrO₂, which constitutes the protective barrier layer on zirconium alloys, e.g. the cladding for nuclear fuel. Indeed, the transport properties of this barrier oxide determine the durability of the fuel assembly itself. Zirconia based materials are also ubiquitous in fuel cell research owing to their properties as solid oxide proton conductors. The added value of such transferability between complementary disciplines is sought by clarifying and utilizing their common contextual framework. In this spirit, in a previous study,¹ the oxidation of zirconium alloys by water was analysed. The process was subdivided into an anode process

Zr + 2O²⁻ → ZrO₂ + 4e⁻ (R1)

and a cathode process which eventually results in hydrogen evolution, occurring at transition metal sites in hydroxylated grain boundaries of ZrO₂ (see Fig. 1). Evidence for grain boundary hydroxides was provided by infrared spectroscopy,² while transition metal decoration was reported by atom probe tomography.^1,3 The cathode reaction was subdivided into two steps, the first of which is the formation of a three-centre hydride

TM^X_GB + Zr^IV + OH⁻ + 2e⁻ → TM^X_GB–H⁻–Zr^IV + O²⁻ (R2a)

or the equivalent

TM^X_GB + Zr^IV + H⁺ + 2e⁻ → TM^X_GB–H⁻–Zr^IV (R2b)

and the second is a subsequent hydrogen evolution reaction

TM^X_GB–H⁻–Zr^IV + OH⁻ → TM^X_GB + Zr^IV + H₂ + O²⁻ (R3a)

or

TM^X_GB–H⁻–Zr^IV + H⁺ → TM^X_GB + Zr^IV + H₂ (R3b)

where X = II or III, and TM = Ti, V, Cr, Mn, Fe, Co, Ni, Cu or Zn. The (R2a) and (R3a) emphasize that reactive protons reside on hydroxide ions. Support for the possible presence of hydride intermediates in hydroxylated grain boundaries was arrived at by comparing computed vibration frequencies¹ to experimental infrared spectra.² When II ions were present, the hydrides were found to form spontaneously for all elements investigated. In contrast, for TM^III the reaction (R2) becomes exothermic for Ti, V, and Cr, while it is endothermic for Mn, Fe, Co, and Ni (see Fig. 2).

Fig. 1 Representative structure for a model of hydroxylated grain boundary ZrO(OH)₂ in ZrO₂. Here, the grain boundary is decorated with Fe ions in oxidation state II. Oxygen is represented as red, zirconium as light blue, iron as purple and hydrogen as white.

Fig. 2 The energy change associated with the formation of TM^III hydrides indicates the feasibility of the reaction channel for H₂ evolution. Negative numbers are favourable, while positive numbers disfavour this channel; TM^III is irrelevant for Cu and Zn.

The energy changes for the hydride–proton recombination reaction (R3) were computed. The resulting H₂ evolution energy versus choice of elements was plotted, i.e. for Ti^III, V^III, Cr^III, Mn^II, Fe^II, Co^II, Ni^II, Cu^II and Zn^II, by using the findings for the oxidation state III (see Fig. 2) as a weight function.

For all 3d transition metals investigated, the 3d orbitals are the ones which interact directly with the hydride. To isolate the properties of pure zirconia, Ca²⁺ was introduced as a reference II ion replacing the 3d transition metal elements of the oxidation state II. Complementary to Ca²⁺, the impacts of inert ions, in oxidation states I and III, were also evaluated. This was achieved by replacing Ca²⁺ by Na⁺ and Sc³⁺, respectively. Thus, a stability test for the hydride–proton recombination energy of pure zirconia is provided, see shaded horizontal band in Fig. 3. Finally, the correlation between the computed reaction energy changes for (R3) and the experimental ratios^4,5 of hydrogen picked up by the alloy to the total amount of hydrogen converted, i.e. the hydrogen pick-up fraction, HPUF, was sought and striking agreement was obtained (see Fig. 3).

Fig. 3 Comparison of theoretical data (blue) at T = 700 K and experimental data (black); * source⁴ and ○ source.⁵ The red spot is Fe^II high-spin. The theoretical data is a weighted average of TM^II and TM^III. The black dashed line is HPUF in pure ZrO₂; source.⁴ The thin blue dashed lines correspond to HE from Zr^IV hydride at grain boundary with Na⁺, Ca²⁺ and Sc³⁺ as “dummy” spectators. The Sc³⁺ corresponds to the top line, Na⁺ to the middle line and Ca²⁺ to the bottom line.

The purpose of the present study is to explore the cause of this agreement and its possible consequences. An analysis of the structural origins of the reaction energy changes in (R3) is included. Moreover, beyond the property of the reaction energy to offer a descriptor for predicting the HPUF, we attempt to unravel the reaction mechanism for the proposed hydride–proton recombination reaction. Finally, the origin and possible implication of the detailed correlation between the energy change associated with hydrogen evolution and the hydrogen pick-up fraction are discussed.

II. Modelling considerations

II.a. The model

The present study utilizes a periodically repeating hydroxylated grain boundary embedded in ZrO₂. It was constructed by inserting one unit cell of monoclinic ZrO(OH)₂ (ref. 6) (5.4 Å × 10 Å × 5.4 Å) between two supercells of monoclinic ZrO₂ (5.4 Å × 10.8 Å × 5.4 Å), where the unit cell doubling is in the b direction. The two subcells were fused “epitaxially” by making contact between the (a,c) planes of each subcell. A periodically layered structure in the b direction was obtained. The starting ZrO(OH)₂ structure was obtained by replacing Li⁺ with H⁺ in Li₂ZrO₃. Upon replacing Li⁺ by H⁺ and subjecting the system to geometry optimization, protons bind to O²⁻ ions thereby forming hydroxide ions, hence the ZrO(OH)₂ structure was formed. Interestingly, an excellent proton conductor has been obtained experimentally by performing ion exchange on Li₂ZrO₃, replacing Li⁺ with H⁺.⁷

Although the stability of the model was extensively investigated, only a subset of all calculations for the system is provided here. The choice of grain boundary model is far from unique. However, for the model to offer a valid chemical representation of the hydroxylated interface between two ZrO₂ grains, there are certain requirements that need to be satisfied.

Essential to the modelling, besides reproducing the large band gap signature of the undoped material (see partial density of states, PDOS, in Fig. 4) and a proton conducting interface (see Fig. 1), is a sufficiently flexible yet cost efficient supercell. The main features in Fig. 4a are: O²⁻ dominating contribution to the occupied p-states states (red) in the valence band below the Fermi level (E_F, dashed vertical line), and Zr^IV contributing mainly to the unoccupied states in the conduction band above the Fermi level (green). The band gap of pure ZrO₂ is affected only marginally by the hydroxylation; compare Fig. 4a and b. Moreover, in Fig. 4b, new states are introduced at 6–8 eV below E_F owing to the hydroxides. A typical impact on the electronic structure owing to the transition metal ions is shown in Fig. 4c. Here, the presence of Fe^II introduces occupied and generally also unoccupied states in the original band gap of ZrO₂.

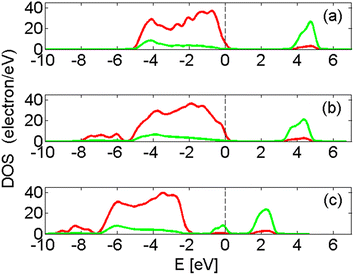Fig. 4 (a) The PDOS for ZrO₂. (b) The PDOS for hydroxylated grain boundary in ZrO₂. (c) The PDOS for hydroxylated grain boundary in ZrO₂ with Fe^II ions in the grain boundary, see Fig. 1. Red represents p-states and green d-states.

The validity of the model must eventually be assessed on its performance. In a previous study,¹ referred to in the introduction, connection was made between reaction energies and corrosion properties, see Fig. 3. The apparent validity of the first-principles model was identified by the horizontal dashed black line representing the hydrogen pick-up fraction during oxidation of pure zirconium by water. Moreover, the experimentally observed trends in HPUFs for the suite, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, and Zn, correlate remarkably well with the corresponding energies. A test of the stability of the model is offered by comparing the sensitivity of the energies to the charge and ionic radii of “dummy” ions (Na⁺, Ca²⁺ or Sc³⁺) embedded in the grain boundary at the site of the transition metal ions to be evaluated. In spite of this harsh test, the seeming correlation between computed hydrogen evolution energies and experimental HPUF for Zr remains.

II.b. Computational details

The present study employs the Perdue, Burke, Erntzerhof generalized gradient approximation,⁸ PBE GGA, as implemented in the DMOL³ engine^9,10 in the Material Studios program package.¹¹ A double-ζ numerical basis set, with an extra polarization function on each heavy atom and a p-function on each hydrogen atom was employed. Systematic spin polarized calculations were made in which a 4 × 1 × 4 k-point set for sampling the Brillouin zone was compared with a 2 × 1 × 2 k-point set, and the latter found to suffice. All of the spin states of reactant and product corresponding to the lowest energies were determined. In a few cases excited states where also taken into account. In those cases the spin state was the same for reactant and product in order to ensure semi-quantitative cancellation of the self-interaction error.^12,13 To reduce the computational effort, inert electrons were described effectively by means of semi-core pseudopotentials. Zero-point corrected free energy was compared with uncorrected energy and the differences were deemed negligible. The entropy contributions to reactant and product were found to cancel. This is because the large entropy contribution commonly assigned to molecular H₂ becomes negligible at the confining grain boundary. Finally, the supercells studied contained approximately 50 atoms; control of the oxidation states of the transition metal ions was achieved by the addition or removal of hydrogen atoms from the supercell. Neutral supercells were employed in all cases.

III. Results and discussion

The correlation between computed hydride–proton recombination energies and observed effective hydrogen pick-up fraction, HPUF, during zirconium oxidation by water implies the existence of a detailed underlying reaction mechanism; this is revealed below. First, structural support for the hydride–proton recombination reaction channel is provided. Second, the origin of the element dependent reaction energy is addressed. Third, properties of H₂ intermediates are presented in support of the emerging understanding.

III.a. Structural support for a hydride–proton reaction channel

Support for the viability of the hydride–proton recombination mechanism is provided here in both reaction energies and structural properties of intermediates along the reaction coordinate, where geometric proximity between reactants and products is understood to favour the efficiency of the proposed reaction channel. Especially for the hydride–proton recombination channel, it is not unexpected to find the resulting hydride–proton affinity reflected in the effective electrostatic potential at the reaction site. Support for this conjecture is provided in Fig. 5 and Table 1, which show how atomic structures depend on the choice of “dummy” ion, Na⁺, Ca²⁺ or Sc³⁺.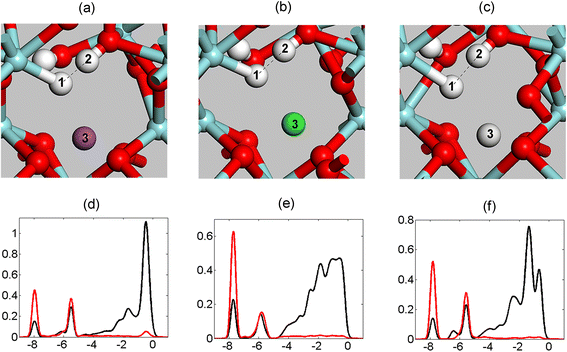

Fig. 5 Three structures of Zr^IV associated hydride (atom no. 1) facing a proton in a hydroxide (atom no. 2). The distance between the hydride and the proton is affected by the charge of the “dummy” ion (atom no. 3) located in the vicinity of the hydride–proton complex. The “dummy” ion is Na⁺, Ca²⁺ and Sc³⁺ for (a), (b) and (c), respectively. (d)–(f) are PDOS corresponding to (a)–(c). Black: H atom no. 1 (hydride); red: H atom no. 2 (hydroxide).

Table 1 Impact of the “dummy” ions, Na⁺, Ca²⁺ and Sc³⁺, on a local surrounding of Zr^IV associated hydride, and the corresponding HER energy. The lack of correlation, between the inter-nuclear distances of adjacent hydride–proton couples and reaction energies for H₂ release into the grain boundary, is noted, as is the smallness of the energy variations. These variations are apparently in spite of the large differences in ionic charges and radii

	Distance [Å]	Energy [eV]
Na^+	1.173	−0.29
Ca^2+	1.262	−0.23
Sc^3+	1.372	−0.42

---

For the three “dummy” elements, an intermolecular hydride–proton bond is inferred i.e. a Zr^IV–H⁻⋯HO–Zr^IV moiety. In Fig. 5 this is shown in the overlapping partial densities of states of hydrogen belonging to hydride and hydroxide moieties. Seemingly, both the reaction energies and the distances between the hydride and the proton are affected by the charges of the proximal “dummy” ions, see Table 1. The distance between the hydride and proton decreases with reduced charge, suggesting effective lower attraction between the hydride and “dummy” ion with reduced ionic charge in conjunction with less repulsion between the “dummy” ion and the proton. If the “dummy” ion is removed altogether, no local minimum on the potential energy surface corresponding to the hydride–proton structure exists. Instead H₂ is formed. Interestingly, no simple correlation between ion charge and reaction energy is seen, see Table 1. This is because the reaction energy is determined to a great extent by the structural relaxations of the product, i.e. subsequent to the H₂ evolution. This relaxation energy depends in a complex way on ionic radius, charge, and change in chemical bonding to the surrounding oxygen ions (mainly for Sc³⁺).

Finally, the impacts of the “dummy” ions on the H₂ evolution reaction energies are shown in Fig. 3 where the black dashed line represents the HPUF for pure zirconium. The three thin blue dashed lines represent hydride–proton recombination energies for the three “dummy” atoms. It is gratifying to note the limited variations in energies, marked by a green shaded band, in spite of the large differences in ionic charges. This offers a stability test for the proposed correlation between the HPUF and reaction energy of the computational methodology.

III.b. Structural origin of hydride–proton recombination energy

The enthalpy drive for any chemical reaction, including the hydrogen evolution reaction, is found in the favourable bonding of the products as compared to the reactants. Hence, the determination of a structural change, driving the hydride–proton recombination, is an important result of the present study. Indeed, the origin of the shape of the graph displayed in Fig. 3 is associated with the changes in the coordination of transition metal ions upon release of H₂ into the grain boundary. In order to see this it becomes helpful to note that most of the transition metal ions investigated here are 6-coordinated. The chemical changes upon HER are associated with the 6^th coordination to TM^II/TM^III; it is a hydride ion in the reactant and an oxide ion in the product, see Fig. 6a–d. When elementary concepts of ligand field theory are used for the quasi-octahedral systems, the differences become controlled by the occupation of e^*_g. Consider that, rather than being released, the H₂ molecule may be viewed as squeezed into the grain boundary by the resulting 6^th TM–O²⁻ coordination. When the incoming oxide lone-pair encounters an occupied matching TM 3d orbital, the energy gains may be small or even negative. However, if this 3d orbital is empty, then the reaction becomes highly favoured. This interpretation is consistent with the overall trend in Fig. 3. Hence, significant stabilizations are obtained when at least one e^*_g component is empty, Ti^III, V^III, Cr^III, and low-spin Fe^II for example. The crucial impact that an unoccupied e^*_g component has on the resulting energy change is clarified in the comparison between low-spin Fe^II and high-spin Ni^II, Fig. 3. For these closely neighbouring ions in the periodic table, this effect is reflected in the structural differences of resulting TM^II–O²⁻ coordinations, see Fig. 6b and d.

Fig. 6 (a) and (c) illustrate Fe and Ni associated three-centre hydrides. In (b) and (d) the TM coordination to the hydride has been replaced by the coordination (dashed line) to O²⁻. Note the difference in TM–O bond distance, 2.12 Å for Fe^II and 2.45 Å for Ni^II, which explains the smaller exothermicity associated with the HER of the latter as compared with the former (see Fig. 3).

This interpretation is further supported by comparing the similar energy changes of high-spin Mn^II with high-spin Fe^II (red dot in Fig. 3), both of which have two unpaired electrons in e^*_g. The semi-quantitative validity of the argument may be more fully appreciated by comparing these two systems to the result for low-spin Fe^II.

In particular, the net endothermic hydrogen evolution reactions for the hydrides of Ni^II and Co^II are due to the insufficient stabilization of TM by the new coordination to O²⁻ as H₂ is released. The smallness of this stabilization is due to the Pauli repulsion between the occupied 3d e^*_g orbital and the incoming O²⁻ lone-pair replacing the hydride. Interestingly, with Co^II it is the low-spin state, which emerges as the ground state. The low-spin 3d⁷ electron configuration implies that one e^*_g is vacant. However, it can be seen that both hydride and the incoming O²⁻ lone-pair interact mainly with the occupied e^*_g component due to a Jahn–Teller distortion. Two other exceptions to the emerging understanding are Cu^II and Zn^II. However, the impact of the occupation of e^*_g is expected to be reduced beyond high-spin Ni^II if one takes into account the effect of the shrinking of the ionic radius upon an increasing atomic number for elements with the same formal charge and belonging to the same period in the periodic table.

Viewing this result from the perspective of catalysis, a slight endothermicity for hydrogen evolution would indeed be an ideal property for a catalyst. However, Ni^II and Co^II are reluctant to release H₂ into the confining metal/oxide interface; this makes Ni^II, which has been used extensively in zirconium based nuclear fuel claddings, a “Trojan horse” for hydrogen pick-up.

III.c. Mechanism for hydride–proton recombination

The hydride–proton recombination reaction, evaluated in the present study, postulates the release of H₂ into a confining hydroxylated ZrO₂ grain boundary. The impact of this confinement is to resist the HER. To pass from the hydride–proton reactants to the corresponding products (as described in Section III.b., see (R3)) two reaction pathways emerge, differing by the presence or absence of a TM–H₂ intermediate. Here, this property offers a complementary perspective, to that given in Section III.b., on the interpretation of the volcano shape of Fig. 3. The stabilities of intermediates relative to their respective reactants and products are shown for a few of the systems investigated (Fig. 7).

Fig. 7 Energy changes for (B) the intermediate TM–H₂ structure and (C) the structure where H₂ is formed relative to (A) the hydride structure; the transition metals are in oxidation state II. The asterisk indicates high-spin state and no asterisk is low-spin state. No stable TM–H₂ structures were found for Mn^II*, Fe^II* and Zn^II.

In unravelling the origin of the disparate behaviours of the different systems, we employ as one important component the same elementary concepts of ligand field theory as used in Section III.b. Hence, we note that low-spin Fe^II and Zn^II display similar reaction energy changes, but what differs is the presence of an Fe^II–H₂ intermediate. The structural characteristics of this intermediate can be appreciated by looking at Fig. 8d and Table 2. Thus, the Fe^II–H₂ moiety has replaced the 6^th Fe^II coordination to the hydride by the one to H₂, compare Fig. 6a and d. The distinct elongation of the H–H bond, see Table 2, is taken to infer that the 1σ² electron pair of H₂ becomes shared with the empty e^*_g component of Fe^II in a three-centre dative bond. The universality of this TM–H₂ intermediate was explored by considering the strongly Jahn–Teller distorted low-spin Ni^II (see Fig. 8c and f), which has one doubly occupied e^*_g orbital and one that coordinates the H₂ molecule. Indeed, similar bonding was observed for low-spin Fe^II–H₂ (see Table 2). The increased elongation of the H–H bond suggests an even stronger dative bonding for low-spin Ni^II than for low-spin Fe^II. This is believed to be due to a larger field acting on H₂ for low-spin Ni^II due to the smaller ionic radius. The inability of 3d¹⁰ Zn^II to provide this bonding situation is the reason why no intermediate H₂ moiety is found for this ion. To emphasize the difference between occupied and unoccupied e^*_g orbitals further, we note that neither high-spin 3d⁶ Fe^II nor high-spin 3d⁵ Mn^II possess any TM–H₂ local minimum along the reaction coordinate considered.

Fig. 8 Depicted are the hydride reactant structures: (a) for Fe^II low-spin, (b) for Ni^II high-spin and (c) for Ni^II low-spin. Also displayed are the intermediate TM–H₂ structures: (d) for Fe^II low-spin, (e) for Ni^II high-spin and (f) for Ni^II low-spin. Energy for the structures can be seen in Fig. 7. Fe^II and Ni^II high-spin have an octahedral coordination, while Ni^II low-spin displays a square planar coordination.

Table 2 Bond distance within the TM–H₂ intermediate structure. The distance between the two hydrogen atoms in the hydrogen molecule in the gas phase is 0.748 Å

	TM–HI [Å]	TM–HII [Å]	HI–HII [Å]
Fe^II low-spin	1.573	1.560	0.815
Ni^II high-spin	1.709	1.682	0.778
Ni^II low-spin	1.494	1.514	0.907

---

An apparent exception to the rule is provided by high-spin 3d⁸ Ni^II–H₂ (see Fig. 8b and d). However, when the H–H bond distance was inspected, only a slight deviation from that of free H₂ was found (see Table 1). Rather than dative bonding between TM and H₂, the molecule remains at the TM site because the oxy-hydroxide ligands do not provide sufficient power to cause the H₂ molecule to detach into the confining hydroxylated interface. This is consistent with high-spin Ni^II displaying the longest TM–H distances, which corresponds to the weakest Coulomb field. These findings are consistent with the resulting endothermicity for the hydrogen evolution reaction (HER) for high-spin Ni^II (see Fig. 7); while both high- and low-spin Ni^II display endothermicity for the HER, the natures of the Ni^II–H₂ moieties are qualitatively different.

Finally, the analogy between low-spin Fe^II and low-spin Ni^II is further substantiated by comparing the corresponding energy changes during TM–H₂ decomposition, whereby H₂ is released and the oxygen coordination sphere of the corresponding TM^II is completed. In both cases this reaction step becomes exothermic by 0.6 eV (see Fig. 7).

III.d. Correlation between hydride–proton recombination energetics and HPUF: implications concerning of nickel

The hydride–proton recombination pathway for hydrogen evolution having been mapped, a connection is made between the experimental observations and the emerging mechanistic interpretation. The correlation observed between HPUF and reaction energy changes, rather than activation energies, suggests the HPUF to be essentially of thermodynamic origin rather than due to kinetics. Thus, instead of controlling reaction barriers, the decisive effects of various transition metal ions on the overall hydrogen evolution reaction are determined by the stabilities of the grain boundary hydride intermediates relative to the H₂ molecule released into the grain boundary. Let the effective potential drop be ∼1.0 eV per H₂. This number is taken from the fact that Ti^III decorated grain boundaries display negligible HPUF (see Fig. 3). Thus, we arrive at the residual net drive, U, for hydrogen evolution inside the hydroxylated interface:

U ≈ 1.0 eV/2e⁻ = 0.50 V. (1)

Now, let the charge associated with the oxide formation due to hydrogen evolution and with the hydrogen pick-up, be Q_HE and Q_HPU, respectively:

Q_tot = Q_HPU + Q_HE. (2)

From the definition, we have

where HEF, hydrogen evolution fraction, is the fraction of water associated protons which are converted to H₂. Eqn (3) allows us to arrive at the observed correlation by acknowledging that

Having determined the correlation between HPUF and the energy changes for hydride–proton recombination, the detrimental impacts of Ni^II or Co^II in the grain boundary may now be understood more fully. Indeed, the harm caused by these ions is dual, in that besides reluctance to release H₂ (Fig. 3 and 7), a “back-door” mechanism for HPU is also provided. Hence, complementary to the endothermicity of the hydride–proton recombination energy changes for Ni^II or Co^II associated hydrides, a priori Co^II or Ni^II decorated grain boundaries display an affinity to any H₂ present in the grain boundary (possibly released from an Fe^II site) to form an Ni^II or Co^II associated hydride in conjunction with a hydroxide proton.

This is illustrated in Fig. 9. In step (A)–(C) the detailed dependence of formation of H₂ on the transition metal is repeated (Fig. 3 and 7). The subsequent step, (C)–(A), demonstrates how Ni^II and Co^II become sinks for the H₂ released.

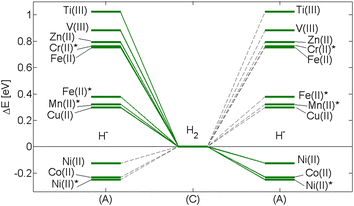Fig. 9 Data from Fig. 3 and 7 are merged in order to illustrate the detrimental impacts of Co^II or Ni^II when present in any complex zirconium alloy, i.e. beyond the binary alloys. Reaction step (A)–(C) describes the energy changes for H₂ formation. Reaction step (C)–(A) is to emphasize the detrimental impact of Ni^II, Co^II and Ni^II* on the fate of H₂. Once H₂ encounters any of these ions, it is converted back to the corresponding Ni^II, Co^II and/or Ni^II* associated hydride in conjunction with a hydroxide proton. Asterisk indicates high-spin state.

IV. Concluding remarks

A hydrogen evolution reaction, HER, mechanism in a hydroxylated zirconia grain boundary was identified, by which H₂ is formed by hydride–proton recombination. This reaction occurs between hydroxide associated protons and transition metal associated hydrides. Characteristic intermediates along this reaction coordinate were described. A similar mechanism for hydrogen evolution was recently proposed for a nickel electrocatalyst supported by seven-membered cyclic diphosphine ligands containing one pendant amine, with the Ni supporting the hydride and the amine providing the proton in the hydride–proton recombination reaction.¹⁴ Moreover, while a di-hydride intermediate was postulated for the Ru catalysed dehydrogenation of methanol,¹⁵ it is conceivable that the hydride–proton recombination reaction is also applicable here. Thus, common ground is implied for the modelling of properties relevant to water induced corrosion of zirconium based alloys and of electrochemical (reverse) fuel cells.

In this way, density functional theory was employed to model the impacts of all 3d elements on the cathode process for the water induced oxidation of zirconium alloys. The robustness of the grain boundary model was also assessed. A major finding of the present study is that the energy change of the HER is determined by the competition for a site in the coordination shell of a transition metal additive, i.e. between a coordinating hydride and an incoming oxygen ion; this is reminiscent of the redox process of NiFe hydrogenase.¹⁶

The energy changes of the HER inside a grain boundary were analysed and the release of H₂ was found to result from a “squeezing” process. Repeatedly, the electron population in the corresponding e^*_g was found to be decisive, i.e. both for the energy changes and for the presence of a bound TM–H₂ intermediate. Consequently, sensitive dependence of the HER on the choice of spin state is observed when the different spin states cause different e^*_g occupations.

The correlation observed between hydrogen pick-up fraction and hydrogen evolution energy changes was discussed; it indicates a purely thermodynamic origin. Dual causes were identified for the detrimental impacts of nickel and cobalt on hydrogen pick-up in zirconium alloys.

Acknowledgements

The Swedish Research Council, Westinghouse Electric Sweden, Sandvik Materials Technology, Vattenfall and the EPRI (Electric Power Research Institute) are gratefully acknowledged for financial support.

References

1. M. Lindgren, G. Sundell, I. Panas, L. Hallstadius, M. Thuvander and H. O. Andrén, in Zirconium in the Nuclear Industry: Seventeenth International Symposium, ed. R. J. Comstock, ASTM and W. Conshohocken, 2013, tentatively accepted for publication.
2. N. Ramasubramanian and P. V. Balakrishnan, in Zirconium in the Nuclear Industry: Tenth International Symposium, ed. A. M. Garde, E. R. Bradley, ASTM and W. Conshohocken, 1994, vol. 1245, pp. 378–399.
3. G. Sundell, M. Thuvander and H. O. Andrén, Corros. Sci., 2012, 65, 10–12.
4. B. G. Parfenov, V. V. Gerasimov and G. I. Venediktova, Corrosion of Zirconium and Zirconium Alloys (Korroziya tsirkoniya i ego splavov), Atomizdat, Moskva, 1976.
5. B. Cox, in Advances in Corrosion Science and Technology, ed. M. G. Fontana and R. W. Staehle, Plenum, N. Y., 1976, vol. 5, pp. 173–391.
6. J. L. Hodeau, M. Marezio, A. Santoro and R. S. Roth, J. Solid State Chem., 1982, 45, 170–179.
7. A. Orera, A. Kuhn and F. G. Alvarado, Z. Anorg. Allg. Chem., 2005, 631, 1991–1993.
8. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
9. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
10. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
11. Materials Studio 6.0, Accelrys Inc..
12. M. Busch, E. Ahlberg and I. Panas, Phys. Chem. Chem. Phys., 2011, 13, 15069–15076.
13. M. Busch, E. Ahlberg and I. Panas, Catal. Today, 2013, 202, 114–119.
14. M. P. Stewart, M.-H. Ho, S. Wiese, M. L. Lindstrom, C. E. Thogerson, S. Raugei, R. M. Bullock and M. L. Helm, J. Am. Chem. Soc., 2013, 135, 6033–6046.
15. M. Nielsen, E. Alberico, W. Baumann, H. J. Drexler, H. Junge, S. Gladiali and M. Beller, Nature, 2013, 494, 85–89.
16. H. S. Shafaat, K. Weber, T. Petrenko, F. Neese and W. Lubitz, Inorg. Chem., 2012, 51, 11787–11797.

---