The hydration structure of Cu²⁺: more tetrahedral than octahedral?

Abstract

A comprehensive multi-technique approach has been used to address the controversial question of the preferred geometric form of the Cu²⁺ aqua-ion hydration shell. A combination of H/D isotopic substitution neutron scattering and X-ray scattering has been used to refine atomistic models of 0.5 m and 2.0 m solutions of Cu(ClO₄)₂, that have also been constrained to simultaneously reproduce detailed local structure information about the cation environment obtained by X-ray Absorption spectroscopy. The adoption of the Empirical Potential Structure Refinement (EPSR) technique as a single unified analytical framework minimises the chances for biasing the result in favour of a specific pre-conceived outcome. The results are consistent with an average coordination for each Cu²⁺ ion of 4.5 ± 0.6 water molecules that matches the more recent picture of five-fold coordination in a 2.0 m solution, but interestingly this combined study highlights that the preferred local geometry of the ion sites is found to have a mixed character of tetrahedral, trigonal bipyramidal and octahedral components. A further point to note is that this new model adds support to a largely ignored result in the literature relating to the linear electric field effect induced g-shifts observed in the electron paramagnetic resonance spectra of glassy Cu²⁺ complexes (Peisach and Mims, Chem. Phys. Lett., 1976, 37, 307–310) that first highlighted the importance of tetrahedral distortions in the cation's hydration shell structure.

---

1 Introduction

In 2001 a state-of-the-art neutron diffraction experiment using ⁶⁵Cu and ⁶³Cu isotopic substitution supported by a first principles molecular dynamics simulation¹ reported a result that suggested that the traditional understanding of the structural chemistry of the Cu²⁺ aqua-ion may be seriously at fault. The controversial finding was that in a 2.0 m solution of Cu(ClO₄)₂, the expected Jahn–Teller distorted octahedral hydration shell of the cation, formed by six coordinating water molecules, was not the most probable aqua-ion structure, but this was instead a five-fold coordinated species of non-octahedral geometry. The result appeared to be quite unambiguous but as it was markedly different to the generally accepted picture of much of the solution chemistry of copper, the work stimulated a number of new studies leading to supporting^2,3 or counter claims.⁴

The issue of the hydration structure and preferred coordinating ligand arrangements of the Cu²⁺ ion has a long history, and the system has been widely studied by a range of spectroscopies^5–12 and radiation scattering techniques,^13–15 as its properties underpin many fundamental chemical,^16–18 environmental^19,20 and biological²¹ issues. In much of the work prior to 2001, the implicit assumption of the majority of authors was that the geometry of the Cu²⁺ environment in aqueous solution was fundamentally octahedral arising from well known crystallographic results.^22,23 For example in the early NMR (nuclear magnetic resonance) work of Swift and Connick⁷ they clearly state, following a brief discussion of the structure of crystalline CuSO₄·5H₂O, that “It is also thought that in aqueous solution the Cu²⁺-ion coordinates with six water molecules to form such a distorted octahedron. This hypothesis can be used to explain the NMR data.” It therefore seems reasonable to ask if so much of the early work on the structure of the aqua-ion could indeed have been incorrect on so basic an issue?

To address this point, many questions immediately spring to mind and include: (1) Is it appropriate to use crystallographic results to explain liquid state structure? (2) What is the sensitivity of the local structure in the solutions to the concentration of species present? (3) How are the findings of the experimental techniques used to investigate the solution structures, affected by their differing sensitivities? (4) Has the interpretation of the results been excessively coloured by the prevailing understanding of copper chemistry at the time the experiments were performed and analysed?

The first question is essential as it appears as if crystallographic results have largely defined the general understanding of structure of the ion. The second question arises from the fact that the controversial study of 2001¹ was performed using a difficult experimental technique that is only possible to apply to quite concentrated systems. This forces us to consider whether the result would be the same for more dilute solutions of the Cu²⁺ aqua-ion. The third question has been highlighted in a number of studies as an important consideration both prior to, and following, the publication of the disputed result.^3,4,6,12 Not only as a wide range of coordination numbers can be found in the literature, ranging from four-fold¹² to six-fold¹⁰ coordination, but equally techniques such as EPR (electron paramagnetic resonance) require the ions to be frozen as glassy structures in glycerine-water solutions to induce sufficient structure in the experimental signal to allow an evaluation of their local structural environment,^5,8 which could perturb the structure compared to the original solution. Lastly, the fourth question highlights an issue that probably affects most studies, but would potentially be more significant if only a single technique is used to evaluate a hypothesis.

To resolve these issues, and to attempt to rationalise the large body of experimental data on the geometric structure of the Cu²⁺ aqua-ion, we have chosen to adopt a recently developed method for building comprehensive atomistic structural models that are consistent with neutron and X-ray scattering data. In consideration of question one, this methodology has no requirement for long-range symmetry in the structural models and thus avoids any crystallographic assumptions. The resulting models are constrained by fundamental issues such as the atomic density and molecular structure of the components, but also by a requirement to reproduce chemically specific X-ray absorption spectra that are known to be highly sensitive to the local structure of the cation environment.²⁴ By requiring model agreement with a range of experimental probes that are analysed within a single coherent and unbiased analytical framework, that is capable of generating any of the proposed models should the data require it, we hope to avoid as much as possible the difficulties associated with questions three and four, and by performing the study at two concentrations, 0.5 m and 2.0 m, to also answer question two.

2 Experiment

To allow us to construct the most comprehensive atomistic models of the 0.5 and 2.0 molal Cu(ClO₄)₂ solutions of interest, it was necessary to combine the results of three structural probes with complementary sensitivities. In this study, we combine (i) neutron scattering with hydrogen-deuterium isotopic substitution to probe the structure of the bulk solvent water network,²⁵ (ii) X-ray scattering to probe the intermediate range hydration structure around the heavier elemental components (copper and perchlorate ions), and (iii) Extended X-ray Absorption Fine Structure (EXAFS), to provide very accurate local structure information on the copper ion sites. It is worth stating at this point that the perchlorate moiety was chosen as the counter ion in this study as it is known not to complex with the cation at the investigated solution concentrations. Although we do not discuss the counter ions in the subsequent sections, no evidence in the structural models was found for contacts <∼5 Å between the Cu²⁺ and the Cl sites of the (ClO₄)⁻ ions. This is consistent with the assumption that no counter ions are present in the direct Cu²⁺ hydration shell.

2.1 Neutron scattering

Neutron scattering data were collected at the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples (SANDALS) at the ISIS pulsed neutron source of the Rutherford Appleton Laboratory, UK. For each solution concentration approximately 3 cm³ of three isotopically distinct but otherwise identical samples were prepared by weight, by dissolving an appropriate amount of Cu(ClO₄)·6H₂O (Sigma-Aldrich 98%) in H₂O, D₂O (Sigma-Aldrich 99.9 atom% D) and a 1 : 1 H₂O : D₂O mixture to give samples with a Cu²⁺ ion to water molecule ratios of 1 : 111 (0.5 m) and 1 : 27.75 (2.0 m). To prevent hydrolysis of the samples each solution was acidified to a pH of ∼1 by the addition of a small quantity (≈0.01 g) of concentrated (65%) HNO₃. For the neutron scattering measurements, 1.4 cm³ of each of the solutions was transferred to null scattering Ti_0.676Zr_0.324 alloy cells, where the cell walls of 1 mm thickness define an internal sample volume of dimensions 1 mm thickness × 35 mm width × 40 mm height. The filled cells were loaded onto the instrument's automatic sample changer and the temperature of each sample was controlled to be 25 ± 0.1 °C.

After collection, the experimental data were corrected for background scattering, absorption, multiple scattering, and normalized to the scattering from a vanadium standard using the Gudrun routines that are based on the algorithms of the widely used ATLAS package.²⁶ The resulting functions were corrected for the self and inelastic scattering contributions following the methods of Soper and Luzar²⁷ and the interference differential scattering cross sections F(Q) shown in Fig. 1 are obtained. F(Q) is defined as

Q is the magnitude of the momentum transfer vector of the scattering process, defined as Q = 4π sin θ/λ where λ is the wavelength of the incident neutron and θ is half the scattering angle, c_α and c_β are the concentrations of the atomic species α and β, whilst b_α and b_β are their neutron scattering lengths.²⁸ S_αβ(Q) are the partial structure factors representing pairwise structural correlations between the atoms and δ_αβ is the Kronecker delta function to avoid double counting the correlations between like atomic species. S_αβ(Q) is related to the corresponding real space partial pair distribution functions, g_αβ(r), by a Fourier transform weighted by the atomic density, ρ, of the system under study.If only a single neutron scattering measurement is made, it is not possible to separate all of the partial structure terms that contribute to the interference differential scattering cross section and a composite structure factor and corresponding pair distribution function is obtained. Table 1 shows the relative contributions of the various partial distribution functions to the total interference differential scattering cross section for the 0.5 m and 2.0 m solutions of Cu(ClO₄)₂ in D₂O. This clearly demonstrates that the sensitivity of the neutron scattering data on this solution is almost entirely weighted towards the structure of the solvent itself, with the cation hydration (Cu–OW and Cu–HW correlations) only contributing a total of ≈2.5% to the signals in the D₂O F(Q) of the two solution concentrations.

Fig. 1 The EPSR model fits (red solid line) and fit residuals (blue dotted line) to the isotopic samples of 0.5 m (left panel) and 2.0 m (right panel) Cu(ClO₄)₂ solutions prepared from D₂O, HDO, and H₂O measured by neutron scattering, and the Cu(ClO₄)₂ in H₂O solutions measured by X-ray scattering. The experimental data are shown as black circles. For clarity the model fits and experimental data are vertically offset by 0.0, 0.75, and 1.5 units, for the D₂O, HDO, and H₂O solutions respectively, and 2.25 units for the X-ray data, while the corresponding fit residuals are vertically offset by −0.25, 0.5, 1.25 and 2.0 units. The error bars in the experimental data are approximately given by the size of the data point symbols.

Table 1 Relative contributions of the partial structure factors to the total interference differential scattering cross section of 0.5 m and 2.0 m solutions of Cu(ClO₄)₂ in D₂O measured by neutron scattering or X-ray scattering at Q = 0 (omitting the very small structural contributions from the ≈0.01 g of HNO₃ used to acidify the solutions and that contribute to the pair correlation terms summing to ≈0.5% and ≈1% to the neutron and X-ray measurements respectively)

Pair Correlation	Neutron Weight (%)		X-ray Weight (%)
	0.5 m	2.0 m	0.5 m	2.0 m
Cu–Cu	0.018	0.026	0.054	0.510
Cu–Cl	0.089	0.128	0.128	1.196
Cu–O	0.217	0.309	0.240	2.251
Cu–OW	0.752	1.073	3.331	7.808
Cu–HW	1.583	1.636	0.833	1.952
Cl–Cl	0.111	0.158	0.075	0.701
Cl–O	0.538	0.768	0.281	2.639
Cl–OW	1.866	2.663	3.906	9.154
Cl–HW	3.930	4.059	0.976	2.288
O–O	0.652	0.930	0.265	2.434
O–OW	4.524	6.454	7.352	17.23
O–HW	9.525	9.838	1.838	4.308
OW–OW	7.846	11.19	51.00	29.88
OW–HW	33.04	34.12	25.50	14.94
HW–HW	34.78	26.01	3.188	1.868

---

2.2 X-ray scattering

X-ray scattering data were collected from samples of 0.5 m and 2.0 m solutions of Cu(ClO₄)₂ in H₂O, prepared identically to the neutron scattering samples, but contained in 2 mm quartz glass capillaries of wall thickness 0.1 mm. The data were collected at room temperature (21 ± 1.0 °C) using an X'pert Pro diffractometer (Panalytical, Almelo, The Netherlands) taking K_α radiation from a Rh-filtered Ag-anode (λ = 0.5609 Å) operating at 60 kV. The data were corrected for polarization and the Bremsstrahlung component of the X-ray beam, absorption, multiple scattering, fluorescence and Compton scattering from the sample, and air background and empty capillary scattering. Finally the reduced data are scaled to oscillate about the self scattering from the sample and normalized to the single atom scattering. The resulting X-ray interference differential scattering cross section is given by:and is shown along side the neutron data in Fig. 1 I(Q) is the X-ray scattering after corrections and scaling to oscillate about the sample self scattering which is given by the summation in the denominator in eqn (3), c_α is the concentration of atomic species α and f_α is the corresponding atomic form factor.

For comparison with the neutron scattering structural sensitivity, the relative structural contributions to the X-ray total interference differential scattering cross sections are also given in Table 1 As X-rays scatter from the electron density in the sample, the weightings are identical for all the isotopic solutions but what is clearly evident from the table is that the F_X(Q) are considerably more sensitive to the water oxygen correlations and the structural contributions from ionic hydration.

2.3 EXAFS and XANES spectroscopy

X-ray absorption spectroscopy data were collected from 0.5 m and 2.0 m solutions of Cu(ClO₄)₂ in H₂O using the scanning branch of the newly constructed I20 versatile X-ray absorption spectroscopy beamline at Diamond Light Source, Oxfordshire, UK.²⁹ At the time of the measurement the Diamond synchrotron was operating at a ring energy of 3 GeV in a 10 min top-up mode for a ring current of 300 mA. The beamline is equipped with a four bounce crystal monochromator working with Si(111) crystals, and harmonic rejection was achieved through the use of two Rh coated mirrors operating at an incidence angle of 5.0 mrad. The absorption spectra were measured in transmission geometry at the copper K absorption edge (8979 eV). The sample was contained in a 0.5 mm light path PTFE cell with 25 μm thick windows made from Kapton foil and the measurements were made at room temperature (22 ± 1.0 °C). The incident and transmitted beam intensities were measured using two 30 cm long ion chambers optimised using a helium-argon gas mixture to absorb 20% and 80% of the beam in I₀ and I_t respectively. The extracted EXAFS signals are shown in Fig. 2 and the near-edge (XANES) region is shown in Fig. 3, where the inset panel highlights the energy region between 8960 eV and 8990 eV, to show the dipole forbidden (electric quadrupole)³⁰ 1s → 3d transition feature at 8977.5 eV that has been correlated with the presence of four-fold coordinated, from square-planar to tetrahedral, coordination sites for Cu²⁺ ions.^30–32

Fig. 2 Experimental data (black circles) and EPSR model predictions (solid red lines) for the Cu K- edge EXAFS spectra for 0.5 m (left panel) and 2.0 m (right panel) Cu(ClO₄)₂ acidified aqueous solutions. The EXAFS signals were calculated using FEFF8³³ with ΔE₀ set to 2 eV and 5 eV for the 0.5 m and 2.0 m solutions respectively. In both cases, FEFF8 evaluated S²₀ to be 0.95.

Fig. 3 Comparison of the normalised Cu K-edge X-ray Absorption Near Edge Structure (XANES) for the 0.5 m and 2.0 m aqueous solutions of Cu(ClO₄)₂. The inset panel highlights the energy region between 8960 eV and 8990 eV, to show the dipole forbidden 1s → 3d transition feature at 8997.5 eV that has been correlated with the presence of four-fold coordinated, from square-planar to tetrahedral, coordination sites for Cu²⁺ ions.^30–32

Sano et al.³² performed a detailed experimental investigation of the intensity of this feature in a range of square planar to tetrahedral Cu–Cl ligand complexes as a function of the ligand plane–Cu²⁺–ligand plane dihedral angle. They found that the feature increased from a magnitude of 0.009 ± 0.003 to 0.023 ± 0.003 in the normalised spectrum, as the local geometry was varied from square planar (dihedral angle close to 0°) to tetrahedral (dihedral angle close to 70.53°). Although this feature is clearly in the solution data, we cannot directly use the published findings³² to estimate the local copper environment geometry. This is because the Cu²⁺ ions in the aqueous solutions of Cu(ClO₄)₂ are coordinated by oxygen and not chlorine, and this change can have a marked influence upon the magnitude of the effect, i.e. the resulting intensities and positions of the quadrupolar transition. However, for completeness we do include in the supporting information† a quantitative comparison of the XANES region of the solution data with two crystalline systems in which copper is octahedrally coordinated by six oxygen atoms.

A second key piece of information that can be taken from the XANES region of the X-ray absorption data relates to the remarkable similarity between the spectra collected for the 0.5 m and 2.0 m solutions. The form of the XANES features is strongly correlated with the geometry of the first coordination shell of atoms around the photo-absorbing atomic sites, and consequently the remarkable equivalence of the spectra shown in Fig. 3 is an unambiguous indicator that tells us to expect geometrically similar local structural environments for the Cu²⁺ ions in both the 0.5 m and 2.0 m solutions, in spite of the obvious differences seen in the X-ray diffraction data (Fig. 1).

3 Structure refinement

To maximise the amount of structural information that can be extracted from the complementary sets of experimental data, we have applied the technique of Empirical Potential Structure Refinement developed by Soper.^34,35 This method uses the available experimental scattering data to generate a set of interatomic perturbation potentials that are used to drive a classical Monte Carlo simulation of the system, into structural configurations that agree with the driving F(Q)s. The modelling framework constrains the resulting three dimensional atomistic structural model to be consistent with the basic physico-chemical constraints of the system's bulk atomic density and the known conformations of the molecular units from which it is built.

Once an acceptable model has been built, that reproduces the driving experimental structure factors, it is then possible to interrogate the structure to obtain an estimate of any of the atomic partial pair distribution functions, despite the fact that only a subset are fully constrained by the experimental data. However, it is important to recognise that any pair distribution functions not heavily constrained by the scattering data will primarilly reflect the prior assumptions made for the underlying interatomic interaction potentials, the packing requirements that result from the imposed basic geometries of the molecules and the requirement that the model conforms to the known bulk density of the system under study. In spite of this, provided that these three primary constraints are reasonable, the models can provide a useful guide for improving our general understanding of how the structure of the system gives rise to its observed physical and chemical properties.

To model the 0.5 m and 2.0 m solutions of Cu(ClO₄)₂, models containing (a) 10 Cu²⁺ ions, 20 (ClO₄)⁻ ions and 1110 water molecules and (b) 40 Cu²⁺ ions, 80 (ClO₄)⁻ ions and 1110 water molecules, were constructed in cubic boxes of side lengths ∼32.6 Å and ∼33.6 Å respectively. These dimensions correspond to the measured atomic density of the solutions of 0.1 atoms Å⁻³. To allow for the small amount of nitric acid added to acidify the solutions to pH ∼ 1, an additional two H⁺ and two NO₃⁻ ions were added to the models. The Lennard-Jones and charge parameters used to describe the reference potentials for the model components are given in Table 2. The parameters for the reference potential used for the water molecules in the simulation are taken from the SPC/E model of Berendsen et al.³⁶

Table 2 Lennard-Jones and charge parameters used in the simulation of Cu(ClO₄)₂ solutions. Within the EPSR model, these are combined using the Lorentz–Berthelot mixing rules σ_αβ = 0.5[σ_α + σ_β] and ε_αβ = [ε_αε_β]^0.5. Note that the coulomb charges on the ionic components used in the model were scaled down by a factor of 2 to increase the observed levels of disorder in the Cu²⁺ ion hydration shell to better match the experimental EXAFS data in the time of the simulation by effectively speeding up the rate at which the simulation can explore the configurational phase space

Atom	ε [kJ mol^−1]	σ [Å]	q [e]	Mass [amu]
Cu	0.1250	1.780	+1.0000	63.5
Cl	0.5660	4.190	0.0000	36
O	0.8000	2.960	−0.1250	16
OW	0.6500	3.160	−0.8476	16
HW	0.0000	0.000	0.4238	2
HH+	0.0075	1.000	+0.5000	2
NNO3^−	0.7000	3.250	0.0000	14
ONO3^−	0.8000	2.960	−0.1667	16

---

These reference potentials are first used to equilibrate the Monte Carlo simulation of the solution, after which the EPSR algorithm is turned on and the experimental data is used to derive the set of perturbation functions that will then drive the structural configurations into consistency with the scattering data. Once this is achieved the simulation is continued and ensemble average information is accumulated from periodic snapshots of the structural configurations of the atoms and molecules. This data can include the partial distribution functions, bond angle distributions, coordination number histograms etc.

The labels assigned to the key atomic sites are Cu for the Cu²⁺ cations, Cl and O for the chlorine and oxygen atoms of the (ClO₄)⁻ anions, OW and HW for the water oxygen and hydrogen sites, and H_H⁺, N_NO3⁻ and O_NO3⁻ for the small number of hydrogen ion and nitrate ion sites that account for the acidification of the investigated solutions. Inside the models the Cu²⁺ cations are incorporated as free ions, whilst the (ClO₄)⁻ ions are incorporated as tetrahedral charged molecular units characterised by an average Cl–O distance of 1.42 Å and a O–Cl–O angle of 109.47°. The water molecules are characterised by an average OW–HW distance of 0.976 Å and a HW–OW–HW angle of 104.5° and lastly, the H⁺ and NO₃⁻ ions are incorporated as free cations, and planar molecular ions characterised by an average N_NO3⁻–O_NO3⁻ distance of 1.21 Å and a O_NO3⁻–N_NO3⁻–O_NO3⁻ angle of 120°.

Fig. 1 shows the fits and fit residuals for the EPSR model to the 0.5 and 2.0 molar Cu(ClO₄)₂ solutions, compared with the experimental neutron scattering data from the three isotopic solvent variants, H₂O, D₂O and HDO and the X-ray scattering data.

3.1 Incorporating the EXAFS information

As the local structural environment of the Cu²⁺ cation is very weakly weighted in three out of the four scattering patterns used to drive the EPSR procedure, the information in the EXAFS spectrum proves particularly useful for optimizing the choice of σ in the Cu²⁺ reference potential used to seed the model.^24,37 Essentially, once the EPSR model has been refined, the simulation is continued and snapshots of the local environments around the Cu²⁺ ions, to a radius of 6 Å, are periodically extracted. These are then input into an EXAFS signal calculation (FEFF 8),³³ and the results ensemble averaged.²⁴

Although the EXAFS information is not directly used to drive the structure refinement, i.e. the EPSR EXAFS estimate is not so much a fit but rather a prediction, it provides a stringent test of how effectively the cation is incorporated into the bulk structural model. In each model >10 000 Cu sites were investigated to generate the ensemble average signals shown in Fig. 2. The only free parameter in the EXAFS signal calculations is ΔE₀, that is used to account for the offset of the energy scale zero point and this essentially is used to align the first oscillation in the theoretical EXAFS signal with the data. It has a rapidly decreasing effect on the phasing of the oscillatory features occurring at higher k-values. This was found to be 2 eV for the 0.5 m system and 5 eV for the 2.0 m system. This variable is purely a model fitting parameter but the small difference may reflect the need to account for slightly different electronic environments in the model signal calculations arising from the markedly different ion concentrations in the two solutions. FEFF8 was used to automatically estimate the EXAFS amplitude reduction factor, S²₀, and this was found to be 0.95.

3.2 Testing the information content of the experimental data and its compatibility with proposed hydration structures

An important question to address in any structure refinement process is the sensitivity of the experimental data to the structural information that is being sought. The EPSR method is particularly advantageous in this regard as it allows for the generation of constrained models that can be used to test our preconceived ideas against the experimental data.^38–40 If all models could generate equally good fits to the scattering data, then clearly they would tell us very little about the issue of interest. In this study, a series of constrained models for the local hydration shell structure of the Cu²⁺ aqua-ion have been generated to favour octahedral, trigonal bipyramidal or either structure. These extra models allowed us to investigate the sensitivity of the scattering and spectroscopy data to the hydration shell environment, and to also benchmark our final model against the classic (octahedral) and revised (trigonal bipyramidal) structures in the current literature. The results of these test refinements are given in the supporting information† and demonstrate that the X-ray diffraction and EXAFS spectroscopy data carry critically important information on the scientific issue under consideration.

4 Results and discussion

The average hydration structure of Cu²⁺ found in the the EPSR models are best summarized in Fig. 4. This shows the Cu–OW and Cu–HW partial distribution functions, and the corresponding running coordination numbers to illustrate the number of atoms involved in each pair correlation. Clearly, on average in both the 0.5 m and 2.0 m solutions, each Cu²⁺ ion is surrounded by between 4 and 5 water oxygen atoms, centred at distance of 1.95(1) Å, and there is a corresponding shell of 8 to 10 water hydrogen atoms centred at a distance of 2.63(1) Å. It is interesting at this point to compare these results with the original ⁶⁵Cu and ⁶³Cu neutron scattering with isotopic substitution results of Salmon et al.¹⁵ who also studied a 2.0 m solution of Cu(ClO₄)₂, taking care to use the same criteria for evaluating the coordination numbers i.e. integration of g_CuOW(r) between 1.6 Å ≤ r ≤ 2.2 Å and g_CuHW(r) between 2.2 Å ≤ r ≤ 3.1 Å, corresponding to the positions of the minima in the first order difference g(r). Salmon et al. obtained a value for n_O of 4.1 ± 0.3, and a value for n_H of 11.3 ± 0.7, which compares with 4.0 ± 0.1 for n_O and 9.9 ± 0.1 for n_H, determined from the current EPSR model. These results show the remarkable similarity in the findings, in particular when one takes into account that the earlier first order difference study could not unambiguously assign the extent of hydrogen atom coordination in the 2.2 Å ≤ r ≤ 3.1 Å range.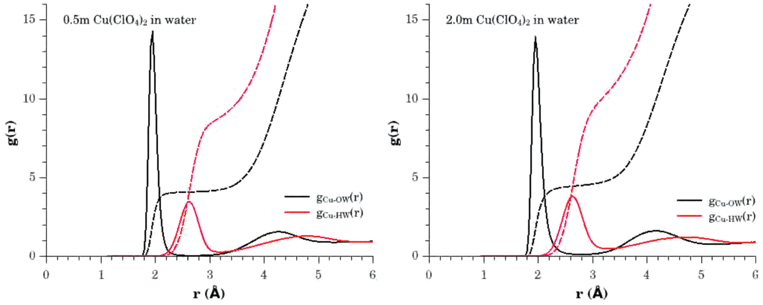

Fig. 4 Pair distribution functions and running coordination numbers relating to the hydration of the Cu²⁺ hydrated ion in 0.5 m (left panel) and 2.0 m (right panel) aqueous solutions of Cu(ClO₄)₂. g_Cu–OW(r) (black solid line), g_Cu–HW(r) (red solid line). The corresponding running coordination numbers are given by the broken lines of the same colour.

However, a particular advantage of the EPSR refinement results is that the resulting atomistic model is generated through ensemble averaging of configurations that are consistent with the experimental data. Consequently more information on the distribution in the number of neighbouring water molecules can be extracted and this is shown in the lower panel of Fig. 5. This tells us that in the 0.5 m solution the dominant hydrated Cu²⁺ species involve 4 neighbouring water molecules with a small fraction of 5 coordinated species, whilst in the 2.0 m solution the distribution shifts to display a reduction in the number of 4 coordinated cations, with a significant growth in the number of 5 coordinated species and small number (≈5%) of 6 coordinated cations. From these distribution functions we obtain an estimation of the mean coordination number of Cu²⁺ to be 4.1 ± 0.3 water molecules in the 0.5 m solution, and 4.5 ± 0.6 water molecules in the 2.0 m solution, based on an interrogation of ≈10 000 Cu²⁺ sites in the models.

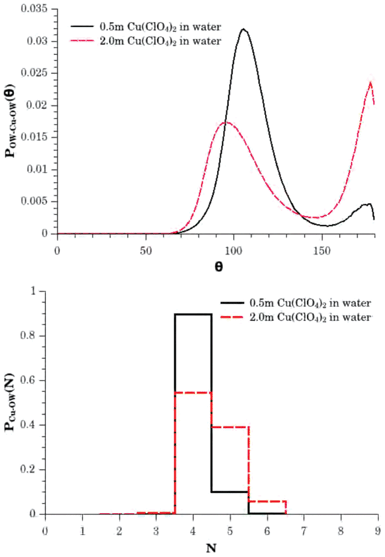Fig. 5 The upper panel shows the first shell OW–Cu²⁺–OW bond angle distributions for 0.5 m (solid black line) and 2.0 m (broken red line) aqueous solutions of Cu(ClO₄)₂. These functions illustrate the relative probabilities of finding 80° to 130° and 150° to 180° configurations consistent with the presence of a range of local hydration shell geometries including tetrahedral, trigonal bi-pyramidal and octahedral environments. The lower panel shows the Cu²⁺–O_water hydration histograms for the 0.5 m (solid black line) and 2.0 m (broken red line) solutions, showing the relative probabilities for finding a water molecule within the first hydration shell, i.e., for the water oxygen atom to be within the distance range between 1.75 Å and 2.80 Å of the cation. These distribution functions correspond to mean coordination numbers of 4.1 ± 0.3 and 4.5 ± 0.6 water molecules in the 0.5 m and 2.0 m solutions respectively.

For the 2.0 m solution, these findings are clearly in agreement with the work of Pasquarello et al.¹ where they first highlighted the mean coordination number of 5 water molecules and where their value was obtained by integrating their measurement of the running coordination number to a distance of 3.02 Å, with an error bar of ±0.15 water molecules estimated from the statistical noise in the neutron scattering data. For the 0.5 m solution, the outcome of the multiple dataset refinement seems to indicate a slightly lower average coordination number and this now deserves some attention.

As mentioned earlier, the identical form of the XANES spectra for the 0.5 m and 2.0 m solutions is indicative of geometrical equivalence of the local environments experienced by the Cu²⁺ ions in each solution. How, then, can we rationalise this with our finding that the average coordination number of the Cu²⁺ ion is slightly different between the two solutions?

First, in the upper panel of Fig. 5 we show the OW–Cu²⁺–OW bond angle distributions for the two solutions, where a water molecule is considered to be bonded to the Cu²⁺ ion if it is found within a distance of 1.75 Å ≤ r ≤ 2.80 Å. For the 2.0 m solution we see two main peaks in this distribution centred at ≈95° and ≈177°. In the 0.5 m solution, the higher angle feature still peaks at the same position but is significantly smaller in intensity, whilst the lower angle feature shifts to higher angles and peaks at ≈105°. Clearly, these distribution functions are highlighting differing probabilities for a range of ligand distributions about the ion. Tetrahedral distributions would result in a preference for 109.5°, whilst for trigonal bi-pyramidal distributions, the dominant angles would be 120°, 90° and 180°, and for octahedral distributions, 90° and 180°. From this perspective, the increasing probability of finding the higher angle feature at ≈177° along side the concomitant reduction in the height of the lower angle peak and shift in its position to angles closer to 90°, indicates an increase in trigonal bi-pyramidal and/or octahedral configurations as the solution moves to higher concentration.

On a first consideration, the change in the bond angle distributions seems at odds with the XANES result, and this discrepancy led us to investigate the spatial density function⁴¹ for the distribution of water molecules about the Cu²⁺ ions. To do this, it is necessary to define a set of coordinate axes (x,y,z) with the origin on a Cu²⁺ ion. This however raises a challenge: As the ion is not part of a molecule, the definition of the reference frame requires us to define a virtual molecule based on the prevailing environment in which it is found.⁴² In this case we take advantage of the fact that we know that on average there are four water molecules found in the immediate local environment about each Cu²⁺ ion, and each of these water molecules is ≈1.95 Å from the ion. The first step in this task is therefore to search for a water oxygen atom in the distance range between 1.55 Å ≤ r ≤ 2.33 Å from the ion, and assign the z-axis of the coordinate reference frame to lie along the identified Cu–OW bond. Next we search for a second water oxygen atom that must satisfy the criterion of 1.55 Å ≤ r ≤ 2.33 Å for the Cu–OW distance, but also a second criterion of 2.20 Å ≤ r ≤ 3.30 Å for the distance of this second water oxygen atom from the water oxygen atom used in the definition of the z-axis. This second water oxygen site is then used to establish an orthogonal x-axis for the coordinate reference frame, and also through the general requirement for axes orthogonality, the y-axis. Once we have established the frame of reference, we can interrogate and ensemble average the spatial distribution of water molecules around each Cu²⁺ ion in the EPSR models. The generation of the spatial density functions themselves was performed through a spherical harmonic reconstruction,⁴³ where no symmetry other than a mirror plane in the x–z axis was specified to reduce the complexity of the calculation to just the real terms of the expansion.

Fig. 6 shows the results of the spatial density analysis of the local ion environments found in the 0.5 m and 2.0 m solutions. The selected probability level of ≈82% highlights the full range of spatial regions and ligand geometries found around the cations. At lower probability levels, the four major lobes are the only spatial regions identified, and indicate a strong preference of close to tetrahedral order, but as the probability levels are increased, one notes the simultaneous appearance of two lower probability features in the −x and −z directions, corresponding to partially occupied sites that would be required for creating trigonal bi-pyramidal (four high probability sites and the −z site) and distorted octahedral (all site) ligand distributions.

Fig. 6 Spatial density functions showing the top ≈82% occupation isosurfaces for water coordination of the Cu²⁺ ion. The left hand panels were generated from the EPSR model of the 0.5 m aqueous solution of Cu(ClO₄)₂ and the right hand panels from the 2.0 m solution. The upper panels show the equatorial view of the ion environment, whilst the lower panels show the corresponding polar view. The figure highlights the underlying similarity of the ion environments in the two solutions that have been investigated. In both cases the ions have a local environment characterised by four sites in a close to tetrahedral configuration that have a high probability of occupation, accompanied by an equatorial and axial site with lower probability of occupation. In total, these six spatial regions define a distorted octahedral hydration structure.

The remarkable feature is that both the 0.5 m and 2.0 m spatial density functions are very similar, with only the relative probabilities of the partially occupied sites being different. These features are slightly larger in the 2.0 m system, indicating the higher probability of finding trigonal bi-pyramidal and distorted octahedral configurations at that concentration. The finding thus explains the unambiguous observation that the XANES spectra for the investigated Cu(ClO₄)₂ solutions are the same within the very high precision of the measurement.

In highlighting the significant role played by tetrahedral configurations in the first hydration shell of the ions, the spatial density functions clearly add support to the explanation of the observed linear electric field effect induced g-shifts in the EPR spectra of frozen solutions of Cu²⁺ ions found by Peisach and Mims.⁵ They were the first to demonstrate that these shifts could be explained by tetrahedral deviations from centrosymmetry in the copper ion environments, and they theorised that this was the result of a spontaneous distortion that occurs in solution that could only be suppressed by coordinating the ion with multidentate ligands to enforce planarity through external bonds. However, their work has largely been neglected in the subsequent years.

5 Conclusions

This comprehensive experimental investigation of the structure of 0.5 m and 2.0 m Cu(ClO₄)₂ in acidified aqueous solution has highlighted the remarkable complexity of the local structure of the Cu²⁺ cation and the underlying resilience of the geometric form of the ion hydration shell. This insight has been gained through the use of three complementary experimental probes with markedly different structural sensitivities, to guide and constrain the generation of a three dimensional atomistic model. Neutron scattering has been used to obtain detailed information on the bulk solvent structure, whilst X-ray scattering provided information on general ion hydration structure and lastly, EXAFS spectroscopy provided chemically specific insight into the Cu²⁺ hydration environment. This analytical approach has allowed us to avoid the need for any prior assumptions about what structural form the ion hydration shell would adopt, and avoid the problems of limited information content specific to each technique.

It is interesting to note that this independent study, based on hydrogen/deuterium isotopic substitution, X-ray scattering and EXAFS, leads to almost identical average structural conclusions as the earlier ⁶⁵Cu and ⁶³Cu isotopic substitution studies of Salmon et al.¹⁵ That being a study that has long been accepted as a key proof in the standard octahedral hydration shell model that has prevailed in the literature for the past five decades. However, expanding the average hydration shell analysis to include the range of observed structural configurations, facilitated by the comprehensive nature of the EPSR generated model, shows strong parallels with the more recent and controversial result of Pasquarello et al.,¹ that showed each Cu²⁺ ion in a 2.0 m aqueous solution Cu(ClO₄)₂ prefers an average coordination of 5 water molecules. Both of these interpretations now however, appear too simplistic, as further detailed analysis of the range of coordination environments found for this important cation, and in particular as one moves to lower solution concentrations, highlights an underlying preference for four-fold coordination in a close to tetrahedral configuration, combined with a partial occupancy picture for two extra sites that would be more consistent with five coordinate (trigonal bi-pyramidal) and six coordinate (distorted octahedral) ligand distributions.

This suggestion of tetrahedral character is particularly intriguing in light of the largely neglected study of the linear electric field effect induced g-shifts in EPR signals performed by Peisach and Mims.⁵ Their work highlighted as far back as 1976, the presence of a non-centrosymmetric component in their data that was consistent with a significant tetrahedral distortion in the ligand distribution for a wide range of Cu²⁺ environments found in structurally disordered “solutions”.

The final interesting observation is that the presented model, established through refinement against neutron and X-ray scattering data, is capable not only of closely reproducing the view of the local Cu²⁺ ion environment seen by EXAFS spectroscopy but also of accounting for the solution concentration invariance of the XANES spectra.

Acknowledgements

The authors thank the ISIS Pulsed Neutron and Muon Facility for access to neutron beamtime on SANDALS and its laboratory based X-ray diffraction support facility, and thank Diamond Light Source Ltd for access to the versatile X-ray absorption spectroscopy beamline, I20. RB acknowledges support from the Ministerio de Economía y Competitividad of Spain.

References

1. A. Pasquarello, I. Petri, P. S. Salmon, O. Parisel, R. Car, É. Tóth, D. H. Powell, H. Fischer, L. Helm and A. E. Merbach, Science, 2001, 291, 856–859.
2. M. Benfatto, P. D'Angelo, S. Della Longa and N. V. Pavel, Phys. Rev. B: Condens. Matter, 2002, 65, 174205.
3. J. Chaboy, A. Muñoz-Páez, P. J. Merkling and E. Sanchez Marcos, J. Chem. Phys., 2006, 124, 064509.
4. I. Persson, P. Persson, M. Sandström and A.-S. Ullström, J. Chem. Soc., Dalton Trans., 2002, 7, 1256–1265.
5. J. Peisach and W. B. Mims, Chem. Phys. Lett., 1976, 37, 307–310.
6. B. R. McGarvey, J. Phys. Chem., 1957, 61, 1232–1237.
7. T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307–320.
8. W. Burton Lewis, M. Alei and L. O. Morgan, J. Chem. Phys., 1966, 44, 2409–2417.
9. T. K. Sham, J. B. Hastings and M. L. Perlman, Chem. Phys. Lett., 1981, 83, 391–396.
10. M. Nomura and T. Yamaguchi, J. Phys. Chem., 1988, 92, 6157–6160.
11. J. Garcia, M. Benfatto, C. R. Natoli, A. Bianconi, A. Fontaine and H. Tolentino, Chem. Phys., 1989, 132, 295–307.
12. A. Filipponi, P. D'Angelo, N. V. Pavel and A. Di Cicco, Chem. Phys. Lett., 1994, 225, 150–155.
13. H. Ohtaki and M. Maeda, Bull. Chem. Soc. Jpn., 1974, 47, 2197–2199.
14. M. Magini, Inorg. Chem., 1982, 21, 1535–1538.
15. P. S. Salmon, G. W. Neilson and J. E. Enderby, J. Phys. C: Solid State Phys., 1988, 21, 1335–1349.
16. Y.-Y. H. Chao and D. R. Kearns, J. Phys. Chem., 1977, 81, 666–668.
17. B. Beagley, A. Eriksson, J. Lindgren, I. Persson, L. G. M. Pettersson, M. Sandström, U. Wahlgren and E. W. White, J. Phys.: Condens. Matter, 1989, 1, 2395–2408.
18. P. D'Angelo, E. Bottari, M. R. Festa, H.-F. Nolting and N. V. Pavel, J. Chem. Phys., 1997, 107, 2807–2812.
19. M. B. McBride, Clays Clay Miner., 1982, 30, 200–206.
20. K. Dyrek, Z. Klapyta and Z. Sojka, Clays Clay Miner., 1983, 31, 223–229.
21. E. I. Solomon, Inorg. Chem., 2006, 45, 8012–8025.
22. C. A. Beevers and H. Lipson, Proc. R. Soc. London, Ser. A, 1934, 146, 570–582.
23. N. V. Mani and S. Ramaseshan, Z. Kristallogr., 1961, 115, 97–109.
24. D. T. Bowron and S. Diaz-Moreno, J. Phys. Chem. B, 2007, 111, 11393–11399.
25. J. L. Finney and A. K. Soper, Chem. Soc. Rev., 1994, 23, 1–10.
26. A. K. Soper, W. S. Howells and A. C. Hannon, ATLAS Analysis of Timeof-Flight Diffraction Data from Liquid and Amorphous Samples, Rutherford Appleton Laboratory Report, Oxfordshire, UK, 1989, vol. RAL-89-046.
27. A. K. Soper and A. Luzar, J. Chem. Phys., 1992, 97, 1320–1331.
28. V. F. Sears, Neutron News, 1992, 3, 29–37.
29. S. Diaz-Moreno, S. Hayama, M. Amboage, A. Freeman, J. Sutter and G. Duller, J. Phys.: Conf. Ser., 2009, 190, 012038.
30. J. E. Hahn, R. A. Scott, K. O. Hodgson, S. Doniach, S. R. Desjardins and E. I. Solomon, Chem. Phys. Lett., 1982, 88, 595–598.
31. G. Onori, A. Santucci, A. Scafati, M. Belli, S. Della Longa, A. Bianconi and L. Palladino, Chem. Phys. Lett., 1988, 149, 289–294.
32. M. Sano, S. Komorita and H. Yamatera, Inorg. Chem., 1992, 31, 459–463.
33. A. L. Ankudinov, B. Ravel, J. J. Rehr and S. D. Conradson, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7565–7576.
34. A. K. Soper, Chem. Phys., 1996, 202, 295–306.
35. A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204.
36. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
37. D. T. Bowron and S. Díaz-Moreno, J. Phys. Chem. B, 2009, 113, 11858–11864.
38. A. K. Soper, J. Phys.: Condens. Matter, 2005, 17, S3273–S3282.
39. A. K. Soper, J. Phys.: Condens. Matter, 2011, 23, 365402.
40. S. Diaz-Moreno, S. Ramos and D. T. Bowron, J. Phys. Chem. A, 2011, 115, 6575–6581.
41. I. M. Svishchev and P. G. Kusalik, J. Chem. Phys., 1993, 99, 3049–3058.
42. A. K. Soper, Empirical Potential Structure Refinement - EPSRshell: a user's guide. Version 18, Rutherford Appleton Laboratory Technical Report, Oxfordshire, UK, 2011, vol. RAL-TR-2011-012.
43. A. K. Soper, J. Chem. Phys., 1994, 101, 6888–6901.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra42400f

‡ These authors contributed equally to this work.

---