 Open Access Article
Open Access ArticleNanocomposite of superparamagnetic maghemite nanoparticles and ferroelectric liquid crystal†
Vladimíra
Novotná
*a,
Jana
Vejpravová
a,
Věra
Hamplová
a,
Jan
Prokleška
b,
Ewa
Gorecka
c,
Damian
Pociecha
c,
Natalia
Podoliak
a and
Milada
Glogarová
a
aInstitute of Physics, ASCR, Na Slovance 2, Prague 8, 182 21, Czech Republic. E-mail: novotna@fzu.cz
bDepartment of Condensed Matter Physics, Faculty of Mathematics and Physics, Charles University Prague, Ke Karlovu 2, 12116 Prague 2, Czech Republic
cLaboratory of Dielectrics and Magnetics, Chemistry Department, Warsaw University, Al. Zwirki i Wigury 101, 02-089 Warsaw, Poland
First published on 25th April 2013
Abstract
In this study we present a novel type of hybrid nanocomposite prepared by mixing maghemite nanoparticles and a chiral liquid crystalline compound. The hybrid system exhibits ferroelectric as well superparamagnetic properties. The impact of nanoparticles and the effect of an applied magnetic field on the ferroelectric liquid crystalline properties were established. The ferroelectric properties are conserved up to a concentration of 5.6% of maghemite. The magnetic behavior of the composites is typical for a system of superparamagnetic nanoparticles with inter-particle dipolar interactions and surface spin disorder.
1. Introduction
Liquid crystals (LCs) are a fascinating state of matter due to their self-assembling properties.1 The presence of orientational and positional order and fluidity at the same time, is inherent to liquid crystalline systems. LCs have a great technological potential due to their electro-optical properties and are widespread in electronic displays, switches, computing, control and measuring devices etc. Omnipresent in nature, they can serve as a model system for biological membranes.The development of the fabrication of particles with nanometric dimensions leads to enormous expectations. Nevertheless, the physical properties of nanoparticles can significantly differ from those of the bulk materials. Magnetic iron oxide nanoparticles, in the magnetite or maghemite phase, have been the subject of numerous studies due to their physical properties, leading to a wide range of applications in biomedicine, spintronics, catalysis and as constituents for bio-sensors.2 As a consequence of their nanometer size, the particles exhibit superparamagnetic (SPM) behavior, associated with the formation of a single-domain state. The magnetic properties of the nanoparticles (NPs) mimic the paramagnetic behavior with a collective response of the individual spins within a particle, which can be attributed to a single giant spin (superspin). The superspin undergoes a SPM relaxation, characterized by the fluctuations of the superspin vector among the directions of easy magnetization.3 This state occurs when the thermal energy, kBT, overcomes the energetic barrier EA of the nanoparticles (proportional to the particle volume, V), which is related to the magnetocrystalline anisotropy, defined for non-interacting nanoparticles by Stoner and Wohlfarth.4 An advantageous fact is that NPs in the SPM regime usually require a lower magnetic field to interact with the magnetization (superspin), in comparison with larger ferromagnetic species. In spite of the fact that the magnetic response of the iron oxide NPs is determined by their shape and size, real effects like interactions between the magnetic NPs,5 finite-size effects6 and the surface effect7 significantly modify their properties. The most obvious effect is the reduction of the saturation magnetization due to surface spin canting. The deviation from the ideal SPM response originates in a varying size distribution, crystallinity and the aggregation of individual NPs, which are imprinted by the preparation procedure. Recently, the suppression of the spurious spin canting effect has been observed in monodisperse highly-crystalline iron oxide NPs coated with oleic acid,8 which enables maximization of the saturation magnetization for a given particle size.
More attention is now paid to novel approaches for organizing NPs and different strategies are used for this purpose. Liquid crystalline materials appear as perfect candidates for such new systems as they combine order and mobility on the molecular level in a unique manner. The capability of LCs to orient small particles has been known for many years.9 The formation of particle aggregates and topological defects have been studied in nematic and cholesteric LCs.10 However, the interaction between particles and LC molecules strongly depends on the particular combination of both materials, on the LC molecular structure and elastic properties and on the type, size and shape of the colloidal particle. NPs can be solvated in LCs or liquid crystalline polymers with the aim of exploiting their self-assembling property and potentially to obtain advantageous electrical, optical or magnetic properties.11 Due to the orientational and positional order in the LC host, one can expect unusual properties, in comparison with conventional colloidal systems. The dispersion of ferromagnetic particles into LCs is done with the aim of enhancing their optical, electrical and magnetic properties.
The preparation of such a hybrid composite can be a way to obtain well organized NPs. A challenge for future studies is to create hierarchically structured composites with a distinct function, to yield a mechanically integrated, multifunctional material, responsive to both electric and magnetic fields. Ordered assemblies are promising in a wide range of applications, for example in high-density media, microelectronics and charge transport devices. Recent work reported the study of a system of iron oxide NPs, prepared by co-precipitation and subsequent dispersion in a lipid-based lyotropic LC, which exhibited orientational order, tunable by the external magnetic field and a photothermal effect.12
This work is concentrated on rod-like molecules that create thermotropic LCs, in which liquid crystalline phases occur, on lowering temperature from the isotropic phase. Besides the nematic phase, which is well-known and widespread in display technology, smectic phases can also appear. In the smectic A phase (SmA), molecules are organized in layers with their molecular axis parallel to the layer normal. If molecules are tilted with respect to the layer normal, the smectic C phase (SmC) is observed. If the molecules are chiral, liquid crystals exhibit ferroelectricity in the tilted SmC* phase. Ferroelectric materials possess a spontaneous polarization that is stable and can be switched by an applied electric field. The ferroelectric properties of the SmC* phase are established by the electric switching and dielectric and optical methods. Chiral smectics are complex systems, certain features of which also manifest in their dielectric behavior.13 Dielectric spectroscopy enables us to characterize the soft mode (the fluctuation of the tilt angle), which contributes to permittivity in the vicinity of the SmA–SmC* phase transition. In the SmC* phase, the phase fluctuations (Goldstone mode) are also present and contribute to the permittivity. The dielectric strength of the Goldstone mode is much larger than that of the soft mode in the whole SmC* phase, except in the vicinity of Tc. If the electric bias field is applied parallel to the smectic layers, the helical structure is unwound and thus the Goldstone mode is suppressed.
We present a new type of hybrid system, consisting of a liquid crystalline compound and magnetic γ-Fe2O3 nanoparticles coated by oleic acid (MNPs). We integrated the magnetic iron oxide nanoparticles into the LC compound (S)-1-(hexyloxy)-1-oxopropan-2-yl 4-(4-(4-(nonyloxy)benzoyloxy)benzoyloxy)benzoate, denoted as 9HL. The studied LC compound exhibits the ferroelectric SmC* phase. The size of the nanoparticles (4 nm) was adjusted, to be close to the length of the LC molecules, to reduce the interference in the LC order. As the efficiency of the possible magneto-electric coupling requires the largest possible value of the superspin for the given MNP size, MNPs with a narrow size distribution were used. We focused on the ferroelectric and magnetic properties of the new hybrid composites. Our objective was to provide a new way to realize the magneto-electric coupling, which is described as the influence of the magnetic (electric) field on the polarization (magnetization) of a material.
2. Results and discussion
2.1. Liquid crystalline compound
The studied thermotropic liquid crystalline host is the lactic acid derivative 9HL, with a molecular core consisting of three phenyl rings, connected by ester linkage groups.14 The compound 9HL exhibits the isotropic (Iso)–SmA–SmC*–crystal phase sequence on cooling with the transition temperatures TA = 401 K (Iso–SmA), TC = 347 K (SmA–SmC*), TCr = 308 K (crystallization). As is characteristic for the SmC* phase, there is a helicoidally periodic arrangement with the characteristic pitch length of 2.1 μm.14a Various hybrid composites were prepared from 9HL and MNPs with a defined weight concentration of γ-Fe2O3 nanoparticles (see the Experimental section).2.2. Mesomorphic properties and textures
The observation of textures is a primary tool for the characterization of the mesomorphic properties of liquid crystalline composites, and differential scanning calorimetry (DSC) complements it. A phase diagram (Fig. 1) shows that the temperature range of the ferroelectric SmC* phase is gradually suppressed with increased MNP concentration and disappears at about 5.6 w/w% of γ-Fe2O3 (20 w/w% of MNP). On the contrary, the Iso–SmA phase transition temperature is not influenced by the presence of magnetic nanoparticles to such a large extent. The coexistence of the isotropic and SmA phases is observed for mixtures with increasing MNPs concentration.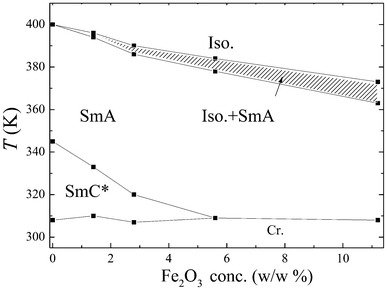 | ||
| Fig. 1 Phase diagram for studied hybrid systems of LC compound 9HL and magnetic nanoparticles (MNPs). The hatched area shows the isotropic–SmA coexistence region. | ||
A transition electron microscope (TEM) photograph is presented for 1.4% of Fe2O3 in 9HL in Fig. 2. The photograph was taken at room temperature on a sample prepared just after the evaporation of hexane from a solution of 9HL and MNPs without heating to the liquid crystalline phase. One can see that magnetic nanoparticles with homogeneous shape and size are uniformly dispersed.
 | ||
| Fig. 2 TEM image of composite 1.4% Fe2O3 in 9HL taken at room temperature. | ||
The textures observed on samples in commercial glass 6 μm thick cells have been studied by polarizing microscopy. For lower MNP concentrations (up to 5.6% of Fe2O3) a typical fan-shaped texture is observed in the SmA phase (see Fig. 3a). Such a texture is also found for the pure compound 9HL and indicates a common tendency of molecules to orient along the sample surface (planar alignment). It results in a sample structure with the smectic planes perpendicular to the sample surface (bookshelf geometry). In the planar texture, slightly elongated dots are visible, which represent defects decorated by clusters of MNPs (see ESI,† Fig. S6). For higher MNP concentrations, a homeotropic texture is preferred, with molecules perpendicular to the sample surface, which is seen as a black area in Fig. 3b. From this fact, one can speculate that there is modification of the anchoring at the surface, from the planar to the homeotropic texture, due to the presence of MNPs. For intermediate concentrations, both types of textures can coexist in one sample (see Fig. 3).
 | ||
| Fig. 3 Microphotograph of the studied 5.6% Fe2O3 in 9HL, embedded into a commercial 6 μm thick cell. (a) A fan-shaped texture observed below the Iso–SmA phase transition; (b) homeotropic texture with birefringent bands. Both textures coexist in different parts of the cell. The width of the photograph is 120 μm. | ||
2.3. Dielectric properties
In the ferroelectric SmC* phase, which is present for mixtures up to a concentration of 5.6% of Fe2O3, the direction of the spontaneous polarization, Ps, can be switched by an electric field. The spontaneous polarization was evaluated by the integration of the peak area in the switching current profile (Fig. 4a). The temperature dependencies Ps(T) have been measured for nanocomposites with 1.4% and 2.8% of Fe2O3 in 9HL, and compared with the Ps(T) of pure 9HL (Fig. 4b). All dependencies show a typical increase in Ps on cooling from the SmA to the SmC* phase. The decrease on the low temperature side reflects a gradual crystallization. The results also reveal a significant decrease of Ps with increasing MNP concentration.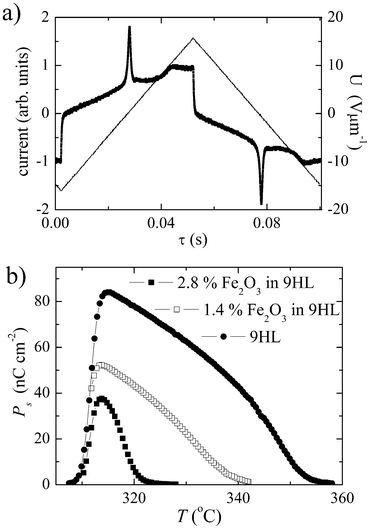 | ||
| Fig. 4 (a) Switching current profile versus intensity of an applied triangular electric field, U, for the composite 1.4% Fe2O3 in 9HL host. (b) Temperature dependencies of the spontaneous polarization, Ps, for pure 9HL and the composite systems 1.4% Fe2O3 in 9HL and 2.8% Fe2O3 in 9HL. | ||
The results of dielectric spectroscopy show that both the Goldstone and the soft modes are suppressed and smeared with increasing MNPs concentration. A similar effect is also observed when inserting another type of nanoparticle into the LC species.15 We have studied the dielectric properties of hybrid nanocomposites under a magnetic field of 9 T, directed along the sample surface. We established the effect of the magnetic particles on the complex permittivity, measured at 1 kHz. Generally, the permittivity in the ferroelectric liquid crystalline compound is given by the Goldstone mode (director-azimuthal fluctuations) besides the vicinity of the SmA–SmC* phase transition, where a peak due to the soft mode (fluctuations of the tilt angle) can be observed. Under a sufficiently high magnetic field, the helix in the SmC* phase is unwound and thus the Goldsone mode is suppressed.16 A comparison of the temperature dependencies of the real, ε′, and imaginary, ε′′, parts of the permittivity without a magnetic field and under a magnetic field of 9 T is shown in Fig. 5. For all studied samples, pure 9HL and the hybrid nanocomposite, the effect of the magnetic field is very similar. In all samples the applied magnetic field strongly suppresses the permittivity in the SmC* phase. In the temperature dependence range, where the Goldstone and soft modes are not active or are suppressed by the applied electric or magnetic field, the losses are very small showing a low concentration of impurities.
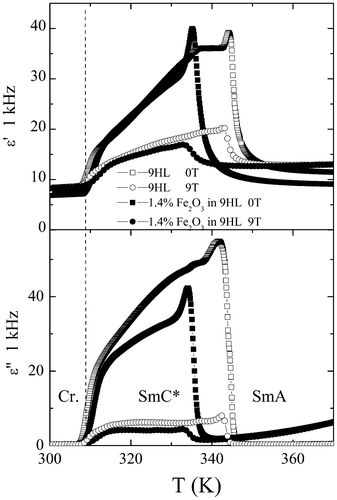 | ||
| Fig. 5 Temperature dependencies of (a) the real part of permittivity, ε′, and (b) the imaginary part of permittivity, ε′′, taken at a frequency of 1 kHz for the pure liquid crystal 9HL (empty symbols) and a mixture 1.4% w/w of Fe2O3 in 9HL (full symbols) without a magnetic field and under a 9 T magnetic field. The studied samples are heated from R.T. to 400 K and then cooled down. | ||
2.4. X-ray scattering data
Small angle X-ray diffraction studies were performed on cooling from the isotropic phase. The layer spacing, d, was evaluated from the peak on diffracted intensity. The temperature dependencies of d, shown in Fig. 6, exhibit a gradual increase in d in the SmA phase. A negative thermal expansion coefficient is common for the SmA phase and is usually explained by the increase of the orientational order on cooling and by the molecular conformation changes due to the ending-chain prolongation. At the SmA–SmC* phase transition, a decrease in d is observed, which is related to the tilt of the molecules in the SmC* phase. An additional significant decrease occurs in the crystalline phase. Qualitatively similar behavior is found for pure 9HL, as well as for the composite with MNPs. The presence of MNPs increases the layer spacing, the increase being more pronounced in the SmC* and crystal phases. One can expect that the presence of nanoparticles influences the process of ending-chain prolongation in the liquid crystalline phase.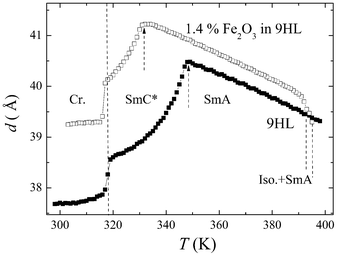 | ||
| Fig. 6 Temperature dependence of the layer spacing value, taken from the X-ray scattering data, for pure 9HL and composite 1.4% of Fe2O3 in 9HL. The SmA–SmC* phase transitions are marked by dashed arrows. | ||
2.5. Magnetic properties
The magnetic response of the original maghemite nanoparticles and the nanocomposites in the studied hybrid system with LC was investigated by means of the temperature dependence of magnetization, magnetization isotherms and a.c. susceptibility. The typical temperature dependence of the zero field cooled (ZFC) and field cooled (FC) curves is shown in Fig. 7. The bifurcation point (TB ∼ 15 K) of the ZFC-FC curves attributed to the blocking temperature of the MNPs, is slightly above the maximum on the ZFC curve (at ∼12 K for all studied samples). The saturation of the FC curve at low temperatures points to dipolar interactions among the MNPs in all studied samples.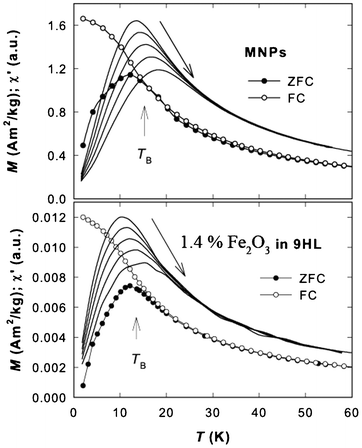 | ||
| Fig. 7 Temperature dependence of the zero field cooled (ZFC) and field cooled (FC) magnetization, M, of the MNPs and the composite containing 1.4% of the Fe2O3 in 9HL. The vertical arrows depict the blocking temperature, TB. The solid lines correspond to the real part of the a.c. susceptibility, χ′; the shift of the maximum with frequency of the applied a.c. magnetic field, increasing from 0.1 to 1 kHz, is schematically shown by the long arrow. | ||
The magnetization isotherms of the original MNPs and the sample containing 1.4% Fe2O3 in 9HL are depicted in Fig. 8. The loops recorded in the block state show a net hysteresis due to the blocked state (Fig. 9), while those above the TB show the expected Langevin character. All curves exhibit a linear paramagnetic-like contribution, which can be attributed to the disordered surface spin layer response; however, the saturation value, Ms, and remnant magnetization, Mr, values are almost comparable to the bulk value (when normalized to Fe2O3 content), suggesting the suppression of the surface spin disorder by the oleic acid coating in the MNPs and the nanocomposite. At the temperature 10 K, the Ms (determined after subtraction of the linear spin-disorder contribution at high magnetic fields) and the Mr values for the MNPs sample are about 12.0 and 4.2 A m2 kg−1, respectively. The corresponding Ms/Mr values for the samples containing 5.6% and 1.4% of Fe2O3 in 9HL are 1.3/0.32 A m2 kg−1 and 0.48/0.12 A m2 kg−1, respectively. These values are in a very good agreement considering the expected MNP content in the composite samples. The important feature observed on the hysteresis loops in the blocked state is the reduction of the coercivity, Hc, in the composite samples to about ½ of the pure MNP value (from 0.1 T to 0.05 T at 2 K, as shown in Fig. 9a). In Fig. 9b the magnetization isotherms recorded at 300 K are shown in order to demonstrate the superparamagnetic nature of the MNPs and the hybrid system. This effect can be attributed to the weakening of the inter-particle interactions. Usually, the dilution of the dipolar interaction is also evidenced by a decrease in the blocking temperature, however, considering the size of our MNPs (4 nm) and the temperature scale, where the transition to the blocked state occurs, the potential shift of the TB would be hardly detectable by analyzing the ZFC-FC dependencies.
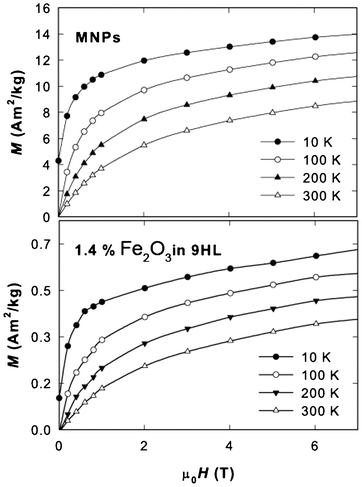 | ||
| Fig. 8 Magnetization isotherms at selected temperatures for the MNPs and the sample containing 1.4% of Fe2O3 in 9HL. | ||
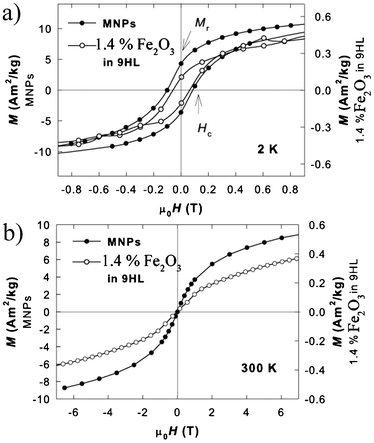 | ||
| Fig. 9 Hysteresis loops (a) in the blocked state at T = 2 K and (b) at T = 300 K for the MNPs (full symbols) and the sample containing 1.4% of Fe2O3 in 9HL (empty symbols). The left-side scale corresponds to the MNPs and the right-side to the composite. The magnetization isotherms recorded at 300 K are shown in order to demonstrate the superparamagnetic nature of the MNPs and the hybrid system. | ||
The superspin relaxation phenomena are inspected by the a.c. susceptibility measurements. The typical temperature dependencies of the real part of the a.c. susceptibility, χ′, are shown in Fig. 7 (solid lines). The maxima of the χ′ curves for the equivalent frequencies occur at slightly lower temperatures for the composite sample, suggesting a modification of the interaction strength between the MNPs. This observation is consistent with the reduction of the Hc. Because the saturation of the FC curve at low temperature suggested the presence of weak inter-particle interactions, the evolution of temperature of χ′ maxima with frequency was inspected using the Vogel–Fulcher (VF) law17 describing the (super)spin relaxation among the weakly interacting MNPs:
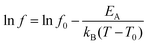 | (1) |
3. Conclusions
The admixture of magnetic nanoparticles, coated by oleic acid, to ferroelectric liquid crystal 9HL, which exhibits the SmA–SmC* phase sequence on cooling from the isotropic phase, gradually suppresses the SmC* temperature range and at about 5.6 w% concentration this phase disappears and only the SmA phase persists on cooling, till crystallization. The crystallization temperature is not affected by the presence of MNPs. In the SmC* phase, the values of the spontaneous polarization, as well as the permittivity, gradually decrease with the particle concentration. A typical planar anchoring of the LC molecules at the sample surface is changed to the homeotropic one, due to the presence of MNPs. The layer spacing in the smectic phase is increased due to the MNP presence, the effect being stronger in the SmC* phase. We present a new hybrid system exhibiting both ferroelectric and superparamagnetic properties. Moreover, we are able to modify the ferroelectric properties by applying a magnetic field. The magnetic behavior is typical for a system of superparamagnetic nanoparticles with inter-particle dipolar interactions and surface spin disorder. The magnetic response of the MNPs in the composite is observed and the unique SPM properties preserved. The magnetic properties are modified due to the reduction of the dipolar interaction strength between the MNPs, which is evidenced by the decrease of the coercivity, superspin relaxation time and VF temperature.4. Experimental section
4.1. Preparation of MNPs and nanocomposites
Magnetic nanoparticles, covered with oleic acid (γ-Fe2O3), were synthesized following the published hydrothermal procedure18 with some modifications: 10 mmol of NaOH was dissolved in 2 ml of water, 10 ml of ethanol and 12 mmol of oleic acid was added with stirring, which led to a clear solution. It was transferred to an autoclave tube and an aqueous solution of 1 mmol of Fe(III) nitrate and 1 mmol of Fe(II) nitrate was added with vigorous stirring and sonication. In total, 20 ml of distilled water was added. The autoclave was closed and placed into a pre-heated, 180 °C oven for 10 h. After cooling, the final mixture was composed of an upper organic phase, a lower aqueous phase and sedimented particles. The liquid phase was discarded. The remaining particles were washed four times by re-dispersion in 5 ml of hexane and precipitation by 15 ml of ethanol. After washing they were re-dispersed in 10 ml of hexane and the dispersion was centrifuged at 4500 rpm to remove large agglomerates.The maghemite particles coated by oleic acid (MNPs) and liquid crystalline material 9HL were dissolved in 5 ml of hexane (p.a.) under heating and stirring. The relative concentrations of the components were adjusted to give 20 mg of the final composite, having an Fe content from 1% to 8% w/w. The hexane solution was then heated up to 60 °C and the solvent was gradually evaporated. The composite was then dried in a vacuum oven for 2 h at room temperature. The content of Fe in the composite was determined by atomic absorption spectroscopy. Samples were mineralized in a mixture of HCl and HNO3 with the addition of a small amount of H2O2. The absorption of the solution was measured on an atomic absorption spectrometer AA240 (Varian) at a wavelength of 248 nm. A flame technique, using an air–acetylene mixture and a deuterium background correction was used. A standard iron stock solution was prepared from iron nitrate. Various hybrid composites were prepared with concentrations of 1.4, 2.8, 5.6 and 11.2% w/w of Fe2O3, which correspond to 5, 10, 20 and 40% w/w of MNPs with the oleic acid admixture.
4.2. Mesomorphic and electro-optical studies
The texture observations and the measurements of the spontaneous polarizations, Ps, were carried out on planar samples, 7 or 12 μm thick, with a 5 × 5 mm2 electrode area. The cells consisted of two glasses provided with transparent ITO electrodes and polyimide layers, ensuring a planar geometry (the layers were perpendicular to the sample surface). The cells were filled by means of capillary action in the isotropic phase. Liquid crystalline samples were examined under a polarizing optical microscope, Nikon Eclipse E-600, equipped with a Linkam heating stage. The temperature was stabilised within ±0.1 °C.4.3. Switching properties and dielectric spectroscopy measurements
The dielectric properties were studied using a Schlumberger 1260 impedance analyser. The frequency dispersions were measured at a cooling rate of about 0.2 K min−1, keeping the temperature of the sample stable during the frequency sweeps in the range of 10 Hz –10 MHz. Details of the fitting procedure are in the ESI.† The spontaneous polarisation, Ps, was determined from the switching current, detected under a triangular electric field profile at a frequency of 50 Hz and an electric field of 20 V μm−1. The current profile was detected with the memory digital oscilloscope, Tektronix.The temperature dependencies of the real and imaginary parts of the dielectric permittivity under an external magnetic field were determined at a frequency of 1 kHz using an ultra-precise capacitance bridge Andeen-Hagerling 2500 A implemented in PPMS 9 T (Physical Property Measurement System).
4.4. Magnetic properties measurements
Magnetic measurements of the samples in the solid state were performed using a commercial SQUID magnetometer MPMS 7XL (Quantum Design, San Diego). The samples, of a typical mass in the order of milligrams, were placed into a gelatine capsule and fixed with glue to avoid rotation of the particles in the direction of the external magnetic field. To determine the values of the blocking temperature, TB, the temperature dependencies of the zero field cooled (ZFC) and field cooled (FC) magnetization were measured in the temperature range of 10–300 K in an external magnetic field equal to 0.01 T. The magnetization isotherms were recorded at selected temperatures in magnetic fields varying up to 7 T in both polarities. The temperature dependencies of the real, χ′ and imaginary, χ′′ parts of the a.c. susceptibility were collected at different frequencies of the altering magnetic field (0.1 Hz–1 kHz) with an amplitude of 0.3 mT in a zero external magnetic field.4.5. X-ray measurements and TEM studies
X-ray studies were performed using the Bruker D8 Discover system (Cu-Kα radiation) equipped with an Anton Paar DCS-350 heating stage (temperature stability 0.1 K), working in the reflection mode. Samples were prepared as one-surface free droplets on a heated surface. The smectic layer thickness, d, was determined using Bragg's law nλ = 2dsinθ, where d is calculated from the diffraction angle θ of the (001) smectic layer peak in the small angle regime.A TEM Libra 120 from Zeiss was used with the highly flexible Koehler illumination system, together with the in-column OMEGA filter, providing an excellent image contrast.
Acknowledgements
This work was supported by grants P204/11/0723 (Czech Science Foundation), M100101211 (Czech Academy of Sciences), COST MP0902 – Coinapo and COST LD12025 (Czech Ministry of Education). Experiments were performed in MLTL (see: http://mltl.eu), which is supported within the program of Czech Research Infrastructures (project no. LM2011025).References
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 1993 Search PubMed.
- (a) S. H. Sun, C. B. Murray, D. Weller, L. Folks and A. Moser, Science, 2000, 287, 1989 CrossRef CAS; (b) B. Y. Geng, J. Z. Ma, X. W. Liu, Q. B. Du, M. G. Kong and L. D. Zhang, Appl. Phys. Lett., 2007, 90, 043120 CrossRef; (c) E. Duguet, S. Vasseur, S. Mornet and J. M. Devoisselle, Nanomedicine, 2006, 1(2), 157 CrossRef CAS; (d) J. L. Dormann and D. Fiorani, Magnetic Properties of Fine Particles, North-Holland, Amsterdam, 1997 Search PubMed.
- L. Neel, Ann. Geophys. (C.N.R.S.), 1949, 5, 99 Search PubMed.
- E. C. Stoner and E. P. Wohlfarth, Philos. Trans. R. Soc. London, Ser. A, 1948, 240, 599 CrossRef.
- (a) E. Tronc, D. Fiorani, M. Nogues, A. M. Testa, F. Lucari, F. D'Orazio, L. M. Greneche, W. Wernsdorfer, N. Galvez, C. Chaneac, D. Mailly and J. P. Jolivet, J. Magn. Magn. Mater., 2003, 262, 6 CrossRef CAS; (b) D. Peddis, C. Cannas, A. Musinu and G. Piccaluga, Chem.–Eur. J., 2009, 15, 7822 CrossRef CAS.
- (a) J. L. Dormann, D. Fiorani and E. Tronc, in Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley & Sons, Inc., Hoboken, NJ, USA, 1997, vol. 98, p. 283 Search PubMed; (b) X. Batlle and A. Labarta, J. Phys. D: Appl. Phys., 2002, 35, R15 CrossRef.
- (a) J. M. D. Coey, Phys. Rev. Lett., 1971, 27, 1140 CrossRef CAS; (b) D. Peddis, M. V. Mansilla, S. Morup, C. Cannas, A. Musinu, G. Piccaluga, F. D'Orazio, F. Lucari and D. Fiorani, J. Phys. Chem. B, 2008, 112, 8507 Search PubMed.
- A. G. Roca, D. Niznansky, J. Poltierova Vejpravova, B. Bittova, M. A. Gonzalez-Fernandez, C. J. Serna and M. P. Morales, J. Appl. Phys., 2009, 105, 114309 CrossRef.
- F. Brochard and P. G. de Gennes, J. Phys., 1970, 31, 691 CAS.
- (a) M. Zapotocky, L. Ramos, P. Poilin, T. C. Lubensky and D. A. Weitz, Science, 1999, 283, 209 CrossRef CAS; (b) H. Stark, Phys. Rep., 2001, 351, 387 CrossRef CAS; (c) P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770 CrossRef CAS; (d) J. A. Moreno-Razo, E. J. Sambriski, G. M. Koenig, E. Diaz-Herrera, N. L. Abbott and J. J. de Pablo, Soft Matter, 2011, 7, 6828 RSC.
- (a) J. Fukuda, J. Phys. Soc. Jpn., 2009, 78, 041003 CrossRef; (b) T. Hegmann, H. Qi and V. M. Marx, J. Inorg. Organomet. Polym. Mater., 2007, 17, 483 CrossRef; (c) U. Shivakumar, J. Mirzaei, X. Feng, A. Sharma, P. Moreira and T. Hegmann, Liq. Cryst., 2011, 38, 1495 CrossRef CAS; (d) O. Stamatoiu, J. Mirzaei, X. Feng and T. Hegmann, in Topics in Current Chemistry, Springer Berlin Heidelberg, 2012, vol. 318, p. 331 Search PubMed; (e) H. K. Bisoyi and S. Kumar, Chem. Soc. Rev., 2011, 40, 306 RSC.
- (a) J. J. Vallooran, S. Bolisetty and R. Mezzenga, Adv. Mater., 2011, 23, 3932 CrossRef CAS; (b) J. J. Vallooran, S. Handschin, S. Bolisetty and R. Mezzenga, Langmuir, 2012, 28, 5589 Search PubMed.
- (a) I. Musevic, R. Blinc and B. Zeks, The Physics of Ferroelectric and Antiferroelectric Liquid Crystals, World Scientific, 2000 Search PubMed; (b) W. Haase and S. Wrobel, Relaxation Phenomenon (Liquid Crystals, Magnetic Systems, Polymers, High-Tc Superconductors, Metallic Glasses), Springer, 2003 Search PubMed.
- (a) M. Kaspar, V. Hamplova, S. A. Pakhomov, A. M. Bubnov, F. Guittard, H. Sverenyak, I. Stibor, P. Vanek and M. Glogarova, Liq. Cryst., 1998, 24, 599 CrossRef CAS; (b) F. Giesselmann, P. Zugenmaier, I. Dierking, S. T. Lagerwall, B. Stebler, M. Kaspar, V. Hamplova and M. Glogarova, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 598 CrossRef CAS; (c) A. Marchetti, V. Domenici, V. Novotna, M. Lelli, M. Cifelli, A. Lesage and C. A. Veracini, ChemPhysChem, 2010, 11, 1641 Search PubMed.
- (a) B. Rozic, M. Jagodic, S. Gyergyek, M. Drofenik, S. Kralj, G. Lahajnar, Z. Jaglicic and Z. Kutnjak, Ferroelectrics, 2011, 410, 37 Search PubMed; (b) G. Cordoyiannis, S. Kralj, G. Nounesis, Z. Kutnjak and S. Zumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021702 CrossRef; (c) G. Cordoyiannis, L.K. Kurihara, L.J. Martinez-Miranda, C. Glorieux and J. Thoen, Phys. Rev. E, 2009, 79, 011702 CrossRef.
- I. Musevic, B. Zeks, R. Blinc, T. Raising and P. Wyder, Phys. Rev. Lett., 1982, 48, 192 Search PubMed.
- S. Shtrikman and E.P. Wohlfarth, Phys. Lett. A, 1981, 85, 467 CrossRef.
- (a) X. Wang, J. Zhuang, Q. Peng and Y. D. Li, Nature, 2005, 437, 121 CrossRef CAS; (b) A. Repko, D. Niznansky and J. P. Vejpravova, J. Nanopart. Res., 2011, 13, 5021 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ra40737c |
| This journal is © The Royal Society of Chemistry 2013 |
