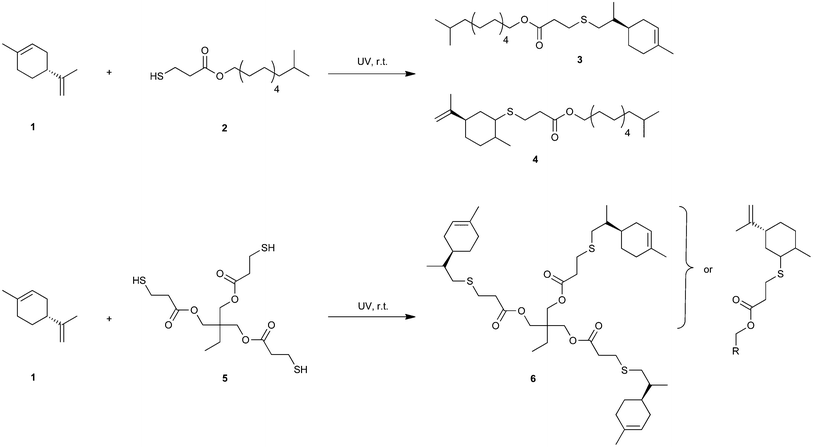
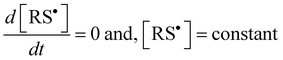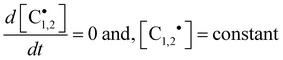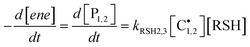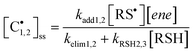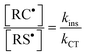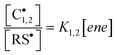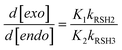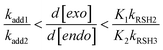DOI:
10.1039/C3RA40696B
(Paper)
RSC Adv., 2013,
3, 11021-11034
Thiol–ene coupling kinetics of D-limonene: a versatile ‘non-click’ free-radical reaction involving a natural terpene†
Received
8th February 2013
, Accepted 4th April 2013
First published on 8th April 2013
Abstract
The free-radical photoinduced thiol–ene reaction between D-limonene, as renewable diolefinic substrate, and two mono-/tri-functional thiols (iso-tridecyl 3-mercaptopropionate and trimethylolpropane tris(3-mercaptopropionate)), has been investigated kinetically to define a relationship between alkene structure and reactivity. Separate thiol–ene solutions of the appropriate thiol in d-chloroform, supplemented with 1.0 wt% of DMPA (Irgacure 651), were subjected to polychromatic UV-irradiation and the chemical changes monitored discontinuously via1H NMR spectroscopy to quantify double bond conversion. The kinetic concentration profiles were modeled analytically and simulated in the application software COPASI for parameter estimation and to verify if the experimental data explained a suggested mechanistic scheme. Empirical results demonstrate that the external vinylidene bond of limonene reacts about 6.5 times faster with thiol than the internal trisubstituted 1-methyl-cyclohexene unsaturation. The selectivity observed for the two unsaturations was successfully explained by means of a simplified steady-state equation derived from the sequential reaction mechanism accounting for propagation and chain-transfer elementary steps with estimated rate coefficients. Kinetic modeling results attribute the difference in selectivity partially to steric impediments controlling thiyl-radical insertion onto the double bonds and predominantly to differences in relative energy between the two tertiary insertion carbon radical intermediates. The rate-limiting step was identified as the third chain-transfer hydrogen-abstraction reaction promoted by the second insertion carbon radical intermediate. High thiol–ene conversions were obtained in a timely fashion without major influence of secondary reactions demonstrating the suitability of this reaction for network forming purposes. The mechanistic and kinetic information collected can be used as a quantitative predictive tool to assess the potential use of D-limonene in thiol–ene network forming systems involving multifunctional alkyl ester 3-mercaptopropionates.
1. Introduction
The pursuit of viable compounds from renewable resources in replacement of petroleum-derived ones is currently seen as one of the major challenges in polymer science on grounds of depleting fossil-oil reserves, environmental awareness and issues of sustainable development. Terpenes represent an extensive class of naturally occurring aliphatic substrates with great potential for the synthesis of biobased polymers.1–3 One of such monomers is D-limonene (also known as (R)-(+)-limonene), characterized as an optically active monocyclic 1,5-diolefin fragrance abundantly present in the peel of oranges and essential oils of citrus fruits, dill, cumin, caraway, among others.4 Limonene possesses two non-conjugated electron-rich double bonds with different degrees of substitution susceptible to polymerization: an endocyclic 1,1,2-trisubstituted 1-methyl-cyclohexene group and an exocyclic 1,1-disubstituted vinylidene (or isopropenyl) moiety. Since the two unsaturations remain virtually unreactive towards free-radical homopolymerization (i.e., chain growth)5 they constitute the ideal alkene for the thiol–ene coupling reaction. Indeed, this intrinsic feature has been explored recently by Meier and co-workers in the synthesis of monofunctional, homodifunctional and hetero-difunctional limonene-modified monomers via the thiol–ene reaction which were then polymerized into linear polymers by use of other chemistries and natural (or bio-derived) monomers.6,7 It would be more interesting, however, if the monoterpene could be directly reacted without any intermediate modifications. This would allow direct incorporation of an abundant and inexpensive bio-renewable monomer into thiol–ene networks by appropriate choice of multifunctional thiol cross-linkers to create novel thermosetting structures not easily accessible via petrochemistry (say, for instance, chirality).
Thiol–ene chemistry, although already known since the early 1900's,8 has not been investigated at the kinetic and/or mechanistic level using limonene as diolefinic substrate. This reaction has grown considerably over the past 10–15 years and many key attributes are currently recognized concerning thermoset synthesis over classical acrylic-based free-radical polymerizations; namely: insensitivity to oxygen inhibition, relatively fast reaction rates, solventless processing when both thiol–ene monomers are compatible, improved photocuring control (both spacial and temporal), ability to initiate polymerization without addition of a photoinitiator enabling the polymerization of thick geometries, and a step-wise radical growth mechanism leading to a late gel-point which results in materials with uniform cross-link density, narrow glass-transition temperatures, reduced volume shrinkage and low stress development at high monomer conversions.9,10 Additionally, thiol–ene photopolymers are optically clear and exhibit improved physical properties, such as flexibility and good adhesion to various substrates.9,11 Due to its high efficiency with few, if any, side-products, the term (‘click’) was recently coined to this reaction12–14 and there is already a vast repertoire of excellent reviews on the subject covering a wide range of scientific fields and applications.9,10,15–17
Conventionally, the thiol–ene coupling reaction proceeds through a two-step free-radical mechanistic pathway mediated by catalytically active thiyl radicals (see Scheme 1 exemplified with limonene).18 At first, the reaction starts via initiation (often UV-induced) which promotes hydrogen transfer from a thiol monomer to one of the primary nucleophilic free-radicals generated for instance from intramolecular α-cleavage of a photoinitiator. The resulting electrophile thiyl radical (RS˙) then reversibly adds across any accessible C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in an anti-Markovnikov fashion (propagation) forming a nucleophilic β-carbon centered radical intermediate (RC˙) which easily captures the electron-poor hydrogen from another weak S–H bond regenerating the thiyl radical (chain-transfer) and gives the final stable thioether (C–S) coupled product. The successive propagation–chain-transfer events allow the mechanism to be repeated in a cyclic reaction sequence until full exhaustion of reactant thiol–ene groups from a starting stoichiometric mixture. Termination reactions can occur via combination of any two intervening radicals (β-carbon and/or thiyl) evocative of a bimolecular termination rate kinetics; although, other yet unidentified mechanisms may also be involved.19
C double bond in an anti-Markovnikov fashion (propagation) forming a nucleophilic β-carbon centered radical intermediate (RC˙) which easily captures the electron-poor hydrogen from another weak S–H bond regenerating the thiyl radical (chain-transfer) and gives the final stable thioether (C–S) coupled product. The successive propagation–chain-transfer events allow the mechanism to be repeated in a cyclic reaction sequence until full exhaustion of reactant thiol–ene groups from a starting stoichiometric mixture. Termination reactions can occur via combination of any two intervening radicals (β-carbon and/or thiyl) evocative of a bimolecular termination rate kinetics; although, other yet unidentified mechanisms may also be involved.19
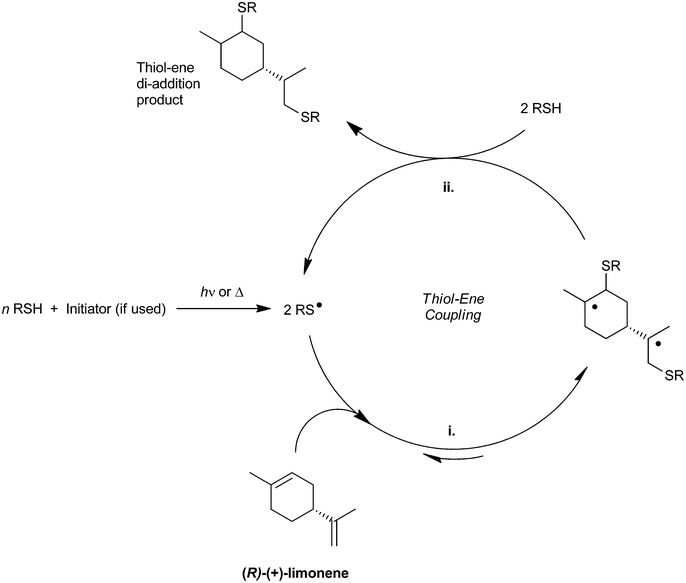 |
| | Scheme 1 General thiol–ene reaction diagram involving the two unconjugated double bonds of (R)-(+)-limonene with alternate propagation (i.) and chain-transfer (ii.) steps. | |
Although virtually any alkene functional group is able to participate in the reaction, the chemical nature of the double bond affects, to large or small extent, the coupling efficiency (‘click’ character) and this much often dictates which alkene monomers can be selected for a specific situation. Most common applications in literature report on the use of terminal (monosubstituted) enes9 and norbornenes20–24 owed to superior reactivity with a variety of thiol compounds; yet, they are derived predominantly from petrochemical feedstocks and alkene monomers that are found in nature usually have to be modified in some way to gain reactivity; vide for instance the acrylation of soybean oil25 and metathesis of triglyceride vegetable oils.26–28 Our recent works have established that cis/trans-1,2-disubstituted alkenes can still undergo direct cross-linking with multifunctional propionate ester mercaptans in high yields via a ‘non-click’ thiol–ene coupling reaction without significant occurrence of side-reactions.29,30 Additionally, multifunctional thiols of this kind may turn advantageous in the preparation of biodegradable thiol–ene networks as thermosetting materials because of the presence of a readily hydrolysable ester group.23 Following the same lines, we would like to investigate if the differences in thiol–ene reactivity observed for the two exotic unsaturations of limonene6 exhibit enough reactive potential for the creation of thermosetting thiol–ene networks that could be of utility for polymer applications, such as clear coatings.
Therefore, in this study, we develop a fundamental kinetic framework explaining the basic reaction mechanism that governs the thiol–ene coupling reaction between D-limonene and thiol compounds having a propionate ester moiety. Experimental and theoretical modeling approaches assisted by computer numerical simulations are combined in an effort to assess thiol–ene reactivity with respect to the two functional alkene structures and obtain rate parameters that can help determine the effectiveness of this monoterpene toward the green production of novel thiol–ene networks that are at least partially based on a bio-renewable resource. In this view, we first perform a general analytic treatment of the kinetics from experimental conversion data followed by dynamic kinetic simulations to confirm a proposed reaction mechanism. Then we attempt at estimating the rate coefficients for the propagation and chain-transfer steps and inspect the reaction model via a sensitivity analysis to better understand which factors contribute more drastically to changes in the model.
2. Materials and methods
2.1. Chemicals
(R)-(+)-limonene (Lim 1, ≥97%) was obtained from Sigma-Aldrich (Sweden). Iso-tridecyl 3-mercaptopropionate (C13MP, 2) and Trimethylolpropane tris(3-mercaptopropionate) (TMPMP, 5) and were kindly provided by Bruno Bock Chemische Fabrik GmbH & Co (Marschacht, Germany). The photoinitiator, 2,2-dimethoxy-2-phenylaceto-phenone (DMPA), was obtained from Ciba Specialty Chemicals Inc. (Switzerland). Deuterated chloroform (CDCl3, 99.8%) was provided by CIL (Cambridge Isotope Laboratories, Inc, USA). All chemicals were commercial products, used as received without purification.
2.2. Instrumentation
2.2.1. UV-light source.
A Hamamatsu L5662 equipped with standard medium pressure 200 W L6722-01 Hg–Xe lamp provided with optical fibers was used as the UV-source for the discontinuous kinetic studies. The UV-intensity was measured using a Hamamatsu UV-light power meter (model C6080-03) calibrated for the main emission line centered at 365 nm.
2.2.2. NMR spectroscopy.
1H NMR spectra of the samples were recorded on a 400 MHz Bruker Aspect NMR spectrophotometer (Karlsruhe, Germany). 1H NMR spectra (128 scans) were acquired with a spectral window of 20 ppm, an acquisition time of 4 s, and a relaxation delay of 2 s. Analytes were prepared by dissolving 8 mg of sample in 800 μl of deuterated chloroform (CDCl3) containing 0.05% of TMS in a 5 mm diameter glass tube. Chemical shifts (δ) were reported in parts per million (ppm) relative either to the tetramethylsilane (TMS) reference signal at 0.00 ppm or residual non-deuterated solvent signal located at 7.26 ppm.
2.3. Procedures
2.3.1. Sample preparation.
Stock solutions of (R)-(+)-limonene (1) and iso-tridecyl 3-mercaptopropionate (2) or TMP-trimercaptopropionate (5) based on a stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 with respect to thiol–ene functionalities were prepared by mixing corresponding mole amounts of each reactant in 50 wt% of d-chloroform (CDCl3) and the resulting solution supplemented with 1.0 wt% of DMPA as photoinitiator. A volume of 2.0 ml from each of the two stock solutions was transferred to small glass vessels of cylindrical geometry (40 × 12 mm) used as photochemical reactors. The samples were protected from visible ambient light before UV-irradiation.
0.5 with respect to thiol–ene functionalities were prepared by mixing corresponding mole amounts of each reactant in 50 wt% of d-chloroform (CDCl3) and the resulting solution supplemented with 1.0 wt% of DMPA as photoinitiator. A volume of 2.0 ml from each of the two stock solutions was transferred to small glass vessels of cylindrical geometry (40 × 12 mm) used as photochemical reactors. The samples were protected from visible ambient light before UV-irradiation.
2.3.2. Reactivity assessment.
Individual samples were exposed to multi-wavelength UV-irradiation (4.2 mW cm−2) in presence of air at room temperature under continuous magnetic stirring (1000 rpm) for a given time interval and then were dissolved in 1.0 ml of d-solvent after the run was finished. Then, 800 μl of the diluted mixtures were analyzed by 1H NMR (128 scans) to determine double-bond conversion throughout time. To check reproducibility, the photo-initiated experiments were executed in triplicate using independent samples. When all reaction runs were terminated the stock solutions were checked with respect to the initial thiol–ene stoichiometry to verify the long-term stability of functional groups. All photoinduced reactions and kinetic measurements were carried out under exactly the same experimental conditions.
2.3.3. Determination of conversion.
1H NMR spectroscopy was used for the discontinuous evaluation of thiol–ene conversions. 1H NMR signals corresponding to the internal and external double-bonds of limonene were used to assess the extent of thiol–ene coupling. Integral areas for the unsaturation proton signals observed at 4.7 ppm (exocyclic, vinylidene) and 5.4 ppm (endocyclic, trisubstituted) were normalized against the areas of the ethyl ester protons from each thiol compound located at 4.1 ppm. Percent conversion of individual unsaturations into C–S bonds was determined according to the formula:| | 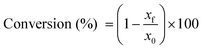 | (1) |
where x denotes normalized double-bond 1H integrations before (x0) and after reaction (xf) for each unsaturated moiety. The sum of individual double-bond conversions (exo + endo) over time provided an estimation of the extent of reacted limonene as a species.
2.3.4. Analytical considerations.
Kinetic conversion data obtained experimentally (see sections VIII. and IX. of the Supplementary Information) were first transformed into chemical species (or functional group) concentrations by means of eqn (2) and the resulting discrete profiles over time subjected to the analytical treatment described in subsection 3.2.
The symbol C(t) represents the molar concentration of each reactant entity at time t, C0 is the initial molarity, and 0 ≤ fc ≤ 1 denotes the fraction of total conversion at each time. Reaction rates were evaluated by computing the first derivative of the fitted curves showing the time-consumption of limonene (or thiol functional groups) and individual alkene functionalities.
2.3.5. Simulation software, modeling and parameter estimation.
Kinetic simulations of the mechanistic reaction were performed using the general software application package COPASI (Complex Pathway Simulator) version 4.8 (build 35). This program is available completely free of charge at http://www.copasi.org/tiki-view_articles.php and was designed for the kinetic modeling, simulation and analysis of biochemical network systems.31 In order to construct the computed output curves, all elementary chemical reactions, stoichiometry, initial reactant concentrations and individual rate coefficients were first entered and the program allowed solving the system of equations as a function of time. A deterministic routine algorithm termed LSODA (Livermore Solver for Ordinary Differential Equations) was used by COPASI to compute the numerical solutions of a set of ordinary differential equations (ODEs) describing a deterministic reaction mechanism. LSODA is a very robust adaptive step-size solver that calculates the stiffness of equations and dynamically switches the method of integration according to this measure.32 The mechanistic model was introduced in the software according to the elements listed in Table 1. To test the fidelity of the model all kinetic curves generated were plotted against the corresponding discrete concentration profiles obtained from experimental 1H NMR measurements of the multifunctional thiol–ene reaction system. Unknown kinetic coefficients specified for propagation and chain-transfer steps were determined via a parameter estimation (optimization) routine that COPASI has built-in. The procedure involved dataset loading of the experimental concentrations for each alkene functional group (exo- and endo-) and thiol/limonene obtained from discontinuous time-course experiments, followed by a recursive calculation task based on the Hooke & Jeeves algorithm (default mode) and objective function for the concurrent experiments until the best convergence between experimental and computed values was finally reached by minimization of their distance. The repetitive process fits the deterministic model to the experimental data. Each experimental concentration profile of the dataset contributes to the objective function, E(p), in accordance with the following weight sum of squares formula derived from a least-squares approach:33| | 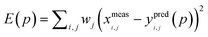 | (3) |
where, p is the tested parameter set, xi,j is an experimental point in the dataset, 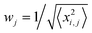 is the mean square weight of each data column, and, yi,j(p), the corresponding simulated value. The subscripts i and j represent rows and columns in the dataset, respectively. The mean square weighing method was chosen because it assures that all data columns containing small and large values contribute with equal weight to the objective function. Computationally predicted rate constants with calculated statistics are given in section XIII. of the Supplementary Information.
is the mean square weight of each data column, and, yi,j(p), the corresponding simulated value. The subscripts i and j represent rows and columns in the dataset, respectively. The mean square weighing method was chosen because it assures that all data columns containing small and large values contribute with equal weight to the objective function. Computationally predicted rate constants with calculated statistics are given in section XIII. of the Supplementary Information.
Table 1 Model definition used to generate the numerical simulations in COPASI
| Reaction Step |
Chemical Equation |
Rate Constants |
|
|
|
Literature Valuesa |
Estimated Valuesb |
|
Partially taken from literature.29
Computed from the parameter estimation task built-in in COPASI.
|
| (1) |

|
— |
k
d = 1.0 × 10−4 s−1 |
| (2) |

|
k
RSH1 = 1.0 × 107 M−1 s−1 |
— |
| (3) |
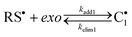
|
k
add1 = 1.6 × 105 M−1 s−1 |
k
add1 = 2.0 × 106 M−1 s−1 |
|
k
elim1 = 2.0 × 107 s−1 |
k
elim1 = 8.5 × 107 s−1 |
| (4) |

|
k
RSH2 = 1.0 × 106 M−1 s−1 |
k
RSH2 = 5.4 × 105 M−1 s−1 |
| (5) |
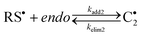
|
k
add2 = 2.9 × 105 M−1 s−1 |
k
add2 = 1.4 × 106 M−1 s−1 |
|
k
elim2 = 1.6 × 108 s−1 |
k
elim2 = 6.6 × 108 s−1 |
| (6) |

|
k
RSH3 = 1.0 × 106 M−1 s−1 |
k
RSH3 = 6.0 × 105 M−1 s−1 |
| (7) |
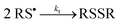
|
k
t = 3.0 × 109 M−1 s−1 |
— |
3. Results and discussion
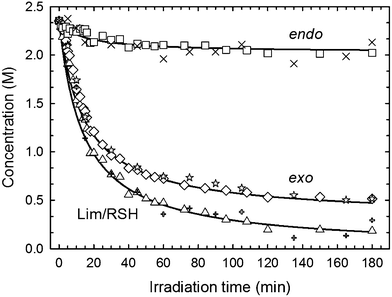
Although thiol–ene kinetics have been extensively studied in the past for a variety of alkene structures, a detailed kinetic examination of the two hydrocarbon alkenes in D-limonene has never been attempted before. Therefore, this study aims to gain primary insight of the free-radical induced thiol–ene coupling of limonene in CDCl3 solution promoted by photogenerated thiyl radicals of the 3-mercaptopropionate ester type (RCH2OC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OCH2CH2S˙) in order to establish a direct relationship between alkene structure and reactivity. Preliminary conversion data displayed in Fig. 1, obtained from the photoreaction of D-limonene (1) with a monothiol, C13MP (2), mixed on a half-mole alkene group stoichiometry with respect to the thiol, highlights a superior reactivity of the terminal vinylidene bond over the internal cyclic ene which reacts at much lower rate. As seen, the terminal (exocyclic) ene achieves almost 80% conversion after 180 min of UV-irradiation, whereas the internal (endocyclic) ene reacts more slowly reaching only 10% conversion after the same reaction period. The observed differences in conversion can be ascribed to a higher regioselectivity of the exocyclic unsaturation toward thiol addition as previously reported.6 It is well-known that free-radicals preferentially attack the less substituted α-carbon atom of alkenes, which is also valid for electrophilic radicals, indicating that regioselectivity is guided mainly by steric effects.34 This explains why most β-thioether products resulting from free-radical thiol–ene coupling of unsymmetrical monosubstituted olefins with alkyl thiols are predominantly secondary in structure exhibiting less exothermicities than primary β-thioether products despite of the latter chemical structure is thermodynamically more stable (more exothermic).35 However, such highly contrasting conversion levels observed for the two olefins in D-limonene cannot be ascribed solely to differences in the steric crowding of the corresponding substituents. Diverse literature studies10,35–37 have shown that the reactivity of a given alkene towards a particular thiol depends on the combinatory effect of a series of elements such as: (i.) chemical structure of the thiol monomer (RSH) as a hydrogen-transfer agent, which controls the ability to donate hydrogen-atoms with respect to RS–H bond-dissociating energy (BDE) due to substituents effects; (ii.) stability, size, polarity and electrophilicity of the thiyl radical RS˙, also determined by the chemical nature of the substituent moiety attached to the sulfur atom; (iii.) location, symmetry, electron-density and conformation of the alkene group (terminal, internal, conjugated, non-conjugated, and substituted), which is responsible for steric hindrance, steroelectronic factors, ring strain energy and ability to partake in side reactions (e.g., competing homolymerization); and, (iv.) geometry, relative energy and relative resonance stability of the intermediate carbon-centered radical adduct formed upon thiyl radical insertion onto the double bond, which determine the propensity for back elimination (β-fragmentation) versus hydrogen-capture ability from a thiol group. For example, the electron density of the ene group and carbon radical stability has been proposed in a previous work21 to explain differences in the propagation-to-chain-transfer ratio, kp/kCT, observed for distinct thiol–ene photopolymerization systems, which also influence gel-point formation.38 Accordingly, the magnitude of kp correlates with the electron density of the reactive ene whereas kCT accounts mainly for the stability of the thioether carbon radical.21 In order to better understand which factors control the thiol–ene reactivity of the two exo and endo double bonds in limonene, we have divided this work into three interconnected parts. The first provides a quantitative measure of the observed double bond selectivity (or relative reactivity) in solution from experimental conversion data resulting from the photo-initiated reaction between D-limonene (1) and a tri-functional propionate ester mercaptan (5), as depicted in Scheme 2. The second, attempts to estimate numerically rate coefficients intrinsic to a proposed reaction scheme describing the observed reaction kinetics and then validate the deterministic model. Finally, we interpret the sequential propagation–chain-transfer elementary steps to verify if the relative reactivity obtained from the detailed mechanism explains the measured selectivity.
OCH2CH2S˙) in order to establish a direct relationship between alkene structure and reactivity. Preliminary conversion data displayed in Fig. 1, obtained from the photoreaction of D-limonene (1) with a monothiol, C13MP (2), mixed on a half-mole alkene group stoichiometry with respect to the thiol, highlights a superior reactivity of the terminal vinylidene bond over the internal cyclic ene which reacts at much lower rate. As seen, the terminal (exocyclic) ene achieves almost 80% conversion after 180 min of UV-irradiation, whereas the internal (endocyclic) ene reacts more slowly reaching only 10% conversion after the same reaction period. The observed differences in conversion can be ascribed to a higher regioselectivity of the exocyclic unsaturation toward thiol addition as previously reported.6 It is well-known that free-radicals preferentially attack the less substituted α-carbon atom of alkenes, which is also valid for electrophilic radicals, indicating that regioselectivity is guided mainly by steric effects.34 This explains why most β-thioether products resulting from free-radical thiol–ene coupling of unsymmetrical monosubstituted olefins with alkyl thiols are predominantly secondary in structure exhibiting less exothermicities than primary β-thioether products despite of the latter chemical structure is thermodynamically more stable (more exothermic).35 However, such highly contrasting conversion levels observed for the two olefins in D-limonene cannot be ascribed solely to differences in the steric crowding of the corresponding substituents. Diverse literature studies10,35–37 have shown that the reactivity of a given alkene towards a particular thiol depends on the combinatory effect of a series of elements such as: (i.) chemical structure of the thiol monomer (RSH) as a hydrogen-transfer agent, which controls the ability to donate hydrogen-atoms with respect to RS–H bond-dissociating energy (BDE) due to substituents effects; (ii.) stability, size, polarity and electrophilicity of the thiyl radical RS˙, also determined by the chemical nature of the substituent moiety attached to the sulfur atom; (iii.) location, symmetry, electron-density and conformation of the alkene group (terminal, internal, conjugated, non-conjugated, and substituted), which is responsible for steric hindrance, steroelectronic factors, ring strain energy and ability to partake in side reactions (e.g., competing homolymerization); and, (iv.) geometry, relative energy and relative resonance stability of the intermediate carbon-centered radical adduct formed upon thiyl radical insertion onto the double bond, which determine the propensity for back elimination (β-fragmentation) versus hydrogen-capture ability from a thiol group. For example, the electron density of the ene group and carbon radical stability has been proposed in a previous work21 to explain differences in the propagation-to-chain-transfer ratio, kp/kCT, observed for distinct thiol–ene photopolymerization systems, which also influence gel-point formation.38 Accordingly, the magnitude of kp correlates with the electron density of the reactive ene whereas kCT accounts mainly for the stability of the thioether carbon radical.21 In order to better understand which factors control the thiol–ene reactivity of the two exo and endo double bonds in limonene, we have divided this work into three interconnected parts. The first provides a quantitative measure of the observed double bond selectivity (or relative reactivity) in solution from experimental conversion data resulting from the photo-initiated reaction between D-limonene (1) and a tri-functional propionate ester mercaptan (5), as depicted in Scheme 2. The second, attempts to estimate numerically rate coefficients intrinsic to a proposed reaction scheme describing the observed reaction kinetics and then validate the deterministic model. Finally, we interpret the sequential propagation–chain-transfer elementary steps to verify if the relative reactivity obtained from the detailed mechanism explains the measured selectivity.
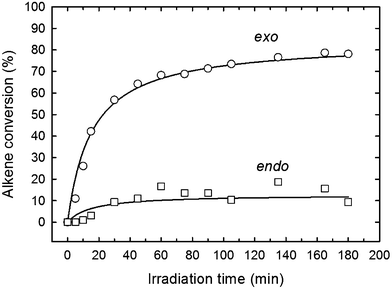 |
| | Fig. 1
1H NMR conversion profiles of exo- and endo-alkene functional groups as a function of time for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mixture based on D-limonene (1) and iso-tridecyl 3-mercaptopropionate (monothiol, 2) in CDCl3 solution (50 wt%). DMPA (1.0 wt%) was used as photoinitiator and the samples irradiated with a polychromatic UV-light irradiance of 4.2 mW cm−2. 0.5 thiol–ene mixture based on D-limonene (1) and iso-tridecyl 3-mercaptopropionate (monothiol, 2) in CDCl3 solution (50 wt%). DMPA (1.0 wt%) was used as photoinitiator and the samples irradiated with a polychromatic UV-light irradiance of 4.2 mW cm−2. | |
 |
| | Scheme 2 Selective thiol–ene coupling between (R)-(+)-limonene (1) and mono- (2) or tri-functional (5) thiol compounds. Reaction conditions: initial stoichiometry (mole ratio of thiol–terpene functional groups): 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, CDCl3 (50 wt%), DMPA (1.0 wt%), UV-intensity: 4.2 mW cm−2, 1000 rpm. 0.5, CDCl3 (50 wt%), DMPA (1.0 wt%), UV-intensity: 4.2 mW cm−2, 1000 rpm. | |
3.1. Generation of thiyl radicals: the initiation process
The production of initiating thiyl radicals was promoted photochemically via photolysis of DMPA (commercially known as Irgacure 651) upon exposure to UV-light in the range 285–370 nm. DMPA is classified as a Norrish type I photoinitiator (α-cleavage) frequently used in thiol–ene photopolymerization kinetic studies39 and thin-film photocurable coatings.40 Under UV-light excitation this initiator decomposes from its lowest triplet state into a benzoyl radical and a tertiary carbon-centered radical, which to a larger or lesser extent have the ability to abstract hydrogens from thiol groups and produce reactive thiyl radicals.41 However, fragmentation of the α,α-dimethoxy-benzyl radical often occurs yielding a methyl radical and a methyl benzoate radical which can also abstract hydrogen-atoms from thiols or add to double-bonds.9 Other intermediary non-radical dimer species are formed, such as the benzil and 1,2-diphenyl-1,1,2,2-tetramethoxyethane molecules, which may also act as transient (secondary) photoinitiators in the beginning of the initiation process.42
The photoinduced decay of a cleavage-type photoinitiator into primary free radicals is typically modeled as simple first-order reaction kinetics with decomposition rate constant, kd, which for useful purposes can be approximated to eqn (4a) adapted from literature19,43 to account for the exposure to polychromatic UV-light
| | 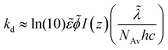 | (4a) |
| | 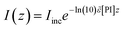 | (4b) |
where the overtilde denotes the weighted mean of each quantity accounting for the principal emission lines of the UV-lamp source exhibiting multi-wavelength spectral distribution. The symbol,
ε, represents the molar absorptivity of DMPA at each wavelength of initiation (
λ); 0 <
ϕ < 1 is the quantum yield for photoinitiation;
I(
z) is the UV-light irradiance available for photolysis as a function of sample depth (
z); [PI] is the transient concentration of DMPA independent of depth;
Iinc the incident UV-light intensity in units of power/area;
NAv denotes the Avogadro's number;
h is the Plank's constant; and,
c the speed of light. Although some values of
ϕ(365 nm) have been estimated for DMPA,
44,45 we cannot apply
eqn (4a) directly to our case study since the dependence
ϕ =
ϕ(
λ) is still unknown for the remaining emission lines. However, typical initiation rates for DMPA
46 are known to range from 10
−6 to 10
−3 M s
−1 giving
decomposition rate constants between 10
−5 to 10
−2 s
−1 when calculated for an initial photoinitiator concentration of 0.05 M (∼1.0 wt% of total reaction mixture) as used herein. We have firstly taken the lower limit offered by this interval since the initial concentration of photoinitiator in solution was considerably low. This assumption is also rationalized by the fact that all reactions were conducted in continuous presence of atmospheric oxygen which acts as natural quencher of photoexcited states of molecules and primary radicals, including the
benzoyl radical, thereby decreasing the amount of radical fragments available for initiation.
5 However, the choice of this value was verified inappropriate as the reaction became too slow when compared to the real experimental profiles. Increasing the value of
kd to 10
−3 s
−1 resulted in the opposite effect and the best value we could obtain was when
kd = 10
−4 s
−1 (
t1/2 ≈ 116 min) (
Fig. 5) as rising or diminishing the value of
kd negatively affected the reaction system kinetics (see section
X. of the Supplementary Information).
The rate coefficient for the decomposition of photoinitiator was then incorporated in a mechanistic model for numerical simulations of the overall reaction system (see later) and to obtain the rate of initiation for this particular set of experimental conditions (Ri = kd[PI]0 = 5.0 × 10−6 M s−1). From the calculated initiation rate and the known thiyl radical self-termination rate coefficient (2kt = 6.0 × 109 M−1 s−1), one obtains an approximation for the steady-state concentration of thiyl radicals, [RS˙]ss = (Ri/2kt)1/2 ≈ 2.9 × 10−8 M.47,48 The first order rate constant of hydrogen-abstraction from thiol by one of the two primary radical centers (I˙) is about kRSH1[RSH]0 = 2.4 × 107 s−1 for kRSH1 = 107 M−1 s−1 (r.t.) and [RSH]0 = 2.4 M, which compared to the overall termination rate parameter‡47, (2ktRi)1/2 ≈ 173 s−1, gives an absolute ratio of about 1.4 × 106, indicating that primary radicals formed upon photolysis of DMPA abstract hydrogen-atoms from thiol groups much faster than termination. However, given that either initiation rate and photoinitiator concentration at start are extremely low, then one might well expect that both the production and development of thiyl radicals will be kinetically controlled by propagation and chain-transfer reactions instead of initiation, i.e., Ri ≪ Rp + RCT. Therefore, throughout this work, we reasonably assume negligible thiol consumption during the initiation process, so that one thiol functional group selectively couples with a single molecule of limonene at the exo or endo double-bonds.
3.2 Observed kinetics
To the best of our knowledge, insufficient quantitative information is currently available in the literature about the absolute values of the intrinsic rate constants of the elementary steps (3)–(6) (Scheme 3) involving the reaction of 3-mercaptopropionate esters with the two unsaturated structures of limonene. Yet, a closer look at the detailed mechanism in Scheme 3 shows that the two sets of addition/elimination–abstraction reactions can be simplified into two overall representative equations by summation of the corresponding elementary chemical reactions as depicted in Scheme 4; where, k1,2 (k1 and k2), denote sub-operational parameters for the external (exo) and internal (endo) thiol–ene coupling routes, respectively. Unfortunately, these two empirical rate parameters are expressed as complex functions of the real intrinsic rate coefficients and equilibrium constants for each coupling route, which greatly complicate any attempt of individualized determination of the true rate coefficients. However, invoking ideal stoichiometry, formation of macromonomer 6 dictates that the net consumption in thiol functional groups should match an exact equal amount of limonene as a species by selective thiol–ene coupling at the two double bonds (i.e., [Lim] = [RSH]). This infers, from a more general perspective, that time-disappearance of limonene could be expressed as a mixed second-order rate law by mutual consumption of thiol–ene reactants:| | 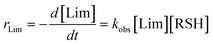 | (5) |
with, kobs, viewed here as a global operational rate parameter. The solution of eqn (5) obtained by integration of rLim with [Lim]0 = [RSH]0, provides the linear inverted model describing the time-depletion of limonene| | 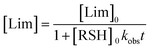 | (6) |
and linearization of eqn (6)viaeqn (7)| | 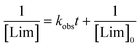 | (7) |
gives the observed rate parameter, kobs = 4.98 × 10−4 M−1 s−1 (Fig. 2), which is function of the reaction conditions for this particular thiol–ene system. Plotting of Δ[ene] vs. Δ[Lim] affords the empirical parameters, m1 and m2, which represent individual fractions of kobs assigned to each thiol–ene coupling route (Fig. 3) and are used to determine double bond selectivity. Consequently, the experimental data points describing the kinetic profiles (Fig. 4) could be reconstructed with extremely high fidelity, covering the entire span of discrete conversion data, by means of eqn (6) for the consumption of limonene and, using the expressions (8)–(10) for depletion of each alkene functional group.| | | [exo] = [exo]0 − m1([Lim]0 − [Lim]) | (8) |
| | | [endo] = [endo]0 − m2([Lim]0 − [Lim]) | (9) |
or,| | | [endo] = [Lim]0 + [Lim] − [exo] | (10) |
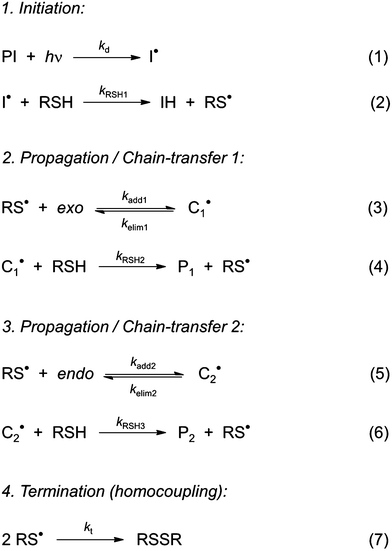 |
| | Scheme 3 Suggested step-wise mechanistic reaction sequence describing thiol–ene coupling between the two double bonds of (R)-(+)-limonene (1) and thiol functional groups (2 and 5). | |
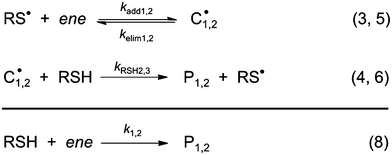 |
| | Scheme 4 Reduction of elementary addition/elimination–abstraction steps into two global thiol–ene coupling reactions. | |
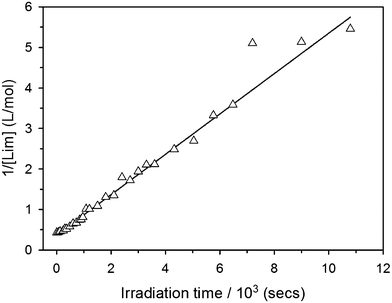 |
| | Fig. 2 Determination of the experimental second-order rate parameter, kobs, from linear regression of the reciprocal data points for the consumption of limonene (R2 = 0.98). | |
![Linear regression fits to the measured variables. Slopes: m1 = d[exo]/d[Lim] = 0.87 (R2 = 0.98) and m2 = d[endo]/d[Lim] = 0.13 (R2 = 0.90). Δ[ene] = [ene]0 − [ene]; and, m1 + m2 = 1.](/image/article/2013/RA/c3ra40696b/c3ra40696b-f3.gif) |
| | Fig. 3 Linear regression fits to the measured variables. Slopes: m1 = d[exo]/d[Lim] = 0.87 (R2 = 0.98) and m2 = d[endo]/d[Lim] = 0.13 (R2 = 0.90). Δ[ene] = [ene]0 − [ene]; and, m1 + m2 = 1. | |
 |
| | Fig. 4 Comparison between fitted curves and overlapped experimental concentration profiles obtained from kinetic evaluations with mono-functional (open signs and star) and tri-functional (closed markers) thiols mixed on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mole stoichiometry (group functionalities). DMPA (1.0 wt%) was used as photoinitiator and the samples exposed to a UV-light irradiance of 4.2 mW cm−2. For clarity the error bars were not plotted. Corresponding double bond conversion data points with errors can be found in sections VIII. and IX. of the Supplementary Information. 0.5 thiol–ene mole stoichiometry (group functionalities). DMPA (1.0 wt%) was used as photoinitiator and the samples exposed to a UV-light irradiance of 4.2 mW cm−2. For clarity the error bars were not plotted. Corresponding double bond conversion data points with errors can be found in sections VIII. and IX. of the Supplementary Information. | |
The remarkable consistent level of superposition between experimental results obtained from mono- and tri-functional thiol–ene systems in solution shows a clear independence of the thiol monomer functionality on conversion rate. By calculating the first derivative of the fitted concentration profiles and then making the ratio of the individual alkene consumption rates, r1,2 = −d[ene]/dt, provides a quantitative measure of the relative reactivity (selectivity) observed between the two distinct double bonds:
| | 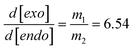 | (11) |
Double bond selectivity (eqn (11)) is independent of the conditions of initiation and is valid throughout the entire course of the reaction, although the absolute values of m1,2 and individual alkene consumption rates, r1,2, are specific for this set of experimental conditions. Because the reactions were performed in solution conditions under high stirring speed, the kinetic measurements are considered unaffected by build-up in viscosity developed at high thiol–ene conversions. Therefore, all kinetic coefficients in this work are assumed to remain constant throughout the reaction (i.e., no diffusional constraints).
3.3. Computational model simulations and parameter estimation
In order to verify the sequential mechanism proposed in Scheme 3 and give a better view of the kinetic behavior of the reaction system, numerical time-course model simulations were performed in COPASI and the computed curves compared with the experimental data profiles. First we entered the best value of kd = 10−4 s−1 we could attain for the photolysis reaction with DMPA accounting for the formation of a single active radical center (I˙), and from literature it is well-known that kRSH1 = 107 M−1 s−1 and kt = 3.0 × 109 M−1 s−1 at room-temperature for the first hydrogen-abstraction and thiyl self-termination reactions in solution, respectively.47,48 Under bulk reaction conditions the value of kt is often decreased by a factor of 10 since the reaction medium viscosity increases, as reported previously in other kinetic systems.49 Subsequently, the values of the second and third hydrogen-abstraction rate coefficients were both set to kRSH2,3 = 106 M−1 s−1,50 one order of magnitude inferior than the value of kRSH1, as two less reactive, sterically hindered, tertiary carbon-centered radicals are formed upon thiyl radical insertion into limonene. Even though accurate kinetic data are normally required to obtain fully reliable simulations, we believe this is a reasonable assumption, since: (i.) the reactivity of alkyl carbon-centered radicals towards hydrogen-abstraction from n-tributyltin hydride (n-Bu3SnH), here regarded as an analogous reference compound with respect to hydrogen-abstraction from thiol, generally follows the order: methyl > primary > secondary > tertiary;51 and, (ii.) the two tertiary carbon-centered radicals formed are expected to have lower reactivity than that of the benzoyl radical fragment resulting from photocleavage of DMPA. An additional support of this hypothesis comes from ‘free-radical clock measurements’ involving the (TMS)3SiH/Thiol Reducing System. It was shown that the primary 3-methyl-1-ene alkyl radical is more efficient in abstracting hydrogen-atoms from a variety of thiol compounds, exhibiting generally higher kRSH values, than the tertiary-substituted 1-methyl-cyclohexane-carbaldehyde acyl radical under similar reaction conditions.37 This evidence points out that the hydrogen-abstractability for a particular thiol–ene system depends on the duality thiol/carbon-centered radical in regard to the hydrogen-donor (thiol) and hydrogen-capture (carbon-radical) abilities.
The mechanistic model was initially tested by entering rate coefficients for addition and fragmentation reactions utilized in a previous kinetic study involving thiyl radical induced isomerization of monounsaturated oils,29 while keeping the remaining rate constants unchanged (Table 1). The output curves shown in Fig. 5-(a) are in excellent trend shape agreement with the experimental data, confirming the underlying mechanism, despite the expected deviations from the observed behavior. Next, we attempted at estimating the ‘apparent’ values of the unknown rate coefficients of the elementary step (3)–(6) accounting for addition, elimination and chain-transfer reactions by best-fitting the experimental data to the kinetic model using the parameter estimation routine that COPASI has built-in. It should be stressed at this point that our mechanistic analysis relies uniquely on relative quantities of the estimated rate coefficients rather than on their absolute values as these are often difficult to measure experimentally. This way, any unknown differences that might exist between the estimated and true rate parameters should be minimized when reporting them in relative terms while allowing the capture of the main fundamental phenomena responsible for the differences in selectivity observed experimentally. Numerical computations are particularly valuable in this regard when the elementary rate constants are absent from experimentation.33 The program was executed using the same literature values for the rate constants as performed in the first run until the best degree of convergence to all experimental data was reached simultaneously. The statistical analysis associated to the fitting process can be found in section XIII. of the Supplementary Information. A preliminary kinetic stability screening of the proposed reaction mechanism run in COPASI found no evidence of the existence of a steady-state regime. All three computed curves for the evolution of exo-, endo- and limonene (or thiol functional groups) are plotted graphically in Fig. 5-(b) and the final values of the estimated (‘apparent’) rate coefficients returned by COPASI are given in Table 1. Increasing the input values of kRSH2,3 from 106 to 107 M−1 s−1,37 does not influence the computed results for the addition/elimination and hydrogen-abstraction rate constants. A maximum value of [RS˙]max = 2.9 × 10−8 M was obtained from the simulation which is in excellent agreement with the steady-state concentration of thiyl radicals estimated in section 3.1. Within tolerance limits, the agreement between the two datasets seems remarkable, again validating the overall reaction scheme. The small discrepancies in the quality of the fitting were anticipated since the analytical treatment of the kinetics assumed ideal thiol–ene mole stoichiometry from start for the propagation and chain-transfer routes, which does not exactly correspond to the real conditions provided by the deterministic mechanism due to initiation. Therefore, the rate coefficients computed should not be regarded as effective (or true) parameters, inherent to the reaction mechanism, but merely as rough estimates and these should be accurately determined via experimentation, if possible, by locally isolating the elementary reactions accounting for the two addition/elimination and hydrogen-abstraction steps.
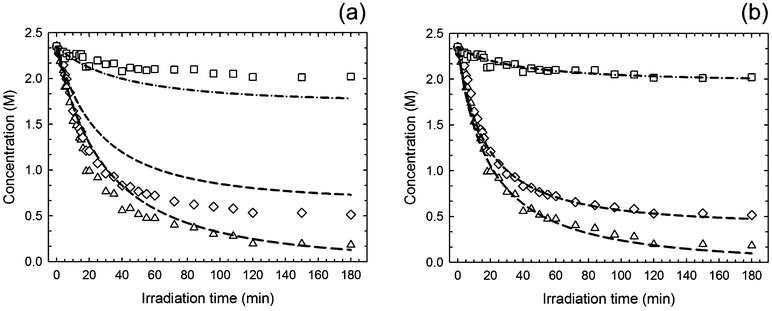 |
| | Fig. 5 Comparison between experimental data (symbols) and simulated model predictions (lines) for the photoreaction of a thiol–ene mixture based on (R)-(+)-limonene (1) and trithiol (5) on a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mole stoichiometry with respect to functional groups. Lim/RSH (triangles), exo-unsaturation (diamonds) and endo-unsaturation (squares). For clarity the error bars were not plotted. Numerically generated output curves based on literature kinetic coefficients from cis/trans-isomerization of monounsaturated oils are represented in plot (a) with kd = 10−4 s−1; and (b) simulation line fits to the experimental data via the estimated parameters presented in Table 1 with the fixed coefficients: kd = 10−4 s−1, kRSH1 = 107 M−1 s−1 and kt = 3.0 × 109 M−1 s−1. 0.5 thiol–ene mole stoichiometry with respect to functional groups. Lim/RSH (triangles), exo-unsaturation (diamonds) and endo-unsaturation (squares). For clarity the error bars were not plotted. Numerically generated output curves based on literature kinetic coefficients from cis/trans-isomerization of monounsaturated oils are represented in plot (a) with kd = 10−4 s−1; and (b) simulation line fits to the experimental data via the estimated parameters presented in Table 1 with the fixed coefficients: kd = 10−4 s−1, kRSH1 = 107 M−1 s−1 and kt = 3.0 × 109 M−1 s−1. | |
It is generally recognized for most alkyl radical addition reactions that double bond reactivity is independent of polar effects and controlled predominantly by the degree of substitution (steric effect) and partially by the stability of the carbon-centered radicals formed.51 For instance, the relative rates of addition of the methyl radical to several olefins have shown the following order in reactivity: isobutylene (1.1) > ethene (1.0) > trans-2-butene (0.33) ≈ trimethylethylene (0.32) > cis-2-butene (0.23) > 2,3-dimethyl-2-butene (0.2), which are also consistent with the trends in reactivity found in another source.52 Furthermore, it has been reported a decrease in the absolute addition rate constants by the methyl and tert-butyl radicals to 1,2-disubstituted and 1,1,2-trisubstituted alkenes by a factor of 5 to 15 when compared to radical addition onto 1,1-disubstituted alkenes (e.g., vinylidene C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond).53 Analogously, the same trend in reactivity should, in principle; hold true for the thiyl radical even though it is more electrophilic than the methyl radical. Hoyle and co-workers also have shown via real-time FT-IR measurements that consumption of 1-hexene (a monosubstituted terminal ene) proceeds about 13-times faster than trans-2-hexene and 25-times faster than trans-3-hexene based on initial equimolar C
C bond).53 Analogously, the same trend in reactivity should, in principle; hold true for the thiyl radical even though it is more electrophilic than the methyl radical. Hoyle and co-workers also have shown via real-time FT-IR measurements that consumption of 1-hexene (a monosubstituted terminal ene) proceeds about 13-times faster than trans-2-hexene and 25-times faster than trans-3-hexene based on initial equimolar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/RSH ratios.54 However, the differences in overall conversion rates was attributed not only because of a restricted stereochemical accessibility due to an increased degree of substitution of the double-bond, causing steric impediments for the approaching thiyl radical, but also given the presence of a reversible isomerization process. The existence of reversibility in thiyl radical additions onto olefins was first noticed by Sivertz and co-workers55 and then confirmed by Walling and Helmreich56 in the late 1950s. In the special case of cis/trans-isomerization involving 1,2-dialkyl substituted olefins the secondary carbon-centered radical conformers formed between the two isomeric Z/E-structures have short lifetimes and similarly low resonance stabilities which reduce the rate of chain transfer hydrogen-abstraction reaction and becomes the rate-limiting step.57 According to our simulated kinetic results, we propose that with limonene (which bears two sterically hindered non-isomerizable unsaturations) the differences in relative reactivity are attributed both to steric hindrance effects, which control the position of thiyl radical attack within the double bonds; and, relative energy of the two intermediary insertion products formed immediately after thiyl radical addition, which determines the extent of the elimination reaction rate. We suggest that the electrophilic thiyl radical regioselectively attacks the primary (less substituted) terminal α-carbon of the vinylidene bond driving the reversible addition-elimination equilibrium towards the formation of a resonance stabilized carbon-centered radical intermediate (C1˙). This shift in the forward direction is driven by a decrease in relative energy of the resulting carbon radical adduct resulting in higher consumption of exocyclic double bonds. On the contrary, the internal unsaturation already exists in a 1,1,2-trisubstituted form, locked inside the cyclohexenyl ring, and favored thiyl radical insertion to the secondary (less crowded) α-carbon-atom again yields a resonance stabilized tertiary carbon-centered radical (C2˙) which in this case fragments back into its former state as reactive species much faster than the first intermediate adduct radical (C1˙) as the result of a smaller activation energy barrier required for elimination.36 Since both tertiary carbon radicals appear to share comparable hydrogen-abstraction abilities for the given thiol (Table 1), probably ascribed to relatively equivalent resonance stabilization, then differences in reactivity may be tentatively explained by means of extent of substitution of the double bond, with thiyl radicals adding faster to enes containing primary isolated carbons than to internal secondary ones and to differences in relative energy of the two thioether carbon radical intermediates. As stated in a previous study, each intermediary carbon-centered radical may very well share relatively comparable resonance stabilization, but reveal different relative energies as consequence of interactions between nonbonded atoms which affect steric strain.36 The high extent of reversibility of the second propagation step (kelim2/kadd2[exo]0 ≈ 2.0 × 102) over the first (kelim1/kadd1[endo]0 ≈ 18) correlates well with the previous trend in reactivity for the methyl radical as both the trans-2-butene and trimethylethylene moieties exhibit similarly low relative addition rates when compared with the isobutylene moiety, indicative of dominance of fragmentation over addition. We also verified a ratio in thiyl radical addition rate constants (kadd1/kadd2) of about 1.4 slightly in favor of consumption of the exo-olefinic bond, whereas the ratio in elimination constants (kelim2/kelim1) was about 7.8 appreciably favoring fragmentation to the endocyclic unsaturation. The substantially high increment of the second elimination rate constant over the first kinetically outweighs the second thiyl–ene propagation route (step 5) also indicating that the main factor governing the reactivity of the two unsaturations with respect to thiol–ene coupling is the relative energy of the C2˙ radical as opposed to intermolecular RS˙ addition which is controlled by steric effects. Indeed, the ‘apparent’ equilibrium constants for addition/elimination (K1,2 = kadd1,2/kelim1,2, in M−1), revealed that K1 ≈ 11.2 × K2 fully supportive of the preceding analysis. Consequently, the rates of the two hydrogen-abstraction reactions occurring immediately after each insertion/elimination step are controlled predominantly by the concentration levels of the ensuing tertiary carbon radicals which both appear to display equivalent radical stabilities towards hydrogen-abstraction (kRSH2/kRSH3 ≈ 0.91) given their structural resemblance. This indicates that the rate-limiting step controlling the overall reaction is the third hydrogen-abstraction reaction promoted by the second insertion product radical given that it is the slowest step.
C/RSH ratios.54 However, the differences in overall conversion rates was attributed not only because of a restricted stereochemical accessibility due to an increased degree of substitution of the double-bond, causing steric impediments for the approaching thiyl radical, but also given the presence of a reversible isomerization process. The existence of reversibility in thiyl radical additions onto olefins was first noticed by Sivertz and co-workers55 and then confirmed by Walling and Helmreich56 in the late 1950s. In the special case of cis/trans-isomerization involving 1,2-dialkyl substituted olefins the secondary carbon-centered radical conformers formed between the two isomeric Z/E-structures have short lifetimes and similarly low resonance stabilities which reduce the rate of chain transfer hydrogen-abstraction reaction and becomes the rate-limiting step.57 According to our simulated kinetic results, we propose that with limonene (which bears two sterically hindered non-isomerizable unsaturations) the differences in relative reactivity are attributed both to steric hindrance effects, which control the position of thiyl radical attack within the double bonds; and, relative energy of the two intermediary insertion products formed immediately after thiyl radical addition, which determines the extent of the elimination reaction rate. We suggest that the electrophilic thiyl radical regioselectively attacks the primary (less substituted) terminal α-carbon of the vinylidene bond driving the reversible addition-elimination equilibrium towards the formation of a resonance stabilized carbon-centered radical intermediate (C1˙). This shift in the forward direction is driven by a decrease in relative energy of the resulting carbon radical adduct resulting in higher consumption of exocyclic double bonds. On the contrary, the internal unsaturation already exists in a 1,1,2-trisubstituted form, locked inside the cyclohexenyl ring, and favored thiyl radical insertion to the secondary (less crowded) α-carbon-atom again yields a resonance stabilized tertiary carbon-centered radical (C2˙) which in this case fragments back into its former state as reactive species much faster than the first intermediate adduct radical (C1˙) as the result of a smaller activation energy barrier required for elimination.36 Since both tertiary carbon radicals appear to share comparable hydrogen-abstraction abilities for the given thiol (Table 1), probably ascribed to relatively equivalent resonance stabilization, then differences in reactivity may be tentatively explained by means of extent of substitution of the double bond, with thiyl radicals adding faster to enes containing primary isolated carbons than to internal secondary ones and to differences in relative energy of the two thioether carbon radical intermediates. As stated in a previous study, each intermediary carbon-centered radical may very well share relatively comparable resonance stabilization, but reveal different relative energies as consequence of interactions between nonbonded atoms which affect steric strain.36 The high extent of reversibility of the second propagation step (kelim2/kadd2[exo]0 ≈ 2.0 × 102) over the first (kelim1/kadd1[endo]0 ≈ 18) correlates well with the previous trend in reactivity for the methyl radical as both the trans-2-butene and trimethylethylene moieties exhibit similarly low relative addition rates when compared with the isobutylene moiety, indicative of dominance of fragmentation over addition. We also verified a ratio in thiyl radical addition rate constants (kadd1/kadd2) of about 1.4 slightly in favor of consumption of the exo-olefinic bond, whereas the ratio in elimination constants (kelim2/kelim1) was about 7.8 appreciably favoring fragmentation to the endocyclic unsaturation. The substantially high increment of the second elimination rate constant over the first kinetically outweighs the second thiyl–ene propagation route (step 5) also indicating that the main factor governing the reactivity of the two unsaturations with respect to thiol–ene coupling is the relative energy of the C2˙ radical as opposed to intermolecular RS˙ addition which is controlled by steric effects. Indeed, the ‘apparent’ equilibrium constants for addition/elimination (K1,2 = kadd1,2/kelim1,2, in M−1), revealed that K1 ≈ 11.2 × K2 fully supportive of the preceding analysis. Consequently, the rates of the two hydrogen-abstraction reactions occurring immediately after each insertion/elimination step are controlled predominantly by the concentration levels of the ensuing tertiary carbon radicals which both appear to display equivalent radical stabilities towards hydrogen-abstraction (kRSH2/kRSH3 ≈ 0.91) given their structural resemblance. This indicates that the rate-limiting step controlling the overall reaction is the third hydrogen-abstraction reaction promoted by the second insertion product radical given that it is the slowest step.
This simple analytic interpretation of the mechanism supported by numerical kinetic modeling clearly highlights the existence of a competing steric effect of both types of ene structures (internal vs. external) towards thiyl radical insertion in straight connection with differences in relative energies of the two intermediary carbon radicals. Our analysis points out that the latter contribution plays a superlative role in the overall reaction kinetics most likely explaining the difference in reactivity observed for the two distinct alkenes. Computational thermodynamics (energetics) should be able to support our kinetic findings while providing further insights about the fundamental factors governing the two reversible additions and chain-transfer steps in the same manner as reported recently for a series of other alkene structures.35
After demonstrating numerically the appropriateness of our empirical and mechanistic approaches in the study of the thiol–ene kinetics of D-limonene we proceeded to test the effect of several parameters such as changes in the values of the ‘apparent’ rate coefficients accounting for addition-elimination and hydrogen-abstraction steps, as well as constant ratios, and their relative impact on the final concentration profiles. From a first inspection, we found the model extremely sensitive towards small changes in the rate coefficient for the decomposition of DMPA and differences in kinetic constants for the second and third hydrogen-abstraction steps as well as perturbations in the two individual equilibrium constants; but remains virtually unresponsive to variations in the ‘apparent’ values of the addition-elimination coefficients as long as K1,2 and the remaining parameters are hold constant. For example, locking K1 = 2.37 × 10−2 M−1 and then increasing kadd1 or kelim1 separately does not have any noticeable effect on the model. Yet, independently reducing these parameters bellow the lower limit offered by the intervals: 6.0 × 105 < kadd1 (M−1 s−1) < 2.0 × 106 and 1.75 × 107 < kelim1 (s−1) < 8.5 × 107 results in tremendous variations into the model. Subjecting the second addition-elimination reaction to the same treatment (locking K2 = 2.12 × 10−3 M−1) resulted in similar outcomes bellow the lower limit of the ranges: 2.8 × 104 < kadd2 (M−1 s−1) < 1.4 × 106 and 2.2 × 107 < kelim2 (s−1) < 6.6 × 108. This analysis suggests that the true kinetic parameters for the equilibrium reactions may be circumscribed to the lower bound offered by those regions given that an increase in kadd1,2 or kelim1,2 has no effective response from the model. Also, high variations in the first hydrogen-abstraction rate constant, kRSH1, shows no detectable kinetic influence in the model whatsoever, a clear indication that a rough guess for its value may suffice for practical purposes. The results of a general sensitivity analysis performed in COPASI can be found in section XIII. of the Supplementary Information with notes.
3.4. Analytical interpretation of the mechanism
Contrarily to a cis/trans-isomerization process catalyzed by thiyl radicals,47,48 the ratio between individual equilibrium constants for the two propagation reactions, Kr = K1/K2, which allows determination of the addition/elimination rate coefficients, cannot be obtained directly from experimental kinetic data at longer times for each unsaturation moiety. Instead, we derive a simple expression (eqn (19)) from the sequential reaction mechanism that relates both chain-transfer rate coefficients and individual equilibrium constants in an effort to determine double bond selectivity by applying the steady-state approximation. Parallel consumption of alkene functional groups via a competing chain-growth route is not considered here as limonene presents very low propensity for radical homopolymerization,5 although is rather common in other types of thiol–ene photopolymerization systems specially those involving thiol–(meth)acrylate based monomers.58 We have also excluded from the mechanistic model the elementary reactions accounting for: (i.) direct thiol cleavage by UV-irradiation; (ii.) trapping of primary radicals by dissolved oxygen; (iii.) addition of primary radicals to the alkene bonds; and, (iv.) terminations by combination of thiyl-carbon and carbon-carbon radicals; as these are secondary effects and should be regarded as of minor importance.48 Additionally, it is anticipated that during initiation the decomposition of photoinitiator will prevail over the UV-induced scission of the RS–H bond as thiols excite predominantly at ∼254 nm light59–61 and at this wavelength the relative UV-light intensity emitted by the lamp source lies below 10%. The same rationale applies for the photolytic dissociation of disulfides formed during thiyl radical bimolecular self-reaction as these absorb essentially at the same wavelength as thiols.62
Under continuous UV-irradiation the stationary-state condition (i.e., when Ri = Rt and d[ene]/d[RSH] = 1) is reached in a relatively short time period, where the two following relations
| | 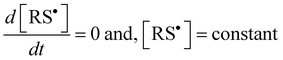 | (12a) |
| | 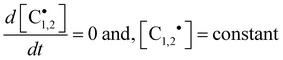 | (12b) |
hold for most of the time-course of the reaction. The consumption rate of each
alkene functional group by propagation should; therefore, remain identical to the production rate of the corresponding coupled product, P
1 or P
2, by chain-transfer as represented by
eqn (13):
| | 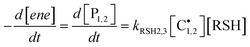 | (13) |
The ratio between formation rates of the two coupled products from chain-transfer steps provides the following expression:
| | 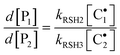 | (14) |
When the individual rates of propagation are essentially equal to the corresponding chain-transfer rates, Rp1,2 = RCT1,2, the concentration of intermediate carbon centered radicals is described by eqn (15)
| | 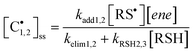 | (15) |
and since we know the ratio of [
exo]
0/[
endo]
0 = 1, as provided by [
exo]
0 + [
endo]
0 = 2[Lim]
0, then the observed selectivity (
eqn (11)), can be approximated to
eqn (14)viaeqn (16) derived from the mechanism:
| |  | (16) |
The denominator of eqn (15) reflects how the consumption of intermediary carbon-centered radicals is distributed along the two propagations and chain-transfer routes, since C1,2˙ competitively partitions in terms of first order kinetic parameters with respect to β-fragmentation (kelim1,2, s−1) and hydrogen-transfer (kRSH2,3[RSH], s−1) in the two thiol–ene coupling channels. Hence, the values of these two rate parameters determine which reaction pathway contributes mostly for the overall propagation–chain-transfer kinetics and define the relative reactivity of the two unsaturations. For example, when elimination by β-fragmentation, kf, is considered insignificant compared with chain-transfer to the thiol (i.e., kf ≪ kCT[RSH]), as commonly encountered in kinetic photopolymerization studies involving thiol–allyl ether, thiol–vinyl ether, thiol–(meth)acrylate, thiol–norbornene and thiol–vinyl silazane systems;21,39,49,58–60,63 then, the rate-limiting step and reaction order of the overall polymerization rate are customarily determined by the steady-state relationship
| | 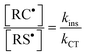 | (17) |
where,
kins and
kCT, denote rate constants for addition and chain-transfer reactions, respectively. In the opposite side, when fragmentation vastly overcomes chain-transfer (
i.e.,
kf ≫
kCT[RSH]), as frequently associated to multi-substituted
olefins,
47,48,64 then the concentration ratio between carbon and thiyl centered radicals is essentially proportional to the concentration of ene, given by:
| | 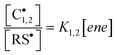 | (18) |
In fact, results from a previous kinetic study involving the thiyl-radical induced cis/trans-isomerization of fatty-acid methyl esters indicate that kCT[RSH] ≪ kEf, since hydrogen-abstraction was determined as the rate-limiting step.29 Additionally, from our real-time model simulations fitted to the experimental data, the estimated values of kRSH2,3[RSH]0 ≪ kelim1,2 (in s−1), decreasing as the reaction proceeds, suggesting that our reaction system tends towards the extreme case represented by eqn (18). This means that expression (16) can be further reduced into a more simplified analytic form:
| | 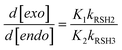 | (19) |
Eqn (19) describes the co-dependence of the selectivity (again expressed as relative consumption rate of ene functional groups) on the individual equilibrium constants, K1,2, and hydrogen-abstraction rate coefficients, kRSH2,3, for each thiol–ene coupling route. Replacing the kinetic parameters by the estimated (‘apparent’) values presented in Table 1 and initial concentration of thiol groups, one obtains for eqn (16), d[exo]/d[endo] ≈ 10.1, and for eqn (19), d[exo]/d[endo] ≈ 10.22, indicating a much higher coupling efficiency for the first reaction route than for the second involving the trisubstituted double bond. Also, we can clearly see that these two quantities differ only marginally from each other demonstrating that both chain-transfer routes contribute very little to the relative double bond reactivity which is determined mostly by propagation. Moreover, the two figures represent slightly less than the double of the observed selectivity (eqn (11)) which proves the suitability of our mechanistic approach in describing the global kinetics. Overall, this analysis agrees well with the following boundary condition for the relative reactivity derived from the mechanism (eqn (16)), when kelim1,2 → 0 (lower limit) or kRSH2,3[RSH] → 0 (upper limit):
| | 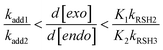 | (20) |
One should note; however, that the numerical values returned by eqn (16) and (19) are also a manifestation of the stationary-state condition with contribution of the estimated model parameters which are affected by computed statistical fluctuations upon execution of the recursive data fitting procedure to the experimental data (see section XIII. of the Supplementary Information). These variations necessarily add a certain degree of uncertainty to the calculated selectivity based on the mechanism which may well explain the small deviation from the measured value.
4. Conclusions
In this work we have systematically examined the kinetics of free-radical thiol–ene photo-additions between D-limonene and two mono-/tri-functional thiol monomers bearing a propionate ester moiety. According to our empirical findings, thiol–ene coupling at the exo-olefinic bond proceeds about 6.5 times faster than at the endocyclic unsaturation in solution conditions. Numerical time-course simulations of the reaction system revealed to be a valuable modeling tool both in describing the overall kinetics and estimating the individual rate parameters for propagation and chain-transfer steps, those of which are still unknown for this particular thiol–ene system. The kinetic behavior observed experimentally was successfully captured by means of a steady-state analytic model derived from the fundamental thiol–ene mechanism conceived for limonene. We propose that the differences observed in double bond conversion are attributed predominantly to a higher relative energy of the second thioether carbon-radical intermediate (C2˙) as opposed to the first carbon radical (C1˙); and, partially to steric hindrance effects which kinetically control thiyl radical insertion onto each of the two distinct double bonds. The third hydrogen-abstraction reaction was identified as the rate-determining step controlling the overall reaction. Reasonable reaction rates were achieved with no significant influence of side-reactions which demonstrates the suitability of the thiol–ene reaction for network forming purposes from D-limonene. The kinetic investigations undertaken in this study will find widespread use in mechanistic and polymer synthesis applications from limonene or any other diolefinic substrate regarding thiol–ene systems. Expansion of this concept to the synthesis of thiol–ene networks from D-limonene and other terpenes is currently in progress in our lab.
Acknowledgements
We kindly acknowledge financial support from the Swedish Research Council (Vetenskapsrådet), grant # 621-2007-5723. The authors would like to thank Mr. Marcus Jawerth for his valuable technical assistance in spectral NMR acquisitions. Mr. Sonny Jonsson is acknowledged for his helpful discussions and widespread knowledge of photochemistry.
References
-
M. N. Belgacem and A. Gandini, in Monomers, Polymers and Composites from Renewable Resources, ed. M. N. Belgacem and A. Gandini, Elsevier, Amsterdam, 2008, ch. 2, pp. 17–38 Search PubMed.
- R. T. Mathers, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 1–15 CrossRef CAS.
- A. Gandini, Green Chem., 2011, 13, 1061–1083 RSC.
-
IARC Monographs on the Evaluation of Carcinogenic Risks to Humans, World Health Organization, Lyon, 1993, vol. 56, pp. 135–162 Search PubMed.
-
G. Odian, in Principles of Polymerization, ed. N. J. Hoboken, 4th edn, John Wiley & Sons, Inc., New Jersey, 2004, ch. 3, pp. 275–279 Search PubMed.
- M. Firdaus, L. M. de Espinosa and M. A. R. Meier, Macromolecules, 2011, 44, 7253–7262 CrossRef CAS.
- M. Firdaus and M. A. R. Meier, Green Chemistry, 2013, 15, 370–380 RSC.
- T. Posner, Ber. Dtsch. Chem. Ges., 1905, 38, 646–657 CrossRef.
- C. E. Hoyle, T. Y. Lee and T. Roper, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 5301–5338 CrossRef CAS.
- C. E. Hoyle, A. B. Lowe and C. N. Bowman, Chem. Soc. Rev., 2010, 39, 1355–1387 RSC.
- N. Moszner, W. Schoeb and V. Rheinberger, Polym. Bull., 1996, 37, 289–295 CrossRef CAS.
- A. Gress, A. Voelkel and H. Schlaad, Macromolecules, 2007, 40, 7928–7933 CrossRef CAS.
- A. Gress and H. Schlaad, Polym. Prepr., 2008, 49, 230–231 CAS.
- K. L. Killops, L. M. Campos and C. J. Hawker, J. Am. Chem. Soc., 2008, 130, 5062–5064 CrossRef CAS.
-
A. F. Jacobine, in Thiol-ene photopolymers, Elsevier, London, 1993, vol. 3, ch. 7, pp. 219–268 Search PubMed.
- C. E. Hoyle and C. N. Bowman, Angew. Chem., Int. Ed., 2010, 49, 1540–1573 CrossRef CAS.
- M. J. Kade, D. J. Burke and C. J. Hawker, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 743–750 CrossRef CAS.
- M. A. Cole and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 4325–4333 CrossRef CAS.
- T. F. Scott, C. J. Kloxin, R. B. Draughon and C. N. Bowman, Macromolecules, 2008, 41, 2987–2989 CrossRef CAS.
- A. F. Jacobine, D. M. Glaser, P. J. Grabek, D. Mancini, M. Masterson, S. T. Nakos, M. A. Rakas and J. G. Woods, J. Appl. Polym. Sci., 1992, 45, 471–483 CrossRef CAS.
- N. B. Cramer, S. K. Reddy, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 7964–7969 CrossRef CAS.
- J. A. Carioscia, L. Schneidewind, C. O'Brien, R. Ely, C. Feeser, N. Cramer and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 5686–5696 CrossRef CAS.
- N. Simpson, M. Takwa, K. Hult, M. Johansson, M. Martinelle and E. Malmstroem, Macromolecules, 2008, 41, 3613–3619 CrossRef CAS.
-
A. F. Jacobine, D. M. Glaser and S. T. Nakos, ACS Symp. Ser., 1990, 417, ch. 13, pp. 160–175 Search PubMed.
- D. W. Janes, K. Shanmuganathan, D. Y. Chou and C. J. Ellison, ACS Macro Lett., 2012, 1, 1138–1142 CrossRef CAS.
- P. A. Fokou and M. A. R. Meier, Macromol. Rapid Commun., 2008, 29, 1620–1625 CrossRef CAS.
- U. Biermann, J. O. Metzger and M. A. R. Meier, Macromol. Chem. Phys., 2010, 211, 854–862 CrossRef CAS.
- U. Biermann, M. A. R. Meier, W. Butte and J. O. Metzger, Eur. J. Lipid Sci. Technol., 2011, 113, 39–45 CrossRef CAS.
- M. Claudino, M. Johansson and M. Jonsson, Eur. Polym. J., 2010, 46, 2321–2332 CrossRef CAS.
- M. Claudino, I. van der Meulen, S. Trey, M. Jonsson, A. Heise and M. Johansson, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 16–24 CrossRef CAS.
- S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074 CrossRef CAS.
-
L. A. H. Petzold, LSODA (Livermore Solver of Ordinary Differential Equations), Livermore, CA, 1997 Search PubMed.
- P. Mendes, S. Hoops, S. Sahle, R. Gauges, J. Dada and U. Kummer, Methods Mol. Biol., 2009, 500, 17–59 CAS.
- B. Giese, Angew. Chem., 1983, 95, 771–782 CrossRef CAS.
- B. H. Northrop and R. N. Coffey, J. Am. Chem. Soc., 2012, 134, 13804–13817 CrossRef CAS.
- T. M. Roper, C. A. Guymon, E. S. Joensson and C. E. Hoyle, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 6283–6298 CrossRef CAS.
- C. Chatgilialoglu, Helv. Chim. Acta, 2006, 89, 2387–2398 CrossRef CAS.
- O. Okay and C. N. Bowman, Macromol. Theory Simul., 2005, 14, 267–277 CrossRef CAS.
- N. B. Cramer, T. Davies, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 4631–4636 CrossRef CAS.
-
N. S. Allen and M. Edge, in UV and electron beam curable pre-polymers and diluent monomers: classification, preparation and properties, Elsevier, London, 1993, vol. 1, ch. 5, pp. 236–237 Search PubMed.
- H. Fischer, R. Baer, R. Hany, I. Verhoolen and M. Walbiner, J. Chem. Soc., Perkin Trans. 2, 1990, 787–798 RSC.
- V. Mucci and C. Vallo, J. Appl. Polym. Sci., 2012, 123, 418–425 CrossRef CAS.
- A. Boddapati, S. B. Rahane, R. P. Slopek, V. Breedveld, C. L. Henderson and M. A. Grover, Polymer, 2011, 52, 866–873 CrossRef CAS.
- J. L. Faria and S. Steenken, J. Chem. Soc., Perkin Trans. 2, 1997, 1153–1159 RSC.
-
M. D. Goodner and C. N. Bowman, ACS Symp. Ser., 1998, vol. 713, ch. 14, pp. 220–231 Search PubMed.
- T. M. Lovestead, K. A. Berchtold and C. N. Bowman, Macromol. Theory Simul., 2002, 11, 729–738 CrossRef CAS.
- C. Chatgilialoglu, A. Altieri and H. Fischer, J. Am. Chem. Soc., 2002, 124, 12816–12823 CrossRef CAS.
- C. Chatgilialoglu, A. Samadi, M. Guerra and H. Fischer, ChemPhysChem, 2005, 6, 286–291 CrossRef CAS.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3673–3680 CrossRef CAS.
-
A. F. Parsons, in An Introduction to Free Radical Chemistry, Blackwell Science, Oxford, 2000 Search PubMed.
-
J. Fossey, D. Lefort and J. Sorba, Free Radicals in Organic Chemistry, Wiley, Chichester, UK, 1995 Search PubMed.
-
K. U. Ingold, in Free Radicals, ed. J. K. Kochi, Wiley-Interscience; John Wiley & Sons, Inc., New York, 1973, vol. 1, ch. 2, pp. 91–93 Search PubMed.
- H. Fischer and L. Radom, Angew. Chem., Int. Ed., 2001, 40, 1340–1371 CrossRef CAS.
- T. M. Roper, T. Y. Lee, C. A. Guymon and C. E. Hoyle, Macromolecules, 2005, 38, 10109–10116 CrossRef CAS.
- C. Sivertz, W. Andrews, W. Elsdon and K. Graham, J. Polym. Sci., 1956, 19, 587–588 CrossRef CAS.
- C. Walling and W. Helmreich, J. Am. Chem. Soc., 1959, 81, 1144–1148 CrossRef CAS.
- K. Griesbaum, Angew. Chem., Int. Ed. Engl., 1970, 9, 273–287 CrossRef CAS.
- L. Lecamp, F. Houllier, B. Youssef and C. Bunel, Polymer, 2001, 42, 2727–2736 CrossRef CAS.
- N. B. Cramer and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 3311–3319 CrossRef CAS.
- N. B. Cramer, S. K. Reddy, M. Cole, C. Hoyle and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 5817–5826 CrossRef CAS.
- A. K. O'Brien, N. B. Cramer and C. N. Bowman, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 2007–2014 CrossRef CAS.
- N. A. Rosenthal and G. Oster, J. Am. Chem. Soc., 1961, 83, 4445–4448 CrossRef CAS.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3681–3687 CrossRef CAS.
-
J. L. Kice, in Free Radicals, ed. J. K. Kochi, Wiley-Interscience; John Wiley & Sons, Inc., New York, 1973, vol. 2, ch. 24, pp. 720–724 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: 1H NMR spectra of: I. (R)-(+)-limonene (1); II.iso-tridecyl 3-mercaptopropionate (2); III. TMP-trimercaptopropionate (5); IV. and V. initial thiol–ene mixtures of compounds 1 with 2 or 5 in CDCl3 solution (respectively); VI. and VII. final thiol–ene product solutions at different reaction times (representative spectra). VIII. average kinetic conversion data; IX. time-conversion plots of exo, endo and (exo + endo); X. effect of changes in the value of kd (numerical simulations) in the overall reaction kinetics; XI. derivation of the empirical expressions for the consumption of exo- and endo-double bonds by free-radical thiol–ene coupling; XII. principal kinetic equations derived from the reaction mechanism; XIII. computer numerical simulations in COPASI (input and output data, parameter estimation results and sensitivity analysis); and, XIV. Supplementary Information references. See DOI: 10.1039/c3ra40696b |
| ‡ Expressed as the reciprocal of the average radical lifetime, τ = (2ktRi)−1/2 = (2kt[RS˙]i)−1 ≈ 5.8 × 10−3 s. |
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in an anti-Markovnikov fashion (propagation) forming a nucleophilic β-carbon centered radical intermediate (RC˙) which easily captures the electron-poor hydrogen from another weak S–H bond regenerating the thiyl radical (chain-transfer) and gives the final stable thioether (C–S) coupled product. The successive propagation–chain-transfer events allow the mechanism to be repeated in a cyclic reaction sequence until full exhaustion of reactant thiol–ene groups from a starting stoichiometric mixture. Termination reactions can occur via combination of any two intervening radicals (β-carbon and/or thiyl) evocative of a bimolecular termination rate kinetics; although, other yet unidentified mechanisms may also be involved.19
C double bond in an anti-Markovnikov fashion (propagation) forming a nucleophilic β-carbon centered radical intermediate (RC˙) which easily captures the electron-poor hydrogen from another weak S–H bond regenerating the thiyl radical (chain-transfer) and gives the final stable thioether (C–S) coupled product. The successive propagation–chain-transfer events allow the mechanism to be repeated in a cyclic reaction sequence until full exhaustion of reactant thiol–ene groups from a starting stoichiometric mixture. Termination reactions can occur via combination of any two intervening radicals (β-carbon and/or thiyl) evocative of a bimolecular termination rate kinetics; although, other yet unidentified mechanisms may also be involved.19
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 with respect to thiol–ene functionalities were prepared by mixing corresponding mole amounts of each reactant in 50 wt% of d-chloroform (CDCl3) and the resulting solution supplemented with 1.0 wt% of DMPA as photoinitiator. A volume of 2.0 ml from each of the two stock solutions was transferred to small glass vessels of cylindrical geometry (40 × 12 mm) used as photochemical reactors. The samples were protected from visible ambient light before UV-irradiation.
0.5 with respect to thiol–ene functionalities were prepared by mixing corresponding mole amounts of each reactant in 50 wt% of d-chloroform (CDCl3) and the resulting solution supplemented with 1.0 wt% of DMPA as photoinitiator. A volume of 2.0 ml from each of the two stock solutions was transferred to small glass vessels of cylindrical geometry (40 × 12 mm) used as photochemical reactors. The samples were protected from visible ambient light before UV-irradiation.
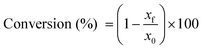
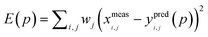
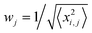 is the mean square weight of each data column, and, yi,j(p), the corresponding simulated value. The subscripts i and j represent rows and columns in the dataset, respectively. The mean square weighing method was chosen because it assures that all data columns containing small and large values contribute with equal weight to the objective function. Computationally predicted rate constants with calculated statistics are given in section XIII. of the Supplementary Information.
is the mean square weight of each data column, and, yi,j(p), the corresponding simulated value. The subscripts i and j represent rows and columns in the dataset, respectively. The mean square weighing method was chosen because it assures that all data columns containing small and large values contribute with equal weight to the objective function. Computationally predicted rate constants with calculated statistics are given in section XIII. of the Supplementary Information.


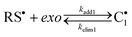

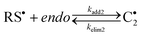

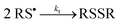
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OCH2CH2S˙) in order to establish a direct relationship between alkene structure and reactivity. Preliminary conversion data displayed in Fig. 1, obtained from the photoreaction of D-limonene (1) with a monothiol, C13MP (2), mixed on a half-mole alkene group stoichiometry with respect to the thiol, highlights a superior reactivity of the terminal vinylidene bond over the internal cyclic ene which reacts at much lower rate. As seen, the terminal (exocyclic) ene achieves almost 80% conversion after 180 min of UV-irradiation, whereas the internal (endocyclic) ene reacts more slowly reaching only 10% conversion after the same reaction period. The observed differences in conversion can be ascribed to a higher regioselectivity of the exocyclic unsaturation toward thiol addition as previously reported.6 It is well-known that free-radicals preferentially attack the less substituted α-carbon atom of alkenes, which is also valid for electrophilic radicals, indicating that regioselectivity is guided mainly by steric effects.34 This explains why most β-thioether products resulting from free-radical thiol–ene coupling of unsymmetrical monosubstituted olefins with alkyl thiols are predominantly secondary in structure exhibiting less exothermicities than primary β-thioether products despite of the latter chemical structure is thermodynamically more stable (more exothermic).35 However, such highly contrasting conversion levels observed for the two olefins in D-limonene cannot be ascribed solely to differences in the steric crowding of the corresponding substituents. Diverse literature studies10,35–37 have shown that the reactivity of a given alkene towards a particular thiol depends on the combinatory effect of a series of elements such as: (i.) chemical structure of the thiol monomer (RSH) as a hydrogen-transfer agent, which controls the ability to donate hydrogen-atoms with respect to RS–H bond-dissociating energy (BDE) due to substituents effects; (ii.) stability, size, polarity and electrophilicity of the thiyl radical RS˙, also determined by the chemical nature of the substituent moiety attached to the sulfur atom; (iii.) location, symmetry, electron-density and conformation of the alkene group (terminal, internal, conjugated, non-conjugated, and substituted), which is responsible for steric hindrance, steroelectronic factors, ring strain energy and ability to partake in side reactions (e.g., competing homolymerization); and, (iv.) geometry, relative energy and relative resonance stability of the intermediate carbon-centered radical adduct formed upon thiyl radical insertion onto the double bond, which determine the propensity for back elimination (β-fragmentation) versus hydrogen-capture ability from a thiol group. For example, the electron density of the ene group and carbon radical stability has been proposed in a previous work21 to explain differences in the propagation-to-chain-transfer ratio, kp/kCT, observed for distinct thiol–ene photopolymerization systems, which also influence gel-point formation.38 Accordingly, the magnitude of kp correlates with the electron density of the reactive ene whereas kCT accounts mainly for the stability of the thioether carbon radical.21 In order to better understand which factors control the thiol–ene reactivity of the two exo and endo double bonds in limonene, we have divided this work into three interconnected parts. The first provides a quantitative measure of the observed double bond selectivity (or relative reactivity) in solution from experimental conversion data resulting from the photo-initiated reaction between D-limonene (1) and a tri-functional propionate ester mercaptan (5), as depicted in Scheme 2. The second, attempts to estimate numerically rate coefficients intrinsic to a proposed reaction scheme describing the observed reaction kinetics and then validate the deterministic model. Finally, we interpret the sequential propagation–chain-transfer elementary steps to verify if the relative reactivity obtained from the detailed mechanism explains the measured selectivity.
OCH2CH2S˙) in order to establish a direct relationship between alkene structure and reactivity. Preliminary conversion data displayed in Fig. 1, obtained from the photoreaction of D-limonene (1) with a monothiol, C13MP (2), mixed on a half-mole alkene group stoichiometry with respect to the thiol, highlights a superior reactivity of the terminal vinylidene bond over the internal cyclic ene which reacts at much lower rate. As seen, the terminal (exocyclic) ene achieves almost 80% conversion after 180 min of UV-irradiation, whereas the internal (endocyclic) ene reacts more slowly reaching only 10% conversion after the same reaction period. The observed differences in conversion can be ascribed to a higher regioselectivity of the exocyclic unsaturation toward thiol addition as previously reported.6 It is well-known that free-radicals preferentially attack the less substituted α-carbon atom of alkenes, which is also valid for electrophilic radicals, indicating that regioselectivity is guided mainly by steric effects.34 This explains why most β-thioether products resulting from free-radical thiol–ene coupling of unsymmetrical monosubstituted olefins with alkyl thiols are predominantly secondary in structure exhibiting less exothermicities than primary β-thioether products despite of the latter chemical structure is thermodynamically more stable (more exothermic).35 However, such highly contrasting conversion levels observed for the two olefins in D-limonene cannot be ascribed solely to differences in the steric crowding of the corresponding substituents. Diverse literature studies10,35–37 have shown that the reactivity of a given alkene towards a particular thiol depends on the combinatory effect of a series of elements such as: (i.) chemical structure of the thiol monomer (RSH) as a hydrogen-transfer agent, which controls the ability to donate hydrogen-atoms with respect to RS–H bond-dissociating energy (BDE) due to substituents effects; (ii.) stability, size, polarity and electrophilicity of the thiyl radical RS˙, also determined by the chemical nature of the substituent moiety attached to the sulfur atom; (iii.) location, symmetry, electron-density and conformation of the alkene group (terminal, internal, conjugated, non-conjugated, and substituted), which is responsible for steric hindrance, steroelectronic factors, ring strain energy and ability to partake in side reactions (e.g., competing homolymerization); and, (iv.) geometry, relative energy and relative resonance stability of the intermediate carbon-centered radical adduct formed upon thiyl radical insertion onto the double bond, which determine the propensity for back elimination (β-fragmentation) versus hydrogen-capture ability from a thiol group. For example, the electron density of the ene group and carbon radical stability has been proposed in a previous work21 to explain differences in the propagation-to-chain-transfer ratio, kp/kCT, observed for distinct thiol–ene photopolymerization systems, which also influence gel-point formation.38 Accordingly, the magnitude of kp correlates with the electron density of the reactive ene whereas kCT accounts mainly for the stability of the thioether carbon radical.21 In order to better understand which factors control the thiol–ene reactivity of the two exo and endo double bonds in limonene, we have divided this work into three interconnected parts. The first provides a quantitative measure of the observed double bond selectivity (or relative reactivity) in solution from experimental conversion data resulting from the photo-initiated reaction between D-limonene (1) and a tri-functional propionate ester mercaptan (5), as depicted in Scheme 2. The second, attempts to estimate numerically rate coefficients intrinsic to a proposed reaction scheme describing the observed reaction kinetics and then validate the deterministic model. Finally, we interpret the sequential propagation–chain-transfer elementary steps to verify if the relative reactivity obtained from the detailed mechanism explains the measured selectivity.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mixture based on D-limonene (1) and iso-tridecyl 3-mercaptopropionate (monothiol, 2) in CDCl3 solution (50 wt%). DMPA (1.0 wt%) was used as photoinitiator and the samples irradiated with a polychromatic UV-light irradiance of 4.2 mW cm−2.
0.5 thiol–ene mixture based on D-limonene (1) and iso-tridecyl 3-mercaptopropionate (monothiol, 2) in CDCl3 solution (50 wt%). DMPA (1.0 wt%) was used as photoinitiator and the samples irradiated with a polychromatic UV-light irradiance of 4.2 mW cm−2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5, CDCl3 (50 wt%), DMPA (1.0 wt%), UV-intensity: 4.2 mW cm−2, 1000 rpm.
0.5, CDCl3 (50 wt%), DMPA (1.0 wt%), UV-intensity: 4.2 mW cm−2, 1000 rpm.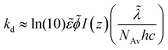
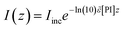
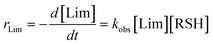
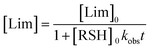
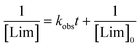



![Linear regression fits to the measured variables. Slopes: m1 = d[exo]/d[Lim] = 0.87 (R2 = 0.98) and m2 = d[endo]/d[Lim] = 0.13 (R2 = 0.90). Δ[ene] = [ene]0 − [ene]; and, m1 + m2 = 1.](/image/article/2013/RA/c3ra40696b/c3ra40696b-f3.gif)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mole stoichiometry (group functionalities). DMPA (1.0 wt%) was used as photoinitiator and the samples exposed to a UV-light irradiance of 4.2 mW cm−2. For clarity the error bars were not plotted. Corresponding double bond conversion data points with errors can be found in sections VIII. and IX. of the Supplementary Information.
0.5 thiol–ene mole stoichiometry (group functionalities). DMPA (1.0 wt%) was used as photoinitiator and the samples exposed to a UV-light irradiance of 4.2 mW cm−2. For clarity the error bars were not plotted. Corresponding double bond conversion data points with errors can be found in sections VIII. and IX. of the Supplementary Information.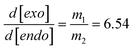

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 thiol–ene mole stoichiometry with respect to functional groups. Lim/RSH (triangles), exo-unsaturation (diamonds) and endo-unsaturation (squares). For clarity the error bars were not plotted. Numerically generated output curves based on literature kinetic coefficients from cis/trans-isomerization of monounsaturated oils are represented in plot (a) with kd = 10−4 s−1; and (b) simulation line fits to the experimental data via the estimated parameters presented in Table 1 with the fixed coefficients: kd = 10−4 s−1, kRSH1 = 107 M−1 s−1 and kt = 3.0 × 109 M−1 s−1.
0.5 thiol–ene mole stoichiometry with respect to functional groups. Lim/RSH (triangles), exo-unsaturation (diamonds) and endo-unsaturation (squares). For clarity the error bars were not plotted. Numerically generated output curves based on literature kinetic coefficients from cis/trans-isomerization of monounsaturated oils are represented in plot (a) with kd = 10−4 s−1; and (b) simulation line fits to the experimental data via the estimated parameters presented in Table 1 with the fixed coefficients: kd = 10−4 s−1, kRSH1 = 107 M−1 s−1 and kt = 3.0 × 109 M−1 s−1.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond).53 Analogously, the same trend in reactivity should, in principle; hold true for the thiyl radical even though it is more electrophilic than the methyl radical. Hoyle and co-workers also have shown via real-time FT-IR measurements that consumption of 1-hexene (a monosubstituted terminal ene) proceeds about 13-times faster than trans-2-hexene and 25-times faster than trans-3-hexene based on initial equimolar C
C bond).53 Analogously, the same trend in reactivity should, in principle; hold true for the thiyl radical even though it is more electrophilic than the methyl radical. Hoyle and co-workers also have shown via real-time FT-IR measurements that consumption of 1-hexene (a monosubstituted terminal ene) proceeds about 13-times faster than trans-2-hexene and 25-times faster than trans-3-hexene based on initial equimolar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/RSH ratios.54 However, the differences in overall conversion rates was attributed not only because of a restricted stereochemical accessibility due to an increased degree of substitution of the double-bond, causing steric impediments for the approaching thiyl radical, but also given the presence of a reversible isomerization process. The existence of reversibility in thiyl radical additions onto olefins was first noticed by Sivertz and co-workers55 and then confirmed by Walling and Helmreich56 in the late 1950s. In the special case of cis/trans-isomerization involving 1,2-dialkyl substituted olefins the secondary carbon-centered radical conformers formed between the two isomeric Z/E-structures have short lifetimes and similarly low resonance stabilities which reduce the rate of chain transfer hydrogen-abstraction reaction and becomes the rate-limiting step.57 According to our simulated kinetic results, we propose that with limonene (which bears two sterically hindered non-isomerizable unsaturations) the differences in relative reactivity are attributed both to steric hindrance effects, which control the position of thiyl radical attack within the double bonds; and, relative energy of the two intermediary insertion products formed immediately after thiyl radical addition, which determines the extent of the elimination reaction rate. We suggest that the electrophilic thiyl radical regioselectively attacks the primary (less substituted) terminal α-carbon of the vinylidene bond driving the reversible addition-elimination equilibrium towards the formation of a resonance stabilized carbon-centered radical intermediate (C1˙). This shift in the forward direction is driven by a decrease in relative energy of the resulting carbon radical adduct resulting in higher consumption of exocyclic double bonds. On the contrary, the internal unsaturation already exists in a 1,1,2-trisubstituted form, locked inside the cyclohexenyl ring, and favored thiyl radical insertion to the secondary (less crowded) α-carbon-atom again yields a resonance stabilized tertiary carbon-centered radical (C2˙) which in this case fragments back into its former state as reactive species much faster than the first intermediate adduct radical (C1˙) as the result of a smaller activation energy barrier required for elimination.36 Since both tertiary carbon radicals appear to share comparable hydrogen-abstraction abilities for the given thiol (Table 1), probably ascribed to relatively equivalent resonance stabilization, then differences in reactivity may be tentatively explained by means of extent of substitution of the double bond, with thiyl radicals adding faster to enes containing primary isolated carbons than to internal secondary ones and to differences in relative energy of the two thioether carbon radical intermediates. As stated in a previous study, each intermediary carbon-centered radical may very well share relatively comparable resonance stabilization, but reveal different relative energies as consequence of interactions between nonbonded atoms which affect steric strain.36 The high extent of reversibility of the second propagation step (kelim2/kadd2[exo]0 ≈ 2.0 × 102) over the first (kelim1/kadd1[endo]0 ≈ 18) correlates well with the previous trend in reactivity for the methyl radical as both the trans-2-butene and trimethylethylene moieties exhibit similarly low relative addition rates when compared with the isobutylene moiety, indicative of dominance of fragmentation over addition. We also verified a ratio in thiyl radical addition rate constants (kadd1/kadd2) of about 1.4 slightly in favor of consumption of the exo-olefinic bond, whereas the ratio in elimination constants (kelim2/kelim1) was about 7.8 appreciably favoring fragmentation to the endocyclic unsaturation. The substantially high increment of the second elimination rate constant over the first kinetically outweighs the second thiyl–ene propagation route (step 5) also indicating that the main factor governing the reactivity of the two unsaturations with respect to thiol–ene coupling is the relative energy of the C2˙ radical as opposed to intermolecular RS˙ addition which is controlled by steric effects. Indeed, the ‘apparent’ equilibrium constants for addition/elimination (K1,2 = kadd1,2/kelim1,2, in M−1), revealed that K1 ≈ 11.2 × K2 fully supportive of the preceding analysis. Consequently, the rates of the two hydrogen-abstraction reactions occurring immediately after each insertion/elimination step are controlled predominantly by the concentration levels of the ensuing tertiary carbon radicals which both appear to display equivalent radical stabilities towards hydrogen-abstraction (kRSH2/kRSH3 ≈ 0.91) given their structural resemblance. This indicates that the rate-limiting step controlling the overall reaction is the third hydrogen-abstraction reaction promoted by the second insertion product radical given that it is the slowest step.
C/RSH ratios.54 However, the differences in overall conversion rates was attributed not only because of a restricted stereochemical accessibility due to an increased degree of substitution of the double-bond, causing steric impediments for the approaching thiyl radical, but also given the presence of a reversible isomerization process. The existence of reversibility in thiyl radical additions onto olefins was first noticed by Sivertz and co-workers55 and then confirmed by Walling and Helmreich56 in the late 1950s. In the special case of cis/trans-isomerization involving 1,2-dialkyl substituted olefins the secondary carbon-centered radical conformers formed between the two isomeric Z/E-structures have short lifetimes and similarly low resonance stabilities which reduce the rate of chain transfer hydrogen-abstraction reaction and becomes the rate-limiting step.57 According to our simulated kinetic results, we propose that with limonene (which bears two sterically hindered non-isomerizable unsaturations) the differences in relative reactivity are attributed both to steric hindrance effects, which control the position of thiyl radical attack within the double bonds; and, relative energy of the two intermediary insertion products formed immediately after thiyl radical addition, which determines the extent of the elimination reaction rate. We suggest that the electrophilic thiyl radical regioselectively attacks the primary (less substituted) terminal α-carbon of the vinylidene bond driving the reversible addition-elimination equilibrium towards the formation of a resonance stabilized carbon-centered radical intermediate (C1˙). This shift in the forward direction is driven by a decrease in relative energy of the resulting carbon radical adduct resulting in higher consumption of exocyclic double bonds. On the contrary, the internal unsaturation already exists in a 1,1,2-trisubstituted form, locked inside the cyclohexenyl ring, and favored thiyl radical insertion to the secondary (less crowded) α-carbon-atom again yields a resonance stabilized tertiary carbon-centered radical (C2˙) which in this case fragments back into its former state as reactive species much faster than the first intermediate adduct radical (C1˙) as the result of a smaller activation energy barrier required for elimination.36 Since both tertiary carbon radicals appear to share comparable hydrogen-abstraction abilities for the given thiol (Table 1), probably ascribed to relatively equivalent resonance stabilization, then differences in reactivity may be tentatively explained by means of extent of substitution of the double bond, with thiyl radicals adding faster to enes containing primary isolated carbons than to internal secondary ones and to differences in relative energy of the two thioether carbon radical intermediates. As stated in a previous study, each intermediary carbon-centered radical may very well share relatively comparable resonance stabilization, but reveal different relative energies as consequence of interactions between nonbonded atoms which affect steric strain.36 The high extent of reversibility of the second propagation step (kelim2/kadd2[exo]0 ≈ 2.0 × 102) over the first (kelim1/kadd1[endo]0 ≈ 18) correlates well with the previous trend in reactivity for the methyl radical as both the trans-2-butene and trimethylethylene moieties exhibit similarly low relative addition rates when compared with the isobutylene moiety, indicative of dominance of fragmentation over addition. We also verified a ratio in thiyl radical addition rate constants (kadd1/kadd2) of about 1.4 slightly in favor of consumption of the exo-olefinic bond, whereas the ratio in elimination constants (kelim2/kelim1) was about 7.8 appreciably favoring fragmentation to the endocyclic unsaturation. The substantially high increment of the second elimination rate constant over the first kinetically outweighs the second thiyl–ene propagation route (step 5) also indicating that the main factor governing the reactivity of the two unsaturations with respect to thiol–ene coupling is the relative energy of the C2˙ radical as opposed to intermolecular RS˙ addition which is controlled by steric effects. Indeed, the ‘apparent’ equilibrium constants for addition/elimination (K1,2 = kadd1,2/kelim1,2, in M−1), revealed that K1 ≈ 11.2 × K2 fully supportive of the preceding analysis. Consequently, the rates of the two hydrogen-abstraction reactions occurring immediately after each insertion/elimination step are controlled predominantly by the concentration levels of the ensuing tertiary carbon radicals which both appear to display equivalent radical stabilities towards hydrogen-abstraction (kRSH2/kRSH3 ≈ 0.91) given their structural resemblance. This indicates that the rate-limiting step controlling the overall reaction is the third hydrogen-abstraction reaction promoted by the second insertion product radical given that it is the slowest step.