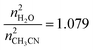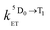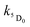Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photophysics of 1,8-naphthalimide/Ln(III) dyads (Ln = Eu, Gd): naphthalimide → Eu(III) energy-transfer from both singlet and triplet states†
Victor F.
Plyusnin
*a,
Arkady S.
Kupryakov
a,
Vyacheslav P.
Grivin
a,
Alexander H.
Shelton
b,
Igor V.
Sazanovich
b,
Anthony J. H. M.
Meijer
b,
Julia A.
Weinstein
b and
Michael D.
Ward
*b
aInsitute of Chemical Kinetics and Combustion SB RAS, Institutskaya 3, 630090 Novosibirsk, Russia. E-mail: plyusnin@kinetics.nsc.ru
bDepartment of Chemistry, University of Sheffield, Sheffield S3 7HF, UK. E-mail: m.d.ward@sheffield.ac.uk
First published on 31st May 2013
Abstract
Transient absorption and time resolved luminescence spectroscopy were used to study photophysical processes in the macrocycle-appended 1,8-naphthalimide compound H3L, and its Eu(III) and Gd(III) complexes Eu·L and Gd·L, in particular the naphthalimide–Eu(III) energy-transfer process. In all cases aggregation of the naphthalimide chromophores results in a low-energy emission feature in the 470–500 nm region in addition to the naphthalimide fluorescence; this lower-energy emission has a lifetime longer by an order of magnitude than the monomer naphthalimide fluorescence. Transient absorption spectroscopy was used to measure the decay of the naphthalimide triplet excited state, which occurs in the range 30–50 μs. In Eu·L, partial energy-transfer from the naphthalimide chromophore results in sensitized Eu(III)-based emission in addition to the naphthalimide-based fluorescence features. Time-resolved measurements on the sensitized Eu(III)-based emission reveal both fast (∼109 s−1) and slow (∼104 s−1) energy-transfer processes from the naphthalimide energy-donor, which we ascribe to energy-transfer occurring from the singlet and triplet excited state of naphthalimide respectively. This is an unusual case of observation of sensitization of Eu(III)-based emission from the singlet state of an aromatic chromophore.
Introduction
Luminescence from lanthanide complexes is of substantial importance in many applications such as biological imaging,1 sensing and analysis,2 optical data transfer,3 and lighting devices.4 Their particular photophysical properties such as narrow line widths, long luminescence lifetimes and (in some cases) hypersensitivity to the coordination environment make them particularly appealing for these applications.1–4 Their main shortcoming however is the very small extinction coefficients for f–f absorptions in these ions, which means that antenna groups – either organic or inorganic chromophores – must be used to harvest the photons as the first step.5 It follows that energy-transfer from the excited state of the antenna group to the Ln(III) centre must be efficient to achieve a high quantum yield for Ln(III)-based emission.One interesting application of Ln(III)-based emission which has attracted recent attention is the preparation of white-light emitting materials in which the strong red luminescence of Eu(III), dominated by the 5D0 → 7F2 transition at 615 nm, is combined with blue or blue/green luminescence from a chromophore with a higher-energy excited state to give luminescence which appears white.6,7 For this to work requires not only that the two emission components are complementary in colour, but that their relative intensities are well balanced so that neither component dominates the emission spectrum. This in turn requires that energy-transfer from the higher-energy (antenna) excited state to the Eu(III) 5D0 level is incomplete, such that the higher-energy blue/green emission component is not fully quenched and is able to balance the sensitised red emission from Eu(III).6,7
With this in mind we recently reported in a preliminary communication7 the synthesis and luminescence properties of a 1,8-naphthalimide/Eu(III) dyad Eu·L (Scheme 1) which afforded white-light emission in some solvents; the Gd(III) analogue Gd·L was also prepared for control purposes, as the excited state of Gd(III) is too high to quench the excited state of the donor and therefore allows study of the unquenched 1,8-naphthalimide unit in an isostructural system. 1,8-Naphthalimide has several properties which make it ideal for this application. It shows short-lived blue fluorescence from the singlet π–π* state, but also has efficient intersystem crossing to the lowest triplet state (ϕ ∼ 0.95).8 The energy of this triplet state (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) is just high enough to sensitise the emissive 5D0 state of Eu(III) (17
500 cm−1) is just high enough to sensitise the emissive 5D0 state of Eu(III) (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1), but is not energetic enough sensitise any of the higher-lying (5D1 and upwards) levels.9 In addition, aggregation of 1,8-naphthalimide units can result in formation of additional fluorescence bands at lower energy than the monomer fluorescence: this is of particular interest in covalently-linked bis-naphthalimides in which the two fluorophores are held close together and provides a convenient way to tune the emission colour of the naphthalimide unit.10
500 cm−1), but is not energetic enough sensitise any of the higher-lying (5D1 and upwards) levels.9 In addition, aggregation of 1,8-naphthalimide units can result in formation of additional fluorescence bands at lower energy than the monomer fluorescence: this is of particular interest in covalently-linked bis-naphthalimides in which the two fluorophores are held close together and provides a convenient way to tune the emission colour of the naphthalimide unit.10
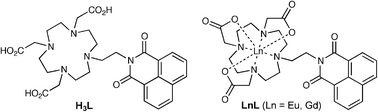 | ||
| Scheme 1 Structural formulae of the species H3L, Eu·L and Gd·L discussed in this paper. | ||
Following our earlier communication,7 in this paper we report a detailed study of the photophysical properties of H3L, Gd·L and Eu·L. In particular we have examined (i) aggregation of the molecules in solution, and (ii) the mechanism of energy-transfer from the 1,8-naphthalimide unit to the Eu(III) centre. In each area some unexpected results emerge, and in particular we have evidence that naphthalimide-to-Eu(III) energy transfer can occur from both the singlet and triplet excited states of the naphthalimide unit.
Experimental
The complexes H3L, Gd·L and Eu·L were available from previous work.7 Laser flash photolysis was carried out using a YAG:Nd laser (the 3rd harmonic at 355 nm, 5 ns pulse duration, 5–30 mJ pulse energy). The excitation and probe light beams entered the solution under investigation in a 1 cm cuvette at a small angle (∼2°) to one another. UV/Visible absorption spectra were recorded using an Agilent 8453 spectrophotometer (Agilent Technologies). To extend the range of detectable concentrations, cuvettes with optical thickness 1 cm–10 μm were used. In numeric kinetic simulations differential equations were solved using proprietary software (SPARK) based on the fourth-order Runge–Kutta method. The program allows calculations and fitting of experimental kinetic curves simultaneously at multiple wavelengths.Spectra and kinetic curves of luminescence were recorded with an Edinburgh Instruments FLSP-920 spectrofluorimeter with either a Xenon lamp or a laser diode EPLED-320 (λex = 320 nm, pulse duration 0.6 ns) as excitation sources. Solutions were prepared using spectroscopically pure solvents and triply distilled water. When necessary, dissolved oxygen was removed from the solutions by bubbling argon through the solution for 30 min. The quantum yield for formation of the triplet excited states was determined using the extinction coefficient ε = 104 M−1 cm−1 for 1,8-naphthalimide.8 Luminescence quantum yields were measured relative to that of anthracene, using the value for the fluorescence quantum yield of anthracene in acetonitrile (0.28), as it has been previously shown that quantum yield of anthracene fluorescence is solvent-independent.11,12 For aqueous solutions the correction factor
All calculations were performed using Gaussian 09, version C.01,13 compiled using Portland compiler v 8.0-2 with the Gaussian-supplied versions of ATLAS and BLAS, using the B3LYP functional of DFT.14 In all calculations we used a Stuttgart/Dresden pseudo potential on Eu15a and D95V on all other atoms.15b As a result, the calculations contained at most 651 basis functions and 354 electrons. No symmetry was taken into account in our calculations. In previous work it was found that this approach results in a reasonably accurate description of transition-metal complexes and their properties,16a,b allowing for qualitative comparison with experiment. In all calculations the bulk solvent was described using PCM,17 whereby the standard parameters as supplied in Gaussian were used.
The following procedure was used in our calculations. The starting structure of Eu·L was obtained by adapting the crystal structure that has been previously reported.18 Using Gaussview19 the pendant naphthalimide unit was attached. Subsequently, the coordination shell was completed by adding the requisite number of water molecules. It was recognized through visual inspection that three different conformers appeared to be possible. Each of these was optimized for both water and MeCN solvent. Frequencies in the harmonic approximation were calculated to confirm that each optimized structure was a minimum. The corresponding structures for MeCN and water are not significantly different, so only the conformers in water will be reported upon.
Results and discussion
1. Absorption and luminescence spectra, and their concentration dependence
The UV/Vis absorption spectrum of unsubstituted 1,8-naphthalimide consists of four intense lines in the UV region. In acetonitrile, the absorption maxima and extinction coefficients of these lines are at 214 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 M−1 cm−1), 234 (49
100 M−1 cm−1), 234 (49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700), 332 (12
700), 332 (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) and 344 (11
500) and 344 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700) nm,11 and very similar spectra were observed in cyclohexane and ethanol. The absorption spectra of H3L and its complexes Eu·L and Gd·L at low concentrations (<10−4 M) are very similar to that of free 1,8-naphthalimide (Fig. 1), with the presence of the lanthanide ions making very little difference as they are separated from the chromophoric unit by a saturated spacer.
700) nm,11 and very similar spectra were observed in cyclohexane and ethanol. The absorption spectra of H3L and its complexes Eu·L and Gd·L at low concentrations (<10−4 M) are very similar to that of free 1,8-naphthalimide (Fig. 1), with the presence of the lanthanide ions making very little difference as they are separated from the chromophoric unit by a saturated spacer.
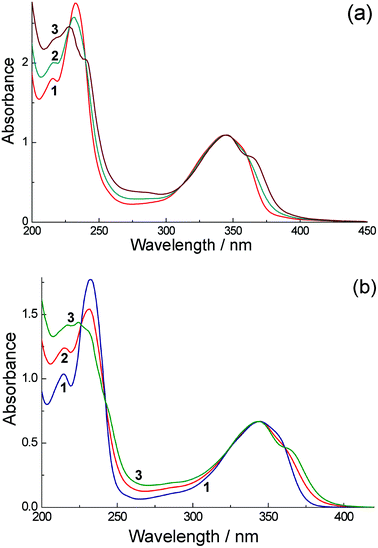 | ||
| Fig. 1 (a) UV/Vis absorption spectra of H3L in water: (1) concentration 9.4 × 10–5 M (path length 1 cm); and (2) 1.75 × 10−2 M (path length 54 μm). The calculated spectrum of a dimer is presented as curve (3) (see text for details). (b) UV/Vis absorption spectra of Eu·L in water: (1) concentration 5.72 × 10−5 M (path length 1 cm); and (2) concentration 2.27 × 10−2 M (path length 25 μm). The calculated spectrum of a dimer is presented as curve (3) (see text for details). | ||
Increasing the concentrations leads to slight but significant changes of the spectra [see Fig. 1(a)]. Fig. 1(a) shows this change in the (normalized) absorption spectra for H3L in water at two different concentrations [spectra (1) and (2)]; Fig. 1(b) shows the similar absorption spectra of Eu·L over the same concentration range. These changes can be explained by aggregation of the aromatic units, and the presence of isosbestic points in both cases confirms conversion between just two spectroscopically distinct species, monomer and aggregate. Such aggregation is a known characteristic of naphthalimides8,10 and was mentioned in our original communication;7 it is discussed in more quantitative detail later. Aggregation is manifested in the absorption spectra by a red-shift of the lowest-energy absorption band to 365 nm and other subtle changes in the absorption profile at higher energy. These changes were only noticeable at concentrations in the region of 10−2 M, which required ultrathin optical cells (path lengths 25 μm or 54 μm) to measure the absorption spectra. Essentially identical behaviour was shown by the absorption spectra of Eu·L (Fig. 1b) and Gd·L (see ESI†) in water. The clear shift of the lowest-energy absorption maximum on aggregation (see curve 3 in both Fig. 1a and 1b) is consistent with formation of a J-aggregate involving stacking of aromatic units,20 and indeed J-aggregates are well known to form with perylene-bisimide dyes which are related to the naphthalimide unit used in this work.20
The fluorescence spectra of H3L in water at a range of concentrations are shown in Fig. 2a. At low concentrations (≈10−4 M) we detect only monomer fluorescence at 395 nm. An increase in concentration up to ≈10−2 M leads to a relative decrease in the intensity of this emission band and an appearance of a new luminescence band at 500 nm (discussed below). Gd·L and Eu·L show essentially identical behaviour (Fig. 2b and ESI†). The naphthalimide-based fluorescence of these complexes behaves as it does for H3L: at low concentrations (10−5–10−4 M) a broad emission band with a maximum at 395 nm is observed, and at higher concentrations (up to 10−2 M) the intensity of this 395 nm band decreases and again we see a lower energy emission band with a maximum at 502 nm (Fig. 2b). In the spectra of Eu·L we also see lines in the red region of the spectrum corresponding to sensitised Eu(III) luminescence, with the most intense component being the 5D0 → 7F2 transition at 614 nm (marked with an arrow). The relative intensity of the Eu(III) emission decreases as the Eu·L concentration increases. The removal of oxygen from the solution leads to an increase in the intensity of Eu(III) emission by an order of magnitude, implying that there is some energy-transfer to Eu(III) from the T1 state of the naphthalimide chromophore, which is reduced in efficiency when this T1 state is partially quenched by O2. This is to be expected and is normal behaviour when a triplet state of a chromophore contributes to sensitisation of Eu(III).5
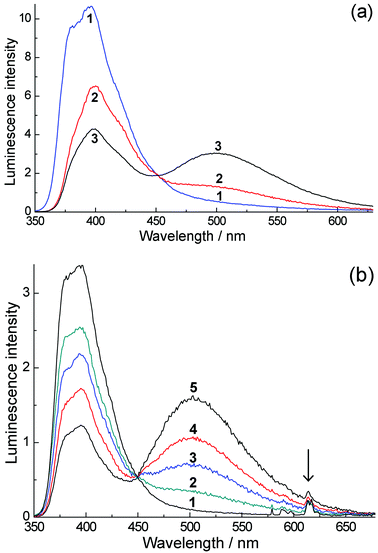 | ||
| Fig. 2 (a) Luminescence spectra of H3L in water with excitation at 320 nm. Spectra (1)–(3) were recorded at concentrations of 9.4 × 10−5, 2.14 × 10−3 and 1.75 × 10−2 M respectively, using 1.0 cm, 0.1 cm and 54 μm cells respectively. (b) Luminescence spectra of Eu·L in O2-equilibrated water (oxygen concentration, 2.8 × 10−4 M) with excitation at 320 nm. Spectra (1)–(5) were recorded at concentrations 5.7 × 10−5, 1.14 × 10−3, 3.45 × 10−3, 9.23 × 10−3 and 2.27 × 10−2 M, respectively. Spectra were measured in a 54 μm cuvette with the exception of spectrum (1) which used a 1 cm cuvette; the normalization of this spectrum with respect to the others is made with the help of the isosbestic point. | ||
The formation of a new low-energy fluorescence band at 470 nm for N-methyl-1,8-naphthalimide (NAP) under high laser intensity has been observed previously11 and was assigned to singlet excimer emission21 arising from triplet–triplet annihilation, i.e.3NAP + 3NAP → 1(NAP:NAP)*. We therefore suggest that the fluorescence band (Fig. 2a and 2b) at 500 nm which appears at high concentrations of H3L, Eu·L and Gd·L is also due to emission from an aggregate in the excited state which involves aromatic interactions. However, in our case, in water this emission originates directly from a pre-formed aggregate (cf. the absorption spectra at high concentration). We can confirm this by excitation spectra recorded measuring the 400 nm (monomer) and 500 nm (excited aggregate) emission bands (Fig. 3a). These are slightly different, with the 500 nm excitation spectrum including features corresponding to aggregate formation in the UV/Vis absorption spectrum at high concentrations, specifically a region of absorbance at around 275 nm and a low-energy tail extending out to 400 nm. These features are clearly more pronounced in the 500 nm excitation spectrum and shown by arrows on spectrum 3 of Fig. 3a.
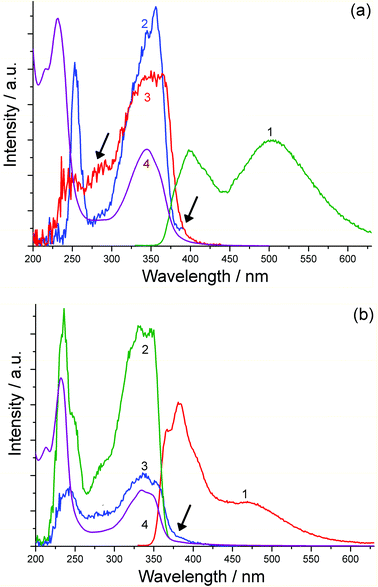 | ||
| Fig. 3 (a) Excitation spectra of H3L in water (17.3 mM using 54 μm cuvette). Spectrum (1): luminescence spectrum using 320 nm excitation. Spectrum (2): excitation spectrum recorded at 400 nm. Spectrum (3): excitation spectrum recorded at 505 nm. Spectrum (4): UV/Vis absorption spectrum. (b) Excitation spectra of H3L in MeCN (8.4 mM using 54 μm cuvette). Spectrum (1): luminescence spectrum using 320 nm excitation. Spectrum (2): excitation spectrum recorded at 382 nm. Spectrum (3): excitation spectrum recorded at 505 nm emission. Spectrum (4): UV/Vis absorption spectrum. | ||
Fig. 1 shows that extinction coefficients of the monomer and a molecule in the aggregate of H3L are the same at 320 nm. This coincidence allows us to calculate the relative quantities of the monomer and the aggregate from the ratio of luminescence intensities at 395 and 500 nm (Fig. 2). Let us assume that emission from the aggregate (500 nm band) does not contribute significantly to the luminescence intensity at 395 nm. Likewise, we assume that there is negligible contribution at 500 nm from the monomer emission (395 nm band). Further, to make some quantitative analysis possible we will assume that the aggregation takes its simplest possible form, of a monomer (M)/dimer (D) equilibrium, which is consistent with the appearance of isosbestic points in the series of normalized absorption spectra at different concentrations. In this case the ratio of the luminescence intensities at these two wavelengths will be determined by eqn (1):
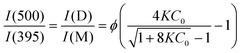 | (1) |
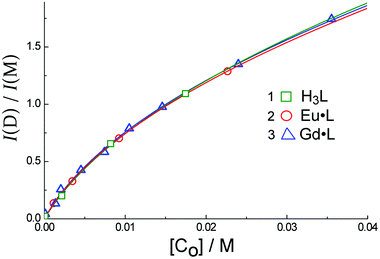 | ||
| Fig. 4 The dependence of the ratio of dimer to monomer luminescence intensity, I(D)/I(M), on the concentration of H3L (1), Eu·L (2) and Gd·L (3) in H2O. Solid lines are the results of calculated fits using eqn (1). | ||
In MeCN the concentration dependences of the spectral properties are quite different, with the absorption spectra of H3L, Eu·L and Gd·L being virtually concentration-independent. This could imply that there is less aggregation of the aromatic chromophores when water is replaced by MeCN (e.g. if aggregation in water is hydrophobic in origin); or it could imply that the spectroscopic consequences of aggregation, which would include changes in solvation between monomer and aggregate, are less apparent in the weaker solvent. Despite this, luminescence spectra of Eu·L and Gd·L in MeCN display not only the expected emission from the naphthalimide monomer at 382 nm, but show an additional band at 470 nm (Fig. 5) similar to what was seen in water. This 470 nm emission component becomes more significant as the concentration of the complexes increases and is again assigned to luminescence from an aggregate. Importantly, time resolved measurements (see later) allow us to rule out excimer formation in a collision process after excitation, which means that the aggregation occurs in the ground state in MeCN even if this is less obvious from the absorption spectra than the aggregation in water. Importantly however excitation spectra recorded at high concentration (Fig. 3b) show that, for the 470 nm emission band but not the 382 nm emission band, the excitation spectrum (curve 3 in Fig. 3b) includes a low-energy tail of absorption at around 400 nm, shown by an arrow, that corresponds well to what we saw in water as a consequence of aggregation; this is absent in the 382 nm excitation spectrum and therefore cannot correspond to the monomer.
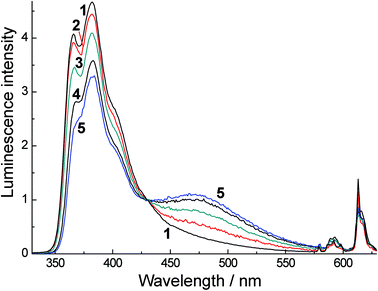 | ||
| Fig. 5 Luminescence spectra of Eu·L in CH3CN with excitation at 320 nm. Spectra (1)–(5) were recorded at concentrations of 6.6 × 10−5, 3.08 × 10−3, 9.51 × 10−3, 1.74 × 10−3 and 2.2 × 10−2 M, respectively. Spectra were measured in a 54 μm cuvette with the exception of spectrum (1) which used a 1 cm cuvette; the normalization of this spectrum with respect to the others is made with the help of the isosbestic point. | ||
Using the analysis described earlier (eqn (1)) based on the intensities of emission from the aggregate (at 470 nm) and monomer (at 382 nm) in MeCN, one can obtain the data shown in Fig. 6. We assume again that the aggregate contains two molecules, like those that form in water in the ground state. Using eqn (1) yields the equilibrium constant K = 52 ± 32 M−1, and quantum yield ratio ϕ = 0.22 ± 0.09 for Eu·L; and K = 89 ± 11 M−1 and ϕ = 0.20 ± 0.02 for Gd·L. Thus the equilibrium constants for aggregation in both solvents are similar, but in MeCN the relative quantum yield of the lower-energy emission component compared to the higher-energy component is only about 20% of the value observed in water: in other words, emission from the aggregate in CH3CN is much weaker than that of the monomer.
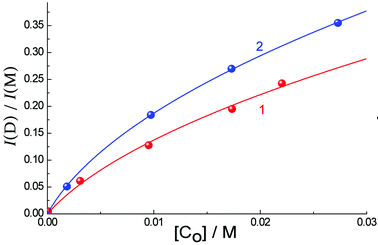 | ||
| Fig. 6 The dependence of ratio of dimer (470 nm) to monomer (382 nm) luminescence intensity. I(D)/I(M), on the concentration of Eu·L (1) and Gd·L (2) in CH3CN (points). Solid lines are the results of calculated fits using eqn (1). | ||
Quantum yield measurements recorded on dilute solutions (with A = 0.5 at λexc = 320 nm) show that the luminescence from the Eu(III) ion (575–750 nm) in CH3CN is ∼34% of the total intensity, whereas in water it is only 7.2% of the total intensity (Fig. 7). This reflects principally the well-known quenching effect on Eu(III) of O–H oscillations from coordinated water molecules which is absent in MeCN.
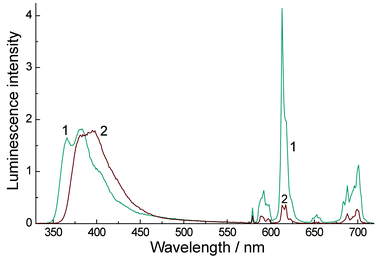 | ||
| Fig. 7 Luminescence spectra of Eu·L (6 × 10−5 M, 1 cm path length) in degassed CH3CN (1) and degassed H2O (2). Excitation was at 320 nm in each case where the two solutions were isoabsorbing (A = 0.5). | ||
2. Time-resolved measurements of the naphthalimide luminescence
Fig. 8 demonstrates the kinetics of luminescence of H3L at 395 nm (the monomer fluorescence emission) in water at a low concentration (9.4 × 10−5 M) and at 500 nm at a high concentration (1.75 × 10−2 M), corresponding to the limiting emission spectra in Fig. 2a. The kinetic behavior in each case required three exponential decay parameters to be modeled satisfactorily, and the solid lines in Fig. 8 show the resultant best fits using parameters given in Table 1. Similar kinetic behaviour for the monomer and aggregate emission bands was shown by Eu·L and Gd·L and the lifetimes used for the three-component decay model for these are also included in Table 1. Between the three compounds the monomer luminescence decay components are very consistent with lifetimes of ca. 0.3, 1.3 and 2.2 ns. The aggregate luminescence decay measured at 1.75 × 10−2 M has two longer-lived components, one at 5–6 ns and one of 15–17 ns, in addition to a ≈0.4 ns component which has a small contribution and is likely to arise from monomer. In the aggregate the presence of ≥2 decay components can be ascribed to variations in the structures of the aggregates and/or complex dynamic behaviour of components within an aggregate. The presence of three luminescence decay components even at high dilution when there is no aggregation present implies the presence of either different conformers of the flexible molecules, or the presence of different degrees of solvation of the naphthalimide unit.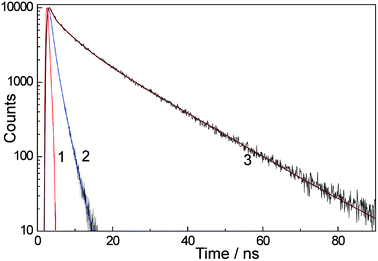 | ||
| Fig. 8 Luminescence decay kinetics of H3L in water with excitation at 320 nm. Curve (1): instrument response function. Curve (2): decay kinetics at 395 nm at low H3L concentration (9.4 × 10−5 M, 1 cm cuvette). Curve (3): decay kinetics at 500 nm at high H3L concentration (1.75 × 10−2 M, 54 μm cuvette). Solid lines in the kinetic traces are the calculated fits using a three exponential approximation (parameters in Table 1). | ||
| Compound | Path length | λ em/nm | τ 1/ns | A 1/% | τ 2/ns | A 2/% | τ 3/ns | A 3/% |
|---|---|---|---|---|---|---|---|---|
| H3L | ||||||||
| 9.4 × 10−5 M | 1 cm | 395 | 0.4 | 29 | 1.3 | 50 | 2.2 | 21 |
| 1.75 × 10−2 M | 54 μm | 500 | 0.5 | 5 | 5.0 | 23 | 15.0 | 72 |
| Eu·L | ||||||||
| 1.0 × 10−4 M | 1 cm | 395 | 0.3 | 28 | 1.3 | 56 | 2.3 | 16 |
| 2.2 × 10−2 M | 54 μm | 395 | 0.5 | 31 | 1.3 | 68 | 4.7 | 1 |
| 2.2 × 10−2 M | 54 μm | 505 | 0.4 | 1 | 6.5 | 22 | 16.5 | 77 |
| Gd·L | ||||||||
| 1.1 × 10−4 M | 1 cm | 393 | 0.3 | 29 | 1.3 | 38 | 2.2 | 33 |
| 7.9 × 10−3 M | 54 μm | 393 | 0.5 | 18 | 1.6 | 73 | 2.6 | 9 |
| 7.9 × 10−3 M | 54 μm | 504 | 0.4 | 2 | 5.9 | 19 | 17.2 | 79 |
Importantly we could detect no rise-time for the long wavelength luminescence component at 500 nm. If this component arose from excimer formation, we would expect a rise time of ≈2 ns at the highest concentration used. As the excitation pulse was of 600 ps duration, such a grow-in would be easily detectable. Its absence confirms that the low energy luminescence arises from aggregates that are pre-formed before excitation (cf. the UV/Vis absorption spectra).
In MeCN, the kinetics of naphthalimide-based luminescence of all three compounds are similar to those in water, again requiring three exponential decay components to obtain a good fit (see Table 2). In MeCN, the emission from the naphthalimide monomers is observed at 382 nm with the two major components having lifetimes of ≈0.3 and ≈1 ns. Emission from aggregates is observed at 470 nm at high concentrations (>10−3 M), and is characterised by longer lifetimes than the monomer, with components of ca. 5 and 20 ns which are similar to the luminescence lifetimes from the aggregates in water. The short lifetime component (<1 ns) detected at 470 nm in MeCN can again be explained by a small contribution from the broad emission band of the monomer which overlaps at this wavelength. Again, the absence of any grow-in means that excimer emission – which requires diffusion of excited molecules – can be ruled out as a mechanism for generating the low-energy luminescence component which must arise from pre-formed aggregates.
| Compound | Path-length | λ/nm | τ 1/ns | A 1/% | τ 2/ns | A 2/% | τ 3/ns | A 3/% |
|---|---|---|---|---|---|---|---|---|
| H3L | ||||||||
| 9.4 × 10−5 M | 1 cm | 382 | 0.3 | 30 | 1.0 | 67 | 2.7 | 3 |
| 1.75 × 10−2 M | 54 μm | 382 | 0.3 | 41 | 1.0 | 58 | 5.2 | 1 |
| 1.75 × 10−2 M | 54 μm | 470 | 0.7 | 12 | 5.0 | 18 | 18.6 | 70 |
| Eu·L | ||||||||
| 6.6 × 10−5 M | 1 cm | 382 | 0.3 | 21 | 1.3 | 77 | 14. 7 | 2 |
| 1.74 × 10−2 M | 54 μm | 382 | 0.3 | 6 | 1.8 | 80 | 3.9 | 14 |
| 1.74 × 10−2 M | 54 μm | 470 | 0.8 | 5 | 6.1 | 33 | 18.6 | 62 |
| Gd·L | ||||||||
| 5.76×10–5 M | 1 cm | 382 | 0.3 | 14 | 1.2 | 85 | 3.7 | 1 |
| 1.04 × 10−2 M | 54 μm | 382 | 0.4 | 15 | 1.1 | 84 | 9.5 | 1 |
| 1.04 × 10−2 M | 54 μm | 470 | 0.8 | 9 | 4.1 | 10 | 20.7 | 81 |
3. Spectra and kinetic properties of the triplet excited state of H3L, Eu·L and Gd·L
Fig. 9 shows the transient absorption spectrum of the triplet excited state of H3L in deoxygenated water recorded 50 ns after 355 nm excitation, and its kinetic behaviour. The 50 ns delay allows the singlet state to disappear completely such that this is the pure triplet–triplet (T–T) absorption spectrum. The shape of this spectrum is very similar to that reported for N-methyl-1,8-naphthalimide.11 In Fig. 9a, spectrum (2) shows the negative contribution to the T–T absorption of photoexcited H3L arising from bleaching of the ground state absorbance at 340 nm. The intensity of this was calculated using the measured optical density of the T–T absorption at 470 nm (spectrum (1)) and ε ≈ 1 × 104 M−1 cm−1. Subtracting spectrum (2) from (1) yields the corrected T–T absorption spectrum, curve (3).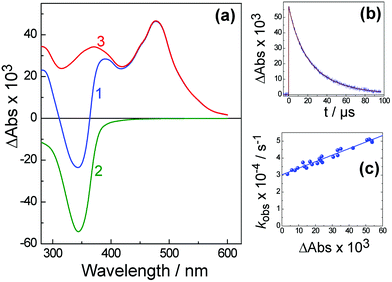 | ||
| Fig. 9 The triplet–triplet absorption spectrum (a) and its decay (b) of H3L in water recorded 50 ns after laser excitation at 355 nm. Curve (c) shows the dependence of kobs of T–T absorption decay at 470 nm on the value of absorption (ΔA). In frame (a): (1), the measured differential T–T absorption; (2), the UV/Vis spectrum of the complex showing the naphthalimide absorption; (3), the difference between (1) and (2), i.e. the T–T absorption spectrum. | ||
The observed rate constant kobs of the triplet–triplet (T–T) absorption decay (see Fig. 9b for an example) as a function of the amplitude of the initial absorbance (ΔA) is presented in Fig. 9(c). This variation in the observed decay rate constant kobs at different concentrations arises because there are both first-order and second-order contributions to the excited-state decay. The observed rate constant in this case can be expressed as
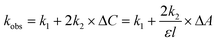 | (2) |
The T–T absorption spectra of Gd·L and Eu·L (see ESI†) are essentially identical to that of H3L, and also display similar kinetic behaviour. From the concentration dependence of the decay kinetics we can again see a combination of first-order and second-order processes contributing to the decay, and analysis using eqn (2) affords the values of k1 (first order decay rate constant) and 2k2/ε (second-order rate constant for triplet–triplet annihilation) that are summarized in Table 3.
| Compound | k 1 × 10−4/s−1 | 2k2/ε × 10−5/cm s−1 |
|---|---|---|
| H3L | 3.0 ± 0.2 | 3.9 ± 0.4 |
| Gd·L | 4.7 ± 0.2 | 2.5 ± 0.2 |
| Eu·L | 5.7 ± 0.2 | 4.4 ± 0.5 |
In the two compounds H3L and Gd·L the value of k1 is determined only by the transition rate from the triplet excited state to the ground state (T1 → S0). For Eu·L, an additional contribution to the T–T decay kinetics arises due to energy-transfer from the ligand triplet state to Eu3+ (T1 → 5D0, responsible for sensitized Eu-based emission) and this also contributes to k1 which is therefore expected to be larger. Assuming that the rate constants of the T1 → S0 transition are identical for Gd·L and Eu·L, the rate constant for naphthalimide (T1) → Eu(5D0) energy transfer kET in Eu·L is given by eqn (3).
| kET = kEu·L1–kGd·L1 | (3) |
The low value of this T1 → 5D0 energy-transfer rate constant could arise for several reasons. These include (i) poor donor/acceptor spectroscopic overlap, arising from the poor energy match between naphthalimide phosphorescence and the Eu(III) f–f absorptions and the narrowness and low intensity of f–f absorptions; and (ii) the separation (and lack of a direct electronic interaction) between the naphthalimide unit and the Eu(III) centre if Dexter energy-transfer is involved.5 These issues will be discussed in more detail later.
The T–T absorption spectrum of H3L in deoxygenated CH3CN recorded 50 ns after a 355 nm, 5 ns laser pulse corresponds closely to what was observed in water (see ESI†). Again, the dependence of the observed T–T absorption decay rate constant on concentration reveals a combination of normal first order decay plus a second order component arising from triplet–triplet annihilation; use of eqn (2) gives k1 = 2.6 × 104 s−1 for the first-order decay, and 2k2/ε = 5 × 104 cm s−1 for the triplet–triplet annihilation. Assuming an extinction coefficient ε ≈ 1 × 104 M−1 cm−1 for T–T absorption intensity,8 we obtain 2k2 = 5 × 108 M−1 s−1. Thus the lifetime of the naphthalimide-based T1 triplet state in CH3CN at low laser powers and low complex concentrations is approximately 50 μs (τ = 1/k1), somewhat longer than was observed in water. Quantum yields for formation of the naphthalimide triplet states for H3L, Eu·L and Gd·L measured in deoxygenated CH3CN and H2O under identical conditions and 355 nm excitation are shown in Table 4; these are of the order of ca. 10%, which is much less than for unsubstituted 1,8-naphthalimide.11
In the same way as described above (eqn (3)) we can compare the behavior of Gd·L and Eu·L to determine the rate constant for naphthalimide(T1) → Eu(5D0) energy transfer in MeCN; the T–T spectra and decay kinetics are in the ESI.† From these we can calculate that kET[T1 → Eu(5D0)] = (1.40 ± 0.05) × 104 s−1, slightly faster than in water.
4. Sensitised luminescence from Eu(III) ion in Eu·L: analysis of energy-transfer
As shown in Fig. 2b, and in the previous section, excitation of the naphthalimide chromophore of Eu·L at 355 nm results in sensitized emission from Eu(III) following naphthalimide(T1) → Eu(5D0) energy transfer. Fig. 10 shows the kinetic behaviour of the Eu(III) emission [measured at 613 nm, curve (2)] of Eu·L in water; there are three components to this. Firstly, Eu(III)-based emission is already present immediately after the laser pulse [see the initial step on the kinetic curve, trace (2), shown in red]. Since direct excitation of Eu(III) must be insignificant or completely absent, this emission cannot be immediate but must arise from a grow-in process that is fast compared to the time resolution of our experiment which is limited by the 5 ns laser pulse. Secondly, there is an additional increase of sensitized Eu(III) emission intensity on the μs timescale; this is synchronous with the decay of the triplet excited state [see Fig. 10, curve (1)] and is associated with the slow (≈104 s−1) energy-transfer process. Thirdly, there is the usual slow decay of Eu(III) emission with a long lifetime (ms timescale). The latter two components are easy to understand, being the grow-in expected for slow energy-transfer from the naphthalimide T1 state (cf. its match with the T–T absorption spectra decay rate), followed by the normal slow radiative decay of Eu(III) on the ms timescale.![The kinetics of T–T absorption at 470 nm [curve (1)] and Eu-based luminescence at 613 nm [curve (2)] for Eu·L in water (1.1 × 10−4 M). Path length 1 cm. Solid lines are the calculated fits using eqn (4) and (5) and the parameters in Table 5.](/image/article/2013/PP/c3pp50109d/c3pp50109d-f10.gif) | ||
| Fig. 10 The kinetics of T–T absorption at 470 nm [curve (1)] and Eu-based luminescence at 613 nm [curve (2)] for Eu·L in water (1.1 × 10−4 M). Path length 1 cm. Solid lines are the calculated fits using eqn (4) and (5) and the parameters in Table 5. | ||
The initial Eu(III)-based emission intensity that appears within 5 ns is unexpected however, and there are two possible explanations for this that need to be considered.
(i) The high Eu-based emission intensity immediately after photoexcitation of naphthalimide could arise from a fast energy transfer process from the singlet excited state of the ligand (S1 → 5D0 transition), which occurs in parallel with the conventional, much slower, T1 → 5D0 energy transfer following S1 → T1 inter-system crossing (ISC). It is reasonable that S1 → 5D0 energy-transfer should be much faster than T1 → 5D0 energy transfer in Eu·L on the basis of a considerably better spectroscopic donor/acceptor overlap in the former case (Fig. 11). The fluorescence from the naphthalimide unit which lies in the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–30
000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 region overlaps with many excited states of Eu(III) in the region above 17
000 cm−1 region overlaps with many excited states of Eu(III) in the region above 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1; there are eight f–f states from 5D0 up to 5D4 at ca. 27
500 cm−1; there are eight f–f states from 5D0 up to 5D4 at ca. 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and direct population of many of these from the 7F0 ground state is allowed according to the selection rules for either Förster or Dexter energy-transfer to lanthanide ions.22 For example population of the 5D2, 5D4 and 5D6 levels (amongst others) would be allowed by multipolar energy-transfer (allowed transitions have ΔJ = 2, 4, 6). The good match between the fluorescence profile of the 1,8-naphthalimide unit of Eu·L and the highest density of f–f absorptions in the UV/Vis spectrum of Eu3+ in water (350–400 nm region) is clear in Fig. 11.
500 cm−1 and direct population of many of these from the 7F0 ground state is allowed according to the selection rules for either Förster or Dexter energy-transfer to lanthanide ions.22 For example population of the 5D2, 5D4 and 5D6 levels (amongst others) would be allowed by multipolar energy-transfer (allowed transitions have ΔJ = 2, 4, 6). The good match between the fluorescence profile of the 1,8-naphthalimide unit of Eu·L and the highest density of f–f absorptions in the UV/Vis spectrum of Eu3+ in water (350–400 nm region) is clear in Fig. 11.
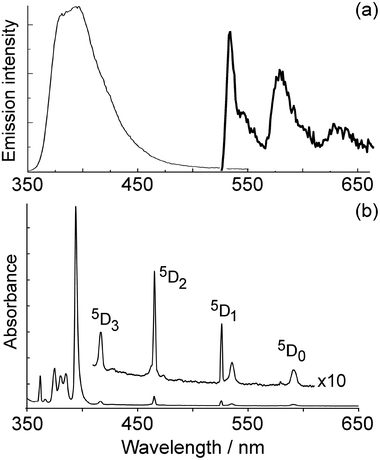 | ||
| Fig. 11 (a) Fluorescence from the naphthalimide unit of Eu·L in aqueous solution (thin line) and phosphorescence of a simple N-substituted naphthalimide recorded at 77 K (thick line, taken from ref. 23); (b) UV/Vis absorption spectrum of Eu(NO3)3 in water. | ||
In contrast the lower-energy phosphorescence of the naphthalimide unit23 occurs in an energy region where there is very little overlap with f–f absorptions of Eu3+, with the only overlapping f–f excited states being 5D0 and 5D1 (Fig. 11). Direct population of the 5D0 level from the 7F0 ground state is forbidden by either Förster or Dexter energy-transfer, as it is a J = 0 → J = 0 transition.22 Population of the 5D1 level is only Dexter-allowed (ΔJ = 1),22 but Dexter energy-transfer will be disfavoured by the lack of orbital contact between donor and acceptor units in Eu·L that are separated by an ethylene spacer. Overall it is reasonable that naphthalimide(S1) → Eu(5D0) energy-transfer should be much faster than T1 → 5D0 energy transfer.
Sensitisation of Eu(III) by the naphthalimide S1 state requires that the S1 → T1 ISC of the naphthalimide unit is slow enough for naphthalimide(S1) → Eu(5D0) energy-transfer to be competitive. With most aromatic ligand sensitisers this is not the case because coordination to a heavy lanthanide ion results in very fast ISC which means that only the T1 state acts as the energy-donor.5 In Eu·L however, if the pendant naphthalimide unit is not directly coordinated to the Eu(III) centre, ISC could be slow enough that the S1 state can also act as an energy donor to Eu(III). In simple N-substituted 1,8-naphthalimides, inter-system crossing is known to occur on the timescale ≈109–1010 s−1,8 which is just slow enough for direct naphthalimide(S1) → Eu(5D0) energy-transfer to occur in parallel in Eu·L (see discussion below). We can see that an additional ISC contribution from the heavy-atom effect is not operating here because the S1 fluorescence is not diminished in intensity in Eu·L and Gd·L compared to H3L: in fact it is more intense (see later), confirming the lack of a direct interaction between the naphthalimide pendant unit and the Eu(III) centre. We note also that there is precedent for sensitization of lanthanide emission by organic dye antenna groups proceeding from the singlet excited state of the donor in a few cases when it is sufficiently fast to complete with inter-system crossing.24
(ii) An alternative possibility which needs to be considered is that Eu·L could contain two conformers, with the naphthalimide energy-donor either close to or remote from the Eu(III) ion. This was investigated using DFT calculations. The final structures of the three conformers investigated are given in Fig. 12 with the structures varying from an unbound “remote” naphthalimide in Fig. 12(a)via a semi-bound one [Fig. 12(b)] to a directly bound unit [Fig. 12(c)]. The relative energies are given in Fig. 12 as well. Our studies show that a conformer with one of the naphthalimide carbonyl groups directly coordinated to Eu(III) is sterically possible, resulting in the ligand being octadentate rather than heptadentate and displacing one water ligand. Moreover, a semi-bound conformer is possible as well, in which the naphthalimide unit is involved in a second-sphere interaction with the Eu(III) via a coordinated water molecule. The co-existence of both ‘bound/close’ and ‘unbound/remote’ naphthalimide units would provide a credible alternative explanation for the presence of slow and fast energy-transfer processes.
![Possible conformations of Eu·L, with the naphthalimide unit either pendant from the metal centre [panel (a)], indirectly coordinated [panel (b)], or directly coordinated [panel (c)] to the metal centre.](/image/article/2013/PP/c3pp50109d/c3pp50109d-f12.gif) | ||
| Fig. 12 Possible conformations of Eu·L, with the naphthalimide unit either pendant from the metal centre [panel (a)], indirectly coordinated [panel (b)], or directly coordinated [panel (c)] to the metal centre. | ||
However several factors lead us to discount this. Firstly, the our calculations show that the ‘bound’ and ‘semi-bound’ conformers in Fig. 12 have Gibbs free energies which are 26.6 kJ mol−1 and 23.9 kJ mol−1 higher than the ‘unbound’ conformer. This rules them out as significant contributors to the structure in solution, if we assume Boltzmann statistics. (Here, we need to point out that we did not consider coordination of water to the carbonyl groups of the naphthalimide unit. However, inclusion of these water interactions will only make the unbound structure even more favourable.) Secondly, as we reported in our earlier communication,7 a value of ≈2 for the number of coordinated water molecules at Eu(III) implies that the ligand L3− is heptadentate (from the macrocycle and three carboxylates) with the naphthalimide not coordinated. Thirdly, a characteristic of conformationally flexible donor–acceptor systems is the presence of a range of energy-transfer rates leading to complex kinetic behavior,25 which would be the case here as well, given the three very different conformations. However, in our experiments only one fast and one slow energy-transfer process is found with no intermediate values that would lead to multi-exponential decay kinetics. Hence, what we see is more consistent with parallel T1 → 5D0 and S1 → 5D0 processes in a single conformer. Finally, as mentioned earlier, direct coordination of naphthalimide to Eu(III) would result in increased ISC and hence a decrease in fluorescence intensity compared to non-metallated H3L, which is clearly not the case (see section 5 below).
Therefore we prefer the first explanation, viz. that energy transfer occurs from both S1 and T1 excited states of naphthalimide. The magnitude of the fast sensitized luminescence component [the step on the kinetic curve (2) in Fig. 10] is significant, and implies that energy transfer from the singlet excited state occurs on a comparable timescale to inter-system crossing. As the lifetime of the naphthalimide S1 state lies in the range 0.28–2.2 ns (Table 1), the rate constant for S1 → 5D0 energy transfer can be estimated as 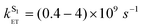 , five orders of magnitude faster than the T1 → 5D0 energy transfer rate. This is in good agreement with the known ISC rate for 1,8-naphthalimides (as required),8 and is consistent with any rise time for the sensitized luminescence being undetectable within the duration of the excitation laser pulse.
, five orders of magnitude faster than the T1 → 5D0 energy transfer rate. This is in good agreement with the known ISC rate for 1,8-naphthalimides (as required),8 and is consistent with any rise time for the sensitized luminescence being undetectable within the duration of the excitation laser pulse.
We can further calculate simultaneously the kinetics of the energy transfer to and from the T1 state (and the decay of Eu3+ luminescence), and the disappearance of T–T absorption, by solving a pair of differential eqn (4) and (5):
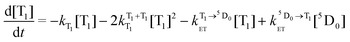 | (4) |
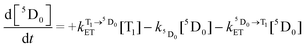 | (5) |
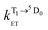 and
and 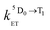 are the rate constants for forward and backward energy transfer processes from and to the naphthalimide T1 state;
are the rate constants for forward and backward energy transfer processes from and to the naphthalimide T1 state; 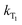 and
and 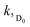 are the rate constants for decay of the T1 and 5D0 states; and
are the rate constants for decay of the T1 and 5D0 states; and 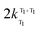 is the rate constant for triplet–triplet annihilation of the naphthalimide unit. The
is the rate constant for triplet–triplet annihilation of the naphthalimide unit. The 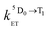 rate constant for back energy-transfer from excited Eu(III) to the naphthalimide sensitiser needs to be introduced, because the energy gradient for forward energy-transfer from T1 (18
rate constant for back energy-transfer from excited Eu(III) to the naphthalimide sensitiser needs to be introduced, because the energy gradient for forward energy-transfer from T1 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) to 5D0 (17
500 cm−1) to 5D0 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) states is only 1000 cm−1, which means that back energy-transfer is possible at room temperature.26
500 cm−1) states is only 1000 cm−1, which means that back energy-transfer is possible at room temperature.26
The naphthalimide T1 concentration, denoted [T1], can be estimated from the values of the optical density at the T–T absorption maximum, and the extinction coefficient of this absorption (ε ≈ 1 × 104 M−1 cm−1).8 The main difficulty in this calculation is the unknown initial fraction of Eu3+ in its 5D0 excited state immediately after the laser pulse, i.e. arising from the fast S1 → 5D0 energy-transfer process. We call this value [5D0]. An estimate of this can be made from the kinetic trace in Fig. 8 which shows that the contributions to Eu-based luminescence intensity arising from this fast formation of the 5D0 state (the height of the initial ‘step’ at time = 0), and the contribution arising from the slower T1 → 5D0 energy-transfer (the additional increase in Eu-based emission intensity), are comparable.
Assuming a 5D0 concentration of approximately half of the T1 concentration as a starting point (cf.Fig. 10) a reasonable estimate of the kinetic parameters can be obtained (see Table 5). The presence of back energy transfer (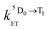 ) is evident from the non-zero concentration of the naphthalimide T1 state observed at later time delays [100–250 μs in Fig. 10, curve (1)]. Thus, whilst the lifetime (1/
) is evident from the non-zero concentration of the naphthalimide T1 state observed at later time delays [100–250 μs in Fig. 10, curve (1)]. Thus, whilst the lifetime (1/ 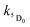 ) of the Eu-based excited-state in Eu·L is about 0.85 ms, the observed luminescence lifetime is shorter because back energy transfer from the 5D0 state to the naphthalimide T1 state provides an additional non-radiative decay pathway. Fitting the kinetic curve (2) in Fig. 10 with a two-exponential approximation for these two processes yields the observed luminescence lifetime of 0.27 ms in water.
) of the Eu-based excited-state in Eu·L is about 0.85 ms, the observed luminescence lifetime is shorter because back energy transfer from the 5D0 state to the naphthalimide T1 state provides an additional non-radiative decay pathway. Fitting the kinetic curve (2) in Fig. 10 with a two-exponential approximation for these two processes yields the observed luminescence lifetime of 0.27 ms in water.
| Solvent | [T1]/M | [5D0]/M | k T1/s−1 |
|
|
|
|
|---|---|---|---|---|---|---|---|
| Water | 7.5 × 10−6 | 3.5 × 10−6 | 4.7 × 104 | 4.4 × 109 | 9.7 × 103 | 3.0 × 103 | 1.2 × 103 |
| MeCN | 1.3 × 10−5 | 5.2 × 10−6 | 5.5 × 103 | 5.0 × 108 | 1.4 × 104 | 1.4 × 103 | 0.9 × 103 |
Fig. 13 shows the same data [kinetics of T–T absorption at 470 nm, and sensitized luminescence from Eu3+ ion (613 nm), following 355 nm excitation of Eu·L] but in CH3CN. The behavior of the sensitized Eu-based emission – with a grow-in component that is fast on the timescale of the laser pulse, and another slower one that matches the T–T decay rate – is similar to what was observed in water and the same explanation is proposed, viz. the presence of energy transfer originating from both the naphthalimide S1 state (fast) and the T1 state (slow). We can see that the balance between the two components is slightly different in MeCN compared to water, with the initial ‘step’ in Eu-based emission (the fast energy-transfer component) being reduced in significance compared to the slower grow-in component. A definitive reason for this is not obvious but may include changes in conformation associated with solvation differences, as energy-transfer by any mechanism is strongly distance dependent. Using the same procedure as described above for the studies in water, and the lifetime of the ligand S1 state in CH3CN of 0.25–1.25 ns (Table 2), one obtains the rate constant of S1 → 5D0 energy-transfer as 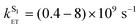 . From the pair of eqn (4) and (5), using the same analysis as was performed for the aqueous solution, we find that the natural lifetime (1/
. From the pair of eqn (4) and (5), using the same analysis as was performed for the aqueous solution, we find that the natural lifetime (1/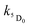 ) of Eu·L luminescence in CH3CN is about 1.1 ms; however the observed lifetime is shorter due to back energy transfer from the 5D0 state to the naphthalimide T1 state. Fitting the data presented in curve (2) in Fig. 13 with a two-exponential approximation yields the observed lifetime of 0.8 ms, which is (expectedly) longer than observed in water (0.27 ms) due to the absence of O–H oscillators, which are known to be effective quenchers of Eu-based emission,27 in MeCN. Kinetic parameters are summarized in Table 5.
) of Eu·L luminescence in CH3CN is about 1.1 ms; however the observed lifetime is shorter due to back energy transfer from the 5D0 state to the naphthalimide T1 state. Fitting the data presented in curve (2) in Fig. 13 with a two-exponential approximation yields the observed lifetime of 0.8 ms, which is (expectedly) longer than observed in water (0.27 ms) due to the absence of O–H oscillators, which are known to be effective quenchers of Eu-based emission,27 in MeCN. Kinetic parameters are summarized in Table 5.
![The kinetics of T–T absorption at 470 nm [curve (1)] and Eu-based luminescence at 613 nm [curve (2)] for Eu·L in CH3CN (1.1 × 10−4 M). Path length 1 cm. Solid lines are the calculated fits using eqn (4) and (5) and the parameters in Table 5.](/image/article/2013/PP/c3pp50109d/c3pp50109d-f13.gif) | ||
| Fig. 13 The kinetics of T–T absorption at 470 nm [curve (1)] and Eu-based luminescence at 613 nm [curve (2)] for Eu·L in CH3CN (1.1 × 10−4 M). Path length 1 cm. Solid lines are the calculated fits using eqn (4) and (5) and the parameters in Table 5. | ||
Conclusions
We have used a combination of laser flash photolysis, emission spectroscopy and DFT calculations to study the photophysical properties of H3L and its lanthanide complexes Eu·L and Gd·L. The two main conclusions are as follows.(i) The compounds aggregate at high concentrations, as shown by appearance of a low-energy fluorescence band in addition to the monomer fluorescence; from the concentration dependence of this effect we could estimate the equilibrium constants for aggregation (assuming a simple monomer/dimer equilibrium) in different solvents.
(ii) We also studied in detail the mechanism of energy transfer in Eu·L. The sensitization of Eu(III)-based emission by the naphthalimide chromophore in Eu·L has both fast (≥109 s−1) and slow (≈104 s−1) contributions. We suggest that this occurs by energy-transfer from both the singlet S1 (fast) and triplet T1 (slow) excited states of the naphthalimide chromophore, with the balance between the two pathways arising because S1 → Eu(5D0) energy-transfer and S1 → T1 inter-system crossing occur on similar timescales such that neither pathway dominates completely. This is different from the usually observed situation where sensitization of lanthanide luminescence occurs exclusively from an aromatic ligand T1 state. However in Eu·L the fact that the naphthalimide unit is separated from the Eu(III) ion by an ethylene spacer, and the poor donor/acceptor overlap, make T1 → Eu(5D0) energy-transfer particularly slow. In addition this spatial separation will weaken the heavy-atom effect which facilitates inter-system crossing, which slows down the S1 → T1 conversion to the extent that S1 → Eu(5D0) energy-transfer becomes competitive. S1 → Eu(5D0) energy-transfer is inherently much faster than T1 → Eu(5D0) energy-transfer because of the much greater donor/acceptor spectroscopic overlap. A photophysical scheme summarising the behaviour of Eu·L is in Fig. 14.
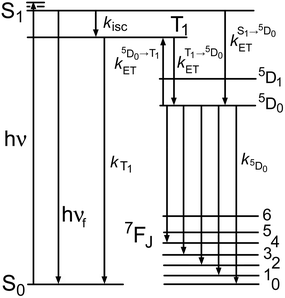 | ||
| Fig. 14 Summary of the photophysical processes occurring in Eu·L. Naphthalimide-based states are on the left; Eu3+-based states are on the right. | ||
Acknowledgements
This work was supported by the Russian Foundation for Fundamental Research (grants 11-03-92605-KO, 11-03-00268, 12-03-00482) and the Program of Integration Projects of SB RAS (grants 33, 88); the Royal Society UK (an International Joint Project grant); the Leverhulme Trust (post-doctoral fellowship to A. H. S.); the EPSRC and the University of Sheffield (UK). All of these institutions are thanked for financial support.References
- (a) J.-C. G. Bünzli, Lanthanide luminescence for biomedical analyses and imaging, Chem. Rev., 2010, 110, 2729 CrossRef; (b) E. Eliseeva and J.-C. G. Bünzli, Lanthanide luminescence for functional materials and biosciences, Chem. Soc. Rev., 2010, 39, 189 RSC; (c) A. Thibon and V. C. Pierre, Principles of responsive lanthanide-based luminescent probes, Anal. Bioanal. Chem., 2009, 394, 107 CrossRef CAS; (d) D. Parker, Critical design factors for optical imaging with metal coordination complexes, Aust. J. Chem., 2011, 64, 239 CrossRef CAS; (e) C. Allain and S. Faulkner, Photo-physical approaches to responsive optical probes, Future Med. Chem., 2010, 2, 339 CrossRef CAS; (f) J.-C. G. Bünzli, Lanthanide luminescent bioprobes, Chem. Lett., 2009, 104 CrossRef; (g) E. J. New, D. Parker, D. G. Smith and J. W. Walton, Development of responsive lanthanide probes for cellular applications, Curr. Opin. Chem. Biol., 2010, 14, 238 CrossRef CAS; (h) H. Uh and S. Petoud, Novel antennae for the sensitization of near infrared luminescent lanthanide cations, C. R. Chim., 2010, 13, 668 CrossRef CAS.
- (a) A. K. Hagan and T. Zuchner, Lanthanide-based time-resolved luminescence immunoassays, Anal. Bioanal. Chem., 2011, 400, 2847 CrossRef CAS; (b) E. G. Moore, A. P. S. Samuel and K. N. Raymond, From antenna to assay; lessons learned in lanthanide luminescence, Acc. Chem. Res., 2009, 42, 542 CrossRef CAS; (c) R. Carr, N. H. Evans and D. Parker, Lanthanide complexes as chiral probes exploiting circularly polarized luminescence, Chem. Soc. Rev., 2012, 41, 7673 RSC; (d) M. L. Cable, D. J. Levine, J. P. Kirby, H. B. Gray and A. Ponce, Luminescent lanthanide sensors, Adv. Inorg. Chem., 2011, 63, 1 CrossRef CAS.
- J.-C. G. Bünzli and S. Eliseeva, Lanthanide NIR luminescence for telecommunications, bioanalyses and solar energy conversion, J. Rare Earths, 2010, 28, 824 CrossRef.
- (a) L. D. Carlos, R. A. S. Ferreira, V. S. Bermudez, B. Julian-Lopez and P. Escribano, Progress on lanthanide-based organic–inorganic hybrid phosphors, Chem. Soc. Rev., 2011, 40, 536 RSC; (b) N. T. Kalyani and S. J. Dhoble, Organic light emitting diodes: energy saving lighting technology – a review, Renewable Sustainable Energy Rev., 2012, 16, 2696 CrossRef; (c) R. C. Evans, P. Douglas and C. J. Winscom, Coordination complexes exhibiting room-temperature phosphorescence: evaluation of their suitability as triplet emitters for light-emitting diodes, Coord. Chem. Rev., 2006, 250, 2093 CrossRef CAS.
- N. Sabbatini, M. Guardigli and J.-M. Lehn, Luminescent lanthanide complexes as photochemical supramolecular devices, Coord. Chem. Rev., 1993, 123, 201 CrossRef CAS.
- (a) P. Coppo, M. Duati, V. Kozhevnikov, J. W. Hofstraat and L. De Cola, White-light emission from an assembly comprising luminescent iridium and europium complexes, Angew. Chem., Int. Ed., 2005, 44, 1806 CrossRef CAS; (b) D. Sykes, I. S. Tidmarsh, A. Barbieri, I. V. Sazanovich, J. A. Weinstein and M. D. Ward, d–f Energy-transfer in a series of Ir(III)/Eu(III) dyads: energy-transfer mechanisms and white-light emission, Inorg. Chem., 2011, 50, 11323 CrossRef CAS.
- A. H. Shelton, I. V. Sazanovich, J. A. Weinstein and M. D. Ward, Controllable three-component luminescence from a 1,8-naphthalimide/Eu(III) complex: white light emission from a single molecule, Chem. Commun., 2012, 48, 2749 RSC.
- V. Wintgens, P. Valat, J. Kossanyi, L. Biczok, A. Demeter and T. Bérces, Spectroscopic properties of aromatic dicarboximides. Part 1. N–H and N-methyl-substituted naphthalimides, J. Chem. Soc., Faraday Trans., 1994, 90, 411 RSC.
- (a) M. de Sousa, M. Kluciar, S. Abad, M. A. Miranda, B. de Castro and U. Pischel, An inhibit (INH) molecular logic gate based on 1,8-naphthalimide-sensitised europium luminescence, Photochem. Photobiol. Sci., 2004, 3, 639 RSC; (b) J. P. Cross, M. Lauz, P. D. Badger and S. Pétoud, Polymetallic lanthanide complexes with PAMAM-naphthalimide dendritic ligands: luminescent lanthanide complexes formed in solution, J. Am. Chem. Soc., 2004, 126, 16278 CrossRef CAS.
- (a) Z. Xu, J. Yoon and D. R. Spring, A selective and ratiometric Cu2+ fluorescent probe based on naphthalimide excimer-monomer switching, Chem. Commun., 2010, 46, 2563 RSC; (b) T. C. Barros, P. B. Filho, V. G. Toscano and M. J. Politi, Intramolecular excimer formation from 1,8-N-alkyldinaphthalimides, J. Photochem. Photobiol. A: Chem., 1995, 89, 141 CrossRef CAS; (c) D. W. Cho, M. Fujitsuka, A. Sugimoto and T. Majima, Intramolecular excimer formation and photoinduced electron-transfer process in bis-1,8-naphthalimide dyads depending on the linker length, J. Phys. Chem. A, 2008, 112, 7208 CrossRef CAS.
- W. H. Melhuish, Quantum efficiencies of fluorescence of organic substances: effect of solvent and concentration of the fluorescent solute, J. Phys. Chem., 1961, 65, 229 CrossRef CAS.
- W. R. Dawson and M. W. Wind, Fluorescence yields of aromatic compounds, J. Phys. Chem., 1968, 72, 3251 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision C.02), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- (a) A. Nicklass, M. Dolg, H. Stoll and H. Preuss, Ab initio energy-adjusted pseudopotentials for the noble gases Ne through Xe: calculation of atomic dipole and quadrupole polarizabilities, J. Chem. Phys., 1995, 102, 8942 CrossRef CAS; (b) X. Y. Cao and M. Dolg, Valence basis sets for relativistic energy-consistent small-core lanthanide pseudopotentials, J. Chem. Phys., 2001, 115, 7348 CrossRef CAS , and references therein; ; (c) T. H. Dunning Jr. and P. J. Hay, Gaussian basis sets for molecular calculations, in Modern Theoretical Chemistry, ed. H. F. Schaefer III, Plenum, New York, 1977, vol. 3, p. 1 Search PubMed.
- (a) C. S. Grange, A. J. H. M. Meijer and M. D. Ward, Trinuclear ruthenium dioxolene complexes based on the bridging ligand hexahydroxytriphenylene: electrochemistry, spectroscopy, and near-infrared electrochromic behaviour associated with a reversible seven-membered redox chain, Dalton Trans., 2010, 39, 200 RSC; (b) J.-M. Herrera, S. J. A. Pope, A. J. H. M. Meijer, T. L. Easun, H. Adams, W. Z. Alsindi, M. W. George and M. D. Ward, Photophysical and structural properties of cyanoruthenate complexes of hexaaza-triphenylene, J. Am. Chem. Soc., 2007, 129, 11491 CrossRef CAS.
- (a) B. Menucci and J. Tomassi, Continuum solvation models: a new approach to the problem of solute's charge distribution and cavity boundaries, J. Chem. Phys., 1997, 106, 5151 CrossRef; (b) M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Ab initio study of ionic solutions by a polarizable continuum dielectric model, Chem. Phys. Lett., 1998, 286, 253 CrossRef CAS and references therein.
- L. J. Charbonnière, S. Faulkner, C. Platas-Iglesias, M. Regueiro-Figueroa, A. Nonat, T. Rodríguez-Blas, A. de Blas, W. S. Perry and M. Tropiano, Ln2M complexes (M = Ru, Re) derived from a bismacrocyclic ligand containing a 4,4′-dimethyl-2,2′-bipyridyl bridging unit, Dalton Trans., 2013, 42, 3667 RSC.
- R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- F. Würthner, T. E. Kaiser and C. R. Saha-Möller, J-Aggregates: from serendipitous discovery to supramolecular engineering of functional dye materials, Angew. Chem., Int. Ed., 2011, 50, 3376 CrossRef.
- (a) M. G. Kuzmin, N. A. Sadovskii, J. A. Weinstein and O. I. Kutsenok, Exciplex mechanism of fluorescence quenching in polar media, Proc. – Indian Acad. Sci., Chem. Sci., 1993, 105, 637 CAS; (b) J. B. Birks and L. G. Christophorou, Excimer formation in polycyclic hydrocarbons and their derivatives, Nature, 1963, 197, 1064 CrossRef CAS.
- (a) G. F. de Sá, O. L. Malta, C. de Mello Donegá, A. M. Simas, R. L. Longo, P. A. Santa-Cruz and E. F. da Silva Jr., Spectroscopic properties and design of highly luminescent lanthanide coordination complexes, Coord. Chem. Rev., 2000, 196, 165 CrossRef; (b) F. R. Gonçalves e Silva, O. L. Malta, C. Reinhard, H.-U. Güdel, C. Piguet, J. E. Moser and J.-C. G. Bünzli, Visible and near-infrared luminescence of lanthanide-containing dimetallic triple-stranded helicates: energy transfer mechanisms in the SmIII and YbIII molecular edifices, J. Phys. Chem. A, 2002, 106, 1670 CrossRef.
- J.-P. Malval, S. Suzuki, F. Morlet-Savary, X. Allonas, J.-P. Fouassier, S. Takahara and T. Yamaoka, Photochemistry of naphthalimide photoacid generators, J. Phys. Chem. A, 2008, 112, 3879 CrossRef CAS.
- (a) G. A. Hebbink, A. I. Klink, L. Grave, P. G. B. Oude Alink and F. C. J. M. van Veggel, Singlet energy transfer as the main pathway in the sensitization of near-infrared Nd3+ luminescence by dansyl and lissamine dyes, ChemPhysChem, 2002, 3, 1014 CrossRef CAS; (b) A. Guenet, F. Eckes, V. Bulach, C. A. Strassert, L. De Cola and M. W. Hosseini, Sensitisation of the near-infrared emission of NdIII from the singlet state of porphyrins bearing four 8-hydroxyquinolinylamide chelates, ChemPhysChem, 2012, 13, 3163 CrossRef CAS.
- (a) T. L. Easun, W. Z. Alsindi, N. Deppermann, M. Towrie, K. L. Ronayne, X.-Z. Sun, M. D. Ward and M. W. George, A luminescence and time-resolved infrared study of dyads containing (diimine)Ru(4,4′-diethylamido-2,2′-bipyridine)2 and (diimine)Ru(CN)4 moieties: solvent-induced reversal of the direction of photoinduced energy-transfer, Inorg. Chem., 2009, 48, 8759 CrossRef CAS; (b) T. L. Easun, W. Z. Alsindi, M. Towrie, K. L. Ronayne, X.-Z. Sun, M. D. Ward and M. W. George, Photoinduced energy-transfer in a conformationally flexible Re(I)/Ru(II) dyad probed by time-resolved infra-red spectroscopy: effects of conformation and spatial localisation of excited states, Inorg. Chem., 2008, 47, 5071 CrossRef CAS; (c) S. J. A. Pope, C. R. Rice, M. D. Ward, A. F. Morales, G. Accorsi, N. Armaroli and F. Barigelletti, Folding of a poly(oxyethylene) chain as probed by photoinduced energy transfer between Ru-and Os-polypyridine termini, J. Chem. Soc., Dalton Trans., 2001, 2228 RSC; (d) M. Frank, M. Nieger, F. Vögtle, P. Belser, A. von Zelewsky, L. De Cola, V. Balzani, F. Barigeletti and L. Flamigni, Dinuclear Ru(II) and/or Os(II) complexes of bis-bipyridine bridging ligands containing adamantane spacers: synthesis, luminescence properties, intercomponent energy and electron transfer processes, Inorg. Chim. Acta, 1996, 242, 281 CrossRef CAS.
- D. Parker, Luminescent lanthanide sensors for pH, pO2 and selected anions, Coord. Chem. Rev., 2000, 205, 109 CrossRef CAS.
- R. M. Supkowski and W. D. Horrocks, On the determination of the number of water molecules, q, coordinated to europium(III) ions in solution from luminescence decay lifetimes, Inorg. Chim. Acta, 2002, 340, 44 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3pp50109d |
| This journal is © The Royal Society of Chemistry and Owner Societies 2013 |