 Open Access Article
Open Access ArticleA kinetic and theoretical study of the borate catalysed reactions of hydrogen peroxide: the role of dioxaborirane as the catalytic intermediate for a wide range of substrates†
Michael E.
Deary
*a,
Marcus C.
Durrant
b and
D. Martin
Davies
b
aFaculty of Engineering and Environment, Northumbria University, Newcastle upon Tyne NE1 8ST, UK. E-mail: michael.deary@unn.ac.uk
bFaculty of Health and Life Sciences, Northumbria University, Newcastle upon Tyne NE1 8ST, UK
First published on 19th November 2012
Abstract
Our recent work has provided new insights into the equilibria and species that exist in aqueous solution at different pHs for the boric acid – hydrogen peroxide system, and the role of these species in oxidation reactions. Most recently, (M. C. Durrant, D. M. Davies and M. E. Deary, Org. Biomol. Chem., 2011, 9, 7249–7254), we have produced strong theoretical and experimental evidence for the existence of a previously unreported monocyclic three membered peroxide species, dioxaborirane, that is the likely catalytic species in borate mediated electrophilic reactions of hydrogen peroxide in alkaline solution. In the present paper, we extend our study of the borate–peroxide system to look at a wide range of substrates that include substituted dimethyl anilines, methyl-p-tolyl sulfoxide, halides, hydrogen sulfide anion, thiosulfate, thiocyanate, and hydrazine. The unusual selectivity–reactivity pattern of borate catalysed reactions compared with hydrogen peroxide and inorganic or organic peracids previously observed for the organic sulfides (D. M. Davies, M. E. Deary, K. Quill and R. A. Smith, Chem.–Eur. J., 2005, 11, 3552–3558) is also seen with substituted dimethyl aniline nucleophiles. This provides evidence that the pattern is not due to any latent electrophilic tendency of the organic sulfides and further supports dioxaborirane being the likely reactive intermediate, thus broadening the applicability of this catalytic system. Moreover, density functional theory calculations on our proposed mechanism involving dioxaborirane are consistent with the experimental results for these substrates. Results obtained at high concentrations of both borate and hydrogen peroxide require the inclusion the diperoxodiborate dianion in the kinetic analysis. A scheme detailing our current understanding of the borate–peroxide system is presented.
Introduction
Our recent work has provided new insights into the equilibria and species that exist in aqueous solution at different pHs when hydrogen peroxide and boric acid are mixed together in concentrations of up to 0.5 M borate and 2.0 M hydrogen peroxide.1–3 In addition, through density functional theory (DFT) calculations, we have determined the species that are likely to be responsible for observed catalysis of electrophilic reactions of hydrogen peroxide with dimethyl sulfide and substituted phenyl methyl sulfides.3Fig. 1 details our current understanding of the hydrogen peroxide–borate system and Table 1 lists the corresponding formation constants; the nomenclature has been retained and expanded, from our previous work.1–3 It is well known that both boric acid, 1, and peroxoboric acid, 3, which are both present at low pH, act primarily as Lewis acids, however our recent DFT study has shown that they are also likely to exhibit a small degree of Brønsted acidity,3 sufficient for the respective anions, structures 4 and 5, to exist in solution at low concentrations. The peroxoborate anion, 5, has a tautomeric form, 8, a previously unreported monocyclic three membered peroxide species named dioxaborirane.3 It is this species that we have proposed as being responsible for the catalysis that is observed for borate mediated electrophilic reactions of hydrogen peroxide with sulfides in alkaline conditions,3 rather than the previously assumed monoperoxoborate, 6, and diperoxoborate, 7, anions, that dominate in alkaline solution, the latter when there are high ratios of hydrogen peroxide to borate. Dioxaborirane, which is in equilibrium with monoperoxoborate via the addition of a water molecule, has a particularly low energy barrier for the reaction with dimethyl sulfide (ca. 2.8 kcal mol−1), though it is likely to be present in only small concentrations.3 For the same reaction monoperoxoborate has an activation barrier of 17.5 kcal mol−1, compared to 10.1 kcal mol−1 for the uncatalysed reaction of hydrogen peroxide, hence monoperoxoborate is unlikely to be catalytically active. The low activation barrier for the dioxaborirane is likely to be due to the intrinsic reactivity of the three membered ring, as has been reported elsewhere for the carbon analogue of dioxirane,4–7 together with the lack of any steric hindrance in the transition state. At low pH, peroxoboric acid, 3, with an activation barrier of 7.4 kcal mol−1, is a plausible catalyst, but it has a low formation constant and so the observed rate enhancement for its reaction with dimethyl sulfide is small. At higher ratios of borate to hydrogen peroxide, the unreactive peroxodiborate dianion, 9, is formed,2,3 and in this paper we adduce evidence that this species can complex with an additional hydrogen peroxide molecule to form the diperoxodiborate dianion, 10.
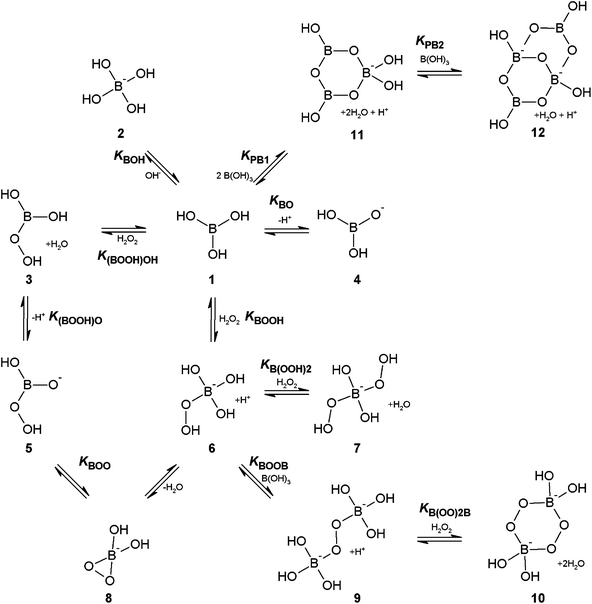 | ||
| Fig. 1 System of equilibria for aqueous mixtures of boric acid and hydrogen peroxide. | ||
| Formation constant | Value | Reference |
|---|---|---|
| a n.d., not determined. | ||
| K BOH | 1.0 × 10−9 M | 14 |
| K BO | 2.51 × 10−10 M−1 | 3 |
| K (BOOH)OH | 0.01 M−1 | 14 |
| K (BOOH)O | n.d.a | 3 |
| K BOOH | 2.0 × 10−8 | 14 |
| K (BOOH)2 | 2.0 M−1 | 14 |
| K BOO | n.d. (small) | 3 |
| K BOOB | 4.3 M−1 | 2 |
| K B(OO)2B | 61 M−1 | This work |
| K PB1 | 1.44 × 10−7 M−1 | 8 |
| K PB2 | 1.52 × 10−8 M−1 | 8 |
Finally we should note that a large number of polyborate species have been proposed to exist at higher borate concentrations,8–13 though literature studies have shown that the trimer, 11 and the tetraborate ion, 12 are the major species present.8,12,13 In addition, we cannot rule out the existence of polyperoxyborates: there is no reason why species 11 and 12 should not complex with hydrogen peroxide in an analogous way to boric acid, 1.
At alkaline pHs the predicted high reactivity of dioxaborirane is consistent, under the Hammond Postulate, with its low selectivity (taken as the Hammett ρ value, −0.65,1 for its reaction with a range of the sulfides) when compared with other hydroperoxides such as hydrogen peroxide (ρ = −1.51), peroxymonocarbonate, HOOCO2− (ρ = −1.4 in 1.76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol
1 ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water15), peroxybenzoic acids (ρ = −1.15, −1.09 and −1.13 for 3-chloro, 4-nitro and 4-methyl perbenzoic acids respectively16), and peroxomonosulfate, HOOSO3− (ρ = −117).
water15), peroxybenzoic acids (ρ = −1.15, −1.09 and −1.13 for 3-chloro, 4-nitro and 4-methyl perbenzoic acids respectively16), and peroxomonosulfate, HOOSO3− (ρ = −117).
The experimental and theoretical work described in the present paper extends the range of substrates for the hydrogen peroxide–borate system to include substituted dimethyl anilines, methyl-p-tolyl sulfoxide, iodide, bromide, thiosulfate, the anion of hydrogen sulfide, HS−, and hydrazine.
The substituted dimethyl anilines are included in order to determine whether the same low selectivity observed for reaction with sulfides is also seen for reactions at a tertiary nitrogen. A similar observation would lend further support to the reactive species being the dioxaborirane since it would rule out the potentially complicating possibility that the observed effects were in part due to the ability of sulfides to act both as nucleophiles and electrophiles with peroxoborates.
Substituted phenyl methyl sulfoxides are included as a comparison because they are considerably less nucleophilic toward hydroperoxides.18,19 Thiosulfate, HS−, iodide and bromide, all anions, are compared with thiocyanate, which was originally used to demonstrate the electrophilic reactivity of peroxoborate.20 Hydrazine is included because borate has previously been reported to be a better catalyst than Cu(II) for the reaction between hydrazine and hydrogen peroxide, and gives the highest hydrogenation efficiency in the diimide hydrogenation of nitrile-butadiene rubber latex using hydrazine and hydrogen peroxide (although these properties were not attributed to peroxoborate formation).21,22
Hydrogen peroxide is an environmentally benign and atom efficient oxidant, and the catalysis of its reactions by borate/boric acid is fundamental chemistry that, as well as offering environmental applications for the destruction of pollutants including dimethyl sulfide, has wider potential importance since sodium perborate is used as a source of peroxide in synthetic chemistry.23–25 Indeed, Chaudhuri et al. have recently reported on the borate catalysed oxidation of organic sulfides by hydrogen peroxide in different media to achieve selective oxidation to sulfoxides and sulfones in high yields, though selectivity in this context arose from the significant difference in oxidation rates of sulfides and sulfoxides towards peroxides and the time allowed for the reaction to take place.26
Results
Kinetic study
Whilst dioxaborirane is a plausible reactive species for the hydrogen peroxide–borate system in alkaline conditions, it does present a problem in terms of analysis of the kinetic data since the equilibrium constant, KBOO, which is likely to be small, is not known. Nevertheless, making the assumption that all of the species depicted in Fig. 1 are in rapid equilibrium with each other, it is valid to analyse the kinetic data relative to the overall concentration of the significant species in solution, i.e. the monoperoxoborate, and monoperoxodiborate for these experiments. This also has the advantage of retaining comparability with our earlier work. Eqn (1) was, therefore, used to analyse the kinetic data for reactions carried out at high ratios of borate to hydrogen peroxide, as with our recent study of the reaction with dimethyl sulfide. Here, kobs is the observed first order rate constant, kP1 is the rate constant for the uncatalysed reaction with hydrogen peroxide, kP1BOH is the rate constant for the reaction of monoperoxoborate, including any reactive species in equilibrium with it, and kP1BOH2 is the rate constant for the reaction of monoperoxodiborate. The dependence of kobs on the total concentration of boric acid is fitted using the approach described previously,1,2 according to eqn (1), with the rate constant for the reaction of monoperoxodiborate, kP1BOH2 set equal to zero. The concentrations of the peroxide species are calculated using the mass balance equations for total boron (2) and peroxide (3) concentrations and the associated equilibrium constants listed in Table 1. The presence of the polyborate species, 11 and 12 were accounted for in the curve fitting analysis using a bisection method that was inserted into the equation editor of Grafit version 7,27 allowing the calculation of the concentrations of the borate species present.| kobs = kP1[H2O2] + kP1BOH[(HO)3BOOH−] + kP1BOH2[(HO)3BOOB(OH)32−] | (1) |
| Bt = B(OH)3 + B(OH)4− + HOOB(OH)3− + (HOO)2B(OH)2− + HOOB(OH)2 + 2(HO)3BOOB(OH)32− | (2) |
| Pt = H2O2 + HOO− + HOOB(OH)3− + 2 (HOO)2B(OH)2− + HOOB(OH)2 + (HO)3BOOB(OH)32− | (3) |
The reactions of two substrates, namely thiosulfate and HS−, were inhibited by borate. For the reaction with thiosulfate, Fig. 2 shows that increasing the total boric acid concentration causes a decrease in kobs. The corresponding values of kP1 and kP1BOH, obtained using eqn (1), with kP1BOH2 set to zero are included in Table 2.
 | ||
| Fig. 2 Effect of total boric acid concentration on the reaction of 8 × 10−3 M sodium thiosulfate and 0.087 M hydrogen peroxide (pH 9.5) and of 2.1 × 10−3 M hydrogen peroxide and 0.0225 M sodium sulfide (pH 10.0), ionic strength 0.2 M with sodium sulfate, curves are best fit values according to eqn (1) or (4) with the rate constants shown in Table 2 and kP1BOH2 set to zero. | ||
| Substrate | k P1/10−6 M−1 s−1 | k P1BOH/10−6 M−1 s−1 |
|---|---|---|
| a Measured at a pH in the range 9.5–10. b Measured at pH 4.3. c Calculated from the data of Wilson.20 d Adjusted for the statistical factor of two for the two nucleophilic nitrogens. | ||
| CH3SCH3 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 6400 600 ± 6400 |
338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 16 000 ± 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| S2O32− | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 200 200 ± 200 |
8120 ± 240 |
| HS− | 299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 15 000 ± 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 9800 000 ± 9800 |
| I− | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 1600 700 ± 1600 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ± 1500 600 ± 1500 |
| Br− | 0.30 ± 0.05 | 25.8 ± 0.3 |
| NH2NH2 | 1.6 ± 0.7d | 23.5 ± 0.6d |
| p-NH2C6H4N(CH3)2 | 1800 ± 60 | 7470 ± 860 |
| p-CH3C6H4N(CH3)2 | 136 ± 5 | 2640 ± 80 |
| C6H5N(CH3)2 | 33 ± 1 | 1520 ± 25 |
| p-BrC6H4N(CH3)2 | 9.1 ± 0.4 | 1040 ± 25 |
| p-CH3C6H4S(O)CH3 | 3.5 (0.76b) | 124 |
| SCN−c | 540 | 5000 |
For the reaction of HS− with hydrogen peroxide in the presence of borate, practicalities of analysis required this to be carried out with the sulfide in excess. In this case the absorbance change reaches a maximum corresponding to maximum polysulfide formation, followed by sulfate formation.28,29 The absorbance change is fitted to two exponential terms, and the effect of boric acid concentration on the rate constant for polysulfide formation is shown in Fig. 2. The corresponding values of kP1 and kP1BOH in Table 2 are obtained, in an analogous way to that used for thiosulfate, using eqn (4) in this case, which is the equivalent form of eqn (1) when the substrate, S, (in this case sulfide) is in excess.
| kobs = (kP1 + kP1BOH[(HO)3BOOH−]/[H2O2] + kP1BOH2[(HO)3BOOB(OH)32−]/[H2O2])[S] | (4) |
For the reaction between hydrogen peroxide and the substrates hydrazine, bromide and iodide, plots of ln(A–A∞) versus time, corresponding to the loss of hydrogen peroxide measured as the Ti(IV) complex, were linear for the duration of measurements, up to three half-lives. Fig. 3 shows the effect of total boric acid concentration on kobs. The corresponding rate constants, obtained using eqn (4) as before, are included in Table 2.
 | ||
| Fig. 3 Effect of total boric acid concentration on the reaction of 0.114 M hydrazine (pH 9.78), 0.02 M iodide (pH 9.84) and 0.2 M bromide (pH 9.79) with, respectively, 0.0416 M, 0.00416 M, and 0.0416 M hydrogen peroxide, ionic strength 0.5 M with sodium sulfate, curves are best fit values according to eqn (4) with the rate constants shown in Table 2 and kP1BOH2 set to zero. | ||
The reactions of the substituted dimethyl anilines with excess hydrogen peroxide showed simple monoexponential loss of absorbance, except in the case of p-amino dimethyl aniline, which was biphasic. The initial, faster, phase is assigned to oxidation at the more nucleophilic tertiary amino group and the slower phase represents reactions involving the primary amino group. Fig. 4 shows the effect of total boric acid concentration on the observed rate constants.
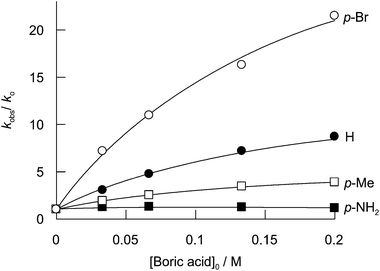 | ||
| Fig. 4 Effect of total boric acid concentration on the reaction of 5 × 10−4 M p-substituted dimethyl anilines and 0.35 M hydrogen peroxide, other conditions as Fig. 2. The curves are the best fits to eqn (6) with kP1BOH2 and kP2B2 set equal to zero. | ||
For the substituted dimethyl aniline reactions, the deviation of the plots from linearity cannot be explained by eqn (1) using the formation constant for monoperoxodiborate, KBOOB, obtained from reaction with dimethyl sulfide. The latter reaction was carried out at low peroxide concentration whereas the dimethyl aniline reactions are carried out at high concentrations of peroxide and the negative deviations occur at high boron concentrations, conditions known to favour the formation of the diperoxodiborate anion 10,30 which can be can be represented as eqn (5). The dependence of kobs on the total concentration of boric acid is, therefore, fitted according to eqn (6) with both kP1BOH2 and the rate constant for the reaction of diperoxodiborate, kP2B2, set equal to zero and the value of KBOOB set equal to that obtained from the dimethyl sulfide data. This yields the best fit values of kP1 and kP1BOH, shown in Table 2, together with KB(OO)2B = 61 ± 16 M−1.
| (HO)3BOOB(OH)32− + H2O2 ⇌ (HO)2B(OO)2B(OH)22− + 2H2O KB(OO)2B | (5) |
| kobs = kP1[H2O2] + kP1BOH[(HO)3BOOH−] + kP1BOH2[(HO)3BOOB(OH)32−] + kP2B2[(HO)2B(OO)2B(OH)2]2− | (6) |
Experimental runs for methyl-p-tolyl sulfoxide at total boric acid and hydrogen peroxide concentrations of 0.11 M and 0.42 M, respectively, yield the rate constants shown in Table 2 at pH 9.58. Sulfoxides are susceptible to nucleophilic attack by peroxoanions, however,18,19 and the concentration of HOO− at pH 9.58 contributes an appreciable amount to the overall reaction of hydrogen peroxide (pKa 11.6) in the absence of boric acid. A better estimate of kP1 is obtained from the run at pH 4.3 shown in Table 2.
Theoretical study
In the absence of an experimental value for KBOO, we began our DFT studies with high level calculations on isomers 5 and 8 (Fig. 1). Using the B3LYP/6-311++G(3df,3pd) method with PCM implicit solvent correction for geometry optimizations and zero point energies, followed by a single point calculation at the same level of theory but with SMD implicit solvent correction, the dioxaborirane 8 was found to be 0.2 kcal mol−1 less stable than the peroxoborate anion 5. Including the calculated entropy term (at 298 K) gave an estimate for ΔG of 0.3 kcal mol−1 in favour of 8, suggesting that KBOO ∼ 1. Calculations on the equilibrium between 9 and 10, using the same level of theory, indicated that 10 is energetically favoured over 9 by 6.9 kcal mol−1, whilst including the entropy term gave ΔG of 14.0 kcal mol−1 in favour of 10.For the catalytic reactions, in our previous work,3 we used the B3LYP/6-31++G(d,p) level of theory, with gas phase optimizations, followed by single point calculations using SMD implicit solvent corrections. All model systems included a single explicit water molecule. This methodology gave calculated energy barriers of 10.1 and 2.8 kcal mol−1 for the reactions of Me2S with H2O2 and dioxaborirane respectively. For the present study, an extra consideration is that some of the systems involve reactions between pairs of anions, such as iodide with dioxaborirane. In such cases, gas phase geometry optimization will not be adequate, since the solvent plays an important role in overcoming electrostatic repulsion. Therefore, we have retained the same level of theory, but geometry optimizations were carried out in implicit solvent using the PCM method, followed by a final single point calculation using the SMD implicit solvent method. Also, in view of the more complex nature of the reactants in the present study, we have not included any explicit water molecules. This model gave barriers for the reactions of Me2S with H2O2 and dioxaborirane of 16.6 and 8.9 kcal mol−1 respectively. These values are ∼6.3 kcal mol−1 higher than in our previous study, nevertheless the data set presented in this work is internally self-consistent.
We have carried out calculations on the reactions of H2O2 and dioxaborirane with all of the species in Table 2, except for the dianion S2O32−. The results are summarised in Table 3, and the calculated structures for Br−, NH2NH2 and SCN− are shown in Fig. 5; structures for the other species are given in the ESI.† The calculations on SCN− were complicated by the possibility that this anion could react at either S or N; we have checked both alternatives, and find that the transition states for attack at S are 12.2 and 10.5 kcal mol−1 lower in energy than the equivalent states for attack at N, for the uncatalysed and catalysed reactions respectively. The final product for attack at S, OSCN−, is calculated to be 13.1 kcal mol−1 more stable than the isomeric ONCS−; hence, the data in Table 3 are for the reaction of SCN− at S.
 | ||
| Fig. 5 Calculated reactant, transition state and product structures for the reactions of H2O2 and (HO)2B(O2) with (a) Br−, (b) NH2NH2 and (c) SCN−. The atoms are rendered as follows: H, B, C plain spheres; O, S, octants; N, Br shaded octants. | ||
| Substrate | H2O2 ΔETS/kcal mol−1 | O–O/Å | H2O2 ΔEP/kcal mol−1 | BH2O4− ΔETS/kcal mol−1 | O–O/Å | BH2O4− ΔEP/kcal mol−1 |
|---|---|---|---|---|---|---|
| a Energies calculated using an intrinsic Coulomb radius of 2.095 Å for Br. b Product assumed to be H2NNHOH rather than H2NNH2O. c Product rearranges to H2NNHOH during geometry optimization. | ||||||
| CH3SCH3 | +16.6 | 1.928 | −6.3 | +8.9 | 1.875 | −3.5 |
| HS− | +13.8 | 1.815 | −38.8 | +9.0 | 1.844 | −38.2 |
| I− | +18.9 | 2.028 | −8.7 | +11.6 | 2.036 | −5.1 |
| Br− | +22.7a | 2.083 | −3.0a | +12.9a | 2.050 | −0.1a |
| NH2NH2 | +22.3 | 1.989 | −33.7b | +14.4 | 1.909 | −42.1c |
| pNH2C6H4N(CH3)2 | +19.0 | 1.989 | −26.2 | +12.5 | 1.958 | −24.0 |
| p-CH3C6H4N(CH3)2 | +20.4 | 2.003 | −25.0 | +13.5 | 1.978 | −22.2 |
| C6H5N(CH3)2 | +20.8 | 2.012 | −24.3 | +14.2 | 1.983 | −21.5 |
| p-BrC6H4N(CH3)2 | +21.7 | 2.020 | −23.5 | +14.5 | 1.995 | −20.0 |
| p-CH3C6H4S(O)CH3 | +22.9 | 1.957 | −59.8 | +13.2 | 1.885 | −54.9 |
| SCN− | +21.9 | 1.947 | −25.5 | +13.8 | 1.918 | −23.7 |
The initial reaction products from all the other calculations are the expected oxo adducts, with the exception of hydrazine, for which a spontaneous proton rearrangement occurred during geometry optimization of the dioxaborirane system to give aminohydroxylamine, H2NNHOH [see Fig. 5(b)]. Although the equivalent H2O2 system did not show such a spontaneous rearrangement, this product is again lower in energy. For all the reactions, the calculated reactant structures involve a hydrogen bond between the substrate heteroatom and an H atom of H2O2 or dioxaborirane, whilst the products generally show hydrogen bonds between the added oxo atom and an H atom of water or BO(OH)2−; in the case of hydrazine, hydrogen bonding in the product H2NNHOH involves the N atoms.
The dioxaborirane systems all show lower transition state barriers than the uncatalysed systems; the reduction in barrier height varies from 4.9 kcal mol−1 for HS− to 9.8 kcal mol−1 for p-CH3C6H4S(O)CH3. The four dimethyl anilines show good linear correlations between the values of ln(k) obtained from Table 2 and the calculated transition state energies in Table 3, with correlation coefficients R2 of 0.986 and 0.997 for H2O2 and dioxaborirane respectively. Indeed, there is a reasonable qualitative correlation between these parameters for all the species in Table 3, as shown in Fig. 6. The only obvious exception to this trend came from our initial calculations on Br−. In this case, the calculated barriers for the uncatalysed reactions were +16.8 and +9.3 kcal mol−1 respectively; these values are much lower than would be expected from the experimentally observed reaction rates. In order to probe the reason for this anomaly, we examined the reactions of H2O2 with halides in more detail. The experimental order of reactivity is known to be I− > Br− > Cl−,31 but using the method described above to calculate the transition state energies gave a predicted order of Br− > I− > Cl−. Using MP4 or alternative basis sets failed to remedy the situation, but a PCM solvent correction with the Gaussian03 defaults rather than the SMD solvent correction gave the correct order. Therefore, we suspect that the current implementation of the SMD method is the source of our difficulties. SMD was parameterized using a range of organobromine compounds,32 and uses an intrinsic Coulomb radius of 3.06 Å for Br. Comparison with the PCM radius of 2.095 Å shows that this value has changed markedly in SMD. We have therefore used the PCM radius with the SMD solvent model for Br in calculating the transition state energies for bromide, recorded in Table 3; this modification gave a much better agreement with experiment (Fig. 6).
 | ||
| Fig. 6 Plot of ln(k) versus transition state energy. Squares and circles are for the uncatalysed and catalysed reactions respectively, with the subset of dimethyl anilines indicated by inset filled symbols. The regression lines are for the four dimethyl anilines. | ||
Discussion
Previous work on the oxidation of substituted phenyl methyl sulfides was carried out at low total boron concentrations, with an excess of hydrogen peroxide, so that the predominant species were the monoperoxoborate and diperoxoborate anions.1 In addition kinetic runs carried out in our recent study on dimethyl sulfide used low concentrations of peroxide and high total boron concentrations, where, in addition to monoperoxoborate, there was a significant concentration of monoperoxodiborate.3 The formation constant of this species, obtained from the kinetic data, was consistent with it being unreactive, in good agreement with data previously obtained from a study of the effect of borate/boric acid on the photochemical decomposition of hydrogen peroxide.2 In contrast, the oxidation of the dimethyl anilines was carried out at high concentrations of peroxide and extended to higher total boron concentrations, where formation of diperoxodiborate dianions has been observed using 11B NMR.30 The formation constant of this species, 61 ± 16 M−1 obtained from the kinetic data, which is consistent with it being unreactive, is the first that has been published.Fig. 7 shows that for each family of substrates the ratio of reactivity with peroxoborate (and reactive species in equilibrium with it) to that with hydrogen peroxide increases as the reactivity toward hydrogen peroxide decreases. This reflects the lower sensitivity of the reaction of peroxoborate to the nature of the substrate compared to that of hydrogen peroxide, as described previously for the substituted phenyl methyl sulfides.1 This could potentially provide a synthetic strategy using these types of substrate and peroxoborate at higher pH that could be used when the products are unstable at the low pH required for activation of hydrogen peroxide as H3O2+.
 | ||
| Fig. 7 Comparison of the rate constants for peroxoborate with those of hydrogen peroxide. The data for the substituted phenyl methyl sulfides is from ref. 1 and the point for thiocyanate from ref. 20. The long dashed line represents log kP1BOH = log kP1 so that points above the line represent catalysis while those below the line represent inhibition. The short dashed line is the best fit for the data for Br−, SCN− and I−. | ||
It can also be seen from Fig. 7 that the result for dimethyl sulfide obtained in the preceding paper3 lies just above the line for the substituted phenyl methyl sulfides. Hence the same factors, that have been fully discussed for the latter,1 apply equally for dimethyl sulfide, where the additional methyl group confers extra nucleophilicity compared to the substituted phenyl groups. The reactivity of peroxoborate with dimethyl sulfide lies between that reported for peroxycarboxylic acids and hydrogen peroxide,33 just as in the case of the substituted phenyl methyl sulfides.1
An important feature of our previous study of organic sulfide substrates is that peroxoborates, compared with other hydroperoxides, are very much less selective, consistent, under the Hammond Postulate, with the highly reactive dioxiborane being the reactive species.3 The present work shows that the oxidation of substituted dimethyl anilines, which results in N-oxide formation, also exhibits the same feature, explained as follows. Hammett plots based on σp values,34 shown in Fig. 8, give the ρ (selectivity) and log k0 (reactivity) values shown in Table 4, where they are compared with the values for peroxomonosulfate obtained from the literature.35 The ρ value for peroxoborate is considerably less than the value, 2.2, expected if a linear reactivity selectivity relationship were to hold. This is strong evidence against the possibility that the unusual selectivity–reactivity relationship reported for the sulfides1 is due to the sulfur atom exhibiting some kind of electrophilic character specifically with peroxoborate, since the dimethyl anilines show the same behavior although the tertiary amine nitrogen atom is incapable of acting as an electrophile because of its filled-shell electronic configuration.
 | ||
| Fig. 8 Hammett plots for the reactions of monoperoxoborate or hydrogen peroxide and p-substituted dimethyl anilines. Hammett ρ-values calculated from the plots are shown in Table 4. | ||
The respective rate constants for the reaction of hydrogen peroxide and HS−, S2O32−, I− and Br− are similar to the accepted literature values.29,36,37 These nucleophiles, and also thiocyanate,38,39 and hydrazine (whose rate constant in Table 2 is about five times lower than the previously reported value)40 are generally considered to react with hydrogen peroxide by mechanisms in which the initial, rate-limiting, step involves heterolytic cleavage of the peroxide bond,18,19,29,41 essentially similar to the organic sulfides and dimethyl anilines. This is supported by the reasonable correlation between theory and experiment seen in Fig. 6. The stoichiometric ratios of the overall reactions are high and under the present experimental conditions the halides catalyse the decomposition of hydrogen peroxide. It is notable that bromide, the pseudohalide, SCN−, and iodide appear to fall on the same line. SCN−, S2O32−, and HS− may also be considered as a group, and, as seen in Fig. 7, thiosulfate is expected to be less reactive toward the dioxaborirane anion compared to hydrogen peroxide because of its doubly negative charge. A similar, but inverse, effect is seen where thiosulfate is more reactive toward H3O2+ than hydrogen peroxide, compared with singly charged nucleophiles.42
Conclusions
This study has examined the reactivity of a wide range of inorganic and organic nucleophiles with peroxoborate, confirming that peroxoborate, and those reactive species in equilibrium with it, is indeed an electrophile. Moreover, the lower than expected selectivity observed for the reaction of peroxoborate with a series of substituted dimethyl anilines, as was also observed for phenylmethyl sulfides,1 further supports the proposed involvement of dioxaborirane as the reactive species. At higher ratios of boron to peroxide there is kinetic evidence for unreactive peroxodiborate species, known in the literature from 11B NMR and Raman studies, and quantified in the current paper, and partly, in our previous paper on the photochemistry of peroxoborates.2 Knowledge of the lack of reactivity of the peroxodiborates will have a bearing on future synthetic strategies for borate catalysed hydrogen peroxide reactions. Finally, we note that dioxiranes such as dimethyldioxirane have found proved to be valuable reagents for oxidation, particularly of hydrocarbons,7 whilst the wider potential of heteroatom dioxiranes as oxidation reagents has been noted, but not yet fully developed.43 Hence, dioxaboriranes are likely to have considerable potential as oxidants.Experimental section
The general procedure has been described previously.1 The substituted dimethyl anilines, methyl-p-tolyl sulfoxide, dimethyl sulfide, sodium thiosulfate, sodium sulfide, potassium bromide, potassium iodide and hydrazine were obtained from Aldrich. Reactions with the dimethyl anilines, the sulfoxide, and thiosulfate were carried out with a large excess of hydrogen peroxide, monitoring the loss of the substrate absorbance spectrophotometrically at a suitable wavelength. When the absorbance of the reaction solution was so large that it was outside the dynamic range of the spectrophotometer, due to the presence of hydrogen peroxide, it was removed, after adjusting an aliquot of the reaction solution to neutral pH, using bovine catalase (BDH). Observed pseudo-first-order rate constants, kobs, were obtained using nonlinear regression of the (in most cases) monoexponential loss of absorbance with time. Reactions with HS−, obtained by adjusting the deoxygenated reaction solution containing sodium sulfide to pH 10.0, were carried out with excess sulfide, monitoring the absorbance of the yellow polysulfides, HSn−, produced.28,29 Reactions with bromide, iodide and hydrazine were carried out with an excess of the substrate, and the reaction followed by removing aliquots of solution and determining the hydrogen peroxide spectrophotometrically as the absorbance, A, of the titanium(IV) complex.1,2 Values of kobs were obtained from linear plots of ln(A–A∞) versus time. All reactions were carried out at 25 °C, and in the pH region 9.5–10.0, unless stated otherwise. All curve fitting was carried out using Grafit, version 7.27All DFT calculations were carried out within Gaussian09W.44 The oxidation reactions were modelled using the B3LYP functional and 6-31++G(d,p) basis set for all atoms except iodine, for which the LanL2DZ basis set was used. A trial calculation on the H2O2−Br− system, using LanL2DZ on bromine, gave a barrier of +24.6 kcal mol−1 which is comparable to the value in Table 3. Geometry optimizations were run using PCM implicit solvent corrections with water as solvent. Output geometries were verified as true minima or first order saddle points by the appropriate frequency calculations. SMD implicit solvent corrections were then obtained for single point jobs using the optimized geometries and water as solvent. The default Coulomb radii were used for all atoms except Br, for which the PCM radius of 2.095 Å was used.
Acknowledgements
We are grateful to Borax Europe for providing the initial funding for this research and to Dr K. Quill for his support for the project.References
- D. M. Davies, M. E. Deary, K. Quill and R. A. Smith, Chem.–Eur. J., 2005, 11, 3552–3558 CrossRef CAS.
- D. M. Davies and S. Rey, Chem.–Eur. J., 2006, 12, 9284–9288 CrossRef.
- M. C. Durrant, D. M. Davies and M. E. Deary, Org. Biomol. Chem., 2011, 9, 7249–7254 CAS.
- W. Adam, R. Curci and J. O. Edwards, Acc. Chem. Res., 1989, 22, 205–211 CrossRef CAS.
- P. Hanson, R. A. A. J. Hendrickx and J. R. L. Smith, Org. Biomol. Chem., 2008, 6, 745–761 CAS.
- P. Hanson, R. A. A. J. Hendrickx and J. R. L. Smith, Org. Biomol. Chem., 2008, 6, 762–771 CAS.
- R. Curci, L. D'Accolti and C. Fusco, Acc. Chem. Res., 2006, 39, 1–9 CrossRef CAS.
- N. Ingri, Acta Chem. Scand., 1963, 17, 581–589 CrossRef CAS.
- A. M. Duffin, C. P. Schwartz, A. H. England, J. S. Uejio, D. Prendergast and R. J. Saykally, J. Chem. Phys., 2011, 134, 154503 CrossRef.
- D. M. Schubert and C. B. Knobler, Phys. Chem. Glasses-B, 2009, 50, 71–78 CAS.
- C. G. Salentine, Inorg. Chem., 1983, 22, 3920–3924 CrossRef CAS.
- L. Maya, Inorg. Chem., 1976, 15, 2179–2184 CrossRef CAS.
- J. E. Spessard, J. Inorg. Nucl. Chem., 1970, 32, 2607–2613 CrossRef CAS.
- R. Pizer and C. Tihal, Inorg. Chem., 1987, 26, 3639–3642 CrossRef CAS.
- D. A. Bennett, H. Yao and D. E. Richardson, Inorg. Chem., 2001, 40, 2996–3001 CrossRef CAS.
- D. M. Davies and M. E. Deary, J. Chem. Soc., Perkin Trans. 2, 1996, 2423–2430 RSC.
- C. A. Bunton, H. J. Foroudian and A. Kumar, J. Chem. Soc., Perkin Trans. 2, 1995, 33–39 RSC.
- R. Curci and J. O. Edwards, Organic Peroxides, Wiley, New York, 1970 Search PubMed.
- Y. Sawaki, Organic Peroxides, Wiley, Chichester, 1992 Search PubMed.
- I. R. Wilson, Aust. J. Chem., 1960, 13, 582–584 CrossRef CAS.
- X. W. Lin, Q. M. Pan and G. L. Rempel, Appl. Catal., A, 2004, 276, 123–128 CrossRef CAS.
- X. W. Lin, Q. M. Pan and G. L. Rempel, Appl. Catal., A, 2004, 263, 27–32 CrossRef CAS.
- A. Mckillop and W. R. Sanderson, Tetrahedron, 1995, 51, 6145–6166 CrossRef CAS.
- J. Muzart, Synthesis, 1995, 1325–1347 CrossRef CAS.
- A. McKillop and W. R. Sanderson, J. Chem. Soc., Perkin Trans. 1, 2000, 471–476 RSC.
- S. Hussain, S. K. Bharadwaj, R. Pandey and M. K. Chaudhuri, Eur. J. Org. Chem., 2009, 3319–3322 CrossRef CAS.
- R. J. Leatherbarrow, GraFit Version 7, Erithacus Software Ltd, Horley, UK, 2009 Search PubMed.
- A. Kamyshny, I. Ekeltchik, J. Gun and O. Lev, Anal. Chem., 2006, 78, 2631–2639 CrossRef CAS.
- M. R. Hoffmann, Environ. Sci. Technol., 1977, 11, 61–66 CrossRef CAS.
- B. N. Chernyshov, Russ. J. Inorg. Chem., 1990, 35, 1333–1335 Search PubMed.
- D. H. Fortnum, C. J. Battaglia, S. R. Cohen and J. O. Edwards, J. Am. Chem. Soc., 1960, 82, 778–782 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- P. Amels, H. Elias and K. J. Wannowius, J. Chem. Soc., Dalton Trans., 1997, 2537–2544 CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- Y. Ogata and I. Tabushi, Bull. Chem. Soc. Jpn., 1958, 31, 969–973 CrossRef CAS.
- E. Abel, Monatsh. Chem., 1907, 28, 1239 Search PubMed.
- A. Mohammad and H. A. Liebhafsky, J. Am. Chem. Soc., 1934, 56, 1680–1685 CrossRef CAS.
- I. R. Wilson and G. M. Harris, J. Am. Chem. Soc., 1960, 82, 4515–4517 CrossRef CAS.
- I. R. Wilson and G. M. Harris, J. Am. Chem. Soc., 1961, 83, 286–289 CrossRef CAS.
- A. S. Gordon, Third Symposium on Combustion, Flame, and Explosion Phenomena, Williams and Wilkins, Baltimore, 1949 Search PubMed.
- R. Curci and J. O. Edwards, Catalytic Oxidations with Hydrogen Peroxide as Oxidant, Kluwer, Dordrecht, 1992 Search PubMed.
- M. Hoffmann and J. O. Edwards, Inorg. Chem., 1977, 16, 3333–3338 CrossRef CAS.
- N. Sawwan and A. Greer, Chem. Rev., 2007, 107, 3247–3285 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09W (Revision A.1), Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ob26842f |
| This journal is © The Royal Society of Chemistry 2013 |
