Structural diversity in iron oxide nanoparticle assemblies as directed by particle morphology and orientation

Abstract

The mesostructure of ordered arrays of anisotropic nanoparticles is controlled by a combination of packing constraints and interparticle interactions, two factors that are strongly dependent on the particle morphology. We have investigated how the degree of truncation of iron oxide nanocubes controls the mesostructure and particle orientation in drop cast mesocrystal arrays. The combination of grazing incidence small-angle X-ray scattering and scanning electron microscopy shows that mesocrystals of highly truncated cubic nanoparticles assemble in an fcc-type mesostructure, similar to arrays formed by iron oxide nanospheres, but with a significantly reduced packing density and displaying two different growth orientations. Strong satellite reflections in the GISAXS pattern indicate a commensurate mesoscopic superstructure that is related to stacking faults in mesocrystals of the anisotropic nanocubes. Our results show how subtle variation in shape anisotropy can induce oriented arrangements of nanoparticles of different structures and also create mesoscopic superstructures of larger periodicity.

---

1 Introduction

Self-assembly of nanoparticles into hierarchical structures is widely investigated for the fabrication of novel functional materials.^1–3 Material properties can be tuned precisely by combining nanoparticles with different physical properties, such as ferro- or superparamagnets, semiconductors, or optically active nanoparticles, thus representing a versatile route to metamaterials.^4–6 A large variety of structure types has been reported for assemblies of nanoparticles including binary nanoparticle superlattices consisting of different species of nanoparticles.^7–9 The structure types accessible by self-assembly can be influenced through variation of interparticle interactions such as electrostatic, dipolar, or van der Waals interactions,^10–14 as well as a controlled swelling^15–17 or modification^18,19 of the surrounding ligand shell. Controlled assembly of shape-anisotropic colloids typically leads to face-to-face oriented assemblies.^20–22 Similarly, the strong preference of face-to-face stacking of anisotropic nanoparticles consistently leads to a size- and shape-selective self-segregation of nanoparticle dispersions containing particles of varying sizes and shapes.^23,24 Defect analysis has been carried out in great depth for larger colloidal particles^25,26 but has been largely overlooked in mesoscopic arrangements of smaller particles (≈10 nm), where the assembly of nanoparticles into mesocrystals inevitably results in the formation of defects, e.g. point defects and stacking faults. Note that the definition of mesocrystals²⁷ includes crystallographic alignment of the nanoparticles.^17,28–33 This class of materials shows great promise for applications where both the anisotropy and size-dependent properties of the nanoparticles are of central importance, e.g. for magnetic and electronic thin-film devices.^34,35

In this work, we investigate assemblies based on iron oxide nanoparticles and the structural diversity that is generated by relatively small variations of the nanoparticle shape. A detailed morphological characterization of different nanoparticles, i.e., nanospheres and truncated nanocubes, combined with a comprehensive structural analysis of their assemblies illustrates the structure-directing influence of the nanoparticle shape. Competing growth orientations are observed in the mesocrystals of the highly truncated cubes, leading to the formation of complex structures. In particular, strong satellite reflections appearing in the GISAXS patterns confirm for the first time the presence of a commensurate mesoscopic superstructure.

2 Experimental

2.1 Synthesis and self-assembly

Monodisperse maghemite (γ-Fe₂O₃) nanoparticles were prepared by thermal decomposition of an iron(III) oleate precursor, according to similar procedures reported earlier.^32,36,37 The nanoparticles were separated by centrifugation from the crude synthesis solution. Several dispersion/precipitation cycles using a solvent–nonsolvent pair (n-hexane/ethanol) followed by centrifugation resulted in the precipitation of a waxy semisolid that was dried in a vacuum. The iron oxide content of the nanoparticle wax was estimated from the residual mass after heating to 800 °C in air employing a Perkin Elmer Thermogravimetric Analyzer TGA-7 at a heating rate of 10 °C min⁻¹. The presence of an ionic surfactant (i.e. sodium oleate) in the synthesis mixture has been reported to be the primary shape-determining factor controlling nanocube faceting, i.e., the degree of truncation of the nanocubes, in agreement with recent observations.^36,38

We also discovered that dispersed nanocubes undergo a change in size and shape upon long time benchtop storage in sealed containers. The highly truncated nanocubes used in this study are the result of a long-time stored (ca. 9 months) dispersion (4.5 × 10¹⁴ particles per mL) of the as-synthesized, moderately truncated nanocubes. No centrifugation or other size selection techniques were used to improve the characteristics of the highly truncated nanocubes prior to their assembly.

Deposition of the nanoparticles onto germanium substrates was performed by drop casting a nanoparticle dispersion in an applied magnetic field, as reported earlier.³⁸ In brief, ∼30 μL of a nanoparticle dispersion of 4.5 × 10¹⁴ particles per mL were deposited onto a substrate of 1 cm². Evaporation took place inside a closed Petri dish, in order to reduce the evaporation rate of the carrier solvent, resulting in drying times in the order of hours. During the drying of the solvent, a magnetic field of ∼30 mT was applied perpendicular to the substrate.

2.2 Characterization

Electron microscopy. TEM images were obtained using a JEOL JEM-2100 microscope equipped with a LaB₆ filament operated at 200 kV (f = 2.7 mm, C_s = 1.4 mm, C_c = 1.8 mm, point resolution = 2.5 Å). The specimens were prepared by depositing a drop of a dilute toluene dispersion of nanoparticles on carbon-coated copper grids and allowing the solvent to evaporate rapidly. Images were calibrated using the γ-Fe₂O₃ lattice plane distance as determined from X-ray powder diffraction (XRPD, see ESI, Fig. S1†). Particle size histograms were built by manually measuring the diameter or edge length of at least 200–300 nanospheres and 50 nanocubes, respectively, on TEM micrographs. The mean size and its standard deviation, σ, were determined by fitting the corresponding histogram with a Gaussian distribution function.

As a measure of the shape anisotropy of the nanocubes, the dimensionless degree of truncation, τ = 2t/l_c, is introduced (see Fig. 1). For comparison, τ = 0 for an ideal cube, whereas τ = 1 for a cuboctahedron. Similar to previous work,³⁸ the degree of truncation of the nanocubes was determined for the aged nanocubes by manually measuring the average truncation length, τ = (τ_a + τ_b)/2, for each of the cube edges l_c using HRTEM images at 800k × magnification. Above 600k × magnification, the uncertainties in t and l_c are δt ∼ 0.145 nm and δl_c ∼ 0.105 nm, respectively. This yields the relatively small maximum uncertainty δτ ∼ 0.03 for the measurement. Four values of τ were obtained from each of 70 particles. The mean degree of truncation and its standard deviation were obtained from fitting the histogram with a Gaussian distribution function.

Fig. 1 Morphology of iron oxide nanocubes. Left: SAXS data with refinements according to a spherical form factor. Data have been scaled for display. Center: sketch of the determined nanocube morphologies of τ = 0.88 (top) and τ = 0.45 (bottom) with illustration of the degree of truncation τ = 2t/l_c (τ = 0: ideal cube, τ = 1: cuboctahedron). Right: HRTEM images of aged (top) and as-synthesized (bottom) nanocubes. The images are FFT-filtered for clarity. Scale bars: 5 nm.

For these measurements, particles oriented close to the [001] zone axis are required (see Fig. S3†). In essence this means that particles are selected based on the preferential orientation which will cause an oversampling of more cube like particles with smaller τ. For the high degree of truncation in the studied samples, a large amount of nanocubes is oriented in the [111] direction, i.e. lying on the truncated facet, and only those nanocubes with a slightly lower degree of truncation are oriented favorably for determination of τ. This results in an oversampling of the nanocubes with a lower truncation.

SEM images of the self-assembled arrays were obtained using a LEO 1550 SEM operated at 20 keV.

SAXS. Small-angle X-ray scattering was performed on dilute nanoparticle dispersions in toluene at the B1 beamline of the DORIS synchrotron at HASYLAB/DESY. During the first experiments (‘as-synthesized’ truncated nanocubes), the incident X-ray energy of 7 keV was chosen, and the scattering data were recorded using a multiwire proportional chamber gas detector (Gabriel detector). At a second measurement 9 months later (‘aged’ highly truncated nanocubes), a Pilatus 300K detector was available, and the incident X-ray energy of 12 keV was chosen. All measurements were carried out using detector distances of 0.93 and 3.63 m, and the scattering data were averaged circularly for evaluation. Details on the SAXS data refinement are given in the ESI.†

GISAXS. Grazing incidence small-angle X-ray scattering measurements on the deposited mesocrystals were performed at the ID01 beamline of the ESRF and the SWING beamline of the Synchrotron SOLEIL. At ID01, a CCD detector with 1242 × 1152 pixels and a pixel size of 55 μm was set at a distance of 0.519 m from the sample. The incident energy was set to 7.105 keV, just below the Fe K edge, and the incident angle of the primary beam was varied between 0.30 and 0.60°. At the SWING beamline, a sample-to-detector distance of 1.600 m and an incident energy of 7.000 keV were chosen. The incident angle of the primary beam was varied between 0.10 and 0.80°. The scattering was recorded on an Aviex CCD detector of 4096 × 4096 pixels with a software binning to 1024 × 1024 pixels with a pixel size of 164 μm. The critical angle of total reflection of the samples at the chosen conditions is 0.125°. Details on the mesocrystal structure determination from GISAXS data are given in the ESI.†

3 Results and discussion

3.1 Morphological characterization

Maghemite (γ-Fe₂O₃) nanocubes and nanospheres were prepared by thermal decomposition of an iron(III) oleate precursor.^32,39 The lattice parameters of the inverse spinel structure determined by XRPD were in both cases close to the literature value of γ-Fe₂O₃(a_γ-Fe2O3 = 8.348 Å, see ESI†).⁴⁰ The morphology of the nanoparticles was characterized by a combination of small-angle X-ray scattering (SAXS) and transmission electron microscopy (TEM). The nanospheres have a diameter of D_sph = 9.2 ± 0.4 nm (TEM) in reasonable agreement with the radius of r_sph = 4.96(1) nm derived from SAXS. The truncated character of the nanocube corners is rationalized using the dimensionless degree of truncation τ.³⁸ The as-synthesized truncated nanocubes have an edge length l_tc = 8.6 ± 0.5 nm with τ_tc = 0.45 ± 0.05 as determined by TEM. Upon 9 months of bench-top storage, the nanocubes dispersed in toluene (4 × 10¹⁵ particles per mL) undergo a change in size and shape resulting in cubes with a higher degree of truncation, l_htc = 8.9 ± 0.7 nm and τ_htc = 0.53 ± 0.07 (TEM). SAXS measurements of the nanocubes with different degrees of truncation are displayed in Fig. 1. Fitting of the data to a spherical form factor yields radii of r_tc = 5.32(2) and r_htc = 5.07(1) nm for truncated and highly truncated cubes, respectively. This indicates that even though the edge length of the nanocubes increases slightly as they age, they display a net reduction of their radius of gyration, which can be correlated geometrically to τ if the edge length of the cube is known (and vice versa, see ESI†). For the as-synthesized nanocubes, assuming a value of τ_tc = 0.45 translates to l_tc = 8.36 nm, correlating well with the edge length derived from TEM. Assuming an edge length of l_htc = 8.9 nm for the highly truncated cubes results in a value of τ_htc = 0.88, close to that of a cuboctahedron (τ = 1). The discrepancy between the values of τ_htc estimated by SAXS and TEM is at least partially a result of oversampling of particles with small τ. The measured SAXS radius of a portion of the nanocubes stored as a powder was consistent with the as-synthesized cubes (r = 5.29(3) nm). The ageing seems to occur by dissolution of material from the {111} facet followed by precipitation at the {100} facets, perhaps mediated by soluble oleates which would explain why the dry powder did not change. This is supported by the constant particle volume of the moderately (τ_tc = 0.45, V_tc = 626(36) nm³) and highly (τ_htc = 0.88, V_htc = 625(51) nm³) truncated nanocubes. Similar ageing processes have been observed for cubic Ag and Pd particles.^41,42

3.2 Self-assembled mesostructures

Drop-casting dispersions of highly monodisperse iron oxide nanoparticles under the influence of an external magnetic field yields well-ordered micron sized assemblies that are several hundred nm in height upon solvent evaporation.^32,38 The arrays formed by nanospheres consist of hexagonally closed packed layers and grow as hexagonal platelets as observed by scanning electron microscopy (SEM) (Fig. 2a and b). All reflections of the grazing incidence small-angle X-ray scattering (GISAXS) pattern presented in Fig. 2c are indexed according to the rhombohedral space group R3̄m (no. 166) with a = 12.4(1) nm and c = 29.5(1) nm, corresponding to a fcc structure with a_fcc = 17.5(1) nm and ≈3% contraction in the [111]_fcc direction perpendicular to the substrate (see ESI†). The lattice parameters can be related to a closed packed array of nanospheres with 10 nm diameter and 1.2 nm ligand shell thickness, as determined from SAXS (see ESI†), in excellent agreement with SEM results. The clear preference for fcc against a possible hcp stacking is in agreement with experiments and simulations of packings of monodisperse hard spheres.^43–45 However, a slight degree of diffuse scattering observed in the Q_z direction between the reflections may indicate the presence of random stacking faults in the assemblies. Nonetheless, the fcc arrangement of the nanospheres can be considered to be the reference structure for isotropic nanoparticles.

Fig. 2 Characterization of nanosphere assemblies. SEM images of (a) a mesocrystal and (b) the lateral arrangement on the mesocrystal surface. Scale bars: 100 nm. (c) GISAXS by nanosphere assemblies (ID01, ESRF). Peaks with (up triangles) and without (down triangles) reflection of the beam at the substrate are indexed according to a fcc packing of nanospheres. The intensities in the Yoneda line are shown below as a red line on the logarithmic scale.

In the case of anisotropic nanoparticles (e.g. cubes, octahedra), a preference for face-to-face orientation in mesocrystals is generally observed.²³ We have recently shown that the moderate degree of truncation in the as-synthesized nanocubes (τ_tc = 0.45) induces a body-centered tetragonal bct arrangement³⁸ in contrast to the simple cubic sc packing found for cubic Pt nanoparticles.⁴⁶

SEM and GISAXS of mesocrystals prepared from highly truncated nanocubes (τ_htc = 0.88) reveal an fcc arrangement similar to the nanospheres, albeit with two different preferred orientations, i.e. tetragonal and rhombohedral configuration. Different preferred growth orientations are found in varying ratios in all assemblies of the highly truncated cubes. This behavior deviates significantly from that of the nanospheres and the nanocubes with a moderate degree of truncation (τ_tc = 0.45), where growth of the assemblies occurs only in one preferred direction. For comparison, the GISAXS patterns of two arrays exhibiting a preference for the two different growth orientations are shown in Fig. 3. Both patterns are compatible with the same fcc lattice (Fm3̄m, no. 225) with a lattice constant a = 20.8(1) nm. The pattern of the [100] oriented fcc lattice (shown in Fig. 3a) is indexed to the tetragonal subgroup I4/mmm (no. 139) with a = 14.7(1) nm and c = 21.0(1) nm, similar to the bct arrangement of the as-synthesized nanocubes (τ_tc = 0.45),³⁸ yet with significantly larger lattice parameters (12 and 18% larger than a = 13.1(1) nm and c = 17.8(1) nm, respectively). The pattern of the [111] oriented fcc lattice (shown in Fig. 3c) is indexed according to the rhombohedral subgroup R3̄m with a = 14.7(1) nm and c = 37.0(1) nm, similar to the arrangement of the nanospheres, again with significantly larger lattice parameters (18 and 25%). A small expansion of the fcc packing perpendicular to the substrate of 1% in [100] and 3% in [111] orientation is attributed to strain during drying of the mesocrystals.

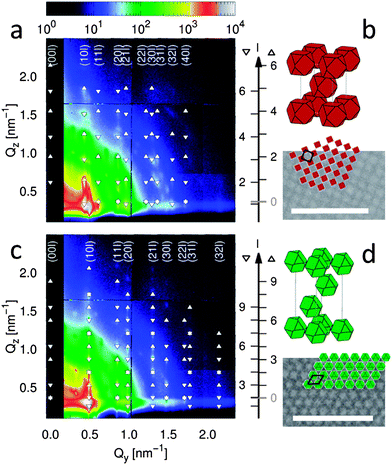Fig. 3 SEM images and GISAXS of mesocrystals of highly truncated nanocubes (SWING, SOLEIL), exhibiting preference of the (a and b) tetragonal and (c and d) rhombohedral configuration of the fcc packing. Peaks with (up triangles) and without (down triangles) reflection of the beam at the substrate are indexed. A possible orientation of the nanocubes in the derived mesocrystal structures is illustrated along with the respective lateral arrangements on the SEM images (scale bars: 100 nm).

Comparing the structure of the isotropic spheres and the anisotropic highly truncated nanocubes, we note that the near fcc unit cell of the highly truncated cubes (a = 20.8(1) nm) is significantly larger than that of the spheres (a = 17.5(1) nm), i.e. 19%. At the same time, the spheres and the highly truncated nanocubes are almost identical in size, i.e. near-identical SAXS radii and similar values of the diameter (D_sph) and edge length (l_htc). It is difficult to motivate this considerably less dense packing (of 28(2)% vs. 39(1)%, see ESI†) based on a random orientational order of the highly truncated nanocubes. Hence, the unit cell expansion strongly indicates alignment of the nanoparticles along their long dimensions, i.e. oriented edge-to-edge or corner-to-corner. Low density structures induced by a high degree of crystal alignment have also been observed in the case of octahedral nanoparticles.²⁹ Because of the relatively large unit cell volume, there are in fact several possible arrangements (see ESI†) with different levels of complexity. The simplest and most symmetric oriented structure is displayed in Fig. 3b and d and is obtained by arranging the nanocubes parallel to the fcc unit cell edge, i.e. [100]_NP parallel to [100]_MC where NP and MC refer to nanoparticle and mesocrystal, respectively. Here, each nanocube is oriented edge-to-edge with respect to its 12 nearest neighbors, which may be justified by the much lower packing density of the highly truncated nanocubes (28(2)%) as compared to the face-to-face arrangement of nanocubes with τ = 0.45 (41(2)%).³⁸ The resulting separation distance of 2.1(2) nm is realistic with respect to the oleic acid chain length and similar to the nearest-neighbor distance in the nanosphere assembly. Furthermore, the growth of the mesocrystals along one of two discrete orientations and the nearly identical lattice parameters of the resulting fcc structures strongly suggest that the oriented structure is the same in both cases.

The orientational order is not necessarily perfect for all of the nanoparticles. The dependence of the orientational ordering of nanoparticles within the array on the organic particle surface coverage has recently been reported by Simon et al.⁴⁷ In our study a quantitative statement on the probability of alignment cannot be made from the available data, however, the observed increase in lattice parameters is significant and justifies the alignment of a significant portion of the highly truncated nanocubes.

3.3 Commensurate superstructure

The GISAXS patterns contain strong satellite reflections which suggest that the highly truncated nanocubes (τ_htc = 0.88) not only result in mesocrystals with different growth orientations but also generate a commensurate mesoscopic superstructure. Satellite reflections observed around the (00l) and (10l) reflection series of the [111] oriented fcc lattice (i.e. the rhombohedral R3̄m configuration) are shown in Fig. 4 and are found to obey the rhombohedral symmetry by following the propagation vectors ± for (10l) reflections and ± for (01l) reflections. For (hhl) reflections, the propagation vectors and are observed for h + l = 2n and h + l = 2n + 1, respectively. Combining all observed propagation vectors, the entire superstructure can be described by either a large supercell with A = 3a, B = 3b, and C = 3c, or a smaller supercell of lower symmetry with A = 3a, B = b, and C = 3c.

Fig. 4 Detail of GISAXS data in Fig. 3c, indicating superstructure reflections of the (00l) and (10l) reflection series of the rhombohedral setting of the mesocrystals. Peaks with (up triangles) and without (down triangles) reflection of the beam at the substrate are distinguished for the basic fcc structure. See ESI† for discussion of the unmarked reflections. Right: observed superstructure reflections according to the propagation vectors.

Laterally, the satellite reflections are related to linear defects observed by SEM for many of the highly truncated nanocube mesocrystals (Fig. 5a). These defects have a lateral period three times larger than the lattice constant, corresponding to the in-plane component of the propagation vector of . Considering the depth sensitivity of the GISAXS technique, the observed periodicity is not a surface effect of a single layer, but ranges deep into the bulk of the mesocrystals as indicated by the l = ±1/3 component of the propagation vector. As the projection of the propagation vector perpendicular to the substrate is equal to the lateral component, a lateral shift of the observed periodicity with each particle layer is deduced.

Fig. 5 Mesocrystal superstructure of highly truncated nanocubes. (a) SEM image of mesocrystals exhibiting linear defects with a periodicity of 3 times the lateral lattice plane distance (blue lines). Square (red) and hexagonal (green) lateral order are highlighted (Scale bars: 100 nm). (b) Supercell derived from the hexagonal basis unit cell as a suggested structure corresponding to the observed satellite reflections (top), view of a single stacking fault (dashed line) resulting in two domains (center, [001] projection), and the detail of the mesocrystal surface for both domains (bottom). In the presented setting, the c axis is oriented perpendicular to the substrate.

The defect lines observed in SEM (Fig. 5a) and the satellite reflections observed by GISAXS (Fig. 4) can be accounted for by a superstructure originating from the occurrence of stacking faults in the [111̄] direction, thus not perpendicular to the substrate, see Fig. 5b. In this model, the C layers in the ABCABC stacking sequence remain unchanged and define an enlarged supercell (A = 3a = 44.1(3) nm, B = b = 14.7(1) nm, and C = 3c = 111.0(3) nm with a monoclinic angle γ = 120°), whereas the order of AB vs. BA layer stacking is random as a result of increased probability of hcp ordering of the C layers. The suggested superstructure gives an average representation of the mesocrystal structure as C{(AB)_1−x(BA)_x}C{(AB)_1−x(BA)_x}C with x being the probability of AB reversal. This means that x = 0 represents the common fcc stacking type also found for the nanospheres, whereas x = 1 represents a fcc configuration with the [123] cubic lattice direction perpendicular to the substrate, i.e. tilted 22.2° with respect to [111]. This structure accounts for the observed satellite reflections and explains in particular the different propagation vectors observed for the (003) and (006) reflections. A comparison of the observed reflection intensities with structure amplitudes calculated from this superstructure model justifies an estimate of x = 0.3–0.35 for the studied mesocrystal sample (see ESI† for details). Note that x does not indicate the amount of stacking faults, but the probability of CBAC stacking in the average representation of the mesocrystal sample (here 30–35%). Thus, it is not possible to distinguish from the reflection intensities alone whether there are large domains with x = 0 and x = 1 or a random order of CABC and CBAC units in the mesocrystal. However, the large structural coherence of the C layers, observed as sharp superstructure reflections with long correlation length, is only compatible with a single stacking fault whereas multiple stacking faults would likely appear in any A, B, or C layer and thus destroy the triple period of the superlattice. A small amount of stacking faults leading to large domains of the different fcc configurations is thus likely. Additional information on the stacking fault-mediated intergrowth of fcc domains might be obtained in a diffraction study on individual mesocrystals as opposed to the 2D powder of mesocrystals studied here. Very similar stacking faults have been reported for larger colloids, illustrating the intergrowth of different fcc domains in otherwise single-crystalline assemblies.²⁶

As can be seen in the detail of the top layer of the suggested superstructure (Fig. 5b), the higher index cleavage planes {123} are not flat and the height variation correlates well with the surface structure of the defected domain (Fig. 5a). In atomic systems, cleavage planes that generate stepped surfaces are often unstable towards surface reconstruction, which is a likely reason as to why a part of the surface layer is rather disordered.⁴⁸ Regardless, the triple periodicity of the top layer is clearly visible, indicating that the unit cell is tripled perpendicular to the observed defect lines. Moreover, a closer look at the SEM in Fig. 5a reveals the preference of a local square arrangement of the nanocubes in the superstructure despite the overall hexagonal lateral symmetry. This observation is consistent with the quasi-square order of particles in the superstructure model and suggests the competition between square and hexagonal coordination as the driving force for the competing stacking types. Indeed, the trigonal prismatic coordination of hcp stacked layers accommodates a square order for at least a part of the involved particles, as opposed to the octahedral coordination of purely fcc layers.²⁶

The observed superstructure is distinctly different from structures resulting from segregation of particles of slightly different shape and size.^23,24 Nanocubes with low degree of truncation preferentially deposit with the cube face, i.e. {100}, parallel to the substrate and aligned to each other, thus maximizing the interaction area. Increasing τ leads to larger {111} facets (with a quadratic dependence ∝ τ²), resulting in a favored alignment of the {111} facet parallel to the substrate. Indeed, a structural transition from a sc to a rhombohedral symmetry has been observed at τ = 0.9 by Monte Carlo simulations of the packing of truncated cubes (0.6 < τ < 1.0) in the absence of anisotropic interactions⁴⁹ and also experimentally by adjusting the ligand and solvent excess.⁵⁰

4 Conclusions

In summary, we have determined the mesostructure of large ordered arrays formed by iron oxide nanoparticles with different morphologies, i.e., nanospheres and highly truncated nanocubes. We find that both the isotropic spheres and the anisotropic highly truncated cubes (τ_htc = 0.88) are ordered in a fcc arrangement. The larger unit cell of the nanocube mesocrystals and the two discrete growth orientations strongly suggest alignment of the crystal axes of the nanocubes, as a consequence of their anisotropic shape. These results complement the structure previously reported for moderately truncated nanocubes (τ_tc = 0.45).³⁸ We have also found that the mesocrystals display a commensurate superstructure, through the satellite reflections determined by GISAXS and defect lines observed by SEM. The superstructure was related to stacking faults which propagate through the mesocrystals. We have presented a model for the supercell which suggests that the superstructure originates from the competition between the square and hexagonal ordering. This intergrowth is in contrast to the more common observation of segregation into different types of assemblies. Our experimental findings, i.e., the coexistence of square and hexagonal lateral order, suggest that a fine balance between the pure packing constraints and anisotropic interactions dictate the symmetry of the mesocrystals. These findings also illustrate the capabilities of using complementary techniques such as electron microscopy and GISAXS for the structural determination of ordered assemblies of anisotropic nanoparticles with unprecedented complexity.

Acknowledgements

We acknowledge the European Synchrotron Radiation Facility, the Synchrotron Soleil, and HASYLAB/DESY for providing the synchrotron radiation facilities at beamline ID01, SWING, and B1, respectively. E.W., G.S.A., and L.B. acknowledge the Swedish Research Council (VR) for financial support. LB and GSA thank Knut and Alice Wallenberg Foundation for support through the project grant 3DEM-NATUR. S.D. acknowledges support from the German National Academic Foundation. E. Brauweiler-Reuters is acknowledged for acquisition of the SEM images and J. Grins is acknowledged for acquisition and refinement of XRPD data.

References

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
2. S. Singamaneni, V. N. Bliznyuk, C. Binek and E. Y. Tsymbal, J. Mater. Chem., 2011, 21, 16819–16845.
3. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
4. F. X. Redl, K. S. Cho, C. B. Murray and S. O'Brien, Nature, 2003, 423, 968–971.
5. Z. Chen, J. Moore, G. Radtke, H. Sirringhaus and S. O'Brien, J. Am. Chem. Soc., 2007, 129, 15702–15709.
6. Y. Wang, M. Ibisate, Z. Y. Li and Y. Xia, Adv. Mater., 2006, 18, 471–476.
7. E. V. Shevchenko, D. V. Talapin, C. B. Murray and S. O'Brien, J. Am. Chem. Soc., 2006, 128, 3620–3637.
8. E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Nature, 2006, 439, 55–59.
9. D. V. Talapin, E. V. Shevchenko, M. I. Bodnarchuk, X. Ye, J. Chen and C. B. Murray, Nature, 2009, 461, 964–967.
10. K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630.
11. H. Chan, A. Demortière, L. Vukovic, P. Kral and C. Petit, ACS Nano, 2012, 6, 4203–4213.
12. J. Chen, A. Dong, J. Cai, X. Ye, Y. Kang, J. M. Kikkawa and C. B. Murray, Nano Lett., 2010, 10, 6103–6108.
13. S. Yamamuro, K. Sumiyama and T. Kamiyama, Appl. Phys. Lett., 2008, 92, 113108.
14. S. Polarz, Adv. Funct. Mater., 2011, 21, 3214–3230.
15. K. Bian, J. J. Choi, A. Kaushik, P. Clancy, D. M. Smilgies and T. Hanrath, ACS Nano, 2011, 5, 2815–2823.
16. Y. Nagaoka, O. Chen, Z. Wang and Y. C. Cao, J. Am. Chem. Soc., 2012, 134, 2868–2871.
17. J. Zhang, Z. Luo, B. Martens, Z. Quan, A. Kumbhar, N. Porter, Y. Wang, D.-M. Smilgies and J. Fang, J. Am. Chem. Soc., 2012, 134, 14043–14049.
18. M. Rycenga, J. M. McLellan and Y. Xia, Adv. Mater., 2008, 20, 2416–2420.
19. J. J. Choi, C. R. Bealing, K. Bian, K. J. Hughes, W. Zhang, D.-M. Smilgies, R. G. Hennig, J. R. Engstrom and T. Hanrath, J. Am. Chem. Soc., 2011, 133, 3131–3138.
20. T. Ming, X. Kou, H. Chen, T. Wang, H.-L. Tam, K.-W. Cheah, J.-Y. Chen and J. Wang, Angew. Chem., Int. Ed., 2008, 47, 9685–9690.
21. J.-M. Meijer, F. Hagemans, L. Rossi, D. Byelow, S. I. R. Castillo, A. Snigirev, I. Snigireva, A. P. Philipse and A. V. Petukhov, Langmuir, 2012, 28, 7631–7638.
22. F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388.
23. Q. Song, Y. Ding, Z. L. Wang and Z. J. Zhang, J. Phys. Chem. B, 2006, 110, 25547–25550.
24. S. Xie, X. Zhou, X. Han, Q. Kuang, M. Jin, Y. Jiang, Z. Xie and L. Zheng, J. Phys. Chem. C, 2009, 113, 19107–19111.
25. E. Vekris, V. Kitaev, D. D. Perovic, J. S. Aitchison and G. A. Ozin, Adv. Mater., 2008, 20, 1110–1116.
26. J. Hilhorst, V. V. Abramova, A. Sinitskii, N. A. Sapoletova, K. S. Napolskii, A. A. Eliseev, D. Byelow, N. A. Grigorievy, A. V. Vasilieva, W. G. Bouwman, K. Kvashnina, A. Snigirev, S. V. Grigoriev and A. V. Petukhov, Langmuir, 2009, 25, 10408–10412.
27. H. Cölfen and M. Antonietti, Angew. Chem., Int. Ed., 2005, 44, 5576–5591.
28. W. Lu, Q. Liu, Z. Sun, J. He, C. Ezeolu and J. Fang, J. Am. Chem. Soc., 2008, 130, 6983–6991.
29. J. Zhang, Z. Luo, Z. Quan, Y. Wang, A. Kumbhar, D. M. Smilgies and J. Fang, Nano Lett., 2011, 11, 2912–2918.
30. F. Dumestre, B. Chaudret, C. Amiens, P. Renaud and P. Fejes, Science, 2004, 303, 821–823.
31. R. Zheng, H. Gu, B. Xu, K. K. Fung, X. Zhang and S. P. Ringer, Adv. Mater., 2006, 18, 2418–2421.
32. A. Ahniyaz, Y. Sakamoto and L. Bergström, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17570–17574.
33. J. J. Choi, K. Bian, W. J. Baumgardner, D.-M. Smilgies and T. Hanrath, Nano Lett., 2012, 12, 4791–4798.
34. S. Sun, C. Murray, D. Weller, L. Folks and A. Moser, Science, 2000, 287, 1989–1992.
35. W.-k. Koh, S. R. Saudari, A. T. Fafarman, C. R. Kagan and C. B. Murray, Nano Lett., 2011, 11, 4764–4767.
36. M. I. Bodnarchuk, M. V. Kovalenko, H. Groiss, R. Resel, M. Reissner, G. Hesser, R. T. Lechner, W. Steiner, F. Schüffler and W. Heiss, Small, 2009, 5, 2247–2252.
37. G. Salazar-Alvarez, J. Qin, V. Šepelák, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. A. A. Macedo, M. Mikhaylova, M. Muhammed, M. D. Baró and J. Nogués, J. Am. Chem. Soc., 2008, 130, 13234–13239.
38. S. Disch, E. Wetterskog, R. P. Hermann, G. Salazar-Alvarez, P. Busch, T. Brückel, L. Bergström and S. Kamali, Nano Lett., 2011, 11, 1651–1656.
39. J. Park, K. An, Y. Hwang, J. Park, H. Noh, J. Kim, J. Park, N. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895.
40. C. Greaves, J. Solid State Chem., 1983, 49, 325–333.
41. Y. Xiong, H. Cai, B. J. Wiley, J. Wang, M. J. Kim and Y. Xia, J. Am. Chem. Soc., 2007, 129, 3665–3675.
42. J. Chen, J. M. McLellan, A. Siekkinen, Y. Xiong, Z. Y. Li and Y. Xia, J. Am. Chem. Soc., 2006, 128, 14776–14777.
43. S. Heitkam, W. Drenckhan and J. Fröhlich, Phys. Rev. Lett., 2012, 108, 148302.
44. L. V. Woodcock, Nature, 1997, 385, 141–143.
45. P. G. Bolhuis, D. Frenkel, S.-C. Mau and D. A. Huse, Nature, 1997, 388, 235–237.
46. A. Demortière, P. Launois, N. Goubet, P. A. Albouy and C. Petit, J. Phys. Chem. B, 2008, 112, 14583–14592.
47. P. Simon, E. Rosseeva, I. A. Baburin, L. Liebscher, S. G. Hickey, R. Cardoso-Gil, A. Eychmüller, R. Kniep and W. Carrillo-Cabrera, Angew. Chem., Int. Ed., 2012, 51, 10776–10781.
48. A. Bartolini, F. Ercolessi and E. Tosatti, Phys. Rev. Lett., 1989, 63, 872–875.
49. N. Volkov, A. P. Lyubartsev and L. Bergström, Nanoscale, 2012, 4, 4765.
50. Y. Zhang, F. Lu, D. van der Lelie and O. Gang, Phys. Rev. Lett., 2011, 107, 135701.

---

Footnotes

† Electronic supplementary information (ESI) available: TEM images and histograms; SAXS data refinement; GISAXS mesocrystal structure determination with comparison of observed and calculated reflections. See DOI: 10.1039/c3nr33282a

‡ Present address: Institut Laue-Langevin, F-38042 Grenoble, France. E-mail: disch@ill.eu

---