 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A “nano-windmill” driven by a flux of water vapour: a comparison to the rotating ATPase†
Patrycja Nitoń,
Andrzej Żywociński*,
Marcin Fiałkowski and
Robert Hołyst*
Institute of Physical Chemistry of the Polish Academy of Sciences, 44/52 Kasprzaka Street, 01-224 Warsaw, Poland. E-mail: rholyst@ichf.edu.pl; Fax: +48 22 343 3333; Tel: +48 22 343 3123
First published on 25th July 2013
Abstract
We measure the frequency of collective molecular precession as a function of temperature in the ferroelectric liquid crystalline monolayer at the water–air interface. This movement is driven by the unidirectional flux of evaporating water molecules. The collective rotation in the monolayer with angular velocities ω ∼ 1 s−1 (at T = 312 K) to 10−2 s−1 (at T = 285.8 K) is 9 to 14 orders of magnitude slower than rotation of a single molecule (typically ω ∼ 109 to 1012 s−1). The angular velocity reaches 0 upon approach to the two dimensional liquid-to-solid transition in the monolayer at T = 285.8 K. We estimate the rotational viscosity, γ1, in the monolayer and the torque, Γ, driving this rotation. The torque per molecule equals Γ = 5.7 × 10−8 pN nm at 310 K (γ1 = 0.081 Pa s, ω = 0.87 s−1). The energy generated during one turn of the molecule at the same temperature is W = 3.5 × 10−28 J. Surprisingly, although this energy is 7 orders of magnitude smaller than the thermal energy, kBT (310 K) = 4.3 × 10−21 J, the rotation is very stable. The potential of the studied effect lies in the collective motion of many (>1012) “nano-windmills” acting “in concerto” at the scale of millimetres. Therefore, such systems are candidates for construction of artificial molecular engines, despite the small energy density per molecular volume (5 orders of magnitude smaller than for a single ATPase).
Introduction
The human endeavour to create artificial molecular machines (AMMs) has become more realistic since the mechanism of biological conversion of chemical energy to mechanical work at the level of a single molecule was understood.1,2 It resulted in the design of many molecules or assemblies of molecules with the ability to perform work.3–5 Very recently a critical assessment on expectations and promise in relation to artificial molecular motors was published by Coskun et al.6 In most of the AMMs the rotation is driven by the cis–trans conformational changes (powered by light) or reaction of tautomerization. Although a switching between the two states usually does not define the direction of rotation, molecules of very special design ensuring a unidirectional rotation were synthesized by the group of B. L. Feringa.7,8 More possibilities can be ensured with more complicated molecules belonging to the big group called rotaxanes.9 These molecules consisting of two parts, which can be treated as the stator and the rotor,10 resemble very much the structure of the most frequently studied rotating protein, i.e. F0F1–ATPase complex. It has to be noted here that most of the AMMs mentioned above are powered by light and rotate at very low angular velocities (often <10−3 Hz) and it was a challenge to increase the speed of rotation up to 87 revolutions per second by a special design of the molecule.11 In this manuscript we show a mechanism of rotation powered by the unidirectional flux of water molecules in the angular velocity range of 1 to 10−2 s−1.None of the papers dealing with AMMs considered the Lehmann effect,12 which describes the collective rotation of chiral molecules of a liquid crystal (LC) driven by a temperature gradient, as a possible mechanism driving the AMMs. Another possible mechanism for powering AMMs was discovered by Tabe and Yokoyama;13 here collective molecular precession occurs in Langmuir monolayers of chiral LC. This phenomenon can be considered as a chemical Lehmann effect because the collective molecular precession is driven by a vapour pressure difference, i.e. a gradient of the chemical potential. Detailed quantitative analysis of the driving forces in this phenomenon over a wide temperature range is the aim of our work. We also consider the following question: how does the chemical Lehmann effect compare with the biological mechanism in ATPase, which is the protein utilizing the gradient of proton concentration to drive the rotation and ADP-to-ATP synthesis?
The chemical Lehmann effect, after its discovery by Tabe and Yokoyama,13 was investigated experimentally in different aspects by us14 and by Gupta et al.15 The discussion presented here is based on the new measurements of the frequency of the collective molecular precession at different temperatures in the range of 285–312 K. This study allowed us to estimate the rotational viscosity in the monolayer and the torque driving this rotation. The torque should be compared to the one generated by other AMMs and especially, by the working proteins among which the rotating ATPase16 seems to be the best candidate. Detailed discussion on that subject is placed at the end of this paper.
The collective molecular rotation or precession mentioned above belongs to the broad class of phenomena called Onsager's cross-effects found in different branches of physics and chemistry, especially irreversible thermodynamics. The most known examples include the Hall effect, Marangoni effect, Soret effect (thermodiffusion), and many others, in which a flux of matter (mass or energy) is coupled with a thermodynamic force. A less known effect of this type is called by the name of Otto Lehmann,12 who observed rotation of droplets of cholesteric LC in a gradient of temperature and described it in 1900. Because of experimental difficulties the Lehmann's experiment was not reproduced for more than 100 years, although it was explained theoretically in 1968 by Leslie17 and later in 1982 it was confirmed indirectly by Éber and Jánossy.18 Finally, in 2008 the Lehmann's observation was reproduced in the sophisticated experiments by Oswald et al.19–21 Very recently Oswald summarized his investigations with emphasis on the microscopic and macroscopic origin of the Lehmann effect.22 Theoretical papers on that subject were also published by Brand et al.23–25 to mention just a few examples of studies on this topic. An assumption that “inverse Lehmann effects can be used as a microscopic pump”, given earlier by Svenšek et al.,24 makes us think that such a mechanism could be involved in the working of F0–ATPase as a proton pump.
Results and discussion
Molecular precession in Langmuir monolayers
Here we present the results for just one liquid-crystalline ferroelectric compound: (S)4-[4-(1-methylheptyloxycarbonyl)phenyl]-4′-[6-(cyanoetanoyloxy)hexyloxy]biphenyl-4-carboxylate, denoted as ferroC, although we studied more ferroelectric compounds and observed the collective rotations with similar behaviour for two of them. The molecules of both compounds self-assemble at the air–water interface and create monolayers of smectic-C* type. The polar molecules of LC are anchored to the water surface with the polar groups present at one end of each molecule. The asymmetric chiral groups attached to the other ends of the molecules' rigid cores stick out into the air. Projections of tilted molecules onto the plane of the water surface, often called a c-director, locally align along one preferred direction and create the specific patterns because of collective rotation driven by a flux of evaporating molecules of water. Molecules of water hitting the asymmetric branches of the chiral groups cause the resultant torque and the molecular precession. This mechanism of rotation was explained and proved by Tabe and Yokoyama.13 The rotation is not coupled to any macroscopic flow within the layer. The lack of flow in the monolayer becomes obvious after longer observation of few domains visible in the two images shown in Fig. 1 recorded using a Brewster angle microscope (BAM) with 8 seconds time delay. A gray-scale intensity of reflected polarized light, being in correlation with the rotating director, changes from black to white and vice versa, but the shapes of the domains with uniform orientation remain unchanged (compare details of both images in Fig. 1). The image analysis of the recorded sequence of images allowed us to measure the frequency of rotation in a particular domain as explained in Fig. S1 in the ESI.† This continuous collective rotation of the molecules is a result of the mechanical balance between the driving force causing a molecular precession and the viscous torque, γ1, proportional to the rotational viscosity. Examples of typical patterns created during molecular precession in the Langmuir film and observed using BAM are shown in Fig. 1 and 2. The mechanism of the pattern formation was explained theoretically and through computer simulations by Svenšek et al.25 This mechanism results in a phase shift of the c-director and macroscopic “in-plane” spirals in the monolayer caused by a winding up process. Detailed analysis of many patterns recorded during our studies has shown clearly a time evolution of these patterns with winding-up causing a shortening of the pitch of spirals in the plane of the monolayer. It can be seen in Fig. 2 showing the early-stage (Fig. 2a) and the late-stage (Fig. 2b) of the pattern evolution. An interesting theoretical explanation of the origin of the patterns with macroscopic chirality of the monolayer, caused by rotation of the axial dynamic preferred direction, was published recently by Brand et al.23 Another theoretical interpretation supported by computer simulations of pattern formation was given (soon after the discovery of this phenomenon by Tabe and Yokoyama13) by Tsori and deGennes.26 The authors assumed26 that the rotation is induced by sudden “bursts” of evaporation (when the threshold of the film elasticity is overcome by the difference of chemical potentials of water in a subphase and in a vapour), and is blocked at the domain walls. Images in Fig. 2 seem to support this model.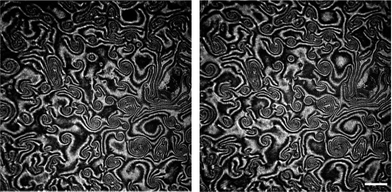 | ||
| Fig. 1 Two images of the same area recorded at 25 °C with 8 seconds of time delay showing that there is no flow in the film in spite of the rotation of the local ordering vector (the c-vector turns here approximately by π/2); the patterns visible under a Brewster Angle Microscope (BAM) show that the shapes of domains remain unchanged and only the intensity of light reflected from bigger domains changes: bright regions turn black and vice versa; white bar shows a length of 500 μm. | ||
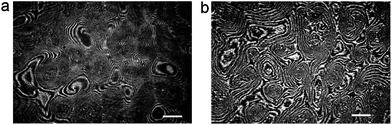 | ||
| Fig. 2 Early (a) and late (b) stages of pattern evolution; image (b) shows stripes tightly “wound-up” around each center of rotation; the images were recorded with a time delay of 1.5 hour; white bars show a length of 500 μm. | ||
Torque and rotational viscosity
The surface torque, Γs, being a driving force causing the rotation of the c-director in the monolayer, is defined as Γs = fr/A, where f is the force acting on the chiral group (treated as vanes of the propeller13), r is the projection of the distance between the polar and the chiral groups on the plane of the water surface and A is the molecular area, i.e. the area occupied by one molecule in the monolayer. Here A is measured during the recording of Langmuir isotherms. Continuous precession of the molecule at constant angular velocity, ω, is a result of the balance between the driving torque and the viscous torque, which can be written as| Γs = γsω, |
The bulk torque, Γ, is proportional to the momentum flux of evaporating water molecules. We estimate the flux from the Hertz–Knudsen relationship. This flux is proportional to the pressure of saturated water vapour, psat (for details see ref. 28). In our case water evaporation occurs at a pressure difference Δp = psat − pw, where pw is the partial pressure of water vapour in a humid atmosphere over the Langmuir film. Thus, the balance between the driving torque and the viscous torque can be written as:
| Γ = νΔp = γ1ω, | (1) |
The last quantity needed to estimate the surface torque and to compare our molecular rotors with biological engines is the area per molecule, A. In our experiments we determined A at the air–water interface for ferroC by the Langmuir trough method. The compound ferroC, when spread from chloroform solution on the water surface, forms a very stable monolayer. The examples of two isotherms of the surface pressure, π, as a function of area per molecule, A, as well as the molecular structure of compound ferroC are given in Fig. 3. In the range of surface pressure, π, accessible on the water surface, the monolayer exhibits 2D transitions between gas, liquid, and solid phases. The morphology of the monolayer was observed using BAM. In Fig. 3, the range of molecular area A > 0.42 nm2 is the region of coexistence of gas and liquid phases. The range marked as 1 with the first pressure increase corresponds to a compression of the compact rotating liquid phase characterized by typical textures shown in Fig. 1 and 2. With our setup it was impossible to distinguish between n and −n orientation of the ordering vector, so the grey-scale intensity variation from black to white and back to black means a rotation by angle π. At the beginning of the plateau (range 2) the phase transition to solid phase occurs. The plateau region corresponds to the liquid–solid phase transition accompanied by the reorientation of the molecules from tilted to vertical orientation (this observation comes from surface potential measurements30 not reported here). On further compression, the second pressure increase, corresponding to a homogenous solid phase, is observed and finally, at the second plateau at π = 38 mN m−1, the monolayer collapses with formation of random aggregates of the solid phase (see Fig. S2 in the ESI†).
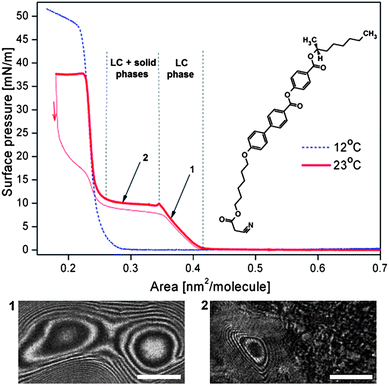 | ||
| Fig. 3 Two isotherms of surface pressure vs. area per molecule for the ferroelectric liquid crystal of a given structure at the air–water interface at temperatures 285.2 and 296.2 K (12 and 23 °C); two BAM images show: (1) texture of the rotating domain recorded at point 1; (2) texture of the two-phase region observed at the plateau of the isotherm at 296.2 K (23 °C). White bar shows a length of 500 μm. | ||
The coherent rotary motion of the c-director gave a characteristic oscillatory pattern of the reflected light observed under a BAM. The rate of rotation was examined at different temperatures of the water subphase in the range of 285–312 K and the results are shown in Fig. 4. The slowest possible to measure rotation (approx. 500 seconds for rotation by 2π angle) was measured at temperature 285.8 K. Below this temperature the oscillatory pattern of the rotating liquid phase vanishes in the transition to the solid phase (see Fig. S3 in the ESI†). We suppose that the diverging time of collective precession of chiral molecules and the decrease of macroscopic chirality of the monolayer support the theoretical model of Brand et al.23 We show in Fig. 4 that the time of molecular revolutions increases with the decreasing temperature. Specifically, the rotation is slowing down from 6 seconds at 312.2 K to almost 8 minutes at 285.8 K.
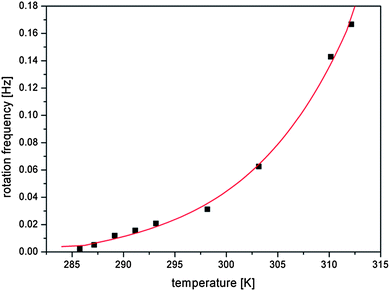 | ||
| Fig. 4 Frequency of rotation by 2π angle as a function of temperature of the water subphase (the line is an exponential fit used for data interpolation). | ||
Spreading the monolayer of our compound on the water surface at temperature 285 K, even at low concentrations, does not give a uniform 2D gas phase. Instead, big rafts of the solid phase are visible in BAM images. In the proximity of the transition to the solid phase (at 285.8 K) the period of the revolution of the vector order parameter diverges. This slowing down of the rotation of the c-vector corresponds to the divergence of the rotational viscosity.
We analyzed the data of ω(T) using eqn (1) with Δp substituted by psat because all the measurements were performed in an atmosphere of dry argon, thus pw = 0. In the equation:
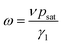 | (2) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p = 16.16629 − 3736.276/(T − 49.577), p = 16.16629 − 3736.276/(T − 49.577),
| (3) |
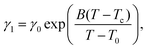 | (4) |
With the values of psat calculated for each temperature from eqn (3), we calculated from eqn (2) the values of the ratio γ1/ν = psat/ω as a function of temperature. These values behave the same way as the rotational viscosity because ν is a constant. We fitted the values of γ1/ν as a function of temperature using the VFT model given by eqn (4) with an experimental value of Tc = 285.0 K and treating γ0, B and T0 as adjustable parameters.
This fitting to eqn (4) gave very reasonable values of the parameters B = −3.564 ± 0.138 and T0 = (282.16 ± 0.55) K. It has to be mentioned that these values are not affected by the multiplication factor ν. The real values of temperature dependence of γ1 (still with accuracy to the multiplication factor) were found by scaling the measured ratios of γ1/ν to typical values of the rotational viscosity of smectic-C* phases in ferroelectric LCs far from any phase transition. For scaling we chose the average value of γ1 = 0.1 Pa s found in the literature34,35 for ferroelectric LCs at a temperature in the middle of the range of SmC* (between the transitions to solid and to SmA phases). The value of γ1 = 0.1 Pa s was taken as the value of the rotational viscosity of the monolayer of compound ferroC at temperature T = 300 K. This scaling and fitting of γ1(T) to eqn (4) gave the value of parameter γ0 = (2.00 ± 0.23) Pa s. Final results of fitting and the fitted curve are shown in Fig. 5. Above scaling allowed us to estimate the chemical Lehmann coefficient, ν, and gave the value ν = 8.8 × 10−6. In this case ν is a dimensionless parameter related to the chiral strength of the molecule characterized by the Lehmann Rotatory Power29 (LRP). Untill now, there has been no theoretical prediction on how the chemical Lehman coefficient relates to the classic Lehmann coefficient, which controls the molecular rotation in a temperature gradient. Very recent measurements by Oswald22 gave the value equal to 2.7 × 10−7 N m−1 K−1. Both of these coefficients are related to the chiral strength of the molecule or LRP, so the relationship between them should also exist.
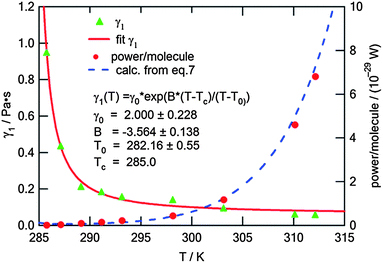 | ||
| Fig. 5 Rotational viscosity, γ1, of the monolayer and the output power of the single molecule vs. temperature of the subphase; the points marked by triangles (▲) are calculated from the angular velocity (see text); the solid curve is a result of fitting to eqn (4) (the equation is also given in the graph together with fitted parameters); dots (●) represent the power output from one molecule calculated for experimental points; the dashed curve is calculated according to eqn (7). | ||
Ferroelectric LC and ATPase: two monomolecular machines
We estimated the viscous torque, ΓfC, of the ferroC monolayer from calculated values of γ1. This quantity is equal to the torque of unit volume, according to eqn (1) and measured in N m−2 unit. For the single-molecule the torque is usually measured in pN nm. To estimate the torque created by a single rotating molecule of ferroC, the viscous torque has to be multiplied by the volume occupied by one molecule. We calculate these values of torque for different temperatures as:| qfC = ΓfCAfCd = γ1ωAfCd, | (5) |
| W = 2πqfC = 2πγ1ωAfCd | (6) |
| P = Wω/2π = γ1ω2AfCd. | (7) |
The energy and power generated during one turn of the molecule calculated from eqn (6) and (7) at T = 310 K are W = 3.5 × 10−28 J and P = 4.9 × 10−29 W, respectively. The values of the power of one molecule calculated for experimental points are shown in Fig. 5 together with the curve P(T) calculated from eqn (7) and smoothed data of γ1(T) and ω(T). In spite of the fact that the energy equivalent to work estimated above is 7 orders of magnitude smaller than kBT (310 K) = 4.3 × 10−21 J, the patterns observed in the film are not destroyed by thermal motion because of the collectiveness of the molecular precession and interactions of the monolayer film with the water surface.
We can compare our result of the torque per molecule, qfC = 5.7 × 10−8 pN nm = 5.7 × 10−29 J, to the value of torque estimated by Tabe and Yokoyama13 for their chiral molecule rotating in the monolayer. They report the value of qT&Y = (10−11 to 10−10)kBT < 4.3 × 10−31 J, approximately 100 times less than our value. The difference is understandable because Tabe and Yokoyama studied molecules of different shapes, although of similar size, in the monolayer spread on the mixture of water and glycerol (more viscous subphase). Also the method of torque estimation was different because their calculation was based on the elasticity of the monolayer and the size of the domain in which the collective precession occurs. Nevertheless, both results drive to similar conclusions given in the next section of this paper.
None of the parameters estimated above for ferroC can be compared directly to the data accessible in the literature for ATPase. The complex of F0F1–ATPase has been investigated by many authors.3,16,36–38 The reported values of torque of ATPase, qATP, ranges from 10 pN nm to 80 pN nm depending on the load connected to the ATPase rotor and the frequency of rotation.37–40 The mechanism of rotation is different in ferroC and in ATPase. The latter is very clearly explained by Aksimentiev et al.41 The coupled units of F0–ATPase and F1–ATPase alternately exchange their roles and when F1 plays the role of a motor, driven by ATP hydrolysis, then F0 acts as a pump generating the proton gradient. In the alternative case, the F0 unit acts as a motor driven by the gradient of protons and F1 synthesizes ATP. Aksimentiev et al.41 reported the results of sophisticated simulations of the system of F0 unit, consisting of more than 111 thousands of atoms, giving the volume of this unit equal to 11.2 × 12.3 × 9.8 nm3. Similar dimensions of the cross-section of the complex of F0F1–ATPase are reported by Stock et al.42 with the height of the complex equal to 19.1 nm. We relate the energy output of our “ferroC molecular motor” to much bigger F0F1–ATPase taking into account differences in their molecular volumes. We calculate the energy density, ε, dissipated during one revolution of a single molecule as a ratio of the output work of one revolution divided by the volume, V, of one molecule,
| ε = W/V = 2πq/V = 2πγ1ω. | (8) |
The volume of the ferroC molecule has already been estimated, so in this case εfC = 2πΓfC = 0.44 N m−2 = 4.4 × 10−7 pN nm−2. The volume of F0F1–ATPase, calculated according to its dimensions from ref. 41 and 42, is equal to 2630 nm3. By using the most frequently reported value of the torque41–43 of ATPase equal to 40 pN nm, we obtain the energy density εATP = 1.5 × 10−2 pN nm−2. Such a comparison of the output energy density, ε, that could be generated by a biological motor, such as ATPase, and by an artificial molecular motor, such as collectively rotating chiral molecules of LC, gives the ratio of energy density equal to 105. Thus, the work per unit molecular volume performed by ATPase driven by ATP hydrolysis is 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times greater than that performed by our ferroC molecule driven by the flux of water molecules. This comparison shows that the future of artificial engines belongs to biological units, possibly working in other environment than living systems. However, the big advantage of AMMs based on liquid crystalline molecules is their simplicity and the easily tuneable, collective rotation involving 1012 molecules. A perfect high energy density machine would comprise these two concepts of collective behaviour (such as in the case of our “nano-windmills”) with a very efficient single entity unit (such as ATPase).
000 times greater than that performed by our ferroC molecule driven by the flux of water molecules. This comparison shows that the future of artificial engines belongs to biological units, possibly working in other environment than living systems. However, the big advantage of AMMs based on liquid crystalline molecules is their simplicity and the easily tuneable, collective rotation involving 1012 molecules. A perfect high energy density machine would comprise these two concepts of collective behaviour (such as in the case of our “nano-windmills”) with a very efficient single entity unit (such as ATPase).
Concluding remarks
In summary, the evaporation of water across a chiral liquid crystalline monolayer can drive a collective molecular precession.13,14 We have shown that in Langmuir monolayers the angular velocity of rotation can be extremely low (of the order of 10−2 Hz), i.e. 14 orders of magnitude lower than that of typical molecular rotations. This unusual slowing down of collective unidirectional rotation is caused by the viscosity of the monolayer and the proximity of the two dimensional liquid–solid phase transition in the monolayer of the smectic-C* phase. We have determined the temperature dependence of the rotational viscosity, γ1, from BAM observations of molecular precession in Langmuir films. The experimental study of temperature dependence of the rotational viscosity, γ1(T), of Langmuir monolayers facilitated estimation of the torque engendered by one rotating molecule. We have related the energy density output of this “molecular motor” to the highly efficient biological motor F0F1–ATPase. Referring to the title of the paper, it can be concluded that the Lehmann rotation has potential to be used to power a “nano-windmill”, however, the power of such an “engine” is 5 orders of magnitude smaller than the power of a single biological motor. But, the potential of the Lehmann effect is hidden in the collective nature of motion of many (>1012) “nano-windmills” acting “in concerto” at the scale of millimetres. We expect that future artificial molecular machines should combine efficient biological units synchronized by a kind of Lehmann effect, utilizing concentration or temperature gradients, and perform their function collectively.Acknowledgements
RH thanks the National Science Centre for funding the project from the funds granted on the basis of the decision number: 2011/02/A/ST3/00143 (Maestro grant). MF acknowledges the financial support from the Foundation for Polish Science Team Programme TEAM/2010-6/4 co-financed by the EU “European Regional Development Fund”.Notes and references
- K. Kinosita, R. Yasuda, H. Noji, S. I. Ishiwata and M. Yoshida, Cell, 1998, 93, 21–24 CrossRef CAS.
- G. Oster and H. Wang, Structure, 1999, 7, R67–R72 CrossRef CAS.
- K. Kinbara and T. Aida, Chem. Rev., 2005, 105, 1377–1400 CrossRef CAS.
- J. Michl and E. C. H. Sykes, ACS Nano, 2009, 3, 1042–1048 CrossRef CAS.
- E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72–191 CrossRef CAS.
- A. Coskun, M. Banaszak, R. D. Astumian, J. F. Stoddart and B. A. Grzybowski, Chem. Soc. Rev., 2012, 41, 19–30 RSC.
- M. Klok, N. Boyle, M. T. Pryce, A. Meetsma, W. R. Browne and B. L. Feringa, J. Am. Chem. Soc., 2008, 130, 10484–10485 CrossRef CAS.
- N. Koumura, R. W. J. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Nature, 1999, 401, 152–155 CrossRef CAS.
- A. Harada, J. Li and M. Kamachi, Nature, 1992, 356, 325–327 CrossRef CAS.
- A. Schalley, K. Beizai and F. Vögtle, Acc. Chem. Res., 2001, 34, 465–476 CrossRef.
- J. Vicario, M. Walko, A. Meetsma and B. L. Feringa, J. Am. Chem. Soc., 2006, 128, 5127–5135 CrossRef CAS.
- O. Lehmann, Ann. Phys., 1900, 2, 649–705 CrossRef CAS.
- Y. Tabe and H. Yokoyama, Nat. Mater., 2003, 2, 806–809 CrossRef CAS.
- P. Milczarczyk-Piwowarczyk, A. Żywociński, K. Noworyta and R. Hołyst, Langmuir, 2008, 24, 12354–12363 CrossRef CAS.
- R. K. Gupta, K. A. Suresh, S. Kumar, L. M. Lopatina, R. L. R. Selinger and J. V. Selinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041703 CrossRef CAS.
- H. Noji, R. Yasuda, M. Yoshida and K. Kinosita, Nature, 1997, 386, 299–302 CrossRef CAS.
- F. M. Leslie, Proc. R. Soc. London, Ser. A, 1968, 307, 359–372 CrossRef CAS.
- N. Éber and I. Jánossy, Mol. Cryst. Liq. Cryst., 1982, 72, 233–238 CrossRef.
- P. Oswald and A. Dequidt, Phys. Rev. Lett., 2008, 100, 217802 CrossRef.
- A. Dequidt, A. Żywociński and P. Oswald, Eur. Phys. J. E, 2008, 25, 277–289 CrossRef CAS.
- P. Oswald, A. Dequidt and A. Żywociński, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061703 CrossRef.
- P. Oswald, Eur. Phys. J. E, 2012, 35, 10 CrossRef CAS , and references therein.
- H. B. Brand, H. Pleiner and D. Svenšek, Eur. Phys. J. E, 2011, 34, 1–10 CrossRef.
- D. Svenšek, H. Pleiner and H. R. Brand, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021703 CrossRef.
- D. Svenšek, H. Pleiner and H. R. Brand, Phys. Rev. Lett., 2006, 96, 140601 CrossRef.
- Y. Tsori and P. G. de Gennes, Eur. Phys. J. E, 2004, 14, 91–96 CrossRef CAS.
- P. Oswald, G. Poy, F. Vittoz and V. Popa-Nita, Liq. Cryst., 2013, 40, 734–744 CrossRef CAS.
- R. Hołyst and M. Litniewski, J. Chem. Phys., 2009, 130, 074707 CrossRef.
- P. Oswald, L. Jųrgensen and A. Żywociński, Liq. Cryst., 2011, 38, 601–613 CrossRef CAS.
- P. Nitoń, Langmuir monolayers of ferroelectric and bolaamphiphilic liquid crystal at the air–water interface, Ph. D. thesis, IPCh PAS, Warsaw, 2012.
- W. Wagner and A. Pruss, International Equations for the Saturation Properties of Ordinary Water Substance. Revised According to the International Temperature Scale of 1990. Addendum to J. Phys. Chem. Ref. Data 16, 893 (1987), J. Phys. Chem. Ref. Data, 1993, 22, 783–787.
- M. Fiałkowski, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 1955–1966 CrossRef.
- J. C. Mauro, Y. Yue, A. J. Ellison, P. K. Gupta and D. C. Allan, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19780–19784 CAS.
- C. Escher, T. Geelhaar and E. Bohm, Liq. Cryst., 1988, 3, 469–484 CrossRef CAS.
- W. Piecek, J. Rutkowska, J. Kędzierski, P. Perkowski, Z. Raszewski and R. S. Dąbrowski, Measurements of Rotational Viscosity of SmC* Mixtures, in Liquid Crystals; International Society for Optics and Photonics, 1998, pp. 148–153 Search PubMed.
- R. Yasuda, H. Noji, M. Yoshida, K. Kinosita Jr and H. Itoh, Nature, 2001, 410, 898–904 CrossRef CAS.
- T. Bilyard, M. Nakanishi-Matsui, B. C. Steel, T. Pilizota, A. L. Nord, H. Hosokawa and R. M. Berry, Philos. Trans. R. Soc., B, 2013, 368, 1611 Search PubMed.
- W. Junge, H. Sielaff and S. Engelbrecht, Nature, 2009, 459, 364–370 CrossRef CAS.
- H. Omote, N. Sambonmatsu, K. Saito, Y. Sambongi, A. Iwamoto-Kihara, T. Yanagida and M. Futai, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 7780–7784 CrossRef CAS.
- O. Pänke, D. A. Cherepanov, K. Gumbiowski, S. Engelbrecht and W. Junge, Biophys. J., 2001, 81, 1220–1233 CrossRef.
- A. Aksimentiev, I. A. Balabin, R. H. Fillingame and K. Schulten, Biophys. J., 2004, 86, 1332–1344 CrossRef CAS.
- D. Stock, A. G. Leslie and J. E. Walker, Science, 1999, 286, 1700–1705 CrossRef CAS.
- T. Ariga, T. Masaike, H. Noji and M. Yoshida, J. Biol. Chem., 2002, 277, 24870–24874 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Three figures showing the method of frequency measurements, Langmuir isotherms and BAM images of different phases of the monolayer. See DOI: 10.1039/c3nr03496h |
| This journal is © The Royal Society of Chemistry 2013 |
