 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A vesicle cell under collision with a Janus or homogeneous nanoparticle: translocation dynamics and late-stage morphology†
Noriyoshi Arai*a,
Kenji Yasuoka*b and
Xiao Cheng Zeng*c
aDepartment of Mechanical Engineering and Intelligent Systems, University of Electro-Communications, Chofu, Tokyo 182-8585, Japan. E-mail: arai@mce.uec.ac.jp
bDepartment of Mechanical Engineering, Keio University, Yokohama, Kanagawa 223-8522, Japan. E-mail: yasuoka@mech.keio.ac.jp
cDepartment of Chemistry, University of Nebraska-Lincoln, Lincoln, Nebraska 68588, USA. E-mail: xzeng1@unl.edu
First published on 1st August 2013
Abstract
We investigate translocation dynamics of a vesicle cell under collision with a Janus or a homogeneous hydrophobic/hydrophilic nanoparticle. To this end, we perform dissipative particle dynamics simulation by setting the nanoparticle with different initial velocities, different chemical patterns of the surface for the nanoparticle, and different orientations (for the Janus nanoparticle). Particular attention is given to translocation dynamics, in-cell water discharge, and the late-stage morphologies of the vesicle/nanoparticle system after the collision. We observe three late-stage states for the Janus nanoparticle, and four late-stage states for the homogeneous nanoparticles. We find that the late-stage state and the associated dynamical pathway not only depend on the relative velocity but also on the chemical pattern of the nanoparticle surface, as well as on the orientation of the incident Janus nanoparticle. We have examined the time-dependent mean radius of the vesicle, the number of in-cell water beads lost from the vesicle, as well as the collision-induced pore size on the lipid membrane during the course of collision. Our simulation provides microscopic insights into the resilience of the vesicle-cell membrane and dynamical behavior of the vesicle under the attack of a foreign nanoparticle. Knowledge and insights gained through the simulation will have implication to the drug delivery with different chemical coatings.
Introduction
A unilamellar vesicle is a micro-spherical organelle enclosed by a lipid bilayer. When prepared artificially, it can be viewed as a model liposome. Vesicles have attracted considerable attention not only due to their biological and medical implications but also their application in food and cosmetic industry. Moreover, vesicles may be exploited as a carrier for drug or gene delivery1–4 owing to their novel properties such as low toxicity, low antigenicity, and metabolizability in vivo, among others. House et al.2 demonstrated that the size of vesicles can be controlled by using patterned substrates. Gözen et al.4 showed two rupture mechanics in bilayer membranes that depend on the stress, i.e., floral and fractal membrane rupture. An improved understanding of the vesicle-size controlling, nanoparticle translocation, and dynamic behavior of membrane rupture under the attack of a nanoparticle is of both fundamental and practical importance for the design of effective carriers for drug and gene delivery, as well as the nano- and micro-reactor. For the application of artificial vesicles, a fundamental issue that requires more attention is the understanding of the chemical interaction between a vesicle and surrounding media and the resilience of the vesicle membrane under the attack by different foreign nanoparticles.Recent developments in nanofabrication and synthesis strategies afford nanoparticles with controlled size, chemical pattern, and structure in large quantities.5–8 Among them, the Janus nanoparticle is a special anisotropic nanoparticle, defined as having two or more distinct functional surface regions. With two distinct chemical and/or physical sections distributed among different surface regions of a single particle, new characteristics arise for the Janus nanoparticle systems, compared with homogeneous nanoparticle systems. To some extent, Janus nanoparticles bear certain resemblance to amphiphilic molecules such as DNA, peptides, and surfactants. Huang et al.9 studied the effect of Janus nanoparticles on the phase separation dynamics of the polymer blends using simulation. They showed that the domain growth can be inhibited by Janus nanoparticles, and the domain size is less than that of the homogeneous nanoparticle. Alexeev et al.10 carried out a simulation of the pore membrane with Janus particles. They show that the Janus particles introduce a controllably “re-sealable” pore in the membrane by diffusing to the edge of the hole and form a stable pore. Yue and Zhang11 investigated how a membrane responds to adsorption of the ligand-coated Janus nanoparticle. They demonstrated that the membrane response depends on the size of the nanoparticle, area density of ligand coating on the nanoparticle, and membrane tension. Ding and Ma12 studied the interaction between Janus nanoparticles and the bilayer membrane and reported two distinct late-stage states for the Janus nanoparticle, namely, the insertion and engulfment. Indeed, there has been a notable surge on the modeling study of nanoparticle–membrane interaction since 2010.13–18 However, to our knowledge, the collision dynamics between the vesicle and the Janus nanoparticle, which includes the breaking and reform process for the vesicle membrane and possible release of in-cell water, has not been investigated from computer simulation. As artificial liposomes and artificial blood vessels will be increasingly used in the future, studies of the interaction between a vesicle and a foreign particle through computer simulation will be valuable. In this article, we perform a comprehensive dissipative particle dynamics (DPD) simulation19,20 to investigate detailed collision and translocation processes between the vesicle and either a Janus or a homogeneous nanoparticle. Particular attention is given to the translocation dynamics, discharge of in-cell water, and late-stage metastable morphologies of the vesicle/nanoparticle system after the collision under different initial relative velocities. In our simulation, typical velocities (excluding the initial speed) are in the range of 10−2 to 10−1 m s−1, as used in a previous simulation study for the translocation of the nanoparticle.14 Such a wide range of initial velocities allow us to examine a variety of phenomena, such as a nanoparticle fully penetrating through a vesicle membrane in a high-speed limit and a nanoparticle bouncing back from the outer membrane in a low-speed limit. Hence, this study not only has practical implications to nanofluidics of drug or gene delivery, but also is of relevance to the fundamental chemistry of the interaction between the nanoparticle and the vesicle and the discharge of the in-cell object.
Simulation method and model
We employ the DPD simulation method to study the collision dynamics between the Janus or homogeneous nanoparticle and the vesicle. DPD simulations involve the use of coarse-grained beads, each composed of a group of atoms or molecules. As such, the DPD method is a computationally more efficient simulation tool over classical molecular dynamics for the study of dynamical behavior of the complex fluid at the mesoscopic level. The DPD method has been used by many researchers on a wide range of complex fluid problems, for example, polymer melts/blends,21–23 self-assembly of the surfactant,24–26 fusion of the membrane and vesicle,27,28 among others.In this method, each DPD bead obeys the Newton's equation of motion,
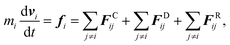 | (1) |
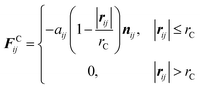 | (2) |
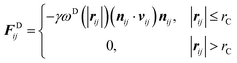 | (3) |
and
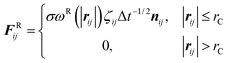 | (4) |
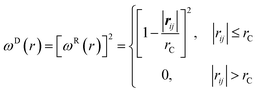 | (5) |
The temperature is controlled through the combination of dissipative and random forces. The noise parameter and friction parameter are related to each other by the fluctuation–dissipation theorem in the following equation
| σ2 = 2γkBT | (6) |
In this study, we adopt a spring force FSij as
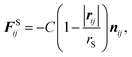 | (7) |
Fig. 1 displays the model system and different initial orientations for the Janus nanoparticle. The Janus nanoparticle is composed of hydrophobic and hydrophilic DPD beads on a diamond lattice with a lattice constant α = 0.78 nm. All DPD beads within the nanoparticle are treated as a rigid body using the rattle constraint algorithm.29 The diameter of the nanoparticle is 6.25 nm. The reason is that we expect it to be used as a carrier in the drug delivery system (DDS). The surface of a nanoparticle can be decorated with a ligand, an antibody, and other materials. The size of the nanoparticle for DDS is typically about 4–8 nm.30,31 We define the orientation vector direction of the nanoparticle from the pole of the hydrophilic side to the pole of the hydrophobic side as shown in Fig. 1. Each Janus nanoparticle consists of 2149 DPD beads: 1024 are hydrophobic (labeled by the letter A) and 1125 are hydrophilic (labeled by the letter B).
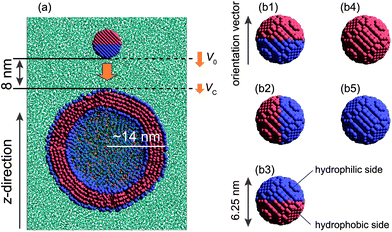 | ||
| Fig. 1 (a) Illustration of initial configuration of the nanoparticle/vesicle system. A view of the cross-section of the system, where cyan dots represent water. Also, V0 and VC represent the initial velocity and the contact velocity, respectively. (b1–b3) Three initial orientations of a model Janus nanoparticle with a hydrophobic side (pink) and a hydrophilic side (blue). (b4) A homogeneous nanoparticle with a hydrophobic surface, and (b5) a homogeneous nanoparticle with a hydrophilic surface. | ||
The vesicle consists of 3024 lipids. We adopt the lipid model of Yamamoto and Hyodo, which was applied to study spontaneous formation of the vesicle.32,33 The thickness of the membrane is about 3 nm, and the flip-flop rate is about 1.1 μs−1, consistent with the simulation results for a cholesterol flip-flop in membranes.34,35 In addition, the estimated bending modulus, κ ∼ 7.9 kBT, and the area per molecule Am ∼ 1.1 nm2 are in very good agreement with the experimental values for lipid membranes.36,37 Each lipid is composed of four DPD beads. One of them is a hydrophilic head group (labeled by H), and the others are hydrophobic tail groups (labeled by T). The water bead (or monomer) is labeled by the letter W. The interaction between any two beads in the solution is described by aAA = aBB = aHH = aTT = aWW = aBW = aHW = 25 kBT and aAB = aAH = aAW = aBT = aTW = 80 kBT.
We note that several improved membrane models have been proposed by other researchers. For example, Shillcock and Lipowsky constructed a membrane model to which the bending potential is applied to amphiphiles so that the membrane area stretch modulus and bending rigidity are consistent with experimental values for typical lipid bilayers.27,38 Meyer et al. proposed a DMPC bilayer model containing cholesterol for simulation using a hybrid dissipative particle dynamics/Monte Carlo method.39,40 This model assumes that the hydrophobic mismatch between the cholesterol and the DMPC hydrophobic tails is an important parameter for regulating the cholesterol–lipid interactions. Relative lengths of hydrophilic and hydrophobic sections in the cholesterol molecule are properly described in this model. Both models, however, require high computation cost due to the adoption of the bending potential and a lipid composed of many DPD beads. In the present study, we perform some hundreds of simulations to achieve a sensible statistical average. Therefore, a relatively simple model is employed here to lower the computation cost, and also to gain insights into the interaction between the vesicle-cell membrane and the nanoparticle, as well as into generic properties not directly related to a membrane model. Actually, we have confirmed that our representative results are qualitatively in agreement with that in the improved membrane model.
In our simulation, the total number of beads is 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156, among which 12
156, among which 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 beads are lipid molecules, 2149 beads are the nanoparticles, and the remaining beads are water. The volume of the simulation box is 37.5 × 37.5 × 50 nm3. The rS is set at 1.075 nm and the spring constant C at 100 kBT/rC2. The cutoff radius rC is based on the length unit in the DPD. The method by Ding et al. for scaling the length and time units is adopted,12,13 which takes into account the thickness of the bilayer and the diffusion constant of lipids. The noise parameter σ is set to 3.0 and the friction parameter γ is set to 4.5. The periodic boundary condition is applied in all three dimensions. All simulations are performed in the constant volume and constant temperature ensemble. We adopt the Lowe's scheme41 to integrate the equation of motion.
096 beads are lipid molecules, 2149 beads are the nanoparticles, and the remaining beads are water. The volume of the simulation box is 37.5 × 37.5 × 50 nm3. The rS is set at 1.075 nm and the spring constant C at 100 kBT/rC2. The cutoff radius rC is based on the length unit in the DPD. The method by Ding et al. for scaling the length and time units is adopted,12,13 which takes into account the thickness of the bilayer and the diffusion constant of lipids. The noise parameter σ is set to 3.0 and the friction parameter γ is set to 4.5. The periodic boundary condition is applied in all three dimensions. All simulations are performed in the constant volume and constant temperature ensemble. We adopt the Lowe's scheme41 to integrate the equation of motion.
A Mean radius of the vesicle
The mean radius of a vesicle Rv is computed through the following procedure: we focus on an innermost bead of a vesicle, which is a terminal tail bead of the lipid molecules. We calculate the distance between the center of mass of the vesicle and each innermost bead, and then average all the distances (d0). Next, we plot end-to-end distance distribution of lipid molecules (Fig. S1a†). The radius of the vesicle is defined by the sum of the maximum value (dee) in the end-to-end distribution and the averaged distance d0 (i.e., Rv = dee + d0). The maximum value in the lipid end-to-end distribution is little changed in the collision process. Hence, we view it as a constant (2.22 nm in this study).B Water beads inside the vesicle and pore size
To monitor time variation of water beads, we need to compute the number of water beads, Nw0, inside a vesicle at t = 0. Nw0 is computed by counting the number of water beads whose distance from the center of mass of the vesicle is less than Rv (Fig. S2a†).During the collision between the nanoparticle and vesicle, pores are created on the surface of the vesicle. The pore is more or less normal to the z-axis, since the nanoparticle always gets into a vesicle along the z-axis. First, the number profile of beads N(z) is computed by dividing the simulation box into thin slices. We consider only the vesicle and initial in-cell water beads. We plot N(z) with the center of mass of the vesicle at z = 0 in the horizontal axis (Fig. S2b†). Then, we count the number of water beads (Nout) that are located outside a vesicle. The number of water beads inside a vesicle, Nw, is defined as Nw0 − Nout. Note that Nw cannot be estimated by the distance from the center of mass of the vesicle because the vesicle can be highly deformed during the collision.
The size of the pore Apore on the vesicle surface is computed via the following procedure: the pore can occur either on the upper hemisphere (first-contact membrane layer) of the vesicle, and sometimes on the lower hemisphere with a high-speed nanoparticle. The nanoparticle always gets into the vesicle along the z-axis. When the pore is created on the surface, a local density near the pore edge should be lower. We compute the local density of the tail beads only. The edge of the pore is defined such that the local density at the edge is less than 70% of the average local density. Once all edge beads are identified, we can calculate the center of mass of these edge beads in the x–y plane. The distance between the center of mass and each edge bead is then averaged and is approximated as the average radius of the pore, Rpore. The size of the pore is estimated by Apore ∼ πRpore.2
Results and discussion
A Possible late-stage states
In the DPD simulations of a collision between a nanoparticle and a vesicle (Fig. 1a), we consider three different orientations for the Janus nanoparticle (Fig. 1b1–b3), two types of the homogeneous nanoparticle (Fig. 1b4 and b5), and forty different initial velocities V0 (0.257–1.626 m s−1) to examine the effect of the collision angle, chemical nature of the nanoparticle, and relative velocity. In all DPD simulations, the nanoparticle is initially located at a distance 8 nm from the vesicle (Fig. 1a). An external force is then applied to the nanoparticle in the negative z-direction. In the simulations involving the Janus nanoparticle, three late-stage states are observed (see Fig. 2a1–a3). When the initial velocity of the nanoparticle is relatively slow (V0 < ∼0.4 m s−1), the Janus nanoparticle bounces back to the solution (Fig. 2a1) after colliding with the vesicle. The vesicle behaves effectively like an elastic band.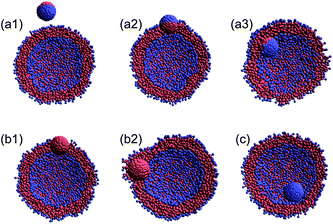 | ||
| Fig. 2 Illustration of various late-stage states for the nanoparticle/vesicle system (cross-section) after the collision. (a1) Detachment state, (a2) outer-surface (or outer insertion) state, (a3) inner-surface (or inner insertion) state, (b1) bi-interface state, (b2) interface embedded (or engulfing) state, and (c) capsule state. | ||
We name this late-stage state as the “detachment” state. The detachment state also arises when the incoming nanoparticle has an initial speed V0 > 1.5 m s−1. In the high speed limit, the Janus nanoparticle can fully penetrate the whole vesicle regardless of the orientation of the nanoparticle. Transient pores are formed when the nanoparticle passes through the vesicle. At the late stage, the spherical lipid membrane recovers. In this case, we still name the late-stage state as the “detachment” state.
The other two late-stage states arise for the initial velocity 0.4 < V0 < 1.5 m s−1, in which the Janus nanoparticle remains either fully or partially inside the vesicle. In both cases, the Janus nanoparticle always occupies a portion of the lipid membrane. If the hydrophobic side of the Janus nanoparticle is inside the lipid while its hydrophilic side is in contact with the outer water, we name this late-stage state as the “outer surface” (or outer-insertion12) state (Fig. 2a2). If the hydrophilic side is in contact with the in-cell water (enclosed by the lipid membrane), we name this state as the “inner surface” (or inner-insertion) state (Fig. 2a3). Which of the two late-stage states is selected depends on the initial velocity and initial orientation of the Janus nanoparticle.
For the system involving a homogeneous nanoparticle, however, four late-stage states are observed after the collision. One of the four is still the detachment state for the initial velocity V0 being either very slow or very fast. For the system with the hydrophobic homogeneous nanoparticle, two late-stage states are named as “bi-interface” (Fig. 2b1) and “interface embedded” (or engulfing12) (Fig. 2b2). The bi-interface state arises for 0.2 < V0 < 0.75 m s−1 or 1.08 < V0 < 1.47 m s−1. In this state, the nanoparticle settles in the middle of the lipid membrane with its partial surface exposing to the outer and in-cell water. On the other hand, the interface-embedded state arises for 0.75 < V0 < 1.08 m s−1, for which the nanoparticle enters into the in-cell water enclosed by the lipid membrane and then moves randomly within the vesicle. Eventually, the nanoparticle is fully embedded (engulfed) by the lipid membrane, a likely metastable state for the nanoparticle. For the system involving the homogeneous hydrophilic nanoparticle, only two late-stage states are observed, i.e., either the “capsule” state (Fig. 2c) for 0.7 < V0 < 0.94 m s−1 or the detachment state otherwise.
B Dynamic behavior and the pathway towards the late-stage state
Next, we study the effect of the initial velocity (B1–B3), surface chemistry (including homogeneous hydrophobic, homogeneous hydrophilic and Janus nanoparticles) (B4), and the orientation of the Janus nanoparticle (B5) on the dynamic behavior and the pathway towards various late-stage states after the collision.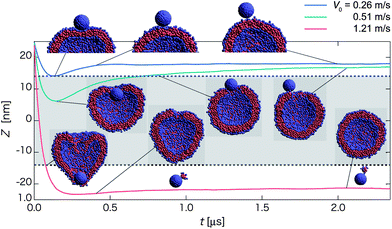 | ||
| Fig. 3 Time-dependent properties and cross-section snapshots (insets) after the collision towards the detachment state for the homogeneous hydrophilic nanoparticle with different initial velocities: V0 = 0.26 m s−1 (blue curve), 0.51 m s−1 (green curve), and 1.21 m s−1 (red curve). The normal axis shows Z = zNP − zv, where zNP and zv represent the z-positions of the nanoparticle and the vesicle center, respectively. The mean radius of the vesicle is denoted by dashed lines, and the gray-shaded region refers to the in-cell water region of the vesicle. (Each curve is plotted based on averaged data over twenty independent simulations.) | ||
For 0.4 < V0 < 0.7 m s−1, the nanoparticle undergoes a different pathway towards the detachment state. The nanoparticle first intrudes partially into the inner water region of the vesicle (see green curve at t ∼ 0.2 μs in Fig. 3), and is then gradually pushed out of the vesicle. A pore is left on the surface of the vesicle after the nanoparticle is expelled from the vesicle (Movie S2†). This expulsion pathway is also observed for 0.98 < V0 < 1.22 m s−1. For the latter, the nanoparticle passes through the lipid membrane of the vesicle and the inner water region, and then penetrates partially to the opposing lipid layer of the vesicle. Eventually, the nanoparticle is pushed out of the vesicle, and leaves a pore on the opposing lipid layer.
For the relatively high initial velocity V0 > 1.22 m s−1 (see red curve in Fig. 3), the nanoparticle can fully penetrate through both the first and the opposing lipid layers of the vesicle and leave behind a highly deformed vesicle within a short period (t ∼ 0.15 μs). Eventually, the spherical membrane of the vesicle is recovered. A tiny micelle is occasionally taken out from the vesicle after the passage of the nanoparticle through the vesicle (see the snapshot at t ∼ 2.1 μs and Movie S3†). This pathway to the detachment state is labeled as penetration. Note that the orientation of the nanoparticle is fairly irregular along all three pathways.
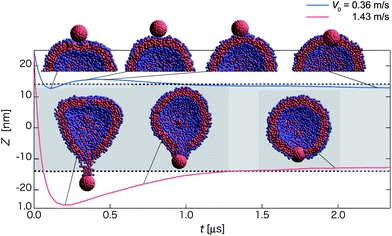 | ||
| Fig. 4 Time-dependent properties and cross-section snapshots (insets) after the collision towards the bi-interface state for the homogeneous hydrophobic nanoparticle with different initial velocities: V0 = 0.36 m s−1 (blue curve), and 1.43 m s−1 (red curve). The normal axis shows Z = zNP − zv. The mean radius of the vesicle is denoted by dashed lines and the gray-shaded region refers to the in-cell water region of the vesicle. (Each curve is plotted based on averaged data over twenty independent simulations.) | ||
Red curves in Fig. 4 describe another new pathway for 1.18 < V0 < 1.48 m s−1 (named as the retraction pathway) towards the bi-interface state. In this pathway, the nanoparticle first penetrates through the first contact lipid layer, then passes through the in-cell water region and then almost penetrates through the opposing lipid layer. However, some lipid molecules can be adsorbed on the surface of the nanoparticle after the contact with the opposing lipid layer (see the snapshot at t ∼ 0.20 and 0.73 μs). These adsorbed lipid molecules effectively act as a spring that can drag the nanoparticle back to the middle of membrane (Movie S5†). A similar pathway is observed for 0.48 < V0 < 0.73 m s−1 except that the nanoparticle is embedded in the first contact lipid layer. For V0 > 1.48 m s−1, the nanoparticle along with adsorbed lipid molecules can break away from the vesicle and reach the detachment state.
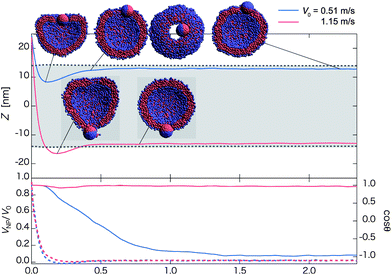 | ||
Fig. 5 Time-dependent properties and cross-section (and top-view in negative z-direction) snapshots (insets) after the collision towards the outer-surface state for the Janus nanoparticle with different initial velocities: V0 = 0.51 m s−1 (blue curve) and 1.15 m s−1 (red curve). The hydrophilic side of the Janus nanoparticle faces the vesicle initially (Fig. 1b1). The upper panel shows time-dependent Z = zNP − zv. The mean radius of the vesicle is denoted by dashed lines, and the gray-shaded region refers to the in-cell water region of the vesicle. The velocity ratio VNP/V0 (dashed lines along with the left axis) and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (solid lines along with right axis) are shown in the lower panel. Here, VNP is velocity of the nanoparticle in the z-direction, V0 is initial velocity in the z-direction, and θ is the angle between an orientation vector of the nanoparticle and the z-axis. (Each curve is plotted based on averaged data over twenty independent simulations.) θ (solid lines along with right axis) are shown in the lower panel. Here, VNP is velocity of the nanoparticle in the z-direction, V0 is initial velocity in the z-direction, and θ is the angle between an orientation vector of the nanoparticle and the z-axis. (Each curve is plotted based on averaged data over twenty independent simulations.) | ||
For 1.04 < V0 < 1.45 m s−1, the normal pathway is observed in which the Janus nanoparticle does not fully turn around during the collision process. As an example, for V0 = 1.15 m s−1, the nanoparticle penetrates the first contact lipid layer and almost penetrates the opposing lipid layer. But the nanoparticle is pulled back by lipid molecules adsorbed on the surface of the hydrophobic side (Movie S7†) as in the case of the homogeneous hydrophobic nanoparticle. The orientation vector of the Janus nanoparticle exhibits little change as cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is nearly a constant 1.0 (see red solid curve in the lower panel of Fig. 5).
θ is nearly a constant 1.0 (see red solid curve in the lower panel of Fig. 5).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ approaches to 0 in all cases (the lower panel in Fig. 6).
θ approaches to 0 in all cases (the lower panel in Fig. 6).
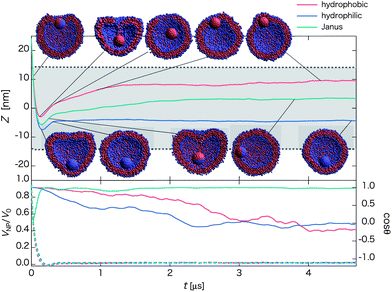 | ||
Fig. 6 Time-dependent properties and cross-section snapshots (insets) after the collision and for nanoparticles with different surface chemical nature: hydrophobic, hydrophilic, and Janus (with initial orientation of Fig. 1b2), and with the same initial velocity V0 = 0.81 m s−1. The upper panel shows time-dependent Z = zNP − zv. The mean radius of the vesicle is denoted by dashed lines, and the gray-shaded region refers to the in-cell water region of the vesicle. The velocity ratio VNP/V0 (dashed lines with the left axis) and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (solid lines with right axis) are shown in the lower panel. (Each curve is plotted based on averaged data over twenty independent simulations.) For a homogeneous nanoparticle, we simply define the orientation vector as a line from the bottom pole to the top pole (in negative z-direction) at the particle's initial position. Once it is defined, the vector is fixed with the nanoparticle. θ (solid lines with right axis) are shown in the lower panel. (Each curve is plotted based on averaged data over twenty independent simulations.) For a homogeneous nanoparticle, we simply define the orientation vector as a line from the bottom pole to the top pole (in negative z-direction) at the particle's initial position. Once it is defined, the vector is fixed with the nanoparticle. | ||
For the hydrophobic nanoparticle, a transient state of “lipid-spring” occurs at t ∼ 0.2 μs due to the adsorption of lipid molecules on the surface of the nanoparticle. This lipid-spring breaks down when overstretched beyond 6.7 nm (a distance depending on the solubility of lipid molecules, curvature of the vesicle, and the surface area of nanoparticle). Thereafter, the nanoparticle fluctuates within the vesicle for relatively long period of time (∼5 μs for the longest time). At a later stage, the hydrophobic nanoparticle arrives at the interface embedded state (Movie S8†) as the nanoparticle dislikes to be surrounded by water. The location in the membrane for the nanoparticle is more likely near the first-contact region because water molecules tend to escape from the transient pore in the first-contact region after the collision.
For the hydrophilic nanoparticle, it can reach deeply to the opposing lipid layer after penetrating through the first lipid layer, followed by recovery of the spherical shape of the vesicle while Z increases slightly (t ∼ 0.3 μs). Thereafter, the nanoparticle continues to be in contact with the membrane from inside (see the snapshot at t ∼ 4.5 μs and Movie S9†) and maintains this state for more than 20 μs in the simulation.
For the Janus nanoparticle with the initial orientation as shown in Fig. 1b2, the orientation of the Janus nanoparticle starts to change right after the collision (t ∼ 0.04 μs) due to the adsorption of lipid molecules on the hydrophobic side. Then the nanoparticle self-rotates 90 degrees as a result of the transient effect of the lipid spring, followed by a contact between the hydrophilic side of the nanoparticle and the membrane from inside (t ∼ 0.25 μs). After the breakage of the lipid-spring, the nanoparticle moves around within the vesicle and eventually reaches the inner surface state with the hydrophobic side embedded in the membrane (Movie S10†). These results indicate that the detachment state is only metastable. Given an extremely long time, the detachment state should be transformed into the true stable state, namely, the outer surface state for the Janus nanoparticle, and the bi-interface state for the hydrophobic nanoparticle.
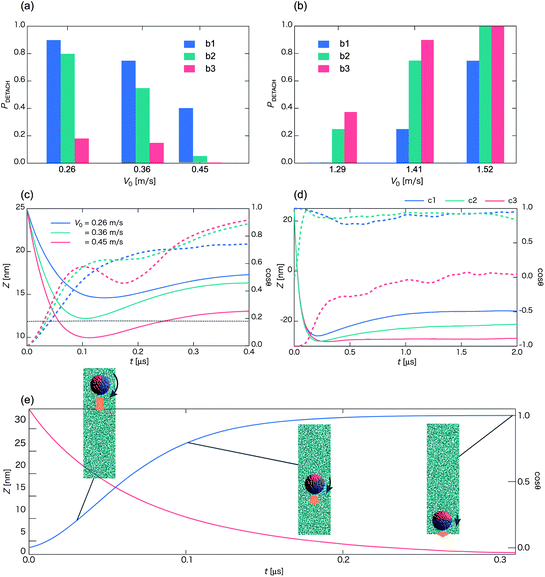 | ||
Fig. 7 Probability PDETACH for the occurrence of the detachment state as a function of the initial velocity V0 with the initial orientation of Fig. 1b1 (blue bar), b2 (green bar), and b3 (red bar), in a low-V0 region (a) and a high-V0 region (b). Each bar represents an average over more than twenty independent simulations. (c) Time sequences of Z (solid lines along with left axis) and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (dashed lines along with right axis) in the low-V0 region, e.g., V0 = 0.26 m s−1 (blue curve), 0.36 m s−1 (green curve), and 0.45 m s−1 (red curve), for the initial orientation of Fig. 1b2. The black dashed line denotes the location of the middle of the lipid membrane. (d) Time sequences of Z (solid lines along with left axis) and cos θ (dashed lines along with right axis) in the low-V0 region, e.g., V0 = 0.26 m s−1 (blue curve), 0.36 m s−1 (green curve), and 0.45 m s−1 (red curve), for the initial orientation of Fig. 1b2. The black dashed line denotes the location of the middle of the lipid membrane. (d) Time sequences of Z (solid lines along with left axis) and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ (dashed lines along with right axis) for V0 = 1.41 m s−1. Blue, green, and red curves represent the initial orientation of the Janus particle of Fig. 1b1–b3, respectively. (e) Self-rotation of the Janus nanoparticle (initial orientation of Fig. 1b2) in water (no vesicle). Time sequences of Z (red line along with left axis) and cos ϕ (dashed lines along with right axis) for V0 = 1.41 m s−1. Blue, green, and red curves represent the initial orientation of the Janus particle of Fig. 1b1–b3, respectively. (e) Self-rotation of the Janus nanoparticle (initial orientation of Fig. 1b2) in water (no vesicle). Time sequences of Z (red line along with left axis) and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (blue line along with right axis) for V0 = 0.57 m s−1. (Each curve is plotted based on averaged data over twenty independent simulations.) θ (blue line along with right axis) for V0 = 0.57 m s−1. (Each curve is plotted based on averaged data over twenty independent simulations.) | ||
In the low-V0 region PDETACH decreases with the increase of V0 in all cases (Fig. 7a). However, values of PDETACH are quite different, depending on the initial orientation of the Janus nanoparticle. If the hydrophilic side faces the vesicle (Fig. 1b1), this side is rolled upward (positive z-axis direction) by the hydrophobic group of lipids as the nanoparticle gets into the middle of the lipid membrane. On the other hand, if the hydrophobic side faces the vesicle (Fig. 1b3), this side interacts favorably with the vesicle when the nanoparticle gets into the middle of the lipid membrane. So the corresponding values of PDETACH are the smallest. In this case, the outer-surface state is most likely observed with the initial orientation of Fig. 1b3. Values of PDETACH for the initial orientation of Fig. 1b2 are close to those of Fig. 1b1 because a portion of the hydrophilic side of the Janus nanoparticle contacts the vesicle first. In fact, the hydrophilic side of the Janus nanoparticle tends to contact the vesicle first provided the nanoparticle can travel sufficiently long distance. The reason is that when the Janus nanoparticle is subjected to a velocity, the orientation vector shown in Fig. 1b1 always tends to align against the velocity direction because in this way, the hydrophilic side would be in contact with the region with higher local water density. This spontaneous self-rotation of the Janus nanoparticle towards a specific orientation (Movie S11†) when traveling in water is consistent with the experimental observation.42
As V0 increases to 0.45 m s−1, PDETACH decreases dramatically for the nanoparticle with the initial orientation of Fig. 1b2. In this case, the center of mass of the nanoparticle crosses the middle line of the membrane (see Fig. 7c). As such, the hydrophobic side of the nanoparticle interacts favorably with the membrane, and thus the probability increases for the outer-surface state.
In the high-V0 region, PDETACH always increases with the increase of V0 (Fig. 7b). Nevertheless, PDETACH for the initial orientation of Fig. 1b1 is evidently lower than that of Fig. 1b3. In the latter case, the hydrophilic side of the Janus nanoparticle faces the vesicle. The pullback force arises after the collision due to the adsorption of lipid molecules on the hydrophobic side like shown in Fig. 4 and 5. In the case of Fig. 1b1, the hydrophilic side faces the vesicle. Lipid molecules do not adsorb on the surface of the Janus nanoparticle after the collision, and as such, the nanoparticle is more likely to penetrate through the vesicle with no lipid-string attached. PDETACH for the initial orientation of Fig. 1b2 is close to that of Fig. 1b3 in the high-V0 region although behavior of the Janus nanoparticle is similar to that in the case of Fig. 1b1, that is, the formation and the breakage of the lipid-spring are observed (see Fig. 7d and Movie S12†). Why do values of PDETACH in the case of Fig. 1b2 become close to those of Fig. 1b3? Again, this is due to self-rotation of the Janus nanoparticle while passing through the vesicle. As such, the lipid-spring is easily broken.
With the initial orientations of b1 and b3 for the Janus nanoparticle, the pathway to the outer-surface and inner-surface states appears anti-symmetrical over each other due to the exact opposite initial orientation vector for the nanoparticles. Next, on the phase boundaries between the detachment state and the outer-surface state for the Janus nanoparticle, the boundaries are shifted towards the higher-V0 region from b3 to b2 and then to b1. Furthermore, that boundary for b1 appears to be overlapping with the boundary between rebound and expulsion pathways for b5, while that the boundary for b3 appears to be overlapping with the boundary between rebound and drag-in for b4. These results suggest that the chemical nature of the incoming side of the Janus nanoparticle plays an important role in the late-stage state when V0 is relatively low (<∼0.5 m s−1).
On the other hand, when V0 is relatively high (>∼1.2 m s−1), there is no obvious correction between the state-boundary for the Janus nanoparticle and the pathway-boundary for the homogeneous nanoparticle due to complex interactions between the Janus nanoparticle with lipid molecules while penetrating through the vesicle. Nevertheless, boundaries between the outer-surface state and the detachment state are still shifted to the higher V0 region from b3 to b2 and to b1, due to the pull-back force by the lipid-spring. Hence, the chemical nature of the rear side of the Janus nanoparticle plays a moderate role when V0 is relatively high.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) are examined. We find that the vesicle is broken for
) are examined. We find that the vesicle is broken for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 21.3 μs−1 beyond which the lipids cannot assemble into a full structure such as a vesicle. We define τ = 1/
> 21.3 μs−1 beyond which the lipids cannot assemble into a full structure such as a vesicle. We define τ = 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 46.9 ns as the characteristic time of this vesicle model.
= 46.9 ns as the characteristic time of this vesicle model.
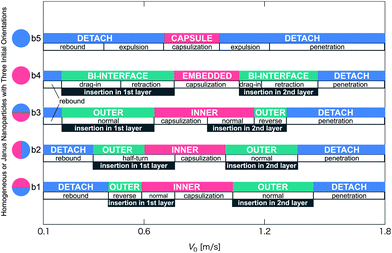 | ||
| Fig. 8 Schematic phase diagram of the late-stage states and pathways for the collision process between a vesicle and a nanoparticle. The vertical axis denotes various initial orientations of the Janus nanoparticle (Fig. 1b1–b3), or homogeneous hydrophobic nanoparticle (Fig. 1b4), or homogeneous hydrophilic nanoparticle (Fig. 1b5). V0 is the initial velocity of the nanoparticle in the z-direction. Short notation for three late-stage states: DETACH: the detachment state (blue); INNER: the inner-surface state (red) and OUTER: the outer-surface state (green). | ||
In addition, a passing time (τp) is defined as the vesicle radius divided by the contact velocity. Note that the contact velocity means the velocity at the time nanoparticle just starts to interact with a vesicle (see Fig. 1a), which is about 30 to 80% of V0, independent of the orientation and the chemical nature of the nanoparticle surface. Now, the vesicle radius, Rv, is about 14 nm. The range of contact velocities is 0.08 < Vc < 1.28 m s−1. Therefore, the range of passing time is 10.9 < τp < 175 ns. Based on the range of passing time, the nanoparticle can penetrate through the vesicle membrane when τp < τ. Otherwise, a nanoparticle bounces back to the water due to low Vc. In our simulation, τp is comparable to τ for V0 ∼ 0.4 m s−1. In Fig. 8, V0 ∼ 0.4 m s−1 corresponds to a boundary between the rebound and other pathways. For orientations b3 and b4, the boundary is located as low as V0 ∼ 0.2 m s−1 in both cases. This is because other pathways arise due to the hydrophobic attraction, allowing the low V0 at which the membrane does not break down.
In addition, we analyze the flip-flop rate for some representative pathways. In the expulsion pathway and the capsulization pathway, the flip-flop rate is ∼150 μs−1 and 115 μs−1, respectively. Besides, the flip-flop rate in the penetration pathway is ∼249 μs−1. Note that each flip-flop rate is based on averaged data over four independent simulations. These values are 100 times greater than those of without collision (1.1 μs−1).
A reason is the reorganization of the membrane. The disordering alignment of lipids located near the pore is caused by the passing of the nanoparticle. Since the state with a pore on the opposing lipid layer is unstable, a large-scale exchange reallocation arises. Actually, in about 2 μs until a pore is closed, the vesicle becomes stable and more than 90% of flip-flop is observed. The reason why the value in the penetration pathway is higher than others is the presence of two pores. Another reason is the increase of the kinetic energy in the vesicle. By the collision, the kinetic energy that a nanoparticle has is passed to the vesicle. Here, the local temperature increases by the delivery of the kinetic energy. Accordingly, the flip-flop rate increases. The flip-flop rate in the rebound pathway is 8.1 μs−1.
C Analysis of discharge of water from opening pores on the surface of the vesicle
Lastly, we analyze time-dependence of the pore size Apore on the lipid membrane, the number of water Nw inside the vesicle, and the mean radius of the vesicle Rv after the collision between the nanoparticle and the vesicle to gain insight into the discharging mechanism of the vesicle. Fig. 9a shows time dependent Apore, Nw, and Rv for a representative rebound pathway at V0 = 0.26 m s−1, an expulsion pathway at V0 = 0.51 m s−1, and a capsulization pathway at V0 = 0.81 m s−1 for the collision between a homogeneous hydrophilic nanoparticle and a vesicle. Because the relative velocities are relatively low, the nanoparticle penetrates the lipid membrane only once at most. As expected, in the rebound pathway, Rv changes only slightly at the moment of the collision, while Nw and Apore exhibit no change. In either the expulsion or the capsulization pathway, the peak values of Apore and Rv appear at t ∼ 0.1 μs. Thereafter, Rv gradually shrinks during the recovery of the lipid membrane. However, Apore exhibits an increase up to t ∼ 1.2 μs, a trend opposite to the decrease of Rv during this time period. The seemingly conflicting trends for Rv and Apore is mainly due to the discharge of in-cell water beads outside, evidenced by the faster reduction of Nw during this period. Meanwhile, the pressure inside the vesicle also decreases due to the discharge of water beads. Interestingly, although V0 in the case of the capsulization is higher, the corresponding pore size Apore is smaller than that of the expulsion pathway for a period of time while the pore shrinks. In the expulsion pathway, the nanoparticle tends to be located near the pore during the expulsion, thereby obstructing the reconstruction of the vesicle. The nanoparticle eventually is expelled from the vesicle as the in-cell water beads get out of the vesicle through the pore (Fig. 9b and Movie S13†). In the capsulization pathway, the nanoparticle reaches the opposing layer of the vesicle. Hence, the vesicle simply repairs itself with the reduction of the size of the pore Apore (Fig. 9c and Movie S14†). Here, the reduction of in-cell water beads Nw is faster initially but when the vesicle is fully recovered, the expulsion pathway looses more in-cell water molecules than the capsulization pathway (Fig. 9a).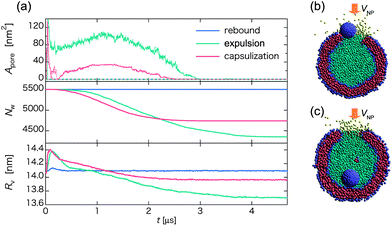 | ||
| Fig. 9 (a) Time-dependent pore size Apore (upper), the number of water beads Nw inside the vesicle (middle), and the average radius of the vesicle Rv (lower) for three different pathways of the collision between a homogeneous hydrophilic nanoparticle and a vesicle. Blue, green, and red curves represent the pathway of rebound, expulsion, and capsulization, respectively. In the upper panel, Apore in the upper hemisphere of the vesicle is illustrated by solid lines, while in the lower hemisphere is illustrated by dashed lines. (b) and (c) Snapshots at t ∼ 0.75 μs in the expulsion and the capsulization pathway, respectively, where water beads inside the vesicle are in cyan, while those outside in yellow. | ||
Next, we analyze the effect of the initial orientation of the Janus nanoparticle on the time-dependence of Apore, Nw and Rv (Fig. 10). Here, the Janus nanoparticle has a relatively low initial velocity V0 = 0.47 m s−1. In all three collision processes, the late-stage state is the outer-surface state but the pathway is different, i.e., reverse for b1, half-turn for b2, and normal for b3. In the latter case, there is no loss of in-cell water beads to outside, and Nw is maintained as a constant (see red curve in Fig. 10b). Unlike the homogeneous nanoparticle, Apore exhibits notable fluctuation around 40 nm2, regardless of the initial orientation. The pore is actually created by the embedded nanoparticle in the outer surface of the vesicle. Hence, Apore is about the same as the cross-sectional area of the nanoparticle. In the cases of b1 and b2, water beads can be released to outside of the vesicle after the collision (t ∼ 0.4 μs). The Janus nanoparticle first arrives at the middle of the membrane, and then turns around to reach the outer-surface state. During the rotation, water beads pass through the membrane (Fig. 10b). Eventually, water outflow is blocked by the cap of the nanoparticle (see Fig. 10c and Movie S14†). The amount of discharge of water beads in b1 is greater than that in b2 since the Janus nanoparticle in b1 rotates more angles than in b2 to reach the late-stage state. These results suggest that water discharge may be controlled by imparting the nanoparticle with tailored chemical surfaces and with different initial orientations.
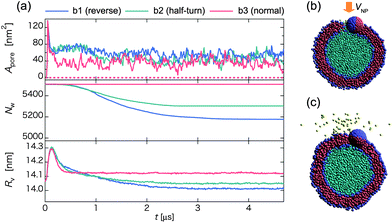 | ||
| Fig. 10 (a) Time-dependent pore size Apore (upper), the number of water beads Nw inside the vesicle (middle), and the average radius of the vesicle Rv (lower) for three different initial orientations of the Janus nanoparticle in the collision process. Blue, green, and red curves represent initial orientations b1, b2, and b3 shown in Fig. 1, respectively. Snapshots in the middle of the reverse pathway at (b) t ∼ 0.4 μs and (c) 1.4 μs. | ||
Fig. 11 is the same as Fig. 10 but for the Janus nanoparticle with a relatively higher initial velocity V0 = 1.44 m s−1. All three collision processes undergo the penetration pathway so that the pore is opened not only in the first-contact layer of the membrane, but also in the opposing layer. A large number of water beads are discharged from the pore created during the extrusion of the nanoparticle in a short time t < 0.08 μs. A weak fluctuation of Rv is observed for t < 0.6 μs during a shrinkage process, a result consistent with experiments.43–45 In both cases of b1 and b2, the hydrophobic side of the Janus nanoparticle initially faces away from the vesicle. When the nanoparticle passes through the first-contact layer, the lipid membrane is stretched inward to the vesicle. When the nanoparticle passes through the opposing layer, the lipid membrane is stretched outward, and some lipid molecules are taken out to form a micelle. Due to the loss of lipid molecules, the pore is harder to close up. Consequently, more water beads leak through the pore in the opposing layer (see Fig. 11b and Movies S16 and S17†). In the case of b3, the pore in the opposing layer closes within t ∼ 1.8 μs. Since the formation of lipid-spring does not occur, most water beads are discharged through the pore in the first-contact layer (see Fig. 11c and Movie S18†).
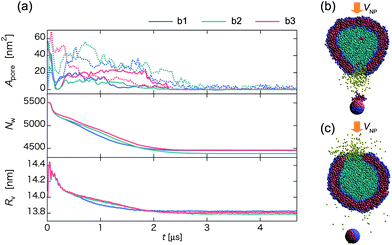 | ||
| Fig. 11 (a) Time-dependent pore size Apore (upper), the number of water beads Nw inside the vesicle (middle), and the average radius of the vesicle Rv (lower) for three initial orientations of the Janus nanoparticle in the collision process. Blue, green, and red curves represent orientations b1, b2, and b3, respectively. Snapshots at (b) t ∼ 0.31 μs for b1, and (c) t ∼ 1.29 μs for b3. | ||
Conclusion
In conclusion, we have performed systematic DPD simulations to investigate translocation dynamics, in-cell water discharge, and the late-stage morphologies of the vesicle/nanoparticle system after the collision between a nanoparticle and a vesicle. Regarding morphologies of the vesicle/nanoparticle system, we have observed three late-stage states for the Janus nanoparticle, and four late-stage states for the homogeneous nanoparticle. Selection of these states and the associated pathway depends on the initial velocity V0, surface chemistry of the nanoparticle, and initial orientation of the Janus nanoparticle. To settle in the stable position, spontaneous rotation and translocation of the nanoparticle are required. For V0 < 0.5 m s−1, the chemical nature of the front surface of the Janus nanoparticle plays an important role in the selection of the late-stage state because it is the front surface of the nanoparticle that interacts with the vesicle when the two species approach each other. In most of these cases, the nanoparticle is bounced back to the outer water due to resilience of the membrane. For V0 > 1.2 m s−1, some lipid molecules can be adsorbed on the surface of the nanoparticle concomitantly with the nanoparticle passing through the opposing lipid layer. Therefore, the chemical nature of the rear surface of the Janus nanoparticle becomes increasingly important. If the chemical nature of the rear surface of the Janus nanoparticle is hydrophobic, the nanoparticle can intrude into the membrane for a wide range of V0 due to the pull-back force by the adsorbed lipids on the surface.We compute time-evolution of the size of the pore on the vesicle surface, the number of water beads inside a vesicle, and the mean radius of a vesicle in several pathways, and we also study the associated discharging mechanism of in-cell water beads from the vesicle. In essence, the nanoparticle can introduce a controllable release of the in-cell object. The targeted amount of discharge of the object may be achieved by changing nanoparticle's properties (the surface chemistry, the orientation, and the initial velocity). We adopted water beads as the in-cell object, and showed controllable release of them but roughly. For the initial velocity (V0 ∼ 0.5 m s−1) of the homogeneous hydrophilic nanoparticle, the nanoparticle first intrudes partially into the inner water region of the vesicle, and is then gradually pushed out of the vesicle. A pore is made on the surface of the vesicle, and the in-cell water discharges during this sequence. As a result, the release of in-cell water beads outside is more substantial than other pathways, for example the nanoparticle penetrates the vesicle, although the initial velocity is slower, i.e. the low-cost input energy to the nanoparticle. Water discharge is more substantial when the initial orientation of the Janus nanoparticle is opposite to the direction of V0. When the Janus nanoparticle has a relatively low initial velocity (V0 ∼ 0.47 m s−1), it rotates to achieve a stable state after collision with the vesicle. Each rotational angle is different depending on the initial orientation of the Janus nanoparticle, and water discharge takes place during the rotation. This result suggests that water discharge from the vesicle may be controlled more precisely by tailoring the chemical pattern on the nanoparticle surface and by changing the initial orientation of the Janus nanoparticle. Note that it is necessary to consider spontaneous self-rotation of the Janus nanoparticle due to the local water density difference. Our results can provide a guide to design the interaction between the nanoparticle and the vesicle for the control of the discharge of the in-cell object in the drug or gene delivery, or nanoscale cargo carriers.
Acknowledgements
N.A. was supported by JSPS KAKENHI Grant number 25870229. K.Y. was supported by JSPS KAKENHI Grant number 24360084. X.C.Z was supported by grants from the NSF (CBET-1066947 and CHE-1306326), ARL (W911NF1020099) and the Nebraska Research Initiative.References
- L. M. Mashburn and M. Whiteley, Membrane vesicles traffic signals and facilitate group activities in a prokaryote, Nature, 2005, 437, 422–425 CrossRef CAS.
- J. R. House, R. A. L. Jones, G. Battaglia, R. E. Ducker, G. J. Leggett and A. J. Ryan, Templated formation of giant polymer vesicles with controlled size distributions, Nat. Mater., 2009, 8, 507–511 CrossRef.
- V. Percec, D. A. Wilson, P. Leowanawat, C. J. Wilson, A. D. Hughes, M. S. Kaucher, D. A. Hammer, D. H. Levine, A. J. Kim, F. S. Bates, K. P. Davis, T. P. Lodge, M. L. Klein, R. H. DeVane, E. Aqad, B. B. Rosen, A. O. Argintaru, M. J. Sienkowska, K. Rissanen, S. Nummelin and J. Ropponen, Self-assembly of Janus dendrimers into uniform dendrimersomes and other complex architectures, Science, 2010, 328, 1009–1014 CrossRef CAS.
- I. Gözen, P. Dommersnes, I. Czolkos, A. Jesorka, T. Lobovkina and O. Orwar, Fractal avalanche ruptures in biological membranes, Nat. Mater., 2010, 9, 908–912 CrossRef.
- P. A. Suci, S. Kang, M. Young and T. A. Douglas, Streptavidin-protein cage Janus particle for polarized targeting and modular functionalization, J. Am. Chem. Soc., 2009, 131, 9164–9165 CrossRef CAS.
- Q. Chen, S. C. Bae and S. Granick, Directed self-assembly of a colloidal Kagome lattice, Nature, 2011, 469, 381–384 CrossRef CAS.
- Q. Chen, E. Diesel, J. K. Whitmer, S. C. Bae, E. Luijten and S. Granick, Triblock colloids for directed self-assembly, J. Am. Chem. Soc., 2011, 133, 7725–7727 CrossRef CAS.
- M. Lattuada and T. A. Hatton, Synthesis, properties and applications of Janus nanoparticles, Nano Today, 2011, 6, 286–308 CrossRef CAS.
- M. Huang, Z. Li and H. Guo, The effect of Janus nanospheres on the phase separation of immiscible polymer blends via dissipative particle dynamics simulations, Soft Matter, 2012, 8, 2834–2845 Search PubMed.
- A. Alexeev, W. E. Uspal and A. C. Balazs, Harnessing Janus nanoparticles to create controllable pores in membranes, ACS Nano, 2008, 2, 1117–1122 CrossRef CAS.
- T. Yue and X. Zhang, Molecular understanding of receptor-mediated membrane responses to ligand-coated nanoparticles, Soft Matter, 2011, 7, 9104–9112 RSC.
- H.-M. Ding and Y.-Q. Ma, Interactions between Janus particles and membranes, Nanoscale, 2012, 4, 1116–1122 RSC.
- H.-M. Ding, W.-D. Tian and Y.-Q. Ma, Designing nanoparticle translocation through membranes by computer simulations, ACS Nano, 2012, 6, 1230–1238 CrossRef CAS.
- K. Yang and Y.-Q. Ma, Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer, Nat. Nanotechnol., 2010, 5, 570–583 CrossRef.
- Y. Li, X. Li, Z. Li and H. Gao, Surface-structure-regulated penetration of nanoparticles across a cell membrane, Nanoscale, 2012, 4, 3768–3775 RSC.
- M. D. Tomasini and M. S. Tomassone, Dissipative particle dynamics simulation of poly(ethylene oxide)–poly(ethyl ethylene) block copolymer properties for enhancement of cell membrane rupture under stress, Chem. Eng. Sci., 2012, 71, 400–408 CrossRef CAS.
- Y. Li, T. Yue, K. Yang and X. Zhang, Molecular modeling of the relationship between nanoparticle shape anisotropy and endocytosis kinetics, Biomaterials, 2012, 33, 4965–4973 CrossRef CAS.
- H. M. Ding and Y. Q. Ma, Role of physicochemical properties of coating ligands in receptor-mediated endocytosis of nanoparticles, Biomaterials, 2012, 33, 5798–5802 CrossRef CAS.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Español and P. Warren, Statistical mechanics of dissipative particle dynamics, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- D. I. Dimitrov, A. Milchev and K. Binder, Capillary rise in nanopores: molecular dynamics evidence for the Lucas-Washburn equation, Phys. Rev. Lett., 2007, 99, 054501 CrossRef CAS.
- J. Cao and A. E. Likhtman, Shear banding in molecular dynamics of polymer melts, Phys. Rev. Lett., 2012, 108, 028302 CrossRef.
- I. C. Pons-Siepermann and S. C. Glotzer, Design of patchy particles using quaternary self-assembled monolayers, ACS Nano, 2012, 6, 3919–3924 CrossRef CAS.
- N. Arai, K. Yasuoka and Y. Masubuchi, Spontaneous self-assembly process for threadlike micelles, J. Chem. Phys., 2007, 126, 244905 CrossRef.
- N. Arai, K. Yasuoka and X. C. Zeng, Self-assembly of surfactants and polymorphic transition in nanotubes, J. Am. Chem. Soc., 2008, 130, 7916–7920 CrossRef CAS.
- S. H. Min, C. Lee and J. Jang, Dissipative particle dynamics modeling of a graphene nanosheet and its self-assembly with surfactant molecules, Soft Matter, 2012, 8, 8735–8742 RSC.
- J. C. Shillcock and R. Lipowsky, Tension-induced fusion of bilayer membranes and vesicles, Nat. Mater., 2005, 4, 225–228 CrossRef CAS.
- A. Grafmüller, J. Shillcock and R. Pipowsky, Pathway of membrane fusion with two tension-dependent energy barriers, Phys. Rev. Lett., 2007, 98, 218101 CrossRef.
- H. C. A. Andersen, “Velocity” version of the shake algorithm for molecular dynamics calculations, J. Comput. Phys., 1983, 52, 24–34 CrossRef CAS.
- J. H. Warner, A. Hoshino, K. Yamamoto and R. D. Tilley, Water-soluble photoluminescent silicon quantum dots, Angew. Chem., Int. Ed., 2005, 44, 4550–4554 CrossRef CAS.
- K. Ma, H. Sai and U. Wiesner, Ultrasmall sub-10 nm near-infrared fluorescent mesoporous silica nanoparticles, J. Am. Chem. Soc., 2012, 134, 13180–13183 CrossRef CAS.
- S. Yamamoto and S. Hyodo, Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules, J. Chem. Phys., 2002, 116, 5842–5848 CrossRef CAS.
- S. Yamamoto and S. Hyodo, Budding and fission dynamics of two-component vesicles, J. Chem. Phys., 2003, 118, 7937–7942 CrossRef CAS.
- S. J. Marrink, A. H. de Vries, T. A. Harroun, J. Katsaras and S. R. Wassall, Cholesterol shows preference for the interior of Polyunsaturated lipid membranes, J. Am. Chem. Soc., 2008, 130, 10–11 CrossRef CAS.
- W. F. D. Bennett, J. L. MacCallum, M. J. Hinner, S. J. Marrink and D. P. Tieleman, Molecular view of cholesterol flip-flop and chemical potential in different membrane environments, J. Am. Chem. Soc., 2009, 131, 12714–12720 CrossRef CAS.
- R. Lipowsky and E. Sackmann, Structure and Dynamics of Membranes, Elsevier, Amsterdam, 1995 Search PubMed.
- A. Pinazo, L. Pérez, M. R. Infante and R. Pons, Unconverntional vesicle-to-ribbon transition behavior of diacyl glycerol amino acid based surfactants in extremely diluted systems induced by pH-concentration effects, Phys. Chem. Chem. Phys., 2004, 6, 1475–1481 RSC.
- J. C. Shillcock and R. Lipowsky, Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations, J. Chem. Phys., 2002, 117, 5048–5061 CrossRef CAS.
- F. J. M. de Meyer, A. Benjamini, J. M. Rodgers, Y. Misteli and B. Smit, Molecular simulation of DMPC-cholesterol phase diagram, J. Phys. Chem. B, 2010, 114, 10451–10461 CrossRef CAS.
- F. de Meyer and B. Smit, Effect of cholesterol on the structure of a phospholipid bilayer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3654–3658 CrossRef CAS.
- C. P. Lowe, An alternative approach to dissipative particle dynamics, Europhys. Lett., 1999, 47, 145–151 CrossRef CAS.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Active motion of a Janus particle by self-thermophoresis in a defocused laser beam, Phys. Rev. Lett., 2010, 105, 268302 CrossRef.
- F. Nomura, M. Nagata, T. Inaba, H. Hiramatsu, H. Hotani and K. Takiguchi, Capabilities of liposomes for topological transformation, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2340–2345 CrossRef CAS.
- F. Nomura, T. Inaba, S. Ishikawa, M. Nagata, S. Takahashi, H. Hotani and K. Takiguchi, Microscopic observations reveal that fusogenic peptides induce liposome shrinkage prior to membrane fusion, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 3420–3425 CrossRef CAS.
- T. Umeda, F. Nomura, T. Inaba, K. Takiguchi and H. Hotani, Stepwise shrinkage of liposomes driven by thermal fluctuations of the membranes, ChemPhysChem, 2005, 6, 1047–1050 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Lipid end-to-end distribution, density profiles for the hydrophobic group, the hydrophilic group and water, and movies for collision or translocation processes are collected. See DOI: 10.1039/c3nr02024j |
| This journal is © The Royal Society of Chemistry 2013 |
