Cyclic twinning and internal defects of boron-rich nanowires revealed by three-dimensional electron diffraction mapping

Abstract

Structural characterization of individual nanosized boron-rich nanowires has been carried out through analysing the three-dimensional (3D) electron diffraction intensity distribution. Not only can the cyclic twinning structure of these nanowires be easily determined, the new approach also reveals the heterogeneous strain relaxation within the intact nanowire, through the accurate determination of the orientation relationship between the constituent crystallites. The quantitative analysis of the fine structure in the 3D diffraction dataset indicates that this may be related to the distribution of defects such as stacking faults, microtwins and dislocations. It is envisaged that the non-destructive nature of this approach could open the way for the in situ study of the structural evolution of complex nanomaterials and polycrystalline materials in general.

---

Introduction

In recent years, both material growth energetics and kinetics have been explored to produce a wide range of nanomaterials with interesting structures and form factors, such as nanotetrapods,¹ icosahedral nanoparticles,² decahedral nanoparticles,^2,3 nanowires,^4–8 and nanostars,⁹ to just name a few well-known examples. Identification and characterization of those complex nanostructures have always been a challenge. Real-space imaging through transmission electron microscopy is the conventional tool of choice to study the internal structure of materials, but it cannot be realized routinely with atomic resolution even using state-of-the-art aberration corrected microscopic techniques because of the large dimensions of the nanostructures involved in many cases. In general, the atomic resolution electron microscopy is a destructive structural characterization technique for complex nanostructures,^10,11 due to the need for preparing ultrathin cross-sectional samples, yet the knowledge on the structure of intact complex nanostructures maybe important as it could be the key behind the enhanced mechanical,^12,13 optical^9,14 and catalytic properties of the nanostructures.^1,9 Non-destructive characterization of the nanostructures can be achieved through real-space electron tomography,¹⁵ however it often suffers from a ‘missing wedge’ problem,¹⁶ and it cannot yet routinely be used to determine the crystallographic information about the internal structure such as orientation relationship and internal strains.

In this paper, we will demonstrate an application of 3D intensity analysis of electron diffraction to a non-destructive study of the internal structure of a cyclic twinned nanowire. Until now, analysis of electron diffraction distribution has only been applied to the determination of crystal structures and the morphology of single crystalline nanoparticles.^17–20 Here we apply the 3D diffraction intensity mapping to reveal information about polycrystalline materials for which cyclic twinned nanowires are special cases with the crystalline components joined by twinning planes. The cyclic twinning nanostructure can have real or pseudo five-fold symmetry that is not seen in the bulk materials, usually it is always due to the result of a balance between the surface energy minimization and the reduction of the strain energy associated with such polycrystalline structures.^21,22 The twinning structure may be a factor influencing the mechanical properties of nanomaterials. For example, five-fold cyclic twinned silver nanowires exhibit anomalous strength and brittle failure.¹² We will show that the retrieval of 3D diffraction intensity distribution allows us to not only identify the cyclic twinned structure directly, but the technique also reveals quantitatively the orientation relationship of the internal crystallites and information about deformation and defects associated with the internal strain relaxation, all non-destructively.

The complex nanostructure we choose to study as a model system is boron-rich cyclic twinned nanowires that have shown promising applications, such as high temperature thermoelectric nanomaterials²³ and reinforcing phases in ceramic composites.²⁴ The boron-rich materials (B₆O, B₄C, etc.) share a common α-rhombohedral crystalline structure with a space group R3̄m (no. 166).²⁵ Despite its complexity, the best way to understand the rhombohedral unit cell is to consider it as a distorted cubic close packing structure with the lattice points occupied by nominally B₁₂ icosahedral clusters and charge balancing atoms such as carbon or oxygen atoms occupying the interstitial sites within this lattice (see Section 1 in the ESI†). Our early studies^7,8 suggest that these multiply twinned nanowires can be understood as a cyclic twinning of five such elongated tetrahedral crystallites sharing a common [001]_r axis (Fig. 1a), where the subscript r refers to the rhombohedral representation.

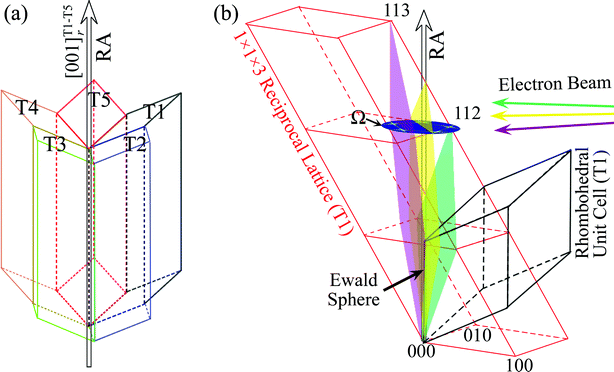Fig. 1 (a) A structural model of a five-fold cyclic twinned boron carbide nanowire. (b) The orientation relationship between the rhombohedral unit cell in one of the five components of the cyclic twinned nanowire (shown in black) and the corresponding reciprocal lattice (as shown in red color). Also shown are diffraction patterns, corresponding to the intersection of the reciprocal lattice points by the Ewald spheres (which are approximated by planes of different colors, corresponding to various plane waves of different incident angles). The Ω plane is defined to be perpendicular to the rotation axis (RA) of the nanowires and passes through the (112)_r lattice point, so it will contain peak intensities of all five (112)_r reflections of the cyclic twinned nanowire as labelled.

Experimental methods

The 3D reconstruction of diffraction intensity distribution is conducted by recording the two-dimensional electron diffraction patterns as a function of systematic tilting of either the incident electron beams or the nanowires (see Section 2 in the ESI†). As the Ewald sphere (which can be approximated as a plane for the scattering of the high energy electron beam typically used in the medium-voltage transmission electron microscopes) intersects with the reciprocal lattice convolved with the shape function of the truncated crystallites, the three-dimensional diffraction intensity distribution can be mapped out through systematic tilting. To study cyclic twinned nanostructures, we have chosen to examine a region of the reciprocal space where the contributions from all the twinning elements form a symmetrical group around the nanowire axis. Fig. 1b shows a real space rhombohedral unit cell of one of the crystalline components labelled T1 in Fig. 1a, together with a part of the corresponding reciprocal lattice structure. The (112)_r and (113)_r are the two reflections close to the [001]_r axial direction of the nanowire, and they are included in the 3D reconstruction of electron diffraction intensity distribution. For clarity, the other four equivalent (112)_r and (113)_r reflections for the remaining crystallites labelled as T2–T5 are not drawn. The scanning of the Ewald sphere through the reciprocal space is achieved through real-space tilting of the nanowire about an axis perpendicular to both the direction of the incident beam and the axis of the nanowire. The tilting is conducted with a regular angular spacing of 0.1° and an overall tilting range of ±10°. Because the resulting tilting of the diffraction pattern is pivoted about the origin of the reciprocal space (defined to be the end of the scattering vector of the incident beam), the volume of the reciprocal space is not sampled uniformly. We have taken this into account and the experimental data shown here have all been converted into a representation with uniform voxels (see Section 3 in the ESI†).

Results and discussion

Fig. 2a shows the experimental result for one such nanowire. We can see clearly two groups of five diffraction peaks situated about a common axis along the axial direction of the nanowire. They form two pentagonal patterns, related by inversion, which can be indexed to the grouping of the (112)_r and (113)_r reflections, respectively, about the axial direction of the nanowire as shown in Fig. 1b. This result directly confirms the cyclic nature of twinning in the boron-rich five-fold twinned nanowires.^7,8 Compared to the more conventional methods of identifying the cyclic twinning internal structure in decahedral nanowires, which requires either one-off destructive cross-sectional sample preparation¹¹ or taking systematic zone-axis diffraction patterns by rotating the nanowire about its axial direction by ±18°,^4,7,8 3D diffraction intensity mapping is visually direct and requires a much smaller tilting range (about ±10°) and can be done non-destructively. The latter is important for in situ experimental investigation of the structural changes inside nanowires, an important area of development in nanoscience research.²⁶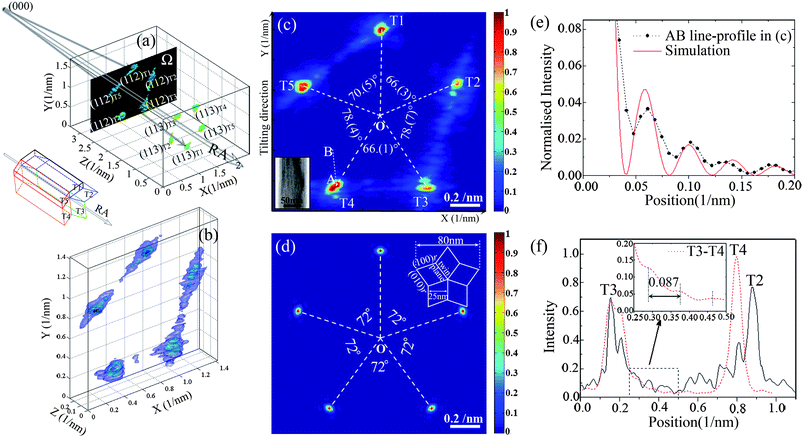

Fig. 2 (a) 3D reconstruction of the diffraction intensity distribution in the reciprocal space around (112)_r and (113)_r lattice points from a boron carbide five-fold twinned nanowire whose orientation is shown at the lower left corner. The plane defined by the peak intensities of all five (112)_r reflections is shaded and is labelled as the Ω plane, as shown in Fig. 1. (b) The magnified view of the 3D distribution of the (112)_r reflections is shown in (a). (c) The 2D intensity distribution of the (112)_r reflections in the Ω plane, with the corresponding boron carbide nanowire with a diameter of about 80 nm is shown in the inset. (d) The 2D intensity map in the Ω plane calculated for the ideal five-fold cyclic twinned nanowire structure whose cross-sectional view is illustrated in the inset. (e) The comparison of the experimental and simulated intensity profiles along the line AB is indicated in (c). (f) Intensity profiles across the (112)_r diffraction peaks of different crystalline segments, the inset is the magnification of the area in the dashed rectangle.

New information can be deduced by studying the three-dimensional reconstruction of the diffraction intensity in detail. We focus on the five-fold (112)_r reflections as shown in Fig. 2b. A striking feature is the large difference between the intensity distributions of the five reflections, showing the inhomogeneous nature of the internal structure of the nanowire. However, it is still possible to define a point, labelled ‘O’, equidistant from the peaks of all five reflections in the cross-sectional map of the five (112)_r reflections shown in Fig. 2c. We regard it as the projection of the [001]_r axial direction of the nanowire on the cross-sectional map. This is supported by the measurement of angles sustained by each reflection with respect to the nanowire axis. They are found to be in the range of 8.1–8.5°, consistent with the angle of 8.4° between [001]_r and (112)_r reflections, calculated using the rhombohedral lattice parameters defined for this boron carbide nanowire (see Section 4 in the ESI†). Therefore, it can be concluded that all five twinning segments of the boron carbide nanowire share the same growth axis, i.e. the common [001]_r twinning axis.

Using the axial direction of the nanowire that we have deduced, we can find out the dihedral angles sustained by each pair of neighbouring planes formed by the (112)_r reflections and the nanowire axis. They define the orientation relationship between the neighbouring crystallites, and more significantly they are also found to be all different, as shown in Fig. 2c. Two of the dihedral angles are about 78°, while the other two are about 66°, very different from the average value of 72° expected of the uniformly strained twin boundary^27,28 or the 73.68° expected of the unstrained twining structure. As we have mentioned before, intrinsic strain is known to be important for decahedral nanostructures because there is an angular misfit in joining five regular crystallites by twinning operation alone.^2,21 For example, in face centered cubic (fcc) materials, there is a well-known angular deficiency of 7.35° in decahedral nanostructures and it is the cause of the intrinsic strain in the fcc cyclic twinned systems such as Au, Ag and Cu nanoparticles and nanowires or that of the related semiconductors (Si, Ge or diamond) and has been subject of extensive studies (see ref. 2 and 21). Using the result of cross-sectional transmission electron microscopy performed on samples prepared by a microtome technique, Chen et al.¹¹ have discovered that the misfit angle of 7.35° is shared by three crystallites in a silver cyclic twinned nanowire with a diameter of 100 nm. However, as Ag nanowires are easily deformed, one has to be careful in extrapolating this result to the intact nanowires.

In the case of boron carbide cyclic twinned nanowires under investigation, because the dihedral angle between neighbouring {100}_r twinning planes is about 73.68°, there is an ‘angular excess’ of about 8.4° when joining five boron carbide crystallites by {100}_r-type twinning. In contrast to the silver nanorods where three of the dihedral angles are very close to the dihedral angle between the {111}_fcc twinning planes,¹¹ our result showed for the first time, on an intact boron-rich nanowire, that none of the five grain boundaries have the pure wedge angle expected of the single twinning relationship.

We can learn more about the possible structural features present by analyzing the fine structure in the individual (112)_r reflection peaks and their flares (or streaks). However to understand them quantitatively, we need to take into account the finite beam coherence, which is different in the transverse and longitudinal beam directions (X direction and Y direction in Fig. 2c, respectively). We estimated the transverse coherence length of the incident beam to be about 22 nm from its angular width (about 0.045 nm⁻¹, after being deconvoluted out of the instrumental broadening effect) without the beam passing through the sample. The transverse coherence is about the same size as the dimension of the crystallites in the cross-sectional plane. Together with the much longer longitudinal coherence length of the beam, the individual components of these cyclic twinned nanowires will be considered to be approximately coherently illuminated in the cross-sectional plane. Examination of the angular widths of the five (112)_r reflections along the axial direction of the nanowire shows that they are in the range of 0.047–0.063 nm⁻¹. These values are similar to the angular width for the incident beam, but significantly smaller than the typical angular widths of the (112)_r reflections seen in the cross-sectional map (Fig. 2c). This shows that the microstructure present in the nanowire is mostly axial. So we will focus on the features in the cross-sectional intensity map now.

The flare in the diffraction patterns of a finite sized nanostructure is known to be affected by shape factors,²⁰ strain and surface relaxation.^29,30 The possible presence of the flare (or the diffuse scattering) has been known because they, for example, are believed to contribute to the forbidden reflections in the zone-axis diffraction patterns.^31,32 The advantage of the 3D diffraction dataset is that it allows us to analyze the intensity of the diffuse scattering more quantitatively. For example, the pure shape effect can be easily simulated. Because of the long extinction distance for boron-rich materials (see Section 5 in the ESI†), a simple kinematic calculation is sufficient. This has been carried out for an ideal five-fold cyclic twinned boron carbide nanowire (i.e. without strain and defects) with the same diameter of 80 nm as that shown in the inset of Fig. 2d and the result is shown in Fig. 2d. A comparison of the simulation and the experimental line profiles along the A–B line marked in the experimental intensity map of Fig. 2c shows a good agreement both in the relative intensity and the pitch of oscillation (0.04 nm⁻¹) (Fig. 2e). However, the simulation result based on an ideal shape effect cannot explain the intense flares along the directions linking (112)_r reflections of T3 and T4, as well as those between T2 and T3 (Fig. 2f).

We believe that these anomalous flares are due to the presence of stacking faults (SF) and microtwins (MT) that are common in such nanowires.^23,33 Fig. 3 shows the high resolution transmission electron microscopy (HRTEM) evidence of their presence in the T3 and T4 crystallites of the nanowire. As a result of the stacking faults or microtwins, the widths of the defect-free regions in T3 are reduced to about 11 nm and 13 nm. This is comparable with the observed spacing of the ripples in the flare from the (112)_r reflection of T3 to that of T4 (about 0.087 nm⁻¹ as indicated in the inset of Fig. 2f, or in other words the width of the coherently diffracting region is about 11.5 nm). This suggests that the flare we have observed is not due to the coherent diffraction from the whole crystallites, but only a small fraction of the volume is involved. To mimic that, we have represented the crystallite segment with microtwin defects (shown in the cross-sectional view in Fig. 4b) by an elongated tetrahedral boron carbide crystallite with 2 layers of parallel regular-spaced {100}_r microtwin lamellae (each lamella has 2 layers of close packing boron clusters). Given the transverse nature of the defect, we have tried to estimate the effect of partial beam coherence by adding the diffraction intensities from those defect-divided subunits either incoherently or coherently. The simulated intensity profiles for both cases have been shown as L2 and L3 (Fig. 4d). We found that the intense L2 profile is more consistent with the experimental observation shown in the inset of Fig. 2f.

Fig. 3 HRTEM of the T3 and T4 twinning segments of the boron carbide nanowire shown in the inset of Fig. 2c. The inset shows the corresponding diffraction pattern of the boron carbide nanowire. At this orientation, T3 and T4 are at [100]_r and [010]_r zone-axis diffraction conditions, respectively, while other crystalline segments (T1, T2 and T5) are far from major zone-axis orientation and do not show atomic scale contrast in the HRTEM image.

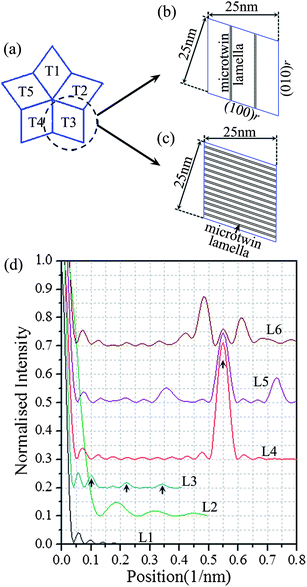Fig. 4 (a) The cross-sectional morphology of an ideal five-fold twinned nanowire with five elongated tetrahedral crystalline segments labelled as T1–T5. (b) and (c) The cross-sectional views of the proposed defective structural model of an elongated tetrahedral boron carbide crystallite oriented as the T3 segment in (a) with 2 and 13 layers of regular-spaced parallel {100}_r microtwin lamellae (each lamella has 2 layers of close packing boron clusters), respectively. The model in (b) is used to simulate the crystalline segment T3 with microtwin lamellae parallel to the twinned plane between T3 and T4. The model (c) assumes that the 13 layers of microtwin lamellae in the T3 segment are parallel to the T2–T3 twinned plane. (d) The comparison of the simulated intensity line-profiles along the direction perpendicular to the twinning plane. All are purely coherent simulation results except for L2 that is obtained by assuming that the intensity is the incoherent summation of the different coherent reflections from microtwin-free regions. L1 is the reference result for the ideal five-fold twinned nanowire shown in (a). L2 and L3 are for the structural model shown in (b). L4 corresponds to the structural model shown in (c). Also shown are the simulated results for structural models with 13 layers of irregular-spaced microtwin lamellae in the sequence of 1-2-3-1-2-3-1-2-3-1-2-3-2-2 (L5) and 2-2-2-1-1-1-3-3-3-2-2-2-1-3 (L6) respectively. The sequence is labelled in the unit of the {100}_r atomic layer.

The flare between T2 and T3 extends further out from the respective diffraction peaks than that between T3 and T4 (Fig. 2c and f). Given the prevalence of the {100}_r-type planar defects (such as microtwins and stacking faults) in such nanowires, it is quite feasible that this reflects much smaller lamella spacing. This possibility has also been investigated through simulation in Fig. 4. As the long longitudinal coherence is more relevant for flares along the T2–T3 directions, only coherent results are shown. The result (L1, L3–L6, Fig. 4d) demonstrated that the presence of microtwin lamellae will indeed increase the intensity of the diffraction flares significantly. For the model structure with regular-spaced microtwin lamellae (Fig. 4b and c), the corresponding intensity plot (L3 and L4, in Fig. 4d) shows an intense flare with a prominent feature (indicated by black arrows in Fig. 4d) reflecting the spatial periodicity of the microtwin lamellae. The comparison with the experimental case can be further improved by considering the case that the microtwin lamellae have irregular spacing. The corresponding simulated intensity distribution shows even more intense flares (L5 and L6 in Fig. 4d correspond to the models with 13 layers of irregular-spaced microtwin lamella) with more diffuse peaks. Therefore we believe that the strong flare between T2 and T3 is due to the high-density irregular spaced planar defects. This prevalence of high-density parallel twins is consistent with the low stacking fault energy that is also responsible for the cyclic twinned structure in the first place.

Finally, we comment on the anisotropy of the diffraction peak broadening observed most strikingly in T3 and T4. In particular, the direction of the elongation of the T4 reflection is not aligned with the flare orientation, suggesting that they have a different origin. It is well known that an array of the edge dislocations, such as those present in a small angle grain boundary capable of fixing the ‘extra-wedge’ problem in the boron carbide cyclic twinned nanostructure, would introduce both a tensile and a compressive strained region respectively around each core of the dislocations. This could be responsible for the anisotropic broadening of the diffraction peaks. The presence of such a small angle grain boundary is consistent with the structural model,³³ where a combination of small angle grain boundary and regular microtwin array can lead to an effective solution of the strain caused by the ‘excess-wedge’ problem in boron carbide cyclic twinned nanowires.

Conclusions

In summary, we have carried out a 3D diffraction intensity reconstruction of cyclic twinned boron-rich nanowires to investigate their internal structures non-destructively. We have found that it is a convenient and direct method to identify the cyclic twinning structures in such nanowires. A quantitative study of the dihedral angles between the diffraction peaks reveals that heterogeneous strain distribution is the norm in nanowires of such size and none of the twinning plane remains strain-free. We expect such nanowires should be considered ‘pre-strained’ when discussing their mechanical responses. We have clearly identified the presence of microtwins and stacking faults, as well as the possibility for dislocation arrays. We believe that these defects, collectively, are responsible for the strain relaxation in such complex nanowires. Given its sensitivity to the microstructure of the complex nanowires, the non-destructive nature of our approach is ideal for the in situ study of nanostructured materials as a function of temperature or external action. With the rapid development of coherent electron diffraction techniques,^29,30 we also expect that this approach can eventually be extended to also include electron diffraction tomography through phasing by the over-sampling method, to obtain real-space structure inversion, once such method becomes more robust in strained systems and a more coherent electron beam is used. This will allow us to study the morphology and strains within individual crystallites in real-space,^20,34 as well as their real-space relationship with each other. Even in its present form, our demonstration has shown that the knowledge on the 3D diffraction intensity distribution is powerful enough in revealing many hitherto unknown states of the complex nanostructure. Therefore, we expect that our current approach and its further extension into electron diffraction tomography can find many more applications in characterization of polycrystalline materials other than the cyclic twinned nanowires.

Acknowledgements

X. Fu would like to thank National Natural Science Foundation of China for the research support (grant no. 51201015). J. Yuan would acknowledge the support of EPSRC (EP/G070474/1) and Royal Society Wolfson Foundation Laboratory Refurbishment Grant. The authors would like to thank Dr Z. Y. Yu and C. Liu for providing boron-rich nanowire samples.

Notes and references

1. L. Manna, E. C. Scher and A. P. Alivisatos, J. Am. Chem. Soc., 2000, 122, 12700–12706.
2. L. D. Marks, Rep. Prog. Phys., 1994, 57, 603–649.
3. Z. Y. Li, N. P. Young, M. Di Vece, S. Palomba, R. E. Palmer, A. L. Bleloch, B. C. Curley, R. L. Johnston, J. Jiang and J. Yuan, Nature, 2008, 451, 46–49.
4. I. Lisiecki, A. Filankembo, H. Sack-Kongehl, K. Weiss, M. P. Pileni and J. Urban, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 4968–4974.
5. C. J. Johnson, E. Dujardin, S. A. Davis, C. J. Murphy and S. Mann, J. Mater. Chem., 2002, 12, 1765–1770.
6. S.-H. Zhang, Z.-Y. Jiang, Z.-X. Xie, X. Xu, R.-B. Huang and L.-S. Zheng, J. Phys. Chem. B, 2005, 109, 9416–9421.
7. J. Jiang, M. H. Cao, Y. K. Sun, P. W. Wu and J. Yuan, Appl. Phys. Lett., 2006, 88, 163107.
8. X. Fu, J. Jiang, C. Liu and J. Yuan, Nanotechnology, 2009, 20, 365707.
9. A. Guerrero-Martínez, S. Barbosa, I. Pastoriza-Santos and L. M. Liz-Marzán, Curr. Opin. Colloid Interface Sci., 2011, 16, 118–127.
10. C. P. Li, C. S. Lee, X. L. Ma, N. Wang, R. Q. Zhang and S. T. Lee, Adv. Mater., 2003, 15, 607–609.
11. H. Y. Chen, Y. Gao, H. R. Zhang, L. B. Liu, H. C. Yu, H. F. Tian, S. S. Xie and J. Q. Li, J. Phys. Chem. B, 2004, 108, 12038–12043.
12. B. Wu, A. Heidelberg, J. J. Boland, J. E. Sader, X. M. Sun and Y. D. Li, Nano Lett., 2006, 6, 468–472.
13. T. Filleter, S. Ryu, K. Kang, J. Yin, R. A. Bernal, K. Sohn, S. Li, J. Huang, W. Cai and H. D. Espinosa, Small, 2012, 8, 2986–2993.
14. M. Song, A. Bouhelier, P. Bramant, J. Sharma, E. Dujardin, D. Zhang and G. Colas-des-Francs, ACS Nano, 2011, 5, 5874–5880.
15. P. A. Midgley and R. E. Dunin-Borkowski, Nat. Mater., 2009, 8, 271–280.
16. I. Arslan, J. R. Tong and P. A. Midgley, Ultramicroscopy, 2006, 106, 994–1000.
17. U. Kolb, T. Gorelik, C. Kübel, M. T. Otten and D. Hubert, Ultramicroscopy, 2007, 107, 507–513.
18. U. Kolb, T. Gorelik and M. T. Otten, Ultramicroscopy, 2008, 108, 763–772.
19. E. Mugnaioli, T. Gorelik and U. Kolb, Ultramicroscopy, 2009, 109, 758–765.
20. R. Dronyak, K. S. Liang, J.-S. Tstai, Y. P. Stetsko, T.-K. Lee and F.-R. Chen, Appl. Phys. Lett., 2010, 96, 221907.
21. H. Hofmeister, in Encyclopedia of Nanoscience and Nanotechnology, ed. H. S. Nalwa, American Scientific Publishers, 2004, pp. 431–452.
22. V. G. Gryaznov, J. Heydenreich, A. M. Kaprelov, S. A. Nepijko, A. E. Romanov and J. Urban, Cryst. Res. Technol., 1999, 34, 1091–1119.
23. Z. Guan, T. Gutu, J. Yang, Y. Yang, A. A. Zinn, D. Li and T. T. Xu, J. Mater. Chem., 2012, 22, 9853–9860.
24. X. Lin and P. Darrell Ownby, J. Mater. Sci., 2000, 35, 411–418.
25. V. I. Matkovich, Boron and refractory borides, Springer-Verlag, Berlin, 1977.
26. H. Zheng, J. Wang, J. Y. Huang, A. Cao and S. X. Mao, Phys. Rev. Lett., 2012, 109, 225501.
27. B. G. Bagley, Nature, 1965, 208, 674–675.
28. R. De Wit, J. Phys. C: Solid State Phys., 1972, 5, 529–534.
29. W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Nat. Mater., 2008, 7, 308–313.
30. W. J. Huang, J. M. Zuo, B. Jiang, K. W. Kwon and M. Shim, Nat. Phys., 2009, 5, 129–133.
31. J. Reyes-Gasga, A. Gómez-Rodríguez, X. Gao and M. José-Yacamán, Ultramicroscopy, 2008, 108, 929–936.
32. Z. Yu, J. Jiang, J. Yuan and J. Zhu, J. Cryst. Growth, 2010, 312, 1789–1792.
33. X. Fu, J. Jiang, W. Zhang and J. Yuan, Appl. Phys. Lett., 2008, 93, 043101.
34. V. Favre-Nicolin, F. Mastropietro, J. Eymery, D. Camacho, Y. M. Niquet, B. M. Borg, M. E. Messing, L.-E. Wernersson, R. E. Algra, E. P. A. M. Bakkers, T. H. Metzger, R. Harder and I. K. Robinson, New J. Phys., 2010, 12, 035013.

---

Footnote

† Electronic supplementary information (ESI) available: Crystal structure of boron carbide, experimental geometry and diffraction pattern registration for the reconstruction of the reciprocal 3D volume, data process for 3D reciprocal volume visualization, rhombohedral lattice parameter refinement of the boron carbide five-fold cyclic twinned nanowire under investigation in this paper, and extinction distance evaluation of (112)_r reflection of boron carbide. See DOI: 10.1039/c3nr01839c

---