On the nature of carrier relaxation and ion–ion interactions in ultrasmall β-NaYF₄:Eu³⁺ nanocrystals – effect of the surface

Abstract

The purely hexagonal phase of ultrasmall (∼10 nm) NaYF₄ nanocrystals (NCs), containing different Eu concentrations, has been obtained by a modified co-thermolysis method. Detailed investigations of the excitation and relaxation mechanisms of the Eu ions in such NCs are reported. Based on the photoluminescence excitation, absorbance, photoluminescence and emission decay times measured as a function of the excitation wavelengths, it has been shown that two Eu sites with different excitation and relaxation characteristics are present in the case of ultrasmall NaYF₄ NCs. It has been shown that, when the Eu concentration increases, strong ion–ion interactions influence the relaxation phenomena in Eu ions, changing their optical properties. Moreover, these ion–ion interactions enable connections between the surface ions and the internal ones via energy transfer from the surface to the NCs core. Furthermore, it has been proposed that the different kinetic properties of the surface Eu ions are mainly caused by the formation of a charge transfer state between the ions and ligand groups attached to the NCs surface.

---

Introduction

NaYF₄ nanocrystals (NCs) have attracted a lot of attention in the last few years as host matrices for luminescent rare earth (RE) ions for applications mainly in the field of optical labelling. The main argument is that, when compared with II–VI NCs (i.e. CdS, CdSe), in addition to lower toxicity, rare earth-doped NaYF₄ NCs have been additionally characterised by narrow emission bands (<10 nm) in the UV–infrared spectral range, large Stokes shifts, long emission decay times (μs or ms), weak bleaching and no blinking.¹ Simultaneously, they can also exhibit magnetic properties^2,3 and can become multifunctional probes. All these factors have strong consequences for their potential applications. For the reasons stated above, a number of papers were recently published that are related to NaYF₄ NCs that are doped or co-doped by lanthanide ions.^4–11 However, in most cases, the obtained NCs are characterised by their size of tens of nanometres (20–200 nm), wide size and shape distribution, and are crystallised in the cubic or a mixture of cubic and hexagonal phases. Moreover, most of them are designed to be excited in the infrared spectral range for up-converting phosphor applications. The size of the smallest reported NCs, usually nanophosphors crystallized in the hexagonal (β) phase (25–50 nm), is not optimal for use as bioimaging probes. To the best of our knowledge, only several groups including ours^11–14 have reported hexagonal NaYF₄ nanoparticles (∼6 to 8 nm) smaller than 10 nm. The reduction of the diameter of the NCs is an important goal, as nanoparticles smaller than 10 nm undergo more efficient body clearance.¹⁵

The number of papers related to physical mechanisms responsible for carrier excitation and relaxation in NaYF₄ is marginal and only a few reports deal with their detailed investigations.^7,13,16 So far, most of the papers have mainly discussed their structural properties^17,18 as well as the application (functionalisation) aspects^19–21 of such NCs, while there are still many fundamental questions to be answered regarding the recombination processes in this type of NCs. RE ions have a very long emission lifetime (μs–ms), thus the interaction between the ions in their excited states becomes significant and many additional processes must be taken into account to describe the relaxation in such systems.²² This is especially important when NCs are co-doped with additional ions (i.e. Gd³⁺, Yb³⁺, Tm³⁺, Er³⁺) that interact simultaneously with each other. The well-known models describing such interactions, which are applied to bulk crystals in the case of well-defined ion positions in the lattice, may not be sufficient when applied to nanoscale matrices. This is mainly caused by the high surface-to-volume ratio and quantum confinement effects. These confinement effects include the slowing down of the single phonon relaxation,²³ changes in their radiative transition rates,²⁴ as well as changes in available phonon frequencies. These changes are especially important for ultrasmall NCs, since the surface to volume ratio significantly increases in this case, and the number of ions placed at the NCs surface increases. These ions are in direct contact with ligand groups or solvent molecules which can influence the optical properties of the marker.

The main purpose of this paper is to investigate the effect of Eu concentration and surface-related effects on the excited carrier relaxation phenomena in ultrasmall β-NaYF₄ NCs.

For this purpose, a set of NCs doped with various Eu mol% have been synthesised from 0.5 up to 100 mol%. For all the samples, EDXS spectra have been collected (Fig. S1 in ESI†). Based on these data, it has been found that the Eu mol% correlates very well with the Eu at.% introduced into the NCs during the synthesis, indicating good control of this parameter in our samples.

Experimental details

Synthesis of NaYF₄:Eu³⁺ hexagonal NCs

The synthetic method for the preparation of β-NaYF₄:Eu³⁺ NCs was similar to the single step co-thermolysis method presented in our previous paper²⁵ and originally proposed by J. Shan et al.²⁶ The sodium trifluoroacetate Na(CF₃COO) (98%), yttrium(III) trifluoroacetate hydrate Y(CF₃COO)₃·xH₂O (99%), europium(III) trifluoroacetate trihydrate Eu(CF₃COO)₃·3H₂O (98%) and trioctylphosphine oxide (TOPO, 90%) were purchased from Sigma Aldrich Ltd, UK and used as received without further purification. In general, mixtures of 1.25 mmol Na(CF₃COO), (0.50 − x) mmol Y(CF₃COO)₃ and x mmol Eu(CF₃COO)₃·H₂O, where x determines the Eu³⁺ intended concentration in the nanocrystals, were prepared. The precursor mixture was added to 10 g of TOPO and was degassed at 120 °C while being stirred. After 30 min the reaction was purged with N₂ and the reaction temperature was increased to 350 °C within 10 min. After 60 min the reaction was cooled to 70 °C and excess methanol was added to precipitate the nanoparticles. The resulting material was collected by centrifugation and excess TOPO was removed by washing with methanol several times.

Structural and optical characterisation

Samples for the TEM experiments were prepared by evaporating a dilute cyclohexane solution of the nanoparticles onto carbon-coated copper grids (S166-3, Agar Scientific) and a FEI Tecnai G2 20 X-TWIN microscope equipped with an energy-dispersive X-ray microanalyser was used to obtain the TEM images and EDXS spectra of the nanoparticles.

X-Ray powder diffraction patterns were obtained using a Philips diffractometer supported by a parallel beam optic and CuK_α1 radiation source, λ = 0.15406 nm. The nanocrystalline domain size was calculated using the Scherrer equation.

In photoluminescence and photoluminescence excitation experiments, the samples were excited by the light from a xenon lamp dispersed through a double Czerny-Turner (CZ) monochromator and the emission was detected by an avalanche Si diode coupled to a single CZ monochromator. Emission decay spectra were recorded by means of a stroboscopic technique, with a pulsed xenon lamp used as an excitation source and a photomultiplier tube used for signal detection. Absorbance spectra were collected with a JASCO V-570 spectrophotometer.

Structural results

It has been shown recently that the relative concentration of a dopant precursor in the reagents is one of the key factors that result in the initial growth of seeds with different crystallographic phases and shapes, which eventually leads to doped nanocrystals with different morphologies.^27,28 Thus, before discussing the optical properties of the β-NaYF₄ NCs doped with different Eu concentrations, their structural properties have been analysed.

As a first step, the XRD spectra were collected for all NaYF₄ samples doped with different Eu contents and compared to reflections of the hexagonal NaYF₄ lattice standard (ICDD no: 28-1192) (Fig. S2 in ESI†). The agreement of the diffraction peak positions with the reference data indicates that all the NCs are of the pure hexagonal phase. The averaged NCs size was calculated from the p-XRD results using the Scherrer equation. The diameters of the β-NaYF₄:Eu NCs for Eu concentrations between 2 and 100 mol% depend slightly on the Eu concentration and varies between 7 and 10 nm when the concentration changes from 2 up to 50 mol%. Only for the NaEuF₄ sample is the average grain size significantly reduced and is equal to ∼4 nm.

Fig. 1 shows the HRTEM images of selected samples (2, 8 and 50 mol%) at two different magnifications, together with the relevant histograms. From these images it is clear that the NCs are monodispersed in size and all have close to spherical morphologies. The obtained histograms show that the average diameters of the β-NaYF₄:Eu NCs differ slightly in Eu content and are equal to 10.7 ± 0.9, 10.1 ± 1.5 and 14.3 ± 1.4 nm for Eu concentrations of 2, 8 and 50 mol%, respectively.

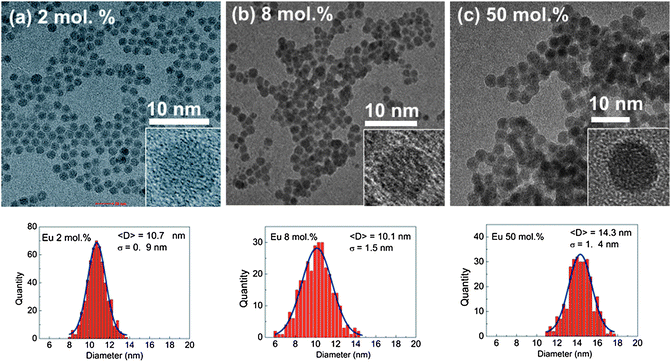Fig. 1 HRTEM images of the β-NaYF₄:Eu³⁺ NCs with (a) 2 mol%, (b) 8 mol% and (c) 50 mol% of Eu³⁺ ions together with calculated histograms.

Optical results

Fig. 2(a) shows the emission spectra recorded for the β-NaYF₄:Eu³⁺ samples with different concentrations of Eu at an excitation wavelength of 395 nm, which is resonant with the transition from the ⁷F₀ energy level to the ⁵L₆ level of the Eu³⁺ ion. Excitation at this wavelength causes the appearance of characteristic emission bands related to transitions between the ⁵D_J and the ⁷F_J energy levels of Eu³⁺ ions, which have been indicated in Fig. 3(a). These band positions correspond to the ones calculated for a free Eu³⁺ ion based on the Judd–Ofelt theory and are shown as bars at the bottom of Fig. 2(a) and (b). As can be seen, the relative intensity of these emission bands depends strongly on Eu concentration, while in all cases the most intense emission band is related to the ⁵D₀–⁷F₂ transition at ∼612 nm.

Fig. 2 (a) Emission spectra and (b) excitation spectra obtained for the β-NaYF₄:Eu samples with different Eu concentrations (0.5, 2, 5, 8, 10, 20, 50 mol%). (c) Absorbance spectra obtained for the β-NaYF₄:Eu samples with different Eu concentrations (2, 5, 8, 10, 20, 50 mol%) together with the reference spectra solution of TOPO + precursor.

Fig. 3 (a) Ratio of ⁵D₁–⁷F₁/⁵D₀–⁷F₃ and ⁵D₁–⁷F₀/⁵D₀–⁷F₁ emission bands of Eu³⁺ ions for NaYF₄ with different Eu concentrations, (b) ratio of ⁵D₀–⁷F₂/⁵D₀–⁷F₁ emission bands and (c) FWHM of the main emission band at two different excitation wavelengths for NaYF₄ with different Eu concentrations.

The band related to the ⁵D₀–⁷F₂ transition is an electric dipole transition and is sensitive to the environmental properties, whilst the band related to the ⁵D₀–⁷F₁ transition is a magnetic dipole transition and is hardly affected by changes in the co-ordination environment. With this assumption, the ratio of electric-dipole and magnetic-dipole transitions intensities (R^0–2_/0–1) can therefore be used as a measure of distortion around the ion. On the other hand, the ratio between ⁵D₁–⁷F₁ and ⁵D₀–⁷F₂ [R^1–1_/0–2(ED)], ⁵D₁–⁷F₀ and ⁵D₀–⁷F₁ [R^1–0_/0–1(MD)] transition intensities can give us information about the efficiency of non-radiative relaxation from the ⁵D_J energy levels down to the lower ⁵D_J−1 energy level. Fig. 3 shows results obtained in such a way. Fig. 3(a) shows R^1–1_/0–2 and R^1–0_/0–1 changing as a function of Eu concentration. Additionally, Fig. 3(b) shows how R^0–2_/0–1 varies with changing Eu concentration at two different excitation wavelengths: 265 and 395 nm. Moreover, Fig. 3(c) shows how the FWHM of the ⁵D₀ → ⁷F₂ transition changes with the Eu concentration at two different excitation wavelengths.

Fig. 2(b) shows the excitation spectra collected for the most intense emission band at 612 nm (⁵D₀ → ⁷F₂) for Eu³⁺ ions. As can be seen, the most intensive excitation band for all samples is the band at 395 nm, which is related to the ⁷F_J–⁵L₆ resonant excitation of the Eu³⁺ ions. Other excitation bands in Fig. 2(b) have a much lower intensity and all of them are related to the resonant excitation of the Eu³⁺ ions. Fig. 2(b) shows that all the spectra look similar for all Eu concentrations and are related with resonant excitations through f–f transitions. However, when one looks closer, it is evident that the PLE signal at the UV excitation overlaps with the broad excitation band whose intensity increases with Eu concentration.

Fig. 2(c) shows the absorbance spectra measured for the samples with different Eu contents. Additionally, a reference sample of solution made from TOPO and Eu precursor has been measured. To remove the effects of scattering and TOPO absorption itself, and to emphasise details in the absorbance spectra, the absorbance spectrum has been collected for TOPO only and has been used to normalise all the other absorbances. It can be seen that, in the case of the TOPO + precursor solution, an evident band at 260 nm appears, which has been related by us to the formation of the charge transfer state (CTS) between the Eu ions from the precursor and oxygen atoms from the TOPO ligands.

A similar, but much weaker band, can also be observed for the sample with 2 mol% Eu. This band became better resolved at higher Eu concentrations and, finally, at 50 mol% it became so intense that it overlapped with the other bands at higher energies in the absorbance spectrum and cannot be well resolved.

To better understand the interactions between the Eu ions in NaYF₄ NCs, computer simulations have been used to estimate the average distance between ions as a function of Eu concentration and NCs size. This has been done in the assumption that the distribution of Eu ions is homogenous over the entire NCs volume.

In our simulation, the positions of Eu ions were randomly chosen according to the crystal structure and Eu concentration.

It should be pointed out, however, that this is only the first estimation since it has been shown already based on synchrotron related experiments by C. Dong et al.,²⁹ that a non-homogenous distribution of ions should be expected. Nevertheless, we believe that even such an idealistic approach can bring some useful information and shed more light on the optical properties of the β-NaYF₄:Eu³⁺ NCs.

The results of simulations are presented in Fig. 4(a–c) and show that, when the Eu concentration decreases, the shape of the Eu–Eu closest neighbour distance distribution is strongly modified. For 0.5 mol% Eu, the Eu–Eu distance distribution is very broad with a long tail, where Eu ions can be separated even by 2.5 nm. Nevertheless, when the Eu content increases, the distribution became very narrow and most of the Eu ions are separated by the same distance of 0.45 nm. In the second step, the average distance between Eu ions has been calculated as a function of Eu content and NCs size and results are presented in Fig. 4(d). It can be seen that, above 5 mol% Eu, there is a strong reduction in the ion–ion distance. This corresponds to the optical results shown in Fig. 3(a), where it has been found that, above 5 mol% Eu, an efficient cross-relaxation mechanism takes place and emission from the higher Eu levels is quenched. This will allow us to introduce a definition of critical distance (L_C) between the Eu³⁺ ions, above which strong ion–ion interactions dominate and emission from the high energy levels of the Eu³⁺ ions become e-times quenched. This correlation between numerical and optical data allows us to recalculate the Eu mol% of the average distance between the Eu ions and see how the ion–ion interaction evolves with the ion–ion distance. Additionally, to exclude the effect of simultaneous NCs size reduction with Eu concentration, similar calculations have been performed for different NCs sizes and is shown in Fig. 4(e).

Fig. 4 (a–c) Distribution of the distances between the closest neighbours of the Eu ions at different concentrations for NaYF4 NCs (D = 10 nm), (d) average and maximum distances between the closest neighbours of the Eu ions as a function of Eu concentration, (e) average Eu–Eu distance as a function of NCs size for two Eu concentrations.

It can be seen that L_C weakly depends on the NCs size for NCs bigger than 5 nm. Thus, the fluctuations in size of the synthesised NCs should not have a significant impact on the conclusion drawn on the basis of the ion–ion interactions.

To obtain better insight into the interactions between the Eu ions, the emission decay times have been measured for the ⁵D₀–⁷F₂ (612 nm) transition recorded for samples obtained at different Eu concentrations. As a first set of data, we analysed the emission decay times measured for NaYF₄:Eu at a 395 nm excitation wavelength for different Eu concentrations. The obtained results have been shown in Fig. 5. Fig. 5(b) shows that, when the Eu concentration increases from 2 up to 100 mol%, the emission decay time (τ_PL) decreases exponentially from 8 down to 4 ms. Again, as has been shown for the PL data, the threshold of this decay is at 5 mol%, which corresponds to L_C = 0.65 nm. This reduction in emission decay time is caused by the ion–ion interaction which appears as 1/τ_NR in the general formula describing emission decay: 1/τ_PL = 1/τ_R + 1/τ_NR. Additionally, Fig. 5(c) shows that, when the Eu ion concentration drops below 5 mol%, a rise time of emission from the ⁵D₀ level becomes evident and increases with a further reduction of concentration up to 1 ms at 0.5 mol% of Eu.

Fig. 5 (a) Emission decay time traces recorded for the β-NaYF₄:Eu samples doped with different Eu concentrations together with exponential fitting curves. Emission decay times (b), rise times and the second component of emission decay times (c), and the energy transfer efficiencies (d), all obtained for β-NaYF₄:Eu samples doped with different Eu concentrations.

Finally, based on a simple dipole–dipole approximation, the efficiency of the ion–ion interactions between the Eu ions has been estimated. It can be seen that this process became saturated when the Eu concentration was above 40 mol%, and reached an efficiency of 45%.

In the next step, the emission decay data was collected for all the samples at different excitation wavelengths. Fig. 6 shows this data recorded for the NaYF₄:Eu samples with different Eu concentrations (2, 5, 8, 10, 20, and 50 mol%) and at different excitation wavelengths corresponding to the main resonant excitation peaks of the Eu ions (see Fig. 3). Fig. 6(a) shows that, when the excitation energy increases above the energy of the resonant excitation to the ⁵D₁ level, the measured decay time (τ_PL) for all of the samples increases as well. However, when the excitation wavelength is shorter than 395 nm (⁵L₆) the decay time starts to significantly decrease. This surprising nonlinear behaviour becomes even more evident when the concentration of the Eu ions decreases. A very similar effect has also been observed for the ⁵D₁–⁷F₁ transition, while much shorter decay times have been obtained for this case [(Fig. 6(b)].

Fig. 6 Emission decay times as a function of excitation wavelength for samples containing different Eu concentrations detected at (a) 612 nm and (b) 550 nm.

To avoid misinterpretation of our results, for one of the samples (8 mol%), the emission decay was recorded as a function of the excitation flux. This was done in the range of power densities available from the excitation source when changing the excitation wavelengths from 250 up to 600 nm (see ESI S3†). No evident dependence of τ_PL on the excitation flux has been obtained, which excludes the excitation flux related effects as the origin of observed nonlinearities in τ_PL. Additionally, we have already observed that there is no dependence of τ_PL on the excitation wavelength for the Tb-doped NaYF₄ sample.¹³ This additionally excludes any setup artefacts which, if any, should be observed for any ions in the same way. Additionally, to rule out solvent effects, we have measured the emission decay times recorded as a function of the excitation wavelengths for two solvents with different polarities, i.e. cyclohexane and chloroform (see ESI S3†). For both solvents, the same nonlinear behaviour has been observed.

Discussion

Emission properties

In Fig. 2 and 3 we can observe that the emission of β-NaYF₄:Eu³⁺ depends both on the excitation wavelength and ion concentration. The concentration dependence is directly related to the ion–ion interactions, while the excitation wavelength dependence is due to the existence of two Eu sites: surface and volume. These two effects manifest themselves clearly in Fig. 3.

Fig. 3(a) shows that R^1–1_/0–2 and R^1–0_/0–1 decreases exponentially when the Eu concentration increases with a decay constant equal to 5 mol% Eu. Assuming that the maximal phonon energy of Eu³⁺-doped NCs does not depend significantly on the Eu³⁺ concentration, some phenomenon other than multiphonon relaxation has to be responsible for the significant decrease of R^1–1_/0–2 and R^1–0_/0–1. A highly possible reason for this is the ion–ion interactions, which dominate above 5 mol%. In this case, non-radiative relaxation from the high energy levels to the lowest ⁵D₀ level is promoted over the radiative relaxation from the higher ⁵D_J levels. This effect is caused by efficient cross-relaxation (CR) between the Eu ions. This 5 mol% corresponds to the average distance between the Eu ions (0.65 nm), which has been estimated already from numerical simulations and is shown in Fig. 4.

Schematically, this CR process has been shown in Fig. 7. As we can see, the CR between [(⁵D₁ → ⁵D₀):(⁷F₀ → ⁷F₃) and other higher levels] transitions will move carriers to the ⁷F₃ level and redistribute thermally over the ⁷F_J levels.

Fig. 7 Schematic interpretation of the relaxation paths (a) within the Eu ion, and (b) between two Eu ions doped into β-NaYF₄ NCs.

From an application point of view, CR is advantageous since the emission spectrum has less emission bands and at the same time the emission efficiency is kept at the same level. This is caused by the fact that the CR processes conserve the number of in and out photons.

Understanding ion–ion interactions can be very useful when analyzing the kinetics of excited electrons. This is because the ion is excited to an energy state with different energy gaps to the next lower levels of the ⁵D_J multiplet. Thus, for small gaps, one phonon can cause very rapid (≪1 ns) non-radiative relaxation. For larger energy gaps, several phonons are required to conserve energy and the decay through the multiphonon relaxation is much slower. For Eu³⁺ ions, the difference between the lowest excited ⁵D_J states is equal to 2900, 2500, 1750 and 12 300 cm⁻¹ for the ⁵D₃–⁵D₂, ⁵D₂–⁵D₁, ⁵D₁–⁵D₀ and ⁵D₀–⁷F₆ transitions, respectively. For β-NaYF₄ the maximum reported phonon frequency is 400 cm⁻¹.³⁰ Therefore, non-radiative decay between these levels would require simultaneous (multiphonon) emission of approximately 8, 7, 5 and 30 phonons. On the other hand, studies of the non-radiative relaxation process of rare earth ions in a number of matrices have demonstrated that multiphonon relaxation involving the emission of as many as five phonons can effectively compete with radiative transitions for decay. Thus, it makes non-radiative relaxation processes between the ⁵D_J levels hardly probable and radiative emission from these levels is expected when no other relaxation channels are active, i.e. CR.

Moreover, from Fig. 3(b) it can be seen that for an excitation wavelength of 395 nm, the R^0–2_/0–1 ratio changes only slightly from 1.32 up to 1.45 when the concentration changes from 0.5 up to 50 mol%. However, in the case of an excitation wavelength of 265 nm, when the concentration of Eu increases, the local environment of emitting Eu ions changes significantly from low centrosymmetry (R^0–2_/0–1 ∼ 2.4) to one with a higher centrosymmetry (R^0–2_/0–1 ∼ 1.45). The lower centrosymmetric site can be attributed to Eu ions placed at the NCs surface, while the high centrosymmetric site can be attributed to europium ions placed inside the NCs core. Following this interpretation, under UV excitation and a low Eu concentration, the contributions from Eu ions placed at two different sites contribute to the observed emission. On the other hand, when an excitation wavelength of 395 nm is used, the emission is mainly from only one site – the volume related site, which contributes to the observed signal.

When the concentration increases, the ion–ion interactions start to dominate and energy migration from the surface ions to the core ions occurs. As a consequence, even under UV excitation, the main contribution to the observed emission comes from the volume ions and the obtained R^0–2_/0–1 ratio is equal to the one obtained at an excitation wavelength of 395 nm. This is because the 395 nm wavelength is not selective and for all Eu concentrations it equally excites Eu at both sites, and the obtained R^0–2_/0–1 ratio is averaged over all the sites with a dominant contribution from the volume sites.

From Fig. 3(c) it can also be seen that, with excitation at 395 nm, the FWHM of the main Eu transition is around 6.5 nm and does not change when the concentration varies over the entire range. However, with excitation at 265 nm , when the ions concentration increases the FWHM is strongly reduced from almost 10 nm at low concentrations down to 6.5 nm at a high concentration. This is because, at low Eu concentration, a wavelength of 265 nm excites two Eu sites, surface and core, and both contribute to the total Eu FWHM and, when the Eu concentration is high due to energy migration, it is mainly the core ions that emit light – thus the line width will be reduced.

What is more, it has been found that the emission peak position related to Eu ions also varies with the excitation wavelength; for the sample with 50 mol% it is constant and equal to 612 nm over the entire range of excitation wavelengths used, while for the sample with 2 mol% Eu it changes from 608 up to 612 nm with different excitation wavelengths.

These results show that, for low Eu concentration, we have a contribution to the emission from two Eu sites. However, for high Eu concentration, where ions strongly interact with each other, the only ions contributing to the observed emission are ions from the NCs core. This is due to dipole–dipole interactions and exciton migration from the surface sites to the core sites, where it is recombined radiatively. Schematically, this has been shown in Fig. 8.

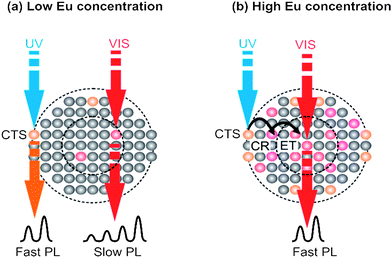Fig. 8 Schematic representation of the excitation and emission mechanism of Eu ions in β-NaYF₄ NCs at two different concentration limits.

Excitation properties

Based on the obtained results shown in Fig. 2, we can conclude that not only are there two different Eu sites in β-NaYF₄ NCs (surface and core), but also the excitation mechanism for them is significantly different. We proposed that UV light excites mainly surface ions while VIS light is not selective and excites all Eu sites within the NCs. The only question arising here is why the UV light excites mainly the surface ions, while the 395 nm and longer wavelengths are not selective for Eu sites.

To explain this result, we had to take into account the absorbance results shown in Fig. 2(c) and the importance of the surface in our ultrasmall NCs, where for 5 mol%Eu³⁺, approximately 20% of the ions are placed at the NCs surface. This means that there is a large number of europium ions in contact with TOPO (C₂₄H₅₁OP) groups, which passivates the NCs surface. In consequence, we should expect many Eu–O bonds at the NaYF₄ surface and the appearance of a charge transfer state (CTS), which can be formed between the Eu ions placed at the NCs surface and ligand groups (TOPO) covering the NCs surface. The position of this band can vary from matrix to matrix, but usually it is expected to be ion the near UV spectral range.^30–32 The position of this band observed by us at 260 nm is also in agreement with predictions of the simple Jörgensen formula, which predicts this band at around 230 nm. Excitation through this band will be also very efficient because CT transitions are spin-allowed and Laporte-allowed as opposed to low probable f–f transitions and will dominate at the UV excitation range. Moreover, the relation of this band to the NCs surface has been proved by us recently.²⁵ This has been done based on the comparison of absorbance spectra for core NaYF₄:Eu³⁺-TOPO NCs and core–shell NaYF₄:Eu³⁺/NaYF₄-TOPO NCs. It has been found that the absorbance band at 260 nm is significantly reduced when the NCs are covered with a NaYF₄ shell.

These results show that the CTS participates in UV light absorption and the significance of such absorption increases with the Eu concentration because the number of Eu–O bonds at the surface increases. However, for excitation with lower energies only, the resonant excitation of Eu³⁺ became possible and, due to statistical reasons, is related with the ions located mainly in the NCs core.

Relaxation mechanisms

Depending on the Eu³⁺ concentration, different relaxation mechanisms in the β-NaYF₄ NCs have been proposed as shown schematically in Fig. 7 and 8.

Low ion concentration regime. The UV light (265–317 nm) excites mainly the ions at the surface through the CTS. Emission from these ions provides the main contribution to the emission decay profile detected at the ⁵D₀–⁷F₂ transition at this excitation wavelength. From the CTS, carriers decay rapidly to fill both ⁵D₁ and ⁵D₀; this is followed by radiative transitions from ⁵D₁ and non-radiative relaxation to ⁵D₀ followed by emission at 608 nm [Fig. 7(a)]. As a consequence, carrier relaxation for these excitation wavelengths is a very fast process and the final decay time is the decay time of the ⁵D₀ level only (τ_uv ≈ τ₀). The decay scenario for the other excitation wavelengths is very different, since the longer excitation wavelengths are not site selective and all Eu ions are excited in this case. Thus, electrons are excited resonantly to higher levels of Eu³⁺ (⁵D_J, ⁵L₆, ⁵G_J) and the only way for them to relax to the lowest emissive ⁵D₀ level is by multiphonon relaxation. As has already been discussed for NaYF₄, this process will be very slow since it needs more than 5 phonons. Thus, the relaxation rate for this process will also be very low. As a consequence, the emission decay time detected in the experiment will be much longer with two or more components τ_vis = τ₀ + ∑τ_i–j increasing the decay time when the excitation energy increases. Finally, when the samples are excited resonantly to the ⁵D₁ level (465 nm), the obtained decay time is again short and equal to τ₀. As a consequence, a nonlinear behaviour of decay time vs. excitation wavelength is observed.

An additional mechanism, which could also be related with this nonlinear behaviour, could be due to the non-radiative interactions between the Eu ions coupled to ligands at the surface forming a CTS, and the neighboring Eu ions. This interaction will influence the emission decay time of ions close to the surface. This could explain the weak contribution of the CT band in the PLE signal, which is contrary to the strong signal in the absorbance spectra.

High ion concentration regime. In this case, the ion–ion interactions change the relaxation scenario. First of all, fast cross-relaxation mechanisms allow the excited carriers to rapidly relax to the emissive ⁵D₀ levels of Eu ions. What is more, because of the high ion concentration, other ion–ion interactions occur, namely energy migration (⁵D₀ → ⁷F_J:⁷F_J → ⁵D₀) between the ions. As a consequence, the only ions participating in the emission are the ions from the NCs volume.²⁵ Evidence of ion–ion interactions can be also observed in the emission rise times of the ⁵D₀–⁷F₂ transition of Eu³⁺ ions. This is because the low Eu concentration population of the ⁵D₀ level is very slow through the multiphonon relaxation, while for high Eu concentration it becomes very fast due to relaxation through CR.

Conclusions

We have shown that, by varying Eu concentration, the NCs size and optical properties of β-NaYF₄:Eu³⁺ NCs can be controlled. For a full concentration range (2–100 mol%) monodisperse ultrasmall (≤10 nm) NCs crystallised in the pure hexagonal phase have been obtained. We have also shown that two different Eu sites, surface and core, are responsible for the observed optical properties of such NCs. These two sites are characterised by different excitation and relaxation characteristics and interact with each other in a complex way depending on the Eu ion concentration. We proposed that under UV excitation, mainly the surface ions are excited via the CTS, while at lower excitation energies, both sites (surface and core) are excited resonantly through f–f transitions. It has been found that, for concentrations higher than 5 mol%, corresponding to the average distance between ions being around 0.65 nm, strong ion–ion interactions appear, which can be used to control the emission properties and kinetics of the Eu³⁺ ions.

Acknowledgements

The authors would like to thank the National Centre for Research and Development for their financial support under the LIDER project no. 014/L-2/10.

Notes and references

1. S. Wu, G. Han, D. J. Milliron, S. Aloni, V. Altoe, D. V. Talapin, B. E. Cohen and P. J. Schuck, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10917–10921.
2. J. Ryu, H. Y. Park, K. Kim, H. Kim, J. H. Yoo, M. Kang, K. Im, R. Grailhe and R. Song, J. Phys. Chem. C, 2010, 114, 21077–21082.
3. G. K. Das, N. J. J. Johnson, J. Cramen, B. Blasiak, P. Latta, B. Tomanek and F. C. J. M. van Veggel, J. Phys. Chem. Lett., 2012, 3, 524–529.
4. Z. Li, L. Wang, Z. Wang, X. Liu and Y. Xiong, J. Phys. Chem. C, 2011, 115, 3291–3296.
5. S. J. Budijono, J. Shan, N. Yao, Y. Miura, T. Hoye, R. H. Austin, Y. Ju and R. K. Prud'homme, Chem. Mater., 2010, 22, 311–318.
6. C. Chen, L. D. Sun, Z. X. Li, L. L. Li, J. Zhang, Y. W. Zhang and C. H. Yan, Langmuir, 2010, 26, 8797–8803.
7. F. Wang, R. Deng, J. Wang, O. Wang, Y. Han, H. Zhu, X. Chen and X. Liu, Nat. Mater., 2011, 10, 968.
8. R. A. Jalil and Y. Zhang, Biomaterials, 2008, 29, 4122–4128.
9. N. Bogdan, F. Vetrone, G. A. Ozin and J. A. Capobianco, Nano Lett., 2011, 11, 835–840.
10. K. A. Abel, J. C. Boyer, C. M. Andrei and F. C. J. M. van Veggel, J. Phys. Chem. Lett., 2011, 2, 185–189.
11. A. Podhorodecki, ECS Transactions, 2012, 45, 191.
12. N. J. J. Johnson, W. Oakden, G. J. Stanisz, R. S. Prosser and F. C. J. M. van Veggel, Chem. Mater., 2011, 23, 3714–3722.
13. A. Podhorodecki, M. Banski, J. Misiewicz, M. Afzaal, P. O'Brien, D. Cha and X. J. Wang, J. Mater. Chem., 2012, 22, 5356–5361.
14. A. D. Ostrowski, E. M. Chan, D. J. Gargas, E. M. Katz, G. Han, P. J. Schuck, D. J. Milliron and B. E. Cohen, ACS Nano, 2012, 6, 2686–2692.
15. M. Longmire, P. L. Choyke and H. Kobayashi, Nanomedicine, 2008, 3, 703.
16. Y. Wang, K. Liu, X. M. Liu, K. Dohnalova, T. Gregorkiewicz, X. G. Kong, M. C. G. Aalders, W. J. Buma and H. Zhang, J. Phys. Chem. Lett., 2011, 2, 2083–2088.
17. K. A. Abel, J. C. Boyer and F. C. J. M. van Veggel, J. Am. Chem. Soc., 2010, 132, 5533.
18. F. Wang, Y. Han, C. S. Lim, Y. Lu, J. Wang, J. Xu, H. Chen, C. Zhang, M. Hong and X. Liu, Nature, 2010, 463, 1061–1065.
19. Z. Li, Y. Zhang, B. Shuter and N. M. Idris, Langmuir, 2009, 25, 12015–12018.
20. Q. Chen, X. Wang, F. Chen, Q. Zhang, B. Dong, H. Yang, G. Liu and Y. J. Zhu, J. Mater. Chem., 2011, 21, 7661–7667.
21. J. Jin, Y. J. Gu, C. W. Y. Man, J. Cheng, Z. Xu, Y. Zhang, H. Wang, V. H. Y. Lee, S. H. Cheng and W. T. Wong, ACS Nano, 2011, 5, 7838–7847.
22. F. Auzel, Chem. Rev., 2004, 104, 139–173.
23. H. S. Yang, S. P. Feofilov, D. K. Williams, J. C. Milora, B. M. Tissue, R. S. Meltzer and W. M. Dennis, Phys. B, 1999, 263, 476–478.
24. R. S. Meltzer, S. P. Feofilov, B. Tissue and H. B. Yuan, Phys. Rev. B: Condens. Matter, 1999, 60, R14012.
25. M. Banski, M. Afzaal, A. Podhorodecki, J. Misiewicz, A. L. Abdelhady and P. O'Brian, J. Nanopart. Res., 2012, 14, 1228.
26. J. Shan, X. Qin, N. Yao and Y. Ju, Nanotechnology, 2007, 18, 445607.
27. Y. Yang, Y. Jin, H. He, Q. Wang, Y. Tu, H. Lu and Z. Ye, J. Am. Chem. Soc., 2010, 132, 13381–13394.
28. A. Podhorodecki, M. Nyk, G. Zatryb, J. Misiewicz and W. Strek, Electrochem. Solid-State Lett., 2009, 12, K33–K36.
29. C. Dong, J. Pichaandi, T. Regier and F. C. J. M. van Veggel, J. Phys. Chem. C, 2011, 115, 15950–15958.
30. M. Banski, A. Podhorodecki, M. Afzaal, A. L. Abdelhady and P. O'Brien, J. Mater. Chem. C, 2012 10.1039/C2TC00132B.
31. P. Ghosh and A. Patra, J. Phys. Chem. C, 2008, 112, 19283–19292.
32. A. Podhorodecki, R. Kudrawiec, M. Nyk, J. Misiewicz and W. Strek, Opt. Mater., 2009, 31, 1252–1255; A. Podhorodecki, R. Kudrawiec, M. Nyk, J. Misiewicz and W. Strek, Electrochem. Solid-State Lett., 2007, 10, H88–H89.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1: EDX spectra for β-NaYF₄ NCs obtained with different Eu concentrations, Fig. S2: XRD spectra of Eu³⁺ doped β-NaYF₄ NCs with (a) different Eu³⁺ molar fractions and (b) obtained at different synthesis times. Fig. S3: (a) emission rise times vs. excitation wavelengths obtained for β-NaYF₄ NCs obtained with different Eu concentrations. (b) Emission decay times vs. excitation wavelengths obtained for the sample with 8 mol% of Eu recorded in two different polarity solvents. Inset: emission decay time recorded as a function of excitation flux. See DOI: 10.1039/c2nr32212a

---