A monomeric form of iNOS can rationalise observed SAR for inhibitors of dimerisation: quantum mechanics and docking compared

Abstract

Two series of compounds that inhibit dimerisation of iNOS have been reported in the literature and studied crystallographically. We have applied a range of docking techniques to these compounds and shown that the geometry of the complexes can be reproduced well but that even within a series of related compounds the docking scores do not rank compounds well. Quantum mechanical studies using a model system for the protein and a range of density functionals are able to reproduce the geometry of the complexes and the corresponding affinities. The combination of docking to generate geometries and quantum mechanical calculations to predict complexation energies is a powerful one for rationalising observed changes and designing improved compounds.

---

Background

The role of nitric oxide as a signalling molecule is well established and the enzymes that generate it from arginine have been studied in great depth.^1,2 Two of these nitric oxide synthases (NOSs) are constitutively expressed (endothelial NOS and neuronal NOS) and play a role in the physiology of blood pressure and of the brain respectively. A third isoform is induced in response to a range of stimuli and hence is called inducible NOS or iNOS. This latter enzyme has been linked to many disease states and is of great interest within the pharmaceutical industry.²

A number of compounds have been described in the literature as inhibitors of iNOS but these have generally been mimics of arginine, the substrate for the enzyme, which is present at high physiological concentrations.² Such molecules have not shown a suitable balance of efficacy and tolerability for clinical progression. This may be because they are unable to compete with the high concentration of natural substrate and may bind at other sites that recognise arginine.

This background has spurred an interest in compounds that inhibit iNOS in ways which are not competitive with arginine. Two series of compounds have been disclosed by workers from Berlex and Kalypsys which were described as inhibiting the dimerisation of iNOS.^3–5 Dimerisation is a prerequisite for enzyme activity and the process requires the cofactor tetrahydrobiopterin which also delivers electrons to the heme iron that is present in the enzyme active site.⁶ This initiates the reaction that leads first to binding of oxygen and then to oxidation of arginine to give NO and citrulline.¹

The compounds described by Berlex derived from a screening library designed to include a group that binds to the heme iron. Two representatives of this series had been studied with protein–ligand crystal structures in which the protein had been engineered to not dimerise.^3,7 The structures of these compounds (1 and 2) in complex with murine iNOS are illustrated in Fig. 1. This shows that a principal feature of these compounds' binding mode is a bond between the heme iron of iNOS and an imidazole nitrogen. An intriguing further feature is the positioning of the dioxolane group in both compounds such that one oxygen is able to form a weak interaction with a backbone NH and one of the polarized CH bonds a weak interaction with a backbone carbonyl. These hydrogen bonding features are shared with the binding mode of compound 3 described below.

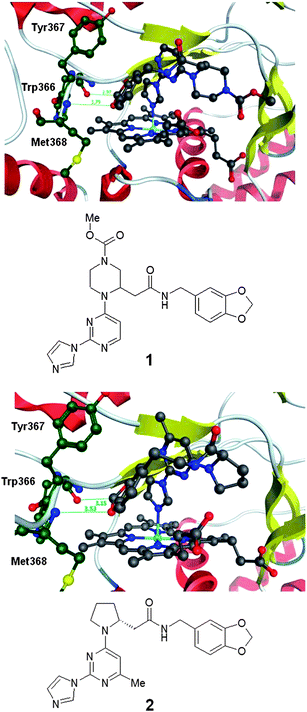Fig. 1 Protein–ligand crystal structure of compounds 1 and 2 in complex with monomeric iNOS.⁸

The compounds described by Kalypsys derived from high throughput screening.⁴ Building on the work that yielded the protein–ligand crystal structures of 1 and 2, we were able to obtain the protein–ligand crystal structure of an exemplar of the series of compounds described by Kalypsys, compound 3 (Fig. 2).⁵ By contrast to 1 and 2, compound 3 reported by Payne et al. is found not to form an interaction with the heme iron.⁵ It relies upon hydrogen bonding between the carbonyl of 3 and the backbone NH of Met368 and the amidic NH of 3 and the backbone carbonyl of Trp366. These interactions are analogous to those involving the weak donor and acceptor of the dioxolane group in 1 and 2. A further key aspect of the interaction between 3 and iNOS is that the aromatic core of 3 stacks onto the extended aromatic system of the porphyrin in the heme group. The contribution of such interactions to binding energies is challenging to quantitate. The imidazopyrazine fragment of 3 protrudes into a water filled part of the pocket and does not make any direct interactions with the protein.

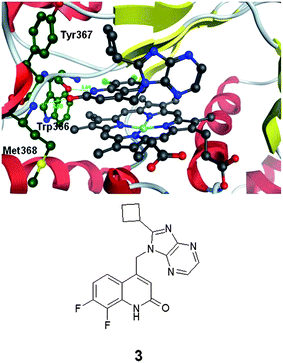Fig. 2 Protein–ligand crystal structure of compound 3 in complex with monomeric iNOS.⁸

The assortment of interaction types involved in the interaction between iNOS monomer and the inhibitors described by both Berlex and Kalypsys make this an extremely complex system for which to make predictions about binding pose and binding energy. It serves as a good test to identify protocols that are able to treat the balance between metal–ligand interactions, hydrogen bonds and π-stacking correctly. There are two stages to achieving this aim, the first is to find a method that predicts the binding pose correctly, the second is to find a method that predicts the binding energy correctly. The first has been approached by studying a small range of commonly available docking protocols. When considering approaches to the second problem, it might be expected that quantum mechanical calculations can achieve an adequate balance between the different interaction types. However, there are many challenges to doing this. An appropriate model system to probe the SAR must be identified and an appropriate level of theory must be found. Hartree–Fock calculations are likely to perform poorly on this balance of interaction types and many of the density functional theory approaches are known to treat dispersion based interactions poorly.⁹ Recently, the Minnesota set of functionals have offered improvements in this area^10,11 and the ωB97XD functional includes an empirical correction to deal with dispersion.¹² Beyond these considerations it has also been of interest to investigate whether the computational methods used are able to describe the SAR for either IC₅₀ or lipophilicity ligand efficiency. This latter property takes into account the enhanced binding to proteins that can come about by simply increasing the lipophilicty of a molecule and hence its tendency to partition into more hydrophobic environments and away from water.

Results and discussion

Compound set

A small number of compounds from two series were selected for our computational study: the two compounds from Berlex (1 and 2) and a set of compounds described by Kalypsys including compound 3 and a set of thirteen compounds from a related series to 3 which share a common substituent (Fig. 3).^3–5 For each of the compounds, an IC₅₀ value is reported in the paper describing the compound and reproduced in the ESI,† Table S2.¹³ Within drug discovery, it has been made clear over recent years that the general partitioning effect caused by increased lipophilicity can lead to compounds that are non-specific binders with poor physical properties. In order to avoid such compounds, it is becoming standard practice to consider a lipophilicity ligand efficiency (LLE) which accounts for these non-specific effects.¹⁴ There are a range of definitions that are employed for this property and we have used pIC₅₀ − clogP, where pIC₅₀ is −log₁₀(IC₅₀) and clogP is a calculated partitioning coefficient for water–1-octanol.¹⁵ It is of value to understand if any of the approaches to SAR modelling described below can model the LLE as this is arguably a more useful property to improve during a lead optimisation process.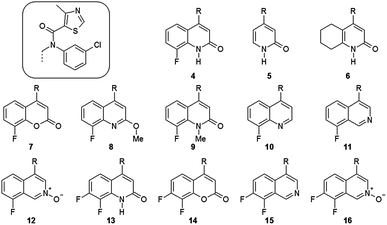

Fig. 3 A series of compounds described by Kalypsys which all share a common sidechain.⁴ Quantum mechanical modelling of these compounds abbreviated this sidechain to methyl and this is designated with (′).

Properties modelled

In the studies described here, two experimental properties have been investigated: pIC₅₀ and LLE. The pIC₅₀ for inhibition of a simple enzymatic reaction can correlate with the pK_i and hence the binding free energy which ideal docking methods seek to compute. As described above, the reaction catalyzed by iNOS is not simple and hence this interpretation of pIC₅₀ values may be in error. LLE for a simple enzyme can be crudely interpreted as proportional to the free energy of binding for an inhibitor partitioning between 1-octanol and the enzyme rather than between water and the enzyme. From a computational perspective this has removed the aqueous environment, which is hard to model. For quantum mechanical calculations, which model the partitioning between isolated protein and ligand in the gas phase and the protein–ligand complex, it seems likely that because the 1-octanol environment is more like the gas phase than water the LLE may be better reproduced by these methods than the pIC₅₀. The ability of docking methods and of QM calculations to provide scores and energy changes that correlate well with either of these measured properties was assessed in a primarily pragmatic fashion; asking if a correlation can be found rather than setting out in the expectation that one should exist. Many docking methods (including GOLD) do not claim that their scores are designed to correlate with free energy of binding but are actually intended to help select good binding poses from among an ensemble for a single compound. The scores for that compound need not be comparable to those for any other compound. QM by contrast should be able to make quantitative comparisons between compounds if the energy change that is computed is appropriate for the experimental measurements.

Docking

This set of structures were studied with several docking protocols. The first three are based on GOLD.¹⁶ These are GOLD using the goldscore fitness function (GOLD1), GOLD using a set of chemscore parameters selected for cytochrome P450 docking (GOLD2) and GOLD using a set of goldscore parameters selected for cytochrome P450 docking (GOLD3).¹⁷ The P450 enzyme system also includes a heme containing iron such that similar interaction types to those likely in iNOS might be expected. All three use a protein in which all water molecules have been deleted. Within Glide,¹⁸ docking has been performed using the SP and XP protocols and using a protein with all the waters in place (SP1 and XP1) or with all waters deleted (SP2 and XP2).^19–21 Both Glide score types (SP and XP) are intended to be able to compute ligand binding free energies. The XP method uses more extensive sampling and a consideration of the effect of hydrophobic enclosure that may make it less comparable to LLE in which this aspect of binding has been deemphasised.²⁰ Docking was into the three protein structures from the complexes of 1, 2 and 3. Throughout this paper, the protein structures derived from these protein–ligand complexes are denoted P1, P2 and P3. Ligand geometries for the docking were obtained by application of corina to a SMILES file of the various ligands. However, the geometries of compound 1 and 2 observed in the crystal structure involve quite different conformations about the pyrrolidine or piperazine ring compared to those generated by corina and hence the crystal structure geometries were also provided as input for these two compounds.

The geometry obtained for compounds 1 to 3 by each method were examined and compared to their crystal structures. For compounds 1 and 2, three distances were measured: the Fe–N distance, the distance between the dioxolane oxygen and the backbone nitrogen of Met368 and the distance between the dioxolane carbon and the backbone carbonyl oxygen of Trp366 (the last two interaction distances are indicated in Fig. 1). For compound 3 the distances between the ligand carbonyl and the backbone nitrogen of Met368 and between the ligand nitrogen (of its NH functional group) and the backbone carbonyl oxygen of Trp366 (the two distances indicated in Fig. 2) were measured in the docked poses. The RMSDs for two fragments of each ligand were also measured after the crystal structures of 1 and 2 and the docked poses for all structures were aligned to that for 3 using the inner (16-membered) ring of the porphyrin. For 1 and 2, the RMSDs for the imidazole-pyrimidine and the benzodioxole estimate how far away these fragments are from where they are in the crystal structures while for 3 the RMSDs for the 10 ring atoms of the quinolinone and for the 13 atoms of the cyclobutylsubstituted imidazopyrazine were computed. All of these parameters are shown in Table S1 in the ESI.†

The geometric parameters in Table S1† show that the poses that GOLD ranks best for either 1 or 2 are incorrect; they do not include any interaction with the heme iron. All of the GOLD protocols are however able to locate a pose for 1 that involves an interaction between the imidazole N and the heme iron when docking into either of P1 or P2, but do not rank these poses best. GOLD is only able to find a pose for compound 2 that includes an interaction with the metal when docking into its own protein P2 and using the GOLD3 method. By contrast, the Glide protocol XP1 is able to correctly position each ligand in its own crystal structure. None of the methods are able to reliably position any of the ligands in any of the proteins other than that from which it was extracted. Examination of the protein structures does not reveal any drastic differences between them other than Glu371 in the complex of 3 which occludes the benzodioxole binding region of 1 and 2 (Fig. 4). The heme also varies slightly both in the orientation of its sidechains and the degree of twisting; the iron atom is depressed away from the ligand in the complex of 3 presumably because it is not forming a direct interaction with the ligand. It remains an impressive achievement that one of the methods is able to correctly place this set of ligands which utilise such a complex array of interaction types when binding to iNOS in its monomeric form.

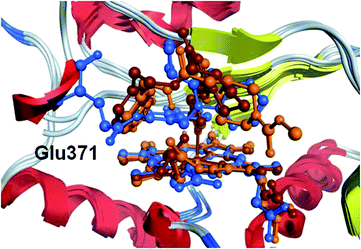Fig. 4 Protein–ligand complex structures of compounds 1 (orange), 2 (brown) and 3 (blue) overlaid using the inner ring of the heme porphyrin.

As the docking protocols are able to dock compound 3 well, albeit with some ambiguity concerning the orientation of the imidazopyrazine, it seemed reasonable that they should also be able to position compounds 4–16 which are expected to bind with the quinolinone in the same position as in 3. This is borne out in practice and the poses for most compounds are those expected although it was notable that only one of the Glide protocols was able to dock the methylated quinolinone 9. The scores arising from each pose are presented in Table S2 in the ESI† and summarised in Table 1 and show that although the binding poses are similar to that observed for 3, the resulting scores do not correlate well with either pIC₅₀ or LLE. The best correlation for pIC₅₀ is with Glide docking into P2 using XP1 which gives an R² value of 0.43 and RMSE of 1.40. For LLE, docking into P2 using XP1 gives R² of 0.6 and RMSE of about 1.8. When the experimental values that fall outside the range of the assay are excluded from the correlation (compounds 5, 8, 9 and 10), the best correlation for pIC₅₀ is for Glide docking into P3 with SP1 which method gives R² of 0.68 and RMSE of 0.77. For LLE it is XP1 docking into P2 which gives R² of 0.61 and RMSE of 1.44, although SP1 using P3 gives similar performance. Given the observations above concerning docking poses, it is of note that this dataset is dominated by compounds that would be expected to dock most similarly to compound 3; it is docking into that structure which is most likely to give the right correlation for the right reasons.

Table 1 Summary statistics describing the relationship between docking scores and observed values of pIC₅₀ or LLE

Protein	Method	pIC50		LLE
		R ^2	RMSE	R ^2	RMSE
P1	SP1	0.04	1.81	0.08	2.67
	XP1	0.01	1.84	0.02	2.76
	SP2	0.22	1.63	0.10	2.64
	XP2	0.00	1.85	0.06	2.71
	GOLD1	0.26	1.64	0.26	2.42
	GOLD2	0.25	1.65	0.45	2.08
	GOLD3	0.20	1.71	0.17	2.56
P2	SP1	0.08	1.77	0.04	2.73
	XP1	0.43	1.40	0.60	1.77
	SP2	0.30	1.55	0.35	2.24
	XP2	0.20	1.70	0.13	2.63
	GOLD1	0.06	1.85	0.05	2.75
	GOLD2	0.24	1.66	0.41	2.16
	GOLD3	0.18	1.73	0.15	2.60
P3	SP1	0.29	1.56	0.32	2.31
	XP1	0.06	1.79	0.15	2.57
	SP2	0.01	1.84	0.00	2.79
	XP2	0.01	1.84	0.02	2.77
	GOLD1	0.13	1.77	0.01	2.80
	GOLD2	0.13	1.78	0.25	2.44
	GOLD3	0.06	1.85	0.00	2.82

---

Quantum mechanics

Although the docking protocols above have been found to give reasonable predictivity for both geometry and interaction energy, it is interesting to see if quantum mechanical methods are able to do as well or better. In particular, there are some subtle features of how the compounds in the set vary in their interactions with the protein that might be illuminated by more physically detailed description.

To perform quantum mechanical calculations on a system such as the iNOS monomer, it is necessary to extract a model for the binding site that includes the atoms that are most important for interacting with the ligands involved. In particular, this has focused on the set of ligands 4 to 16. The binding pose of these compounds is expected to be close to that of 3 which suggested that a good description of the binding site could be provided by: (i) the backbone of residues 364–368 (ii) the Cys that interacts with the iron reduced to SMe (iii) iron porphyrin with the various sidechains on the heme porphyrin ligand removed. The required atoms were obtained by editing the protein–ligand crystal structure of 3 and are shown in Fig. 5. In order to mimic the scaffolding effect of the rest of the protein, the carbon and nitrogen atoms of the back bone (coloured orange and purple respectively) as well as the four bridging carbons of the porphyrin which are chosen to be remote from the iron centre both in terms of distance and electronically are all fixed in space using the fixed Cartesian redundant coordinate feature in Gaussian09. To further simplify these studies, the common sidechain to compounds 4–16 was abbreviated to a methyl group to give compounds 4′ to 16′. For these compounds because the rest of the molecule remains the same, the methyl substituted compounds should have parallel SAR to the fully elaborated compounds. Compounds 1 and 2 that interact with the heme iron directly and the backbone of the protein through parts of the molecule that are remote from one another were studied as the full molecule. Initial positioning of these two compounds was performed by overlaying the heme inner ring of their protein–ligand complexes with that of the QM model system. It is expected that because the model receptor excludes Glu371 and allows the porphyrin ligand to change shape that it should allow 1 and 2 to bind appropriately.

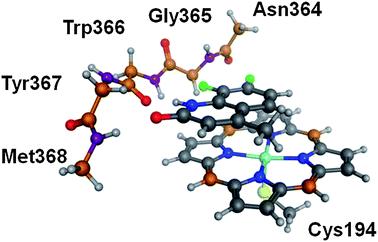Fig. 5 The quantum mechanical model system extracted from the complex of 3 with monomeric iNOS.

One matter that crystal structures are not able to probe directly is the spin state of iron. While it is assumed in this case that the iron is in its +3 oxidation state, it remains possible for it to adopt a high spin sextet or low spin doublet electronic configuration. It may also be able to adopt an intermediate spin quartet but this possibility is more difficult to treat computationally and has not been considered further. In order to address this issue, the calculations have been performed for both spin states of the iron.

A range of quantum mechanical methods were used in these studies. A set of calculations using HF were performed although these had to be combined with the quadratic convergence protocol which slows the calculations down. The B3LYP functional has long been favoured as showing a good balance of speed and accuracy although it is known to treat dispersion based interactions poorly.^9,22,23 The M06, M06-2X, M06L and M06HF functionals have all been described by the Truhlar group.^10,11 M06 is described as having general applicability, M06-2X as being good at treating aromatic–aromatic interactions but poor at transition metal chemistry, M06L as more accurate for transition metals and M06HF for a number of weakly bonded states. Because it includes an HF component M06HF was also used with the quadratic convergence protocol. The iNOS system represents a good test for this set of functionals. Finally, the ωB97XD includes an empirical correction for dispersion.¹² All of these functionals were combined with the 6-31G* basis set for all atoms apart from iron which used the lanl2dz basis set and pseudopotential.^24–26 All calculations were performed in Gaussian09 and ligand geometries were also optimized and characterized by frequency calculations whereas calculations involving the Cartesian constraints did not include frequency calculations.²⁷ The geometry of all complexes and ligands obtained by these calculations are provided as ESI.†

The geometry of the complexes of compounds 1 to 3 (the latter modelled by 13′) obtained by each method was examined and the same distances as studied for the docking methods were measured. In addition the Fe–S distance (which was not variable in the docking studies) which depends on the spin state of the iron was measured. These distances are reported in Table S3 in the ESI† and show that for all methods and all three compounds the distances found in the QM system for the doublet state of iron agree better with those observed in the crystal structures and suggest that in the crystallographic construct the iron is in the low spin state regardless of whether the ligand forms a direct interaction with the metal or not. Of the various methods studied, the M06 and M06L methods fare best overall in terms of predicting the bond lengths studied whereas M06-2X fares best for the set of distances excluding Fe–S. M06-2X is the only method that predicts that the Fe–S distance should be shorter in the sextet than the doublet and also has a smaller difference between the spin states for the Fe–N distance than other methods, this supports the suggestion that this method is less good for transition metal systems.

Finally the energy of complexation for each ligand binding to the QM model system in the two spin states has been computed, using separate optimizations of an empty receptor with the Cartesian constraints still applied. Full optimization of the isolated ligands complete the set of components needed to compute the energy change, E_complex, that corresponds to eqn 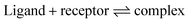(1).

The geometry of the complex for compounds 4′ to 16′ was generally obtained by editing that of the model for compound 13′ which in turn came from the crystal structure of compound 3. The ligand geometries were extracted from the complex but as with the docking, corina was used to generate a conformation for compounds 1 and 2. In both cases following optimization by all methods the geometry obtained from the complex was found to be lower in energy than that generated by corina. Compound 6′ has two possible chair conformations and both were generated for the isolated ligand and the complex and the lowest energy conformation of each was used in the resulting energy changes. The other model compounds do not have any conformational degrees of freedom and so were not studied in any more detail.

The complexation energies for the different ligands to the model receptor in doublet and sextet states are provided in Table S4 in the ESI† and performance statistics summarise this in Table 2.²⁸ In general the various methods perform well, with the best method for pIC₅₀ being M06HF with the receptor in the doublet state. This method gives an R² of 0.67 and RMSE of 0.96. By comparison, for the same set of compounds, the best docking method is GOLD1 docking into P3 which gives R² of 0.67 and RMSE of 0.98. When LLE is considered instead, the quantum mechanical methods perform significantly better and the best is once again M06HF binding to the doublet state which gives R² of 0.94 and RMSE of 0.46; the accuracy is similar to that expected in most biological assays. Many of the QM methods give excellent R² values over 0.8 and RMSE below 0.9. By contrast for the same set of LLE values, the best docking method is GOLD3 docking into P3 which gives R² of only 0.47 and RMSE of 1.56. The QM approach is sufficiently accurate to guide the design of compounds in lead optimisation where small structural changes leading to small changes in binding energy are attempted and where docking methods are often found wanting. It is worth considering why the QM methods perform so much better when modelling LLE than pIC₅₀. The model system for the QM calculations is actually each of the species shown in eqn (1) in the gas phase. No account is taken of the solvation energy of the different ligands. The clogP term takes this into account to a certain degree, to the extent that 1-octanol provides a good model for the gas phase.

Table 2 Summary statistics describing the relationship between computed E_complex and observed values of pIC₅₀ or LLE

Methods	Spin state	pIC50		LLE
		R ^2	RMSE	R ^2	RMSE
B3LYP	Doublet	0.19	1.53	0.52	1.48
HF	Doublet	0.28	1.46	0.41	1.65
M06	Doublet	0.53	1.16	0.79	0.98
M062X	Doublet	0.64	1.00	0.84	0.85
M06HF	Doublet	0.67	0.96	0.94	0.46
M06L	Doublet	0.66	0.99	0.81	0.94
ωB97XD	Doublet	0.61	1.06	0.78	0.99
B3LYP	Sextet	0.22	1.51	0.52	1.48
M06	Sextet	0.50	1.20	0.76	1.04
M062X	Sextet	0.63	1.03	0.84	0.86
M06L	Sextet	0.61	1.06	0.79	0.99
ωB97XD	Sextet	0.27	1.45	0.37	1.69

---

Although it is gratifying to find computational methods that are able to correctly rank compounds, it is arguably of more use to obtain structural insight from those calculations to guide future design. For instance, there is an increase in LLE upon addition of an extra fluorine atom going from 4 to 13 and also on going from 12 to 16. This is mirrored in an increased E_complex computed by M06HF. Examination of the geometries obtained by M06HF show that the more fluorinated compound is moved slightly away from the protein backbone (the carbon bearing H or F moves by 0.15 Å) suggesting weaker interaction at that point while the donor–acceptor pair move less which suggests that the increased E_complex must be due to an improvement in the π–π interaction caused by addition of fluorine.

It is of interest that the binding energies of compounds 1 and 2 are predicted to be smaller than those of model compounds 4′ to 16′ despite the fact that 1 and 2 are measured to be tight binding compounds. It is possible that this discrepancy arises because of errors introduced by reducing to model compounds, or an inadequacy of the description of the gap between doublet and sextet states or due to a kinetic barrier to spin flipping that prevents some of the compounds from achieving their lowest energy state (Scheme 1). Although the sextet state is generally higher in energy than the doublet, it is possible that only the sextet state is kinetically accessible. For compounds 4′ to 16′, the gap between the doublet and the sextet is computed to change by no more than about 1 kcal mol⁻¹ upon complexation. However, for compounds 1 and 2, the gap is made larger by around 8–12 kcal mol⁻¹ according to B3LYP, M06 and M06L. This would provide a significantly higher driving force for the spin flip for these two compounds than for the others. If the compounds that do not form direct bonds to iron (4 to 16) are not able to access the doublet state of the complex whereas compounds, like 1 and 2 can then this would provide them a significant extra binding energy. It may also instill these compounds with slow off rate kinetics. This interesting possibility could be the subject of experimental studies.

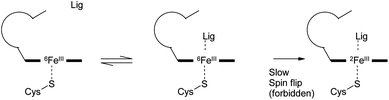Scheme 1 Potential mechanism of inhibition for compounds that form a direct interaction with iron not available to other ligand types.

Conclusions

The key observation is that if a carefully selected model receptor is used with well considered model compounds, quantum mechanics can provide useful insight to understand the interaction between proteins and ligands across substantial numbers of compounds. Docking can also provide useful input but doubts will always remain about the quality of the parameterisation of any given ligand and its interactions, whereas in principle QM methods should not have the same problem. This is particularly important in lead optimisation where unusual functionality might be considered as a way to modulate the pharmaceutical properties of a compound. The QM methods can also be used to provide insight into the origin of changes in interaction energy. QM calculations of E_complex in the gas phase are found to model LLE better than pIC₅₀ itself, likely due to the lipophilicity term accounting for solvation effects; this also might be viewed as a positive feature of the approach. The XP1 methodology in Glide performs well for obtaining binding poses for compounds in this system which involves a complex balance of polar interactions, π–π stacking and direct interactions with a metal atom. Of the functionals examined, the M06, M06L and M06HF methods perform well in terms of reproducing experimental geometries and correlating with LLEs. The combination of docking to generate interaction geometries and QM to predict binding constants could be a powerful tool for medicinal chemistry.

Acknowledgements

We would like to acknowledge the great efforts from many co-workers at AstraZeneca towards understanding of the iNOS system. In particular those from former AstraZeneca sites at Montreal and Charnwood are recognised.

Notes and references

1. W. K. Alderton, C. E. Cooper and R. G. Knowles, Biochem. J., 2001, 357, 593–615,  DOI:10.1042/0264-6021:3570593.
2. A. C. Tinker and A. V. Wallace, Curr. Top. Med. Chem., 2006, 6, 77–92,  DOI:10.2174/156802606775270297.
3. D. D. Davey, M. Adler, D. Arnaiz, K. Eagen, S. Erickson, W. Guilford, M. Kenrick, M. M. Morrissey, M. Ohlmeyer, G. Pan, V. M. Paradkar, J. Parkinson, M. Polokoff, K. Saionz, C. Santos, B. Subramanyam, R. Vergona, R. G. Wei, M. Whitlow, B. Ye, Z. Zhao, J. J. Devlin and G. Phillips, J. Med. Chem., 2007, 50, 1146–1157,  DOI:10.1021/jm061319i.
4. C. Bonnefous, J. E. Payne, J. Roppe, H. Zhang, X. Chen, K. T. Symons, P. M. Nguyen, M. Sablad, N. Rozenkrants, Y. Zhang, L. Wang, D. Severance, J. P. Walsh, N. Yazdani, A. K. Shiau, S. A. Noble, P. Rix, T. S. Rao, C. A. Hassig and N. D. Smith, J. Med. Chem., 2009, 52, 3047–3062,  DOI:10.1021/jm900173b.
5. J. E. Payne, C. Bonnefous, K. T. Symons, P. M. Nguyen, M. Sablad, N. Rozenkrants, Y. Zhang, L. Wang, N. Yazdani, A. K. Shiau, S. A. Noble, P. Rix, T. S. Rao, C. A. Hassig and N. D. Smith, J. Med. Chem., 2010, 53, 7739–7755,  DOI:10.1021/jm100828n.
6. C. Wei, B. R. Crane and D. J. Stuehr, Chem. Rev., 2003, 103, 2365–2383,  DOI:10.1021/cr0204350.
7. K. McMillan, M. Adler, D. S. Auld, J. J. Baldwin, E. Blasko, L. J. Browne, D. Chelsky, D. Davey, R. E. Dolle, K. A. Eagen, S. Erickson, R. I. Feldman, C. B. Glaser, C. Mallari, M. M. Morrissey, M. H. J. Ohlmeyer, G. Pan, J. F. Parkinson, G. B. Phillips, M. A. Polokoff, N. H. Sigal, R. Vergona, M. Whitlow, T. A. Young and J. J. Devlin, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 1506–1511,  DOI:10.1073/pnas.97.4.1506.
8. Compound 1 is taken from structure with pdb code 1dd7, compound 2 from structure with pdb code 2oro while compound 3 is taken from an analogous structure obtained at AstraZeneca.
9. K. E. Riley, M. Pitonak, P. Jurecka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063,  DOI:10.1021/cr1000173.
10. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
11. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
12. J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620,  10.1039/b810189b.
13. Compounds 1 and 2 are studied in a different assay to compounds 3 to 16 but related examples have been studied in an assay within AstraZeneca and the reported IC₅₀ values are broadly in line with what is found for them.
14. P. D. Leeson and B. Springthorpe, Nat. Rev. Drug Discovery, 2007, 6, 881–890.
15. clogP, version 4.71; Daylight Chemical Information Systems, Santa Fe, NM.
16. G. Jones, P. Willett and R. C. Glen, J. Mol. Biol., 1995, 245, 43–53,  DOI:10.1016/S0022-2836(95)80037-9.
17. S. B. Kirton, C. W. Murray, M. L. Verdonk and R. D. Taylor, Proteins: Struct., Funct., Bioinf., 2005, 58, 836–844,  DOI:10.1002/prot.20389.
18. Glide, version 5.7, Schrödinger, LLC, New York, NY, 2011.
19. R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley, J. K. Perry, D. E. Shaw, P. Francis and P. S. Shenkin, J. Med. Chem., 2004, 47, 1739–1749,  DOI:10.1021/jm0306430.
20. R. A. Friesner, R. B. Murphy, M. P. Repasky, L. L. Frye, J. R. Greenwood, T. A. Halgren, P. C. Sanschagrin and D. T. Mainz, J. Med. Chem., 2006, 49, 6177–6196,  DOI:10.1021/jm051256o.
21. T. A. Halgren, R. B. Murphy, R. A. Friesner, H. S. Beard, L. L. Frye, W. T. Pollard and J. L. Banks, J. Med. Chem., 2004, 47, 1750–1759,  DOI:10.1021/jm030644s.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
23. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
24. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
25. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
26. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009.
28. Because compounds 1 and 2 are not part of the series with 4 to 16 in which a common sidechain is abbreviated to a methyl group, it is difficult to include all of the compounds in any statistical summary and so the experimental data for 4 to 16 only has been used and compared to the complexation energies for 4′ to 16′.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2md20159c

---