 Open Access Article
Open Access ArticleScaling and systems biology for integrating multiple organs-on-a-chip†
John P.
Wikswo
*abc,
Erica L.
Curtis
ab,
Zachary E.
Eagleton
ab,
Brian C.
Evans
ab,
Ayeeshik
Kole
ab,
Lucas H.
Hofmeister
ab and
William J.
Matloff
ab
aVanderbilt Institute for Integrative Biosystems Research and Education, Vanderbilt University, Nashville, TN 37235, USA. E-mail: john.wikswo@vanderbilt.edu; Fax: +1 615-322-4977; Tel: +1 615-343-4124
bDepartment of Biomedical Engineering, Vanderbilt University, Nashville, TN 37235, USA
cDepartment of Molecular Physiology & Biophysics and Department of Physics & Astronomy, Vanderbilt University, Nashville, TN 37235, USA
First published on 14th June 2013
Abstract
Coupled systems of in vitro microfabricated organs-on-a-chip containing small populations of human cells are being developed to address the formidable pharmacological and physiological gaps between monolayer cell cultures, animal models, and humans that severely limit the speed and efficiency of drug development. These gaps present challenges not only in tissue and microfluidic engineering, but also in systems biology: how does one model, test, and learn about the communication and control of biological systems with individual organs-on-chips that are one-thousandth or one-millionth of the size of adult organs, or even smaller, i.e., organs for a milliHuman (mHu) or microHuman (μHu)? Allometric scaling that describes inter-species variation of organ size and properties provides some guidance, but given the desire to utilize these systems to extend and validate human pharmacokinetic and pharmacodynamic (PK/PD) models in support of drug discovery and development, it is more appropriate to scale each organ functionally to ensure that it makes the suitable physiological contribution to the coupled system. The desire to recapitulate the complex organ–organ interactions that result from factors in the blood and lymph places a severe constraint on the total circulating fluid (∼5 mL for a mHu and ∼5 μL for a μHu) and hence on the pumps, valves, and analytical instruments required to maintain and study these systems. Scaling arguments also provide guidance on the design of a universal cell-culture medium, typically without red blood cells. This review presents several examples of scaling arguments and discusses steps that should ensure the success of this endeavour.
 John P. Wikswo | John Wikswo received the B.A. degree from the University of Virginia in 1970 and M.S. and Ph.D. degrees, all in physics, from Stanford University in 1973 and 1975, respectively. He joined the Vanderbilt University faculty in 1977, where he is now the Gordon A. Cain University Professor, the A. B. Learned Professor of Living State Physics, and Professor of Biomedical Engineering, Molecular Physiology and Biophysics, and Physics. He uses novel instrumentation, quantitative measurements, and mathematical models to study and control cellular metabolism and signaling in organs on chips. |
 Erica L. Curtis | Erica Curtis received the B.E. degree in biomedical engineering from Vanderbilt University in 2013. As a participant in SyBBURE (Systems Biology and Bioengineering Undergraduate Research Experience), a program funded by Gideon Searle at Vanderbilt, she developed and tested a platform for performing quasi-real-time integration of microfluidics with mass spectrometry instrumentation for the purpose of studying yeast systems biology. In 2013 she was awarded a National Science Foundation Graduate Research Fellowship. |
 Zachary E. Eagleton | Zachary Eagleton received the B.E. degree in biomedical engineering from Vanderbilt University in 2013. At Vanderbilt he worked on the development of a low resource diagnostic test for malaria. The focus of his research was the use of optical coherence tomography to study flow patterns in small colloidal drops. He is currently a research and development engineer at Philips North America. |
 Brian C. Evans | Brian Evans received the B.S.E. degree in biomedical engineering from Case Western Reserve University in 2010 and the M.S. degree in biomedical engineering from Vanderbilt University in 2013. He is currently pursuing his Ph.D. in biomedical engineering at Vanderbilt University and is a National Science Foundation Graduate Research Fellow. At Vanderbilt he works on the development of novel biomaterials to enhance the intracellular delivery of biomacromolecular therapeutics for applications ranging from cardiovascular disease to cancer therapy. |
 Ayeeshik Kole | Ayeeshik Kole received the B.E. degree in biomedical engineering with honors from Vanderbilt University in 2012. At Vanderbilt his research focused on the use of high-resolution mass spectrometry in conjunction with microfluidics for the demonstration of cell system control. He is currently in the Medical Scientist Training Program at Indiana University School of Medicine, where he will earn a dual degree with a doctorate from the Purdue University Weldon School of Biomedical Engineering. |
 Lucas H. Hofmeister | Lucas Hofmeister received the B.S. degree in biomedical engineering from the University of Tennessee at Knoxville in 2010. He is currently pursuing his Ph.D. in biomedical engineering at Vanderbilt University, where he is an American Heart Association Graduate Research Fellow. At Vanderbilt Lucas's research is focused on developing targeted nanoparticle drugs to prevent and treat atherosclerosis, and he is a research coordinator for SyBBURE (Systems Biology and Bioengineering Undergraduate Research Experience), a program funded by Gideon Searle. |
 William J. Matloff | Will Matloff received the B.E. degree in biomedical engineering and mathematics from Vanderbilt University in 2013. As a participant in SyBBURE (Systems Biology and Bioengineering Undergraduate Research Experience), a program funded by Gideon Searle at Vanderbilt, he worked on building automated microfluidic chemical mixing tools for systems biology research. |
Introduction
Organ-on-chip (OoC) microphysiological systems (MPS) programs funded by a variety of governmental agencies in the United States, Europe, and Asia are developing individual organs-on-a-chip and, more important, coupling human-cell, multi-organ, organ-on-chip and larger human organ construct (HoC) systems for drug development and studies of drug toxicity and efficacy. While individual OoC technologies have advanced considerably in the past decade,1–6 significant technical challenges must be met before multiple organs can be integrated into a single system of coupled organs.1 Only limited reports describe coupled organs,2,3 and there is not yet a full understanding of how biological scaling laws apply to multiple, coupled OoCs. To replicate human physiology and drug response with interconnected human OoCs/HoCs, it is critical that each OoC/HoC has the correct relative size. Extensive literature describes differences in organ size between animal species whose body mass, Mb, spans 6 orders of magnitude from shrew to whale. Organ size does not scale proportionally (isometrically) with Mb, but instead obeys a number of different allometric power laws that describe, for example, how as the animal's linear dimension L increases, its mass increases as L3, and hence the cross-sectional area of the bones must increase non-linearly.4 Metabolic rates may exhibit Mb3/4 scaling,5–8 pulmonary and vascular networks exhibit Mb3/4 scaling,9,10 and blood circulation time scales as Mb1/4.11Table 1 shows the coefficients A and B, derived from primates with body masses of 10 g to 100 kg,12 to compute organ mass M = AMbB. When multiple organs are connected, their relative size could be normalized to mass, surface area, volumetric flow, or other geometric measures. The challenge is to specify the appropriate scaling law(s) for specific applications, whether it be to construct a physically functional organ (e.g., a pumping heart), a pharmacodynamic model (3D co-culture systems), or both simultaneously in a MPS.| Human | milliHuman (mHu) | microHuman (μHu) | Organ mass ratios | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Body mass: | 60 kg | 60 g | 60 mg | |||||||
| Organ | A | B | M, g | Organ/Body | M, g | Organ/Body | M, mg | Organ/Body | M mHu /MHu | M μHu /MHu |
| a Coefficients for human brain scaling: 80–90. The corresponding number for monkeys is 20–30, and great apes 30–40. | ||||||||||
| Liver | 33.2 | 0.93 | 1496 | 2.5% | 2.4 | 4.0% | 3.9 | 6.6% | 1.62E-03 | 2.63E-06 |
| Brain | 85 | 0.66a | 1268 | 2.1% | 13 | 22% | 139 | 232% | 1.05E-02 | 1.10E-04 |
| Lungs | 9.7 | 0.94 | 455 | 0.76% | 0.69 | 1.2% | 1.0 | 1.7% | 1.51E-03 | 2.29E-06 |
| Heart | 5.2 | 0.97 | 276 | 0.46% | 0.34 | 0.57% | 0.42 | 0.70% | 1.23E-03 | 1.51E-06 |
| Kidneys | 6.3 | 0.87 | 222 | 0.37% | 0.54 | 0.91% | 1.3 | 2.2% | 2.45E-03 | 6.03E-06 |
| Pancreas | 2.0 | 0.91 | 83 | 0.14% | 0.15 | 0.26% | 0.29 | 0.48% | 1.86E-03 | 3.47E-06 |
| Spleen | 1.5 | 0.85 | 49 | 0.081% | 0.14 | 0.23% | 0.39 | 0.64% | 2.82E-03 | 7.94E-06 |
| Thyroid | 0.15 | 1.12 | 15 | 0.025% | 0.0064 | 0.01% | 0.0028 | 0.0047% | 4.37E-04 | 1.91E-07 |
| Adrenals | 0.53 | 0.7 | 9.3 | 0.016% | 0.07 | 0.12% | 0.59 | 0.98% | 7.94E-03 | 6.31E-05 |
| Pituitary | 0.03 | 0.49 | 0.00081% | 0.0044 | 0.0074% | 0.040 | 0.067% | 9.12E-03 | 8.32E-05 | |
For convenience we select three scales for our discussion: Human (Hu), milliHuman (mHu), and microHuman (μHu); we assume an adult Hu mass of 70 kg and hence a mHu mass of 70 g and a μHu mass of 70 mg. In theory, a system with multiple organs could be designed to represent any fraction of a human, possibly a nanoHuman (nHu). In this paper we discuss the factors that guide the specification of the size of each organ in a coupled system. We hope that this will provide guidance to the ongoing efforts to design and implement coupled organ systems.
Allometric scaling
However, this scaling may not produce valid parameters for mHu and μHu systems. The most notable observation from Table 1 is that the large human brain size (a = 85) and its allometric scaling exponent (b = 0.66) would produce a μBrain that has twice the body mass of the μHuman. The nature of this problem can be seen in Fig. 1. The intersections of the allometric scaling lines for each organ with the vertical mHu and μHu lines in Fig. 1A indicate the allometric mass of the mHu and μHu organ in Table 1. The scaling of each organ relative to its mass for a 1.0 Hu is shown in Fig. 1B, which suggests that allometric scaling for the brain, pituitary, and adrenals will produce larger than average organs, while that for the thyroid will be smaller. Given its median position, one might consider using the pancreas scaling as a starting point, with B = 0.91.
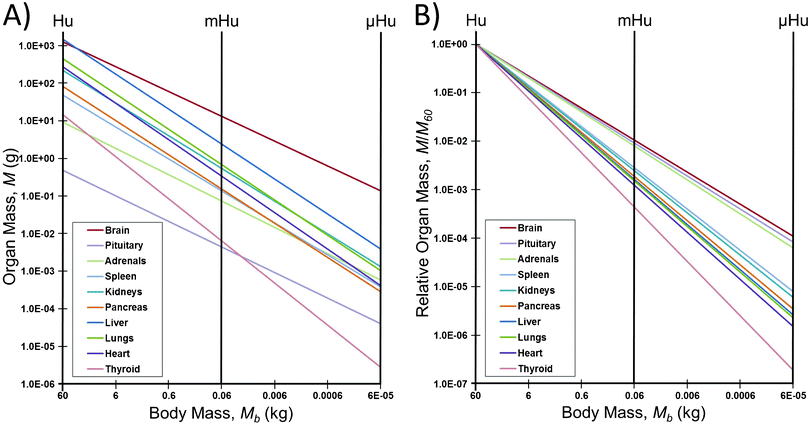 | ||
| Fig. 1 How allometric scaling might (mis)inform mHu and μHu scaling when known power laws12 are used to extrapolate from humans. A) Organ mass in grams. B) The mass of each organ relative to that for a 1.0 Hu. Note the range in allometric slopes for different organs, and that a 106 reduction in body mass leads to only a 104 reduction in the mass of the brain, pituitary, and adrenals, leading to a μBrain with twice the mass of the μHuman. | ||
There would be similar issues were allometric scaling used to set the heart rates and blood circulation times. The heart rate of a mouse is approximately one hundred times that of an adult human,11 and hence one would not want to assemble a mHu whose organs and the connecting vasculature would require perfusion at rates that would not be realistic for a human. Human cells might not function properly or for long when placed in organs sized to a mouse.
Simple scaling will also fail for other reasons. A working heart cannot be less than one cardiomyocyte thick. Key endothelial layers must be one cell thick, and only one cell, independent of organ size. Certain immune cells function at such a low density (3000 leukocytes per ml of cerebral spinal fluid (CSF)) that the breadth of acquired immune response may not be replicable in a μBrain with a CSF volume of ∼1 μL that would contain about 3 leukocytes. Cellular heterogeneity should not scale.
Interconnected “histological sections”
This approach is advantageous when one desires to recapitulate only a subset of an organ's function, for example, a lung alveolus with epithelial, endothelial, immune, and mechanical interactions but without requiring gas transfer,17,18 a heart-on-a-chip that elucidates drug effects on cardiac electrophysiology or mechanical activity but doesn't pump blood,19,20 or a gut-on-a-chip that does not consider bile activity, nutrient and water uptake, or abluminal transport.21 In this case, the system may scale linearly, and in effect one is creating a local system with inputs, outputs, and selected physiological controls.22
However, the situation becomes more complex when two or more “histological sections” are coupled in series or parallel. Correct representation of organ-organ interactions is now determined by the size of each section and the volume of their shared fluid. A scaling mismatch of the two organs could make one section either oblivious of the other or dominated by it. Too large a fluid volume would delay or minimize organ-organ interactions. Furthermore, a small histological section may not be representative of the complexity of the organ as a whole and may be missing essential biological features that can alter biological responses to stimuli.
However, engineering all in vivo conditions artificially would fundamentally eliminate the need to couple the organ systems, and the same results could be achieved by running each organ in its own microenvironment. This contradicts the purpose of coupling the organ systems together, in which the goal is to observe the most physiologically accurate response and intra-organ signaling to perturbations in the system without a priori biases. Hence we need functional scaling of our “sections”.
Functional scaling
One limitation of the approach is that functional scaling may result in oversimplification of OoCs and limit the translatability of the results achieved. Another is that it may not be possible to create an organ that recapitulates more than one organ function. Just as we saw in Fig. 1, different functions may scale differently with respect, for example, to surface-volume ratio. One could devise two-part organs, e.g., a heart with separate chambers for recapitulating mechanical and electrophysiological functions.19,20
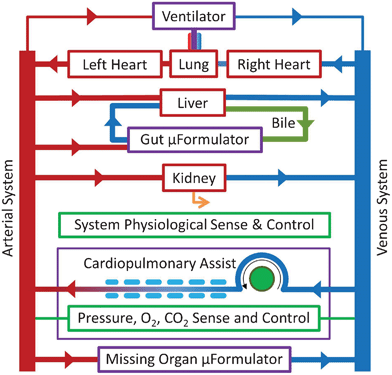 | ||
| Fig. 2 The mHu Advanced Tissue-engineered Human Ectypal Network Analyzer (ATHENA), a milliHuman (Homo chippus) being developed by Los Alamos National Lab, Vanderbilt University, Charité Universitätsmedizin Berlin, University of California–San Francisco, Harvard University, and CFD Research Corporation with the support of the Defense Threat Reduction Agency (DTRA).23 Figure from Wikswo et al., 2013, with permission.1 | ||
Examples of organ scaling
We now present several examples of scaling considerations that might apply to the creation of individual organs. In the ESI† Scaling Spreadsheet, we present an extensive compilation, with appropriate references from a vast and often inconsistent literature, of ∼250 anatomical and functional parameters for the brain, heart, kidney, liver, lung, and blood that can be used to guide the design, modeling, and validation of OoCs and HoCs, using either allometric or functional scaling. In the following paragraphs we provide a brief discussion of the importance of several of the parameters for each organ.Our examples are limited to the major organs that are common therapeutic targets and do not include other significant tissues such as adipose, bone, endocrine, skeletal muscle, or skin tissues. When attempting to recapitulate in vivo metabolic and physiologic demands of a coupled organ system, one must consider that these tissues also play a key role in metabolic demands and biochemical signaling. As a result, design criteria for OoC scaling should take into consideration the presence, absence, and simulation of various organs when scaling certain physiologic parameters. The ESI† Scaling Spreadsheet and the discussion of each example below should provide guidelines for a rational approach to the design of integrated HoC/OoC systems.
Brain
There are a growing number of reports on in vitro, flow-based models of the neurovascular unit (NVU) and blood-brain barrier (BBB),27–31 and other neural co-cultures.32–35 For this scaling analysis, we choose to reduce the brain from its extreme structural and functional complexity and focus our analysis on scaling of the NVU, which is the most important functional unit for ADMET (absorption, distribution, metabolism, and excretion toxicity) studies and functionally represents the BBB. The NVU consists of a capillary and its surrounding cell types, including endothelial cells, pericytes, astrocytes, microglia, and neurons. Correct and, importantly, feasible scaling of an NVU will require a unique combination of geometrical and biochemical scaling.This is important because the brain is particularly complex, and the literature is riddled with inconsistent physiological data. For example, one of the most common misconceptions of brain physiology is that glial cells outnumber neurons by ten to one, where in fact the ratio for neocortical glia to neurons is 1.2, and the ratio of non-neuronal to neuronal cells ranges from 0.2 to 1.5, depending upon the brain region. These ratios are of exquisite importance when constructing a brain-on-a-chip.
Many of these misconceptions arise from the difficulty of studying the brain. Brain tissue is very diverse across species, and therefore studying the physiological parameters of rodent or other brains will not give an accurate representation of human physiology. The best understanding we can gain from non-human studies comes from the primate brain. The architectural complexity of the brain also complicates the analysis of simple parameters such as capillary density and cell numbers. Neurons can traverse multiple brain regions. Significant advances have been made in this regard by Herculano-Houzel et al., with their isotropic fractionator technique,36 and improvements will continue to be made with more advanced analytical techniques such as the transparent brain recently developed by Chung et al.37
As the ESI† Scaling Spreadsheet indicates, gray matter and white matter may also contain different ratios of cell types and orientations. These parameters are important for scaling in brain region-specific ways. The task of assembling these parameters is complicated because most groups studying the brain make empirical measurements on a specific brain region and not the whole-brain scale. In addition, metabolic parameters such as oxygen consumption are difficult to measure for specific brain regions, but capillary density and cell number distribution are far easier to measure for isolated brain regions. To further complicate gathering this information, many of these parameters had to be assembled by studying the control groups from manuscripts investigating a specific disease state. Finally, it is unclear which of these parameters will be most important for the end goal of creating and integrating a brain-on-a-chip. Therefore, in the Scaling Spreadsheet we present our best understanding of the necessary physiological parameters and their sources for the reader to evaluate and employ as necessary. We envision this table of parameters as evolving alongside our understanding of the human brain and the challenges of building HoCs.
Functional scaling of the brain is largely driven by metabolism. In humans the brain represents 20% of the overall metabolic load and 2% of overall body mass.38,39 Moreover, the relative metabolic demand of the brain grows more slowly than body and brain mass (allometric exponent 0.873).40,41 The total energy consumption by the brain varies linearly with the number of neurons in the brain at a rate of 5.79 × 10−9 μmol glucose min−1 neuron−1.40 However, it is unclear if an in vitro brain-on-a-chip (BoC) can recapitulate the metabolic rate of the in vivo case. Therefore, we believe that a mHu and μHu BoC, for example, should be scaled linearly by the number of neurons in the adult human brain, and the remaining components of the brain should be scaled according to the metabolic demand of the number of neurons in the BoC. Autoregulation of the BBB by all cellular components of the NVU also necessitates correct scaling of the cell numbers in the BoC and capillary surface areas in relation to the metabolic demand of the neurons which they support. According to the cellular composition of the cerebral cortex, the NVU should consist of 1.2 astrocytes/neuron, 0.46 vascular cells/neuron, and 0.2 microglia/neuron.42
The greatest challenge in geometrical scaling of the brain is realization of the capillary density of the brain, which has one of the largest capillary densities of any organ. The average human adult has between 12 and 18 m2 of BBB, or 150 to 200 cm2 g−1 of tissue. The necessity of providing neurons with such a high capillary surface area per neuron (174 μm2 neuron−1) will challenge fabrication techniques and is most feasible in microfluidic systems.42,43 In association with the vasculature, pericytes cover around 30% (5 m2, 667 cm2 g−1) and astrocytes cover around 99% (18 m2, 200 cm2 g−1) of the abluminal surface of brain microvasculature.44–46
Scaling of blood flow in a BoC relative to other OoCs could present significant challenges. The human brain has a flow rate of 7 L min−1, which accounts for 13% of total blood flow.47–50 This number should scale functionally with the size and metabolism of the BoC in order to supply sufficient glucose, oxygen, and other nutrients and remove resulting metabolites. Values such as the central metabolic rate for oxygen (CMRO2) of 3.2 mL/100 g min should remain constant with decreased size and will be a useful readout of BoC success.47 Another critical factor is maintenance of the shear stress at the endothelial barrier. Blood surrogate flow must be supplied to a BoC with a sufficiently small capillary cross-sectional area to maintain a shear of around 1.5 Pa without excessive volumetric flow rates.51–53 This value will also determine the pharmacokinetic parameters of the brain by influencing the residence time and Péclet number of the BoC capillaries.
In summary, the scaling of a BoC revolves around the NVU and is focused on delivering the correct metabolic demand relative to other organs and the unique transport properties of the BBB. As these technologies develop it will become more clear which of these scaling laws are critical to success, and also where scaling can or must be broken in favor of realistic implementation of these technologies for routine studies.
Heart
The scaling considerations that apply to the development of heart tissue revolve around tissue architecture and composition, electrical conduction, biochemical factors, metabolism, and fluid flow. An important decision that must be addressed early in the development of an OoC/HoC heart is whether it is to be a working heart, i.e., support the flow of blood against a mechanical load (including the pulmonary or peripheral vasculature),54–58 or serve as an electromechanical sensor of the effects of drugs and their metabolites on cardiac performance.19,20The cardiac parameters in the ESI† Scaling Spreadsheet support several of the major cardiac scaling issues we have discussed. For example, if a heart construct is to be used as the fluidic pump that provides and supports circulation of a blood surrogate through a coupled OoC system, then functional parameters such as transport capacity, ejection fraction, and fractional cell shortening become scaling issues of paramount importance. The ESI† Scaling Spreadsheet is constructed to circumvent the need to look up individual organ parameters, which often vary throughout the literature and species type. Furthermore, a desired organ size can be used to quickly calculate approximate parameter values for an organ of a certain size based upon both allometric and functional scaling. Thus the table is a valuable resource for quickly and efficiently approximating functional and structural parameters for OoC design, and it also highlights a number of the scaling issues that must be considered in terms of design criteria.
Composition and biochemical factors are of significant import in modeling mammalian heart tissue, which is intrinsically heterogeneous, containing cardiomyocytes, fibroblasts, vascular smooth muscle cells, endothelial cells, and neuronal cells among other less abundant non-myocytic cells.59 These cell types all interact through a variety of biochemical factors and signaling mechanisms to maintain cardiomyocyte phenotype and tissue function.60–65 In terms of these fundamental signaling pathways, one may need to consider exogenous sources of biochemical factors that are scaled to the targeted tissue construct's mass, volume, and composition. One must also consider that the size of the organ construct will limit the ability to accurately recreate features of the mammalian heart (e.g., if the size of a heart construct is limited to 1–2 cells thick, as would be required for a μHeart, then the realization of an endocardium and the incorporation of all native cell types will not be feasible, whereas this might be possible with a 15-myocyte thick mHeart).
Tissue architecture and metabolism must also be considered. The specialized cells that comprise heart tissue are organized in a highly specific structure that results in a transendothelial biochemical gradient that forms the blood-heart barrier. Furthermore, the fibers in the heart are aligned in anisotropic, helically wound layers that impart unique, spatiotemporally dynamic biomechanical properties to heart tissue. This issue is of key importance when considering the use of a scaffold or substrate as a culture platform, since mismatched substrate and tissue properties can result in a significant reduction in cardiac pump function. In addition to its complex architecture, heart tissue is very metabolically active and requires sufficient oxygenation. Thus, scaling cellular metabolism is another concern, as the balance of energy supply and demand is essential for maintaining cardiac pump function. To meet this demand, native heart tissue contains a dense, complex network of myocardial capillaries that penetrate orthogonally through the myocardium. However, recapitulating a complex network of small diameter capillaries may not yet be feasible in vitro, although recent developments are promising.66,67 As a result, the utilization of planar diffusion may suffice for now, as the reduced thickness of the cultured myocardium of engineered heart tissue may allow for adequate oxygenation without vascular perfusion.
Fluid flow and other biomechanical stimulation of cardiac tissue are integral to a variety of the heart's intrinsic control mechanisms. Synchronized cardiomyocyte contraction results in complex mechano-electrical feedback mechanisms through the activation of stretch-activated channels and modulation of cellular calcium handling, the endocardium responds to both fluid shear stresses and pulsatile cyclical strain by releasing paracrine and endocrine factors, and baroreceptors transduce sensory feedback into various forms of cellular signaling. Under normal fluid shear conditions, endothelial and vascular smooth muscle cells have relatively low rates of proliferation, whereas abnormal hemodynamic conditions result in pathological cellular phenotypes that are associated with a number of cardiovascular diseases.68 The proper scaling of biomechanical properties in conjunction with fluid dynamics is therefore crucial to modeling both normal and pathological cardiac tissue. In order to achieve physiologic fluid shear stresses in miniaturized working heart constructs, one must appropriately apply volumetric and resistance scaling by modulating flow rates and blood surrogate/media viscosity in accordance with the geometry of the bioreactor and tissue construct. These scaling issues only gain significance when integrating heart-on-a-chip technologies into multi-organoid constructs, especially if the heart tissue is to be responsible for cardiac output to perfuse the entire organ network. Here, cardiac output (i.e., stroke volume, heart rate, ejection fraction, etc.), tissue size, metabolic and perfusion demands of other tissues, total peripheral resistance, and resident blood surrogate volume are all variables that need to be properly scaled relative to each other. However daunting it may be, the scaling of biological variables for the integration of multiple human organ constructs provides a basis for fabricating functional mHu or μHu constructs that would streamline drug development and discovery and produce a more realistic cellular microenvironment than monolayer monocultures in Petri dishes or well plates.
Overall, each of these scaling issues merits consideration in the design of engineered heart constructs, and optimization of heart-on-a-chip technologies, not to mention all organ-on-a-chip technologies, is a compromise between verisimilitude and a functional abstraction.
Kidney
Building an in vitro kidney model necessitates architectural, functional, and biochemical scaling. The nephron consists of three structurally and functionally distinct subunits – glomerular filtration, proximal reabsorption and secretion, and urine concentration–which must scale individually as well as relative to one another in order to preserve whole organ functionality.The ESI† Scaling Spreadsheet provides examples and literature references for a range of functional and structural factors that need to be considered in kidney scaling. First and foremost, the kidney model must scale in order to sufficiently filter the circulating volume of blood in the HoC construct and achieve physiologically relevant rates of the glomerular filtration. Second, the model must be manipulated to facilitate physiological rates of fractional reabsorption, a challenging feat due to the wide discrepancies between in vivo functionality and in vitro performance. The kidney also provides a unique example of an organ in which the preservation of geometrical features, such as the countercurrent mechanism and exchanger, is critical to realizing an accurate model of the human kidney.
Functional scaling begins in the glomerulus. The glomerular filtration rate (GFR) in a 70 kg human produces 125 mL min−1 of ultrafiltrate and therefore 125 μL min−1 in a functional milliHuman (mHu).39 The ratio of the surface area of the glomerular hemofilter to porous surface area can be optimized in the model to achieve this rate of filtration, given that a physical filter will be different from a biological one.
Recapitulation and subsequent scaling of the specific transport, metabolic, endocrine, and immune activities of the renal tubules pose formidable fabrication and scaling challenges.69,70 A potential approach begins with functional scaling of active solute reabsorption rate in the proximal tubule. For example, a 70 kg human normally filters 180 g per day of D-glucose, almost all of which is reabsorbed in the proximal tubule; therefore, a mHu kidney must scale to filter and subsequently reabsorb about 180 mg of glucose per day.71 Because metabolic activity and active transport abilities of the proximal cells in vitro may differ significantly from in vivo quantities, preliminary in vitro studies must be conducted to characterize the phenotype of human proximal tubule cells in single hollow fibers. From these results, we can predict the number of cells and surface area required for functional scaling of solute reabsorption. Manipulation of geometric dimensions or the use of parallel proximal tubule modules can ensure that the proximal tubule model can receive the appropriate volume of ultrafiltrate from the glomerular unit.
Although the scaling of the urine-concentrating mechanism must encompass functional scaling concepts, the approach must also pay particular attention to scaling the critical architecture of the loop of Henle. Although the relation of absolute loop length and urine-concentrating ability between species is highly debated, the creation of the corticomedullary osmotic gradient is unequivocally linked to active reabsorption of Na+ as well as the complex geometry of the loop of Henle.72,73 In an approach similar to that of the proximal tubule model, functional scaling in the loop of Henle can be achieved by scaling the rate of Na+ reabsorption. Active reabsorption of Na+ by Na/K-ATPase pumps located in the thick ascending limb of the loop of Henle (TAL) effectively drives the passive H2O reabsorption in the descending limb. Additionally, the Na/K-ATPase pump has been extensively characterized and is tunable with a variety of solutes, hormones, and drugs, and therefore may serve as a point of modulation for scaling purposes.74 Successful scaling may be impossible without the preservation of architectural features such as the countercurrent mechanism and exchanger. Computational modeling can be used to optimize the length and surface area to volume ratios needed to establish a physiologically relevant osmotic gradient for a human, 300 to 1200 mOsm regardless of size.75 Additionally, “preconditioning” of long loops with short loops, as seen in vivo in a ratio of 85 short to 15 long in humans, may help to maximize urine-concentrating ability.73,76
The kidney is an excellent example of a key OoC/HoC design concept: while functional and biochemical scaling may provide the best approach to scaling a histological section of a human, some organ functionalities cannot be achieved without reproduction and scaling of certain physiological architectures.
Liver
The ESI† Scaling Spreadsheet provides an overview of the available allometric scaling laws for the liver and a basis from which we can evaluate parameters that will scale and those that will not.77 Intuitively, we can identify certain parameters that will not scale. For example, cellular parameters such as sinusoidal endothelial cell (SEC) fenestration size will remain 100–1000 nm in diameter.78 Additionally, hepatocyte density (1.39 × 108 cells g−1 liver), protein concentration (90 mg g−1 liver), and liver density (1.03 g liver mL−1) are not expected to show appreciable scaling in our milli/microliver.39,79There are, however, central design parameters for which there are allometric scaling laws, but from which we can justifiably deviate for functional scaling. For functional scaling, we argue that the hepatic mass will not follow the allometric power law and instead represent 1/103 or 1/106 of what is found in a normal human. For example, although an allometric power law exists for oxygen consumption, we instead use functional scaling given that the metabolic demand per hepatocyte—approximately 0.3 to 0.9 nmol s−1/106 cells—will be equivalent in our scaled OoC.80,81 The allometric value for oxygen consumption in the mHu (O2 = 0.035 Mb0.69, with Mb in g, such that a 60 g mHu would have a hepatic oxygen consumption of 0.59 ml min−1) underestimates consumption when compared to a functional proportion of a normal human (2.06 ml min−1).9 Note that if oxygen transport through the blood surrogate is insufficient, a system of hydrophobic hollow fibers could be used to increase the interstitial oxygen concentration without affecting interstitial or blood volumes, as has been done quite successfully for liver HoCs.82,83
In addition to proper oxygen delivery, there is also a need to seed the appropriate number of cells with sufficient exposure to a blood surrogate. In vivo hepatocytes sit adjacent to the 1.4 μm perisinusoidal space (i.e., the space of Disse), which separates the hepatocytes from the sinusoidal capillary that averages 10 μm in diameter and 275 μm in length. Appropriate concerns are whether a longer and larger in vitro model of a hepatic sinusoid unit via hollow fiber (HF) bioreactors will affect nutrient delivery, create unwanted oxygen gradients, and/or add to necessary volume given the limitations of HF fabrication. Although the number of hepatocytes needed for a functional mHu is calculated to be 3 × 108 cells, it is unclear if current HF technology can support this.83–85 Neither 3-D, planar microfabricated, or hollow-fiber livers have yet achieved collection of bile, generated by the liver canaliculi, into bile ducts.
Validation of the milli- and microliver models will primarily occur via iterative in vitro–in vivo correlation of xenobiotic clearance. Several groups have conducted correlation studies, with a general belief that each drug compound, unsurprisingly, may have its own allometric power law across species (due to metabolic variations) and also a different scaling factor (due to assumptions made in their model such as diffusional barriers).86–93 For example, Naritomi et al. found that they could predict human in vivo clearance rates of eight model compounds from human in vitro data by using an animal scaling factor (Clin vivo/Clin vitro) from either a rat or a dog. Scaling factors were similar across species for each of the eight compounds, but varied from 0.3 to 26.6-fold among the compounds.89
While this variation may prove to be troublesome in the analysis of unknown compounds during drug evaluation and discovery stages, awareness of the properly scaled input parameters and thorough analysis of a wide range of model compounds (e.g., acetaminophen, diazepam) will assist in building predictive pharmacokinetic/pharmacodynamic (PK/PD) models of the OoC system.
Lastly, Boxenbaum notes in an early paper on allometric scaling of clearance rates that these models may not prove to be accurate, particularly at small masses, as the intercept of the allometric equation predicts a non-zero clearance rate at 0 g. This collapse of allometric theory at the micro- and milliscale gives credence to the necessity to scale based on organ function.22
Lung
Within the lung, the bronchial tree and the alveoli can be scaled separately. The main structures in the lung that do not scale with system size are the individual cell parameters, such as cell volume and radius. While one might not expect to scale the percent distribution of cells, this may be necessary if the efficiency of a particular cell type in a mHu or μHu differs from that in a Hu.The ESI† Scaling Spreadsheet provides a collection of both functional and structural lung variables. Inconsistencies between the allometric exponents show a disconnect between structure and function, illustrating a novel problem when constructing HoCs. As we have discussed, additional support systems, such as assistance from a microformulator, may be necessary to ensure the most accurate structure/function μLung construct incorporated onto a HoC. A robust table of scaling values is therefore a valuable reference tool when making the inevitable compromises while designing a coupled OoC system.
Allometric scaling in the bronchial region is found in the diameters of the trachea and bronchioles. Allometrically, the diameter of the terminal bronchiole scales with an exponent of 0.21, while the radius of the trachea scales with an exponent of 0.39. However, this presents a problem: allometrically scaled, a μHu would have a terminal bronchiole diameter of 30 μm, which is near the limit of current soft-lithographic microfabrication technology; were hollow fibers used for the larger bronchial tubes, with a minimum diameter of 200 μm, the microfluidic network would require approximately six binary splittings to achieve a 240 μm diameter. Either scaling laws must be broken or novel fabrication techniques94 utilized to accommodate and create a viable μHu trachea/bronchi system.9
Allometric scaling in the alveoli is critical as well. The most important function of the alveolus is oxygenation, so scaling should be addressed to meet oxygenation needs, if required for the MPS. The critical parameter to be properly scaled is surface area, as it is the main component of Fick's law and governs diffusion capacity across the alveolar-capillary barrier. Pulmonary diffusing capacity (DLO2) scales linearly with body mass with an exponent of ∼1.95 This means that the DL02/body mass ratio is relatively constant in all mammals. Diffusing capacity is related to alveolar surface area, mean barrier thickness, and capillary blood volume, and the allometric coefficients are 0.95 for surface area, 0.05 for barrier thickness, and about 1 for capillary blood volumes.95
To replicate a μHu, alveolar diameter would be 21 μm–an order of magnitude less than the average 200 μm diameter of a human. The diameter of a type 1 epithelial cell is around 20 μm. Thus any individual μHu alveolus would require only a single epithelial cell,9,96 but the entirety of alveolae for a 0.1 μHu might well be modeled by a rectangular membrane of the appropriate area.17,18
Another scaling argument that should be considered is the mass-of-tissue to volume-of-media, in this case lung tissue volume to blood volume. Blood volume is linearly related to body mass in mammals (allometric exponent of 1). Thus scaling lung tissue surface area and blood substitute volume in the HoC depends on the total mass of the system, and if both are scaled correctly then oxygen concentration should be sufficient. If scaling is ignored, problems could arise with the surface area required to supply the blood with sufficient oxygen for metabolic needs.95
A μLung would have 184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells in the alveolar region. Around 37% of those (the interstitial cells) could be eliminated, since only endothelial, type I and II cells, and macrophages are needed to create a functional alveolar-capillary unit. The correct percentage breakdown of cells is important to assure sufficient paracrine factors and surfactant production.97–99
000 cells in the alveolar region. Around 37% of those (the interstitial cells) could be eliminated, since only endothelial, type I and II cells, and macrophages are needed to create a functional alveolar-capillary unit. The correct percentage breakdown of cells is important to assure sufficient paracrine factors and surfactant production.97–99
The scaling factor that appears to present the greatest challenge to a μLung is respiration rate. Were we to use allometric scaling, a μLung would have to inspire 643 times per minute to maintain proper oxygenation. Due to the strain this would put on a 1 μm thick polymer membrane, it is likely that this frequency would have to be slowed to prevent rupture. As a result, more surface area would need to be added or higher oxygen concentrations used to compensate for the loss of rate in order to maintain a minute volume of 0.17977 mL min−1 consumption of oxygen. This highlights the challenges of scaling, especially into the micro- and nano-scales, where the limitations imposed by non-biological fabrication technologies prevent meeting design parameters without violating scaling laws,100 which could result in a less accurate abstraction. Hence it is critical to specify the desired lung functions and scale the device to achieve them.
Blood
A universal media, or blood surrogate, for HoCs and OoCs must be able to support each cell type in addition to recapitulating the blood's critical role in homeostasis through the transport of dissolved gases, carrier proteins with bound molecules, soluble nutrients, metabolites, and signaling molecules. Since blood “maintenance” is dynamic but tightly controlled by several organs and biochemical processes, development of a blood surrogate is non-trivial.Allometric scaling of blood components gives some insight into how the surrogate should be constructed. The ESI† Scaling Spreadsheet corroborates the scaling issues that must be considered in designing a blood surrogate. First, it can be seen that the concentrations of blood remain virtually the same in organisms of all sizes: conveniently, the concentrations of a remarkably large number of blood components do not scale with body mass.101 This means that the creation of a blood surrogate can benefit from the large body of work that has been completed on creating cell media. Second, it can be noted that blood volume scales linearly with mass; thus, the total volume of the blood surrogate in an OoC/HoC device should be proportional to the entire size of the device. For all non-aquatic mammals, the blood volume is about 6–7% of the total body volume.100 Scaling the blood surrogate volume with the size of the OoC/HoC device is necessary to ensure that signaling and other transported molecules are not excessively diluted and that the total mass of transported blood surrogate components is enough to support the organs. Third, the spreadsheet shows the critical functional parameters for ensuring that the cells behave in a physiological manner. The epithelial cells in contact with the blood surrogate must have the same shear stress that cells experience in the body to achieve the requisite polarization. In addition, the cells must experience the same levels of oxygen and carbon dioxide, which are dictated by the gas transport capabilities of the blood surrogate, in order to maintain the physiological metabolism of the cells. The physical properties of a number of different oxygen carriers are also shown. The spreadsheet is based upon the scaling of a complete system; as discussed above, it may be necessary to correct for the hydrodynamic, metabolic, and chemical activity of organs that are not included in the system.
Hence, little should be changed in normal blood to form a blood surrogate. However, there are other scaling issues that must be considered to ensure that the cells in the mHu and μHu behave physiologically.
First, the blood surrogate must recapitulate physiological oxygen transport properties. Experiments have shown that the rate of oxygen delivery to the cells affects the cells' metabolic rate.102 There are programmatic differences relative to the suitability of serum in an OoC/HoC system: the Defense Threat Reduction Agency (DTRA) program announcement23 precludes the use of serum, whereas the Defense Advanced Research Projects Agency (DARPA) program103 does not. If simple serum-free aqueous culture media is used, the low concentration of dissolved oxygen in the media may limit metabolic rates and affect capillary surface-to-volume scaling. Therefore, the level of oxygen transport that cells experience in vivo as enabled by hemoglobin must be functionally mimicked with the blood surrogate. Were erythrocytes not used, perfluorocarbons and hemoglobin-based oxygen carriers may be very effective for achieving this.104–106 If human or animal serum is not utilized, appropriate concentrations of carrier proteins such as albumin may be required to replicate organ-organ chemical communication.
For the purpose of supporting HoCs, the blood surrogate must maintain multiple cell types while also optimizing physiological processes. While there is no known universal serum-free media, a number of different formulations of minimal media can be used as a starting point for the creation of a medium that can support multiple cell types.107,108 To achieve optimal cell functionality and longevity, supplements must be added to this minimal medium.109
Although a number of effective medium formulations for the growth and maintenance of multiple cell types have been developed, these media mixtures have not been widely tested for interconnected HoCs. For OoC/HoC systems, this represents a significant challenge due to differential scaling, simultaneous maintenance of multiple cell types, and the recirculatory nature of HoCs. Logic dictates that during flow-through of the blood surrogate within a HoC, some components will be absorbed or metabolized, while others will be added to the blood surrogate, with a negative impact on downstream HoCs.
One method that has been successfully used to create a common blood surrogate for a number of different cells in an OoC/HoC first involves combining the established serum-free mediums of each cell type, which can be found in the literature, to create a base medium. Next, various other components, such as growth factors and supplements, are added to optimize for physiological functionality, based on a number of different physiological measures. Finally, since some of the components of the medium support one type of cell but hinder others, one of several different techniques is used to ensure that each organ receives an optimal subset of the components of the blood surrogate. Zhang et al.108 demonstrated this method by creating a blood surrogate that supported four cultured cell types: liver (C3A), lung (A549), kidney (HK-2), and adipose (HPA). Another option is to grow cells in isolated OoC/HoCs on their preferred media, and then gradually, through controlled valves, wean them slowly from this media to the universal one.
In addition, some properties of blood and related structures that exist physiologically cannot yet be replicated with HoCs. For example, capillaries, which have relatively constant size across species, are too small to be recreated at present, so care must be taken to design the HoCs such that the physical characteristics of the blood surrogate, such as flow, volume, and shear stress, match those found in the tiny capillaries. It is imperative to match the wall shear stress in HoCs to that of microvessels to achieve the same mechanotransduction and gene expression in endothelial cells as in humans.52 This might be addressed by self-organizing on-chip microvasculature.66,67
Furthermore, it is important to understand PK/PD scaling in order to add drugs to the HoC/OoCs at proper levels and to use the HoC/OoCs to predict the pharmacokinetics in humans.2,3 The classical scaling relationship for drug/signal dosing is that the body's ability to use and metabolize drugs/signals varies with surface area.110 But these scaling laws are critically dependent on the biochemical mechanisms and physical properties of the organs.111 If the organs do not functionally mimic physiology, they could fail to predict the PK/PD of humans. Differences in drug transport and metabolism in the HoC can render typical allometric PK/PD scaling useless. This can be seen clearly by the fact that PK/PD varies significantly between infants and adults.112
Finally, the blood surrogate will require supporting systems that can provide missing functionality required for blood surrogate and organ maintenance. As required, a microformulator108 can provide media supplements specific to each organ.108 The microformulator could be used to locally add media components to a particular organ. A size-exclusion filter or an affinity capture chamber or matrix (Donna Webb, personal communication) could be used to remove any toxic molecules produced by one organ before they reach other organs. Computer-controlled microformulators could also provide the regulated injection of molecules that cannot be maintained by the system alone and those from organs not in the HoC.24,113
Cellular heterogeneity
In contrast to the common monocultures and occasional co-cultures used in much of cellular biology, organs present a much richer cellular heterogeneity. Cellular heterogeneity is a key issue to consider when applying scaling laws to OoCs, since downscaling an organ may result in a reduction in the number of cell types present. Furthermore, achieving a complex co-culture system that preserves native cellular heterogeneity in an organ, much less coupled organs, is still far from realization. As a result, in addition to scaling issues, the choice of cell types used to develop an OoC may also be altered in order to focus on a biological response that is specific to a certain cell population in the organ of interest. Table 2 indicates the relative fractions of the most common cells in each of the organs considered. In the ESI†, we present these data in terms of Shannon-Wiener Index (SWI),114,115 a useful method to quantify cellular heterogeneity. We were unable to identify from the literature a self-consistent set of cell distributions for the kidney. One could also argue that the erythrocytes and leukocytes could be treated separately.| Organ | # of cell types, N | Cell type | % |
|---|---|---|---|
| Brain (neocortex)42 | 4 | Glia | 41% |
| Neurons | 33% | ||
| Vascular | 17% | ||
| Microglia | 8% | ||
| Total | 100% | ||
| Heart59,60 | 5 | Cardiomyocytes | 55% |
| Fibroblasts | 25% | ||
| Vascular smooth muscle | 10% | ||
| Endothelial | 7.0% | ||
| Neuronal | 3.0% | ||
| Total | 100% | ||
| Liver116 | 4 | Hepatocyte | 60% |
| Sinusoidal endothelial | 20% | ||
| Kupffer | 15% | ||
| Hepatic stellate | 5.0% | ||
| Total | 100% | ||
| Lung (alveolar) 97 | 5 | Endothelial | 39% |
| Interstitial | 29% | ||
| Type II epithelial | 18% | ||
| Type I epithelial | 11% | ||
| Alveolar macrophages | 3% | ||
| Total | 100% | ||
| Blood117 | 6 | Erythrocytes | 99% |
| Neutrophils | 0.50% | ||
| Lymphocytes | 0.30% | ||
| Monocytes | 0.050% | ||
| Eosinophils | 0.025% | ||
| Basophils | 0.007% | ||
| Total | 99.9% |
Engineering challenges
We have discussed a number of criteria for scaling mHu and μHu organs as required to design and validate realistic, coupled HoC/OoC systems. That said, there are also a number of engineering challenges that must be met before it is possible to construct a realistic mHu as shown in Fig. 2 or a μHu as shown schematically in Fig. 3. These challenges are cataloged in detail elsewhere,1 and include determining the proper size of each organ, fluidic control of mL and μL volumes, analytical chemistry in μL and nL volumes, including comprehensive molecular characterization in real time, maintaining and controlling coupled organ systems, vascularizing organs with appropriate surface-to-volume ratios, developing a universal blood surrogate, accounting for missing organs and the adjustment of blood surrogate, modeling coupled organ systems, characterization of organ health and disease, and minimizing organ cost to enable high-content screening. Several of these can be revisited based upon our detailed scaling analysis.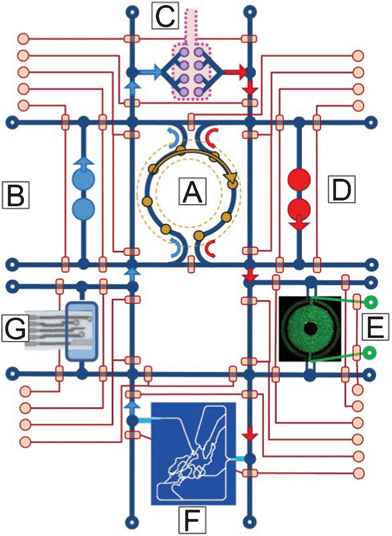 | ||
| Fig. 3 A concept drawing of a four-organ μHu (Homo chippiens). A) An on-chip peristaltic ventricular assist, B) Right heart, C) Lung, D) Left heart, E) Liver (courtesy of Kapil Pant), F) Peripheral circulation118 (courtesy of Kapil Pant), G) Microchemical analyzer of metabolic activity.119 The system would operate on a single microfluidic chip, with on-chip pneumatic valves controlling system functions and connections. | ||
The circulating volume of perfusate of an OoC/HoC must match organ size, lest metabolites, hormones, and paracrine signals be diluted to the point that each organ operates in a large reservoir independent of the other organs, thereby precluding accurate study of the desired organ-organ interaction so necessary for PK/PD,120 ADMET,121 and drug safety/toxicity studies.122,123 The aforementioned ∼4.5 mL and ∼4.5 μL blood volumes for a mHu and μHu will place severe constraints on not only the fraction of an organ bioreactor that must be occupied by cells, but also limits the size of in-system sensors and the volume that can be withdrawn for analysis of the system's state and subsequent control adjustments. The scaling arguments applied to the organs also apply to the instruments that will analyze their performance.
One might also wonder whether the ratio of cell-to-perfusate volumes alone precludes the use of conventional well plate cell culture in creating properly coupled HoC/OoC systems: blood and interstitial fluid volumes for organs in vivo are a small fraction of the volume of the organ itself. Well-plate tissue cultures without internal vascularization can seldom support tissues thicker than 100 to 300 μm without necrosis, so the height of fluid above such tissues grown in a well plate would have to be a small fraction of the thickness of the cell layer to maintain the proper tissue-fluid volume ratios. Because of surface tension effects, it is difficult to pipette fluid from such a thin layer of fluid without damaging the underlying cells. This argues for flow-based HoC/OoC systems that can function within the aforementioned volume constraints. The capabilities of microfluidic systems will be critical to produce compact organs with both appropriate temporal responses and the ability to produce and react to circulating cytokines,124–126 and to work with small quantities of rare or expensive human cells.127
Another issue that has been largely overlooked yet is critical to consider in OoC/HoC design is temporal scaling in reference to disparate cell growth and turnover rates between tissues and between in vivo and in vitro conditions, particularly when studying drugs with slow kinetics. It is well recognized that cellular co-cultures are subject to being overrun by one of the two cell types, although components can be added to culture media to retard proliferation of one species128 or accelerate the growth of the other. It may be possible to design a mechanical means to address cellular turnover, for example by adding or removing sections of cells from an organ as the entire MPS ages.
While fluorescence sensors can be used to record metabolic signals such as acidification and oxygenation, it may be wise to reserve optical bandwidth for intracellular fluorescent probes, and instead utilize miniature, wide-bandwidth electrochemical sensors matched to small cell populations129–131 or single cells.132–135 It is a great advantage that, typically, the signal-to-noise ratio of electrochemical sensors does not increase as the electrodes are miniaturized,136 and it has been shown possible to make electrochemical measurements of single cells and small cell populations.134,135,137,138
A larger problem is to characterize the circulating molecules either consumed or produced by each organ, given the small volumes and the need to track concentrations of many molecules over long periods of time. Nanospray injection, ion mobility-mass spectrometry (nESI-IM-MS) may prove to be the key technique for rapid OoC state monitoring, given that IM separations require milliseconds rather than the hour or so of high pressure liquid chromatography,139,140 with the recognition that nESI requires desalting of the media that can now be done on-line.141 Ultimately, the sensors and controllers might be interconnected in a way that would lead to automated inference of model-based control algorithms.22,142
An additional implication of the small fluid volumes in a mHu or μHu is that adjustment of the chemical concentrations of the perfusion media, for example to simulate humoral control of organ function, requires injection of small volumes of precisely mixed fluids. While a high-throughput screening fluidic robot or droplet injector can handle nl to pl volumes, it is a non-trivial to connect one of these into a closed, circulating system of coupled HoCs/OoCs. It is yet another problem to achieve the dynamic range of concentrations of different chemical species found in typical cell culture media without the use of large volumes of media and serial dilution techniques. It will also be necessary to provide the signaling molecules and metabolites from missing organs, as well as apply localized biochemical perturbations to assess the response of the other organs, but note that this has to be done as a small perturbation of the mL to μL volume of the blood surrogate with a temporal resolution guided by the requisite controller bandwidth. A microfluidic microformulator as we discussed earlier may meet these needs.
As the complexity of a coupled OoC system increases with the number of organs integrated, organ scaling will become more complicated, since the metabolic demands and relative scaling between organs will undoubtedly be affected. We also believe that the scaling in multi-organ OoC/HoC systems, particularly for dynamic metabolic phenomena, will require systematic design such that the functional scaling of any organ system is not significantly altered by another organ, and no single organ receives a substantial, unintended scaling priority.
Coupled non-linear biological systems can spontaneously oscillate and may require external stabilization, which in turn will require the use of sensors and controllers, possibly at the level of each organ. The neurohumoral control of human homeostasis may in fact be simulated by a properly configured sensor and control system, which in turn will benefit from both properly scaled sensors and the ability to rapidly reformulate the perfusion media. That said, regulatory noise may contain useful information about system interconnections.
It will be interesting to determine whether cellular heterogeneity in mixed cultures, critical to cellular signaling mechanisms in vivo, can be maintained for long times in vitro in coupled HoC/OoC systems. Given the regulatory role of the cellular microenvironment in vivo,143,144 there would be reason to expect that it might in fact become easier to maintain heterogeneity as multiple cell types are grown together in balanced environments with self-conditioned media. The Shannon-Wiener Index may prove important in assessing and controlling this.
We have not yet addressed in detail the scaling issues associated with microfluidics, oxygen carrying capacity of the blood surrogate, and the distributed hydraulic impedance of both the individual organs and the coupled system. This is of particular significance for mHu and μHu systems with working hearts. One would expect that designing around these constraints would benefit greatly from multiphysics, computational biology modeling tools.145,146 Optimized microfluidic design using a first-principles optimization of vascular branching147–149 may be better suited than approaches that assume a particular scaling law.9
Ultimately, there may be significant technical and economic advantages to creating a μHuman on a single microfluidic chip as shown schematically in Fig. 3. Simpler implementations are already being developed.108 The total volume of fluidic interconnects is minimized. On-chip valves can be utilized to bypass individual organs while the organs are being seeded and grown to a stable state, and to adjust the duty cycle by which they are connected to the entire system so that conditioning of media can be gradual rather than sudden, providing time for cellular up- and down-regulation of signaling and control genes. Multi-organ integration is not, however, a practical approach until each organ has been perfected individually, albeit at the correct size. Hence as we gain experience in this field, we need to make our HoCs and OoCs small, but not too small.
Conclusions
It is reasonable to assume that the many issues addressed in this review can be resolved through careful attention to engineering and physiological details, particularly with the large number of well-funded investigators now working on this worldwide. Clearly, this does represent a Lab-on-a-Chip challenge of unprecedented complexity and significance. It is most important to recognize that there are obvious trade-offs between realism and simplicity, since the ability to sense and control the microscale environment in microfabricated organs-on-a-chip may provide a solution to the current impasse in extending existing in vitro models, most of which are based upon single-layer cellular monoculture, to greater realism and utility.150There will undoubtedly be requests to make these OoC/HoC systems ever-more realistic, and to criticize them for their shortcomings. There have been similar drives for perfect reductionist representations, particularly in the regulatory networks and systems biology communities, where computational models continue to grow in complexity and may operate at a very small rate compared to real time. It is important to realize that OoC/HoC systems reside in a niche of abstraction that will improve constantly with technology but will never exactly recreate a full human, which represents ∼109 years of evolutionary engineering. It may be most useful if OoCs and HoCs are viewed as simplified model systems for PK/PD and systems biology studies, not small humans.
The drive to perfect reductionism is put in perspective by both Jorge Luis Borges and Lewis Carroll, in which a map of an empire/country the size of an empire/country is not found useful.151,152 Just as a perfect map resolves few problems and produces others, the creation of a near-to-perfect in vitro replica of a human may accomplish little at great expense. We believe that with the proper application of scaling and a balance between abstraction and realism, we should be able to learn much about the complexity of human biology153 and its interaction with drugs from each implementation of a HoC/OoC. Ultimately, we may be able to create OoC/HoC surrogates for specific genetic or disease subgroups for drug development or for individual patients to optimize their treatment.
Acknowledgements
We thank Rashi Iyer and Kapil Pant for their contributions to Fig. 2 and 3, and Allison Price and Don Berry for their editorial assistance. We have benefitted from extensive discussions with Frank E. Block, Jr., Frank E. Block III, David Cliffel, William Fissell, Geraldine Hamilton, Donald Ingber, Rashi Iyer, Daniel Levner, John McLean, Kapil Pant, Kevin Kit Parker, Andrzej Przekwas, and Philip Samson regarding microfluidic devices and organs-on-a-chip. This research has been funded in part by Defense Threat Reduction Agency grants HDTRA1-09-1-00-13 and DTRA100271A-5196; NIH grants R01GM092218, RC2DA028981, and, through the NIH Common Fund, NCATS grant 1UH2-TR000491-01; DARPA grant W911NF-12-2-0036; the NSF Graduate Research Fellow Program (BCE); and the Vanderbilt Institute for Integrative Biosystems Research and Education (VIIBRE), the Systems Biology and Bioengineering Undergraduate Research Experience (SyBBURE) funded by Gideon Searle, and a Vanderbilt University Discovery Grant. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies and institutions.References
- J. P. Wikswo, F. E. Block III, D. E. Cliffel, C. R. Goodwin, C. C. Marasco, D. A. Markov, D. L. McLean, J. A. McLean, J. R. McKenzie, R. S. Reiserer, P. C. Samson, D. K. Schaffer, K. T. Seale and S. D. Sherrod, IEEE Trans. Biomed. Eng., 2013, 60, 682 CrossRef.
- M. B. Esch, T. L. King and M. L. Shuler, Annu. Rev. Biomed. Eng., 2011, 13, 55 CrossRef CAS.
- M. Shuler, Ann. Biomed. Eng., 2012, 40, 1399 CrossRef.
- K. Schmidt-Nielsen, J. Exp. Zool., 1975, 194, 287 CrossRef CAS.
- M. Kleiber, Hilgardia, 1932, 6, 315 CAS.
- M. Kleiber, Proceedings of the Society for Experimental Biology and Medicine. Society for Experimental Biology and Medicine (New York, N.Y.), 1941, 48, 419 CAS.
- K. Schmidt-Nielsen, in Scaling: Why is animal size so important?, Cambridge University Press, New York, 1984, ch. 8, pp. 90–98 Search PubMed.
- P. S. Dodds, D. H. Rothman and J. S. Weitz, J. Theor. Biol., 2001, 209, 9 CrossRef CAS.
- G. B. West, J. H. Brown and B. J. Enquist, Science, 1997, 276, 122 CrossRef CAS.
- J. H. Brown, V. K. Gupta, B. L. Li, B. T. Milne, C. Restrepo and G. B. West, Philos. Trans. R. Soc. London, Ser. B, 2002, 357, 619 CrossRef.
- S. L. Lindstedt and W. A. Calder, Quart. Rev. Biol., 1981, 56, 1 CrossRef.
- W. R. Stahl, Science, 1965, 150, 1039 CAS.
- T. N. Johnson, A. Rostami-Hodjegan and G. T. Tucker, Clin. Pharmacokinet., 2006, 45, 931 CrossRef CAS.
- M. Danhof, J. de Jongh, E. C. M. De Lange, O. Della Pasqua, B. A. Ploeger and R. A. Voskuyl, Annu. Rev. Pharmacol. Toxicol., 2007, 47, 357 CrossRef CAS.
- H. W. Leung, in General, Applied and Systems Toxicology, John Wiley & Sons, Ltd, 2009 Search PubMed.
- M. Hadi, I. M. Westra, V. Starokozhko, S. Dragovic, M. T. Merema and G. M. M. Groothuis, Chem. Res. Toxicol., 2013, 26, 710 CrossRef CAS.
- D. Huh, D. C. Leslie, B. D. Matthews, J. P. Fraser, S. Jurek, G. A. Hamilton, K. S. Thorneloe, M. A. Mcalexander and D. E. Ingber, Sci. Transl. Med., 2012, 4, 159ra147 CrossRef CAS.
- D. Huh, B. D. Matthews, A. Mammoto, M. Montoya-Zavala, H. Y. Hsin and D. E. Ingber, Science, 2010, 328, 1662 CrossRef CAS.
- A. Grosberg, P. W. Alford, M. L. McCain and K. K. Parker, Lab Chip, 2011, 11, 4165 RSC.
- P. W. Alford, A. W. Feinberg, S. P. Sheehy and K. K. Parker, Biomaterials, 2010, 31, 3613 CrossRef CAS.
- H. J. Kim, D. Huh, G. Hamilton and D. E. Ingber, Lab Chip, 2012, 12, 2165 RSC.
- P. R. LeDuc, W. C. Messner and J. P. Wikswo, Annu. Rev. Biomed. Eng., 2011, 13, 369 CrossRef CAS.
- Chemical and Biological Defense Innovations and Technologies, Grants.gov, 12 Dec. 2011. http://www.grants.gov/search/search.do?mode=VIEW&oppId=133833.
- C. L. Hansen, M. O. A. Sommer and S. R. Quake, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 14431 CrossRef CAS.
- C. L. Hansen, Caltech, 2004 Search PubMed.
- R. Yang, M. Zhang and T. J. Tarn, in Life science automation fundamentals and applications, ed. M. Zhang, B. Nelson and R. Felder, Artech House, Norwood, MA, 2007, ch. 6, pp. 153–196 Search PubMed.
- L. Cucullo, N. Marchi, M. Hossain and D. Janigro, J. Cereb. Blood Flow Metab., 2011, 31, 767 CrossRef CAS.
- R. Booth and H. Kim, Lab Chip, 2012, 12, 1784 RSC.
- A. K. H. Achyuta, A. J. Conway, R. B. Crouse, E. C. Bannister, R. N. Lee, C. P. Katnik, A. A. Behensky, J. Cuevas and S. S. Sundaram, Lab Chip, 2013, 13, 542 RSC.
- L. M. Griep, F. Wolbers, B. de Wagenaar, P. M. ter Braak, B. B. Weksler, I. A. Romero, P. O. Couraud, I. Vermes, A. D. van der Meer and A. van den Berg, Biomed. Microdevices, 2013, 15, 145 CrossRef CAS.
- B. Prabhakarpandian, M. C. Shen, J. B. Nichols, I. R. Mills, M. Sidoryk-Wegrzynowicz, M. Aschner and K. Pant, Lab Chip, 2013, 13, 1093 RSC.
- Y. Gao, D. Majumdar, B. Jovanovic, C. Shaifer, P. Lin, A. Zijlstra, D. Webb and D. Li, Biomed. Microdevices, 2011, 13, 539 CrossRef CAS.
- D. Majumdar, Y. Gao, D. Li and D. J. Webb, J. Neurosci. Methods, 2011, 196, 38 CrossRef.
- J. Park, H. Koito, J. Li and A. Han, Lab Chip, 2012, 12, 3296 RSC.
- M. Shi, D. Majumdar, Y. Gao, B. M. Brewer, C. R. Goodwin, J. A. McLean, D. Li and D. J. Webb, Lab Chip, 2013 10.1039/C3LC50249J.
- S. Herculano-Houzel, P. Ribeiro, L. Campos, A. V. da Silva, L. B. Torres, K. C. Catania and J. H. Kaas, Brain Behav. Evol., 2011, 78, 302 CrossRef.
- K. Chung, J. Wallace, S. Y. Kim, S. Kalyanasundaram, A. S. Andalman, T. J. Davidson, J. J. Mirzabekov, K. A. Zalocusky, J. Mattis, A. K. Denisin, S. Pak, H. Bernstein, C. Ramakrishnan, L. Grosenick, V. Gradinaru and K. Deisseroth, Nature, 2013, 497, 332 CrossRef CAS.
- S. Herculano-Houzel, Front. Hum. Neurosci., 2009, 3 CrossRef , Article 31.
- B. Davies and T. Morris, Pharm. Res., 1993, 10, 1093 CrossRef CAS.
- S. Herculano-Houzel, PLoS One, 2011, 6 CAS , Article e17514.
- J. Karbowski, BMC Biol., 2007, 5 CrossRef CAS , Article 18.
- L. Lyck, I. D. Santamaria, B. Pakkenberg, J. Chemnitz, H. D. Schroder, B. Finsen and H. J. G. Gundersen, J. Neurosci. Methods, 2009, 182, 143 CrossRef.
- P. Kreczmanski, H. Heinsen, V. Mantua, F. Woltersdorf, T. Masson, N. Ulfig, R. Schmidt-Kastner, H. Korr, H. W. M. Steinbusch, P. R. Hof and C. Schmitz, Acta Neuropathol., 2009, 117, 409 CrossRef.
- A. Armulik, G. Genove and C. Betsholtz, Dev. Cell, 2011, 21, 193 CrossRef CAS.
- T. M. Mathiisen, K. P. Lehre, N. C. Danbolt and O. P. Ottersen, Glia, 2010, 58, 1094 CrossRef.
- D. E. Sims, Tissue Cell, 1986, 18, 153 CrossRef CAS.
- H. Ito, I. Kanno, C. Kato, T. Sasaki, K. Ishii, Y. Ouchi, A. Iida, H. Okazawa, K. Hayashida, N. Tsuyuguchi, K. Ishii, Y. Kuwabara and M. Senda, Eur. J. Nucl. Med. Mol. Imaging, 2004, 31, 635 CrossRef.
- L. C. Mchenry, N. Engl. J. Med., 1966, 274, 82 CrossRef.
- L. C. Mchenry, N. Engl. J. Med., 1965, 273, 562 CrossRef.
- P. Lebrungrandie, J. C. Baron, F. Soussaline, C. Lochh, J. Sastre and M. G. Bousser, Arch. Neurol., 1983, 40, 230 CrossRef CAS.
- L. Cucullo, M. Hossain, V. Puvenna, N. Marchi and D. Janigro, BMC Neurosci., 2011, 12, 40 CrossRef CAS.
- A. G. Koutsiaris, S. V. Tachmitzi, N. Batis, M. G. Kotoula, C. H. Karabatsas, E. Tsironi and D. Z. Chatzoulis, Biorheology, 2007, 44, 375 Search PubMed.
- J. M. Tarbell, Cardiovasc. Res., 2010, 87, 320 CrossRef CAS.
- Y. Tanaka, K. Morishima, T. Shimizu, A. Kikuchi, M. Yamato, T. Okano and T. Kitamori, Lab Chip, 2006, 6, 362 RSC.
- J. Park, I. C. Kim, J. Baek, M. Cha, J. Kim, S. Park, J. Lee and B. Kim, Lab Chip, 2007, 7, 1367 RSC.
- J. C. Nawroth, H. Lee, A. W. Feinberg, C. M. Ripplinger, M. L. McCain, A. Grosberg, J. O. Dabiri and K. K. Parker, Nat. Biotechnol., 2012, 30, 792 CrossRef CAS.
- E. J. Lee, D. E. Kim, E. U. Azeloglu and K. D. Costa, Tissue Eng. A, 2008, 14, 215 CrossRef CAS.
- G. A. Giridharan, M. D. Nguyen, R. Estrada, V. Parichehreh, T. Hamid, M. A. Ismahil, S. D. Prabhu and P. Sethu, Anal. Chem., 2010, 82, 7581 CrossRef CAS.
- I. Banerjee, J. W. Fuseler, R. L. Price, T. K. Borg and T. A. Baudino, Am. J. Physiol. Heart, 2007, 293, H1883 CrossRef CAS.
- D. L. Brutsaert, Physiol. Rev., 2003, 83, 59 CAS.
- M. Horackova and J. A. Armour, Cardiovasc. Res., 1995, 30, 326 CrossRef CAS.
- M. Horackova and Z. Byczko, Exp. Cell Res., 1997, 237, 158 CrossRef CAS.
- M. Horackova, M. H. Huang, J. A. Armour, D. A. Hopkins and C. Mapplebeck, Cardiovasc. Res., 1993, 27, 1101 CrossRef CAS.
- K. Lemmens, V. F. M. Segers, M. Demolder and G. W. De Keulenaer, J. Biol. Chem., 2006, 281, 19469 CrossRef CAS.
- T. M. Leucker, M. Bienengraeber, M. Muravyeva, I. Baotic, D. Weihrauch, A. K. Brzezinska, D. C. Warltier, J. R. Kersten and P. F. Pratt, J. Mol. Cell. Cardiol., 2011, 51, 803 CrossRef CAS.
- Y. H. Hsu, M. L. Moya, P. Abiri, C. C. W. Hughes, S. C. George and A. P. Lee, Lab Chip, 2013, 13, 81 RSC.
- M. L. Moya, Y.-H. Hsu, A. P. Lee, C. C. W. Hughes and S. C. George, Tissue Eng. Pt. C, 2013 DOI:10.1089/ten.tec.2012.0430.
- T. G. Papaioannou, E. N. Karatzis, M. Vavuranakis, J. P. Lekakis and C. Stefanadis, Int. J. Cardiol., 2006, 113, 12 CrossRef.
- W. H. Fissell, J. Kimball, S. M. Mackay, A. Funke and H. D. Humes, Ann. N. Y. Acad. Sci., 2001, 944, 284 CrossRef CAS.
- H. D. Humes, S. M. Mackay, A. J. Funke and D. A. Buffington, Kidney Int., 1999, 55, 2502 CrossRef CAS.
- E. M. Wright, Am. J. Physiol. Renal, 2001, 280, F10 CAS.
- S. Abrahams, L. Greenwald and D. L. Stetson, Am. J. Physiol., 1991, 261, R719 CAS.
- C. A. Beuchat, J. Theor. Biol., 1990, 143, 113 CrossRef CAS.
- R. Greger, Physiol. Rev., 1985, 65, 760 CAS.
- S. Kurbel, K. Dodig and R. Radic, Adv. Physiol. Educ., 2002, 26, 278 CAS.
- C. A. Beuchat, Am. J. Physiol-Reg. I., 1996, 271, R157 CAS.
- J. W. Prothero, Comparative Biochemistry and Physiology Part A: Physiology, 1982, 71, 567 CrossRef CAS.
- Y. Nahmias, F. Berthiaume and M. L. Yarmush, Adv. Biochem. Eng. Biotechnol., 2007, 103, 309 CrossRef.
- A. K. Sohlenius-Sternbeck, Toxicol. in Vitro, 2006, 20, 1582 CrossRef CAS.
- B. D. Foy, A. Rotem, M. Toner, R. G. Tompkins and M. L. Yarmush, Cell. Transplant., 1994, 3, 515 CAS.
- U. J. Balis, K. Behnia, B. Dwarakanath, S. N. Bhatia, S. J. Sullivan, M. L. Yarmush and M. Toner, Metab. Eng., 1999, 1, 49 CrossRef CAS.
- S. C. Balmert, D. McKeel, F. Triolo, B. Gridelli, K. Zeilinger, R. Bornemann and J. C. Gerlach, Int. J. Artif. Organs, 2011, 34, 410 CrossRef.
- K. Zeilinger, T. Schreiter, M. Darnell, T. Soderdahl, M. Lubberstedt, B. Dillner, D. Knobeloch, A. K. Nussler, J. C. Gerlach and T. B. Andersson, Tissue Eng., Part C, 2011, 17, 549 CrossRef CAS.
- J. M. Piret and C. L. Cooney, Biotechnol. Bioeng., 1991, 37, 80 CrossRef CAS.
- W. G. Whitford and J. J. S. Cadwell, BioProcess Int., 2009, 7, 54 CAS.
- I. Mahmood, J. Pharm. Sci., 2005, 94, 883 CrossRef CAS.
- T. Lave, S. Dupin, C. Schmitt, R. C. Chou, D. Jaeck and P. Coassolo, J. Pharm. Sci., 1997, 86, 584 CrossRef CAS.
- Y. Naritomi, S. Terashita, A. Kagayama and Y. Sugiyama, Drug Metab. Dispos., 2003, 31, 580 CrossRef CAS.
- Y. Naritomi, S. Terashita, S. Kimura, A. Suzuki, A. Kagayama and Y. Sugiyama, Drug Metab. Dispos., 2001, 29, 1316 CAS.
- H. Boxenbaum, J. Pharmacokinet. Biopharm., 1980, 8, 165 CrossRef CAS.
- D. J. Carlile, K. Zomorodi and J. B. Houston, Drug Metab. Dispos., 1997, 25, 903 CAS.
- G. Ghibellini, L. S. Vasist, E. M. Leslie, W. D. Heizer, R. J. Kowalsky, B. F. Calvo and K. L. R. Brouwer, Clin. Pharmacol. Ther., 2007, 81, 406 CrossRef CAS.
- R. J. Riley, D. F. McGinnity and R. P. Austin, Drug Metab. Dispos., 2005, 33, 1304 CrossRef CAS.
- J. S. Miller, K. R. Stevens, M. T. Yang, B. M. Baker, D. H. Nguyen, D. M. Cohen, E. Toro, A. A. Chen, P. A. Galie, X. Yu, R. Chaturvedi, S. N. Bhatia and C. S. Chen, Nat. Mater., 2012, 11, 768 CrossRef CAS.
- E. R. Weibel, Annu. Rev. Physiol., 1987, 49, 147 CrossRef CAS.
- C. Hou and M. Mayo, Phys. Rev. E, 2011, 84, 061915 CrossRef.
- J. D. Crapo, B. E. Barry, P. Gehr, M. Bachofen and E. R. Weibel, Am. Rev. Respir. Dis., 1982, 126, 332 CAS.
- W. A. H. Wallace, M. Gillooly and D. Lamb, Thorax, 1992, 47, 437 CrossRef CAS.
- A. O. S. Fels and Z. A. Cohn, J. Appl. Physiol., 1986, 60, 353 CAS.
- W. R. Stahl, J. Appl. Physiol., 1967, 22, 453 CAS.
- M. Kjeld and O. Olafsson, Can. J. Zool., 2008, 86, 890 CrossRef.
- M. F. Brown, T. P. Gratton and J. A. Stuart, Am. J. Physiol-Reg. I., 2007, 292, R2115 CAS.
- Microphysiological Systems, Solicitation no. DARPA-BAA-11-73 FedBizOpps.gov, 11 Sept. 2011. https://www.fbo.gov/index?s=opportunity&mode=form&id=956b160c42aaa386cf5762f12c21be9f&tab=core&_cview=0.
- G. Chen and A. F. Palmer, Biotechnol. Prog., 2009, 25, 1317 CrossRef CAS.
- D. R. Spahn, Crit. Care, 1999, 3, R93 CrossRef CAS.
- M. Yamazaki, R. Aeba, R. Yozu and K. Kobayashi, Circulation, 2006, 114, I220 CrossRef.
- V. Jager, J. Lehmann and P. Friedl, Cytotechnology, 1988, 1, 319 CrossRef CAS.
- C. Zhang, Z. Q. Zhao, N. A. A. Rahim, D. van Noort and H. Yu, Lab Chip, 2009, 9, 3185 RSC.
- J. van der Valk, D. Brunner, K. De Smet, A. F. Svenningsen, P. Honegger, L. E. Knudsen, T. Lindl, J. Noraberg, A. Price, M. L. Scarino and G. Gstraunthaler, Toxicol. in Vitro, 2010, 24, 1053 CrossRef CAS.
- D. Pinkel, Cancer Res., 1958, 18, 853 CAS.
- C. Hall, E. Lueshen, A. Mosat and A. A. Linninger, J. Pharm. Sci., 2012, 101, 1221 CrossRef CAS.
- V. Sharma and J. H. McNeill, Br. J. Pharmacol., 2009, 157, 907 CrossRef CAS.
- A. H. Diercks, A. Ozinsky, C. L. Hansen, J. M. Spotts, D. J. Rodriguez and A. Aderem, Anal. Biochem., 2009, 386, 30 CrossRef CAS.
- L. Jost, Oikos, 2006, 113, 363 CrossRef.
- C. J. Keylock, Oikos, 2005, 109, 203 CrossRef.
- D. E. Malarkey, K. Johnson, L. Ryan, G. Boorman and R. R. Maronpot, Toxicol. Pathol., 2005, 33, 27 CrossRef CAS.
- L. Sherwood, in Human physiology: from cells to systems, Cengage-Brooks/Cole, Belmont, CA, 7th edn, 2010 Search PubMed.
- B. Prabhakarpandian, Y. Wang, A. Rea-Ramsey, S. Sundaram, M. F. Kiani and K. Pant, Microcirculation, 2011, 18, 380 CrossRef CAS.
- L. A. Hiatt, J. R. McKenzie, L. F. Deravi, R. S. Harry, D. W. Wright and D. W. Cliffel, Biosens. Bioelectron., 2012, 33, 128 CrossRef CAS.
- J. H. Sung, C. Kam and M. L. Shuler, Lab Chip, 2010, 10, 446 RSC.
- K. Viravaidya and M. L. Shuler, Biotechnol. Prog., 2004, 20, 590 CrossRef CAS.
- F. D. Sistare and J. J. DeGeorge, Biomarkers Med., 2011, 5, 497 CrossRef CAS.
- B. Ma, G. Zhang, J. Qin and B. Lin, Lab Chip, 2009, 9, 232 RSC.
- J. P. Wikswo, A. Prokop, F. Baudenbacher, D. Cliffel, B. Csukas and M. Velkovsky, IEE Proc.: Nanobiotechnol., 2006, 153, 81 CrossRef CAS.
- A. Prokop, Z. Prokop, D. Schaffer, E. Kozlov, J. P. Wikswo, D. Cliffel and F. Baudenbacher, Biomed. Microdevices, 2004, 6, 325 CrossRef CAS.
- S. Faley, K. Seale, J. Hughey, D. K. Schaffer, S. VanCompernolle, B. McKinney, F. Baudenbacher, D. Unutmaz and J. P. Wikswo, Lab Chip, 2008, 8, 1700 RSC.
- S. L. Faley, M. Copland, D. Wlodkowic, W. Kolch, K. T. Seale, J. P. Wikswo and J. M. Cooper, Lab Chip, 2009, 9, 2659 RSC.
- A. Suzumura, S. Bhat, P. A. Eccleston, R. P. Lisak and D. H. Silberberg, Brain Res., 1984, 324, 379 CrossRef CAS.
- S. E. Eklund, D. E. Cliffel, E. Kozlov, A. Prokop, J. P. Wikswo Jr and F. J. Baudenbacher, Anal. Chim. Acta, 2003, 496, 93 CrossRef CAS.
- S. E. Eklund, R. M. Snider, J. Wikswo, F. Baudenbacher, A. Prokop and D. E. Cliffel, J. Electroanal. Chem., 2006, 587, 333 CrossRef CAS.
- S. E. Eklund, R. G. Thompson, R. M. Snider, C. K. Carney, D. W. Wright, J. Wikswo and D. E. Cliffel, Sensors, 2009, 9, 2117 CrossRef CAS.
- I. A. Ges and F. Baudenbacher, Biosens. Bioelectron., 2010, 26, 828 CrossRef CAS.
- I. A. Ges and F. Baudenbacher, Biosens. Bioelectron., 2010, 25, 1019 CrossRef CAS.
- I. A. Ges, I. A. Dzhura and F. J. Baudenbacher, Biomed. Microdevices, 2008, 10, 347 CrossRef.
- I. A. Ges and F. Baudenbacher, J. Exp. Nanosci., 2008, 3, 63 CrossRef CAS.
- D. Grieshaber, R. MacKenzie, J. Voeroes and E. Reimhult, Sensors, 2008, 8, 1400 CrossRef CAS.
- M. Ciobanu, D. E. Taylor, J. P. Wilburn and D. E. Cliffel, Anal. Chem., 2008, 80, 2717 CrossRef CAS.
- J. R. McKenzie, A. M. Palubinsky, J. E. Brown, B. McLaughlin and D. E. Cliffel, ACS Chem. Neurosci., 2012, 3, 510 CrossRef CAS.
- J. R. Enders, C. C. Marasco, A. Kole, B. Nguyen, S. Sundarapandian, K. T. Seale, J. P. Wikswo and J. A. Mclean, IET Syst. Biol., 2010, 4, 416 CrossRef CAS.
- J. R. Enders, C. R. Goodwin, C. C. Marasco, K. T. Seale, J. P. Wikswo and J. A. Mclean, Spectroscopy Supp. Curr. Trends Mass Spectrometry, 2011, July, 18 Search PubMed.
- J. R. Enders, C. C. Marasco, J. P. Wikswo and J. A. Mclean, Anal. Chem., 2012, 84, 8467 CrossRef CAS.
- M. D. Schmidt, R. R. Vallabhajosyula, J. W. Jenkins, J. E. Hood, A. S. Soni, J. P. Wikswo and H. Lipson, Phys. Biol., 2011, 8, 055011 CrossRef.
- L. G. Griffith and M. A. Swartz, Nat. Rev. Mol. Cell Biol., 2006, 7, 211 CrossRef CAS.
- D. E. Ingber, Semin. Cancer Biol., 2008, 18, 356 CrossRef CAS.
- R. Kannan and A. Przekwas, Int. J. Numer. Methods Biomed. Eng., 2011, 27, 13 CrossRef.
- A. J. Przekwas, M. R. Somayaji and Z. J. Chen, CoBi Tools for model Guided Manufacturing of Biologics from Synthetically Stimulated Biofactories, 2011 Search PubMed.
- A. Bejan and S. Lorente, Phys. Life Rev., 2011, 8, 209 CrossRef.
- S. Lorente, W. Wechsatol and A. Bejan, Int. J. Heat Mass Transfer, 2002, 45, 3299 CrossRef.
- W. Wechsatol, S. Lorente and A. Bejan, Int. J. Heat Mass Transfer, 2002, 45, 4911 CrossRef.
- A. D. van der Meer and A. van den Berg, Integr. Biol., 2012, 4, 461 RSC.
- J. L. Borges and N. T. tr- Di Giovanni, in A Universal History of Infamy, Penguin, London, 1975 Search PubMed.
- L. Carroll, in The complete Sylvie and Bruno, Mercury House, San Francisco, 1991, ch. 11, pp. 262–267 Search PubMed.
- S. Huang and J. Wikswo, in Reviews of Physiology, Biochemistry and Pharmacology, ed. S. G. Amara, E. Bamberg, T. Gudermann, S. C. Hebert, R. Jahn, W. J. Lederer, R. Lill, A. Miyajima and S. Offermanns, 157 edn, 2007, vol. 157, pp. 81–104 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Discussion of the Shannon-Wiener Index, and a Scaling Spreadsheet that provides an extensive table describing scaling parameters for brain, heart, kidney, liver, lung, and blood. See DOI: 10.1039/c3lc50243k |
| This journal is © The Royal Society of Chemistry 2013 |
