 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel ToF-SIMS operation mode for improved accuracy and lateral resolution of oxygen isotope measurements on oxides
Gerald
Holzlechner†
*,
Markus
Kubicek†
,
Herbert
Hutter
and
Jürgen
Fleig
Institute of Chemical Technologies and Analytics, Vienna University of Technology, Vienna, Austria. E-mail: gerald.holzlechner@tuwien.ac.at; Fax: +43 1 58801 15899; Tel: +43 1 58801 15821
First published on 22nd April 2013
Abstract
Oxygen isotope exchange with subsequent time-of-flight secondary ion mass spectrometry (ToF-SIMS) is a highly valuable tool for determining oxygen diffusion coefficients in oxides. Since ToF-SIMS analysis enables an elemental and chemical mapping, it can also be used to visualize oxygen exchange-active zones by determining the local oxygen isotopic fraction. However, measuring accurate isotopic fractions can be a challenging analytical task owing to secondary ion interaction and signal saturation, particularly when dealing with high secondary ion intensities as commonly found when analyzing oxygen ions from oxides. It is shown that in many cases the calculated 18O− fraction erroneously shifts to higher values and can lead to systematic errors in the determination of diffusion coefficients. A novel ToF-SIMS operation mode, called “Collimated Burst Alignment” (CBA) mode, is therefore introduced to enable a more accurate determination of oxygen isotopic fractions with an optimized lateral resolution of sub-100 nm. Both improvements are rendered possible by a modified beam guidance in the primary ion gun. This modification reduces detector dead time effects and ion interactions to a minimum and secondary ion intensities can be obtained more accurately. The result of this optimization is demonstrated in measurements of the natural isotope abundance of several different oxides including SrTiO3 and Sr-doped LaCoO3.
Introduction
Functional oxides find application in many different fields, ranging from solid oxide fuel cells (SOFCs) to ferroelectric memories, piezoelectric actuators and gas sensors. In most fields the oxide ion motion plays a role either in preparation, operation or degradation. For example, the ion transport in solid electrolytes or the oxygen reduction at cathodes crucially affects the cell efficiency of SOFCs.1–33 In ferro- and piezoelectric oxides degradation phenomena such as an increasing leakage current upon DC load or fatigue are often related to oxide ion motion.34–50A powerful tool to quantify oxide ion diffusion and to visualize electrochemically active zones of oxides is the combination of tracer oxygen incorporation with subsequent secondary ion mass spectrometry (SIMS) analysis.4,6,8,9,11,13–15,17,19,20,22,26–33,43,45–47,51–55 By using time-of-flight- (ToF-) SIMS, detailed 2D and 3D information about the chemical composition of a surface and the elemental distribution can then be obtained.56,57 Elemental or isotope ion ratios can be determined for quantitative data interpretation.58,59 Among others, oxygen tracer diffusion coefficients and surface exchange coefficients can therefore be evaluated from ToF-SIMS depth profiles of the local oxygen isotopic fraction.60
The main challenge when measuring isotopic fractions is to achieve sufficient ion intensities for minor isotopes while preventing the major isotope signals from saturation.58 This is far from trivial since SIMS analysis of oxygen in oxides can result in high negative secondary ion intensities due to an enhanced oxygen ionization yield and high primary ion intensities in established ToF-SIMS modes. High secondary ion intensities can cause significant collision-induced ion interactions58,61 and detector dead time effects,62–64 both leading to an underestimated value for the detected major isotope intensities. Consequently, high secondary ion intensities can lead to systematic errors in the quantitative data interpretation, as detailed in this paper. One approach to minimize the error of oxygen isotopic fractions is described in the literature by De Souza et al.61 Operating ToF-SIMS in BA-burst mode reduces the intensity per primary ion pulse by chopping several pulses (bursts) out of a larger one. The determination of accurate diffusion profiles in BA-burst mode, however, requires an elaborate analysis of the raw data. Moreover, the lateral resolution is reduced. As an indication for an accurate measurement of the isotopic fraction the 18O level of oxides can be measured after equilibration in ambient air and compared with the expected natural abundance value. This corresponds to the test of the accuracy of a SIMS operation mode in that part of a tracer concentration profile where the major isotope intensity (here I16O) is at its maximum and shows the greatest impact on the error of the isotopic fraction.
In this contribution, we first show that measurements of 18O intensities in several oxides such as SrTiO3, MgO and Sr-doped LaCoO3−δ consistently show an erroneously high fraction when using ToF-SIMS analysis in established “Burst Alignment” (BA) and “High Current Bunched” (HCBU) mode, despite varying primary ion emission current and cluster size. The aim was therefore to develop an optimized ToF-SIMS mode in order to improve this situation by shifting secondary ion intensities to an optimal level to guarantee an accurate determination of both the major (16O−) and minor (18O−) secondary ion intensities. These developments were performed on an ION-TOF instrument but all basic ideas can also be applied to other instruments. It is shown that a novel mode called “Collimated Burst Alignment” (CBA) mode indeed leads to highly accurate tracer fraction values. Simultaneously it enables an improved lateral resolution of sub-100 nm compared to ∼250 to 300 nm in BA or BA-burst mode. Moreover, the CBA mode gives the possibility of increasing the mass resolution to m/Δm > 6000 by bursting the primary ion beam – thus being able to differentiate between secondary ions of the same mass number, e.g.16O2 and 32S, as we detailed in ref. 65. Reasons for the improved performance of the CBA mode are discussed by detailed analysis of secondary ion mass peaks and effects of dead time and ion interaction.
Experimental
All SIMS measurements were performed on a TOF.SIMS 5 instrument (ION-TOF, Münster, Germany) using 25 kV Bixy+ primary ions. The 18O− fractions were determined by operating the instrument in the novel “Collimated Burst Alignment” (CBA) mode as well as in the conventional modes commonly called “Burst Alignment” (BA) and “High Current Bunched” (HCBU) mode. During operation the primary ion gun typically scans a field of view of 100 × 100 μm2 applying a 1024 × 1024 pixel measurement raster. For sequential sputtering a 2 kV Cs+ sputter gun (400 × 400 μm2 sputter area, 2 s sputtering, 1 s pause time) was used. Charge compensation was achieved by 20 eV electrons.66,67Once the primary ion gun is aligned, a ToF-SIMS mass spectrum is generated by summing the detected secondary ion intensities and plotting them against the mass channels. The mass peak integration limit was set to the peak center plus/minus half the dead time of τ = 65.4 ns. Since the primary ion peak width was adjusted to 50 ns FWHM, the 50 ns of the main secondary ion mass peak as well as 7.7 ns before and after this main peak were considered in the integration. Since preceding ion counts can saturate the detector even before ions of the actual mass peak impinge, underestimated intensity counts could have a greater impact to the entire counts of a ∼1 ns pulse than to a longer one. When a single secondary ion peak width is smaller than the detector's dead time (pulse width ≤ τ), the intensity correction using Poissonian contribution simplifies to the equation58
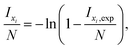 | (1) |
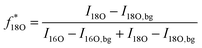 | (2) |
The lateral resolution was determined by imaging a part of the certified reference material BAM-L200 (ref. 68) as suggested in ref. 69. The reference sample consisted of AlGaAs/GaAs gratings with finely grated periods from 6.9 nm to 587 nm. Mass spectra, the 18O natural abundance level and details on oxygen isotope mass peaks were obtained on a number of functional oxides. The properties of these oxides range from high electronic and high ionic conductivity ((La0.6Sr0.4)CoO3−δ, (La0.6Sr0.4)FeO3−δ) to moderate or low electron/hole and ion conduction (SrTiO3, Pb(Zr,Ti)O3) to almost no electronic but high ionic conductivity ((Zr,Y)O2−δ) or highly insulating material (MgO). Thin films of (La0.6Sr0.4)CoO3−δ (LSC) and (La0.6Sr0.4)FeO3−δ (LSF) were produced by pulsed laser deposition (PLD) onto (Zr,Y)O2−δ (YSZ) single crystals (9.5 mol% Y2O3). The deposition procedures are described elsewhere.19 The 18O fractions in LSC and LSF were obtained immediately after PLD preparation as well as after pre-annealing the samples in an ambient atmosphere for 30 minutes at 600 °C. Commercially available single crystals of undoped SrTiO3 (STO), YSZ and MgO were investigated as-received (Crystec, Germany). A Pb(Zr1−xTix)O3 (PZT) ceramic sample was supplied by Graz University of Technology (Graz, Austria). For surface polishing of the latter one, diamond suspensions (DiaPro 9 and 3 μm, Struers, Germany) were used with MD-disk Largo (Struers) on a Planopol-3 Pedemax polishing machine (Struers).
ToF-SIMS measurements: problems and conventional operation modes
Dead time function and intensity saturation
Sputtering a target surface with a positive primary ion beam of suitable energy leads to interactions that cause the emission of secondary ions. Immediately after the sputtering process the secondary ions are extracted from the surface into the ToF-analyzer by an electrostatic field. After acceleration, the secondary ions get separated according to their mass to charge ratio. Secondary ions arriving at the detector with either only positive or only negative polarity are counted and their arrival times are recorded. Such a detector consists of a microchannel plate for ion-to-electron conversion, a scintillator for electron-to-photon conversion and finally a photomultiplier for recording impinged ions.58 Since ToF-SIMS is equipped with a single ion counting detector, it is impossible to distinguish between multiple ions arriving within a certain time interval τ denoted as the detector dead time. Hence, all ions arriving at the detector simultaneously or within the dead time τ are counted as just one single ion. The Poissonian correction (see eqn (1)) is often suitable to correct the experimentally obtained counts. However, an accurate correction is particularly troublesome for highly intensive secondary ion mass peaks (e.g. O− on oxides) with almost no “zero” events and pronounced dead time effects.The theory of single ion counting, dead time effects and Poissonian correction has been discussed in detail by Stephan, Zehnpfenning and Benninghoven, who concluded that in many cases a simple correction according to the Poissonian distribution is sufficient, but for a precise correction the dead time function has to be known in detail.64 This dead time function reflects the probability that the detector is not able to detect new ions after a time τ. It was also demonstrated that when being saturated once, the detector is still not fully recovered even after 300 ns. For the sake of illustration we simulated the impact of differently shaped dead time functions (DTFs) to secondary ion intensity mass peaks with a long pulse width of about 5 τ (Fig. 1). All DTFs start near unity detector saturation but differ in their decay characteristics. A simple step function leads to a secondary ion mass peak oscillating with a period of dead time τ (Fig. 1b). Such oscillations are generally not found in measurements and can be reduced by more complex DTFs. For example, an exponential- or logistic-like DTF results in a secondary ion signal, which is in better agreement with typical experimentally obtained secondary ion mass peaks such as the 16O mass peak in Fig. 2. The latter shows a typical example of the dead time impact on a very intensive mass peak (BA mode, Bi1+, 0.5 pA pulsed, 160 ns pulse width). From the time dependence of the saturated intensity signal in Fig. 2 the actual dead time τ can be determined and found to be τ = 65.4 ns full-width-half-maximum (FWHM) for our ToF-SIMS setup.
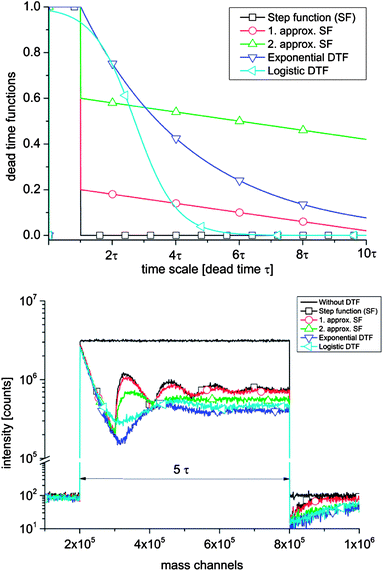 | ||
| Fig. 1 (a) Differently shaped dead time functions (DTFs) giving the probability that the detector is still dead after the detection of an ion in dead time τ. (b) Impact of the different DTFs to a simulated secondary ion mass spectrum for a ∼5 τ long pulse. | ||
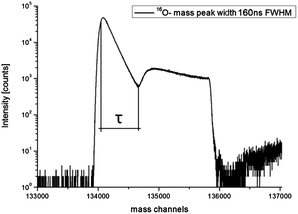 | ||
| Fig. 2 Experimentally obtained 16O− secondary ion mass peak on an as-received SrTiO3 sample in “Burst Alignment” (BA) mode. High secondary ion intensities saturate the single ion counting detector. | ||
The high oxygen sputter ionization rate together with high primary ion currents in conventional operation modes like “Burst Alignment” or “High Current Bunched” leads to very intensive secondary ion mass peaks in many functional oxides. The main challenge in measuring isotopic fractions is to prevent the major isotope signal from strong saturation of the detector with dead time losses, while achieving sufficient ion intensities for the minor isotope, in order to minimize counting statistical errors.58,61 Hence, for an accurate isotopic measurement it is essential to ensure the linearity of the detection system over a wide dynamic range.
“High Current Bunched”, “Burst Alignment” and “Collimated” mode
The primary ion gun can be operated in different modes that mainly differ in their mass resolution, primary ion intensity and achievable lateral resolution.70 In the commonly called “High Current Bunched” (HCBU) mode, a bunched and very intensive primary ion beam increases mass resolution (m/Δm > 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), however, at the cost of lateral resolution (2–10 μm). The “Burst Alignment” (BA) mode is particularly used for fast imaging with moderate mass resolution (m/Δm > 200) and improved lateral resolution (250–300 nm).
000), however, at the cost of lateral resolution (2–10 μm). The “Burst Alignment” (BA) mode is particularly used for fast imaging with moderate mass resolution (m/Δm > 200) and improved lateral resolution (250–300 nm).
In the BA mode, in the primary ion column two out of three ion optical lenses are energized. After the “Liquid Metal Ion Source” (LMIS) the first lens “Lens Source” positions a beam crossover in the blanking aperture 2, as visualized in Fig. 3. The second lens “Lens Target” is used to focus the primary ion beam to a minimal spot size on the target surface. Relatively high primary ion currents in the range of 1 pA are obtained by running the primary ion gun in pulsed mode (Bi1+, 100 μs cycle time, 50 ns pulse width). The BA mode is also the starting point to activate the BA-burst mode. The burster activation energizes a sine blanker consisting of a dual set of blanking plates. The so-called chopper cuts a large beam pulse into several smaller ion packages. In this way mass resolution is increased and secondary ion intensity per primary ion pulse is decreased. For very intensive mass peaks such as 16O− in oxides the first burst nevertheless saturates the detector, thus affecting the burst following within the detector dead time τ.
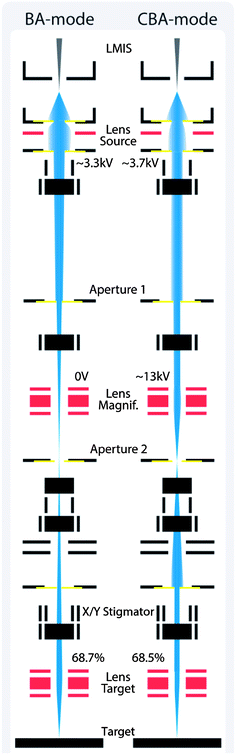 | ||
| Fig. 3 Primary ion gun scheme of the beam guidance for the BA (Burst Alignment) and CBA (Collimated Burst Alignment) modes on an ION-TOF instrument. | ||
Since the dead time function is not precisely known, the Poissonian correction is applied to the first single burst only. To obtain the total ion counts of saturated bursts the corrected intensity of the first burst has to be multiplied by the number of following bursts.61 In ref. 64 it is even discussed that particularly when the dead time of a high-intensity signal influences the following mass peaks, a dead time correction becomes almost impossible. However, owing to the decreased saturation problems, the intensity of minority isotope peaks can be summed over the entire bursts. The determination of accurate diffusion profiles therefore implies separation of the calculation into different parts, since the 18O fraction may vary from almost unity to natural abundance. Consequently, accurate analysis of 18O diffusion profiles in the “BA-Burst” mode requires a complicated calculation of 18O fractions. Compared to the HCBU and the BA mode, the conventional “Collimated” mode for imaging can show an enhanced performance in terms of higher lateral resolution and accuracy due to the reduced primary ion intensity (not shown). However, particularly the modified beam guidance in the CBA mode enables essential advantages. This is discussed in the following section.
The novel “Collimated Burst Alignment” mode
Beam guidance of the CBA mode
The “Collimated Burst Alignment” (CBA) mode is a novel primary ion gun mode optimized to accurately determine oxygen isotopic fractions and to enable a significantly improved lateral resolution. In the CBA mode all three ion optical lenses are energized. Compared to the conventional BA mode a higher voltage is applied to the “Lens Source” in order to diverge the bismuth beam. Aperture 1 blanks out bismuth ions deviating from the optical axis whereas the collimated near-axis ions pass. Hence, increasing the “Lens Source” voltage collimates the primary ion beam and decreases the primary ion intensity in a first step. Owing to the collimation, however, the beam crossover shifts from aperture 2 towards the target. A high voltage applied to “Lens Magnification” repositions the beam crossover in aperture 2. The current measurements (scope 1 and 2) on aperture 1 and 2 show the actual beam position. Moreover, a first step of focusing can be done by aligning “Lens Magnification” in such a way that the current signal on aperture 2 (scope 2) achieves a rectangular-like shape. Since the ion beam is focused on and oscillating over aperture 2 during the current measurement, a rectangular-like current signal indicates a small primary ion beam spot size, at least at aperture 2. A second step of focusing is done by adjusting the “Lens Target” and “X/Y Stigmator”, all the same as in the BA mode alignment.Having the beam crossover position in aperture 2 supports a time-effective alignment and focusing of the primary ion beam due to in situ spot size information. Therefore, the CBA mode enables a simple performance tuning in terms of either higher lateral resolution or secondary ion yield. Compared to the “Collimated” mode the CBA mode is also supposed to show higher performance in terms of increased mass resolution when using the burster, see ref. 65. A detailed description of the CBA alignment procedure is given in the Appendix.
Lateral resolution of the CBA mode
Secondary Ion Mass Spectrometry (SIMS) not only enables a detailed surface chemical analysis but also a nano-scaled chemical imaging. A critical review on “SIMS imaging of the nanoworld” is given by Senoner and Unger.71 In the surface analysis community different approaches for the quantification of image resolution are used. In the commonly applied “knife edge method”, for example, an image over a straight edge is evaluated. But the latter determines the sharpness of an image and differs from the original meaning of lateral resolution. A very well defined procedure to determine the lateral resolution is suggested by Senoner, Wirth and Unger and is based on the separation of stripes.69,72 Therefore, we measured the lateral resolution of the CBA mode on the certified reference material BAM-L200 (ref. 68) by imaging well defined 3-stripe-gratings. The reference material includes several parts, each consisting of two AlGaAs stripes separated by one GaAs stripe, all of the same width, see Fig. 4c. As a reasonable resolution criterion to determine whether an image profile of a grating is resolved, a signal-to-noise ratio D/σNR ≥ 4 is suggested in ref. 69. Fig. 4a and b show ToF-SIMS image line scan (Al+) profiles in the CBA mode (Bi1+, Bi3++) obtained from the BAM-L200 reference sample. The calculated signal-to-noise ratios between 4.3 for Bi1+ and 5.4 for Bi3++ are in agreement with the resolution criterion; therefore five gratings are resolved in Fig. 4a and four in Fig. 4b. A higher signal-to-noise ratio can be reached by increasing the measurement acquisition time. Owing to instrumental drifts caused by the experimental environment, however, in our measurements a shorter acquisition time had to be chosen. For analysis, the Al+ intensity signal of a 7 × 7 μm2 large area was summed over 100 scans. After an optimal primary ion beam alignment, a lateral resolution (l.r.) of 68 nm < l.r. < 96 nm for Bi3++ and 96 nm < l.r. < 136 nm for Bi1+ (both ∼0.05 pA primary ion current, 75 μs cycle time) is obtained. The higher lateral resolution obtained for the doubly charged Bi3++ ions results from their doubled kinetic energy. With increased kinetic energy the importance of Coulomb repulsion of the primary ions is supposed to decrease; therefore a smaller spot size can be reached. The achievable lateral resolution in ToF-SIMS imaging depends on an optimized focus of the primary ion beam and an increased efficiency of desorbed secondary ions.73 These properties and further data on the modes considered in this paper are summarized in Table 1.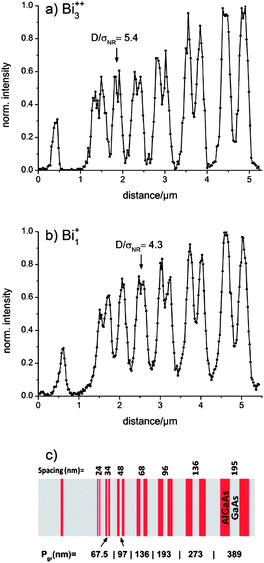 | ||
| Fig. 4 Profiles resulting after summing 100 scans (Al+) of the certified BAM-L200 reference material in the CBA mode using (a) Bi3++ and (b) Bi1+ primary ion clusters. A grating period Pgr of 97 nm (a) and 136 nm (b) could be resolved laterally according to the criterion in ref. 69. (c) Scheme of the nano-scale stripe pattern of BAM-L200. | ||
| Operation mode | HCBU (High Current Bunched) | BA (Burst Alignment) | Collimated | CBA (Collimated Burst Alignment) | |
|---|---|---|---|---|---|
| Lateral resolution (l.r.) | ∼2 to 10 μm* | ∼250 to 300 nm* | ∼100 nm* | Bi1+: 96 < l.r. < 136 nm | Bi3++: 68 < l.r. < 96 nm |
| Mass resolution | ∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000*† 000*† |
∼200*† | ∼200*† | ∼200 | ∼200 |
| Activated burster | — | >6000† | >6000† | >6000 | >6000 |
| DC-current | 16 nA | 0.4–0.75 nA | 50 pA | 70 pA | 210 pA |
| Lens Source | ∼3150 V | ∼3300 V | ∼3900 V | ∼3750 V | ∼3500 V |
| Lens Magnification | ∼15 kV | 0 V | 0 V | ∼13 kV | ∼12 kV |
| Ion fluence [ions per cm2] | ∼3.3 × 1011 | ∼3.1 × 1011 | ∼2.7 × 1011 | ∼2.8 × 1011 | ∼2.8 × 1011 |
Analysis of 18O isotope fractions in different modes
A (La0.6Sr0.4)CoO3−δ (LSC) thin layer on YSZ was analyzed to obtain the 18O natural abundance. The primary ion gun was operated in both the conventional BA and the novel CBA mode. For analysis, Bi1+ primary ions with an emission current of 1 μA were used. Fig. 5 displays the results of 40 analysis cycles for BA and CBA modes. The uncertainty of measurements expressed as a standard deviation is related to only statistical errors. The bar in Fig. 5 represents the natural 18O abundance range of (2.05 ± 0.14) × 10−3 given by the National Institute of Standards and Technology (NIST). The average 18O fraction obtained in the BA mode shows an erroneously high abundance of 2.58 × 10−3. Performing analyzes in the CBA mode results in an 18O fraction of 2.07 × 10−3. The more accurate determination of the oxygen isotopic fraction is enabled by shifting the secondary ion intensities to an optimal level, with details being given in the following sections. Owing to the low primary ion intensity in the CBA mode the count rates of the major and minor isotopes are decreased. The resulting low count rates for the minor isotope 18O− show the greatest impact on the counting statistics. Compared to the standard deviation of (±0.058) × 10−3 obtained in BA mode, therefore, a slightly larger deviation of (±0.092) × 10−3 could be determined in CBA mode.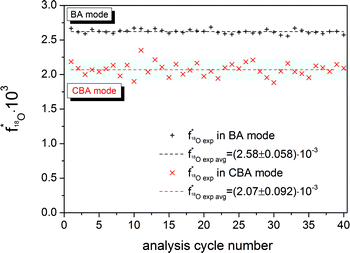 | ||
| Fig. 5 18O fraction in a (La0.6Sr0.4)CoO3−δ (LSC) thin film obtained using Bi1+ primary ions and 1 μA emission current operating the primary ion gun in both the BA and the CBA mode. The bar represents the NIST values given for the 18O natural abundance. The dashed lines show the arithmetic mean of the 18O fraction of 40 analysis cycles. After PLD preparation, the LSC layer was annealed in an ambient atmosphere for 30 min at 600 °C. | ||
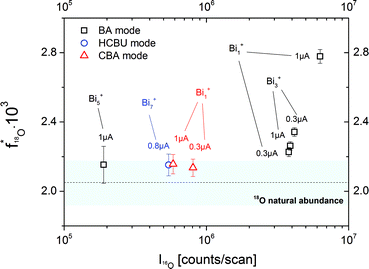
This raises the question whether the BA mode always leads to erroneous results. As a first optimization of the BA mode, the relatively high primary ion current (Bi1+, 1 pA pulsed, 20 μs cycle time) was decreased to reach lower intensities in the 16O major isotope mass peak. In Fig. 6 the resulting 18O fraction is plotted versus the 16O intensity for the SrTiO3 sample. The determined 18O tracer fractions for different operation modes, cluster sizes and primary ion emission currents are also included. Each presented experimental value is the arithmetic means of at least 40 analysis cycles and the standard deviation represents the statistical errors.
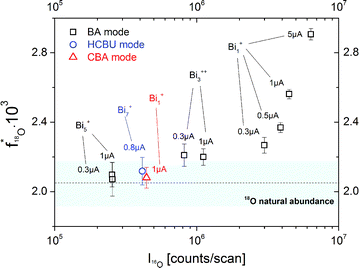 | ||
| Fig. 6 18O fractions in an as-received SrTiO3 single crystal obtained for different operation modes (BA, HCBU, CBA), bismuth emission currents (0.3 to 5 μA) and bismuth cluster sizes (Bi1+, Bi3++, Bi5+, Bi7+). The bar represents the NIST values given for the 18O natural abundance. | ||
A clear correlation between the 16O intensity and the detected 18O tracer fraction was found. The higher the major isotope intensity I16O the larger is the deviation from the correct 18O fraction. Operating the BA mode with the lowest stable emission current (in our ToF-SIMS setup 0.3 μA) results in an 18O fraction of 2.27 × 10−3 compared to 2.56 × 10−3 at 1.0 μA. However, despite lowering the emission current to a minimum, the natural 18O abundance value is not reached. This can only be achieved when using low intensive clusters in BA mode (Bi5+) or HCBU mode (Bi7+).
The measurement in CBA mode, on the other hand, results in an oxygen isotopic fraction of 2.08 × 10−3 and thus leads to an accurate value even though a high emission current (1 μA) and Bi1+ primary ions were used. This is attributed to the fact that in CBA mode still low secondary ion intensities are reached, even when Bi1+ primary ions are used. Accordingly, the 18O fraction could be accurately determined without limitations of emission current or cluster sizes.
In Fig. 7 the oxygen isotopic fractions are displayed for a (La0.6Sr0.4)FeO3−δ (LSF) thin layer on (Zr,Y)O2−δ (YSZ) analyzed immediately after PLD preparation (without annealing in ambient air). All general trends observed above (SrTiO3, Fig. 6) are found again. As long as 16O intensities are very high, 18O tracer fractions are systematically too high. Irrespective of the mode, low I16O values yield correct values but only the CBA mode can achieve the correct results with all Bi clusters.
 | ||
| Fig. 7 Dependency of the 18O fraction in a (La0.6Sr0.4)FeO3−δ (LSF) thin layer for different operation modes (CBA, BA, HCBU), bismuth emission currents (0.3 to 1 μA) and bismuth cluster sizes (Bi1+, Bi3+, Bi5+, Bi7+). The sample was investigated immediately after preparation by pulsed laser deposition. A higher 18O fraction of 2.16 × 10−3 was obtained due to higher 18O2 amount in the 16O2 gas bottle (cf.ref. 54). | ||
Interestingly, the results obtained at low I16O also show a slightly enhanced 18O tracer fraction in this case; for the CBA mode 2.16 × 10−3 is obtained. Such enhanced values after PLD production were repeatedly found, also for an as-prepared LSC layer a fraction of 2.14 × 10−3 was determined. Therefore, annealing for 30 min at 600 °C in ambient air was performed and caused a decrease to 2.07 × 10−3 and thus to the correct natural abundance value. These results can be understood from the fact that the 18O fraction in bottled (pure) oxygen is often not at the natural abundance level; values between 2.2 × 10−3 and 5.2 × 10−3 are reported in ref. 54. When using such O2 during PLD layer preparation, a higher 18O fraction results in the samples but subsequent annealing in ambient air leads to a complete oxygen exchange due to the high diffusion coefficients27 and thus to the natural abundance value.
Fig. 8 presents experimental data on the 18O fraction in several oxides measured by operating ToF-SIMS in both the BA and the CBA mode. The ordinate corresponds to the measured oxygen fraction given in percent and the abscissa assigns the analyzed oxides ordered from the left to the right in terms of increasing sputter yield. 18O “natural abundance” values obtained in the BA mode consistently show erroneously high 18O fractions, whereas analysis in the CBA mode enables an accurate determination. The higher the sputter yield, the higher is the error of the determined oxygen isotopic fractions. These results also show that both the high accuracy for all Bi clusters and the optimized lateral resolution result from low SI intensities and can only be reached due to the modified beam guidance in CBA mode.
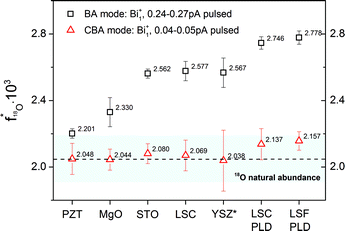 | ||
| Fig. 8 18O fractions measured on Pb(Zr,Ti)O3 (PZT), MgO, SrTiO3 (STO), (La,Sr)CoO3−δ (LSC), YSZ, (La,Sr)FeO3−δ (LSF) in both the “Burst Alignment” (BA) and the “Collimated Burst Alignment” (CBA) operation mode. The 18O fraction on YSZ* was measured with very low count rate, therefore the standard deviation increased due to counting statistics. PLD indicates thin films measured before annealing. The bar represents the values given by NIST for the natural 18O abundance. | ||
Discussion of the improved accuracy in CBA mode
Fig. 9 displays a typical example how the dead time affects the major isotope (16O) mass peak. The mass spectrum shows the part around the oxygen isotopes in a negative secondary ion mass spectrum and reveals very significant differences in secondary ion signals between the BA and the CBA mode. In the BA mode the 18O mass peak is not significantly affected by saturation due to dead time. The 16O peak, however, exhibits a shoulder at lower masses which suggests that some ions arrive at the detector earlier than the main part of the secondary ions. We suppose that the primary ion pulse deviates from an ideal rectangular pulse shape due to Coulomb repulsion in the highly intensive primary ion beam. Both noise signal and preceding ions can already saturate the detector which erroneously causes a lower intensity maximum. The following main peak of the major isotope 16O in BA mode strongly saturates the single ion counting detector. The latter is not able to recover from the huge amount of secondary ions per primary ion pulse before the next analysis cycle starts. Therefore channel by channel lower secondary ion intensities are detected. The pronounced dead time effect gets visible as a steep intensity descent during the entire major isotope mass peak. In such a case of very high intensities the Poissonian correction is supposed to be not sufficient to recalculate the true number of ions impinging the detector and the analysis results in underestimated 16O intensity.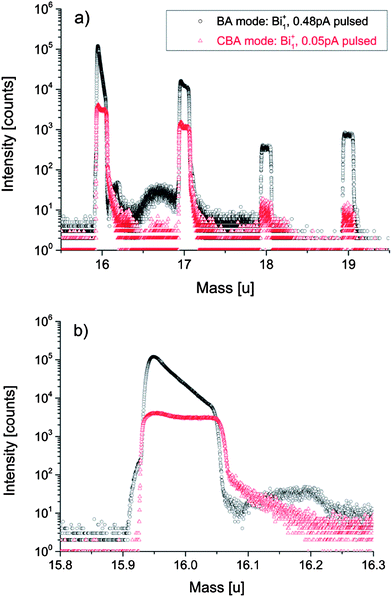 | ||
| Fig. 9 Negative secondary ion mass spectrum including all oxygen isotopes (a) and at a magnification around 16 u (b) obtained in the “Burst Alignment” (BA) and the “Collimated Burst Alignment” (CBA) for a SrTiO3 sample. The BA mass spectrum shows the dead time effect on the signal intensity in addition to preceding ions and collision-induced delayed ions. The significantly decreased intensities in CBA mode reduce the dead time effect and ion interactions. The peaks around 17 u and 19 u are mainly caused by 16OH− and F−, 18OH−, respectively. | ||
A very broad and intensive background signal between 16 u and 17 u follows the major isotope mass peak. The increase of the ion counts between the masses 16.09 u and 16.23 u indicates that the detector recovers from the previous saturation. However, intensities are so high that another saturation of the detector sets in. This is visualized by the steep intensity descent, followed by increasing counts due to renewed recovering of the detector. Two possible explanations of the background signal between 16 u and 17 u are offered in the literature: in ref. 58 the background signal is ascribed to electrons disturbing the negative mass spectra; these electrons partially result from charge compensation or they are generated from primary ion and secondary ion interactions with various surfaces within the instrument. Analysis in ref. 61 suggest that the background signal is due to ion collisions in the analyzer caused by the huge number of 16O ions.
In accordance with the latter interpretation we assume that due to their collisions 16O ions could be detected as delayed or do not arrive at the detector at all. As a consequence of the underestimated 16O signal, the calculated 18O fraction erroneously shifts to a higher value. Owing to preceding ions, ions of the following masses 17 u and 18 u could be affected by dead time effects even before the corresponding secondary ions arrive at the detector. Since the dead time probability function is not precisely known and the dead time affects the following nominal masses, a Poissonian correction becomes almost impossible. This further affects the calculated 18O fraction.
In the CBA mode, primary ion currents are adjusted in order to reduce effects caused by the dead time and ion interactions. The corresponding colored mass spectrum in Fig. 9 shows a decreased intensity for both major and minor isotopes. Preceding the 16O mass peak a very low noise signal is detected. The steeply rising slope indicates the first 16O ions arriving at the detector. The detector gets slightly saturated, which is indicated by the small decrease of the signal. However, after a time interval of ∼20 ns detection recovers (see Fig. 9b), resulting in an intensity plateau. The chosen integration interval, which corresponds to the dead time τ = 65.4 ns, sums the preceding counts as well as the counts of the entire mass peak. Because of low intensity saturation, Poissonian statistics is now suitable to correct the experimentally obtained counts. Since preceding ions are included in the integration interval, a possible saturation of the first part in the mass peak of interest is taken account of Poissonian correction.
Even if a low primary ion current in CBA mode minimizes ion interactions there are still decelerated ions following the major isotope mass peak. However, in contrast to the broad background peak in the BA mode there is no dead time effect observable in the low intensity background signal of the CBA mode. As a result, a more accurate oxygen isotopic fraction can be determined in addition to an improved lateral resolution. The performance of the CBA mode is discussed in more detail in ref. 65 featuring different measurement techniques and application examples. There, also more information on the still high mass resolution of the CBA mode is given, which would, for example, allow a separation of H216O and 18O.
Conclusions
The operation of established ToF-SIMS modes often results in high primary ion and secondary ion intensities. Pronounced dead time effects and ion interactions can lead to an underestimated value of 16O counts due to saturation of the major isotope mass peak. Consequently, the determination of oxygen isotopic fractions is affected in such a way that the calculated 18O fraction shifts to a higher value. Analysis in BA and HCBU modes therefore shows an erroneously high 18O fraction except for very low primary ion currents resulting when using the largest bismuth clusters (Bi5+, Bi7+). Applying the novel CBA mode enables determination of accurate oxygen isotopic fractions irrespective of the chosen primary ion currents and cluster sizes. Owing to the lower primary ion intensity, a further advantage of the CBA mode is a significantly optimized lateral resolution. Operating CBA with Bi1+ and Bi3++ clusters enables a lateral resolution of sub-100 nm. Owing to the modified primary ion beam guidance also the mass resolution can be increased. Moreover, a simple tuning is possible for either achieving higher lateral resolution or an improved detection limit.Appendix: how to align the CBA mode
The following instructions detail the alignment procedure of the CBA mode when operating a bismuth ion gun on a TOF.SIMS 5 machine manufactured by ION-TOF. The fundamental idea of the CBA mode, however, can be applied to all ion guns with at least three main ion lenses. Although the same general tendencies can be expected, the exact changes in lateral resolution or intensity will depend on the individual ion gun setup.Based on an already aligned BA mode, we activated the DC mode and used the “Faraday Cup” to run a target current measurement (manual) in positive mode with illumination turned off. The voltage applied on “Lens Source” has to be increased to ∼3500 to 4000 V in order to collimate the primary ion beam. While increasing “Lens Source” voltage, the “Direct Current” (DC) is observed to decrease simultaneously. If Bi1+ ions are used for analysis, a good “Lens Source” voltage is aligned when a target current of ∼140 pA is reached. Owing to the voltage increase, the ion beam can shift out of the previously aligned center in the BA mode. In order to measure the correct DC current, the beam should be re-centered using the scope function in apertures 1 and 2. The upper part of the beam is aligned when scope 1 and 2 signals are centered as visualized in Fig. 10a and b. Then, the scope function is stopped to re-center the near-target part of the beam by optimizing “X/Y Blanking”. “X/Y Blanking” voltages are adjusted when the target current (DC) reaches its maximum. When the first alignment procedure is finished, an additional adjustment cycle (like increasing “Lens Source” voltage and re-centering of the upper and near-target beam) would be necessary to finally reach a target current of ∼140 pA. The current signal in scope 1 of aperture 1 should now show a decreased amplitude like that displayed in Fig. 10a.
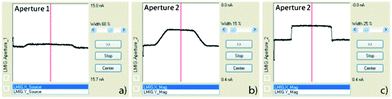 | ||
| Fig. 10 Primary ion current measurements on primary ion gun aperture 1 (scope 1) and aperture 2 (scope 2) of an already aligned ion beam. (a) Current signal on aperture 1 after primary ion beam collimation with already decreased intensity. (b) Current signal on aperture 2 after collimation without any voltage applied to “Lens Magnification”. (c) Current signal on aperture 2 shows a rectangular shape after an optimal voltage was applied to “Lens Magnification”. | ||
As a next important step, the voltage on “Lens Magnification” is gradually increased from zero to approximately 12–13 kV while observing the current signal of scope 2 approaching a rectangular-like shape. The optimal voltage is reached when the steepness of the rectangular-like current signal reaches its maximum, see Fig. 10c. The upper and near-target parts of the beam have to be re-centered again. The DC current is expected to be approximately 70 pA, otherwise “Lens Source” and “Lens Magnification” voltages can be fine-tuned. The primary ion gun is aligned to a DC current of ∼70 pA optimized for oxygen isotopic measurements using Bi1+. Since bismuth clusters like Bi3++ have a lower relative intensity in the DC beam than Bi1+, a higher DC current has to be aligned to finally reach a pulsed primary ion beam current of ∼0.05 pA (20 μs cycle time). The relative primary ion currents of several Bi clusters in the DC beam are given in ref. 74.
The following fine-focusing steps are monitored by observing a “Secondary Electron” (SE) image on the “A-Grid” (chopper grid, 100 μm spacing) with a “Field of View” (FoV) of at least 30 × 30 μm2, the reference height is already adjusted. When focusing the beam for the first time in the CBA mode, the “X/Y Stigmator” should be set to zero before the “Lens Target” is optimized for the best focus. Adjusting the “X/Y Stigmator” will compensate possible astigmatism of the beam resulting in a better resolution. After successful focusing, the SE image is expected to well-resolve at least 10 × 10 μm2 (FoV). When the primary ion beam is aligned and focused once, a setting file should be saved. For further beam alignment it is just necessary to load the CBA setting file, to maximize the DC current by optimizing “X/Y Blanking” and fine-focusing as in the BA mode.
The higher the desired lateral resolution the lower has the primary ion current to be adjusted. The minimum limit, however, is exceeded when the amplitude in the scope 1 signal disappears and therefore an alignment of the ion beam is impossible. As an optimal value to determine accurate oxygen isotopic fractions, a DC current of ∼70 pA for Bi1+ and ∼210 pA for Bi3++ (0.03–0.05 pA pulsed at 100 μs cycle time) is suggested. The voltages and currents applied to modify the CBA mode may vary on other ToF-SIMS instruments, for example, due to different aperture abrasion or primary ion species.
Acknowledgements
Financial support by Christian Doppler Laboratory of Ferroic Materials and Austrian Science Fund (FWF) project F 4509-N16 is gratefully acknowledged. We also thank Klaus Reichmann, Graz University of Technology, for providing PZT samples and Sandra Kogler for providing LSF samples.References
- S. B. Adler, Chem. Rev., 2004, 104, 4791–4843 CrossRef CAS.
- W. C. Chueh, Y. Hao, W. Jung and S. M. Haile, Nat. Mater., 2012, 11, 155–161 CrossRef CAS.
- J. L. M. Rupp, Solid State Ionics, 2012, 207, 1–13 CrossRef CAS.
- T. Horita, T. Shimonosono, H. Kishimoto, K. Yamaji, M. E. Brito, Y. Hori and H. Yokokawa, Electrochem. Solid State Lett., 2010, 13, B135–B138 CrossRef CAS.
- J. Mizusaki, K. Amano, S. Yamauchi and K. Fueki, Solid State Ionics, 1987, 22, 313–322 CrossRef CAS.
- T. Horita, D. Cho, T. Shimonosono, H. Kishimoto, K. Yamaji, M. E. Brito and H. Yokokawa, J. Electrochem. Soc., 2012, 159, F476–F481 CrossRef CAS.
- J. Mizusaki, K. Amano, S. Yamauchi and K. Fueki, Solid State Ionics, 1987, 22, 323–330 CrossRef CAS.
- M. Sase, K. Yashiro, K. Sato, J. Mizusaki, T. Kawada, N. Sakai, K. Yamaji, T. Horita and H. Yokokawa, Solid State Ionics, 2008, 178, 1843–1852 CrossRef CAS.
- M. Sase, F. Hermes, K. Yashiro, K. Sato, J. Mizusaki, T. Kawada, N. Sakai and H. Yokokawa, J. Electrochem. Soc., 2008, 155, B793–B797 CrossRef CAS.
- A. Chroneos, B. Yildiz, A. Tarancon, D. Parfitt and J. A. Kilner, Energy Environ. Sci., 2011, 4, 2774–2789 CAS.
- I. D. Seymour, A. Tarancon, A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, Solid State Ionics, 2012, 216, 41–43 CrossRef CAS.
- E. Mutoro, S. Gunther, B. Luerssen, I. Valov and J. Janek, Solid State Ionics, 2008, 179, 1835–1848 CrossRef CAS.
- S. Fearn, J. C. H. Rossiny, J. A. Kilner and J. R. G. Evans, Solid State Ionics, 2012, 211, 51–57 CrossRef CAS.
- N. Sakai, T. Horita, K. Yamaji, M. E. Brito, H. Yokokawa, A. Kawakami, S. Matsuoka, N. Watanabe and A. Ueno, J. Electrochem. Soc., 2006, 153, A621–A625 CrossRef CAS.
- D. P. Rupasov, A. V. Berenov, J. A. Kilner, S. Y. Istomin and E. V. Antipov, Solid State Ionics, 2011, 197, 18–24 CrossRef CAS.
- Z. Cai, M. Kubicek, J. Fleig and B. Yildiz, Chem. Mater., 2012, 24, 1116–1127 CrossRef CAS.
- R. Hancke, S. Fearn, J. A. Kilner and R. Haugsrud, Phys. Chem. Chem. Phys., 2012, 14, 13971–13978 RSC.
- J. Janek, B. Luerssen, E. Mutoro, H. Fischer and S. Gunther, Top. Catal., 2007, 44, 399–407 CrossRef CAS.
- M. Kubicek, A. Limbeck, T. Frömling, H. Hutter and J. Fleig, J. Electrochem. Soc., 2011, 158, B727–B734 CrossRef CAS.
- R. A. De Souza, M. J. Pietrowski, U. Anselmi-Tamburini, S. Kim, Z. A. Munir and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2067–2072 RSC.
- N. J. Simrick, A. Bieberle-Hutter, T. M. Ryll, J. A. Kilner, A. Atkinson and J. L. M. Rupp, Solid State Ionics, 2012, 206, 7–16 CrossRef CAS.
- H. Aydin, C. Korte, M. Rohnke and J. Janek, Phys. Chem. Chem. Phys., 2013, 15, 1944–1955 RSC.
- J. L. Hertz and H. L. Tuller, Solid State Ionics, 2007, 178, 915–923 CrossRef CAS.
- M. Burriel, J. Pena-Martinez, R. J. Chater, S. Fearn, A. V. Berenov, S. J. Skinner and J. A. Kilner, Chem. Mater., 2012, 24, 613–621 CrossRef CAS.
- A. K. Opitz and J. Fleig, Solid State Ionics, 2010, 181, 684–693 CrossRef CAS.
- A. Opitz, A. Schintlmeister, H. Hutter and J. Fleig, Phys. Chem. Chem. Phys., 2010, 12, 12734–12745 RSC.
- M. Kubicek, Z. Cai, W. Ma, B. Yildiz, H. Hutter and J. Fleig, ACS Nano, 2013, 7, 3276–3286 CrossRef CAS.
- M. Gerstl, T. Frömling, A. Schintlmeister, H. Hutter and J. Fleig, Solid State Ionics, 2011, 184, 23–26 CrossRef CAS.
- R. A. De Souza, J. A. Kilner and J. F. Walker, Mater. Lett., 2000, 43, 43–52 CrossRef CAS.
- M. Y. Oh, A. Unemoto, K. Amezawa and T. Kawada, J. Electrochem. Soc., 2012, 159, F659–F664 CrossRef CAS.
- V. B. Vert, J. M. Serra, J. A. Kilner and M. Burriel, J. Power Sources, 2012, 213, 270–274 CrossRef CAS.
- E. N. Coker, J. A. Ohlhausen, A. Ambrosini and J. E. Miller, J. Mater. Chem., 2012, 22, 6726 RSC.
- D. Pergolesi, E. Fabbri, S. N. Cook, V. Roddatis, E. Traversa and J. A. Kilner, ACS Nano, 2012, 6, 10524–10534 CAS.
- G. Y. Yang, G. D. Lian, E. C. Dickey, C. A. Randall, D. E. Barber, P. Pinceloup, M. A. Henderson, R. A. Hill, J. J. Beeson and D. J. Skamser, J. Appl. Phys., 2004, 96, 7500–7508 CrossRef CAS.
- H. M. Duiker, P. D. Beale, J. F. Scott, C. A. P. Dearaujo, B. M. Melnick, J. D. Cuchiaro and L. D. McMillan, J. Appl. Phys., 1990, 68, 5783–5791 CrossRef CAS.
- M. F. Zhang, Y. Wang, K. F. Wang, J. S. Zhu and J. M. Liu, J. Appl. Phys., 2009, 105 CAS.
- R. Waser, T. Baiatu and K. H. Hardtl, J. Am. Ceram. Soc., 1990, 73, 1645–1653 CrossRef CAS.
- S. Rodewald, J. Fleig and J. Maier, J. Am. Ceram. Soc., 2000, 83, 1969–1976 CrossRef CAS.
- N. J. Donnelly and C. A. Randall, J. Appl. Phys., 2011, 109 Search PubMed.
- N. J. Donnelly and C. A. Randall, J. Am. Ceram. Soc., 2009, 92, 405–410 CrossRef CAS.
- N. Balke, D. C. Lupascu, T. Granzow and J. Rodel, J. Am. Ceram. Soc., 2007, 90, 1081–1087 CrossRef CAS.
- R.-A. Eichel, Phys. Chem. Chem. Phys., 2011, 13, 368–384 RSC.
- R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85 Search PubMed.
- N. J. Donnelly and C. A. Randall, Appl. Phys. Lett., 2010, 96 Search PubMed.
- J. Claus, M. Leohardt and J. Maier, J. Phys. Chem. Solids, 2000, 61, 1199–1207 CrossRef CAS.
- T. Frömling, A. Schintlmeister, H. Hutter and J. Fleig, J. Am. Ceram. Soc., 2011, 94, 1173–1181 CrossRef.
- T. Frömling, H. Hutter and J. Fleig, J. Am. Ceram. Soc., 2012, 95, 1692–1700 CrossRef.
- K. Reichmann, E. Volkl, M. Ahrens, J. Fleig and J. Votsch, J. Mater. Sci., 2010, 45, 1473–1477 CrossRef CAS.
- L. Andrejs and J. Fleig, J. Eur. Ceram. Soc., 2013, 33, 779–794 CrossRef CAS.
- E. Völkl, P. Hillebrand and J. Fleig, J. Electroceram., 2011, 27, 66 CrossRef.
- J. A. Kilner, S. J. Skinner and H. H. Brongersma, J. Solid State Electrochem., 2011, 15, 861–876 CrossRef CAS.
- T. Horita, K. Yamaji, N. Sakai, Y. Xiong, T. Kato, H. Yokokawa and T. Kawada, Appl. Surf. Sci., 2003, 203–204, 634–638 CrossRef CAS.
- R. A. De Souza and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2356–2367 RSC.
- R. A. De Souza and R. J. Chater, Solid State Ionics, 2005, 176, 1915–1920 CrossRef CAS.
- T. Horita, K. Yamaji, N. Sakai, Y. Xiong, H. Yokokawa and T. Kawada, Ionics, 2002, 8, 108–117 CrossRef CAS.
- A. Benninghoven, Angew. Chem., Int. Ed. Engl., 1994, 33, 1023–1043 CrossRef.
- A. Benninghoven, Surf. Sci., 1973, 35, 427–457 CrossRef CAS.
- T. Stephan, Planet. Space Sci., 2001, 49, 859–906 CrossRef CAS.
- A. J. Fahey and S. Messenger, Int. J. Mass Spectrom., 2001, 208, 227–242 CrossRef CAS.
- P. Fielitz and G. Borchardt, Solid State Ionics, 2001, 144, 71–80 CrossRef CAS.
- R. A. De Souza, J. Zehnpfenning, M. Martin and J. Maier, Solid State Ionics, 2005, 176, 1465–1471 CrossRef CAS.
- J. L. S. Lee, I. S. Gilmore and M. P. Seah, Surf. Interface Anal., 2012, 44, 1–14 CrossRef.
- M. R. Keenan and P. G. Kotula, Surf. Interface Anal., 2004, 36, 203–212 CrossRef CAS.
- T. Stephan, J. Zehnpfenning and A. Benninghoven, J. Vac. Sci. Technol., A, 1994, 12, 405–410 CAS.
- M. Kubicek, G. Holzlechner, A. Opitz, S. Larisegger, H. Hutter and J. Fleig, Appl. Surf. Sci., 2013, submitted Search PubMed.
- B. Hagenhoff, D. van Leyen, E. Niehuis and A. Benninghoven, J. Vac. Sci. Technol., A, 1989, 7, 3056–3064 CAS.
- H. W. Werner and N. Warmoltz, J. Vac. Sci. Technol., A, 1984, 2, 726–731 CAS.
- M. Senoner, T. Wirth, W. Unger, W. Osterle, I. Kaiander, R. L. Sellin and D. Bimberg, Surf. Interface Anal., 2004, 36, 1423–U1429 CrossRef CAS.
- M. Senoner, T. Wirth and W. Unger, J. Anal. At. Spectrom., 2010, 25, 1440–1452 RSC.
- R. N. S. Sodhi, Analyst, 2004, 129, 483–487 RSC.
- M. Senoner and W. Unger, J. Anal. At. Spectrom., 2012, 27, 1050 RSC.
- PD ISO/TR 19319:2013: Surface chemical analysis, Fundamental approaches to determination of lateral resolution and sharpness in beam-based methods, British Standards Institution, 2013 Search PubMed.
- B. Hagenhoff, Mikrochim. Acta, 2000, 132, 259–271 CAS.
- F. Kollmer, Appl. Surf. Sci., 2004, 231–232, 153–158 CrossRef CAS.
Footnote |
| † Authors with equal contribution. |
| This journal is © The Royal Society of Chemistry 2013 |
