Sphingolipid metabolites modulate dielectric characteristics of cells in a mouse ovarian cancer progression model

Abstract

Currently, conventional cancer treatment regimens often rely upon highly toxic chemotherapeutics or target oncogenes that are variably expressed within the heterogeneous cell population of tumors. These challenges highlight the need for novel treatment strategies that (1) are non-toxic yet able to at least partially reverse the aggressive phenotype of the disease to a benign or very slow-growing state, and (2) act on the cells independently of variably expressed biomarkers. Using a label-independent rapid microfluidic cell manipulation strategy known as contactless dielectrophoresis (cDEP), we investigated the effect of non-toxic concentrations of two bioactive sphingolipidmetabolites, sphingosine (So), with potential anti-tumor properties, and sphingosine-1-phosphate (S1P), a tumor-promoting metabolite, on the intrinsic electrical properties of early and late stages of mouse ovarian surface epithelial (MOSE) cancer cells. Previously, we demonstrated that electrical properties change as cells progress from a benign early stage to late malignant stages. Here, we demonstrate an association between So treatment and a shift in the bioelectrical characteristics of late stage MOSE (MOSE-L) cells towards a profile similar to that of benign MOSE-E cells. Particularly, the specific membrane capacitance of MOSE-L cells shifted toward that of MOSE-E cells, decreasing from 23.94 ± 2.75 to 16.46 ± 0.62 mF m⁻² after So treatment, associated with a decrease in membrane protrusions. In contrast, S1P did not reverse the electrical properties of MOSE-L cells. This work is the first to indicate that treatment with non-toxic doses of So correlates with changes in the electrical properties and surface roughness of cells. It also demonstrates the potential of cDEP to be used as a new, rapid technique for drug efficacy studies, and for eventually designing more personalized treatment regimens.

---

Insight, innovation, integration

This study presents the first investigation of the relationship between treatment with non-toxic doses of an exogenous metabolite and changes in the electrical properties and surface roughness of cells. A relatively new and innovative technique for label-free rapid cell manipulation, contactless dielectrophoresis (cDEP), was used. cDEP eliminates contact between electrodes and the biological sample, thereby avoiding some challenges of traditional dielectrophoresis-based techniques. The results of this integrative study reveal that sphingolipid modulation therapy, which acts independent of variably expressed biomarkers, partially reversed the aggressive phenotype of the malignant cancer cells to a benign or slow-growing state. These new insights can lead to the development of new techniques for drug efficacy studies, and eventually more personalized treatment regimens.

Introduction

Ovarian cancer, the most frequent cause of death from gynecological malignancies in women and the fifth leading cause of death from cancer in women,^1,2 is a genetically and histologically heterogeneous disease. The lack of common genetic markers hinders both cancer detection at earlier stages and the development of successful treatment options. Development of treatment regimens and detection techniques that do not rely upon the expression of specific genes or surface markers could ameliorate these challenges.

The operating principle for our cell manipulation and characterization strategy is dielectrophoresis (DEP), the movement of polarized particles in a non-uniform electric field.³ DEP can be applied as a cell manipulation technique^4–7 that does not rely on genotype-dependent biomarkers, in contrast to other cell isolation techniques such as flow cytometry⁸ and magnetic bead cell separation.⁹ DEP has been successfully used for drug screening applications,¹⁰ to distinguish between multidrug-resistant and sensitive cancer cells by their cytoplasmic conductivity,^11,12 and to determine cytoplasm and membrane conductivity of drug-treated red blood cells.¹³ Further applications of DEP include cell viability determination^10,14 and investigations of drug-stimulated cell surface roughness increase.¹⁵ In conventional DEP techniques, metallic electrodes are used to create a non-uniform electric field.^10–15 However, contact between electrodes and the sample fluid creates challenges in manipulating biological samples including Joule heating, sample contamination, and bubble formation due to electrolysis. To address these issues, we have developed contactless DEP (cDEP), a microfluidic cell manipulation strategy which eliminates direct contact between electrodes and the sample.¹⁶ In cDEP, an electric field is generated using electrode channels that are separated from the sample channels by a thin insulating barrier. These electrode channels are filled with a highly conductive fluid and under an alternating current (AC) signal are capacitively coupled to the sample channel.^17–20 cDEP has been used to isolate prostate tumor initiating cells from prostate cancer cells,²¹ cancer cells from blood cells,^22,23 viable cells from dead cells,¹⁷ and different stages of breast cancer cell lines.²⁴

Moreover, we have previously utilized cDEP to quantify dielectric properties of a syngeneic mouse cell model for progressive ovarian cancer.²⁵ In this model, isolated primary mouse ovarian surface epithelial (MOSE) cells undergo transformation in vitro and progress to malignant stages.²⁶ Since human cell lines exhibiting different stages of ovarian cancer derived from one genetic source are not available for study, the MOSE model represents a useful alternative that avoids the potential confounding variable of inter-subject genetic differences. Based on their phenotype, MOSE cells were categorized into early, intermediate, and late stages of malignancy. An increasingly dysregulated cytoskeleton organization and changes in the expression of cytoskeleton genes and their regulators were observed during neoplastic progression, accompanied by an increase in membrane ruffles and protrusions.^26,27 Cytoskeletal changes were associated with stage-specific changes in cellular biomechanical properties.²⁸ Also, we have recently shown for the first time that the dielectric responses of cells are different in different stages of progression.²⁵ We compared the crossover frequency and membrane capacitance of different stages of MOSE cells, finding that the membrane capacitance was greater in malignant cells compared to benign cells.²⁵ Aggressive MOSE cells also showed different dielectric responses from peritoneal cells, specifically macrophages and fibroblasts,²⁹ indicating that cDEP may be an option for isolating ovarian cells from peritoneal fluid for cancer detection.

Current cancer treatments rely upon highly toxic doses of chemotherapeutics and can cause severe adverse side effects. In addition to achieving early detection, the development of less aggressive treatment options that at least partially reverse the aggressive phenotype of the disease to an earlier, more benign state and therefore may turn a deadly cancer into a chronic disease could be highly beneficial for patients. In this regard, we have used orally administered complex sphingolipids to successfully suppress colon and breast cancer.^30–34Sphingolipidmetabolites influence membrane biology and as lipid second messengers modulate cellular homeostasis, functions and responses to extracellular stimuli. Sphingolipids are involved in the regulation of cell growth, cell death, migration, angiogenesis, and metabolism, among many other cell functions.^35,36 Dysregulation in metabolic pathways of sphingolipids can cause progression of some diseases, including cancer.^37,38 The sphingolipidmetabolites, ceramide (Cer), sphingosine (So), and sphingosine-1-phosphate (S1P), can stimulate opposing cellular responses depending upon their relative levels in a cell, forming the so-called sphingolipid rheostat.^39,40 In general, So and Cer are known as cell death-promoting factors leading to apoptosis, inhibition of cell growth, differentiation, migration, and angiogenesis⁴¹ and thus could be considered tumor suppressors. However, Cer has also been associated with inflammation,⁴² suggesting a tumor promoting effect. In contrast, S1P acts to support growth and survival of numerous cell types. As such, it has tumor-promoting effects, including the inhibition of apoptosis and the stimulation of angiogenesis, cell proliferation, differentiation, and migration.^39,41 Elevated levels of S1P have been reported in human ascites fluid of patients with ovarian cancer⁴³ and may promote the survival, adherence, and outgrowth of peritoneal metastases. Interestingly, therapies targeting S1P generation and signaling have led to a decreased tumor formation in mice.⁴⁴

In the present study, we used cDEP to characterize MOSE cells' electrical properties after So and S1P treatment to compare the effects of exogenous sphingolipidmetabolites associated with anti- and pro-cancer effects, respectively. We demonstrate that sphingolipid modulation therapy induced distinct changes in the bioelectrical properties of cancer cells. Importantly, the treatments were non-toxic, allowing us to use cDEP to discriminate among viable MOSE-derived cancer cells. We report that So treatment correlated with a shift in electrical properties of the aggressive MOSE cells towards a profile reminiscent of more benign stages, whereas S1P did not significantly impact the electrical properties of either early or late stage MOSE cells. The association of the altered electrical phenotype of the So treated cells with cancer suppression and the potential for use of the electrical phenotype as a marker for treatment efficacy will be explored in future studies.

Theory

A particle located within the boundaries of an applied non-uniform electric field will become polarized and experience a dielectrophoretic force described by

F⃑_DEP = (p_eff·▽)E⃑_RMS (1)

p_eff is the effective induced dipole moment of the particle and E⃑_RMS is the root mean square electric field. For a lossy spherical particle where

p_eff = 4πε_mr³Re[K(ω)]E⃑_RMS (2)

and ε_m is the permittivity of the suspending medium, r is the radius of the particle, and the Clausius–Mossotti factor is represented as

The real part of the Clausius–Mossotti factor is theoretically bound by −0.5 and 1, and and represent the complex permittivity of the particle and the suspending medium, respectively, where the complex permittivity is ε* = ε + σ/jω. The sign of the frequency-dependent Clausius–Mossotti factor determines the direction of translational particle movement, either toward a region of high electric field gradient (positive DEP, pDEP) or low electric field gradient (negative DEP, nDEP). Biological particles are more complex than a simple spherical particle, and models of varying complexity have emerged that can approximate a biological particle, such as a cell, with sufficient accuracy. In a multi-shell model,⁴⁵ the membrane of the bioparticles, the nucleus, and even the nucleus membrane can be considered, and parameters can be tailored to a specific cell of interest. For the work presented here, a single shell model that considers the cell's thin lipid membrane and the internal cytoplasm is used. Thus the effective permittivity can be written as

where γ³ = r/(r − d), d is the thickness of the membrane, r > d, and and are the cytoplasm and membrane complex permittivity, respectively.

For each cell type, within a specific media, there exists a unique crossover frequency, f_xo. At this frequency the real part of f_CM equals zero, thus, there is no net DEP force acting on the cells. The first crossover frequency of mammalian cells in low conductivity buffer of 100 μS cm⁻¹ occurs between 10–100 kHz, and the second crossover frequency is typically on the order of 10 MHz.⁴⁶ Cell size, shape, cytoskeleton, and membrane morphology affect the first crossover frequency, while cytoplasm conductivity, nuclear envelope permittivity, nucleus–cytoplasm (N/C) volume ratio, and endoplasmic reticulum influence the second crossover frequency.⁴⁷ Thus, the crossover frequency can be used as a tool to monitor the effect of treatments that physically alter the cell. The crossover frequency can be determined by setting Re{K(ω)} equal to zero and solving for frequency. Then, f_xo is found by

For frequencies less than 1 MHz, dielectric properties of cells are related to membrane properties.⁴⁸ The specific capacitance of the cell membrane, C_mem, and conductance associated with the transport of ions across the membrane, G_mem, can be defined as

and the total effective conductance per unit area of the cell membrane, as⁴⁶

K _ms is the surface conductance of the membrane related to the electrical double layer around the cell, and G_mem is the conductance associated with the transport of ions across the membrane.^46,49 At low frequencies, <100 kHz, the low value of G_mem, representing the membrane bulk conductivity, prevents the applied electric field from penetrating the interior of the cell. As the frequency increases beyond 100 kHz, membrane resistance begins to short-circuit and the electric field penetrates inside the cell. Then, for frequencies below 100 kHz eqn (5) can be simplified to the form of⁴⁶

The second term on the right hand side can be neglected for . This inequality is valid for low conductivity media, such as the cell solution in this work (conductivity of approximately 100 mS m⁻¹). Thus, the second term is negligible and the crossover frequency can be calculated from:

Eqn (10) shows that there is an inverse relation between the ratio of crossover frequency to sample conductivity, f_xo/σ_m, and C_mem. Also it shows that the electrical properties of cells, such as specific membrane capacitance, can be calculated from their crossover frequency, as will be investigated further in the rest of the article.

Although the single-shell model has been successful for predicting the biophysical properties of cells, it sometimes deviates from the experimental results⁵⁰ since the real cellular structure is more complex than that assumed by the single-shell model. For instance, this model assumes that cells have a thin and spherical membrane which surrounds a spherical homogeneous interior, and thus does not take into account membrane inhomogeneity and cytoplasm and nuclear structural features.⁵¹ Consequently, this model cannot correlate specific membrane capacitance, C_mem, with membrane morphological complexity.

Materials and methods

Device layout

Our microdevice, shown in Fig. 1, consists of a straight main channel and parallel fluid electrode channels, each 50 μm in depth. The main channel has an inlet and outlet with a series of rounded ‘sawtooth’ features that constrict the main channel from 500 μm width to 100 μm. These sawtooth features create high electric field gradients in the region where the sample channel is constricted, and the series of features increases the length of time that the cells are exposed to the DEP force, based on the approach developed by Sano et al.²² Fluidic electrode channels are separated from the sample channel by 20 μm thick insulating barriers. Throughout this article, the side of the channel which has sawtooth features will be referred to as the top side of the channel and the opposite side of the channel which is a straight wall will be referred to as the bottom side of the channel.

Fig. 1 The overhead view schematic of the microfluidic device. The inset shows a detailed view of a sawtooth feature and the thin insulating barrier separating the sample channel and electrode channels.

Device fabrication

A stamp of the microdevice design was made for the use with standard soft lithography techniques. An AZ 9260 photoresist (AZ Electronic Materials, Somerville, NJ, USA) was spun onto a clean silicon wafer and exposed to UV light for 60 s through a mask patterned with the device design. The exposed photoresist was removed using an AZ 400 K developer (AZ Electronic Materials, Somerville, NJ, USA). Deep Reactive Ion Etching (DRIE) was used to etch microchannels to a depth of 50 μm. Surface roughness on the side walls was removed by 5 minutes wet etching with tetramethylammonium hydroxide (TMAH) 25% at 70 °C. A thin coating of Teflon, which improved the release of the device from the stamp, was deposited by DRIE.

The devices were fabricated using polydimethylsiloxane (PDMS). PDMS was mixed in a 10 : 1 ratio of elastomer to curing agent (Sylgard 184, Dow Corning, USA). The liquid-phase PDMS was left under vacuum for 30 minutes to remove air bubbles, and was then poured onto the silicon master stamp and cured for 45 minutes at 100 °C. Upon removal from the wafer, the device was trimmed and fluidic connections were punched in the inlet and outlet of each channel with a 1.5 mm blunt puncher (Howard Electronic Instruments, USA). The PDMS device and a glass microscope slide were cleaned before treating with air plasma for two minutes and bonding together.

Cell culture and drug treatment

MOSE cells were cultured in high glucose DMEM (Sigma Aldrich) supplemented with 4% fetal bovine serum (Atlanta Biologicals), 3.7 g L⁻¹ NaHCO₃, and 1% penicillin/streptomycin (Sigma Aldrich). MOSE-E and MOSE-L cells were treated with 1.5 μM So or 500 nM S1P as BSA complexes (BSA, fatty acids-free fraction V, Calbiochem) for three passages, allowing 3–4 days between each passage. These treatments were not toxic to the cells.

Cell preparation

The cells were harvested by trypsinization, washed and resuspended in low conductivity buffer (8.5% sucrose [w/v], 0.3% glucose [w/v], 0.725% RPMI [w/v])⁵² to a concentration of 3 × 10⁶ cells per mL. The cells were stained with Calcein-AM (Molecular Probes Inc., Carlsbad, CA, USA), at a concentration of 2 μL dye per mL cell suspension. The final cell suspension had an averaged conductivity of 96.97 ± 4.15 μS cm⁻¹, measured using a conductivity meter (Horiba B-173 Twin Conductivity/Salinity Pocket Testers, Cole-Parmer).

Experimental setup

The PDMS device was placed under vacuum for 30 minutes immediately prior to priming the main channel with the cell suspension. The cell suspension was introduced into the main channel inlet through Teflon tubing attached to a syringe with a needle tip (Cole-Parmer Instrument Co., Vernon Hills, IL). The fluidic electrode channels were filled with phosphate-buffered saline (PBS) solution of conductivity 1.4 S m⁻¹ and pipette tip reservoirs filled with PBS were inserted into the fluid electrode channel inlet and outlet. Aluminum electrodes connected to the low frequency electronics were inserted into the fluidic electrode reservoirs. After priming, a syringe pump (PHD Ultra, Harvard Apparatus, Holliston, MA, USA) was used to supply the flow rate of 0.005 mL h⁻¹ during the experiments.

To generate the AC electric field, the output signal from a function generator (GFG-3015, GW Instek, Taipei, Taiwan) was amplified (Model AL-50 HF-A/VT, West Nyack, NY, USA) to produce output voltages ranging from 0–200 V_RMS at frequencies between 5 and 70 kHz. Voltage and frequency were monitored using an oscilloscope (TDS-1002B, Tektronics Inc. Beaverton, OR, USA) connected to the output of the function generator.

An inverted light microscope (Leica DMI 6000B, Leica Microsystems, Bannockburn, IL) equipped with a digital camera (Leica Microsystems) was used for monitoring cells in the main channel, and Leica Application Suite 3.8 software (Leica Microsystems) was used for recording videos of cell response at systematically varied frequencies. Microdevices were kept under vacuum for thirty minutes prior to priming the sample channel with cell suspension and fluid electric channels with PBS. The cell suspension was pumped through the sample channel at 0.005 ml h⁻¹ using a syringe pump.

Image processing was accomplished using MATLAB (R2012a, MathWorks Inc., Natick, MA, USA). For each two minute video, the spatial distribution of cells through the sample channel was determined by recording the position of each cell as it passed a superimposed vertical line. The centerline of each distribution was then compared to the average centerline of control cell distributions (to which no electric field was applied) and the crossover frequency was found by interpolating.

Computational modeling

Device performance was modeled computationally. DEP force was predicted using the Electric Currents module and the shear rate and fluid flow were modeled using the Laminar Flow module of COMSOL Multiphysics 4.3a (Comsol Inc., Burlington, MA, USA). Table 1 presents the values of electrical conductivity and permittivity used in the computational modeling. PBS properties were applied to the fluid electrode channels and low conductivity buffer properties were used for the sample channel. The electrical properties of PDMS used in the model were reported by the manufacturer (Sylgard 184, Dow Corning, USA). The viscosity and density of water, 0.001 Pa s and 1000 kg m⁻³, respectively, were used as the viscosity and density of the sample in the main fluidic channel, given the characteristics of low conductivity buffer.

Table 1 Electrical properties of the materials used in the computational modeling

Material	Electrical conductivity [S m^−1]	Relative permittivity
PDMS	0.83 × 10^−12	2.65
PBS	1.4	80
Low conductivity buffer	0.01	80

---

Fig. 2a illustrates the shear rate inside the sample channel. The inlet velocity was set to 56 μm s⁻¹ based on the experimental flow rate of 0.005 mL h⁻¹. The outlet boundary was set to no viscous stress (Dirichlet condition for pressure). No slip boundary conditions were applied to the walls of the sample channel. Then, the Navier–Stokes equations were solved for an incompressible laminar flow. The maximum shear rate (∼2 s⁻¹) was found to be significantly lower than the shear rate threshold (approximately 5000 s⁻¹) that can cause cell lysis.^53,54

Fig. 2 Computational modeling of the sample channel: (a) shear rate, (b) electric field magnitude, and (c) ▽(E⃑_RMS·E⃑_RMS).

To model the electric field, uniform potentials and ground at the source and sink fluid electrode channels, respectively, were applied as the boundary conditions. The governing equation ∇ (σ*∇ϕ) = 0, where σ* = σ + iωε represents the complex conductivity, was solved to yield the potential distribution, ϕ. Fig. 2b and c present the magnitude of the electric field and the gradient ▽(E⃑_RMS·E⃑_RMS) inside the sample channel, respectively.

To have more accurate computational results, mesh was refined in the sample channel where the sawtooth features were located. A mesh resolution study was performed to ensure that the computational results were mesh-independent. To do so, the mesh was refined and compared to the results of previous iteration. Mesh refinement continued until there were maximum 0.01% and 2% differences in the computed values of ϕ and ▽(E⃑_RMS·E⃑_RMS), respectively, compared to the previous iteration.

The Particle Tracing for Fluid Flow module was used to predict the trajectories of particles at different frequencies. Trajectories of 10 particles with uniform initial position distribution were simulated (Fig. 3). Drag and DEP forces were added to the model using velocity and electric fields computed from Laminar Flow and Electric Currents modules. The simulations were based on untreated MOSE-L cell properties. Since DEP and drag forces are both proportional to the size of the cells, the smallest cell radius, 5.85 μm, reported previously,²⁹ was used in the simulations. Also, Re[K(ω)] at 5 and 20 kHz was estimated to be −0.37 and 0.36, respectively, from the Re[K(ω)] graph reported previously.²⁵Fig. 3a and b demonstrate cell trajectories at 5 and 20 kHz, respectively. At frequencies less than the crossover frequency, cells experience nDEP, thus they are repelled from higher ▽(E⃑_RMS·E⃑_RMS) and move towards the bottom half of the sample channel (Fig. 3a). At frequencies higher than the crossover frequency cells experience pDEP, thus they are attracted towards higher ▽(E⃑_RMS·E⃑_RMS) and the top half of the sample channel (Fig. 3b). In Fig. 3b, some particle trajectories meet the top wall of the sample channel. The plot does not continue to display these trajectories, leading to the appearance of fewer trajectories down the channel.

Fig. 3 Predicting the particle trajectories at (a) 5 kHz and (b) 20 kHz in red lines for 10 particles. Trajectories appear to diminish down the channel due to a simulation artifact that occurs when trajectories encounter a wall. ▽(E⃑_RMS·E⃑_RMS) is also presented in the background. Darker areas indicate higher ▽(E⃑_RMS·E⃑_RMS). The scale bar represents 500 μm.

Results and discussion

Fig. 4a–c demonstrate cell movement in the sample channel without any applied electric field, and due to applying 200 V_RMS and at frequencies lower and higher than the crossover frequency, respectively. As was shown in the computational results, ▽(E⃑_RMS·E⃑_RMS) is much greater at the top side of the channel due to the sawtooth features, which induce non-uniformities into the electric field. When applying a frequency less than the first crossover frequency of cells, cells will experience a negative DEP force and will be repelled from the sawtooth features. Then, they will move towards the bottom half of the channel. However, when applying a frequency higher than the first crossover frequency, cells will experience pDEP force and will be attracted towards sawtooth features and the top side of the channel. Fig. 4d–f demonstrate the normalized cell distribution corresponding to no DEP force from Fig. 4a, nDEP from Fig. 4b, and pDEP from Fig. 4c, respectively. Fig. 4d shows the distribution of cells without an applied voltage to verify that the cells were randomly distributed in the absence of an electric field. Cell distributions were normalized by the total number of cells crossing the red line in Fig. 4 to make a comparison of cell distributions in different experiments possible since the number of cells crossing the line is not exactly equal in all of the experiments. The results presented in Fig. 4(b) and (c) are in agreement with the computational modeling of the trajectories of particles at 5 and 20 kHz.

Fig. 4 Finding the crossover frequency of cells based on their movement towards top or bottom half of the channel. MOSE-L cell movement in the sample channel (a) without applying any electric field, (b) due to applying 200 V_RMS and negative DEP at 5 kHz and (c) 200 V_RMS and positive DEP at 30 kHz. Normalized cell distributions corresponding to (d) no DEP force in the control (a), (e) negative DEP in (b), and (f) positive DEP in (c).

As shown in Fig. 4, cells experience a stronger pDEP force than nDEP and they are focused in a narrower stream at the top side of the channel while experiencing pDEP force than when they experience nDEP force, due to two reasons. First, since K(ω) is constrained between −0.5 and 1, the maximum possible value of pDEP force, regardless of the applied frequency, is twice as strong as the nDEP force. Also, ▽(E⃑_RMS·E⃑_RMS) in cDEP increases as the applied frequency is increased, and because, pDEP for cells occurs at higher frequencies than nDEP, cells experience a stronger DEP force during pDEP than nDEP.

The average crossover frequency for the benign MOSE-E and malignant MOSE-L cells under each treatment condition was calculated. Since the sample conductivity of each cell sample was slightly different, the crossover frequency from each experiment was divided by the sample conductivity in that experiment, based on the linear relationship between conductivity of the sample and crossover frequency (eqn (10)). These values, f_xo/σ_m, were compared by a student t-test (Fig. 5a). The ratios of crossover frequencies to sample conductivity, f_xo/σ_m, for untreated, So-treated, and S1P-treated MOSE-E cells were 1.96 ± 0.16, 2.06 ± 0.18, and 2.00 ± 0.39 MHz m S⁻¹, respectively, which were not statistically different, indicating that exogenous sphingolipids do not affect the crossover frequencies of MOSE-E. Under identical treatment conditions, f_xo/σ_m of MOSE-L cells was 1.35 ± 0.07, 1.94 ± 0.07, and 1.21 ± 0.14 MHz m S⁻¹, respectively. f_xo/σ_m for So-treated MOSE-L cells was significantly higher than the control or S1P treated MOSE-L cells (p < 0.001). Importantly, there was no statistically significant difference between f_xo/σ_m of So-treated MOSE-L cells and control MOSE-E cells (p = 0.29), indicating that So treatment effectively reversed the crossover frequency of MOSE-L cells to that observed in MOSE-E cells. The crossover frequency of MOSE-L cells did not change after the treatment with S1P, indicating that the change in electrical properties was due to the So or its metabolites rather than the conversion to S1P or a generic reaction to sphingolipid treatment.

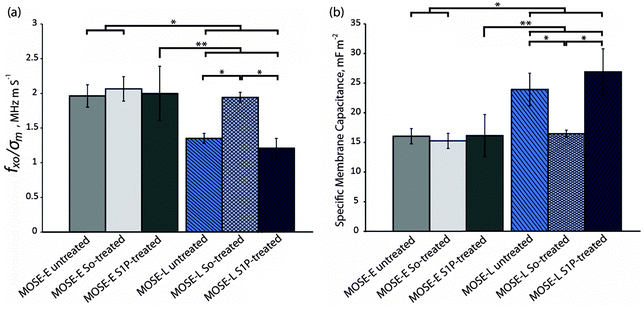Fig. 5 So-treated late stage cells revert back to an early stage based on their electrical signature. (a) f_xo/σ_m and (b) specific membrane capacitance of untreated, So-treated, and S1P-treated of MOSE-E and -L cells. * and ** represent p < 0.001 and 0.01, respectively (n = 3 for treated cells and n = 6 for untreated cell experiments).

Given the conductivity of the media and the known crossover frequency and radius of the cells, the specific membrane capacitance, C_mem, can be calculated using eqn (10). For MOSE-E control, So or S1P-treated cells, C_mem was 16.05 ± 1.28, 15.26 ± 1.38, and 16.15 ± 3.55 mF m⁻², and for MOSE-L cells with identical treatments, C_mem was found to be 23.94 ± 2.75, 16.46 ± 0.62, and 26.89 ± 3.91 mF m⁻², respectively. Neither So nor S1P treatment caused a significant change in C_mem of MOSE-E cells. The specific membrane capacitance of MOSE-L cells was significantly higher (p < 0.01) than MOSE-E cells; treatment with So, however, significantly decreased C_mem to the levels of MOSE-E cells while S1P treatment was not associated with a change in C_mem of MOSE-L cells (Fig. 5b). The results indicate that the decrease in C_mem is specific for So treatment of aggressive cancer cells and benign cells are not affected. The measured radius of 7.185 ± 1.004 and 7.050 ± 1.195 μm of the MOSE-E and MOSE-L cells, respectively, was used to calculate C_mem.

The following discussion explores possible physiological sources for the observed properties, although currently, the underlying events that determine these changes in the dielectric properties during cancer progression are unknown. The specific membrane capacitance of cells can be elevated by an increase in surface protrusions, roughness, and membrane ruffling, traits known to manifest with progressing malignancy, invasiveness, and metastatic potential.⁵⁵ This has been shown for leukemia, breast cancer lines, transformed rat kidney, murine erythroleukemia, and oral cancer cells.^48,56–58 Consistent with these studies, we observed an elevated specific membrane capacitance with progressing malignancy of MOSE cells (Fig. 5b).

Along these lines, Gascoyne et al.^59,60 defined a membrane-specific area parameter, φ, the ratio of the actual membrane area to the membrane area that would be required to cover a smooth cell with the same radius. Thus, φ can be defined as φ = C_mem/C₀, where C₀ is the membrane capacitance of a smooth cell, approximately C₀ = 9 mF m⁻².⁶¹ The amount of surface folding and protrusions, and morphological features such as microvilli, villi, ruffles, ridges, and blebs are quantified by φ.⁵⁹ These complexities increase the membrane surface area and consequently the membrane capacitance. Cells with irregular surfaces will have φ greater than unity, while a perfectly smooth cell will have φ = 1. In the current study, φ increases from 1.78 ± 0.14 for MOSE-E cells to 2.66 ± 0.31 for untreated MOSE-L cells (p < 0.001), based on the results presented in Fig. 5b, demonstrating that malignant cells have more surface irregularities than early cells. In our previous study we also showed that φ for MOSE-I cells is 2.01 ± 1.61, which is in between φ values of MOSE-E and MOSE-L cells.²⁵ After treating MOSE-L cells with So, φ decreased to 1.83 ± 0.07, which is statistically significantly different (p < 0.01) from untreated MOSE-L cells. However, treatment of MOSE-L cells with S1P increased φ to 2.99 ± 0.43 (p = 0.06) which is an indicator of an increased surface roughness associated with S1P treatment.

To relate the membrane properties of suspended cells to cells in an attached state, Gascoyne recently measured C_mem and φ of the cell lines in the NCI-60 panel,⁶⁰ and also examined the exterior morphology of these cell lines by defining a membrane area morphological score, M. M includes three characteristics of cells when attached to a cell culture flask: flattening on the culture flask surface, cell elongation and the long dendritic projections, and small features, such as ruffles, folds and microvilli on the cell surface.⁶⁰ They also showed that there is a correlation between φ and M which means that the cell DEP characteristics depend not only on cell size and morphology when suspended, but also on the exterior morphology of cells before releasing from the site of origin or the cell culture flask.⁶⁰ It was shown previously that MOSE-E cells exhibit a more cobble-stone like appearance, whereas the cells take on a more spindle-like morphology as they subsequently progress to more aggressive phenotypes.²⁶ This observation indicates that M, membrane area morphological score, increases during cancer progression and results, consequently, in increasing φ and changes in dielectric properties of cells, which is consistent with our experimental results.

Changes in dielectric properties of MOSE cells during cancer progression might also result from dysregulation of the cytoskeleton.²⁵ This dysregulation is common in cancer progression and alters the cellular architecture of cancer cells, affecting cellular functions, growth, and signaling events. The MOSE cell model recapitulates these changes in cellular architecture: MOSE-E cells have well-organized, long, cable-like bundles of actin fibers while MOSE-L cells have a highly disorganized actin and microtubule cytoskeleton,^26,27 critical for the viscoelasticity of the cells.²⁸ Stage-dependent, step-wise changes in gene expression levels during MOSE neoplastic progression have been reported previously by using mouse whole genome microarray and gene ontology analyses.^26,27 Specifically, progression was associated with a significant change in the expression or subcellular distribution of key cytoskeletal regulatory proteins, including focal adhesion kinase, α-actinin, and vinculin.²⁷ Moreover, after treating MOSE-L cells with So, a significant change in the expression levels of these proteins was observed (unpublished observations). These observations are in agreement with the noted changes in dielectric properties of MOSE-derived cancer cells and suggest that the dielectric properties of cells could be correlated to a cell gene expression profile.⁶⁰

Sphingolipid metabolites have been shown to be involved in the regulation of the cytoskeleton architecture, increasing or decreasing stress fibers and affecting surface topography.^62,63 This may have contributed to the calculated φ decrease after So treatment (from 2.66 ± 0.31 for untreated MOSE-L to 1.83 ± 0.07) but increase after S1P treatment (to 2.99 ± 0.43). Overall, the observed shift in dielectric properties of So-treated MOSE-L cells towards a more benign-like MOSE-E profile appears consistent with our previous findings indicating direct associations between changes in cytoskeleton architecture^26,27 elasticity,²⁸ and dielectric properties^25,29 throughout progression, and the effects of sphingolipids on MOSE cell morphology.

Conclusions

In this study, we investigated the effect of non-toxic concentrations of the sphingolipidmetabolites, So, a potential anti-cancer agent, and S1P, which is regarded as a tumor promoting metabolite, on the intrinsic electrical properties of benign and aggressive stages of ovarian cancer. Our results show that in contrast to S1P treatment, So treatment correlates with a partial reversal of the aggressive phenotype of late-stage ovarian cancer cells defined by a shift (decrease) in the membrane specific capacitance of MOSE-L cells towards that observed for less aggressive cells. In addition, S1P increased surface membrane protrusions whereas So-treated cells overall exhibited a smoother surface. The basis of these results is in agreement with our previous study showing that the specific membrane capacitance of cells increases during ovarian cancer progression in a synergic model of ovarian cancer cells.²⁵ These studies suggest that the electrical properties of cancer cells can be targets of cancer preventive and promoting efforts. Future studies need to correlate these changes with the tumorigenicity of the cells and structural and molecular events for the design of effective prevention and treatment strategies. It is foreseeable that in the future, we may use cDEP to not only detect cancer cells of different stages but also determine the effectiveness and predict the success of chemopreventive drugs. For instance, the effectiveness of So or conventional chemotherapeutic drugs that impact the cells' surface topography and the actin cytoskeleton may be ascertained by monitoring changes in the cells' electrical signature. The underlying molecular or structural alterations responsible for the changes in dielectric properties and the response to treatment may be critical for the design of devices for cancer detection and treatment control. This would be an advantage over methods that rely solely upon expressed surface receptors, not only for applications such as cell identification and enrichment but also for targeted treatments. Utilizing cDEP for mapping electrical properties of treated cancer cells to specific disease stages of non-treated cells may allow a new, rapid method for determining drug efficacy and for performing dosage studies.

Acknowledgements

This material is based upon work supported in part by NIH 1R21 CA173092-01 (to RVD), NIH RO1 CA118846 (to EMS and PCR), by the National Science Foundation under grant no. EFRI 0938047, and by the Virginia Tech Institute for Critical Technology and Applied Science (ICTAS). The authors would like to thank Dr. Schmelz's laboratory member, Angela Anderson, and Bioelectromechanical Systems (BEMS) laboratory members, Michael Sano, for building the electronics and writing the software, and Catlin Swaffar and Karli Brittain, for their contributions.

Notes and references

1. I. Visintin, Z. Feng, G. Longton, D. C. Ward, A. B. Alvero, Y. Lai, J. Tenthorey, A. Leiser, R. Flores-Saaib, H. Yu, M. Azori, T. Rutherford, P. E. Schwartz and G. Mor, Clin. Cancer Res., 2008, 14, 1065–1072.
2. I. J. Jacobs and U. Menon, Mol. Cell. Proteomics, 2004, 3, 355–366.
3. H. A. Pohl, Dielectrophoresis, Cambridge University Press, 1978.
4. S. Shim, P. Gascoyne, J. Noshari and K. S. Hale, Integr. Biol., 2011, 3, 850–862.
5. D. M. Vykoukal, P. R. Gascoyne and J. Vykoukal, Integr. Biol., 2009, 1, 477–484.
6. Z. R. Gagnon, Electrophoresis, 2011, 32, 2466–2487.
7. Z. Gagnon, J. Mazur and H.-C. Chang, Lab Chip, 2010, 10, 718–726.
8. A. Lostumbo, D. Mehta, S. Setty and R. Nunez, Exp. Mol. Pathol., 2006, 80, 46–53.
9. K. Kato and A. Radbruch, Cytometry, 1993, 14, 384–392.
10. L. C. Hsiung, C. L. Chiang, C. H. Wang, Y. H. Huang, C. T. Kuo, J. Y. Cheng, C. H. Lin, V. Wu, H. Y. Chou, D. S. Jong, H. Lee and A. M. Wo, Lab Chip, 2011, 11, 2333–2342.
11. F. H. Labeed, H. M. Coley, H. Thomas and M. P. Hughes, Biophys J., 2003, 85, 2028–2034.
12. H. M. Coley, F. H. Labeed, H. Thomas and M. P. Hughes, Biochim. Biophys. Acta, Gen. Subj., 2007, 1770, 601–608.
13. Y. Hubner, K. F. Hoettges, G. E. N. Kass, S. L. Ogin and M. P. Hughes, IEE Proc.: Nanobiotechnol., 2005, 152, 150–154.
14. K. Khoshmanesh, J. Akagi, S. Nahavandi, J. Skommer, S. Baratchi, J. M. Cooper, K. Kalantar-Zadeh, D. E. Williams and D. Wlodkowic, Anal. Chem., 2011, 83, 2133–2144.
15. R. Pethig, V. Bressler, C. Carswell-Crumpton, Y. Chen, L. Foster-Haje, M. E. Garcia-Ojeda, R. S. Lee, G. M. Lock, M. S. Talary and K. M. Tate, Electrophoresis, 2002, 23, 2057–2063.
16. H. Shafiee, J. L. Caldwell, M. B. Sano and R. V. Davalos, Biomed. Microdevices, 2009, 11, 997–1006.
17. H. Shafiee, M. B. Sano, E. A. Henslee, J. L. Caldwell and R. V. Davalos, Lab Chip, 2010, 10, 438–445.
18. A. Salmanzadeh, H. Shafiee, R. V. Davalos and M. A. Stremler, Electrophoresis, 2011, 32, 2569–2578.
19. M. B. Sano, E. A. Henslee, E. Schmelz and R. V. Davalos, Electrophoresis, 2011, 32, 3164–3171.
20. M. B. Sano, A. Salmanzadeh and R. V. Davalos, Electrophoresis, 2012, 33, 1938–1946.
21. A. Salmanzadeh, L. Romero, H. Shafiee, R. C. Gallo-Villanueva, M. A. Stremler, S. D. Cramer and R. V. Davalos, Lab Chip, 2011, 12, 182–189.
22. M. B. Sano, J. L. Caldwell and R. V. Davalos, Biosens. Bioelectron., 2011, 30, 13–20.
23. A. Salmanzadeh, M. B. Sano, H. Shafiee, M. A. Stremler and R. V. Davalos, presented in part at the EMBC, San Diego, CA, 2012.
24. E. A. Henslee, M. B. Sano, A. D. Rojas, E. M. Schmelz and R. V. Davalos, Electrophoresis, 2011, 32, 2523–2529.
25. A. Salmanzadeh, M. B. Sano, R. C. Gallo-Villanueva, P. C. Roberts, E. M. Schmelz and R. V. Davalos, Biomicrofluidics, 2013, 7, 011809.
26. P. C. Roberts, E. P. Mottillo, A. C. Baxa, H. H. Heng, N. Doyon-Reale, L. Gregoire, W. D. Lancaster, R. Rabah and E. M. Schmelz, Neoplasia, 2005, 7, 944–956.
27. A. L. Creekmore, W. T. Silkworth, D. Cimini, R. V. Jensen, P. C. Roberts and E. M. Schmelz, PLoS One, 2011, 6.
28. A. N. Ketene, P. C. Roberts, A. A. Shea, E. M. Schmelz and M. Agah, Integr. Biol., 2012, 4, 540–549.
29. A. Salmanzadeh, H. Kittur, M. B. Sano, P. C. Roberts, E. M. Schmelz and R. V. Davalos, Biomicrofluidics, 2012, 6, 24104.
30. E. M. Schmelz, P. C. Roberts, E. M. Kustin, L. A. Lemonnier, M. C. Sullards, D. L. Dillehay and A. H. Merrill Jr., Cancer Res., 2001, 61, 6723–6729.
31. E. M. Schmelz, M. C. Sullards, D. L. Dillehay and A. H. Merrill Jr., J. Nutr., 2000, 130, 522–527.
32. L. A. Lemonnier, D. L. Dillehay, M. J. Vespremi, J. Abrams, E. Brody and E. M. Schmelz, Arch. Biochem. Biophys., 2003, 419, 129–138.
33. K. W. Simon, L. Tait, F. Miller, C. Cao, K. P. Davy, T. Leroith and E. M. Schmelz, Food Funct., 2010, 1, 90–98.
34. J. C. Mazzei, H. Zhou, B. P. Brayfield, R. Hontecillas, J. Bassaganya-Riera and E. M. Schmelz, J. Nutr. Biochem., 2011, 22, 1160–1171.
35. C. R. Gault, L. M. Obeid and Y. A. Hannun, Adv. Exp. Med. Biol., 2010, 688, 1–23.
36. P. Gangoiti, L. Camacho, L. Arana, A. Ouro, M. H. Granado, L. Brizuela, J. Casas, G. Fabrias, J. L. Abad, A. Delgado and A. Gomez-Munoz, Prog. Lipid Res., 2010, 49, 316–334.
37. R. Kolesnick and D. W. Golde, Cell, 1994, 77, 325–328.
38. R. N. Kolesnick and M. R. Hemer, J. Biol. Chem., 1990, 265, 18803–18808.
39. S. Spiegel and S. Milstien, Nat. Rev. Mol. Cell Biol., 2003, 4, 397–407.
40. M. Maceyka, S. G. Payne, S. Milstien and S. Spiegel, Biochim. Biophys. Acta, Mol. Cell Biol. Lipids, 2002, 1585, 193–201.
41. C. Chalfant and M. Del Poeta, Sphingolipids as signaling and regulatory molecules, Springer Science+Business Media; Landes Bioscience, New York, N.Y. Austin, Tex, 2010.
42. V. Teichgraber, M. Ulrich, N. Endlich, J. Riethmuller, B. Wilker, C. C. De Oliveira-Munding, A. M. van Heeckeren, M. L. Barr, G. von Kurthy, K. W. Schmid, M. Weller, B. Tummler, F. Lang, H. Grassme, G. Doring and E. Gulbins, Nat. Med., 2008, 14, 382–391.
43. D. Wang, Z. Zhao, A. Caperell-Grant, G. Yang, S. C. Mok, J. Liu, R. M. Bigsby and Y. Xu, Mol. Cancer. Ther., 2008, 7, 1993–2002.
44. B. Visentin, J. A. Vekich, B. J. Sibbald, A. L. Cavalli, K. M. Moreno, R. G. Matteo, W. A. Garland, Y. L. Lu, S. X. Yu, H. S. Hall, V. Kundra, G. B. Mills and R. A. Sabbadini, Cancer Cell, 2006, 9, 225–238.
45. A. Irimajiri, T. Hanai and A. Inouye, J. Theor. Biol., 1979, 78, 251–269.
46. R. Pethig and M. S. Talary, IET Nanobiotechnol., 2007, 1, 2–9.
47. R. Pethig, Biomicrofluidics, 2010, 4, 022811.
48. Y. Huang, X. B. Wang, F. F. Becker and P. R. C. Gascoyne, Biochim. Biophys. Acta, Gen. Subj., 1996, 1282, 76–84.
49. W. M. Arnold and U. Zimmermann, J. Electrost., 1988, 21, 151–191.
50. X. Wang, F. F. Becker and P. R. Gascoyne, Chaos, 2010, 20, 043133.
51. X. B. Wang, Y. Huang, P. R. Gascoyne, F. F. Becker, R. Holzel and R. Pethig, Biochim. Biophys. Acta, 1994, 1193, 330–344.
52. L. A. Flanagan, J. Lu, L. Wang, S. A. Marchenko, N. L. Jeon, A. P. Lee and E. S. Monuki, Stem Cells, 2008, 26, 656–665.
53. R. Skalak and S. Chien, Handbook of Bioengineering, McGraw-Hill, New York, 1987.
54. Y. C. Fung, N. Perrone and M. Anliker, Biomechanics, Its Foundations and Objectives, Prentice Hall, Englewood Cliffs, NJ, 1972.
55. W. G. Jiang, Eur. J. Surg. Oncol., 1995, 21, 307–309.
56. F. F. Becker, X. B. Wang, Y. Huang, R. Pethig, J. Vykoukal and P. R. C. Gascoyne, J. Phys. D: Appl. Phys., 1994, 27, 2659–2662.
57. F. F. Becker, X. B. Wang, Y. Huang, R. Pethig, J. Vykoukal and P. R. C. Gascoyne, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 860–864.
58. H. J. Mulhall, F. H. Labeed, B. Kazmi, D. E. Costea, M. P. Hughes and M. P. Lewis, Anal. Bioanal. Chem., 2011, 401, 2455–2463.
59. P. R. Gascoyne, X. B. Wang, Y. Huang and F. F. Becker, IEEE Trans. Ind. Appl., 1997, 33, 670–678.
60. P. R. Gascoyne, S. Shim, J. Noshari, F. F. Becker and K. Stemke-Hale, Electrophoresis, 2013, 34, 1042–1050.
61. W. M. Arnold and U. Zimmermann, Naturwissenschaften, 1982, 69, 297–298.
62. G. M. Strub, M. Maceyka, N. C. Hait, S. Milstien and S. Spiegel, Adv. Exp. Med. Biol., 2010, 688, 141–155.
63. A. N. Hanna, L. G. Berthiaume, Y. Kikuchi, D. Begg, S. Bourgoin and D. N. Brindley, Mol. Biol. Cell, 2001, 12, 3618–3630.

---