 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparing simulated and experimental molecular cluster distributions†
Tinja
Olenius
*a,
Siegfried
Schobesberger
a,
Oona
Kupiainen-Määttä
a,
Alessandro
Franchin
a,
Heikki
Junninen
a,
Ismael K.
Ortega
a,
Theo
Kurtén
b,
Ville
Loukonen
a,
Douglas R.
Worsnop
ac,
Markku
Kulmala
a and
Hanna
Vehkamäki
a
aDepartment of Physics, University of Helsinki, FIN-00014 Helsinki, Finland. E-mail: tinja.olenius@helsinki.fi
bDepartment of Chemistry, University of Helsinki, FIN-00014 Helsinki, Finland
cAerodyne Research Inc., Billerica, Massachusetts 01821, USA
First published on 16th April 2013
Abstract
Formation of secondary atmospheric aerosol particles starts with gas phase molecules forming small molecular clusters. High-resolution mass spectrometry enables the detection and chemical characterization of electrically charged clusters from the molecular scale upward, whereas the experimental detection of electrically neutral clusters, especially as a chemical composition measurement, down to 1 nm in diameter and beyond still remains challenging. In this work we simulated a set of both electrically neutral and charged small molecular clusters, consisting of sulfuric acid and ammonia molecules, with a dynamic collision and evaporation model. Collision frequencies between the clusters were calculated according to classical kinetics, and evaporation rates were derived from first principles quantum chemical calculations with no fitting parameters. We found a good agreement between the modeled steady-state concentrations of negative cluster ions and experimental results measured with the state-of-the-art Atmospheric Pressure interface Time-Of-Flight mass spectrometer (APi-TOF) in the CLOUD chamber experiments at CERN. The model can be used to interpret experimental results and give information on neutral clusters that cannot be directly measured.
1 Introduction
Atmospheric new particle formation has been observed in numerous sites around the world1 and is estimated to be a significant source of aerosol particles and cloud condensation nuclei.2–4 Atmospheric aerosol particles influence the global climate and have adverse effects on visibility and human health.5,6 Currently, the effect of aerosols forms the dominant uncertainty in predicting radiative forcing and global temperature change.7Sulfuric acid is known to be involved in atmospheric particle formation (see for example ref. 8–10), but the identity and role of other compounds remains uncertain. Atmospheric bases, such as ammonia and amines, as well as other organic compounds and ions have been proposed to enable or enhance sulfuric acid driven particle formation.11–14 Nevertheless, the understanding of the initial formation mechanisms remains incomplete.New particle formation starts with gas phase molecules clustering into small molecular clusters. The main limitations in the experimental examination of the initial clusters are their low concentrations and the insufficient size resolution or selective sensitivity of instruments. Understanding the formation and growth of the clusters requires information on both size distribution and chemical composition, which are challenging to determine experimentally for clusters consisting of only few molecules. Implementation of high-resolution mass spectrometry, together with electrical mobility spectrometry, enables the concentration measurements and chemical characterization of charged small particles from the molecular scale upward.15,16 The experimental observation of electrically neutral clusters is possible down to approximately 1 nm in mobility diameter.17 Nevertheless, all available methods for determining the chemical composition of the clusters require charging, which is likely to have an effect on the measurement result for example via changing the composition of the clusters.18
The challenges involved in the experimental studies make theoretical methods giving information on both charged and neutral clusters necessary for exploring atmospheric cluster formation. In this work we used the kinetic collision and evaporation model ACDC19 to study the steady-state concentrations and kinetics of a set of small molecular clusters under conditions relevant to the CLOUD experiment at CERN.20 We show a good agreement between the modeled steady-state concentrations of negatively charged clusters and experimental concentrations measured with a mass spectrometer in the CLOUD experiment. After showing that the model is able to reproduce the experimental results for the concentrations of charged clusters, we demonstrate how the model can also give information on electrically neutral clusters and thus improve our knowledge of atmospheric particle formation mechanisms.
2 Methods
2.1. Theoretical methods and model system
The model system is a set of molecular clusters consisting of sulfuric acid (H2SO4) and ammonia (NH3) molecules. Electrically neutral, and negatively and positively charged clusters are included. In principle the clusters can contain 0–5 sulfuric acid and 0–5 ammonia molecules, forming a so-called 5 × 5 simulation box. However, as some of these clusters can be predicted to be highly unstable because of an unfavorable composition, they were omitted from the simulation to reduce the computational burden. These unstable clusters include negatively charged clusters containing more or as many ammonia molecules as acid molecules, positively charged clusters containing more acid than ammonia molecules, and neutral and positive clusters that have a very high ammonia![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid ratio. All the clusters included in the simulation are listed in Table 1.
acid ratio. All the clusters included in the simulation are listed in Table 1.
| a) Electrically neutral clusters | |
| Number of NH3 molecules | |
| 0 acids | 1–4 |
| H2SO4 | 0–4 |
| (H2SO4)2 | 0–4 |
| (H2SO4)3 | 0–4 |
| (H2SO4)4 | 0–5 |
| (H2SO4)5 | 0–5 |
| b) Negatively charged clusters | |
| Number of NH3 molecules | |
| HSO4− | 0–1 |
| (H2SO4)·HSO4− | 0–1 |
| (H2SO4)2·HSO4− | 0–2 |
| (H2SO4)3·HSO4− | 0–3 |
| (H2SO4)4·HSO4− | 0–4 |
| c) Positively charged clusters | |
| Number of NH3 molecules + H+ | |
| 0 acids | 1–3 |
| H2SO4 | 1–3 |
| (H2SO4)2 | 1–4 |
| (H2SO4)3 | 2–5 |
| (H2SO4)4 | 3–5 |
| (H2SO4)5 | 5 |
The steady-state concentrations of the cluster set were solved with the kinetic model ACDC (Atmospheric Cluster Dynamics Code).19 Since the current version of the model is described in detail in ref. 21, the basic features are discussed only briefly here. The code writes out the birth–death equations, in other words, the time derivatives of the cluster concentrations, for a given set of clusters assuming all possible collision and evaporation processes. The time evolution of the cluster concentrations is simulated using the Matlab ode15s solver for sets of differential equations until the time-independent steady-state is achieved. The clusters are formed in collisions of smaller clusters and evaporations of larger clusters, and they are destroyed by colliding with other clusters and by fragmenting into smaller clusters. Hence the time derivative can be written as
 | (1) |
For collisions between electrically neutral clusters, the collision coefficients are calculated according to the kinetic gas theory:
 | (2) |
Cluster evaporation rates are calculated as in ref. 25:
 | (3) |
In this study we used two additional sink terms reported in the experimental studies: a wall loss term corresponding to the sticking of the clusters onto the walls of the experiment chamber and a dilution term. The dilution sink has a constant value of 1.06 × 10−4 s−1, and the wall loss factor, determined by experimental means (see for example ref. 26), has been parameterized to depend on the size of the cluster as
 | (4) |
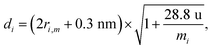 | (5) |
When cluster collisions result in clusters outside of the simulation box, they are allowed to grow out of the system if their composition is favorable and they can be assumed to grow further instead of re-evaporating immediately. The boundary conditions are based on the relative stability of the clusters in terms of the acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) base ratio (see for example ref. 25). Neutral clusters are allowed to leave the system if they contain at least six acid and five ammonia molecules; the requirement for negatively charged clusters is at least six acids (including the negative ion) and one base, and for positively charged clusters at least five acids and six bases (including the positive ion). If these conditions are not satisfied, the cluster is brought back to the system by evaporating monomers out of it until it reaches the nearest boundary of the simulation box.
base ratio (see for example ref. 25). Neutral clusters are allowed to leave the system if they contain at least six acid and five ammonia molecules; the requirement for negatively charged clusters is at least six acids (including the negative ion) and one base, and for positively charged clusters at least five acids and six bases (including the positive ion). If these conditions are not satisfied, the cluster is brought back to the system by evaporating monomers out of it until it reaches the nearest boundary of the simulation box.
2.2. Measurements and conditions in the CLOUD experiment
Concentrations of negatively charged sulfuric acid–ammonia clusters were measured in the CLOUD experiment at CERN (for more details, see ref. 20) using an Atmospheric Pressure interface Time-Of-Flight mass spectrometer (APi-TOF).15 The instrument obtains the ion signal as counts per unit time as a function of mass-to-charge ratio. The signal was converted to concentrations by applying a mass dependent conversion function. For deriving this function, its mass-dependency was first derived by dedicated laboratory experiments: ammonium bisulfate particles were size-selected by a high-resolution differential mobility analyzer and sampled by both the APi-TOF and an electrometer that served as the reference, covering most of the size-range the APi-TOF can detect. For the data from the CLOUD experiment, we compared the ion signal measured by the APi-TOF with the results of an ion mobility spectrometer (Neutral cluster and Air Ion Spectrometer, NAIS, Airel Ltd.)27 that sampled in parallel and measured ion concentrations as a function of mobility-equivalent size. Losses in each instrument's sampling line were taken into account, and the corrected ion concentrations from the NAIS were used as reference for determining the final setup-specific conversion function, and for assessing uncertainties.The APi-TOF data was measured under steady-state conditions with constant sulfuric acid and ammonia concentrations at temperatures of 248, 278 and 292 K. The sulfuric acid concentration was measured with a Chemical Ionization Mass Spectrometer (CIMS)28,29 and varied between approximately 106 and 109 cm−3 in individual experiments. The ammonia concentration was measured with a Long-Path Absorption Photometer (LO-PAP)30 and a Proton Transfer Reaction Mass Spectrometer (PTR-MS).31Ammonia was not added to the experiment chamber intentionally in all the runs, but a trace amount of ammonia (below the experimental detection limit of 35 ppt) is known to have been present in the chamber anyway, because clusters containing ammonia molecules were detected by the APi-TOF. In the experiments with intentionally added ammonia, the ammonia mixing ratio was in the range of approximately 100 to 1000 ppt, corresponding to 2.6 × 109 cm−3 to 2.6 × 1010 cm−3.
We ran the simulations using the same range of sulfuric acid and ammonia concentrations that were reported in the experiment. In the case of ammonia, we fixed the concentration of single ammonia molecules. For comparison with the experiments with no added ammonia, the simulated ammonia concentration was set to either 5 ppt or to the experimental detection limit of 35 ppt. In the case of sulfuric acid, the total concentration of all electrically neutral clusters consisting of one acid molecule and any number of ammonia molecules was fixed instead of the concentration of single acid molecules. This was considered to correspond better to the measured acid concentration since according to theoretical calculations, the CIMS can also detect acid molecules clustered with base molecules as acid monomers.18 However, under the conditions studied in this work the sum of all neutral clusters containing one acid was practically equal to the concentration of pure acid monomers.
Ions were produced in the experiments either by only natural ionization due to galactic cosmic rays (GCR), or additionally by a pion beam which allowed higher total ion production rates. In the simulations, we used the rates 3 ion pairs s−1 cm−3, corresponding to natural GCR ionization, and 40 ion pairs s−1 cm−3, corresponding to the ionization at the average pion beam intensity of 60 kHz.
3 Results and discussion
3.1. Comparison of modeled and measured concentrations of negatively charged clusters
The data presented and discussed in the Results and discussion section are for 278 K and ionization rate due to GCR (3 ion pairs s−1 cm−3). Results for 248 K, 292 K and beam-augmented ionization are qualitatively similar and are presented in the supplementary information.†Fig. 1 shows the modeled and experimental distributions of negatively charged clusters containing 1–5 sulfuric acid molecules (including the bisulfate ion), denoted from now on as mono-, di-, tri-, tetra- and pentamers, respectively, under representative experimental conditions at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt. Concentrations of clusters with different numbers of ammonia molecules are shown as separate lines. The shapes of the modeled and experimental distributions of pure acid clusters are qualitatively similar with the exception that according to the measurements, the monomer clearly has a higher concentration compared to the dimer than what is predicted by the model (note that this might not be clearly visible in the logarithmic scale). The model also predicts higher concentrations than observed for the ammonia-containing tetra- and pentamers. These discrepancies can be due to cluster fragmentation processes inside the instrument; at least the ratio of the dimer and monomer concentrations has been observed to be easily affected by the instrument settings. Moreover, it is possible that trimers can break into monomers and dimers in the atmospheric pressure interface, and hence the measured concentrations of the smallest clusters should be examined with caution. The fragmentation issues are discussed in more detail in Section 3.3.![Modeled (solid lines) and experimental (dashed lines) concentrations of negatively charged clusters containing sulfuric acid and varying number of ammonia molecules as a function of number of acid molecules (including the ion) at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt. Note that the smallest observed cluster containing three ammonia molecules is the pentamer.](/image/article/2013/FD/c3fd00031a/c3fd00031a-f1.gif) | ||
| Fig. 1 Modeled (solid lines) and experimental (dashed lines) concentrations of negatively charged clusters containing sulfuric acid and varying number of ammonia molecules as a function of number of acid molecules (including the ion) at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt. Note that the smallest observed cluster containing three ammonia molecules is the pentamer. | ||
 | ||
| Fig. 2 Modeled and experimental concentrations of negatively charged sulfuric acid mono-, di-, tri-, tetra- and pentamers as a function of sulfuric acid concentration. Concentrations of i-mers containing only sulfuric acid and total concentrations of pure i-mers plus i-mers containing ammonia molecules are shown as separate lines and markers. Note the different scales in the y-axes. | ||
Although it seems that the model is also able to cover the experiments at background-level ammonia concentrations, certain caution should be used in the interpretation of these results. ACDC is an acid–base model and, as stated in Section 2.1, allows clusters to leave the simulation box if they contain a certain amount of acid and base molecules. On the other hand, it is possible that during the background-level experiments the ammonia concentration in the chamber may have been so low that it did not significantly enhance cluster formation. If the growth in reality occurred mostly via different mechanisms, presumably binary acid–water clustering, the simulated conditions are not directly comparable to the experiments. This should be kept in mind especially when comparing with the experiments where the detected clusters generally do not contain ammonia.
 | ||
| Fig. 3 Ratios of the concentrations of negatively charged clusters as a function of sulfuric acid concentration. Ratios of pure sulfuric acid i-mer concentrations and ratios of total i-mer concentrations including clusters both with and without ammonia are shown as separate lines and markers. Note the different scales in the y-axes. | ||
3.2. Modeled concentrations of electrically neutral clusters
As the ACDC model is capable of reproducing the experimental results for the concentrations of charged clusters qualitatively and even quantitatively under some conditions, it can be used to give reliable estimates of the concentrations of electrically neutral clusters. Modeling results for the distribution of neutral clusters at [H2SO4] = 5 × 107 cm−3, [NH3] = 100 ppt and 278 K (conditions corresponding to Fig. 1) are presented in Fig. 5. Under these conditions, the number of ammonia molecules in the most abundant neutral clusters is either equal to or one less than the number of acid molecules. This is a general feature in the acid–ammonia system, and follows from the stabilizing effect of ammonia in neutral sulfuric acid clusters.![Modeled concentrations of electrically neutral clusters containing sulfuric acid and a varying number of ammonia molecules as a function of the number of acid molecules at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt.](/image/article/2013/FD/c3fd00031a/c3fd00031a-f5.gif) | ||
| Fig. 5 Modeled concentrations of electrically neutral clusters containing sulfuric acid and a varying number of ammonia molecules as a function of the number of acid molecules at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt. | ||
The relative stability of the clusters can be predicted from the evaporation rates derived from the formation free energies,25 but the relative abundances cannot be estimated solely based on them, as kinetic effects also play a role. Although the most stable (and abundant) neutral clusters contain approximately the same number of acid and ammonia molecules, the exact relative concentrations of the clusters also depend on the concentrations of acid and ammoniavia the collision rates of monomers with the clusters. In addition, the dynamics of the neutral clusters are affected by the presence of ionizing species and charged clusters. Finally, external loss terms, such as the wall loss term in this study, affect the concentrations of all the clusters and ions. Assessment of the concentrations and kinetics of neutral clusters requires that the various dynamic effects are taken into account. To better understand these effects, we studied how the neutral clusters are formed under the conditions corresponding to Fig. 1 ([H2SO4] = 5 × 107 cm−3, [NH3] = 100 ppt and T = 278 K). The growth occurs by the successive addition of acid and ammonia molecules, which is expected from the distribution of the neutral clusters (Fig. 5). However, we found that under other conditions a notable fraction of the neutral clusters can be formed by the recombination of charged clusters, either with other charged clusters of the opposite polarity, or with the generic ionizing species. These formation routes become significant for example at low acid concentration or higher temperature. This is likely due to the fact that under the aforementioned conditions the evaporation processes of neutral clusters are relatively significant. Ions are more tightly bound due to electrostatic interaction, and consequently the ionic formation routes of neutral clusters are more prominent when the growth along neutral pathways is limited by a too high evaporation rate of some cluster compared to its collision rate with any species that can grow it further. The dependence of the formation routes of the neutral clusters on the ambient conditions reflects how interactions with ions can affect the concentrations of neutral clusters.
3.3. Sources of uncertainty
From the experimental point of view, the greatest source of uncertainty, also qualitative, is probably due to fragmentation processes possibly occurring inside the APi-TOF. These include the breaking of the clusters in collisions, and the evaporation of molecules from the clusters. The first-mentioned process is due to the accelerations of the ions in the electric fields created by the various ion guiding and focusing elements. The ions are therefore subjected to more energetic collisions with gas molecules than in the ambient, and one or more molecules may be lost from cluster ions. It can be noted that the magnitude of this type of fragmentations depends on the instrumental settings, and that their effect is probably most significant for the smallest clusters, such as the mono- and dimers. Relative concentrations of the larger clusters are less affected. The evaporation-type fragmentation can occur if some molecules in the cluster are relatively loosely bound. These molecules can be lost if the evaporation is fast enough to take place during the time between the cluster entering the instrument and its detection. Water is the only compound that is known for sure to evaporate so rapidly that it will not be detected in the clusters, although there is water vapor in the chamber (and thus water molecules attached to a significant fraction of the clusters). Overall the de-clustering inside the instrument is still poorly understood. However, its effect must be limited since comparisons with ion mobility spectrometers show good agreement, as shown previously by Ehn et al. (ref. 16) and as was also seen when comparing the APi-TOF with the NAIS ion data for this study.Another source of uncertainty is the data conversion from ion count rates to ion concentrations. Variations in the comparison between the APi-TOF and the NAIS during the measurement campaign were taken into account by calculating a mean and a standard deviation. The mean was used for the conversions, and the uncertainties of the conversion function were assessed from the standard deviation. A representative example of the error bars calculated from the standard deviation by applying the propagation of uncertainty is presented in Fig. S1 in the supplementary information.† Although the error bars are relatively large, they are not enough to fully cover the differences between experimental and modeling results.
Some of the corrections for sampling losses, which were included in the conversion, were based on simplified theoretical assumptions,33 which could also lead to some systematic error. In any case, the resulting uncertainties and errors are mostly in the absolute numbers, whereas the shape of the cluster distribution would hardly be affected.
From the model perspective, the most significant error source is likely the uncertainties in the Gibbs free energies that can be estimated to be around ±1 kcal mol−1. Therefore test simulations were performed with either stabilizing or de-stabilizing all the clusters by 1 kcal mol−1. This changes the absolute concentrations up to around an order of magnitude, as can be expected, while the qualitative behavior remains the same. Possible uncertainties in the collision frequencies are more difficult to assess. On the other hand, the same methods for calculating the collision coefficients between neutral molecules and ionic clusters have been applied in the modeling study by Kupiainen et al. (ref. 23), which reported good agreement with experimental data. The relative abundance of different clusters can also be somewhat affected by the boundary conditions determining which clusters are allowed to grow out from the system. However, the currently used conditions are reasonable based on the existing experimental and modeled distributions of acid–ammonia clusters.
The modeled clusters do not contain water molecules. Kinetic modeling of the full multicomponent acid–base–water system is impossible, as the collision frequency of water with the clusters (as well as the water evaporation rate) is approximately ten orders of magnitude higher than that of acid or base molecules. This results in a numerically extremely stiff set of equations, which cannot be solved practically for our system. Water can, nevertheless, be implemented in the model implicitly by calculating the effective collision and evaporation rates of the hydrated clusters.34 However, the computational effort of the quantum chemical calculations required to obtain the formation free energies of the hydrates is significant as multiple additional molecules are added to the clusters, both due to configurational sampling and to the time required by each energy or force evaluation. In light of the other considerable sources of uncertainty in the comparison of the modeled and experimental data (see above), estimating the effect of water was considered to be beyond the scope of this study.
4 Conclusions
We modeled the kinetics of a set of neutral and charged molecular clusters consisting of sulfuric acid and ammonia molecules and studied the steady-state concentrations and growth pathways of the clusters. Evaporation rates of the clusters were derived from quantum chemical formation free energies with no free parameters. We compared the concentrations of negatively charged clusters to experimental results measured with the APi-TOF (Atmospheric Pressure interface Time-Of-Flight mass spectrometer) in the CLOUD experiment20 and found good agreement. After demonstrating the validity of the model in the case of charged clusters, we showed how the model can be used to obtain information on neutral clusters that cannot be directly measured.The behavior of the concentrations of negative clusters with respect to variations in the acid and ammonia concentrations is well predicted by the model, although there are some discrepancies between the measured and modeled absolute cluster concentrations. However, taking into account the experimental uncertainties that are mainly due to the still poorly understood cluster fragmentation inside the mass spectrometer, the agreement is impressive. The model also correctly predicts that the smallest negative ammonia-containing clusters have four acid molecules. The discrepancies in the number of ammonia molecules in the clusters might be explained by the evaporation of ammonia inside the instrument. As the instrumental effects are not well known, the modeling results can help in the interpretation of the measurements. The dynamic model and the high-resolution experiments are complementary methods to study the properties of atmospheric molecular clusters, and provide necessary tools to understand the growth mechanisms of these clusters.
Acknowledgements
This work was supported by FP7-MOCAPAF project no. 257360 (ERC Starting Grant), FP7-ATMNUCLE project no. 227463 (ERC Advanced Grant), FP7 Marie Curie Initial Training Network CLOUD-ITN no. 215072, Vilho, Yrjö and Kalle Väisälä Foundation, Maj and Tor Nessling Foundation project no. 2011200 and Academy of Finland Center of Excellence project no. 1118615 and LASTU project no. 135054. The authors thank CSC- IT Center for Science in Espoo, Finland for the computing time, tofTools development team for providing the TOF-MS analysis tools and the CLOUD consortium for providing the experimental data.References
- M. Kulmala, H. Vehkamäki, T. Petäjä, M. Dal Maso, A. Lauri, V.-M. Kerminen, W. Birmili and P. H. McMurry, J. Aerosol Sci., 2004, 35, 143–176 CrossRef CAS.
- D. V. Spracklen, K. S. Carslaw, M. Kulmala, V.-M. Kerminen, G. W. Mann and S.-L. Sihto, Atmos. Chem. Phys., 2006, 6, 5631–5648 CrossRef CAS.
- D. V. Spracklen, K. S. Carslaw, M. Kulmala, V.-M. Kerminen, S.-L. Sihto, I. Riipinen, J. Merikanto, G. W. Mann, M. P. Chipperfield, A. Wiedensohler, W. Birmili and H. Lihavainen, Geophys. Res. Lett., 2008, 35 Search PubMed.
- J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS.
- J. C. Cabada, A. Khlystov, A. E. Wittig, C. Pilinis and S. N. Pandis, J. Geophys. Res., 2004, 109, D16S03 1–13 CrossRef.
- A. Nel, Science, 2005, 308, 804–806 CrossRef CAS.
- IPCC, The Intergovernmental Panel on Climate Change, Climate Change 2007: The Physical Science Basis, Cambridge University Press, New York, 2007 Search PubMed.
- R. J. Weber, J. J. Marti, P. H. McMurry, F. L. Eisele, D. J. Tanner and A. Jefferson, J. Geophys. Res., 1997, 102, 4375–4385 CrossRef CAS.
- S.-L. Sihto, M. Kulmala, V.-M. Kerminen, M. Dal Maso, T. Petäjä, I. Riipinen, H. Korhonen, F. Arnold, R. Janson, M. Boy, A. Laaksonen and K. E. J. Lehtinen, Atmos. Chem. Phys., 2006, 6, 4079–4091 CrossRef CAS.
- C. Kuang, P. H. McMurry, A. V. McCormick and F. L. Eisele, J. Geophys. Res., 2008, 113, D10209 CrossRef.
- T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef.
- V. Loukonen, T. Kurtén, I. K. Ortega, H. Vehkamäki, A. A. H. Padua, K. Sellegri and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 4961–4974 CrossRef CAS.
- A. B. Nadykto and F. Yu, Chem. Phys. Lett., 2007, 435, 14–18 CrossRef CAS.
- F. Yu and R. P. Turco, Geophys. Res. Lett., 2000, 27, 883–886 CrossRef CAS.
- H. Junninen, M. Ehn, T. Petäjä, L. Luosujärvi, T. Kotiaho, R. Kostiainen, U. Rohner, M. Gonin, K. Fuhrer, M. Kulmala and D. R. Worsnop, Atmos. Meas. Tech., 2010, 3, 1039–1053 CrossRef CAS.
- M. Ehn, H. Junninen, S. Schobesberger, H. E. Manninen, A. Franchin, M. Sipilä, T. Petäjä, V.-M. Kerminen, H. Tammet, A. Mirme, S. Mirme, U. Hõrrak, M. Kulmala and D. R. Worsnop, Aerosol Sci. Technol., 2011, 45, 522–532 CrossRef CAS.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petäjä, M. Sipilä, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Järvinen, M. Äijälä, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkilä, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin III, J. Duplissy, H. Vehkamäki, J. Bäck, A. Kortelainen, I. Riipinen, T. Kurtén, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V.-M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS.
- T. Kurtén, T. Petäjä, J. Smith, I. K. Ortega, M. Sipilä, H. Junninen, M. Ehn, H. Vehkamäki, L. Mauldin, D. R. Worsnop and M. Kulmala, Atmos. Chem. Phys., 2011, 11, 3007–3019 CrossRef.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes, A. Kurten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkilä, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petäjä, R. Schnitzhofer, J. H. Seinfeld, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tome, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS.
- T. Olenius, O. Kupiainen, I. K. Ortega, T. Kurtén and H. Vehkamäki, Free energy barrier in the growth of sulfuric acid–ammonia and sulfuric acid–dimethylamine clusters, J. Chem. Phys., 2013 Search PubMed , in press.
- T. Su and M. T. Bowers, J. Chem. Phys., 1973, 58, 3027–3037 CrossRef.
- O. Kupiainen, I. K. Ortega, T. Kurtén and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 3591–3599 CrossRef CAS.
- H. Israël, Atmospheric Electricity, vol. I., Israel Program for Sci. Transl. & NSF, Jerusalem, 1970 Search PubMed.
- I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 225–235 CrossRef CAS.
- J. Voigtländer, J. Duplissy, L. Rondo, A. Kürten and F. Stratmann, Atmos. Chem. Phys., 2012, 12, 2205–2214 CrossRef.
- S. Mirme, A. Mirme, A. Minikin, A. Petzold, U. Hõrrak, V.-M. Kerminen and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 437–451 CrossRef CAS.
- H. Berresheim, T. Elste, C. Plass-Dülmer, F. L. Eisele and D. J. Tanner, Int. J. Mass Spectrom., 2000, 202, 91–109 CrossRef CAS.
- T. Petäjä, R. L. Mauldin III, E. Kosciuch, J. McGrath, T. Nieminen, P. Paasonen, M. Boy, A. Adamov, T. Kotiaho and M. Kulmala, Atmos. Chem. Phys., 2009, 9, 7435–7448 CrossRef.
- F. Bianchi, J. Dommen, S. Mathot and U. Baltensperger, Atmos. Meas. Tech., 2012, 5, 1719–1725 CrossRef CAS.
- M. Norman, A. Hansel and A. Wisthaler, Int. J. Mass Spectrom., 2007, 265, 382–387 CrossRef CAS.
- B. R. Bzdek, J. W. DePalma, D. P. Ridge, J. Laskin and M. V. Johnston, J. Am. Chem. Soc., 2013, 135, 3276–3285 CrossRef CAS.
- P. Gormley and M. Kennedy, Proc. R. Irish Acad., 1949, 52A, 163–169 Search PubMed.
- P. Paasonen, T. Olenius, O. Kupiainen, T. Kurtén, T. Petäjä, W. Birmili, A. Hamed, M. Hu, L. G. Huey, C. Plass-Duelmer, J. N. Smith, A. Wiedensohler, V. Loukonen, M. J. McGrath, I. K. Ortega, A. Laaksonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2012, 12, 9113–9133 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available: See DOI: 10.1039/c3fd00031a |
| This journal is © The Royal Society of Chemistry 2013 |

![Modeled and experimental fractions of negatively charged tetra- and pentamers containing different numbers of ammonia molecules at [H2SO4] = 5 × 107 cm−3 and [NH3] = 100 ppt.](/image/article/2013/FD/c3fd00031a/c3fd00031a-f4.gif)