Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Internal dynamics in helical molecules studied by X-ray diffraction, NMR spectroscopy and DFT calculations†
Martin
Dračínský
 *a,
Jan
Storch
b,
Vladimír
Církva
b,
Ivana
Císařová
c and
Jan
Sýkora
*b
*a,
Jan
Storch
b,
Vladimír
Církva
b,
Ivana
Císařová
c and
Jan
Sýkora
*b
aInstitute of Organic Chemistry and Biochemistry, Czech Academy of Sciences, Flemingovo 2, 16610 Prague, Czech Republic. E-mail: dracinsky@uochb.cas.cz
bInstitute of Chemical Process Fundamentals, Czech Academy of Sciences, Rozvojová 135, 16502 Prague, Czech Republic. E-mail: sykora@icpf.cas.cz
cFaculty of Science, Charles University in Prague, Hlavova 2030, 12840 Prague, Czech Republic
First published on 3rd January 2017
Abstract
The conformational behaviour of a prototype helical molecule, [6]helicene, and its derivatives was studied in solution and the solid state. Available crystal structures of [6]helicene revealed surprisingly large flexibility of this molecule and variable-temperature NMR experiments provided unusual temperature dependence of chemical shifts of hydrogen, carbon and fluorine atoms in the peripheral aromatic rings of [6]helicene and tetrafluoro[6]helicene. These chemical shift changes were interpreted as a consequence of the helicene ‘pitch’ opening with elevated temperature, and the experimental data were corroborated by DFT calculations of the chemical shift dependence on the helicene conformation and by variable-temperature DFT molecular dynamics simulations.
Introduction
Helicenes are polycyclic aromatic compounds consisting of ortho-fused benzene rings with nonplanar helical topology, resulting from the steric repulsive interaction between peripheral aromatic rings.1 This helical character makes helicenes chiral even though they have no centre of chirality. Furthermore, helicene molecules also possess a twofold axis of symmetry perpendicular to the axis of helicity.The highly delocalised large π-electron system of fully aromatic helicenes along with the previously mentioned inherent chirality provide them with unique optical and electronic properties. The helicenes achieve e.g. exceptionally high values of specific rotation (thousands of degrees per mole).2 They also provide strong circular dichroism,3 electroluminescence,4,5 circularly polarised luminescence,6,7 and non-linear optical properties.8–11 Furthermore, helicenes exhibit semi-conductive behaviour.12,13 All of these properties predetermine their utilisation in a wide range of applications in organic electronic devices.14–16 The chirality of helicenes has also been utilised in the chiral discotic liquid-crystalline materials, or these molecules have served as ligands in asymmetric catalysis.17–19 In addition, they can be used as building blocks in functional polymers.20 Undoubtedly, these valuable properties are closely connected with the overall structure of the molecule.
Unsubstituted helicenes usually crystallise in non-centrosymmetric space groups (P21, P212121) despite the fact that the helicenes are racemic.21–25 This phenomenon involves so-called ‘lamellar twinning’, where the layers of individual enantiomers alternate within a single crystal, forming homo-chiral domains.26 Some of the derivatives have a tendency towards co-facial stacking in bulk state forming macroscopic fibres consisting of columnar aggregates. Similar self-assembly motifs can be also found in Langmuir–Blodgett films prepared by dip or spin coating.27,28 Due to the perpendicular arrangement of the aromatic rings with respect to the surface, the deposited films are usually anisotropic.29
Starting from [6]helicene, the twisted molecule of helicenes is highly constrained due to the steric hindrance of the peripheral rings, which gives the impression of rigidity. However, a comparison of accessible crystal structures of [6]helicene reveals surprising flexibility within a certain range of the molecular conformation. On the one hand, there is a crystal structure of a charge-transfer complex of [6]helicene with trimesic acid, which has provided the most compressed conformation of the [6]helicene molecule with the distance between C2 and C2′ atoms of the peripheral rings of 3.94 Å (Fig. 1).30 On the other hand, the helicene conformation can be stretched by the insertion of another molecule or atom into the helicene pitch, such as in the crystal structure of plain [6]helicene (the C2–C2′ distance of 4.58 Å in the original structure from 1973),21 which consists of pairs of interlocked helicene molecules, or a [6]helicene complex with silver salts, where the silver ion is bound by η1 bond to C2 and C2′ atoms, giving the C2–C2′ distance of 4.61 Å.31 The adopted conformation is a consequence of intra- and intermolecular interactions in the crystal lattice and induces deformations of individual aromatic rings.
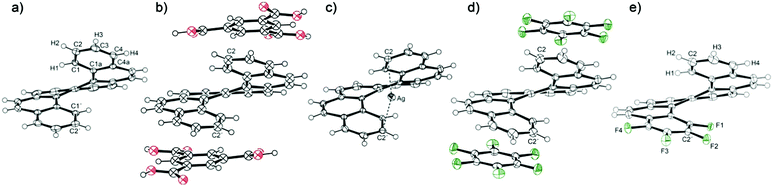 | ||
| Fig. 1 The crystal structure of (a) [6]helicene, (b) [6]helicene-trimesic acid (benzene-1,3,5-tricarboxylic acid), (c) Ag–[6]helicene complex, (d) [6]helicene–perfluorobenzene complex and (e) tetrafluoro[6]helicene. Complete atom numbering is shown in the ESI.† | ||
This paper presents an original study of internal dynamics in [6]helicenes both in solution and the solid state with special attention to the helicene pitch opening. It analyses the temperature dependence of the structural parameters determined by X-ray diffraction and of NMR chemical shifts. The experimental results are subsequently confronted with DFT calculations and molecular dynamics simulations. It is shown that a combination of experimental and theoretical approaches allows a precise description of the conformational behaviour of helicenes.
Methods
[6]Helicene (puriss., ≥99%) was purchased from Lach-ner, Czech Republic. Single crystals of [6]helicene suitable for X-ray structure analysis were obtained by crystallisation from chloroform. The charge-transfer complex of [6]helicene with perfluorobenzene was obtained by crystallisation from chloroform–perfluorobenzene mixture. 1,2,3,4-Tetrafluoro[6]helicene was prepared by intramolecular photocyclisation of tetrafluoro-2,7-distyrylnaphthalene using the Mallory-type reaction.32 The detailed synthesis will be published separately. Single crystals of 1,2,3,4-tetrafluoro[6]helicene were obtained by crystallisation from chloroform.Diffraction data were collected at 150 K on a Nonius Kappa CCD diffractometer (Enraf-Nonius) with graphite-monochromated Mo-Kα radiation. A Cryostream Cooler (Oxford Cryosystem) was used for low-temperature measurements. The structures were solved by direct methods (SIR92,33 SHELXL9734) and refined by full-matrix least-squares on F2 values (CRYSTALS35). All heavy atoms were refined anisotropically. Hydrogen atoms were localised from the expected geometry and difference electron density maps and were refined isotropically. PARST9736 was used for the calculation of ring-puckering parameters.37 The details of atom numbering and the complete list of puckering parameters are listed in the ESI.† ORTEP-338 was used for structure presentation.
X-ray of [6]helicene
C26H16, M = 328.41 g mol−1, orthorhombic system, space group P212121, a = 7.3280(3), b = 13.0400(4), c = 17.4490(5) Å, Z = 4, V = 1667.4(1) Å3, Dc = 1.31 g cm−3, μ(MoKα) = 0.074 mm−1, T = 150 K, crystal dimensions of 0.1 × 0.15 × 0.2 mm. The structure converged to the final R = 0.0345 and Rw = 0.0797 using 1682 independent reflections for 299 parameters (θmax = 27.50°). The obtained structure is almost identical to that obtained by De Clercq.21 Variable-temperature X-ray structure analysis was performed at 100, 150 and 300 K, CCDC 1514732 (100 K), 1514734 (150 K) and 1514735 (300 K). The hydrogen atoms of the crystal structure measured at 300 K were located from the expected geometry and were not refined. The variable-temperature calculation results are summarised in the ESI† (Table S1).X-ray of the [6]helicene–perfluorobenzene complex
C26H16.CF6, M = 514.47 g mol−1, monoclinic system, space group C2/c, a = 7.4459(4), b = 17.9293(9), c = 17.1981(10) Å, β = 98.529(2), Z = 4, V = 2270.6(2) Å3, Dc = 1.51 g cm−3, μ(MoKα) = 1.21 mm−1, T = 150 K, crystal dimensions of 0.20 × 0.40 × 0.61 mm. The structure converged to the final R = 0.0404 and Rw = 0.0926 using 2301 independent reflections for 205 parameters (θmax = 27.52°), CCDC 1514731.X-ray of tetrafluoro[6]helicene
C26H12F4, M = 400.36 g mol−1, monoclinic system, space group P21/n, a = 7.5783(6), b = 20.3575(16), c = 11.4292(8) Å, β = 101.178(3), Z = 4, V = 1729.8(2) Å3, Dc = 1.54 g cm−3, μ(MoKα) = 1.15 mm−1, T = 150 K, crystal dimensions of 0.16 × 0.39 × 0.67 mm. The structure converged to the final R = 0.0410 and Rw = 0.0869 using 3750 independent reflections for 319 parameters (θmax = 27.43°), CCDC 1514733.NMR spectra were measured at room temperature on a Bruker Avance III spectrometer operating at 600.1 MHz for 1H and at 150.9 MHz for 13C in DMSO-d6 and aceton-d6. A combination of 1D and 2D experiments (COSY, HSQC, HMBC) was used for the assignment of all 1H and 13C resonances. Variable-temperature NMR experiments were performed on a Bruker Avance II spectrometer operating at 499.9 MHz for 1H, 470.3 MHz for 19F and at 125.7 MHz for 13C. Temperature was calibrated with methanol and ethyleneglycol; a 200–400 K temperature range with 50 K steps was used for the experiments. To minimise the solvent effects and temperature dependence of bulk magnetic susceptibility on the reported variable-temperature NMR data,39 relative chemical shift dependences on temperature with respect to a selected signal are reported, i.e. the chemical shift of zero ppm was attributed to the selected signal at every temperature in both solvents. Signals of hydrogen H8, carbon C8 and fluorine F4 were selected for the referencing because the signals of these atoms are the least affected by the through-space ring-current effects of peripheral aromatic rings.
Two different approaches were used for DFT computations. First, geometry optimisation of isolated molecules with B3LYP40,41 and PBE42 functionals and standard Pople-type basis sets were performed with the Gaussian09 program package.43 The NMR parameters were calculated using the GIAO method and B3LYP functional. Second, geometry optimisation and molecular dynamics (MD) simulations of fully periodic systems and of isolated molecules were run in the CASTEP program,44 which exploits periodic plane waves as the basis-set functions. DFT molecular dynamics (MD) simulation of crystalline [6]helicene under periodic boundary conditions was done using an NVT ensemble maintained at a constant temperature of 300 K using a Langevin thermostat, a 0.5 fs integration time step, total simulation length of 20 ps, ultrasoft pseudopotentials,45 a planewave cutoff energy of 500 eV, and with integrals taken over the Brillouin zone using a Monkhorst–Pack46 grid of a minimum k-point sampling of 0.1 Å−1. Electron-correlation effects were modelled using the generalised gradient approximation of Perdew, Burke and Ernzerhof.42 The atomic positions were optimised at the same computational level prior to the MD runs, while lattice parameters were fixed to the experimental values. No symmetry constraints were applied during the runs as these are only relevant to the time-averaged structure. The same procedure was used for MD simulations of isolated [6]helicene at 200 and 300 K modelled as an isolated molecule in a cubic periodic box of 20 × 20 × 20 Å3. The effect of empirical corrections for dispersion47 was also examined both in the simulations of isolated molecules and crystals.
Results
X-ray diffraction
Five crystal structures of [6]helicene were selected for the conformational analysis based on X-ray diffraction experiments (Fig. 1). The structures of [6]helicene (the structure recollected at 100 K) and the Ag–[6]helicene complex31 were taken as examples of structures with a stretched helix; the complex of [6]helicene with trimesic acid represents a compressed structure. The newly prepared complex of [6]helicene with perfluorobenzene provides a more or less relaxed helicene conformation because no significant influence of intermolecular interactions could be observed. The last structure is a new compound, tetrafluoro[6]helicene, which should reflect the intramolecular interaction between electron-deficient (tetrafluoro-) and the opposite electron-rich peripheral aromatic rings. This structure also represents a relaxed helicene skeleton as the influence of the intermolecular interaction on the helix seems to be negligible.As mentioned above, the overall conformation of the helicene molecule is reflected in the distance between the peripheral rings. Extreme values were found in the complex of [6]helicene with trimesic acid (C2–C2′ distance of 3.94 Å) and, surprisingly, in the structure of plain [6]helicene (4.64 Å at 100 K). Both values describe conformations severely influenced by intermolecular interactions: compression produced by the grid of the crystallisation partner (trimesic acid) on the one hand and the insertion of the second helicene molecule into the pitch on the other. The insertion of a silver cation induced a similar opening of the pitch to 4.62 Å. The two extreme values gave a surprisingly large conformational range of 0.7 Å. The relaxed helicene molecule in the structure of the charge-transfer complex with perfluorobenzene provided a C2–C2′ distance of 4.31 Å, which is close to the middle of the observed conformational range (4.29 Å). On the other hand, the C2–C2′ distance found in the relaxed structure of tetrafluoro[6]helicene is shorter (4.14 Å); the π–π interaction of the electron-deficient with the electron-rich aromatic ring leads to a significant shortening of the distance between the peripheral rings.
A detailed conformational analysis of individual aromatic rings based on a comparison of standard ring-puckering parameters37 has revealed the central aromatic rings as the most distorted from planarity, while the peripheral rings remain almost planar. The total puckering amplitude Q ranges from 0.01 to 0.07 Å for the peripheral rings 1 and 6, from 0.11 to 0.16 Å for the rings 2 and 5, and from 0.18 to 0.21 Å for the central rings 3 and 4. According to standard visualisation of the ring-puckering parameters, the conformations of all aromatic rings are located near the ‘equator’, adopting relatively narrow range of twisted or boat conformations 2T4–B4,1–3T1 for right-handed helix (Fig. 2) and 1T3–1,4B–4T2 for the left-handed helix. For a detailed explanation and the list of puckering parameters, see the ESI.† The range of the individual benzene ring conformations is similar to that found in previous computational studies of benzene and other aromatic compounds.48–52
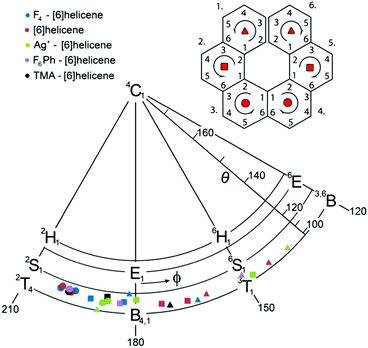 | ||
| Fig. 2 The visualisation of ring-puckering parameters calculated for the right-handed helix. Only the most relevant part of the conformational space is depicted. For full details see the ESI.† | ||
As the main focus of this paper is on the internal dynamics in these helical molecules, a variable-temperature X-ray diffraction study of [6]helicene in the temperature range of 100–300 K has also been performed. The analysis has shown that the higher temperature increases only the oscillations of individual atoms manifested by larger thermal ellipsoids without any significant effect on molecular conformation. The C2–C2′ distance even slightly decreases with the elevated temperature, which may look surprising at first sight; however, this is only a consequence of higher amplitudes of librational motion, which leads to shorter distances between average atomic positions.53 A similar shortening of the C2–C2′ distance has also been observed in the structure of the [6]helicene–trimesic acid complex measured at 105 K and room temperature.30 Nevertheless, the restricted motion of the [6]helicene molecule fixed in the crystal lattice is in contrast to the prolongation of the cell parameters. Especially, the cell parameters b and c were extended by 0.21 and 0.14 Å, respectively, which corresponds to 1.6% and 0.8% of their value, respectively. The elongation of the parameter a was significantly smaller (0.04 Å, 0.5%). A detailed analysis of the crystal packing revealed a noticeable change only in the intermolecular distance between the two interlocked molecules, which increased by 0.14 Å (measured as the distance between molecular centroids) in the temperature range studied. This effect takes place mainly in the direction [012] and therefore strongly affects solely the cell parameters b and c in the corresponding ratio. The increased thermal atomic motion results in the ousting of the second molecule from the helicene pitch rather than in any observable conformational change (Fig. 3).
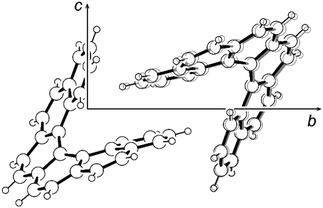 | ||
| Fig. 3 The ousting of the second molecule from the helicene pitch in the structure of [6]helicene. The structure measured at 100 K in black, at 300 K in grey. | ||
NMR spectroscopy
Valuable information about the geometry of helicene molecules including the ‘pitch’ opening can be provided by NMR spectroscopy. NMR chemical shifts reflect the electronic environment in the surroundings of a studied nucleus. In helicene molecules, the resonances of the atoms in peripheral aromatic rings can be affected through space by the aromatic ring on the other side of the molecule. Ring-current effects can be particularly important in these molecules. They make the nuclei below and above an aromatic system more shielded (i.e. with a lower chemical shift) than similar nuclei in systems without this spatial interaction. For NMR data acquired for diluted helicene solutions, intermolecular solute–solute interactions, such as those leading to the ‘pitch’ opening in the crystal structure of [6]helicene, cannot be expected. Therefore, the NMR data are more likely related to isolated molecules and the adopted conformation is formed without the influence of intermolecular interactions.Chemical shifts of hydrogen and carbon atoms in an unsubstituted peripheral ring of [6]helicene and tetrafluoro[6]helicene molecules are shown in ESI.† The largest 1H chemical-shift differences in the studied compounds were found for the H1 atom, which is found at 7.43 ppm in the spectrum of unsubstituted [6]helicene and at 7.01 ppm in the spectrum of tetrafluoro[6]helicene. The hydrogen atom H1 is the closest atom to the opposite peripheral aromatic ring in helicenes, as a result of which it is the most affected by the ring-current effects. The fact that the H1 in tetrafluoro[6]helicene is more shielded indicates that its helix is more ‘squeezed’ and the H1 is closer to the opposite fluorinated aromatic ring. The described chemical-shift difference can mostly be attributed to through-space effects as the fluorine atoms are separated by at least eight covalent bonds. On the other hand, the chemical-shift differences of the hydrogen atoms H2, H3 and H4 in [6]helicene and tetrafluoro[6]helicene are rather small. The slightly higher values of these chemical shifts in tetrafluoro[6]helicene can be explained by the slightly lower electron density in this ring caused by electron-density transfer to electron-withdrawing fluorine substituents on the other side of the molecule. Similar chemical-shift changes were also found in 13C NMR spectra. The carbon atoms C1, C1a and C2 in [6]helicene are significantly less shielded than the corresponding atoms in tetrafluoro[6]helicene.
The flexibility of helicene molecules found in various crystal structures might be reflected in large conformational fluctuations of the isolated molecules. Therefore, variable-temperature NMR measurements in a broad temperature range (200–400 K) have been performed to gain insight into the dynamics of the studied helicenes. In the absence of any structural changes, chemical shifts usually exhibit only weak temperature dependence caused by vibrational averaging.54–56 The temperature dependence of 1H and 13C chemical shifts in [6]helicene is shown in Fig. 4. The atoms H1 and C1 in this molecule have revealed significant temperature dependence leading to higher chemical shifts at higher temperature. This behaviour may be explained by increased molecular dynamics at higher temperatures, leading to a larger average distance between the opposite peripheral aromatic rings and hence to a decrease of the effects of the ring currents. The effect of temperature on H2, H3 and H4 chemical shifts is significantly lower than in the case of H1, and the rest of the hydrogen chemical shifts are almost temperature-independent. Similar behaviour was also observed for 13C resonances, where C1 shielding is significantly more temperature-dependent than the shielding of other carbons. The 1H, 13C and 19F chemical shifts in tetrafluoro[6]helicene have revealed similar temperature dependence (ESI†). The atoms that are close to the opposite peripheral ring are significantly deshielded at a higher temperature, while the temperature effect on other chemical shifts is much less pronounced. For comparison, the temperature dependence of chemical shifts of phenanthrene (a reference planar aromatic compound without through-space shielding by ring-current effects) is also shown in the ESI.†
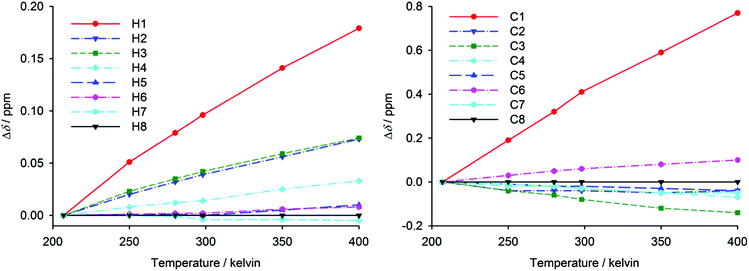 | ||
| Fig. 4 The temperature dependence of relative 1H chemical shifts with respect to H8 (left) and of 13C chemical shifts with respect to C8 (right) in [6]helicene measured in acetone and DMSO. For atom numbering see Fig. 1 and ESI.† | ||
DFT calculations
In order to gain further insight into the structure and dynamics of the studied helicenes, a number of DFT computations were performed. First, the geometries of the molecules in vacuum and in periodic crystal structures were optimised and subsequently compared with those found experimentally. Then energy and shielding dependence on the ‘opening’ of the helicene molecule was calculated, and finally, DFT molecular dynamics simulations of isolated and crystalline helicenes at various temperatures were performed.Geometry optimisation under fully periodic conditions performed in the CASTEP provided excellent agreement of the optimised geometries with X-ray structures. The inclusion of empirical corrections for dispersion did not change the resulting geometry much, probably because the crystal packing itself forces the molecules to adopt the preferred conformation and neglecting dispersion leads to error cancelation of intramolecular and intermolecular weak interactions.
On the other hand, when geometry optimisation is performed at the same computational level but for isolated molecules, the resulting conformation is significantly different from the X-ray structure and the inclusion of dispersion significantly affects the conformation (Table 1). The structure of tetrafluoro[6]helicene optimised in vacuum with dispersion correction is almost identical to that found in the crystalline state, while [6]helicene in the crystal is ca. 0.4 Å more ‘open’ than in vacuum, which can be explained by the intermolecular interactions discussed above (the interlocking of helicene molecules). The influence of the functional and basis set used for the geometry optimisation was also examined (see details in the ESI†).
| Compound | Exp. | Calc. | |||
|---|---|---|---|---|---|
| X-ray | Periodic | Periodic + D | Isolated | Isolated + D | |
| [6]Helicene | 4.622 | 4.627 | 4.622 | 4.460 | 4.198 |
| F4[6]helicene | 4.141 | 4.152 | 4.159 | 4.254 | 4.153 |
The intramolecular potential along the C2–C2′ distance was obtained by geometry optimisations of both compounds with the distance fixed at selected values (Fig. 5). These calculations confirm the results found in fully relaxed structures, i.e. the dispersion correction leads to a shortening of the C2–C2′ distance and [6]helicene is more ‘open’ than tetrafluoro[6]helicene. The potential is, however, relatively flat in both compounds (an increase of the distance by 0.4 Å leads to an increase of potential energy by only 0.5 kcal mol−1). At room temperature, Boltzmann thermal energy quantum kBT corresponds to ca. 0.6 kcal mol−1, hence the distance may significantly fluctuate around the equilibrium value.54 These small energy penalties for the deformation of the helicene molecule may be easily paid by intermolecular interactions in crystals, which explains the conformational variability of helicenes in the solid state.
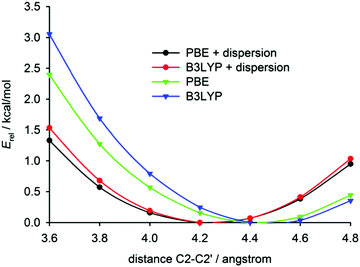 | ||
| Fig. 5 The calculated relative energy dependence on the C2–C2′ distance in isolated [6]helicene. For tetrafluoro[6]helicene, see the ESI.† | ||
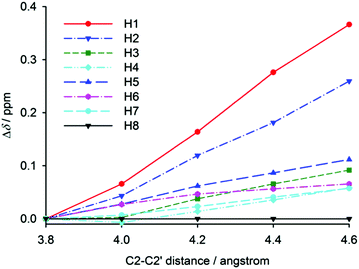
Chemical shifts of [6]helicene were also calculated for partially optimised structures with a fixed C2–C2′ distance (used above for the construction of the intramolecular potential). The distance dependence of hydrogen chemical shifts is shown in Fig. 6, which clearly resembles the experimental temperature dependence of relative hydrogen chemical shifts in [6]helicene (Fig. 4 left). The chemical shift of H1 is the most distance dependent with higher shifts observed for larger distances. This observation thus confirms the influence of ring-current effects on nuclear shielding, and the similarity with the experimental temperature dependence of chemical shifts confirms the expected trend in the helix opening with increasing temperature. At higher temperatures, the helix is more open, the effect of ring currents is weaker, and the chemical shift of H1 increases. Through a comparison of the calculated chemical-shift dependence on the C2–C2′ distance with the experimental temperature dependence, the opening of the helix in an isolated [6]helicene molecule can be estimated to be ca. 0.2 Å per 100 K.
The temperature dependence of experimental chemical shifts in [6]helicene and tetrafluoro[6]helicene indicates significant internal dynamics in these helical molecules. In order to explore this internal dynamics in detail, molecular dynamics simulations of a fully periodic crystal structure of [6]helicene at 300 K and of isolated [6]helicene at 200 and 300 K were performed.
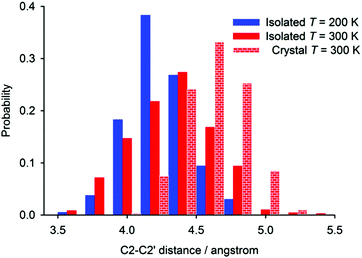
The distance found with the highest probability in the periodic simulation (4.6 Å) is very close to the experimental C2–C2′ distance found in the crystal (Fig. 7). The crystal packing restricts the flexibility of individual [6]helicene molecules, which leads to a relatively sharp and symmetric distribution of the distance probability around the most probable value.
On the other hand, the helix is less open in the isolated molecule of [6]helicene than in the crystalline state; this is reflected in a shift of the probability function in the case of the isolated molecule to a smaller distance than in periodic simulations, both performed at 300 K. The probability distribution function is also slightly broader, which can be explained by the lack of crystal-packing forces. The distance probability distribution calculated for isolated molecules is significantly affected by the temperature of the simulation. With increasing temperature, the distribution function broadens and moves towards higher values, which reflects larger amplitudes of motion and a larger average C2–C2′ distance at higher temperatures. The most probable C2–C2′ distance increases by ca. 0.2 Å when going from 200 to 300 K, which is in excellent agreement with the estimate made from the comparison of experimental and calculated chemical-shift changes. Average C2–C2′ distance calculated throughout the whole MD simulations increased by 0.1 Å.
Conclusions
Despite the impression of rigidity, the conformational flexibility of molecules related to [6]helicene is surprisingly large. Every aromatic ring is distorted from planarity in these molecules, with the distorsion being significantly larger in the central rings than in the peripheral rings. The overall conformation of the molecule is reflected in the distance between peripheral aromatic rings, the value of which has been found in a wide range of 3.9–4.6 Å. The conformation of crystalline [6]helicene has been shown to be almost temperature-independent. On the other hand, variable-temperature NMR experiments performed in a 200–400 K range have revealed significant temperature dependence of the nuclear shielding of peripheral atoms, which are the most strongly influenced by through-space ring-current effects. The chemical shifts of these atoms are always higher at elevated temperatures, which can be explained by a larger distance between the peripheral rings.DFT calculations have confirmed high flexibility of [6]helicene conformation; the intramolecular ‘opening’ potential is surprisingly flat with the minimum at 4.2 Å, and the 0.4 Å stretching/squeezing penalty being well below 1 kcal mol−1, which can be easily overcome by intermolecular interactions in solid materials. Furthermore, DFT calculations have confirmed the trend of increasing chemical shifts of peripheral atoms in conformations with a larger opening of the helicene molecule. A comparison of the experimental chemical-shift dependence on temperature with the calculated chemical-shift dependence on the helicene opening has made it possible to estimate that the helicene opening in isolated molecules increases by approximately 0.2 Å per 100 K. A similar result was provided by molecular dynamics simulations of isolated molecules, where the most populated C2–C2′ distance increased by 0.2 Å between the simulations performed at 200 and 300 K.
The experimental and theoretical investigation performed within this work describes the unexpectedly large conformation flexibility and dynamic behaviour of [6]helicene molecules. These properties should be taken into account in the design of helicene-like structures for future applications.
Acknowledgements
This work was supported by the Czech Science Foundation (M. D.: grant No. 15-11223S, J. S. and I. C.: grant No. 15-12719S).References
- M. Gingras, Chem. Soc. Rev., 2013, 42, 1051–1095 RSC
.
- A. Moradpour, H. Kagan, M. Baes, G. Morren and R. H. Martin, Tetrahedron, 1975, 31, 2139–2143 CrossRef CAS
.
- A. Jančařík, J. Rybáček, K. Cocq, J. V. Chocholoušová, J. Vacek, R. Pohl, L. Bednárová, P. Fiedler, I. Císařová, I. G. Stará and I. Starý, Angew. Chem., Int. Ed., 2013, 52, 9970–9975 CrossRef PubMed
.
- D. J. Morrison, T. K. Trefz, W. E. Piers, R. McDonald and M. Parvez, J. Org. Chem., 2005, 70, 5309–5312 CrossRef CAS PubMed
.
- Y. Ooyama, G. Ito, H. Fukuoka, T. Nagano, Y. Kagawa, I. Imae, K. Komaguchi and Y. Harima, Tetrahedron, 2010, 66, 7268–7271 CrossRef CAS
.
- J. E. Field, G. Muller, J. P. Riehl and D. Venkataraman, J. Am. Chem. Soc., 2003, 125, 11808–11809 CrossRef CAS PubMed
.
- Y. Q. Tang, T. A. Cook and A. E. Cohen, J. Phys. Chem. A, 2009, 113, 6213–6216 CrossRef CAS PubMed
.
- T. Verbiest, S. Van Elshocht, A. Persoons, C. Nuckolls, K. E. Phillips and T. J. Katz, Langmuir, 2001, 17, 4685–4687 CrossRef CAS
.
- S. Van Elshocht, T. Verbiest, G. de Schaetzen, L. Hellemans, K. E. S. Phillips, C. Nuckolls, T. J. Katz and A. Persoons, Chem. Phys. Lett., 2000, 323, 340–344 CrossRef CAS
.
- T. Verbiest, S. Van Elshocht, M. Kauranen, L. Hellemans, J. Snauwaert, C. Nuckolls, T. J. Katz and A. Persoons, Science, 1998, 282, 913–915 CrossRef CAS PubMed
.
- A. Bossi, E. Licandro, S. Maiorana, C. Rigamonti, S. Righetto, G. R. Stephenson, M. Spassova, E. Botek and B. Champagne, J. Phys. Chem. C, 2008, 112, 7900–7907 CAS
.
- T. Hatakeyama, S. Hashimoto, T. Oba and M. Nakamura, J. Am. Chem. Soc., 2012, 134, 19600–19603 CrossRef CAS PubMed
.
- Y. Yang, R. C. da Costa, M. J. Fuchter and A. J. Campbell, Nat. Photonics, 2013, 7, 634–638 CrossRef CAS
.
- S. Sahasithiwat, T. Mophuang, L. Menbangpung, S. Kamtonwong and T. Sooksimuang, Synth. Met., 2010, 160, 1148–1152 CrossRef CAS
.
- L. Q. Shi, Z. Liu, G. F. Dong, L. Duan, Y. Qiu, J. Jia, W. Guo, D. Zhao, D. L. Cui and X. T. Tao, Chem. – Eur. J., 2012, 18, 8092–8099 CrossRef CAS PubMed
.
- J. Storch, J. Zadny, T. Strasak, M. Kubala, J. Sykora, M. Dusek, V. Cirkva, P. Matejka, M. Krbal and J. Vacek, Chem. – Eur. J., 2015, 21, 2343–2347 CrossRef CAS PubMed
.
- T. Verbiest, S. Sioncke, A. Persoons, L. Vyklicky and T. J. Katz, Angew. Chem., Int. Ed., 2002, 41, 3882–3884 CrossRef CAS PubMed
.
- M. T. Reetz, E. W. Beuttenmuller and R. Goddard, Tetrahedron Lett., 1997, 38, 3211–3214 CrossRef CAS
.
- S. D. Dreher, T. J. Katz, K. C. Lam and A. L. Rheingold, J. Org. Chem., 2000, 65, 815–822 CrossRef CAS
.
- J. Hrbac, J. Storch, V. Halouzka, V. Cirkva, P. Matejka and J. Vacek, RSC Adv., 2014, 4, 46102–46105 RSC
.
- C. de Rango, G. Tsoucaris, J. P. De Clercq, G. Germain and J. P. Putzeys, Cryst. Struct. Commun., 1973, 2, 189 CAS
.
- K. Mori, T. Murase and M. Fujita, Angew. Chem., Int. Ed., 2015, 54, 6847–6851 CrossRef CAS PubMed
.
- P. T. Beurskens, T. E. M. Beurskens and v. d. Hark, Cryst. Struct. Commun., 1976, 5, 241 CAS
.
- G. Le Bas, A. Navaza, Y. Mauguen and C. De Rango, Cryst. Struct. Commun., 1976, 5, 357 CAS
.
- G. Le Bas, A. Navaza, M. Knossow and C. De Rango, Cryst. Struct. Commun., 1976, 5, 713 CAS
.
- B. S. Green and M. Knossow, Science, 1981, 214, 795–797 CAS
.
- A. J. Lovinger, C. Nuckolls and T. J. Katz, J. Am. Chem. Soc., 1998, 120, 264–268 CrossRef CAS
.
- C. Nuckolls, T. J. Katz, T. Verbiest, S. Van Elshocht, H. G. Kuball, S. Kiesewalter, A. J. Lovinger and A. Persoons, J. Am. Chem. Soc., 1998, 120, 8656–8660 CrossRef CAS
.
- P. Henderson, D. Beyer, U. Jonas, O. Karthaus, H. Ringsdorf, P. A. Heiney, N. C. Maliszewskyj, S. S. Ghosh, O. Y. Mindyuk and J. Y. Josefowicz, J. Am. Chem. Soc., 1997, 119, 4740–4748 CrossRef CAS
.
- O. Ermer and J. Neudorfl, Helv. Chim. Acta, 2001, 84, 1268–1313 CrossRef CAS
.
- E. Makrlík, J. J. Dytrtová, P. Vaňura, I. Císařová, J. Sýkora, V. Církva, J. Storch and M. Polášek, Struct. Chem., 2016, 27, 627–635 CrossRef
.
- K. B. Jørgensen, Molecules, 2010, 15, 4334–4358 CrossRef PubMed
.
- A. Altomare, G. Cascarano, G. Giacovazzo, A. Guagliardi, M. C. Burla, G. Polidori and M. Camalli, J. Appl. Crystallogr., 1994, 27, 435 Search PubMed
.
-
G. M. Sheldrick, SHELXL97, Program for Crystal Structure Refinement from Diffraction Data, University of Göttingen, Göttingen, 1997 Search PubMed
.
- P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, J. Appl. Crystallogr., 2003, 36, 1487 CrossRef CAS
.
- M. Nardelli, J. Appl. Crystallogr., 1995, 28, 659 CrossRef CAS
.
- D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS
.
- L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565 CrossRef CAS
.
- M. Dračínský and P. Bouř, J. Chem. Theory Comput., 2010, 6, 288–299 CrossRef PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, X. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS
.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State., 1976, 13, 5188–5192 CrossRef
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- O. V. Shishkin, P. Dopieralski, I. V. Omelchenko, L. Gorb, Z. Latajka and J. Leszczynski, J. Phys. Chem. Lett., 2011, 2, 2881–2884 CrossRef CAS
.
- P. Cysewski, J. Mol. Model., 2011, 17, 2249–2257 CrossRef CAS PubMed
.
- P. Cysewski, Phys. Chem. Chem. Phys., 2011, 13, 12998–13008 RSC
.
- M. V. Zhigalko, O. V. Shishkin, L. Gorb and J. Leszczynski, J. Mol. Struct., 2004, 693, 153–159 CrossRef CAS
.
- A. Laaksonen, J. Wang and R. J. Boyd, Chem. Phys. Lett., 1995, 241, 380–386 CrossRef CAS
.
- M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712 RSC
.
- M. Dračínský, P. Bouř and P. Hodgkinson, J. Chem. Theory Comput., 2016, 12, 968–973 CrossRef PubMed
.
- M. Dračínský and P. Bouř, J. Comput. Chem., 2012, 33, 1080–1089 CrossRef PubMed
.
- M. Dračínský, J. Kaminský and P. Bouř, J. Chem. Phys., 2009, 130, 094106 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental and computational data. CCDC 1514731–1514735. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cp07552e |
| This journal is © the Owner Societies 2017 |