Searching for the thermodynamic limit – a DFT study of the step-wise water oxidation of the bipyramidal Cu₇ cluster

Abstract

Oxidative degradation of copper in aqueous environments is a major concern in areas such as catalysis, electronics and construction engineering. A particular challenge is to systematically investigate the details of this process for non-ideal copper surfaces and particles under the conditions found in most real applications. To this end, we have used hybrid density functional theory to study the oxidation of a Cu₇ cluster in water solution. Especially, the role of a large water coverage is explored. This has resulted in the conclusion that, under atmospheric H₂ pressures, the thermodynamically most favored state of degradation is achieved upon the generation of four H₂ molecules (i.e. Cu₇ + 8H₂O → Cu₇(OH)₈ + 4H₂) in both condensed and gas phases. This state corresponds to an average oxidation state below Cu(I). The calculations suggest that the oxidation reaction is slow at ambient temperatures with the water dissociation as the rate-limiting step. Our findings are expected to have implication for, among other areas, the copper catalyzed water-gas shift reaction, and for the general understanding of copper corrosion in aqueous environments.

---

1 Introduction

Despite the large amount of effort that has been invested in studying the water–copper system over the years, it remains a subject of active debate and controversy. Some of the unresolved matters concern the suggested corrosion of copper in anoxic water, which seemingly contradict the long established thermodynamic bulk properties of copper and its oxidized phases.^1–9 Other questions are triggered by the catalytic behavior of copper in e.g. the industrially important water-gas shift reaction (WGSR).^10–16 Additionally, much attention is motivated by the conceptually interesting behavior of water at the water–copper interfaces.^17–25 The above-mentioned topics have in common their connection to the surface properties of the copper material.

The interface between water and copper (and other metals) is rather well-documented,^17–25 theoretically as well as experimentally, albeit experimentally mainly under low-temperature high vacuum conditions on ideal mono-crystalline surfaces. Under the typical conditions in real applications, e.g. rough, disrupted surfaces at water coverage close to and above one mono-layer, the available information is sparser and the systems become much more difficult to model. In the present work we attempt to shed light on some questions with implications for the ongoing debate, by using a density functional theory (DFT) approach and a Cu₇ cluster model for the non-ideal copper surface with a high water coverage (for computational reasons cluster models are advantageous for studying reactions in water solution‡). Especially, we strive to identify to what extent it is thermodynamically feasible to oxidize the surface of the copper cluster by pure water.

It has previously been established that single water molecules adsorb exothermically on various copper surfaces.^11,15,23,24 The adsorption is (partially) dissociative on the low density copper [110] crystallographic plane,^21–25 but molecularly intact on the denser [100]²⁶ and [111]²⁵ surfaces. To accommodate the wetting of copper surfaces, adsorbed hydroxyl groups have been found to play an important role; the Cu[110] surface is hydrophilic while Cu[111] is hydrophobic due to the lack of the anchoring hydroxyl groups (formed upon water dissociation) on the latter surface.²⁵ The water splitting is, moreover, facilitated by assisting water, driven by the strong OH–H₂O H-bond formed upon dissociation, and thus more favored at high water coverage, i.e. around one mono-layer.^13,22 In addition, the water dissociation has proven to be the rate-limiting step in the Cu-catalyzed WGSR.^11,15 Activation energies in the gas-phase in the order of 0.62–1.25 eV (theoretical)^{14,15,27–32} and 0.91–1.17 eV (experimental)^11,33 have been reported. The values vary, e.g., with the crystallographic plane, where the denser surfaces typically are associated with a larger barrier. Similar values have also been determined by cluster calculations.^10,14,29 At high water coverage has, nevertheless, a much lower experimental barrier of 0.53 eV been observed for the [110] surface,²¹ an effect which is attributed to the strong H-bond formed during the dissociation.^13,22

In order to generate hydrogen gas, a second H₂ forming step must follow the dissociation of water. This step is typically associated with a slightly lower barrier than the water dissociation, in the order of 0.56–1.07 eV depending on the surface, cluster size and water coverage. It is usually reported as endothermic (ΔH^o > 0) but exergonic (ΔG^o < 0) (due to the large translational entropy of gaseous H₂) on both mono- and polycrystalline surfaces as well as on nano-sized clusters.^{1,9,11,28,30,34,35}

The non-ideal character of real systems can be approached by different means: for instance, Tang et al.³⁶ revealed that water adsorbs stronger at stepped surfaces, e.g. [221] or [211], compared to flat surfaces, e.g. [111]. Another way to study the influence of surface roughness and defects is by using finite cluster models. This may, for some systems, be a better representation, or at least a sufficiently accurate but less computationally demanding approach for studies of defective surfaces compared to extended models employing periodic boundary conditions. However, nanoparticles are not only interesting as models. Their unique properties compared to the bulk metals have attracted massive interest during the recent decades. It should thus be emphasized that the increased activity of copper nanoparticles in catalysis is sufficient motivation for investigations of Cu-clusters.

The Cu₇ cluster model used throughout this study has been identified as the smallest stable three dimensional copper cluster by theoretical investigations.³⁴ It is also the smallest three dimensional Cu-cluster to be observed experimentally.§^38,39 A particular stability has, furthermore, been assigned to the cluster, and it may be considered a ‘super-atom’ with the seven (original) 4s-electrons forming an outer valence-shell in resemblance to a halogen atom⁴⁰ (and hence allowing for a rich redox chemistry).

Adsorption of small molecular species on the Cu₇ cluster has been studied before. Of particular interest to this work, Chen et al.¹⁰ used density functional theory (DFT) methods to model water adsorption and dissociation on the Cu₇ cluster in the gas-phase. Likewise the gas-phase interactions of H₂,^34,35,41,42 O₂,^43–45 CO^43,46 and CO₂⁴⁷ with Cu₇ have been explored earlier. In addition, larger cluster models have been employed to study the water dissociation^10,14,29,48 as well as the water catalyzed H₂ formation reaction.^9,35 However, to the best of the authors' knowledge, none of the earlier theoretical studies of copper clusters or surfaces have investigated the complete formation of H₂ gas from water at large water coverage in the condensed phase, nor taken the H₂ generation process as far as this work. The oxidative reactivity of copper surfaces with water is of fundamental interest in corrosion processes and, as such, for, e.g., the long term (geological time-scale) application of copper in nuclear fuel repositories.

The present work is divided into two parts: (i) an adsorption and properties part where the performance of the hybrid PBE0⁴⁹ functional is compared to other functionals as well as previous studies and (ii) the identification of the favored mechanisms for water dissociation and H₂-gas generation, including a study of the oxidation of Cu₇ by water up until the formation of five H₂ molecules.

2 Computational details

All structures have been fully optimized in both gas and condensed phases with the Jaguar 7.9⁵⁰ or Gaussian 09⁵¹ software packages, using the hybrid DFT functional PBE0⁴⁹ along with the double zeta effective core potential (Los Alamos) basis set LACVP*+.⁵² An unrestricted spin scheme was employed throughout the study to properly treat the spin-polarization of Cu₇. The reported energies are taken from single-point calculations on the PBE0/LACV3P**++ level of theory, if not otherwise specified. Additionally, the water adsorption energies were evaluated using a set of other functionals: the pure DFT GGA (general gradient approximation) functional PBE,⁵³ the meta GGA M06-L⁵⁴ and the double-hybrid PW6B95 functional.⁵⁵ Moreover, dispersive forces were accounted for by adding Grimme and co-worker's D3-type corrections^56,57 on top of some of the aforementioned functionals, see Table 3. For comparison, the water adsorption structures were also optimized with the meta hybrid M06⁵⁸ functional of Zhao and Truhlar, referred to as M06(opt) in Table 3. Relativistic all-electron calculations with the ZORA Hamiltonian and spin–orbit coupling were, furthermore, performed on the optimized adsorption structures within the ADF2012^59,60 program suite using the PBE functional and a Slater-type triple-ς quality basis set including two sets of polarization functions augmented with diffuse functions (AUG/ATZ2P).

Frequency calculations were carried out in order to characterize all reported geometries as either minima (no imaginary frequency) or transition-states (one imaginary frequency). The calculated Hessian was also used to estimate the thermal corrections to the standard enthalpies and free energies by employing standard conditions of 298.15 K and 1 bar, and assuming the rigid rotor, harmonic oscillator and ideal/non-interacting gas approximations. The condensed phase calculations were performed using the Poisson–Boltzmann solver^61,62 in Jaguar 7.9, for the adsorption calculations, with ε = 80.0, and the IEFPCM^63,64 implementation in Gaussian 09 and ε = 78.4 for the remaining structures. The use of continuum models to represent the water solvent has previously been successful for studying metal ions and the hydroxyl anion in aqueous solutions.^65–69 It has been shown that by using an explicit first solvation shell and representing long-range effects by PCM, accurate geometries, hydration energies and reaction barriers can be determined for aqueous systems. This especially in the case of moderately charged ions as those encountered in the present study. For the condensed phase all reported free energies have been recalculated to a standard state of 55 M water from the programs' default concentration of 0.041 M (i.e. 1 bar at 298.15 K) by

ΔΔG^o = ΔG^o (55 M) − ΔG^o (1 bar) = − RT ln(K_55M/K_1bar) (1)

The K_55M and K_1bar above are equilibrium constants for a given water adsorption reaction. The correction term, (ΔΔG^o), for a single water adsorption (i.e. K_55M/K_1bar = 55/0.041) is approximately −0.185 eV, which means a stronger adsorption. Standard states of 1 bar for H₂ gas and gaseous H₂O have been used throughout this study.

The average standard adsorption enthalpy (ΔH^o_ad), and standard Gibbs free energy (ΔG^o_ad) of water, is defined as (the same definition for ΔG^o_ad)¶

ΔH^o_ad = [H(Cu₇(H₂O)_n) − H(Cu₇) − nH(H₂O)]/n (2)

where n refers to the number of adsorbed water molecules, and H(Cu₇), H(H₂O) and H(Cu₇(H₂O)_n) to the calculated enthalpies (or free energies) of the Cu₇, H₂O and Cu₇(H₂O)n species respectively.

Sequential addition of water to Cu₇ was also considered. The standard enthalpy is defined as (equivalent definition for the free energy):

ΔH^o_ad,seq = H(Cu₇(H₂O)_n) − H(Cu₇(H₂O)_n−1) − H(H₂O) (3)

Molecular hyperfine parameters (in particular the Fermi contact parameter, A_iso) for Cu₇ were obtained from a spin-unrestricted, relativistic ZORA calculation at the PBE0 level with (i) the AUG/ATZ2P basis set and (ii) a Slater-type quadruple-ς basis set with four sets of added polarization functions (QZ4P), as implemented in ADF2012.⁷¹ The electrostatic potential surface of Cu₇ was calculated with Jaguar 7.9 at the 0.001 electron per bohr³ iso-density surface. The natural bond orbital electron population and charge analyses were performed using the NBO 3.1 program⁷² as implemented in the Gaussian 09 package.

3 Results and discussion

3.1 Cu₇ properties

3.1.1 General features. The bipyramidal, D_5h symmetry Cu₇-cluster consists of a pentagonal ring (equatorial copper) with capped atoms on both sides of the ring plane (axial copper), see Fig. 1. From electron spin resonance spectroscopy (ESR) experiments in inert matrices at low temperature (neon³⁹ and deuterated cyclohexane³⁸) it is known that the single unpaired electron of the doublet (S = 1/2) Cu₇ is predominantly located on the axial copper atoms. This has previously been reproduced with DFT calculations.^71,73,74 Calculations performed in this work using the PBE0 functional give reasonable hyperfine parameters (A_iso) and spin-densities,|| within 6% of axial copper's experimental values (Table 1). Similar to previous theoretical studies, the estimated A_iso values for the equatorial copper atoms are negative. Although the values are of the same magnitude as experimental values, they are of opposite sign.

Fig. 1 Electrostatic potential of Cu₇ in the gas phase mapped on the 0.001 electron per bohr³ iso-density surface. The potential ranges from −0.45 eV to 0.90 eV. Equatorial copper atoms are negative and electrophilic while the hollow and bridge sites are positive and nucleophilic.

Table 1 Hyperfine (Fermi contact) parameters of Cu₇

Method	A iso(ax)^a	A iso(eq)^b	Ref.
a Axial (ax). b Equatorial (eq) copper. c With additional tight s functions. d All-electron mixed-basis set, see ref. 74 and 75. e Unclear if Aiso or A⊥ was observed.
PBE0/(AUG/ATZ2P)	1690	−68	This work
PBE0/QZ4P	1846	−72	This work
B3LYP/6-31G*	1195	−21	73
B3LYP/6-311+G*	1806	−43	73
B3LYP/6-311+G*^c	1787	−53	73
PB3PW91/6-311+G*	1747	−73	73
DFT-LSDA/AEMB^d	1750	−51	74
Exp. (ESR)	1747	54	39
Exp. (ESR)^e	1749	43	38

---

Furthermore, the geometrical parameters of the optimized cluster structures obtained with the PBE0 functional in the gas-phase are in close resemblance with those previously determined with pure DFT functionals (Table 2). Repeating the calculations with the M06 functional gives similar structures. Upon optimization in the condensed phase (water simulated by a polarizable continuum model) the cluster is flattened (distance between axial atoms reduced by ca. 5%) and the ring size is extended (equatorial–equatorial distance enlarged by an average of ca. 3%).

Table 2 Geometric parameters for the Cu₇ cluster, distances in Å

Method	eq–eq^a	eq–ax^a	ax–ax^a	Ref.
a Equatorial (eq) and axial (ax) copper. b Extra polarization functions. c Employing effective core potentials. d A frozen core approximation. e An all electron basis set with the ZORA Hamiltonian and spin–orbit coupling.
PBE0/lacvp*+ (aq)	2.569	2.569	2.442	This work
PBE0/lacvp*+ (g)	2.499	2.499	2.579	This work
M06/lacvp*+ (g)	2.464	2.464	2.600	This work
PBE/double-ς^b^,^c (g)	2.468	2.486	2.660	10
BPW91/triple-ς^b^,^d (g)	2.444	2.440	2.555	46
PBE/triple-ς^b^,^e (g)	2.414	2.420	2.559	40

---

The HOMO–LUMO gap is determined to be 1.59 eV with PBE0, which, as expected, is much larger than that of the pure DFT functional PBE (0.33 eV).¹⁰

3.1.2 Adsorption. The left picture of Fig. 1 shows the electrostatic potential of the Cu₇-cluster plotted on the 0.001 electron per bohr³ iso-density surface. Such maps are useful for identification of nucleophilic (negative) and electrophilic (positive) sites, as well as for comparison of their relative reactivity (see e.g.ref. 76 for a recent review). According to the electrostatic surface potential the equatorial ring sites are electrophilic, which is consistent with their affinity for water (a nucleophile),¹⁰ whereas the axial coppers seemingly are inactivated. Moving on over the cluster, nucleophilic sites can be found on the bridges between any two copper atoms (equatorial–equatorial or axial–equatorial) and, especially, in the 3-fold hollow sites in the center of the triangles formed by an axial atom and two equatorial atoms. This analysis is in agreement with the identified preference for water to bind equatorially over axial (a difference of about 0.14 eV in the gas phase and 0.11 eV in the condensed phase†) as well as the difficulty to find minima for bridge and hollow site adsorption of water. The picture is further cemented by the results that the more electrophilic proton and the OH radical prefer to add to the hole and bridge sites.†

The water molecule adds to the copper by donating electron density primarily from the oxygen's p_z orbital, to the 4p-orbitals of copper (NBO analysis⁷²). To accommodate the interaction, electron density is moved from the 4s orbitals to the 4p orbitals of Cu₇ by a sp orbital hybridization, accompanied to a small degree by a reorganization of the 3d band where electron density is moved from the interacting copper atom to the non-interacting atoms. These processes facilitate water adsorption by reducing the Pauli repulsion and increasing the (+) charge of the active copper atom. The interacting water orbitals are re-hybridized via the bonding 1b₂ and 3a₁ orbitals to allow for a stronger p_z polarization. All in all the adsorption leads to a small charge transfer from water to copper in the order of 0.05e⁻. The LUMO of Cu₇ is dominated by the 4p orbitals of the axial copper atoms, and it is also to these 4p orbitals that the main part of the electron density is transferred. The presented NBO analysis agrees well with earlier experimental and theoretical studies of water interacting with ideal surfaces.^77–79

Upon adsorption the water molecule binds at a distance of 2.156 Å to the equatorial position and 2.190 Å to the axial, considerably shorter distances than those obtained via PBE optimizations.¹⁰ The equatorial adsorption enthalpy of −0.45 eV is in accordance with experimentally determined values on surfaces (−0.42 eV on the [110] surface).¹¹ M06 yields similar results to that of PBE0 for the geometries and energies (e.g. equatorial adsorption has an enthalpy of −0.46 eV and a slightly shorter bond distance of 2.132 Å).

Adding another water molecule to Cu₇ is slightly less favorable (enthalpically) than the first addition (Table 3) and may occur at any equatorial copper atom (the adjacent and opposite sites with respect to the first water are essentially energetically degenerate in the gas phase, whereas the adjacent site is slightly favored in the condensed phase). The third water preferentially adsorbs at the opposite side to the previously adsorbed water molecules (given that the two first molecules are adsorbed next to each other) in the condensed phase, while in the gas phase the sites are energetically degenerate (see Fig. 2).† Up to five water molecules can be adsorbed at once on the cluster (all at the equatorial sites), but any attempt to place an additional water on the free axial sites results in the migration of the (added) water molecule to a second adsorption layer, outside the already adsorbed water molecules. This is in agreement with the observations by Chen et al.¹⁰ using the pure DFT PBE functional.

Table 3 Average enthalpies and standard Gibbs free energies (298.15 K) of adsorption for n = 1–5 water molecules onto Cu₇ in eV

nH2O	PBE0			PBE0-D3	PBE	PBE-AE^a	PBE-D3	M06 (opt)	M06-D3	M06-L	PW6B95-D3
	ΔH^oad	ΔG^oad	ΔG^oad,S^b	ΔH^oad	ΔH^oad	ΔH^oad	ΔH^oad	ΔH^oad	ΔH^oad	ΔH^oad	ΔH^oad
a Including all electrons and using the ZORA Hamiltonian and spin–orbit coupling scheme. b Solvent (water) free energies corrected to the standard state of 55 M water.
1	−0.45	−0.03	−0.23	−0.51	−0.47	−0.47	−0.53	−0.46	−0.48	−0.47	−0.47
2	−0.39	−0.05	−0.20	−0.45	−0.42	−0.42	−0.48	−0.41	−0.42	−0.42	−0.42
3	−0.37	−0.03	−0.16	−0.43	−0.40	−0.39	−0.45	−0.37	−0.40	−0.39	−0.39
4	−0.34	−0.00	−0.13	−0.41	−0.38	−0.38	−0.44	−0.35	−0.37	−0.37	−0.38
5	−0.32	0.02	−0.10	−0.39	−0.35	−0.36	−0.42	−0.34	−0.36	−0.35	−0.35

---

Fig. 2 Geometries for water adsorption on Cu₇.

The average adsorption enthalpy decreases with the number of added water molecules and the trend is consistent for all the applied functionals. By re-optimizing the structures with M06, essentially the same geometric parameters and energies are reproduced. Noteworthy is, moreover, that the PBE0 determined adsorption enthalpies decline steeper than the PBE binding energies observed by Chen et al.,¹⁰ possibly as a result of the shorter adsorption distance for the PBE0 optimized geometries which would result in a larger steric water–water repulsion.

Adsorption of the fifth water is still considerably exothermic (see Tables 3 and 4), although slightly endergonic in the gas phase. In fact, the standard Gibbs free energy for adsorption in the gas phase is not particularly favorable for adsorption of any number of water molecules (Tables 3 and 4). This is reasonable when considering the entropic advantage of a free water molecule in the gas phase at 298.15 K. The effect will be even more pronounced if pressures below 1 bar are considered (e.g. valid for applications under atmospheric conditions). For the condensed phase the analysis is not as straightforward since it is difficult to define a representative reference state for the bare Cu₇ cluster within the PCM approach. Nevertheless, at high coverage the error is not as large as for low coverage. Thus, the free energies can be used to analyse the sequential water adsorption in order to determine the size of the first coordination sphere. The results in Table 4 suggest that four to five water molecules are adsorbed on the Cu₇ cluster in the condensed phase (probably under dynamic equilibrium). In the gas phase the same analysis yields an adsorption of two to three water molecules (note, however, that values around 0.01 eV is well within the accuracy of the applied method).

Table 4 Enthalpies and standard Gibbs free energies [eV] for sequential adsorption of H₂O to Cu₇ using the PBE0 functional

nH2O	ΔH^oad,seq	ΔG^oad,seq	ΔG^oad,seq,S^a
a Solvent (water) free energies corrected to the standard state of 55 M water.
1	−0.45	−0.03	−0.23
2	−0.33	−0.06	−0.18
3	−0.33	−0.01	−0.08
4	−0.28	0.10	−0.04
5	−0.22	0.09	0.02

---

The various functionals yield strikingly similar adsorption enthalpies (Table 3). Inclusion of the D3 dispersion correction shifts the values ca. 0.05 eV towards stronger adsorption, consistent with previous reports.⁸⁰ In a benchmark study of the performance of different functionals, the PW6B95-D3 functional was identified as producing the most reliable results⁸¹ and it has also given very promising results for transition metal interactions.⁸² Here the energies of PBE0 and PW6B95-D3 are quite similar, differing by only 0.03 eV, which is lower than, for instance, the basis set superposition error (ca. 0.06 eV). The popular PBE functional gives results even closer to PW6B95-D3 (essentially the same values), however PBE0 has been found to out-perform PBE for energetic evaluation of H-bond strengths in small water clusters.⁸³ Furthermore, for the case of non-metallic molecules, it is well-known that hybrid Hartree–Fock/DFT typically gives a more accurate description for potential energy surfaces far from equilibrium geometries, e.g. TS structures.⁵⁴ Lately it has been found that it is necessary to include Hartree–Fock exchange in order to reproduce experimental data also for late transition metal complexes⁸⁴ and metal oxides.^85,86 An example is the H₂O₂ dissociation where non-hybrid DFT largely underestimates the activation energy compared to experiments.⁸⁷ Hence the use of the hybrid PBE0 functional in this work is motivated.

To conclude the adsorption analysis, the effect of considering relativistic effects in all electron calculations – hence also including the ten innermost core electrons – was tested. However, in the present work the relativistic effects did not affect the adsorption enthalpies to any large degree, see entry PBE-AE in Table 3.

3.2 Water dissociation and H₂ formation

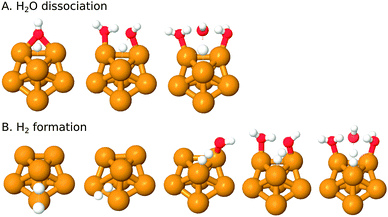
It has been argued in the context of H₂ generation on aluminium clusters that the water dissociation is much favored by a close proximity of electrophilic and nucleophilic sites (i.e. a Lewis acid–Lewis base pair)⁸⁸ – the electrophilic site governs adsorption of the water molecule and the nucleophilic site accepts the hydrogen during H-transfer/dissociation. As discussed in the adsorption Section (3.1.2) above, the ring and hollow positions of the Cu₇-cluster offer such a close pair of antagonistic reactive sites (see also Fig. 1).

The most plausible mechanisms for water dissociation and H₂ generation on Cu₇ are discussed below, concluding in a complete scheme for formation of H₂ gas on Cu₇ and an evaluation of the thermodynamic limit for consecutive production of H₂.

3.2.1 Fundamental steps. The dissociation energy for homolytic cleavage of water is 5.10 eV in the gas phase.⁸⁹ The OH bond of water can thus be greatly activated by copper (with experimentally determined dissociation barriers of 0.91–1.17 eV).^11,33 On the Cu₇ cluster a number of different mechanisms can be imagined for the water dissociation, for instance: (i) a direct, unassisted dissociation, (ii) dissociation catalyzed by H-bonding of an adjacently adsorbed water, or (iii) dissociation of a water molecule in the second coordination shell, H-bonded by two surface adsorbed water molecules (Fig. 3A). In summation:

H₂O_ad → OH_ad˙ + H_ad˙ (4)

2H₂O_ad → OH_ad˙–H₂O_ad + H_ad˙ (5)

2H₂O_ad + H₂O → OH_ad˙–H₂O(aq)–H₂O_ad + H_ad˙ (6)

If the reactions above are accompanied by an electron uptake (i.e. a reduction by adding e⁻ to the left of and changing OH_ad˙ to OH_ad⁻ on the right side of the reaction arrow) the reactions (4)–(6) above are examples of the alkaline Volmer reaction.

Fig. 3 TS structures at reduced water coverage.

To confirm the findings of Chen et al.¹⁰ that water dissociation is possible at room temperature on the Cu₇ cluster, we first investigated the above-stated mechanisms at minimal cover.

In all cases the optimal site for H acceptance during the course of reaction (and in the product) is the hollow sites. This is in contrast to the findings by Chen et al.,¹⁰ where the transition state (TS) structures were located at the bridge sites. At the PBE0 level used in the present study and at high water coverage, these (bridge) sites are instead the TS for H diffusion and thus associated with an energetic penalty (of around 0.45 eV† at full coverage), which rationalizes the reluctance to form a dissociation TS at these sites. All efforts to find a bridge site transition state for comparison converged back to the hollow position.

The activation enthalpies and free energies of the various dissociation mechanisms are reported in Table 5. It was found that the reaction becomes more favored with the number of assisting water molecules, owing to a greater H-bond stabilization in the TS. Moreover, the energetics of the condensed phase reactions are in general shifted upwards by a factor of ca. 0.1–0.2 eV compared to the gas phase, i.e. the reaction in water solution is seemingly slower than in the gas phase. However, the water dissociation reaction greatly benefits from interaction with a second water coordination sphere, which is more likely to form in the condensed phase than in the gas phase. Consequently one can argue that the water dissociation should proceed with comparable rates in gas and condensed phases due to a mechanistic switch from the gas to condensed phase – compare ΔG^o‡ of entry 2H₂O_ad for the gas phase (1.05 eV) and of entry 2H₂O_ad + H₂O for the condensed phase (0.97 eV).

Table 5 Activation energies [eV] for different mechanisms of water dissociation and H₂ formation

	ΔH^o‡	ΔG^o‡
Water dissociation
H2Oad	1.17	1.34	1.42
2H2Oad	0.78	1.05	1.26
2H2Oad + H2O	0.65	0.76	0.97
H2 formation
2Had˙ (Hollow)	1.26	1.28	1.24
2Had˙ (Bridge)	1.18	1.18	1.20
Had˙ + H2Oad	0.40	0.55	0.75
Had˙ + 2H2Oad	0.09	0.18	0.47
Had˙ + 2H2Oad + H2O	0.06	0.16	0.35

---

The kinetics changes somewhat at full coverage. The dissociation in the condensed phase is slightly quicker, where the activation energies differ by 0.06 eV. In the gas phase the energy barrier is decreased by 0.15 eV, see Table 5 and Fig. 4. If one considers only the enthalpy contribution, the reaction barrier is also lowered (by 0.20 eV to 0.58 eV) at full coverage,† a result that agrees well with the results obtained by Chen et al.¹⁰ using the PBE functional.** Although the dissociation is rather slow at room temperature, it is still feasible over longer time-scales.

Fig. 4 Reaction diagram for the generation of the first H₂ from H₂O on Cu₇. The displayed structures are optimized in the gas phase and the TS5 structure is flipped-over compared to the other structures for clearer visualization. The condensed phase energies, ΔG^o_S, are generally higher than the gas phase energies, ΔG^o.

Subsequent H₂ formation has previously proven to be relatively fast, in comparison to the water dissociation.^{1,9,11,28,30,34,35} This reaction can also proceed via a number of mechanisms. We have investigated the reactions below (see also Fig. 3B):

2H_ad˙ → H₂(g) (Hollow) (7)

2H_ad˙ → H₂(g) (Bridge) (8)

H_ad˙ + H₂O_ad → H₂(g) + OH_ad˙ (9)

H_ad˙ + 2H₂O_ad → H₂(g) + OH_ad˙–H₂O_ad (10)

H_ad˙ + 2H₂O_ad + H₂O → H₂(g) + OH_ad˙–H₂O(aq)–H₂O_ad (11)

Among the presented mechanisms the first two are the simple addition of two adsorbed H_ad to form H₂ gas, studied at different sites (bridge and hollow). The remaining reactions resemble those of the dissociation above in that sense that we studied reaction between H_ad and a H₂O_ad with different numbers of catalytic water – uncatalyzed as well as catalyzed by one or two adsorbed waters. In the case of two catalyzing water molecules, the active H-donating water is situated in the second coordination shell and the two assisting molecules are adsorbed directly on Cu₇. Attempts were made to locate a reaction path for the direct formation of H₂via 2H₂O_ad → 2OH_ad + H₂, but without success.

Using electrochemical terminology, reaction (7) and (8) above are variants of the so-called Tafel reaction. Reaction (9)–(11) are examples of the alkaline Heyrovsky reaction, given that a simultaneous reduction takes place to form OH_ad⁻.

It was found that the reaction proceeds preferably at the equatorial–axial bridge sites and can be greatly enhanced by water catalysis (Table 5). In the gas-phase the unassisted H₂ formation (H_ad + H_ad) has a larger barrier (1.18 eV) than the water-catalyzed water dissociation (1.05 eV), which would identify the H₂ formation as the rate-limiting step. However, at minimal water coverage, which is probable for situations where the uncatalyzed H₂ formation mechanism applies, the water dissociation is also likely to be uncatalyzed. The latter mechanism is associated with a large barrier (1.34 eV) which suggests that, in fact, the dissociation reaction is the rate-limiting step in the gas-phase. Moving on to the condensed phase, the unassisted addition between two H_ad has a barrier height of 1.20 eV, which is comparable to the barrier of water dissociation (1.26 eV for directly adsorbed water, although the barrier for H₂O dissociation is reduced to 0.97 eV when considering reaction from a second coordination shell). Hence, based solely on the unassisted H₂ formation mechanism, it is not clear which step is rate-limiting in the condensed phase. Nevertheless, the H_ad + H_ad mechanism is not likely to take place at the large water coverage that is expected in water solution. By allowing the H₂ formation reaction to proceed via a direct mechanism between H_ad and a H₂O_ad (direct in the respect that a second dissociation of water to produce another H is avoided), the reaction barrier is reduced to 0.55 eV and 0.75 eV in gas and condensed phase respectively. At higher coverage, one or two extra catalytic water molecules can further reduce the barrier: for one additional water the barrier is 0.18 eV (gas phase) and 0.47 eV (condensed phase), and for two waters it is 0.16 eV (gas) and 0.35 eV (condensed phase). When considering all investigated mechanisms, one can clearly identify the water dissociation as the rate-limiting step for the overall reaction in the condensed phase and likely also for the gas phase, although the gas phase rate-limiting step may vary with water coverage.

The result that formation of H₂via H_ad + H₂O_ad is more rapid than via combination of 2H_ad was also found in a previous study employing a Cu₅₀ cluster displaying a [100] surface and applying the PW91 functional.⁹ In general, among the here-in proposed mechanisms, those that are mediated by water are clearly attenuating the reaction barrier compared to bare H_ad + H_ad; it is evident that the presence of water greatly speeds up the H₂ formation reaction on the Cu₇ cluster.

The adsorbed reactants (i.e. water) prefer not to be H-bonded, neither in the H₂O dissociation nor the H₂ formation reactions (except for the cases when a solvent molecule from an outer adsorption layer is actively participating), but during the reaction the formation of H-bonds lowers the activation barrier. In the condensed phase reactions the H-bond formation in the TS structure is not as favorable as in the gas phase. This may be explained by considering stabilization of the partial charges of the reacting water molecules. These charges are stabilized by the polarizable continuum model (PCM) applied to represent the condensed phase. Similar stabilities does not exist in the gas phase. Consequently, the reaction barriers are generally lower in the gas phase, since the stabilizing H-bonding effect is larger in gas. An exception is the direct formation of H₂ (2H_ad → H₂) where no H-bonding is possible and accordingly the PCM does not affect the reaction barrier in the same way.

To summarize the findings for the various steps of the complete H₂ generation from water, the water dissociation is in general the reaction with the largest activation energy and is most likely the rate-controlling step under all reaction conditions. The reaction is greatly facilitated by surrounding water molecules, but even at situations where a large or moderate coverage is anticipated, the rate of the overall reaction is expected to be modest – although observable – at ambient temperatures. At a minimal coverage, i.e. only non-interacting water, the reaction rate is expected to be very slow, if observable at all.

3.2.2 Mechanism at high coverage. For the high coverage, consecutive generation of H₂ from Cu₇(H₂O)₅ (R1 in Fig. 4), we studied two possible reaction mechanisms: a two-step (direct) and a three-step (dissociative) mechanism. The direct and dissociative mechanisms are often referred to as the Volmer–Heyrovsky and Volmer–Tafel mechanisms respectively. The direct mechanism consists of an initial, water catalysed dissociation of H₂O_ad (TS1) followed by formation of hydrogen gas via a reaction between the H_ad and two H₂O_ad species (TS3). This path is the most favorable when considering the individual steps at low coverage (Table 5). The dissociative mechanism proceeds firstly via two water catalyzed dissociations (TS1 and TS2) before a final H_ad + H_ad addition (TS4) to form the H₂ gas. Although the last step of the dissociative mechanism is not the most favorable of its kind (i.e. H₂ formation), its barrier at minimal coverage is comparable in size to the dissociation's (in the condensed phase) and can accordingly not be over-looked (Table 5). It was also found that at full water coverage the reaction barriers for the various mechanisms are shifted compared to the case of low coverage (cf.Table 5 and Fig. 4), thus further validating the inclusion of the dissociative mechanism in the evaluation. The mechanisms including reaction from a second coordination shell were not considered at high coverage.

Dissociation of the first water on the Cu₇ cluster is a slow but strongly exergonic process. The reaction barrier is larger in the condensed phase than in the gas phase. Additionally, the barriers at high coverage are reduced compared to the case of low coverage: by about 0.12 eV and 0.06 eV for gas and condensed phase respectively (cf. 2H₂O_ad in Table 5 and TS1 in Fig. 4). This is consistent with the results of Chen et al.,¹⁰ ** The corresponding enthalpy change is in the order of 0.2 eV in the gas phase.† The reaction is still slow, but at 298 K it should occur at a (for many applications) relevant time-scale. Note, however, that the reaction kinetics is likely to be faster for a dissociation mechanism that proceeds through H-transfer from a second coordination shell. At low water coverage this mechanism was associated with a 0.29 eV lower barrier (see Table 5).

Further dissociation from the first intermediate (I1)†† has a substantially reduced barrier compared to the first – in the gas phase the activation energy is lowered by 0.28 eV, and by 0.15 eV in the condensed phase. The second dissociation is very exergonic and the resulting intermediate (I2) is in fact the most stable species for the whole first H₂ generation reaction series (Fig. 4). Forming H₂ from this intermediate demands passing over a 1.31–1.43 eV reaction barrier and is therefore not a very likely path – thus ruling out the dissociative reaction mechanism for H₂ generation at moderate (e.g. room) temperatures.

Although kinetically disfavored (see discussion below), the I2 structure is likely to form to some extent at longer time-scales. Thus the cluster would be trapped in an energetic minimum, which could eventually inhibit the activity of the cluster surface. However, the formation of H₂ gas via a direct mechanism between one of the H_ad and H₂O_ad from I2 has a relatively low barrier of 0.85 eV in the gas phase (from the step I4 to TS6 in Fig. 5), and offers a reasonable route out of the local minimum (see Fig. 6 for the global minimum). The barrier is reduced by the adsorption of another water molecule to stabilize the TS by H-bonding (structure I4) and the final product (P2) after addition of a second additional water is lower than I2 in both gas and condensed phases. In the condensed phase the activation energy from I4 to TS6 is 1.33 eV, i.e. even larger than the activation energy for the first dissociation. Consequently, deactivation by formation of the I2 and I4 compounds is possible in water solution.

Fig. 5 Reaction path out of the I2 structure. In the various stages, the non-reacting H atom has diffused to its favored hollow site. The condensed phase energies, ΔG^o_S, are generally higher than the gas phase energies, ΔG^o.

Fig. 6 Sequential oxidation of Cu₇: H₂ generation of up to 5H₂ molecules (or 10 adsorbed OH) on Cu₇. The displayed structures correspond to local minima in the gas phase. In each step 0.5H₂ is generated. Condensed phase free energies have been corrected to 55 M of water. The condensed phase energies, ΔG^o_S, are generally higher than the gas phase energies, ΔG^o. See the ESI† for the corresponding graph compensated to atmospheric H₂ pressure.

A more accessible way of generating H₂ is via the direct mechanism. From I1 the adsorbed H can interact with a water hydrogen and form H₂ at a bridge site. This process has a relatively small barrier of 0.34/0.74 eV (gas/condensed phase), which is distinctly lower than dissociation of a second H₂O_ad. Direct formation of H₂ from I1 is exergonic in the gas phase, but endergonic in the condensed phase. The formed H₂ attaches vertically at the axial copper (favored adsorption geometry for H₂†) and leaves essentially without energy barrier (0.02 eV) to form the products, P1 + H₂(g). Clearly, however, the reaction proceeds further (see Fig. 4 and 6, and the discussion below), and a global minimum can only be identified by searching beyond the first H₂ generation product (P1).

The energy shift between the condensed phase and the gas phase beyond I1 can be explained in terms of the formed H-bonds (an equivalent argument was proposed for the reactions at low coverage). Compared to the condensed phase, the H-bonds between the adsorbed species in the gas-phase are ca. 1% shorter, an indication of the increased bond strength. At the R1 stage the water molecules prefer not to H-bond thereby staying at the optimal equatorial copper positions. Upon dissociation the situation changes and formation of H-bonds between the OH and H₂O is greatly favored. Nevertheless the effect of OH bonding is not as pronounced in the condensed phase calculations since the dielectric continuum helps to stabilize the partial charges of the reactants. The effect is present already at I1 but becomes larger at later stages.

Since the dissociation of H₂O_ad is the rate-controlling step, and therefore determines whether or not the reaction will proceed, a first dissociation TS (TS5) for the subsequent (second) H₂ generation from R2 was located in order to evaluate if further reaction is plausible. We find that neither the gas nor the condensed-phase activation energies for dissociation are shifted much going from R1 to R2 (now 1.02 eV and 1.13 eV, respectively, see Fig. 4) and hence water splitting, and presumably also the consecutive H₂ formation, is likely to proceed beyond R2.

The process of forming a H₂ molecule on Cu₇ from water drains the metal cluster of electrons, i.e. oxidizes it. An NBO analysis (Table 6) reveals that the copper atoms of the product cluster (P1) have acquired a significant positive charge during the reaction. Hence, at the first product stage (P1), the discovery that adsorption of additional nucleophilic (electron donating) water at the previously unoccupied axial copper atoms is strongly exergonic is reasonable (P1 → R2 in Fig. 4), since the electron donation stabilizes the charged copper atoms. The two axially coordinated water molecules in R2 are bound with an average 0.36 eV per molecule. This can be compared to axial coordination of water in R1, which was found to be repulsive (see 3.1.2 Adsorption). The addition of two extra water molecules on the cluster drives the reaction and the R2 species is almost as stable as the I2. This can also be interpreted in terms of wetting properties; the formation of hydroxyl groups on the surface facilitates adsorption of water and hence makes the cluster more hydrophilic, in agreement with experimental results on the Cu[110] and Cu[111] surface.²⁵

Table 6 Charge (NBO) evolution for the Cu₇-cluster and the first and second dissociating hydrogens (H1 and H2) and hydroxyl groups (OH1 and OH2) over the course of the gas-phase H₂ generation reaction^a

	q (Cu7)	q (H1)	q (H2)	q (OH1)	q (OH2)
a For reference, H of water has a NBO charge of ca. 0.46e and O a charge of ca. −0.92e. b Not yet dissociated. c H neutrally charged.
R1	−0.29	0.49^b	0.49^b	−0.43^b	−0.43^b
TS1	0.33	0.12	0.49^b	−0.66	−0.45^b
I1	0.77	−0.29	0.50^b	−0.67	−0.43^b
TS2	1.32	−0.29	0.13	−0.67	−0.61
TS3	1.15	−0.23	0.31	−0.68	−0.64
I2	1.75	−0.26	−0.26	−0.66	−0.66
TS4	1.45	−0.09	−0.07	−0.66	−0.67
I3	1.22	−0.06	0.06	−0.68	−0.68
P	1.29	−0.00^c	0.00^c	−0.68	−0.67

---

Analyzing the NBO charges more in detail gives a better understanding of the reaction.‡‡ The evolution of partial charges on the active species during the reaction (Table 6) indicates that the proton-like character of the H-atom of H₂O_ad changes to a hydride-like state after dissociation. Obviously, a second dissociation results in another adsorbed “hydride”. Hence, the H atoms go from positively to negatively charged. Furthermore, during the reaction the atoms of the adsorbed (and H-bonded) OH acquire an additional 0.22e negative charge. The build up of negative charge on the atoms of the dissociated water is balanced by a build-up of positive charge on the copper atoms of Cu₇. The Cu-atoms gain a charge of approximately 1.06e during the first dissociation step. At the end of the total reaction the copper atoms have in summary gained ca. 1.58e positive charge, which is accompanied by a reduction of two water molecules to 2OH_ad⁻ and H₂(g). In total, the reduced species are associated with a change in charge of −1.46e (the remaining charge difference is spread over the adsorbed water molecules). This analysis demonstrates the oxidation process of Cu₇ over the course of the complete H₂ generation reaction. Compare, however, only the relative proportions of the charges not their exact magnitudes.

Noteworthy is that the partially negatively charged H_ad, adsorbed on the cluster, prefers to react to form H₂ with a partially positively charged H-atom of H₂O_ad over reaction with another adsorbed H_ad.

3.2.3 Thermodynamic limit of surface oxidation. Thermodynamically, bulk copper in pure oxygen-free water is stable with respect to any of the known oxide, hydroxide or hydride phases (i.e. ΔG^o for oxidation of copper by water to any of these phases is positive with a large absolute value). This means that copper should not corrode in water. Nevertheless, locally the situation may be different; surfaces, which have a dissimilar physico-chemical environment than the bulk, may e.g. exhibit a thermodynamic shift compared to bulk copper which could facilitate formation of some of the known meta-stable phases of Cu, O and H^92–96 (to a limited degree). Surface defects such as grain boundaries or localized nanoparticles attached to the surface may, in addition, shift the thermodynamics further.⁹⁶ Accounting for these types of local effects, and the fact that rough, unpolished metal surfaces have a larger effective (microscopic) surface area than ideal surfaces (for a given apparent macroscopic area) may help to explain the observations of H₂ gas partial pressures substantially larger than what corresponds to the equilibrium pressures of any known phase of oxidized copper.^2–8 Regardless, the thermodynamic stability of small Cu clusters in water and on surfaces as, e.g., different metal oxides (for instance Fe₃O₄ and Zn₂O are typical supports for Cu-catalysts in the WGSR) is poorly understood, and the knowledge of the redox behavior of these species may turn out to be of vast importance with implications for areas such as corrosion, catalysis and electrochemistry in general. A few theoretical studies have, nevertheless, been conducted. Apart from the aforementioned studies,^{9,10,14,29,48} a notable example is a quantum chemical investigation of the anchoring process for the Cu₇ cluster, among others, on a ZnO surface.⁹⁷ However, the study did not consider interaction with water.

Fig. 6 shows the free energy landscape for the sequential water oxidation of Cu₇. The oxidation is favorable compared to intact water on copper up to the formation of eight adsorbed OH in both gas and condensed phases. Within the investigated span of surface oxidation, a global free energy minimum is found at the oxidation stage of three or five formed OH-groups. These two structures are more or less energetically degenerate, with five OH being slightly favored in the condensed phase and three OH slightly favored in gas. Consequently the oxidation of Cu₇ should stop at either of these stages when considering standard states. However, if an atmospheric partial pressure of H₂ gas is applied (i.e. using a pressure of 5.31 × 10⁻⁷ bar⁹⁸ instead of the standard state of 1 bar), the equilibrium is driven to the right of Fig. 6. Using an equivalent to eqn (1) we can calculate the free energy correction to the atmospheric H₂ pressure; since 0.5H₂ is produced in each step in Fig. 6, each step will be 0.185 eV more exergonic compared to the previous (ΔΔG = −0.5RT ln (p_1bar/p_atm)). This results in the 8OH structure as the most favored state for both gas and condensed phases.†

As discussed previously (3.2.2 Mechanism at high coverage), the shift between the gas and the condensed phase may be explained by a more pronounced stabilization by H-bonding in the gas-phase.

Moreover, the oxidation is seemingly exergonic as long as strong H-bonds can be formed. As the oxidation proceeds, the number of available, H-donating water molecules is reduced (water is consumed). With this in mind, it is possible that a continued process could be found beneficial if a larger number of explicit solvent water molecules from a second coordination shell were to be considered. Additionally, further oxidation may be feasible if the structure of the cluster is disrupted. However, this is beyond the scope of this investigation.

As seen in Fig. 6, the Cu₇ cluster starts to deform at higher oxidation. This can be seen already at the formation of three OH, but is clearer further into the oxidation process. The Cu₇ cluster expands and flattens (shorter axial–axial distance) up until nine OH and at ten OH it loses its bipyramidal shape and adopts a cage-like structure – possibly starting to dissolve, or reconstruct on its way to form a more favored oxide structure.

A clear odd–even oscillating behavior of the free energy for the oxidation was found beyond two OH, with even numbers being less favored (Fig. 6). Such periodicity has been observed for other properties with varying copper cluster size, for instance ionization energies or electron affinities.^41,99 The behavior can most conveniently be explained by electron pairing – where formation of paired electrons (odd number of OH, since Cu₇ has an odd number of electrons) results in an increased stability. The deviation from the periodic behavior between seven and eight OH can be explained by the exergonic adsorption of another water.

The oxidation process can be illustrated by the total NBO charges of the Cu₇ copper atoms, which are steadily increasing going from zero to ten OH (Fig. 7). Again, it is mainly the trend for the NBO charges over the oxidation process that is of interest, not so much the absolute magnitudes of the charges. A closer look at the charge and spin/electron distributions reveals that a rearrangement process accompanies the charge evolution.† Up until the formation of five OH, the characteristic spin polarization of Cu₇ as well as the surplus of electrons at the axial atoms are retained, although all copper atoms are continuously drained of electrons from zero to five OH. The same applies to the NBO charge, with the axial copper atoms consequently being less positively charged compared to equatorial atoms. The results can be interpreted in terms of a Cu(I) oxidation state for the equatorial copper and Cu(0) for the axial. This indicates that the more under-coordinated equatorial copper atoms (4 close neighbours for equatorial copper compared to 5 for axial copper) are more easily oxidized, which agree with the picture that dense copper surfaces are less active than sparse (and thus more under-coordinated) surfaces for dissociation of water.^21–26

Fig. 7 NBO charge on Cu₇ during oxidation up to the formation of 10OH and 5H₂. The asterisk (*) indicates two added water molecules. Consider the trend, not the exact magnitudes of the NBO charges.

Beyond five OH, the axial atoms begin to adjust and the partial charges and electrons are more evenly distributed. At the point of nine OH the transformation is essentially completed (i.e. all Cu atoms are more or less equivalent). Moving towards the highest considered oxidation state (10OH), structural changes are induced. These are associated with a new pattern for the charge and electron population distributions, where the copper atoms can be divided between two kinds of sites: (i) four sites where copper is coordinated to three other copper atoms, and (ii) three sites with a Cu-coordination of four. In other words, a new kind of copper complex. The 9OH cluster can perhaps be identified as a transition structure from the bipyramidal structure to a cage-like structure – a structure that may prove more beneficial for continued oxidations. However, the possibility of accessing more stable structures (with respect to Cu₇(H₂O)₂(OH)₅) for oxidation post 10OH is limited by the large barrier associated with passing over the 9OH for the here-in identified pathway.

4 Conclusions

The water splitting/hydrogen formation reaction at the surface of the bipyramidal (D_5h) Cu₇ cluster has been investigated using hybrid density functional theory. Water adsorbs exergonically to the equatorial copper atoms of the Cu₇ cluster, while coordination to the axial copper atoms is clearly weaker. Beyond full adsorption to the favored equatorial sites, it was found that the axial copper atoms repel water – which means that the inner coordination shell consists of five water molecules. This motivated the choice of the Cu₇(H₂O) as a model for a saturated surface state of the Cu₇ cluster in water.

In the condensed phase the dissociation of water on the Cu₇(H₂O) cluster is found to have a rather high activation energy (1.20 eV). However, from calculations at low water coverage it was found that including H-bonded water molecules in a second coordination shell reduces the activation energy significantly (by ca. 0.3 eV).

The most rapid mechanism for formation of H₂ in the condensed phase is not via a direct combination of two adsorbed H-atoms at the cluster surface (1.31 eV), but through the reaction of an adsorbed H-atom with water (0.77 eV), yielding H₂ and an adsorbed hydroxyl group.

Formation of up to four H₂ molecules is exergonic with respect to the initial Cu₇(H₂O) cluster, albeit under standard conditions the most stable state of surface oxidation was found to be the Cu₇(H₂O)₂(OH)₅ cluster, which is accomplished by the formation of 2.5H₂ molecules. Under atmospheric conditions, it is, however, possible to regard the formation of four H₂ as the thermodynamic limit of the corrosive water splitting/hydrogen formation reaction on the Cu₇ surface. Nevertheless it cannot be excluded that the reaction can proceed through extensive reconstruction of the cluster geometry.

The present investigation indicates that the oxidation/degradation of the copper clusters in pure, oxygen-free water is slow and stops at a relatively early stage. This is particularly interesting for applications of copper nanoparticles which, with their unique properties, anchored to oxide surfaces play an important role in many catalytic processes. The question whether or not these conclusions can be applied to an extended metallic surface cannot be univocally answered at this point and should be addressed by larger clusters or periodic models. Moreover, in order to accurately reproduce the solvent effects, inclusion of an extended number of explicit water molecules in the model may be necessary.^100,101 This is currently considered in an ongoing study by the authors. To capture the dynamics of copper–water systems one may alternatively make use of parametrized force fields (e.g. the reaxFF¹⁰² formulation) in molecular dynamics simulations.

Acknowledgements

The authors wish to thank the Swedish Nuclear Fuel and Waste Management Co (SKB) for financial support. JHS would like to acknowledge Björn Dahlgren for fruitful discussions. Christina Lilja is warmly acknowledged for much useful input.

References

1. A. J. Johansson and T. Brinck, Mechanisms and energetics of surface reactions at the copper-water interface, TR-12-07, Swedish Nuclear Fuel Management Co., Stockholm, Sweden, 2012.
2. G. Hultquist, Corros. Sci., 1986, 26, 173–177.
3. Q. Lu, G. Hultquist, K. L. Tan and T. Åkermark, Surf. Interface Anal., 1993, 20, 645–650.
4. G. Hultquist, L. Gråsjö, Q. Lu and T. Åkermark, Corros. Sci., 1994, 36, 1459–1471.
5. P. Szakálos, G. Hultquist and G. Wikmark, Electrochem. Solid-State Lett., 2007, 10, C63–C67.
6. G. Hultquist, P. Szakálos, M. J. Graham, A. B. Belonoshko, G. I. Sproule, L. Gråsjö, P. Dorogokupets, B. Danilov, T. Aastrup, G. Wikmark, G.-K. Chuah, J.-C. Eriksson and A. Rosengren, Catal. Lett., 2009, 132, 311–316.
7. G. Hultquist, M. Graham, P. Szakalos, G. Sproule, A. Rosengren and L. Gråsjö, Corros. Sci., 2011, 53, 310–319.
8. J. Simpson and R. Schenk, Corros. Sci., 1987, 27, 1365–1370.
9. A. J. Johansson, C. Lilja and T. Brinck, J. Chem. Phys., 2011, 135, 084709.
10. L. Chen, Q. Zhang, Y. Zhang, W. Z. Li, B. Han, C. Zhou, J. Wu, R. C. Forrey, D. Garg and H. Cheng, Phys. Chem. Chem. Phys., 2010, 12, 9845.
11. J. Nakamura, J. M. Campbell and C. T. Campbell, J. Chem. Soc., Faraday Trans., 1990, 86, 2725–2734.
12. J. Ren and S. Meng, J. Am. Chem. Soc., 2006, 128, 9282–9283.
13. J. Ren and S. Meng, Phys. Rev. B, 2008, 77, 054110.
14. P. Liu and J. A. Rodriguez, J. Chem. Phys., 2007, 126, 164705.
15. G.-C. Wang and J. Nakamura, J. Phys. Chem. Lett., 2010, 1, 3053–3057.
16. C. Callaghan, I. Fishtik, R. Datta, M. Carpenter, M. Chmielewski and A. Lugo, Surf. Sci., 2003, 541, 21–30.
17. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385.
18. M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308.
19. A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381–451.
20. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
21. K. Andersson, A. Gómez, C. Glover, D. Nordlund, H. Öström, T. Schiros, O. Takahashi, H. Ogasawara, L. Pettersson and A. Nilsson, Surf. Sci., 2005, 585, L183–L189.
22. K. Andersson, G. Ketteler, H. Bluhm, S. Yamamoto, H. Ogasawara, L. G. M. Pettersson, M. Salmeron and A. Nilsson, J. Am. Chem. Soc., 2008, 130, 2793–2797.
23. A. Spitzer and H. Lüth, Surf. Sci., 1982, 120, 376–388.
24. C. Ammon, A. Bayer, H.-P. Steinrück and G. Held, Chem. Phys. Lett., 2003, 377, 163–169.
25. S. Yamamoto, K. Andersson, H. Bluhm, G. Ketteler, D. E. Starr, T. Schiros, H. Ogasawara, L. G. M. Pettersson, M. Salmeron and A. Nilsson, J. Phys. Chem. C, 2007, 111, 7848–7850.
26. A. Spitzer, A. Ritz and H. Lüth, Surf. Sci., 1985, 152–153(Part 1), 543–549.
27. J. L. C. Fajín, F. Illas and J. R. B. Gomes, J. Chem. Phys., 2009, 130, 224702.
28. A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402–1414.
29. C. D. Taylor, M. Neurock and J. R. Scully, J. Electrochem. Soc., 2008, 155, C407–C414.
30. Q.-L. Tang, Z.-X. Chen and X. He, Surf. Sci., 2009, 603, 2138–2144.
31. Q.-L. Tang and Z.-X. Chen, J. Chem. Phys., 2007, 127, 104707.
32. G. Wang, L. Jiang, Z. Cai, Y. Pan, X. Zhao, W. Huang, K. Xie, Y. Li, Y. Sun and B. Zhong, J. Phys. Chem. B, 2003, 107, 557–562.
33. C. T. Campbell and K. Daube, J. Catal., 1987, 104, 109–119.
34. G. H. Guvelioglu, P. Ma, X. He, R. C. Forrey and H. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155436.
35. R. C. Forrey, G. H. Guvelioglu, P. Ma, X. He and H. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155437.
36. Q.-L. Tang and Z.-X. Chen, Surf. Sci., 2007, 601, 954–964.
37. J. Howard and B. Mile, in Electron Spin Resonance (Specialists Periodic Reports vol. 11B, London, 1988).
38. J. Howard, R. Sutcliffe, J. Tse and B. Mile, Chem. Phys. Lett., 1983, 94, 561–564.
39. R. J. Van Zee and W. Weltner, J. Chem. Phys., 1990, 92, 6976–6977.
40. A. Muñoz-Castro, D. Mac-Leod Carey and R. Arratia-Pérez, ChemPhysChem, 2010, 11, 646–650.
41. G. H. Guvelioglu, P. Ma, X. He, R. C. Forrey and H. Cheng, Phys. Rev. Lett., 2005, 94, 026103.
42. X.-J. Kuang, X.-Q. Wang and G.-B. Liu, J. Chem. Sci., 2011, 123, 743–754.
43. Y. Wang, G. Wu, M. Yang and J. Wang, J. Phys. Chem. C, 2013, 117, 8767–8773.
44. L. Padilla-Campos, THEOCHEM, 2007, 815, 63–69.
45. X. Yuan, L. Liu, X. Wang, M. Yang, K. A. Jackson and J. Jellinek, J. Phys. Chem. A, 2011, 115, 8705–8712.
46. A. Poater, M. Duran, P. Jaque, A. Toro-Labbé and M. Solà, J. Phys. Chem. B, 2006, 110, 6526–6536.
47. S. Gautam, K. Dharamvir and N. Goel, Comput. Theor. Chem., 2013, 1009, 8–16.
48. A. Belonoshko and A. Rosengren, Philos. Mag., 2012, 92, 4618–4627.
49. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
50. Jaguar, version 7.9, Schrödinger, LLC, New York, NY, 2012.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.1, Gaussian Inc., Wallingford CT, 2009.
52. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
54. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
55. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
56. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
57. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
58. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130.
59. ADF2012, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam.
60. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
61. B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788.
62. D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard, J. Am. Chem. Soc., 1994, 116, 11875–11882.
63. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
64. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.
65. J. M. Martínez, R. R. Pappalardo, E. Sánchez Marcos, B. Mennucci and J. Tomasi, J. Phys. Chem. B, 2002, 106, 1118–1123.
66. D. Asthagiri, L. R. Pratt, M. E. Paulaitis and S. B. Rempe, J. Am. Chem. Soc., 2004, 126, 1285–1289.
67. I. Tunon, D. Rinaldi, M. F. Ruiz-Lopez and J. L. Rivail, J. Phys. Chem., 1995, 99, 3798–3805.
68. F. P. Rotzinger, Helv. Chim. Acta, 2000, 83, 3006–3020.
69. J. Li, C. L. Fisher, J. L. Chen, D. Bashford and L. Noodleman, Inorg. Chem., 1996, 35, 4694–4702.
70. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
71. E. van Lenthe, A. van der Avoird and P. E. S. Wormer, J. Chem. Phys., 1998, 108, 4783–4796.
72. E. D. Glendening, A. Reed, J. Carpenter, J. Bohmann and F. Weinhold, NBO version 3.1.
73. R. Arratia-Perez, L. Alvarez-Thon and P. Fuentealba, Chem. Phys. Lett., 2004, 397, 408–411.
74. M. S. Bahramy and Y. Kawazoe, Mater. Trans., JIM, 2007, 48, 1883–1885.
75. M. S. Bahramy, M. H. F. Sluiter and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045111.
76. F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691.
77. T. Schiros, K. Andersson, L. Pettersson, A. Nilsson and H. Ogasawara, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 85–98.
78. T. Schiros, H. Ogasawara, L.-Å. Näslund, K. J. Andersson, J. Ren, S. Meng, G. S. Karlberg, M. Odelius, A. Nilsson and L. G. M. Pettersson, J. Phys. Chem. C, 2010, 114, 10240–10248.
79. T. Schiros, O. Takahashi, K. J. Andersson, H. Öström, L. G. M. Pettersson, A. Nilsson and H. Ogasawara, J. Chem. Phys., 2010, 132, 094701.
80. J. Carrasco, J. Klimeš and A. Michaelides, J. Chem. Phys., 2013, 138, 024708.
81. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670.
82. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
83. B. Santra, A. Michaelides and M. Scheffler, J. Chem. Phys., 2007, 127, 184104.
84. M. M. Quintal, A. Karton, M. A. Iron, A. D. Boese and J. M. L. Martin, J. Phys. Chem. A, 2006, 110, 709–716.
85. S. C. Ammal and A. Heyden, J. Chem. Phys., 2010, 133, 164703.
86. C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803.
87. C. M. Lousada, A. J. Johansson, T. Brinck and M. Jonsson, Phys. Chem. Chem. Phys., 2013, 15, 5539.
88. P. J. Roach, W. H. Woodward, A. W. Castleman, A. C. Reber and S. N. Khanna, Science, 2009, 323, 492–495.
89. O. V. Boyarkin, M. A. Koshelev, O. Aseev, P. Maksyutenko, T. R. Rizzo, N. F. Zobov, L. Lodi, J. Tennyson and O. L. Polyansky, Chem. Phys. Lett., 2013, 568–569, 14–20.
90. F. Maseras and K. Morokuma, Chem. Phys. Lett., 1992, 195, 500–504.
91. F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379.
92. P. A. Korzhavyi, I. Soroka, M. Boman and B. Johansson, Solid State Phenom., 2011, 172–174, 973–978.
93. P. A. Korzhavyi, I. L. Soroka, E. I. Isaev, C. Lilja and B. Johansson, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 686–689.
94. I. L. Soroka, A. Shchukarev, M. Jonsson, N. V. Tarakina and P. A. Korzhavyi, Dalton Trans., 2013, 42, 9585.
95. E. Protopopoff and P. Marcus, Electrochim. Acta, 2005, 51, 408–417.
96. A. B. Belonoshko and A. Rosengren, Langmuir, 2010, 26, 16267–16270.
97. S. A. French, A. A. Sokol, C. R. A. Catlow and P. Sherwood, J. Phys. Chem. C, 2008, 112, 7420–7430.
98. P. C. Novelli, P. M. Lang, K. A. Masarie, D. F. Hurst, R. Myers and J. W. Elkins, J. Geophys. Res.: Atmos., 1999, 104, 30427–30444.
99. H. Åkeby, I. Panas, L. G. M. Pettersson, P. Siegbahn and U. Wahlgren, J. Phys. Chem., 1990, 94, 5471–5477.
100. V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719.
101. V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. Goddard III, J. Phys. Chem. A, 2008, 112, 9104–9112.
102. A. C. T. van Duin, V. S. Bryantsev, M. S. Diallo, W. A. Goddard, O. Rahaman, D. J. Doren, D. Raymand and K. Hermansson, J. Phys. Chem. A, 2010, 114, 9507–9514.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional figures and enthalpy diagrams for the adsorption and the water oxidation reactions. Also provided is an analysis of the preferred adsorption sites for the H⁺, H˙, H₂, OH˙, and H₂O species on Cu₇ as well as natural population analysis data. See DOI: 10.1039/c3cp53865f

‡ Partly since cluster model calculations are computationally affordable in general, but also, and importantly, since the available programs for cluster calculations offer the possibility of using polarizable continuum models to represent the dielectric properties of the surrounding solvent.

§ Howard et al. first assigned their ESR spectra to a bipyramidal Cu₅ but later reinterpreted it as belonging to Cu₇.³⁷

¶ The basis set superposition errors were estimated by the counterpoise procedure of Boys et al.⁷⁰ to be ca. 0.06 eV for H₂O and ca. 0.01 eV for H₂ upon adsorption to Cu₇, but are not included in the reported energies.

|| van Zee et al. determined the s-electron spin-density of the axial and equatorial coppers of Cu₇ to be 0.291 and ±0.009, respectively, from EPR spectra. NBO⁷² (and Mulliken) analysis at the DFT PBE0/LACV3P**++ level yields a total atom average spin-density of 0.49(0.26) and 0.004(0.098) at the axial and equatorial copper atoms.

** Note that in Chen et al.'s work¹⁰ the energies are reported as zero-point corrected energies, whereas in this study the results are given as either enthalpies or free energies. For the most valid comparison between the studies, cf. the ΔH^o‡ entries of Table 3 and the enthalpy diagrams in the ESI.†

†† Note that H has moved the site from TS1 to I1. An adsorbed H can diffuse between hollow sites with a free energy barrier of ca. 0.45 eV.†

‡‡ Care should, however, be taken with this kind of analysis. An atom's charge in a molecule is neither a physical observable nor uniquely defined. The NBO charges should not be seen as exact absolute values and are here only used in relation to other charges for qualitative evaluations. NBO charges are, nevertheless, considered more reliable and robust than, for instance, Mulliken charges. Note, furthermore, the debate on whether or not to include higher valance p-orbitals in the NBO assessment of transition metals and NBO's pros and cons.^90,91

---