Incoherent dynamic light scattering by dilute dispersions of spherical particles: wavelength-dependent dynamics

Abstract

Dynamic light scattering (DLS) was performed on dilute suspensions of colloidal particles, where the scattering intensity was minimised by ellipsometric optics as in ellipsometric light scattering. Measurements at minimum intensity settings are dominated by the incoherent scattering properties, i.e. the deviations from the average scattering properties. The observed relaxation dynamics does not vary with the scattering angle, but depends on the wavelength λ of the employed light. Therefore, the process has a λ-dependence beyond the dependence included in the scattering vector. Such incoherent ellipsometric DLS could be applied to determine the residence time of particles in volumes with an extension comparable to λ, and to obtain detailed information on the dynamics of complex systems which is usually hidden by the dominating diffusive process.

---

The investigation of sample dynamics forms an intrinsic part of soft matter science. Different techniques exist to probe dynamical properties spanning decades of length- and time scales, such as rheological measurements,¹ dielectric relaxation experiments,² neutron spin echo,³ fluorescence correlation spectroscopy (FCS),⁴ dynamic light scattering (DLS),⁵ and nuclear magnetic resonance.⁶

DLS developed into a routine characterisation method for polymers and colloids. The dominating scattering contribution in polarised (VV) experiments is the coherent scattering contribution. Coherent scattering is analysed in virtually all cases in routine analytics, where the characteristic relaxation time τ of a measured intensity correlation function of the scattered light is related to the diffusion coefficient D, which is, via the Stokes–Einstein relationship, transformed into a hydrodynamic radius R_h of the material under study. In coherent scattering, the nature of an observed relaxational mode is shown in the dependence of τ on the magnitude of the scattering vector . The scattering angle is denoted as Θ, the wavelength in vacuum by λ, while n is the refractive index at λ of the solvent. The q-dependence of τ is usually described as a power law of the form τ ∝ q^−N, with the characteristic exponent N. The most prominent behaviour is N = 2, characteristic of diffusion,⁵ which is found in the overall majority of DLS studies. Other values of N > 0 characterize different processes with characteristic length scales, such as reptation, membrane fluctuations, or internal modes.^7,8 In contrast, in a process in which τ ∝ q⁰ the relaxation time is independent of the length scale. While this dominance of the diffusive process is useful for particle sizing, it often disguises more interesting features in the dynamics of complex systems. One possible experiment to extract further information is depolarised (VH) DLS, which probes rotational diffusion. Currently, DLS can only under special circumstances probe internal modes. Suppressing the dominant coherent scattering contribution might open a route to access shape fluctuations of soft colloidal systems.

Even though coherent scattering dominates the total scattered intensity in most DLS experiments, incoherent scattering is inevitably present, which has been demonstrated experimentally.^5,9 An experiment measuring purely incoherent cross-correlation functions has been applied to study sedimentation and flow in complex fluids.¹⁰

Ellipsometric light scattering (ELS) was introduced by applying the principles of ellipsometry to scattered light, to analyse the interface between colloidal particles and the surrounding solution,^11–14 or to analyse non-concentric core–shell particles.¹⁵ Similar measurements of Mueller matrix elements have been used to characterise the internal structure of algae.¹⁶ Using ELS, the coherent scattering contribution can be selectively analysed.^17,18 In this work, ellipsometric dynamic light scattering (EDLS) is introduced.

The setup used here has been described in detail elsewhere.¹⁸ Briefly, an ALV-3000 light scattering goniometer (ALV, Langen, Germany), equipped with two laser sources at λ = 633 nm and 532 nm, was modified with a polariser and a compensator before the sample, and with a compensator and an analyser after the sample. Scattered light was collected using a single mode optical fibre and fed into an actively quenched avalanche photodiode detector (APD). The curves of static ELS reported so far have been obtained by minimizing the intensity at the detector at a certain scattering angle.^{11–13,15,17,18} Ideally, e.g. with perfectly parallel incident light and detection, monodisperse particles, and infinitely sharp laser lines, scattered light is purely coherent; hence it can be completely extinguished by ellipsometric polarisation optics. Experiments do have deviations from idealized conditions, with a distribution of the setup and sample parameters. Due to this distribution, an incoherent intensity remains at the ellipsometric intensity minimum. In EDLS experiments, the autocorrelation function of this residual intensity was investigated.

The results of EDLS are compared to correlation functions measured in VV and VH geometry. In VV scattering, the polarisation of incident light is set perpendicular (vertical) to the scattering plane, and only scattered light with the same polarisation is analysed. Experimentally, this is achieved by setting the compensator parallel to the polariser and the analyser. For VH geometry, the incident polarisation is the same as for VV, but on the analyser side, the polarisation is parallel (horizontal) to the scattering plane. For additional measurements in VH geometry at a third wavelength of 488 nm, a home-built goniometer with illumination via an Ar⁺ laser was used. All measurements have been performed at T = 25 °C, unless noted otherwise. The regularization program CONTIN was used to determine the relaxation time distribution h(log(t)) based on electric field correlation function g₁(t), employing a regularisation parameter α ≈ 1.5 × 10⁻⁴.^19,20 The τ of different modes are extracted as the centres of peaks of this distribution on a logarithmic time scale.

Fig. 1 shows three field correlation functions g₁(t) obtained at Θ = 30° of a dispersion of poly(methyl methacrylate)-b-poly(N-isopropyl acrylamide)-b-poly(ethylene glycol) (PMMA–PNIPAM–PEG) particles in water together with the inverted correlation functions h(t). Particle synthesis and temperature-dependent behaviour of the particle's shell have been described elsewhere.^11,21 The VV correlation function shows a single process, which is diffusive (τ ∝ q⁻²). EDLS shows the relaxation observed in the VV scattering only as a minor component. Hence, the main diffusive mode in the coherent scattering contribution is suppressed in EDLS. The main component in EDLS is a process that is one order of magnitude faster than the diffusive process observed in VV scattering. The VH correlation function shows both modes. The major component is equivalent to the mode visible in VV scattering, and the minor component is identical to the mode visible in EDLS. For the spherical particles under investigation, the presence of the VV scattering mode in the VH signal probably originates from imperfections in the polarisation optics. The intensity extinction ratio I_VH/I_VV is typically between 1 × 10⁻⁴ and 5 × 10⁻⁴, i.e. ≈10 times as high as the extinction ratio of the polarisation optics without a sample.

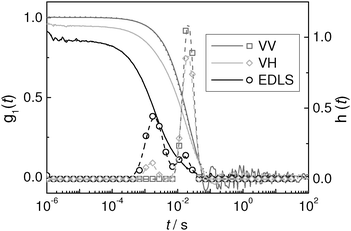Fig. 1 Example of correlation functions g₁(t) ([thick line, graph caption]), fits to g₁(t) (⋯) from PMMA–PNIPAM–PEG particles (w_b = 8.6 × 10⁻⁵, R_h = (176 ± 2) nm, 15 °C) and inverted correlation functions h(t) (□, ○, ◊) at Θ = 30°, in the indicated polarisation geometry; h(t) have been fit with overlapping Gaussian peaks ([dash dash, graph caption]).

The observation of a fast relaxational mode in EDLS is made in a number of samples, including different poly(styrene) [PS] latices, which have been used for a detailed analysis of the characteristics of the relaxational mode. A well-characterised set of dispersions has been used here,^13,18 diluted to a mass fraction w_b, whereas in VV scattering only single scattering is observed. The q-dependence obtained from measurements with a PS latex is shown in Fig. 2. As expected, the process in the VV scattering shows τ ∝ q⁻². Data obtained from several λ fall on the same line in the double logarithmic plot in Fig. 2. The second process, which is not detected in VV, but represents the major component in EDLS, shows a dependence τ ∝ q⁰, i.e. it is q-independent. In a plot of τ⁻¹ against q², the slope is 0 within the error. Also included in Fig. 2 is the calculated rotational dynamics⁵ for the investigated spherical particles with R_h = 60 nm,¹⁸ which should show up in VH measurements for particles with internal anisotropy. The differences in q-dependence and τ between measured EDLS dynamics and rotational diffusion, as well as the λ-dependence of EDLS, exclude an interpretation of the observed dynamics on the basis of rotational diffusion. The absence of the rotational τ in the data further indicates that here internal anisotropy contrast does not contribute significantly to the intensity in the ellipsometry minimum.

Fig. 2 Dependence of τ on q at the different wavelengths for a PS latex dispersion Eur41,¹⁸ mass fraction w_b = 3.5 × 10⁻⁵.

The q-independence of the process observed in EDLS should imply that the underlying process has no characteristic length scale. Inconsistent with this interpretation, EDLS measurements show a dependence on λ as τ ∝ λ^k with k = 1.67 ± 0.04 (Fig. 2), which is unexpected for coherent scattering.

The temperature dependence of the EDLS process between 20 °C and 32 °C for PS latices follows an Arrhenius behaviour τ⁻¹ ∝ exp(E_a/(RT)) (R – gas constant, T – temperature), where the activation energy E_a has been determined to be 14.3 ± 1.8 kJ mol⁻¹. This value is close to E_a of diffusion, which is governed by E_a of the viscous flow of the surrounding water. From the viscosity of water,²² this value has been evaluated to be 15.8 ± 0.3 kJ mol⁻¹.

The q-independent, λ-dependent process has been observed in a wide variety of samples. The fast mode was present in all investigated aqueous dispersions. Also for micelles formed from poly(styrene)-b-poly(isoprene) in decane, a selective solvent for poly(isoprene), the q-independent process was observed. The characteristics are always as displayed in Fig. 2. While at Θ ≤ 65°, the two processes are well-separated, their respective τ get closer at higher Θ. Consequently, it is hard to separate the two processes at high q using CONTIN. Notwithstanding, the resulting inverted correlation functions show a much wider peak in EDLS compared to VV, hinting at the presence of the two processes in EDLS. The q of intersection for the two processes is unaffected by R_h, which shifts both τ. Though not diffusive, the process dominating EDLS is therefore coupled to the diffusion of particles.

In solutions of polymers and amphiphiles, q-independent processes have been reported. For semidilute polymers in the theta state, a q-independent structural relaxation of a transient network has been predicted²³ and found.^24,25 Density fluctuations in highly concentrated polymer solutions are q-independent.^26,27 Triblock copolymer micelles above the overlap concentration show a q-independent process attributed to viscoelastic properties of a network of micelles,²⁸ supported by theoretical arguments.²⁹ Slow, q-independent modes have been found in sols nearing a sol–gel transition,³⁰ in dilute solutions of certain polymers,³¹ and in a sponge phase in a 4-component system.³² The latter mode has been attributed to a topology relaxation.³² All these modes are not supposed to show a λ-dependent behaviour, though none of these studies have investigated λ-dependence. For metal colloids, a λ-dependence has been observed, attributed to plasmon excitation.^33,34 This mechanism can be excluded for dielectric particles as used here.

Using a PS latex, the concentration dependence of the intensity I of the fast process has been found to be I ∝ w_b^(1.2±0.6). This result is close to the expected dependence I ∝ w_b¹ for single scattering events, as opposed to I ∝ w_b² for multiple scattering.³⁵ Therefore, multiple scattering can be ruled out as the responsible mechanism for process dominating in EDLS. Two processes with a similar behaviour of the q-dependence of τ have been reported and explained by multiple scattering.^36,37 Agreement with the theoretical predictions is, however, rather poor especially because the theory predicts only one process, while experimentally two processes have been observed. The λ-dependence was not studied there.³⁶

The λ-dependence cannot originate from light absorption and associated local heating, as in this case, both the diffusive and non-diffusive processes are expected to show a λ-dependence beyond q. Furthermore, experimental effects due to a finite laser line width Δλ or the angular smearing ΔΘ of Θ because of the weak focussing of the incident light can be excluded. These effects can be summarized as a smearing Δq of q. Any prediction connected to particle diffusion ends up with τ⁻¹ ∝ DΔq² for dimensional reasons. Since Δλ ≪ λ and ΔΘ ≪ Θ, one gets Δq ≪ q, so slow dynamics results, similar to the scattering at small Θ. Although such an approach can produce a q-independent incoherent process, it cannot capture the observed fast relaxation, which fits better to Θ ≈ 180°. Sample polydispersity can also be ruled out as an origin for the observed q⁰ dynamics. A large increase in polydispersity was required to enhance slightly the intensity in the ELS minimum,¹⁸ implying that the main source of incoherent intensity for monodisperse samples has a different origin. Furthermore, incoherent scattering due to sample polydispersity is expected to show τ ∝ q⁻², as observed e.g. in the chain self-diffusion of block-copolymer samples.³⁸

For an interpretation of all observations, reflections at the cuvette walls are considered. The superposition of 4 different paths in Fig. 3 is similar to related problems.³⁹ Path 1 is the desired case, where laser light is scattered towards the detector. Paths 2–4 involve one or two reflections at the cuvette walls, and the contribution to the detected field is reduced by a reflection coefficient. Multiple reflections slightly change the weight of the different light components; however, no additional propagation direction is included, as long as only a single scattering event is considered. The 4 paths in general have different polarisation signatures when they reach the analyser. The setting of minimum intensity of the optics corresponding to the coherent signal is determined by the average of the 4 paths. Overall, path 1 dominates scattering intensity, and thus minimum intensity is found for a set of polarisation optics which almost extinguishes path 1. The deviations from the average, which constitute the incoherent signal, are of comparable amplitude for all 4 paths. For paths 1 and 3 as well as for paths 2 and 4, the involved q are of identical magnitude, but of opposite direction, resulting in an overall q-independence. The resulting interference of the 4 beam paths from scattering from a single particle can be constructive or destructive. The situation is similar to the scattering of a particle in a standing wave. The summed scattering signals of a particle change from bright to dark when the particle diffuses over the distance λ/4. For the diffusion of a particle out of a volume element with smallest extend ∼λ, τ ∝ λ². The deviation from the observed τ ∝ λ^1.67 might originate from neglect of re-entry or entry in neighbour illumination volumes of the particle.

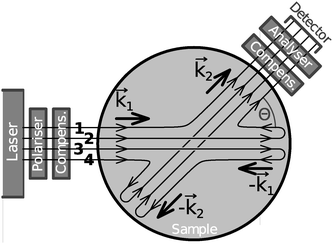Fig. 3 Scheme of light paths in a cuvette which contribute to the scattering at Θ. The wave vectors ±k⃑₁ and ±k⃑₂ indicate the directions of the incident and the scattered components, respectively.

In conclusion, the main achievement of EDLS is the isolation of low intensity incoherent contributions, and the almost complete suppression of the coherent, diffusive process of the colloidal particles. The observation of a dynamic process with a relaxation time τ independent of the scattering vector q but dependent on the wavelength λ is explained by the superposition of 4 scattering contributions which superimpose due to reflection at the cuvette walls. Future applications of EDLS are expected in situations where information about system dynamics can be extracted from the background after extinguishing the major coherent component. For instance, for colloids with large polydispersity, the incoherent scattering should be determined by the polydispersity,^17,18 a contribution often dominating incoherent scattering but negligible here due to the low sample polydispersity. A second application may yield data similar to FCS, where number density fluctuations are probed.⁴ Therefore, it is expected that under identical conditions, both the collective and self-diffusion coefficients could be obtained. Interesting applications with major insight into the internal dynamics may arise from experiments on complex systems.

The authors thank Klaus Tauer for providing samples.

References

1. A. Y. Malkin, Polym. Sci., Ser. A, 2009, 51, 80.
2. U. Kaatze and Y. Feldman, Meas. Sci. Technol., 2006, 17, R17.
3. D. Richter, J. Phys. Soc. Jpn., 2006, 75, 111004.
4. Y. Tian, M. M. Martinez and D. Pappas, Appl. Spectrosc., 2011, 65, 115A.
5. B. J. Berne and R. Pecora, Dynamic Light Scattering with Applications to Chemistry, Biology, and Physics, Dover, Mineola, NY, 2000.
6. R. Kimmich and N. Fatkullin, Adv. Polym. Sci., 2004, 170, 1.
7. S. Safran, Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, Addison-Wesley, Reading, MA, 1994.
8. P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, London, 1979.
9. W. Härtl and H. Versmold, J. Chem. Phys., 1984, 80, 1387.
10. K.-Q. Xia, Y.-B. Xin and P. Tong, J. Opt. Soc. Am. A, 1995, 12, 1571.
11. A. Erbe, K. Tauer and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 031406.
12. A. Erbe and R. Sigel, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 22, 303.
13. A. Erbe, K. Tauer and R. Sigel, Langmuir, 2007, 23, 452.
14. R. Sigel, Curr. Opin. Colloid Interface Sci., 2009, 14, 426.
15. D. J. Ross and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 056710.
16. Ø. Svensen, J. J. Stamnes, M. Kildemo, L. M. S. Aas, S. R. Erga and Ø. Frette, Appl. Opt., 2011, 50, 5149.
17. R. Sigel and A. Erbe, Appl. Opt., 2008, 47, 2161.
18. A. Erbe, K. Tauer and R. Sigel, Langmuir, 2009, 25, 2703.
19. S. Provencher, Comput. Phys. Commun., 1982, 27, 213.
20. S. Provencher, Comput. Phys. Commun., 1982, 27, 229.
21. K. Tauer and V. Khrenov, Macromol. Symp., 2002, 179, 27.
22. Taschenbuch für Physiker und Chemiker. Band 1 - Physikalisch - chemische Daten, ed. M. Lechner, Springer Verlag, Berlin, Heidelberg, 1992.
23. F. Brochard and P. G. de Gennes, Macromolecules, 1977, 10, 1157.
24. T. Nicolai, W. Brown, R. M. Johnsen and P. Štěpánek, Macromolecules, 1990, 23, 1165.
25. S. W. Provencher and P. Štěpánek, Part. Part. Syst. Charact., 1996, 13, 291.
26. C. Koňák and W. Brown, J. Chem. Phys., 1993, 98, 9014.
27. G. Fytas, G. Floudas and K. L. Ngai, Macromolecules, 1990, 23, 1104.
28. K. Thuresson, S. Nilsson, A.-L. Kjøniksen, H. Walderhaug, B. Lindman and B. Nyström, J. Phys. Chem. B, 1999, 103, 1425.
29. U. Genz, Macromolecules, 1994, 27, 3501.
30. M. C. Blanco, D. Leisner, C. Vázquez and M. A. López-Quintela, Langmuir, 2000, 16, 8585.
31. T. A. P. Seery, M. Yassini, T. E. Hogen-Esch and E. J. Amis, Macromolecules, 1992, 25, 4784.
32. T. D. Le, U. Olsson, H. Wennerström, P. Uhrmeister, B. Rathke and R. Strey, J. Phys. Chem. B, 2002, 106, 9410.
33. E. Antoniou, P. Voudouris, A. Larsen, B. Loppinet, D. Vlassopoulos, I. Pastoriza-Santos and L. M. Liz-Marzán, J. Phys. Chem. C, 2012, 116, 3888.
34. M. Haghighi, M. A. Plum, G. Gantzounis, H.-J. Butt, W. Steffen and G. Fytas, J. Phys. Chem. C, 2013, 117, 8411.
35. P. N. Pusey and R. J. A. Tough, Dynamic light scattering, ed. R. Pecora, Plenum Press, New York, London, 1985.
36. A. N. Semenov, A. E. Likhtman, D. Vlassopoulos, K. Karatasos and G. Fytas, Macromol. Theory Simul., 1999, 8, 179.
37. G. Fytas, D. Vlassopoulos, G. Meier, A. Likhtman and A. N. Semenov, Phys. Rev. Lett., 1996, 76, 3586.
38. R. Sigel, S. Pispas, N. Hadjichristidis, D. Vlassopoulos and G. Fytas, Macromolecules, 1999, 32, 8447.
39. A. Stocco, T. Mokhtari, G. Haseloff, A. Erbe and R. Sigel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011601.

---