 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calculating and assigning rovibrational energy levels of (15N2O)2, (15N14NO)2, 14N2O–15N2O and 15N14NO–15N2O
James Brown, Xiao-Gang Wang and Tucker Carrington Jr.
Queen's University, Kingston, Ontario K7L 3N6, Canada
First published on 24th September 2013
Abstract
In this paper we report transition frequencies and rotational constants computed for several isotopologues of the nitrous oxide dimer. A previously reported intermolecular potential, the symmetry adapted Lanczos algorithm and an uncoupled product basis set are used to do the calculations. Rotational transition frequencies and rotational constants are in good agreement with experiment. We calculate states localized in both polar and nonpolar wells on the potential surface. Two of the four isotopologues we study have inequivalent monomers. They have wavefunctions localized over a single polar well.
1 Introduction
In recent years there have been several experimental1–15 and theoretical16–20 studies of the nitrous oxide Van der Waals dimer. The (N2O)2 potential energy surface (PES) has several accessible minima. A non-polar C2h slipped anti-parallel structure was first identified and characterized.2,5 Later, a polar form of (N2O)2 was predicted16 and observed.9,11,12,14In previous papers we reported transition frequencies and rotational constants for (14N2O)2,18,19 which agree well with experimental results. Experimentalists have also studied, (15N2O)2,11,14,17 (15N14NO)2,514N2O–15N2O,13,14 and 15N14NO–15N2O.14 For all of these isotopologues they have determined rotational constants for the ground vibrational state of the polar and/or nonpolar forms. Rotational constants for the torsion, geared bend, and antigeared bend states have also been reported for some of the isotopologues.10,13,15 In this paper we compare the experimental numbers with results we obtain using the PES of ref. 18 and confirm that both the adiabatic separation of inter- and intra-molecular coordinates employed in ref. 18 and 19 and the PES of ref. 18 are accurate. According to the Born–Oppenheimer approximation, spectra for all isotopologues can be computed from one PES. It is known that for light molecules non-Born–Oppenheimer effects can shift energy levels by ∼1 cm−1.21 As the experimentalists' results for nitrous oxide dimer are very precise, it is important to know how well the Born–Oppenheimer approximation works.
Nitrous oxide dimers with equivalent monomers have two identical polar wells, and each polar wavefunction has amplitude in both polar wells. Isotopologues with different monomers are of particular interest because, although the polar wells are identical, each wavefunction has amplitude in only one of the two wells, due to the fact that there is almost no tunnelling between the wells. The transition frequencies and rotational constants we compute could facilitate the assigning of experimentally observed transitions, help experimentalists discover transitions that have heretofore not been observed, and understand spectral patterns. See for example ref. 22.
2 Calculating rovibrational levels
The rovibrational Schrödinger equation is solved using the approach of ref. 18 and 19. The full potential can be written as a sum of an intra-molecular term, an inter-molecular term, and a coupling term. The inter-molecular term is the potential of ref. 18. We neglect the coupling term and use an adiabatic approximation to separate inter- and intra-molecular coordinates. To make the kinetic energy operator (KEO) for the effective inter-molecular Hamiltonian we use experimental constants. Three vectors:![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,
1, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2, and
2, and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 define the intermolecular coordinates. See Fig. 1. Vectors
0 define the intermolecular coordinates. See Fig. 1. Vectors ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1 and
1 and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2 point toward O and are aligned with the monomers. Vector
2 point toward O and are aligned with the monomers. Vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 points from the centre of mass of monomer 1 to that of monomer 2. The four vibrational coordinates ϕ2, θ1, θ2, and r0 are defined in the standard fashion. θk is the angle between
0 points from the centre of mass of monomer 1 to that of monomer 2. The four vibrational coordinates ϕ2, θ1, θ2, and r0 are defined in the standard fashion. θk is the angle between ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 and
0 and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k, ϕ2 is the dihedral angle from
k, ϕ2 is the dihedral angle from ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1 to
1 to ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2 around
2 around ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0; and r0 is the length of
0; and r0 is the length of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0. Euler angles specify the orientation of a body-fixed frame attached such that the z-axis is along
0. Euler angles specify the orientation of a body-fixed frame attached such that the z-axis is along ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 and the x-axis is along the vector (
0 and the x-axis is along the vector (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 ×
0 × ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1) ×
1) × ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0. The kinetic energy operator in these coordinates is well known.23–25
0. The kinetic energy operator in these coordinates is well known.23–25 | ||
| Fig. 1 (N2O)2 coordinates. O is red and N is blue. | ||
To specify the KEO, we must choose masses and monomer rotational constants. The masses used to calculate the reduced mass for the inter-monomer distance (r0) are 14.0030740052 u,26 15.000108973 u,26 and 15.9949146221 u27 for 14N, 15N, and O respectively. We calculate energy levels for a particular intra-molecular state of the dimer. For different intra-molecular states we use different monomer rotational constants in the dimer KEO. For the ground state of a dimer we use monomer rotational constants for the ground state of the monomers. For the various monomer isotopologues, they are taken from ref. 28. For excited states of dimers with different monomers we calculate energy levels for an intra-molecular dimer state with one monomer in its ground state and another excited in its ν1 = 1 state. To do these calculations we use the ν1 = 1 monomer rotational constant for 14N2O from ref. 28 and the ν1 = 1 monomer rotational constant for 15N2O from ref. 29. For dimers with identical monomers, there are two excited states: the symmetric combination (in-phase) and the anti-symmetric combination (out-of-phase). The in-phase state of the non-polar isomer is infra-red inactive because it has symmetry Ag in the C2h point group. Therefore we only calculate energy levels for the out-of-phase state 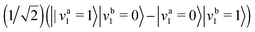 , where a and b label the two monomers. In this case, the appropriate rotational constant, for both monomers is (B0 + B1)/2, where B0 is the monomer rotational constant for the ground state and B1 is the monomer rotational constant for the ν1 = 1 state.
, where a and b label the two monomers. In this case, the appropriate rotational constant, for both monomers is (B0 + B1)/2, where B0 is the monomer rotational constant for the ground state and B1 is the monomer rotational constant for the ν1 = 1 state.
Energy levels and wavefunctions of a basis representation of the inter-molecular Hamiltonian are computed using a symmetry adapted Lanczos (SAL) algorithm.30,31 Filter Diagonalization is another option.32,33 Potential matrix elements are computed by quadrature. Matrix-vector products required to use the Lanczos algorithm are computed by evaluating sums sequentially using techniques described in ref. 25 and 34–39. Wavefunctions were obtained from the eigenvectors of the Hamiltonian matrix using methods described previously.36,37
Basis functions are functions of the four inter-molecular coordinates. For r0 we use 25 potential optimized discrete variable representation (PODVR) functions40,41 for a cut reference potential obtained by setting the other three coordinates equal to equilibrium values of the nonpolar configuration. The PODVR functions are computed in a sine basis, defined in the range [4.5 Bohr, 18.0 Bohr].42 For the angular and rotational coordinates, we use parity adapted rovibrational functions,36,43
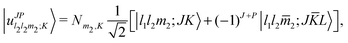 | (1) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 2 = −m2 and
2 = −m2 and ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) = −K, and Nm2,K = (1 + δm2,0δK,0)−1/2. The ket in this equation is defined by
= −K, and Nm2,K = (1 + δm2,0δK,0)−1/2. The ket in this equation is defined by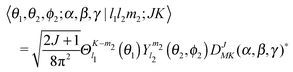 | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. A potential ceiling34 was used to reduce the spectral range. About 82 percent of the quadrature points are below the ceiling value of 5240 cm−1.
000. A potential ceiling34 was used to reduce the spectral range. About 82 percent of the quadrature points are below the ceiling value of 5240 cm−1.The use of the parity adapted-basis makes it possible to separately compute even and odd parity levels. For complexes with different monomers (15N14NO–15N2O and 14N2O–15N2O), the only symmetry operation is (space-fixed) inversion and states are labelled only by their parity: even (+) or odd (−). When the monomers are identical ((15N2O)2 and (15N14NO)2) the Hamiltonian also commutes with permutation of the monomers and states are labelled (A+, B+, A−, B−) where A/B indicates whether a state is symmetric or antisymmetric with respect to permutation of the monomers. A and B states are computed separately using Symmetry Adapted Lanczos.30,31,35
2.1 Using the potential for other isotopologues
According to the Born–Oppenheimer approximation, the potential of ref. 18, made to compute the spectrum of (14N2O)2, can be used for any isotopologue. However, the potential of ref. 18 is a function of coordinates (ϕ2, θ1, θ2, and r0) defined from Jacobi vectors that are mass-dependent. Therefore, to use the potential for other isotopologues, a coordinate transformation is required. To compute the spectrum of isotopologue b we must evaluate the potential at (quadrature and DVR) points in coordinates qb, where qb represents all four coordinates. We know the potential as a function of the coordinates qa and thus require V(qa(qb)).To obtain qa from qb we proceed as follows. The four coordinates ϕ2, θ1, θ2, and r0 of isotopologue b are the same as the corresponding coordinates of a virtual 4-atom molecule (NX)2, where the X atom is at the centre of mass of the inner N atom and the neighbouring O atom of a monomer and the mass of X is MN + MO. We denote the lengths of the two NX bonds as r1′ and r2′. From r1′ and r2′ and the four qb coordinates we obtain Cartesian coordinates for the three Jacobi vectors ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0,
0, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1′, and
1′, and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2′ by (arbitrarily) attaching a Cartesian axis system to the molecule. Knowing these Cartesian coordinates we can determine Cartesian components of position vectors of the atoms of the virtual molecule,
2′ by (arbitrarily) attaching a Cartesian axis system to the molecule. Knowing these Cartesian coordinates we can determine Cartesian components of position vectors of the atoms of the virtual molecule,
| Ξi = J−1ρi. | (4) |
In this equation,
 | (5) |
3 Results
3.1 Energies and labels for J = 0
The low lying states for the isotopologues with equivalent and inequivalent monomers are shown in Tables 1 and 2 respectively. In all tables, we report four decimal places (in cm−1) because the energies in the tables are relative to zero point energy (ZPE). Relative errors are little affected by non-adiabatic and non-Born–Oppenheimer effects. The labels for the states are of the form (type; vt (torsion), vg (geared bend), vr (VdW-stretch), va (anti-geared bend)), where type is the well above which the wavefunction is localized. N is the label for the nonpolar well and P is the label for the polar wells. When the monomers are equivalent, polar levels are split by less than 0.0001 cm−1 and polar wavefunctions have amplitude in both polar wells. Previous calculations19 demonstrated this for (14N2O)2, and in this paper we show that it is also true for (15N2O)2.| A+ | B+ | A− | B− |
|---|---|---|---|
| (15N2O)2 | |||
| 0.0000(N;0000) | 41.2860(N;0100) | 25.3644(N;1000) | 64.7030(N;1100) |
| 49.9506(N;2000) | 85.4353(N;0110) | 73.3442(N;3000) | 108.2692(N;1110) |
| 51.6079(N;0010) | 89.0123(N;2100) | 75.8042(N;1010) | 112.2575(N;3100) |
| 79.2953(N;0200) | 112.5860(N;0300) | 102.5049(N;1200) | 136.6005(N;1300) |
| 96.3946(N;4000) | 126.6917(N;0120) | 119.2646(N;5000) | 149.5334(N;1120) |
| 97.0473(N;0001) | 130.9050(N;2110) | 120.2643(N;1001) | 152.3685(N;3110) |
| 99.2091(N;0020) | 134.2485(N;0101) | 122.4350(N;3010) | 156.2541(N;1101) |
| 100.0734(N;2010) | 135.3983(N;4100) | 123.0847(N;1020) | 157.4220(N;5100) |
| 114.9930(N;0210) | 141.8673(N;0310) | 139.1094(N;1210) | 164.7427(P;1000) |
| 126.0668(N;2200) | 143.6184(P;0000) | 148.1570(N;3200) | |
| 138.5227(N;0400) | 162.0301(N;1220) | ||
| 141.4709(N;6000) | 162.3369(N;7000) | ||
| 142.4823(N;2001) | 164.3517(N;5010) | ||
| 143.4326(N;0011) | 164.7427(P;1000) | ||
| 143.6184(P;0000) | |||
| 145.0899(N;4010) | |||
| (15N14NO)2 | |||
| 0.0000(N;0000) | 41.2680(N;0100) | 25.3588(N;1000) | 64.6846(N;1100) |
| 49.9675(N;2000) | 85.7062(N;0110) | 73.3787(N;3000) | 108.5322(N;1110) |
| 52.0146(N;0010) | 89.0003(N;2100) | 76.1595(N;1010) | 112.2495(N;3100) |
| 79.3263(N;0200) | 112.7371(N;0300) | 102.5525(N;1200) | 136.7507(N;1300) |
| 96.4881(N;4000) | 126.9851(N;0120) | 119.3375(N;5000) | 149.8323(N;1120) |
| 97.2825(N;0001) | 131.1331(N;2110) | 120.5656(N;1001) | 152.6032(N;3110) |
| 99.7066(N;2010) | 134.3627(N;4100) | 122.7463(N;3010) | 156.3860(N;1101) |
| 100.5825(N) | 135.5489(N;2110) | 123.6696(N;1020) | 157.5508(N;5100) |
| 115.2980(N;0210) | 142.2876(N;0310) | 139.4306(N;1210) | 164.6524(P;1000) |
| 126.1184(N;2200) | 143.5421(P;0000) | 148.2189(N;3200) | |
| 138.8338(N;0400) | 162.3374(N;1220) | ||
| 141.5690(N;6000) | 162.4907(N;1400) | ||
| 142.8702(N;2001) | 164.6059(N;5010) | ||
| 143.5421(P;0000) | 164.6524(P;1000) | ||
| 143.9925(N;2020) | |||
| 145.3756(N;4010) | |||
| 14N2O–15N2O | 15N14NO–15N2O | ||
|---|---|---|---|
| + | − | + | − |
| 0.0000(N;0000) | 25.5633(N;1000) | 0.0000(N;0000) | 25.3616(N;1000) |
| 41.5625(N;0100) | 65.1640(N;1100) | 41.2770(N;0100) | 64.6939(N;1100) |
| 50.3632(N;2000) | 73.9630(N;2000) | 49.9607(N;2000) | 73.3634(N;3000) |
| 52.1940(N;0010) | 76.5353(N;1010) | 51.8109(N;0010) | 75.9811(N;1010) |
| 79.8406(N;0200) | 103.2530(N;1200) | 79.3109(N;0200) | 102.5288(N;1200) |
| 86.1021(N;0110) | 109.1243(N;1110) | 85.5722(N;0110) | 108.4023(N;1110) |
| 89.6636(N;2100) | 113.0796(N;3100) | 89.0062(N;2100) | 112.2532(N;3100) |
| 97.0881(N;4000) | 120.2768(N;5000) | 96.4496(N;0001) | 119.3078(N;5000) |
| 97.5102(N;2010) | 120.9475(N;1001) | 97.1600(N;2010) | 120.4127(N;1001) |
| 100.1038(N;0001) | 123.2829(N;3010) | 99.4651(N;4000) | 122.5906(N;3010) |
| 101.0014(N;0020) | 124.1754(N;1020) | 100.3217(N;0020) | 123.3769(N;1020) |
| 113.2866(N;0300) | 137.4908(N;1300) | 112.6620(N;0300) | 136.6762(N;1300) |
| 115.8601(N;0210) | 140.1793(N;1210) | 115.1456(N;0210) | 139.2704(N;1210) |
| 126.9682(N;2200) | 149.1896(N;3200) | 126.0928(N;2200) | 148.1881(N;3200) |
| 127.5887(N;0120) | 150.6165 | 126.8406(N;0120) | 149.6858 |
| 131.8691(N;2110) | 153.4795(N;3110) | 131.0207(N;2110) | 152.4866(N;3110) |
| 134.8914(N;0101) | 157.9916(N;1110) | 134.3082(N;0101) | 156.3220(N;1101) |
| 136.2645(N;4100) | 158.5032(N;5100) | 135.4704(N;4100) | 157.4839(N;5100) |
| 139.3557(N;0400) | 163.0892(N;1220) | 138.6809(N;0400) | 162.1979 |
| 142.6543(N;6000) | 163.5930(N;7000) | 141.5287(N;6000) | 162.4099(N;7000) |
| 142.8754(N;0301) | 164.6521(PB;1000) | 142.0781(N;0301) | 164.4812(N;5010) |
| 143.3810(PB;0000) | 165.0188(PA;1000) | 142.6808(N;4100) | 164.6898(PB;1000) |
| 143.4422(N;4100) | 165.4287(N;5010) | 143.5725(PB;0000) | 164.7056(PA;1000) |
| 143.7674(PA;0000) | 166.4179 | 143.5882(PA;0000) | 165.5514 |
| 144.3883(N;2001) | 166.6013 | 143.7067(N;2001) | 165.6570 |
To label the J = 0 states, probability density (PD) plots were made by integrating over all but two coordinates. The PDs are normalized with a volume element with a sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ factor for each θ angle and an r02 factor for r0. The only wavefunctions we examined that are localized above more than one well are those for polar states of dimers with identical monomers. It is thus easy to identify the ground state for each type. The vt = 1, vg = 1, vr = 1, and va = 1 fundamentals can be labelled on the basis of the nodal structure of the PDs. Four single-node wavefunctions were observed. PDs for the vr = 2 stretch and va = 1 anti-gear fundamental are shown in Fig. 2. For some combination and overtone states, it was not possible to label using only PDs. In these cases, energies of the fundamentals were also used. The energy of the (15N2O)2 state with E + 64.7030 cm−1, assigned to (N;1100), is approximately the sum of the energy of the vt = 1 state (≈25.4 cm−1) and the energy of the vg = 1 state (≈41.3 cm−1). The strategy of using fundamental energies to guide the assignment is more important when labelling the anti-gear and VdW stretch combinations and overtones because the corresponding PDs are more complicated due to coupling.18,19
θ factor for each θ angle and an r02 factor for r0. The only wavefunctions we examined that are localized above more than one well are those for polar states of dimers with identical monomers. It is thus easy to identify the ground state for each type. The vt = 1, vg = 1, vr = 1, and va = 1 fundamentals can be labelled on the basis of the nodal structure of the PDs. Four single-node wavefunctions were observed. PDs for the vr = 2 stretch and va = 1 anti-gear fundamental are shown in Fig. 2. For some combination and overtone states, it was not possible to label using only PDs. In these cases, energies of the fundamentals were also used. The energy of the (15N2O)2 state with E + 64.7030 cm−1, assigned to (N;1100), is approximately the sum of the energy of the vt = 1 state (≈25.4 cm−1) and the energy of the vg = 1 state (≈41.3 cm−1). The strategy of using fundamental energies to guide the assignment is more important when labelling the anti-gear and VdW stretch combinations and overtones because the corresponding PDs are more complicated due to coupling.18,19
![PD plots of the (N;0020)[(a) and (b)] at 99.2091 cm−1, and (N;0001)[(c) and (d)] at 97.0473 cm−1 states for the (15N2O)2 isotopologue. There is clear coupling between the coordinates so the use of fundamental energies to guide assignment becomes important.](/image/article/2013/CP/c3cp52548a/c3cp52548a-f2.gif) | ||
| Fig. 2 PD plots of the (N;0020)[(a) and (b)] at 99.2091 cm−1, and (N;0001)[(c) and (d)] at 97.0473 cm−1 states for the (15N2O)2 isotopologue. There is clear coupling between the coordinates so the use of fundamental energies to guide assignment becomes important. | ||
Our fundamental energies can be compared with experimental counterparts. A torsion band was observed for (14N2O)2 in 2009.17 Very recently the same band has been discovered for (15N2O)2.15 For (14N2O)2, the experimental torsion frequency, 27.3(1.0) cm−1, is close to the theoretical value, 25.7599 cm−1, of ref. 18. For (15N2O)2, the experimental frequency is 26.9(1.0) cm−1 and we find (Table 1) 25.3644 cm−1. Although for both isotopologues, the calculated and experimental frequencies are not equal, the difference in the torsion frequency between the two isotopologues is 0.4 cm−1, for both experiment and theory. For the geared (disrotatory) bend fundamental, the (14N2O)2 frequency is 42.3(1.0) cm−1 (ref. 13 and 17) and the calculated value is 41.8609 cm−1. For (15N2O)2, the experimental value is 41.6(1.0) cm−1 and we compute 41.2860 cm−1. In this case, the the experimental and calculated frequencies do agree to within experimental error. According to experiment, the geared frequencies of the two isotopologues differ by −0.7 cm−1; according to our calculation the difference is −0.6 cm−1. Recently, the anti-gear fundamental was observed at 96.0926 cm−1 and 95.4913 cm−1 for (14N2O)2 and (15N2O)2 respectively.15 The calculated values are 97.5221 cm−1 and 97.0473 cm−1. Once again, the theoretical calculations and experimental measurements have similar frequency shifts (−0.5 cm−1 and −0.6 cm−1).
In ref. 14 the monomer with an N inside is denoted A and the monomer with an N outside is denoted B. When the monomers are not equivalent, notation is required to distinguish the two wells and their associated states. In this work, a dimer for which monomer A is lighter is called PA and a dimer for which monomer B is lighter is called PB. For 14N2O–15N2O, the dimer denoted by N(A,1)N(A,2) in ref. 14 is called PA in this work. For 15N14NO–15N2O, the dimer denoted by N(A,2) in ref. 14 is called PA in this work. See Fig. 3 and 4 for illustrations. For dimer X–Y, r1 and θ1 are coordinates of monomer X and r2 and θ2 are coordinates of monomer Y. In order to assign the wavefunctions to either PA or PB, we look at probability density (PD) plots. Wavefunctions with amplitude in the PA well have θ1 > 90° and θ2 > 90°, as is shown in Fig. 3.
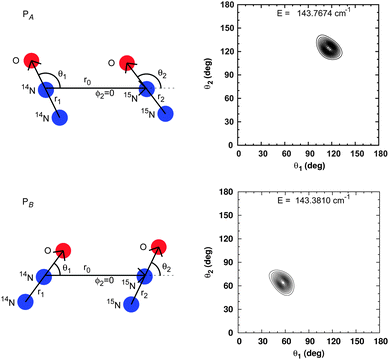 | ||
| Fig. 3 Polar equilibrium geometries and probability densities for the 14N2O–15N2O complex. | ||
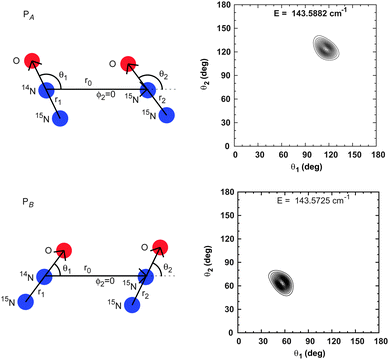 | ||
| Fig. 4 Polar equilibrium geometries and probability densities for the 15N14NO–15N2O complex. | ||
For isotopologues with different monomers, although the two polar wells have the same shape and depth, vibrational wavefunctions are localized in only one polar well. See Fig. 3 for plots of probability density for the 14N2O–15N2O. The energy of the PA vibrational state is higher than the energy of the PB vibrational state. For 15N14NO–15N2O, plots of probability density of PA and PB states are shown in Fig. 4. Also in this case, the vibrational energy of the PA state is higher, however, the difference between the PA and PB energies (0.015 cm−1) is much smaller than the 14N2O–15N2O difference (0.386 cm−1), presumably due to the smaller difference between the monomer masses. The order of the PA and PB vibrational energies for the dimers with inequivalent monomers, predicted by our calculations, has not been confirmed by the experiment. This could perhaps be done in the infrared. Of course, the energy of the polar isomers of the dimers with equivalent monomers studied in this work have not been measured either.
3.2 J > 0 energy levels and rotational constants for ground and fundamentals
J > 0 levels have also been calculated for each isotopologue. The J = 1 energies and rotational constants, for nonpolar and polar levels are shown in Tables 3 and 4 respectively. Where possible, comparisons have been made to experimental rotational constants. These are the italicized numbers in the tables. The experimentalists determine rotational constants by adjusting the parameters of an effective rotational Hamiltonian so that its eigenvalues reproduce rotational energy levels consistent with transitions associated with a particular vibrational state. With the definition that monomer A has an N on the inside and monomer B has an N on the outside, as indicated in Fig. 3 of ref. 14, columns 2 and 3 and also columns 4 and 5 of ref. 14 must be permuted.45 Rotational constants we report are obtained directly from the J = 1 levels we compute by assigning them to vibrational states.| J = 0 (W; vt, vg, vr, va) (sym) | 101 (sym) | 111 (sym) | 110 (sym) | A | B | C |
|---|---|---|---|---|---|---|
| (15N2O)2 | ||||||
| 0.0000(N;0000)(A+) | 0.1036(B−) | 0.3424(B−) | 0.3515(A+) | 0.2952 | 0.0564 | 0.0473 |
| (N;0000)11 | 0.2940 | 0.0564 | 0.0472 | |||
| 25.3645(N;1000)(A−) | 25.4680(B+) | 25.6966(B+) | 25.7051(A−) | 0.2846 | 0.0560 | 0.0475 |
| 41.2860(N;0100)(B+) | 41.3873(A−) | 41.6414(A−) | 41.6504(B+) | 0.3092 | 0.0552 | 0.0462 |
| 51.6079(N;0010)(A+) | 51.7089(B−) | 51.9543(B−) | 51.9630(A+) | 0.3003 | 0.0548 | 0.0461 |
| 97.0473(N;0001)(A+) | 97.1496(B−) | 97.3778(B−) | 97.3863(A+) | 0.2836 | 0.0554 | 0.0469 |
| (15N14NO)2 | ||||||
| 0.0000(N;0000)(A+) | 0.1056(B−) | 0.3437(B−) | 0.3532(A+) | 0.2957 | 0.0575 | 0.0481 |
| (N;0000)5 | 0.2944 | 0.0575 | 0.0480 | |||
| 25.3588(N;1000)(A−) | 25.4643(B+) | 25.6921(B+) | 25.7009(A−) | 0.2850 | 0.0571 | 0.0483 |
| 41.2680(N;0100)(B+) | 41.3713(A−) | 41.6248(A−) | 41.6342(B+) | 0.3098 | 0.0563 | 0.0470 |
| 52.0146(N;0010)(A+) | 52.1173(B−) | 52.3624(B−) | 52.3714(A+) | 0.3009 | 0.0559 | 0.0469 |
| 97.2825(N;0001)(A+) | 97.3865(B−) | 97.6172(B−) | 97.6263(A+) | 0.2873 | 0.0566 | 0.0474 |
| 14N2O–15N2O | ||||||
| 0.0000(N;0000)(+) | 0.1067(−) | 0.3463(−) | 0.3559(+) | 0.2978 | 0.0581 | 0.0485 |
| (N;0000)13 | 0.2966 | 0.0581 | 0.0485 | |||
| 25.5633(N;1000)(−) | 25.6698(+) | 25.8993(+) | 25.9082(−) | 0.2872 | 0.0577 | 0.0488 |
| 41.5624(N;0100)(+) | 41.6668(−) | 41.9219(−) | 41.9314(+) | 0.3120 | 0.0569 | 0.0474 |
| 52.1940(N;0010)(+) | 52.2978(−) | 52.5445(−) | 52.5536(+) | 0.3032 | 0.0564 | 0.0474 |
| 100.1038(N;0001)(+) | 100.2049(−) | 100.4258(−) | 100.4329(+) | 0.2750 | 0.0542 | 0.0470 |
| 15N14NO–15N2O | ||||||
| 0.0000(N;0000)(+) | 0.1046(−) | 0.3431(−) | 0.3524(+) | 0.2954 | 0.0570 | 0.0477 |
| 25.3616(N;1000)(−) | 25.4661(+) | 25.6943(+) | 25.7030(−) | 0.2848 | 0.0566 | 0.0479 |
| 41.2770(N;0100)(+) | 41.3793(−) | 41.6331(−) | 41.6423(+) | 0.3095 | 0.0558 | 0.0466 |
| 51.8109(N;0010)(+) | 51.9127(−) | 52.1581(−) | 52.1669(+) | 0.3006 | 0.0553 | 0.0465 |
| 96.4496(N;0001)(+) | 96.5530(−) | 96.7582(−) | 96.7650(+) | 0.2603 | 0.0551 | 0.0483 |
| J = 0 (W; vt, vg, vr, va) (sym) | 101 (sym) | 111 (sym) | 110 (sym) | A | B | C |
|---|---|---|---|---|---|---|
| (15N2O)2 | ||||||
| 143.6184(P;0000)(A+) | 143.7147(B−) | 143.9598(A−) | 143.9677(B+) | 0.2972 | 0.0521 | 0.0442 |
| 143.6184(P;0000)(B+) | 143.7147(A−) | 143.9598(B−) | 143.9677(A+) | 0.2972 | 0.0521 | 0.0442 |
| (P;0000)11,14 | 0.2981 | 0.0518 | 0.0440 | |||
| 164.7427(P;1000)(A−) | 164.8430(B+) | 165.1925(A+) | 165.2010(B−) | 0.4039 | 0.0544 | 0.0459 |
| 164.7427(P;1000)(B−) | 164.8430(A+) | 165.1925(B+) | 165.2010(A−) | 0.4039 | 0.0544 | 0.0459 |
| (15N14NO)2 | ||||||
| 143.5421(P;0000)(A+) | 143.6402(B−) | 143.8849(A−) | 143.8931(B+) | 0.2979 | 0.0531 | 0.0450 |
| 143.5421(P;0000)(B+) | 143.6402(A−) | 143.8849(B−) | 143.8931(A+) | 0.2979 | 0.0531 | 0.0450 |
| 164.6524(P;1000)(A−) | 164.7546(B+) | 165.1047(A+) | 165.1135(B−) | 0.4056 | 0.0555 | 0.0467 |
| 164.6524(P;1000)(B−) | 164.7546(A+) | 165.1047(B+) | 165.1135(A−) | 0.4056 | 0.0555 | 0.0467 |
| 14N2O–15N2O | ||||||
| 143.3811(PB;0000)(+) | 143.4802(−) | 143.7262(−) | 143.7345(+) | 0.2997 | 0.0537 | 0.0454 |
| (PA;0000)14 | 0.3006 | 0.0534 | 0.0453 | |||
| 143.7674(PA;0000)(+) | 143.8651(−) | 144.1180(−) | 144.1260(+) | 0.3058 | 0.0528 | 0.0449 |
| (PB;0000)14 | 0.3065 | 0.0524 | 0.0447 | |||
| 164.6521(PB;1000)(−) | 164.7554(+) | 165.1029(+) | 165.1120(−) | 0.4037 | 0.0562 | 0.0471 |
| 165.0188(PA;1000)(−) | 165.1204(+) | 165.4833(+) | 165.4918(−) | 0.4180 | 0.0550 | 0.0466 |
| 15N14NO–15N2O | ||||||
| 143.5725(PB;0000)(+) | 143.6698(−) | 143.9146(−) | 143.9226(+) | 0.2975 | 0.0526 | 0.0446 |
| (PA;0000)14 | 0.2983 | 0.0524 | 0.0444 | |||
| 143.5882(PA;0000)(+) | 143.6854(−) | 143.9304(−) | 143.9385(+) | 0.2977 | 0.0526 | 0.0446 |
| (PB;0000)14 | 0.2985 | 0.0523 | 0.0444 | |||
| 164.6898(PB;1000)(−) | 164.7911(+) | 165.1408(+) | 165.1494(−) | 0.4046 | 0.0549 | 0.0463 |
| 164.7056(PA;1000)(−) | 164.8068(+) | 165.1567(+) | 165.1653(−) | 0.4049 | 0.0549 | 0.0463 |
To assign ro-vibrational levels to vibrational states we use the two methods described in ref. 19. The first uses line strengths calculated from a sum-of-dipoles model for the dipole moment of (N2O)2. Equations for computing the line strengths are given in ref. 19 If vibrational states were widely spaced it would be easy to assign ro-vibrational levels to vibrational states. This is not the case for the nitrous oxide dimer. However, vibrational states localized above polar wells are widely spaced and therefore if we can extract the ro-vibrational levels associated with polar vibrational states from the full list of ro-vibrational levels they can be attributed to vibrational states by using previously established assignments of J = 0 energy levels. This is successful, even if the polar states are embedded in a region with many nonpolar (dark) energies. R(0) transitions that are intense must be to J = 1 states of polar vibrational states. As the dipole moment is in the plane perpendicular to the c-axis, only a-type and b-type transitions will be bright. The R(0) transitions are therefore to 101 and 111 states only. 110 states can be identified by computing Q(1) transition line strengths. Fig. 11 of ref. 19 illustrates these transitions. A list of the bright R(0) and Q(1) transition frequencies and their line strengths for (P;0000) is in Table 7.
Using line strengths it is not possible to assign nonpolar states nor is it possible for polar states of dimers with equivalent monomers to identify which of the two tunnelling states should be assigned to a polar ro-vibrational state participating in a bright transition (for the dimers with non-equivalent monomers, ro-vibrational states can be assigned to one of the two tunneling states of the polar isomer, due to their splitting). Both of these deficiencies of the line-strength method can be rectified by using the second method of ref. 19, called vibrational parent analysis (VPA). Using VPA we also confirm the assignments from the intensity analysis. To do VPA, the calculated rovibrational wavefunctions are expanded in terms of vibrational wavefunctions.19,46 Once one has assigned a vibrational label (with a known symmetry) to a rovibrational state (also of known symmetry) it is possible, to determine the symmetry of the rotational function, using the product rule, Γvr = ΓvΓr. For states localized in the nonpolar well, the symmetries of the 101, 111, and 110 rotational functions are B−, B−, and A+ respectively. This is denoted case a in ref. 19. For polar states, the symmetries are B−, A−, and B+ which is denoted case b. In ref. 19, the bright transitions occur both within and across a tunnelling pair. When the monomers are not equivalent, the exchange symmetry is broken and there are two distinct polar states (as shown in Fig. 3). In this case bright transitions occur only among states associated with one of the polar wells. The 101, 111, and 110 rotational functions have symmetries −, −, and + for states localized above either well. For the nonpolar well, the rotational functions are also −, −, and +.
For the ground nonpolar state, computed rotational constants can be compared to experimental values for (15N2O)2, (15N14NO)2 and 14N2O–15N2O. The discrepancy between the theoretical and fitted experimental values is similar for all isotopologues. The A rotational constants differ by between 0.0012 and 0.0013 cm−1, the calculated and observed B constants are equal (to within the number of digits we report), and the C constants differ by <0.0001 cm−1. These differences are all close to those reported in ref. 18. The nonpolar ground state rotational constants for 14N2O–15N2O of ref. 17, computed from the geometry of the nonpolar configuration on their PES are A = 0.2943 cm−1, B = 0.06058 cm−1, and C = 0.05024 cm−1. They are considerably further from the experimental values than are the results in Table 3.
For the ground polar state, the discrepancy between experiment and theory is larger for some isotopologues than for others. For the equivalent-monomer isotopologue (15N2O)2, the theory–expt differences are −0.0009 cm−1, +0.0003 cm−1, and +0.0002 cm−1 for A, B, C, respectively. The same differences are reported for (14N2O)2 in ref. 19. Similar differences are obtained for 15N14NO–15N2O and PA of 14N2O–15N2O. PB of 14N2O–15N2O has differences of −0.0007 cm−1, +0.0004 cm−1, and +0.0002. Berner et al. also computed rotational constants from equilibrium geometries of the polar 14N2O–15N2O. However, they failed to notice that columns 2 and 3 and also columns 4 and 5 of Table 2 of ref. 14 must be permuted.
Ref. 14 reports some observed polar transitions for several isotopologues and Table 5 shows the comparison between the calculated and observed transition frequencies along with line strengths calculated using the method of ref. 19. For (15N2O)2, all lines with J < 3 are compared. The difference between the calculated and observed transitions frequencies is fairly constant for all observed transitions.
| Polar | JKa′′Kc′′′′ → JKa′Kc′′ | νcal(cm−1) | νobs(cm−1) | νcal − νobs(cm−1) | S |
|---|---|---|---|---|---|
| (15N2O)2 | |||||
| 110 → 101 | 0.2530 | 0.2541 | −0.0011 | 3.68 | |
| 000 → 111 | 0.3414 | 0.3421 | −0.0007 | 2.45 | |
| 212 → 111 | 0.1847 | 0.1838 | 0.0009 | 2.16 | |
| 202 → 101 | 0.1924 | 0.1914 | 0.0010 | 2.88 | |
| 211 → 110 | 0.2005 | 0.1994 | 0.0011 | 2.16 | |
| 211 → 202 | 0.2611 | 0.2621 | −0.0010 | 6.04 | |
| 212 → 101 | 0.4298 | 0.4301 | −0.0003 | 3.68 | |
| 313 → 212 | 0.2756 | 0.2769 | −0.0013 | 3.84 | |
| 303 → 202 | 0.2867 | 0.2881 | −0.0014 | 4.32 | |
| 312 → 211 | 0.2990 | 0.3007 | −0.0017 | 4.32 | |
| 312 → 303 | 0.2744 | 0.2736 | 0.0007 | 8.25 | |
| 14N2O–15N2O | |||||
| B | 000 → 111 | 0.3451 | 0.3453 | −0.0002 | 2.47 |
| A | 000 → 111 | 0.3506 | 0.3512 | −0.0006 | 2.43 |
| 15N14NO–15N2O | |||||
| B | 000 → 111 | 0.3421 | 0.3427 | −0.0007 | 2.45 |
| A | 000 → 111 | 0.3422 | 0.3429 | −0.0007 | 2.45 |
| B | 110 → 101 | 0.2529 | 0.2539 | −0.0011 | 3.67 |
| A | 110 → 101 | 0.2531 | 0.2542 | −0.0011 | 3.67 |
| B | 101 → 212 | 0.4312 | 0.4315 | −0.0003 | 3.67 |
| A | 101 → 212 | 0.4314 | 0.4317 | −0.0003 | 3.67 |
| B | 202 → 303 | 0.2909 | 0.2894 | 0.0015 | 4.34 |
| A | 202 → 303 | 0.2907 | 0.2892 | 0.0015 | 4.35 |
| B | 303 → 404 | 0.3869 | 0.3850 | −0.0019 | 5.79 |
| A | 303 → 404 | 0.3867 | 0.3847 | −0.0020 | 5.79 |
Results for the case when one of the monomers is in an excited state are shown in Table 6 for the ground and fundamental states of 14N2O–15N2O. In these calculations, the monomer in the excited state with ν1 = 1 is 14N2O. The calculated rotational constants for the (N;0000) state differ from the experimental values by 0.0015, 0.0001, and 0.0001 cm−1 for A, B, and C respectively. These differences are slightly larger than the differences between calculated and experimental values for the case when both monomers are not excited when they are 0.0012, 0.0000, and 0.0001 cm−1.
| J = 0 (W; vt, vg, vr, va) (sym) | 101 (sym) | 111 (sym) | 110 (sym) | A | B | C |
|---|---|---|---|---|---|---|
| a The in-phase ν1 = 1 polar from ref. 11.b The out-of-phase ν1 = 1 polar from ref. 17. | ||||||
| (15N2O)2 | ||||||
| 0.0000(N;0000)(A+) | 0.1036(B−) | 0.3418(B−) | 0.3510(A+) | 0.2946 | 0.0563 | 0.0472 |
| (N;0000)13 | 0.2937 | 0.0562 | 0.0471 | |||
| 25.3399(N;1000)(A−) | 25.4434(B+) | 25.6714(B+) | 25.6799(A−) | 0.2840 | 0.0560 | 0.0475 |
| (N;1000)15 | 0.2812 | 0.0561 | 0.0474 | |||
| 41.2497(N;0100)(B+) | 41.3511(A−) | 41.6045(A−) | 41.6136(B+) | 0.3086 | 0.0552 | 0.0461 |
| (N;0100)13 | 0.3061 | 0.0553 | 0.0461 | |||
| 51.6015(N;0010)(A+) | 51.7024(B−) | 51.9473(B−) | 51.9560(A+) | 0.2997 | 0.0548 | 0.0461 |
| 96.9822(N;0001)(A+) | 97.0844(B−) | 97.3126(B−) | 97.3212(A+) | 0.2836 | 0.0554 | 0.0468 |
| (N;0001)15 | 0.2874 | 0.0551 | 0.0462 | |||
| 143.6359(P;0000)(A+) | 143.7322(B−) | 143.9768(A−) | 143.9847(B+) | 0.2967 | 0.0521 | 0.0442 |
| 143.6359(P;0000)(B+) | 143.7322(A−) | 143.9768(B−) | 143.9847(A+) | 0.2967 | 0.0521 | 0.0442 |
(P;0000)11,12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a | 0.2970 | 0.0517 | 0.0439 | |||
(P;0000)17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b | 0.2955 | 0.0519 | 0.0440 | |||
| 164.7414(P;1000)(A−) | 164.8416(B+) | 165.1907(A+) | 165.1992(B−) | 0.4034 | 0.0544 | 0.0459 |
| 164.7414(P;1000)(B−) | 164.8416(A+) | 165.1907(B+) | 165.1992(A−) | 0.4034 | 0.0544 | 0.0459 |
| 14N2O–15N2O | ||||||
| 0.0000(N;0000)(+) | 0.1066(−) | 0.3458(−) | 0.3554(+) | 0.2973 | 0.0581 | 0.0485 |
| (N;0000)13 | 0.2958 | 0.0580 | 0.0484 | |||
| 25.5633(N;1000)(−) | 25.6448(+) | 25.8738(+) | 25.8827(−) | 0.2867 | 0.0577 | 0.0488 |
| 41.5275(N;0100)(+) | 41.6318(−) | 41.8863(−) | 41.8959(+) | 0.3114 | 0.0569 | 0.0474 |
| 52.1881(N;0010)(+) | 52.2919(−) | 52.5381(−) | 52.5471(+) | 0.3026 | 0.0564 | 0.0473 |
| 100.0692(N;0001)(+) | 100.1704(−) | 100.3899(−) | 100.3970(+) | 0.2736 | 0.0541 | 0.0470 |
| 143.3966(PB;0000)(+) | 143.4957(−) | 143.7412(−) | 143.7496(+) | 0.2992 | 0.0537 | 0.0454 |
| 143.7866(PA;0000)(+) | 143.8863(−) | 144.1386(−) | 144.1465(+) | 0.3051 | 0.0528 | 0.0449 |
| 164.6470(PB;1000)(−) | 164.7503(+) | 165.0978(+) | 165.1068(−) | 0.4037 | 0.0561 | 0.0471 |
| 165.0220(PA;1000)(−) | 165.1236(+) | 165.4857(+) | 165.4941(−) | 0.4171 | 0.0550 | 0.0466 |
| Polar | JKa′′Kc′′′′ → JKa′Kc′′ | νcal(cm−1) | S |
|---|---|---|---|
| (15N2O)2 | |||
| 000 → 101 | 0.0963 | 1.44 | |
| 000 → 111 | 0.3414 | 2.45 | |
| 110 → 101 | 0.2531 | 3.68 | |
| 110 → 111 | 0.0079 | 2.16 | |
| (15N14NO)2 | |||
| 000 → 101 | 0.0963 | 1.44 | |
| 000 → 111 | 0.3414 | 2.45 | |
| 110 → 101 | 0.2531 | 3.68 | |
| 110 → 111 | 0.0079 | 2.16 | |
| 14N2O–15N2O | |||
| B | 000 → 101 | 0.0992 | 1.42 |
| A | 000 → 101 | 0.0977 | 1.47 |
| B | 000 → 111 | 0.3451 | 2.47 |
| A | 000 → 111 | 0.3506 | 2.43 |
| B | 110 → 101 | 0.2543 | 3.71 |
| A | 110 → 101 | 0.2608 | 3.64 |
| B | 110 → 111 | 0.0083 | 2.13 |
| A | 110 → 111 | 0.0079 | 2.20 |
| 15N14NO–15N2O | |||
| B | 000 → 101 | 0.0972 | 1.45 |
| A | 000 → 101 | 0.0972 | 1.45 |
| B | 000 → 111 | 0.3421 | 2.45 |
| A | 000 → 111 | 0.3422 | 2.45 |
| B | 110 → 101 | 0.2529 | 3.67 |
| A | 110 → 101 | 0.2531 | 3.67 |
| B | 110 → 111 | 0.0081 | 2.17 |
| A | 110 → 111 | 0.0080 | 2.17 |
For the (15N2O)2 complex, non-polar levels and rotational constants, for the out-of-phase ν1 = 1 state, are also shown in Table 6. There are results for the ground state, and for torsion, geared and anti-geared fundamentals. Experimentally, only transitions to the out-of-phase ν1 = 1 band are observed because the in-phase band is infrared inactive. The (N;0000) rotational constants differ from their experimental counterparts by 0.0009, 0.0001, and 0.0001 cm−1 for A, B, and C respectively. Compared to the ν1 = 0 (N;0000) state, the A constant is slightly closer to and the B constant is slightly further from the experimental value while the difference is the same for the C constant. For the (N;1000) state, the theory–expt differences are 0.0028, −0.0001, and 0.0001 cm−1 for A, B, and C respectively. While the B and C constants are still close to experiment, the difference in the A constant is about three times as large as for (N;0000) state. For the geared (N;0100) excited monomer state, the theory–expt differences are 0.0025, −0.0001, and 0.0000 cm−1 for A, B, and C respectively. Once again, the A constant is significantly over-estimated in our calculations. For the anti-gear (N;0001) state, the theory–expt differences are −0.0038, 0.0003, and 0.0006 cm−1 for A, B, and C respectively. These differences are larger than for any other state. The larger differences might be due in part to the fact that the fit of the experimental levels to eigenvalues of the standard rotational Hamiltonian is not as good. The order of magnitude of the error on the fitted constants for energy levels of J < 2 is about two orders of magnitude larger than for the other states. A possible explanation for this is coupling with the (N;0010) or (N;0020) states. The coupling with the (N;0010) state is shown in Fig. 9 of ref. 19 and the coupling with (N;0020) is shown in Fig. 2.
For the nonpolar isomer, only the in-phase monomer stretching vibration is infrared inactive. This differs from the polar isomer which has two bands, for both the in-phase and out-of-phase ν1 = 1 upper states.17 With the adiabatic approximation we use, out-of-phase and in-phase upper states have identical energies. However, from experimental results in Table 6, a noticeable difference in the rotational constants is observed. The theory–expt difference is −0.0003, 0.0004, and 0.0003 cm−1 for the in-phase, and 0.0012, 0.0002, 0.0002 cm−1 for the out-of-phase constants A, B, and C respectively. This compares to the ν1 = 0 differences of −0.0009, 0.0003, 0.0002 cm−1.
4 Conclusion
Ro-vibrational energy levels and line strengths have been computed for four isotopologues of the N2O dimer. Wavefunctions of polar and nonpolar states were analyzed to assign states. In most cases, vibrational frequencies, rotational constants, and ro-vibrational transition frequencies agree well with available experimental values. For nonpolar states, differences between calculated and experimental rotational constants for all the isotopologues are similar to those previously reported for (14N2O)2 in ref. 19. For polar states, the differences are also similar for isotopologues with equivalent monomers. Dimers with different monomers do not have polar states that occur in degenerate pairs with both members of each pair having wavefunction amplitude in both polar wells. Instead, the polar vibrational wavefunctions are localized in only one polar well. We find that the energy of the polar vibrational state localized above the well for which the lighter monomer has N inside is higher than the energy of the polar vibrational state localized above the well for which the heavier monomer has N inside, for both the dimers with different monomers we studied. For 15N14NO–15N2O, the calculated and experimental rotational constants agree well for states localized in each of the polar wells. However, for polar states of 14N2O–15N2O the agreement is better for one well than for the other.Acknowledgements
This work has been supported by the Natural Sciences and Engineering Research Council of Canada. Calculations were done on computers purchased with money from the Canadian Foundation for Innovation.References
- T. E. Gough, R. E. Miller and G. Scoles, J. Chem. Phys., 1978, 69, 1588–1590 CrossRef CAS.
- R. Miller, R. Watts and A. Ding, Chem. Phys., 1984, 83, 155–169 CrossRef CAS.
- R. Miller and R. Watts, Chem. Phys. Lett., 1984, 105, 409–413 CrossRef CAS.
- M. Gauthier, J. Chem. Phys., 1988, 88, 5439–5449 CrossRef CAS.
- Z. S. Huang and R. E. Miller, J. Chem. Phys., 1988, 89, 5408–5416 CrossRef CAS.
- Y. Ohshima, Y. Matsumoto, M. Takami and K. Kuchitsu, Chem. Phys. Lett., 1988, 152, 294–298 CrossRef CAS.
- B. H.-B. Qian, W. A. Herrebout and B. J. Howard, Mol. Phys., 1997, 91, 689–696 CrossRef.
- A. Hecker, I. Scheele and M. Havenith, Phys. Chem. Chem. Phys., 2003, 5, 2333–2336 RSC.
- M. Dehghani, M. Afshari, Z. Abusara, N. Moazzen-Ahmadi and A. R. W. McKellar, J. Chem. Phys., 2007, 126, 164310 CrossRef CAS PubMed.
- M. Dehghany, M. Afshari, N. Moazzen-Ahmadi and A. R. W. McKellar, Phys. Chem. Chem. Phys., 2008, 10, 1658–1661 RSC.
- M. Dehghany, M. Afshari, Z. Abusara, C. V. Eck and N. Moazzen-Ahmadi, J. Mol. Spectrosc., 2008, 247, 123–127 CrossRef CAS PubMed.
- M. Dehghany, M. Afshari, R. Thompson, N. Moazzen-Ahmadi and A. McKellar, J. Mol. Spectrosc., 2008, 252, 1–4 CrossRef CAS PubMed.
- M. Dehghany, M. Afshari, Z. Abusara and N. Moazzen-Ahmadi, Phys. Chem. Chem. Phys., 2009, 11, 7585–7588 RSC.
- N. R. Walker, A. J. Minei, S. E. Novick and A. C. Legon, J. Mol. Spectrosc., 2008, 251, 153–158 CrossRef CAS PubMed.
- M. Rezaei, K. H. Michaelian and N. Moazzen-Ahmadi, J. Chem. Phys., 2012, 136, 124308 CrossRef CAS PubMed.
- H. Valdes and J. A. Sordo, J. Phys. Chem. A, 2004, 108, 2062–2071 CrossRef CAS.
- G. M. Berner, A. L. L. East, M. Afshari, M. Dehghany, N. Moazzen-Ahmadi and A. R. W. McKellar, J. Chem. Phys., 2009, 130, 164305 CrossRef CAS PubMed.
- R. Dawes, X.-G. Wang, A. W. Jasper and T. Carrington, Jr., J. Chem. Phys., 2010, 133, 134304 CrossRef PubMed.
- X.-G. Wang, T. Carrington, Jr., R. Dawes and A. W. Jasper, J. Mol. Spectrosc., 2011, 268, 53–65 CrossRef CAS PubMed.
- L. Zheng, Y. Lu, S.-Y. Lee, H. Fu and M. Yang, J. Chem. Phys., 2011, 134, 054311 CrossRef PubMed.
- M. Pavanello, L. Adamowicz, A. Alijah, N. F. Zobov, I. I. Mizus, O. L. Polyansky, J. Tennyson, T. Szidarovszky, A. G. Császár, M. Berg, A. Petrignani and A. Wolf, Phys. Rev. Lett., 2012, 108, 023002 CrossRef.
- S. A. Peebles and R. L. Kuczkowski, Mol. Phys., 2001, 99, 225–237 CrossRef CAS.
- J. Tennyson and A. van der Avoird, J. Chem. Phys., 1982, 77, 5664–5681 CrossRef CAS.
- F. Gatti and C. Iung, Phys. Rep., 2009, 484, 1–69 CrossRef CAS PubMed.
- M. J. Bramley and T. Carrington, Jr., J. Chem. Phys., 1993, 99, 8519–8541 CrossRef CAS.
- G. Audi and A. Wapstra, Nucl. Phys. A, 1993, 565, 1–65 CrossRef CAS.
- G. Audi and A. Wapstra, Nucl. Phys. A, 1995, 595, 409–480 CrossRef.
- R. A. Toth, J. Opt. Soc. Am. B, 1987, 4, 357–374 CrossRef CAS.
- A. Bauer, J. Teffo, A. Valentin and T. McCubbin, J. Mol. Spectrosc., 1986, 120, 449–454 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2001, 114, 1473–1477 CrossRef CAS.
- R. Chen and H. Guo, J. Chem. Phys., 2001, 114, 1467–1472 CrossRef CAS.
- V. A. Mandelshtam and H. S. Taylor, J. Chem. Phys., 1997, 106, 5085–5090 CrossRef CAS.
- S.-W. Huang and T. Carrington, Jr., Chem. Phys. Lett., 1999, 312, 311–318 CrossRef CAS.
- M. J. Bramley, J. W. Tromp, T. Carrington, Jr. and G. C. Corey, J. Chem. Phys., 1994, 100, 6175–6194 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2001, 115, 9781–9796 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2003, 118, 6946 CrossRef CAS.
- X.-G. Wang, T. Carrington, Jr., J. Tang and A. R. W. McKellar, J. Chem. Phys., 2005, 123, 034301 CrossRef PubMed.
- P. Sarkar, N. Poulin and J. T. Carrington, J. Chem. Phys., 1999, 110, 10269–10274 CrossRef CAS.
- X.-G. Wang and J. T. Carrington, J. Chem. Phys., 2008, 129, 234102 CrossRef PubMed.
- H. Wei and T. Carrington, Jr., J. Chem. Phys., 1992, 97, 3029–3037 CrossRef CAS.
- J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225–230 CrossRef CAS.
- D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2004, 121, 2937–2954 CrossRef CAS PubMed.
- R. Zare, Angular momentum: understanding spatial aspects in chemistry and physics, Wiley, 1988 Search PubMed.
- N. Walker, private communication, 2013.
- E. Matyus, C. Fabri, T. Szidarovszky, G. Czako, W. D. Allen and A. G. Csaszar, J. Chem. Phys., 2010, 133, 034113 CrossRef PubMed.
| This journal is © the Owner Societies 2013 |
