Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism and microkinetics of the Fischer–Tropsch reaction†
R. A. van Santen*ab, A. J. Markvoortac, I. A. W. Filotab, M. M. Ghouriab and E. J. M. Hensenb
aInstitute for Complex Molecular Systems, Eindhoven University of Technology, PO Box 513, 5600MB, Eindhoven, The Netherlands. E-mail: R.A.v.Santen@tue.nl
bLaboratory of Inorganic Materials Chemistry, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, PO Box 513, 5600MB, Eindhoven, The Netherlands
cComputational Biology group, Department of Biomedical Engineering, Eindhoven University of Technology, PO Box 513, 5600MB, Eindhoven, The Netherlands
First published on 21st August 2013
Abstract
The increasing availability of quantum-chemical data on surface reaction intermediates invites one to revisit unresolved mechanistic issues in heterogeneous catalysis. One such issue of particular current interest is the molecular basis of the Fischer–Tropsch reaction. Here we review current molecular understanding of this reaction that converts synthesis gas into longer hydrocarbons where we especially elucidate recent progress due to the contributions of computational catalysis. This perspective highlights the theoretical approach to heterogeneous catalysis that aims for kinetic prediction from quantum-chemical first principle data. Discussion of the Fischer–Tropsch reaction from this point of view is interesting because of the several mechanistic options available for this reaction. There are many proposals on the nature of the monomeric single C atom containing intermediate that is inserted into the growing hydrocarbon chain as well as on the nature of the growing hydrocarbon chain itself. Two dominant conflicting mechanistic proposals of the Fischer–Tropsch reaction that will be especially compared are the carbide mechanism and the CO insertion mechanism, which involve cleavage of the C–O bond of CO before incorporation of a CHx species into the growing hydrocarbon chain (the carbide mechanism) or after incorporation into the growing hydrocarbon chain (the CO insertion mechanism). The choice of a particular mechanism has important kinetic consequences. Since it is based on molecular information it also affects the structure sensitivity of this particular reaction and hence influences the choice of catalyst composition. We will show how quantum-chemical information on the relative stability of relevant reaction intermediates and estimates of the rate constants of corresponding elementary surface reactions provides a firm foundation to the kinetic analysis of such reactions and allows one to discriminate between the different mechanistic options. The paper will be concluded with a short perspective section dealing with the needs for future research. Many of the current key questions on the physical chemistry as well as computational study of heterogeneous catalysis relate to particular topics for further research on the fundamental aspects of Fischer–Tropsch catalysis.
 R. A. van Santen | Rutger Anthony van Santen obtained his doctorate from the University of Leiden, Netherlands. After an initial career at Shell Research in 1988, he joined the Eindhoven University of Technology as a Professor of Catalysis, and in 2005 he was made Royal Netherlands Academy of Science and Arts Professor. He is a member of the Royal Dutch Academy of Arts and Sciences, Dutch Academy of Engineering, and is a Knight in the order of the Dutch Lion. Professor van Santen is the author or editor of 13 books, over 700 research papers and 22 patents, and has been awarded several national and international awards and visiting professorships. |
 A. J. Markvoort | Albert Jan Markvoort is an Assistant Professor in the Computational Biology group and member of the Institute for Complex Molecular Systems at the Eindhoven University of Technology (the Netherlands), where he received his MSc in Applied Physics and PhD in Computer Science. Currently he is part of the Program for Evolutionary Dynamics at Harvard University (USA). His main research interests focus on molecular simulation and modeling of various self-assembling and self-organizing systems. |
 I. A. W. Filot | Ivo Filot finished his Master’s Degree in Chemical Engineering in 2009. He is currently a PhD student at the Laboratory for Inorganic Materials Chemistry and Institute of Complex Systems at Technical University Eindhoven. His thesis research concerns the quantum-chemistry and microkinetics of Fischer–Tropsch catalysis. |
 M. M. Ghouri | Minhaj M. Ghouri received his MS degree in ‘Molecular Sciences and Nanotechnology’ and PhD in engineering from Louisiana Tech University, Louisiana, USA, in the year 2009. He then moved to Eindhoven, NL, where he started his current position as the postdoctoral researcher working with Prof. Rutger van Santen at the Schuit Institute of catalysis, Eindhoven University of Technology. His current research interests include atomistic and multiscale modeling, computational catalysis and kinetics and materials science. |
 E. J. M. Hensen | Emiel Hensen studied Chemical Engineering at Eindhoven, where he received a PhD in Chemical Engineering and Chemistry in 2000. He held junior positions at the University of Amsterdam and Eindhoven University of Technology, before becoming a full professor of heterogeneous catalysis in Eindhoven in 2009. He is recipient of VENI, VIDI and Casimir awards of the Netherlands Organization for Scientific Research. He is chairman of the Netherlands Institute for Catalysis Research (NIOK). His research interests are in the field of catalysis and include mechanism of heterogeneous catalysis, computational modeling, kinetics, porous solids, nanoparticles and materials science. |
1 Introduction
The past decades have seen major advances in the study of heterogeneous catalysis on a molecular level.1–5 A significant contribution to this state of affairs has been the development of instrumentation, with the use of surface model systems (Somorjai,1 Ertl2), that enabled access to molecular events at the catalyst surface. This in combination with computational catalytic advances6–10 created the opportunity to put the relation between the chemistry of catalytically reactive surfaces and catalyst performance on a firm footing. Moreover, apart from providing a bridge between surface chemistry and kinetics of catalytic reactions, the possibility of ab initio simulation of catalytic reactivity is also essential for fruitful development of physical chemical theories of catalytic reactivity, since it provides the essential data on the energies of reaction intermediates and transition barriers to test such theories.This perspective will describe advances in our current understanding, based on molecular catalysis research of the past decade,11–36 of the mechanism of one particular heterogeneous catalytic reaction of significant current interest, that is, the Fischer–Tropsch reaction. This reaction which converts synthesis gas into liquid hydrocarbons is used in commercial processes to provide alternative fuel to that derived from crude oil, as the synthesis gas (a mixture of mainly CO and H2) can be produced by reforming coal, natural gas or biomass with steam and oxygen.37 As synthesis gas from different sources has different ratios of H2 to CO, different catalysts are being used. Synthesis gas derived from coal, with a low H2 to CO ratio, for instance, is preferentially converted by Fe based catalysts, whereas Co is the preferred catalytic material for Fischer–Tropsch processes involving synthesis gas with a higher H2/CO ratio derived from natural gas. However, although discovered nearly a century ago,38 the exact mechanisms of the Fischer–Tropsch reaction are still unknown and many conflicting mechanistic theories persist.
Elucidation of the mechanisms is important for the design of novel catalysts that increase selectivity of the reaction. Since synthesis gas production is an expensive process, there is a practical incentive to reduce non-selective methane and light gas production. Whereas the main products of the Fischer–Tropsch reaction are hydrocarbons, efficient ways to produce other products selectively are desirable.39 Moreover, there is a need to improve the stability of the catalysts so as to reduce catalyst cost.
One particular aspect we will focus on is the relation between catalyst performance and catalyst structure. Such information is especially relevant for synthesis of improved catalytic systems. The other focus of our attention will be on the implications of our increased understanding for existing kinetics models of the Fischer–Tropsch reaction. We will discuss the molecular basis of the catalytic reactivity of metals such as Fe, Ni, Co, Rh and Ru with respect to the Fischer–Tropsch reaction and especially focus on how structural differences of catalytic reaction sites affect catalyst performance.
Structural effects are known in different forms. Fe, for instance, will be converted to the carbide phase,40 with computational studies of this system in its carbidic phase available.12,41 Other structural effects include the activation by promoters. Such promoters are especially used in Fe based catalysis, where often alkali and S are used,42 but also in Rh based catalysts, which are of interest for higher alcohol production promoted by reducible oxides.39 The state of the surface of such systems is not well understood and computational studies of such complex systems are in an initial stage.43–46
It is also well known that catalysts that remain mainly metallic during the Fischer–Tropsch reaction change structure accompanied by an initial increase in the rate of CO consumption. Schulz47,48 has called this phenomenon catalyst self-organization. A striking experimental observation of surface reconstruction of a Co single surface terrace is a STM study by Wilson et al.,49 which demonstrated that an initially planar Co(0001) terrace converts into small nanoparticles when exposed to the Fischer–Tropsch reaction condition. Computational studies50 indicate that most likely increasing coverage with adsorbed C atoms provides a driving force for these transformations by stabilization of the more open surfaces.
Computational studies, as we will discuss here, that study the performance of a catalytic reaction for a chosen surface structure and composition provide a reference to an understanding of the very different reactivity patterns for the different surface phases. The microkinetics approach implies that we limit ourselves to the intrinsic kinetics of the reaction that exclude mass and heat transfer effects. In practical catalysis the latter are essential to consider as for instance discussed by Iglesia and others.51,52
A molecular catalysis approach will first of all have to focus on the mechanism of the reaction. As for many of the heterogeneous reactions, there is considerable debate about the reaction mechanism of the Fischer–Tropsch reaction. Two essentially different mechanistic proposals which describe the reaction steps of the hydrocarbon chain growth reaction, i.e., the carbide mechanism38versus the CO insertion mechanism,53 are at the center stage of this debate. As has been discussed already in a very early theoretical study of this reaction,54 the key issue concerns the nature of the monomeric single C atom containing “C1” intermediate that is incorporated into the growing hydrocarbon chain. According to the proponents of the carbide mechanism, the C1 intermediate is formed by initial cleavage of the C–O bond of carbon monoxide. In a consecutive step the partially hydrogenated CHx intermediate is inserted into the growing hydrocarbon chain. According to the CO insertion and related theories, the “C1” species to be inserted into the growing hydrocarbon chain still contains a C–O bond, which is broken only after the insertion of that species into the growing chain.
Because of these conflicting mechanistic theories, there is no consensus on the elementary rate expressions to be used in kinetics expressions. To resolve these issues is one of the main goals of this paper. We will see that computational catalysis currently can help significantly to resolve the mechanistic issues. It provides information on the relative stability of reaction intermediates as well as elementary rate constant parameters as activation energy barriers and transition state entropies. The availability of such catalyst surface structure and composition dependent quantitative data makes microkinetics simulations useful for catalyst performance studies. Using these data, different mechanistic models can be tested against experiments and evaluated. The kinetics simulations integrate elementary reaction steps into a catalytic cycle that for the Fischer–Tropsch reaction may have varying elementary reaction controlling steps dependent on catalyst or reaction conditions. Therefore it is essential to determine the steady-state concentrations of reaction intermediates and products with solution methods that solve the partial differential equations (PDEs), that compute their rate of change without assuming a rate controlling step.55 We will add to the theory of Fischer–Tropsch kinetics by formulating the analytical kinetics expressions that apply in reaction regimes with different rate controlling steps.
Information on the state of the surface under reaction conditions is critical. Surface thermodynamics methods56–58 are available to predict overlayer formation as a function of reaction conditions. These methods incorporate interaction of adatoms and local surface reorganization. However, on the atomistic level so far such surface reorganization effects have only been combined computationally with an ongoing catalytic reaction for less complex reactions using approximate grid dependent methods.59
In this review we will therefore limit ourselves to mechanistic and kinetics considerations on static surfaces, except that the quantum-chemical calculations include local changes in metal–metal bond distances when reaction intermediates change. With these limitations, microkinetics simulations based on first principle input of elementary reaction rates and relative stability or reaction intermediates can give predictions of catalyst performance as a function of surface structure and composition. As we will see, microkinetics simulations of the catalytic reaction are essential to properly identify the relative importance of particular reaction intermediates.
The microkinetics simulations and computational quantum-chemical catalytic data will lead to the interesting conclusion that for the systems studied so far, the carbide mechanism is the most likely candidate. The benefit of the identification of a particular mechanism is that it provides the link between catalyst performance and catalyst structure and composition. It gives theoretical insight into the relation between the chemistry of catalyst surface and catalyst performance. It appears that surface reaction centers of unique topology consisting of at least 5 or 6 metal atoms in a surface step-edge type arrangement are needed for high chain growth.
Using a similar combined quantum-chemical and microkinetics approach we will also address a fundamental assumption of Fischer–Tropsch kinetics based on empirical observations.55,60–66 This is the intriguing assumption that the rate of CO consumption is independent of chain growth probability. This is counterintuitive since within the carbide mechanistic scheme the rate of CO to CHx transformation will have to be fast compared to the rate of methane formation from CHx. Otherwise, as we will discuss, the CHx surface concentration will be too low and chain growth will have a low probability.
We will also highlight essential results from the extensive and very relevant experimental literature51,60,67–76 on the mechanism of the Fischer–Tropsch reaction to illustrate the different mechanistic proposals. One of the most important experimental observations of the past decade is the metal particle size sensitivity of the Fischer–Tropsch reaction in the nanometer regime of the reaction.77 Generally, the CO consumption rate of the reaction per exposed surface metal atom (turnover frequency) decreases steeply when the particle size becomes less than 6 nm. Steady-state isotopic transient kinetic analysis (SSITKA) transient experiments have shown that in some cases this relates to the decrease in the surface concentration of a uniquely reactive site.78 There are indications in the case of Co79,80 that also the reactivity of these centers is affected by particle size. Interestingly, quantum-chemical data show that some of the key elementary reaction steps of the Fischer–Tropsch reaction, such as CO dissociation and M–C bond cleavage reactions, are very sensitive to site structure, whereas other elementary reactions such as the chain growth reaction are less structure demanding.
In the next section, we will introduce the molecular chemistry of the Fischer–Tropsch reaction. We will discuss different mechanistic proposals as well as the most important elementary reaction steps and reaction intermediates. This will be followed in Section 3 by a short review of the most important quantum-chemical insights into surface reactivity and relative stability of key elementary reaction intermediates and corresponding reaction rates. The numerical data used are based on state of the art quantum-chemical DFT calculations, for details of which we refer to the original papers. These two sections on reaction intermediates provide a basis for the microkinetics of the Fischer–Tropsch reaction's analysis of Section 4. There we will discuss the kinetics consequences of different mechanistic options and also present analytical expressions for the rate of CO consumption and chain growth probability valid in different reactivity regimes. The section will be concluded with a summarizing discussion where we will relate the mechanistic and kinetics insights with the results of transient kinetics experiments on catalyst particle size dependence. In the final perspective section we will evaluate the current status of fundamental insights into the Fischer–Tropsch reaction and indicate open questions for future research.
2 The reaction mechanism
The Fischer–Tropsch reaction is a surface polymerization reaction. In such a reaction one distinguishes reaction initiation, chain growth and reaction chain termination. In this section we will discuss the different proposals on the chemistry of these three different reactions, the kinetic consequences of the carbide versus the CO insertion chain growth mechanistic proposals as well as the main experiments that are supporting each mechanism.Chain growth of an adsorbed hydrocarbon intermediate occurs through insertion of an adsorbed C1 reaction intermediate that contains one carbon atom. In the carbide mechanism the generation of a CHx intermediate initiates the overall reaction, where the CHx intermediate is formed by dissociation of the C–O bond of adsorbed CO. In contrast according to the CO insertion mechanism chain growth occurs in two separate steps. After the initial dissociation of a CO molecule, another CO inserts into the CHx species that has been generated. Then the C–O bond of the inserted CO cleaves and an initial C2Hy species is generated. Further chain growth occurs by consecutive insertion steps of CO into adsorbed hydrocarbon fragments followed by C–O bond cleavage. The reaction intermediates and reaction steps that correspond to these carbide and CO insertion chain growth mechanisms are schematically shown in Fig. 1a and b, respectively.
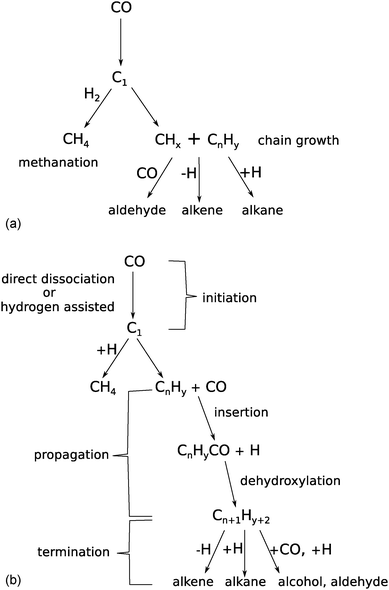 | ||
| Fig. 1 Reaction scheme of the Fischer–Tropsch reaction according to (a) carbide mechanism and (b) CO insertion chain growth mechanism (adapted from ref. 74). | ||
As we will discuss in the following, the chain growth reaction is to be followed by a chain termination step that liberates adsorbed hydrocarbon from the surface. The termination reaction can be due to addition of hydrogen, β-CH cleavage or CO insertion resulting in the formation of paraffins, olefins and oxygenates, respectively.
Additionally, within the carbide mechanism, there is the issue of the particular “CHx” intermediate to be inserted into the growing hydrocarbon chain, for which CH32 as well as CH2 (ref. 81 and 82) species have been proposed. The nature of the CHx species to be inserted relates to the nature of the adsorbed growing hydrocarbon chains that are generated during the polymerization stage of the reaction and on which no consensus exists. We will discuss the three main chain growth proposals, i.e., the proposals by Brady–Pettit, Maitlis, and Gaube, which have been summarized in Fig. 2.
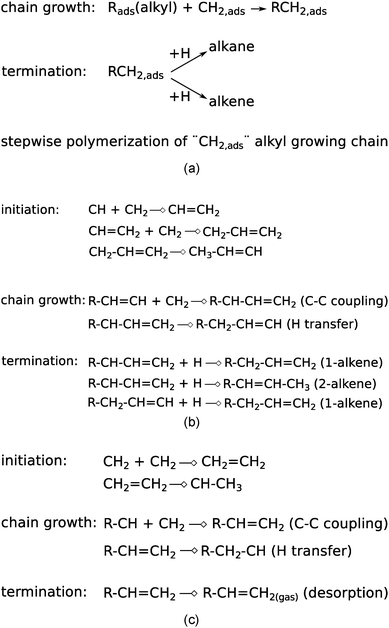 | ||
| Fig. 2 The three main chain growth reactions proposed within the carbide scheme. (a) Brady–Pettit,81,82 (b) Maitlis,71,83–85 and (c) Gaube.86 | ||
With the exception of the Maitlis proposal “CH2”71,83–85 is proposed to be the inserting “C1” species, but the nature of the growing hydrocarbon chain can be alkyl, alkenyl or alkylidene. According to the Maitlis proposal, to form the “C2” intermediate, recombination of “CH” with “CH2” type growing chains occurs. As we will see in the next section, quantum-chemical results indicate that instead of “CH2”, “CH” may play a much more dominant role than assumed according to the other mechanisms of Fig. 2. Gaube et al.86 proposed chain growth through recombination of “CH2” with carbene terminated hydrocarbon chains.
Chain growth through CO insertion has been originally proposed by Pichler and Schulz.87 In addition to direct CO insertion, also insertion of partially hydrogenated intermediates such as CHO or CHOH16,37,69,88,89 has been proposed. Oxygenate desorption and chain growth compete. Hence production of longer oxygenates will not occur through the CO insertion chain growth mechanism, but occurs through the carbide mechanism.
Within the carbide mechanism, the main competing process with the chain growth reaction is formation of methane. A high rate of CO to CHx transformation and a high “C1” insertion rate into the growing chain, but a low rate of “CHx” hydrogenation and hydrocarbon chain termination, are conditions for high production of long hydrocarbons. We will show that the C–O bond cleavage reaction will have to be fast compared to methane formation. When this condition is satisfied, a high selectivity for formation of longer hydrocarbons is possible as long as the rate of “C1” insertion into the growing hydrocarbon chain is fast and the rate of chain growth termination is slow compared to the latter. Then the rate of chain growth may be fast compared to the C–O bond activation and “C1” formation can be considered rate controlling.
This situation with respect to CO dissociation is different for the CO insertion mechanism case. Here the CO dissociation rate has to be slow compared to the rate of CO insertion into the growing chain and the rate of chain growth termination. The rate of methanol formation from CO also has to be slow. The rate of C–O bond cleavage after insertion into the growing hydrocarbon chain has to be fast.
As we will see later in the section on the microkinetics of the reactions, the different mechanistic schemes lead to very different expressions for the chain growth probability α and the rate of CO consumption. Then we will also discuss the consequences of computational and experimental data of the relative stability of reaction intermediates on Fischer–Tropsch performance.
It has been realized already in the seventies of the previous century90,91 that there is a relation between metals that readily dissociate CO and Fischer–Tropsch activity. However it has also been realized that the activation energies92 for direct activation of CO on the transition metal terraces are not consistent with the measured apparent activation energies of the CO consumption rate. A recent experiment by Salmeron et al.93 convincingly demonstrated low activation energy of CO bond cleavage in adsorbed CO on Co particles when promoted by H2. Computational studies also show that on less reactive surfaces H activated C–O bond cleavage through intermediate formyl formation has a lower barrier than direct CO dissociation.29,31–33 This barrier can be comparable to that of the activation energy of the overall reaction.
The most convincing experiments in favor of the carbide mechanism are those by Biloen and Sachtler94,95 and by Brady and Pettit.81,82 By decomposing 13CO on a Ru catalyst and exposing this surface to a mixture of synthesis gas with 12CO, Biloen et al. found that more than one 13C isotope label was incorporated into the growing chain, which proves that “C1” generated by decomposition of CO is the monomer that is inserted into the growing hydrocarbon chain. Brady and Pettit decomposed CH2N2 on a metal catalyst and discovered upon exposure to hydrogen longer hydrocarbon formation. Koerts et al.96,97 decomposed CH4 on different metal surfaces, and found longer hydrocarbons upon exposure to hydrogen gas near room temperature. Even Pt will generate longer hydrocarbons from C1 species generated from methane. The latter experiments indicate not only that a “CHx” species is responsible for chain growth, but also that this property is not limited to the familiar Fischer–Tropsch active metals where “CHx” is generated by dissociation of CO.97 Low selectivity can be due to non-reactive carbon formation and rapid competitive formation of methane.
These experiments also support the idea that not the chain growth reaction but CO activation is the CO consumption rate limiting step. This is one of the reasons that the Fischer–Tropsch reaction occurs at a higher temperature than required for the chain growth reaction. The other reason is that at low temperature CO adsorption will block the surface and no dissociation reaction can occur.
On the other hand, the high pressure needed for Fischer–Tropsch reactivity and the resulting high coverage with CO are consistent with the CO insertion chain growth mechanism. An elegant infrared experiment by Beitel et al.98,99 demonstrates rapid CO consumption with the formation of adsorbed hydrocarbon. A recent transient kinetics experiment by Schweicher et al. also suggests a relation between CO coverage and rate of chain growth.149 Based on kinetics simulations we will evaluate these experiments and discuss consistency with the carbide and/or CO insertion mechanism in later sections.
3 Quantum-chemistry of the Fischer–Tropsch reaction
The ability of computational quantum-chemical techniques to study quantitatively the relative stability of reaction intermediates on surfaces representative of the experimental condition has made a major impact on theories of catalysis.100–103 Even more important is the possibility to calculate not only the energies positioned in their local minima, but also transition state structures and energies. The latter possibility to calculate the rate constants of elementary reaction steps provides the connection between surface chemistry and catalyst performance. It enables one to do the microkinetics simulations discussed in the next section.Quantum-chemistry relates surface chemistry to the nature of the surface chemical bond. Based on state of the art quantum-chemical methods in the eighties, the basic molecular orbital descriptions of the surface chemical bond have been developed. These are highlighted in the very instructive book of Hoffmann,104 that is still useful to rationalize the many DFT based computational results that are available today.
The quantitative data we will use are based on more recent DFT quantum-chemical studies. Preferred recombination reactions sensitively depend on the structure of the metal surface. Barriers for overall C–C bond formation are relatively low compared to those of C–O bond activation and chain growth termination. These barriers are indeed found to be rather insensitive to the composition of the catalyst surface.
CO activation will be discussed in detail in the following subsection. It will appear that direct CO activation is very sensitive to surface structure. Only surface step-type reaction sites provide activation energies low enough that CO activation competes with undesirable hydrogenation of “CHx” species to methane. Hydrogen activated CO activation is the dominant route to “CHx” formation on less reactive surfaces, which however are expected to give low chain growth probability.
Within the carbide mechanism CO insertion into a growing hydrocarbon chain will lead to chain growth termination with the formation of oxygenates. When the CO insertion chain growth mechanism is operational this will not necessarily be the case. A detailed discussion of the available quantum-chemical information on the corresponding elementary steps will be given. It will appear that available data indicate that direct C–C bond formation through “CHx” insertion has a significantly lower overall activation energy barrier than that through CO insertion as long as x < 3. The barrier known for CO insertion is consistent with the possibility that it terminates the growing hydrocarbon chain.
3.1 C–C bond formation and chain termination
On metal surface terraces chain growth by recombination of a CH3,ads species with growing alkyl chains has a barrier higher than 200 kJ mol−1. This agrees with early extended Hückel method results by Zheng et al.105 which explained this by the umbrella effect arising when two parallel adsorbed CH3 species become close to each other on a surface. The spatially extended CH bonds will then make the first contact, which leads to a repulsive interaction and inhibits the formation of C–C bonds.The recombination of CHx species with x < 3 with a growing hydrocarbon chain is substantially more favorable because then the umbrella repulsion effect is reduced and other partially occupied orbitals on the CHx species are available to stabilize the activation energy. Calculated activation energies of CHx–CHy fragments adsorbed to a CO terrace and step site are shown in Table 1.14
| C + C | C + CH | C + CH2 | C + CH3 | CH + CH | CH + CH2 | CH + CH3 | CH2 + CH2 | CH2 + CH3 | |
|---|---|---|---|---|---|---|---|---|---|
| Flat | 1.22 | 0.91 | 0.74 | 0.94 | 0.86 | 0.76 | 1.05 | 0.70 | 1.11 |
| Step | 2.43 | 1.96 | 1.34 | 1.09 | 1.76 | 1.32 | 1.55 | 0.22 | 0.73 |
The data of Table 1 can be used to evaluate the relative barriers for C–C bond formation in the chain growth reaction by considering one of the CHx species to be the analogue of a growing adsorbed hydrocarbon chain. One observes that recombination with adsorbed C or CH is favorable on a terrace site but recombination with a CH2 species is more favorable on the stepped site. Also the more strongly bonded C and CH species tend to have higher activation energies for recombination than the CH2 species. The weaker adsorption energy of the adsorbed C atom is the reason for the preferential formation of a carbonaceous overlayer on a flat terrace, rather than on the stepped site where it would deactivate the site responsible for selective Fischer–Tropsch catalysis.
Activation energies between recombining CHx species tend to decrease with x. The increased coordinative saturation of the carbon atom decreases the energy of the metal–C bond. This has been predicted by Shustorovich,106 which he ascribed to bond order conservation, and has been validated by Nørskov et al.,107 who gave this phenomenon the name “scaling law” (see also ref. 7).
Except for C–C bond formation with “CH2” fragments, recombination on the more weakly adsorbate binding terraces is generally preferred. The CH and CH2 recombination reaction on the terrace competes with CH2 and CH3 recombination in the step edge. CH2 with CH2 recombination has an extremely low barrier. However, to complete the chain growth reaction hydrogen atom transfer reactions have to occur. The isomerization of adsorbed ethylene by H atom transfer proposed by Gaube86 (see Fig. 2c) to generate the chain growth intermediate increases the apparent activation energy of this reaction substantially.17 The CH2 and CH2 recombination reaction refers to the Gaube mechanism, the CH2 and CH3 recombination to the Brady–Pettit chain growth reaction, and the CH and CH2 recombination to the Maitlis mechanism. All three types of chain growth reactions appear to have comparable activation energies, but site requirements differ.
Efficient C–C bond formation is possible on terraces as well as on step-edge sites. The nature of the growing chain and “CHx” species inserted determines the specific structure dependence of the chain growth reaction. A comparison of activation energies of CHx–CHy recombination for different metals can be found in Table 2.
| C + C | C + CH | C + CH2 | C + CH3 | CH + CH | CH + CH2 | CH + CH3 | CH2 + CH2 | CH2 + CH3 | |
|---|---|---|---|---|---|---|---|---|---|
| Co | 2.46 | 0.96 | 1.36 | 1.12 | 1.74 | 1.34 | 1.57 | 0.27 | 0.76 |
| Rh | 2.26 | 1.66 | 1.58 | 1.50 | 1.44 | 1.56 | 1.60 | 0.86 | 0.89 |
| Ru | 1.80 | 1.29 | 1.13 | 1.28 | 1.26 | 1.25 | 1.62 | 0.92 | 1.17 |
One notes substantial activation energy differences for C–C bond formation when Cads is involved. The activation energies of CH and CH2 bond formation or CH and CH3 bond formation are found to be insensitive to changes in the M–C bond energies. Larger variation is found for CH2 and CH2 recombination than for CH2 and CH3 recombination. But barriers remain relatively low. This agrees with the experimental observations mentioned in the previous section, which indicate that the rate constant of the chain growth reaction is not very sensitive to the catalytically active metal used.
Within the carbide mechanism rapid chain growth requires that hydrogenation of Cads or CHads to give methane is a relatively slow reaction. Otherwise no “CHx” species is available for incorporation into the growing hydrocarbon chain. Since to produce methane the M–C bond has to be completely ruptured, whereas to form a C–C bond from a CHx species the M–C bond has to remain partially intact,108 the activation energies for methane formation tend to vary more strongly with variation in the surface adsorption strength than the activation energy for C–C bond formation. Methane formation from adsorbed CHx species has been studied by many authors.40 On surface terraces of Co, Ru or Rh, the overall activation energy to form CH4 from CHads is at least 100 kJ mol−1 and can increase to 140 kJ mol−1. This is substantially higher than that of the lower activation energy C–C bond forming reactions, which for several coupling pathways is of the order of 70 kJ mol−1.
The quantum chemistry of CO insertion is quite analogous to that of C–C bond formation by recombination of CH3 species. The CO insertion reaction produces oxygenates within the carbide mechanism and is part of the chain growth reaction within the CO insertion chain growth mechanism. Similarly as for C–C bond formation from the recombination of two adsorbed CH3 species on the metal surface, the activation energy for CO insertion into adsorbed alkyl is high (of the order of 150 kJ mol−1,12 see also ref. 109) because of the umbrella effect of adsorbed CH3, which hinders the approach of CO.
As for the chain growth reaction, CO will insert with lower activation energy into a CH or CH2 type hydrocarbon chain. This was originally proposed by Zhuo et al.,36 who reported on Co(0001) an activation energy of 80 kJ mol−1 for insertion of CO into “CH2”. The reaction is endothermic by 60 kJ mol−1. On the open Ru surface, Filot et al.110 report activation energy of the CO with “CH” reaction to be 60 kJ mol−1, which is 30 kJ mol−1 endothermic. The effective rate constant for chain growth termination though requires at least one additional hydrogen addition step (see Fig. 3), which can be as high as 90 kJ mol−1. Hence, the apparent activation energies for termination through CO insertion can be estimated to vary between 120 and 180 kJ mol−1.12,16 This is higher than that of termination of the hydrocarbon chain as an alkane or alkene, which has an activation energy of the order of a hydrogen transfer activation energy.
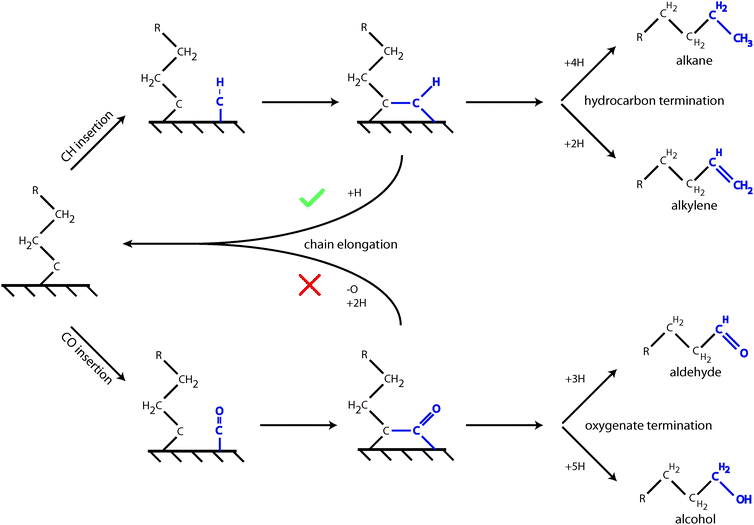 | ||
Fig. 3 CO insertion into the growing Cn hydrocarbon chain competes with CHx insertion. Hydrocarbon chain propagation requires rapid H atom insertion after the CHx introduction step, where the hydrogen atoms are generated by dissociative adsorption of H2. It is indicated by  sign that the hydrocarbon chain is continued after insertion of CHx, but is discontinued (denoted by sign that the hydrocarbon chain is continued after insertion of CHx, but is discontinued (denoted by  ) once CO has been inserted. ) once CO has been inserted. | ||
These quantum-chemical results imply that CO will not insert into the growing alkyl chain of the Brady–Pettit chain growth mechanism. When alkenyl or alkylidyne type adsorbates as in the Maitlis or Gaube mechanisms dominate the chain growth reaction, long hydrocarbon chain oxygenate formation is possible. It is important to realize that the CO insertion step competes with insertion of a “CHx” species to lengthen the growing hydrocarbon chain. This is schematically indicated in Fig. 3.
As illustrated in Fig. 3 CO insertion competes with CHx insertion into a Cn growing chain to form a hydrocarbon of chain length Cn+1. Cn+1 olefin formation and chain growth compete in the second step. One predicts therefore that oxygenate formation becomes suppressed with respect to alkane or alkene formation when a chemical change on the surface suppresses methane formation.111 This will result in an increased concentration of “C1” species to be inserted into the growing hydrocarbon chain. Generally, when the chain growth probability α increases, selectivity towards oxygenate formation will decrease.
The activation energy of formation of a C–C bond in combination with the relative stability of a CHx species determines which of the three chain growth mechanisms operate. C–CH3, CH–CH, CH–CH2, CH–CH3 and CH2–CH3 tend to have similar activation energies. The relative stability of adsorbed C, CH, CH2 and CH3, as found in the calculations of CH4 decomposition,20,21,88,107,112–117 thus determines the dominance of one of these species for insertion. Generally, on the transition metals, CHads tends to be substantially more stable than Cads (hydrogen atom addition to Cads is exothermic by 40 kJ mol−1). This suggests that the C atom is not directly involved in the chain growth reaction. The relative stability of CHads and CH2,ads varies. CH tends to be more stable by a few kJ mol−1 than “CH2”, but on open surfaces the two may have similar energies. CH3,ads is the least stable of the four “CHx” species, but has usually an energy comparable to or slightly less than that of Cads. Hence CH and CH2 will be the dominant inserting species. Their respective overall insertion rates may depend on the surface structure. It implies a low probability for the Brady–Pettit mechanism, which proposes alkyl chains as growing hydrocarbon chains. In addition to CH2, CH is a good candidate for insertion into the growing hydrocarbon chain.
According to the CO insertion chain growth mechanism, CO has to insert into the growing hydrocarbon chain and C–O bond cleavage has to follow. Once the CO bond is activated by hydrogen, the activation energy of C–O bond cleavage is relatively low.22,36,89 For instance, a typical activation energy for CO bond cleavage in adsorbed formyl is 40 kJ mol−1,27,29,31,32 but formyl formation from adsorbed CO and hydrogen is endothermic by 100 kJ mol−1. We already discussed that insertion of CO into adsorbed CH3 has a high barrier due to the umbrella effect. Insertion of CO into CH2 or CH has lower activation barriers. However, low barrier C–O bond cleavage then is only found after the insertion of additional hydrogen atoms until the carbonyl group becomes attached to the growing hydrocarbon chain as an aldehyde substituent by reaction steps as illustrated in Fig. 3. This implies an additional energy cost of the order of 90 kJ mol−1. The overall activation barrier for insertion of CO into the growing hydrocarbon chain will vary between 120 and 180 kJ mol−1.36,118 The overall rate of CO insertion then is slow compared to the rate of C–O bond cleavage of inserted CO.
The desorption energy of oxygenates is of the order of 80–90 kJ mol−1.12,22 This competes with the comparable activation energy of C–O bond cleavage and the growing hydrocarbon chain.118 However the activation energy for hydrocarbon chain termination is substantially lower than the apparent activation energy of chain growth through CO insertion.
In summary, overall chain growth by CO insertion followed by C–O cleavage will be expected to be slower than overall chain growth according to the carbide mechanism, unless the rate of CHx formation from adsorbed CO is too slow. The two mechanisms will be further compared in Section 4 dealing with microkinetics.
3.2 CO activation
The activation of diatomic molecules with a π-bond is highly structure sensitive.18,32,77,88,102,116,119–121 This is illustrated in Fig. 4 for the activation of CO on a Ru surface.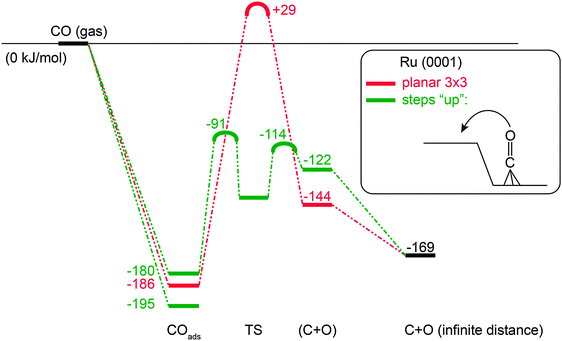 | ||
| Fig. 4 Comparison of adsorption, reaction energies and activation energies (kJ mol−1) of CO activation on dense Ru(0001) surface versus stepped surface according to PBE-GGA based DFT calculations as implemented in VASP (adapted from ref. 7). | ||
Whereas on the terraces of Ru or Co the activation energies for CO bond cleavage can be in excess of 200 kJ mol−1, activation on step-edge sites may reduce activation energies by 100 kJ mol−1 or more. At such sites, in the adsorbed state, the CO bond is weakened. In the side-on bonded adsorption mode of CO substantial electron transfer into the anti-bonding C–O bond weakening orbitals occurs. The local topology of the surface metal atoms requires limited stretching of the C–O bond from its ground state to the transition state. Also in the transition state there is no sharing of chemical bonds between the dissociating molecular atoms and surface metal atoms,7 which otherwise would increase the activation energy.
On the terraces and surfaces on which direct CO activation has a high activation barrier, a different C–O bond cleavage mechanism may take over. C–O bond cleavage through intermediate hydrogen activation of CO and intermediate formyl formation may become more favorable.29–33 On most surfaces this reduces the overall activation energy to convert CO to CHx to approximately 120 kJ mol−1. This value appears to be rather insensitive to the surface or the metal. A comparison of the energetics of conventional and hydrogen-assisted activation reaction paths on a reactive Ru surface site is given in Fig. 5.33
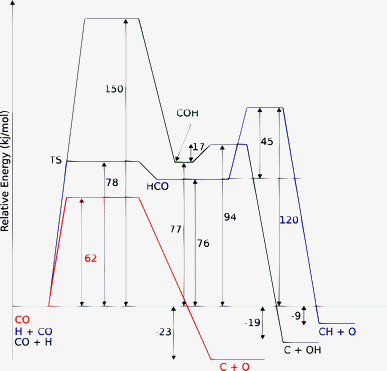 | ||
Fig. 5 Comparison of the energetics of hydrogen assisted versus direct CO dissociation on Ru(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface according to PBE-GGA based DFT calculations as implemented in VASP (adapted from ref. 33). 1) surface according to PBE-GGA based DFT calculations as implemented in VASP (adapted from ref. 33). | ||
One notes that on the step-edge site, activation of the C–O bond by addition of a hydrogen atom has an energy cost of 120 kJ mol−1 when the reaction proceeds through intermediate formyl formation, but even more when the hydrogen atom attaches initially to the CO oxygen atom. On the (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface, direct CO activation is more favorable because of its low value of 62 kJ mol−1. The overall activation energy to form “CH” will also be low because of the comparable activation energy to convert Cads on this site to CHads.26
1) surface, direct CO activation is more favorable because of its low value of 62 kJ mol−1. The overall activation energy to form “CH” will also be low because of the comparable activation energy to convert Cads on this site to CHads.26
In agreement with the proposal that direct low activation energy CO activation requires step-edge sites, which are expected to be stable only on larger particles, an elegant experiment by Salmeron et al.93 demonstrated that on small Co particles the hydrogen activated CO bond cleavage mechanism gives C–O bond cleavage, whereas direct CO activation does not occur at the low temperature used in their experiment. Behm et al.122 also provide experimental indications that formyl intermediates are stable only on larger Ru particles.
3.3 In summary
Hydrocarbon chain growth is possible at a low temperature and will proceed over many metals and surfaces as long as CHx species are available. The competitive reaction is methane formation, so the rate of CHx consumption to give methane has to be slow. Metals or surfaces with relatively weak M–C bond energies are less suitable because of rapid methane formation. In the Fischer–Tropsch reaction, CO activation generates the CHx species that is inserted into the growing hydrocarbon chain. Hence CO activation has to be fast compared to methane formation. The activation energy to convert CHx,ads to methane is typically between 100 and 140 kJ mol−1.When the carbide mechanism is operational, the Fischer–Tropsch reaction will be highly structure sensitive, since only on specific sites CO activation, be it direct or through H-assisted activation, has the overall activation energy that it can deliver CHx fast enough for the chain growth reaction to have a reasonable rate.
The experiments by Bezemer et al.,123 which demonstrate that metallic Co particles less than a few nanometers have low Fischer–Tropsch activity, suggest that the larger particles stabilize the step-edge sites and that the smaller particles loose this capability. This is in line with earlier work on N2 activation,124,125 which also indicates that molecular π bond activation becomes inhibited on the smaller particles because the step-edge type sites are absent.
The CO insertion route to give chain growth is less structure sensitive than the carbide path, but we have seen that CO insertion tends to be slow compared to direct C–C bond formation and therefore within the CO insertion mechanism will not lead to high chain growth parameter α values.
We will discuss the kinetics of the Fischer–Tropsch reaction based on the quantum-chemical studies of the relative stability of relevant reaction intermediates and their elementary rate constants in the next section. This is important because the relative concentrations of the reaction intermediates of the surface adsorbate overlayer under reaction conditions need to be known for definitive comparisons of the kinetic consequences of the different mechanistic proposals.
To conclude this section we show in Fig. 6 for a reactive site on the Ru(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface the subsequent energies of CO adsorption and dissociation followed by C–C bond formation according to the carbide and CO insertion mechanisms. In this particular case, CO insertion into CH has a lower barrier than that of the CH–CH recombination reaction step. However the barrier of CH–CH recombination is lower than the overall activation barrier for CHC formation via CO insertion because of the high C–O bond cleavage activation energy. Hence the carbide chain growth mechanism will dominate. In view of its low activation energy CO insertion into CH is a reasonable reaction path for acetaldehyde formation. Whether this will be actually formed depends on the competitive formation of methane. In this case of reaction on the very open (11
1) surface the subsequent energies of CO adsorption and dissociation followed by C–C bond formation according to the carbide and CO insertion mechanisms. In this particular case, CO insertion into CH has a lower barrier than that of the CH–CH recombination reaction step. However the barrier of CH–CH recombination is lower than the overall activation barrier for CHC formation via CO insertion because of the high C–O bond cleavage activation energy. Hence the carbide chain growth mechanism will dominate. In view of its low activation energy CO insertion into CH is a reasonable reaction path for acetaldehyde formation. Whether this will be actually formed depends on the competitive formation of methane. In this case of reaction on the very open (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) Ru surface the overall activation energies to form methane and acetaldehyde from “CH” are respectively 196 kJ mol−1 and 137 kJ mol−1.110 Note the higher overall activation energy of aldehyde formation, compared to the CO insertion barrier. It is due to consecutive reaction steps with adsorbed H atoms as discussed above. The rather favorable overall activation energy for oxygenate formation compared to that of methane formation is consistent with the observation of high oxygenate yield in the Fischer–Tropsch reaction catalyzed by Ru nanoparticles at low temperatures.126
1) Ru surface the overall activation energies to form methane and acetaldehyde from “CH” are respectively 196 kJ mol−1 and 137 kJ mol−1.110 Note the higher overall activation energy of aldehyde formation, compared to the CO insertion barrier. It is due to consecutive reaction steps with adsorbed H atoms as discussed above. The rather favorable overall activation energy for oxygenate formation compared to that of methane formation is consistent with the observation of high oxygenate yield in the Fischer–Tropsch reaction catalyzed by Ru nanoparticles at low temperatures.126
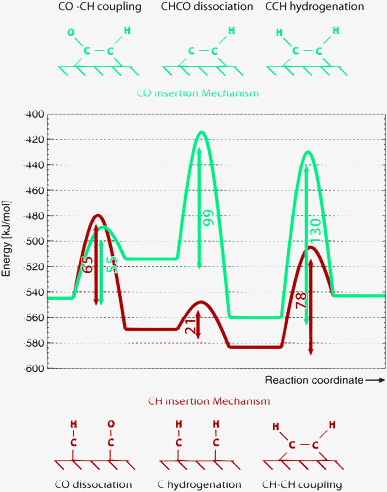 | ||
Fig. 6 Comparison of activation barriers of elementary reaction steps for C–C coupling according to the carbide mechanism and the CO insertion chain growth mechanism on Ru (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface according to PBE-GGA based DFT calculations as implemented in VASP. Energy reference is CO and H2 in gas phase.110 1) surface according to PBE-GGA based DFT calculations as implemented in VASP. Energy reference is CO and H2 in gas phase.110 | ||
On the (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1) surface low activation energy CO dissociation and chain growth by CH insertion take place on different sites. Cads is generated at a fourfold site to which it preferentially binds. On the other hand CHads prefers coordination to a threefold site. The two sites are connected through a CH diffusion step.26 This Fischer–Tropsch dual site allows for chain growth without blocking the CO dissociation reaction by adsorbed growing hydrocarbon chains. Also CO dissociation will not be poisoned by carbonaceous overlayer formation since this preferentially occurs on the terrace sites instead of the stepped surface sites.
1) surface low activation energy CO dissociation and chain growth by CH insertion take place on different sites. Cads is generated at a fourfold site to which it preferentially binds. On the other hand CHads prefers coordination to a threefold site. The two sites are connected through a CH diffusion step.26 This Fischer–Tropsch dual site allows for chain growth without blocking the CO dissociation reaction by adsorbed growing hydrocarbon chains. Also CO dissociation will not be poisoned by carbonaceous overlayer formation since this preferentially occurs on the terrace sites instead of the stepped surface sites.
4 The microkinetics of the Fischer–Tropsch reaction
One of the most intriguing issues concerning the kinetics of the Fischer–Tropsch reaction is that empirical kinetics modeling approaches, developed in a reactor engineering context,61–67,127–131 indicate that the rate of CO consumption is independent of chain growth. We will compare here the results of microkinetics simulations based on the carbide mechanism132 with those based on the CO insertion mechanism.133 Interestingly, the empirical kinetics model is found to be consistent with only the carbide mechanism. The elementary rate condition that has to be satisfied is that the apparent rate of CO transformation to CHx is slow compared to the rate of chain growth. Paradoxically, but only seemingly, this appears to be in conflict with the requirement that within the carbide mechanism the rate of CO activation has to be fast compared to the rate of methane formation or the rate of chain growth termination.A classical observation on the product distribution of the Fischer–Tropsch reaction is that, beyond a chain length of three carbon atoms, within a significant chain length interval the hydrocarbon concentration depends logarithmically on its chain length. The slope of this relation defines the chain growth probability α that is independent of hydrocarbon chain length. This is called the Anderson–Schulz–Flory (ASF) product distribution.134–136 Deviations of this dependence may relate to product readsorption137,138 that we will ignore in the following. We will also assume that Oads generated by C–O bond cleavage is removed fast compared to the other reaction steps, so that the catalyst surface can be considered metallic during reaction. Generally, excess methane and suppressed C2 hydrocarbon concentration is found compared to the ASF distribution that we will also comment on in the subsequent subsections.
We will initiate this section with a discussion of kinetics according to the carbide mechanism that in a later section will be compared with chain growth according to the CO insertion growth mechanism. The microkinetics results to be discussed here are based on a single site model of the Fischer–Tropsch reaction. For a comparison of kinetics according to the single or dual site model we refer to Markvoort et al.132
4.1 Kinetics according to the carbide mechanism
The quantum-chemical results of the previous section indicated that CH2–CH2 recombination is an easy reaction. Suppressed C2 formation, as found experimentally, indicates that this is an unlikely reaction. This suggests that “CH2” is not the dominant C1 species active in the growing chain reaction, as suggested within the Gaube mechanism. Instead, “CH” seems to be the preferred intermediate for C1 insertion into the growing chain. This is in agreement with suggestions of low activation energies of CH–CH recombination and the CH insertion reaction by Ciobîcă” et al.17 and Shetty et al.26 For this reason we have performed molecular kinetics simulations of the chain growth reaction based on this assumption.55Molecular kinetics simulations explicitly contain all elementary steps of the reaction. The corresponding ordinary differential equations132 can be solved without assuming a rate controlling step, so that the possibility of a change in the rate controlling step with changed surface reactivity or reaction condition can be investigated. This is essential since we will observe that the kinetics of the reaction depends on the ratios of key elementary rate constants. We will discuss the results of molecular kinetics simulations based on activation energies as typically obtained from quantum-chemical calculations for metals such as Co or Ru. Elementary reactions in which molecules exchange between gas phase and surface require inclusion of entropy loss or gain in their activation entropies. Adsorbates have been assumed to be immobile and their transition states to be tight103 so that activation entropies for elementary reaction steps on the surface could be ignored. Apart from methane formation only linear olefins are products. The elementary rates of reaction of hydrocarbons have been assumed to be independent of chain length. Different parameter choices relate to different surface topologies or metal choice. The results presented in Fig. 7 have been obtained without including re-adsorption of product molecules of the gas phase. Details of parameter choices and elementary reaction steps included are given in ESI.† The results are representative for a stepped CO or Ru surface.
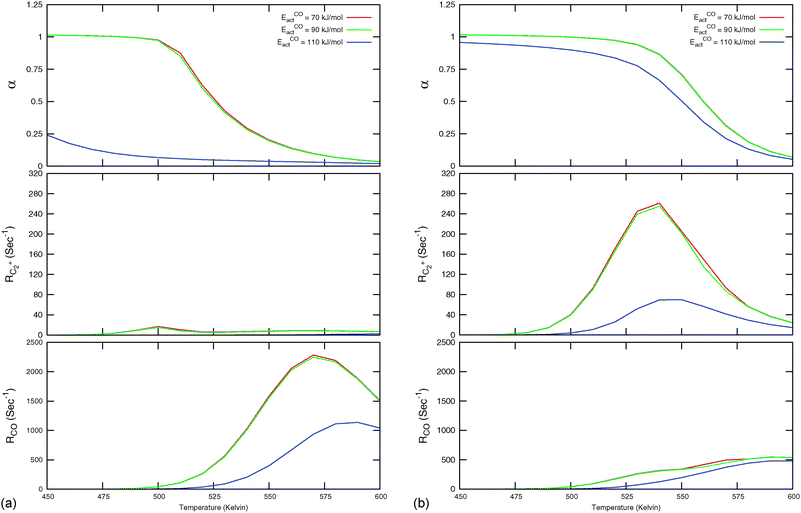 | ||
Fig. 7 Microkinetics simulations of the chain growth parameter α, C2+ yield RC2+ and the rate of CO consumption RCO as a function of temperature. Total pressure PCO = 5 bar and PH2 = 15 bar. The rates are expressed as turnover frequencies (TOFs) of CO, where the unit is the number of CO molecules consumed per site per second. Default elementary rate parameter values as in ESI.† (a) α, RC2+ and RCO for three different values of ECOact. (b) α, RC2+ and RCO for three values of ECOact, where 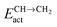 is now increased from 70 kJ mol−1 to 90 kJ mol−1 (reproduced with permission from ref. 132). is now increased from 70 kJ mol−1 to 90 kJ mol−1 (reproduced with permission from ref. 132). | ||
In Fig. 7, rates of CO consumption, the chain growth parameter α and C2+ yield RC2+ are plotted as a function of temperature. Fig. 7a illustrates the dependence of catalyst performance on the activation energy of C–O bond cleavage and the rate of methane formation. As discussed previously within the carbide mechanism these parameters are critical to the selectivity of the reaction. Increased rate of CO bond cleavage will enhance the surface concentration of CHads intermediates and hence increase the probability of chain growth. Reduced rate of methane formation is also expected to increase the surface CHads concentration. In the section that follows also the effect of changes in the chain growth rate and chain growth termination will be discussed.
Most striking are the very different temperature regimes observed for optimum C2+ yield versus methane production. The optimum in CO consumption rate at the higher temperature is mainly determined by the latter. The reaction starts at a temperature where CO starts to desorb and CO dissociation becomes possible. At the lower temperature the elementary rates of methane formation and chain growth termination are slow, because of their relatively high overall activation energies. This is the reason for the preference of lower temperatures for the Fischer–Tropsch reaction.
Fig. 7 indicates that below an activation energy of CO of 110 kJ mol−1 the CO conversion rate RCO and the chain growth parameter α do not change. This indicates a change in the rate controlling step of the reaction. We will discuss this more extensively in the next subsection. There we will demonstrate that Fischer–Tropsch kinetics behaves very differently in the two limiting cases that we have called chain growth limited kinetics and monomer formation limited kinetics. The results in Fig. 7 illustrate chain growth limited kinetics when the activation energy of CO is below 110 kJ mol−1. The rate of chain growth termination then is the rate controlling step and CO bond cleavage is fast compared to the chain growth reaction. When CO activation limits, catalyst performance kinetics behavior is according to the monomer formation limit. Then the chain growth reaction as well as chain growth termination is faster. However, as we illustrate in Fig. 7b, in order to have chain growth selectivity the rate of methane formation from “CHx” will have to be slower than the CO bond activation reaction.
In both limits the selectivity of the reaction towards formation of longer hydrocarbons is strongly enhanced when the rate of methane formation from adsorbed “CH” is suppressed. This is simulated by a decrease of the rate constant for formation of CH2,ads from CHads. At low temperatures the overall rate of CO consumption RCO is not affected by this change in the elementary rate. At the higher temperatures the rate of methane formation becomes limiting and the overall rate of CO consumption decreases.
Fig. 8 shows pressure dependence for three microkinetics simulations with different activation energies for CO activation, chain growth termination and methane formation. Chain growth limited and monomer kinetics limit cases are shown. One notes that the CO consumption rate and the chain growth probability agree with usually observed experimental behavior. The rate of C2+ formation is found to have a negative order in CO pressure, but positive in H2 pressure.37 The dependence of the chain growth parameter on H2 pressure is very sensitive to the rate limiting step of methane formation. As Fig. 8b indicates the chain growth parameter α will decrease with H2 pressure when instead of the transformation CHads to CH2,ads the transformation of CH2,ads to CH3,ads is assumed to be rate limiting. Since now more hydrogen is consumed in methane formation this rate has become higher order in H2 pressure.
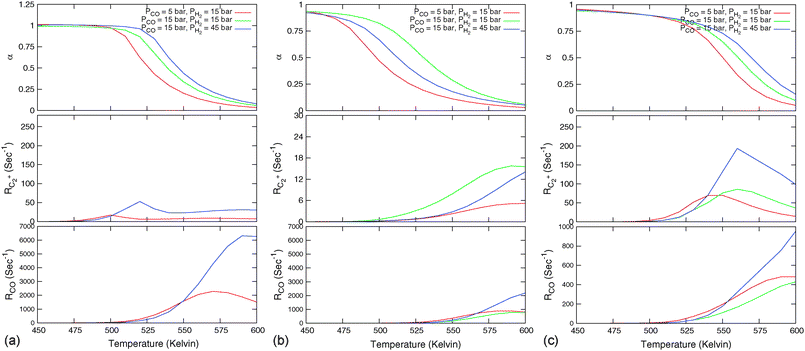 | ||
Fig. 8 Microkinetics simulations of the chain growth parameter α, C2+ yield RC2+ and the rate of CO consumption RCO as a function of temperature. Three different partial pressures of H2 and CO are compared as indicated in the figures. Default parameters are given in ESI.† Note that for clarity not all figures use the same scale. (a) Chain growth kinetics limit; low elementary rate constant of chain growth termination: 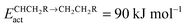 ; (b) chain growth kinetics limit; altered rate controlling step of methanation elementary rate constant: ; (b) chain growth kinetics limit; altered rate controlling step of methanation elementary rate constant: 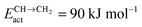 ; (c) monomer formation limit; ECOact = 110 kJ mol−1; ; (c) monomer formation limit; ECOact = 110 kJ mol−1; 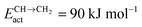 .111 .111 | ||
As one can observe from Table 3, high chain growth and the rate of CO consumption are consistent with a high surface concentration of CO. When the rate of termination becomes very slow, the rate of CO consumption decreases since the surface becomes poisoned by an overlayer of growing hydrocarbon chains. The slowing down of the chain growth termination rate has been done in the microkinetics simulations by decreasing the rate constant of one of the essential hydrogen atom transfer steps in the chain growth termination reaction. This decrease in the CO consumption rate when the rate of chain growth has become limiting is caused by the suppression of the rate of CO dissociation because of the lack of surface vacancies.
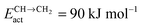 ; third column, default values as in ESI except for
; third column, default values as in ESI except for 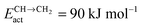 and
and 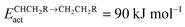 111
111
| High
| Low
| Low kC–Ct | |
|---|---|---|---|
| Tmax (C2+) | 500 K | 520 K | 540 K |
| Sel. CH4 | 50% | 0% | 0% |
| α | 0.99 | 0.96 | 0.99 |
| Coverage CO | 91% | 76% | 28% |
| Vacancy | 2% | 6% | 7% |
| Coverage C | 0% | 1% | 4% |
| Growing chains | 7% | 17% | 61% |
| Coverage of CO without reaction | 91% | 80% | 60% |
The very different surface compositions that are consistent with high chain growth probability relate to kinetics operating in different relative rate constant regimes. This is the topic of the next subsection.
The classical kinetics scheme of the Fischer–Tropsch reaction that corresponds to the carbide mechanism is represented by Scheme 1.
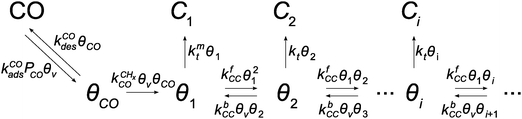 | ||
Scheme 1 Schematic representation of the lumped reaction steps of the carbide mechanism, their rate constants, and their dependencies on reactants, where θCO represents adsorbed CO, θi adsorbed chains of i carbons, θv vacant surface sites and Ci desorbed alkanes of length i. CO adsorbs to and desorbs from vacant surface sites with rate constants kCOads and kCOdes. Adsorbed CO can dissociate with the rate constant 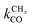 , resulting in an adsorbed C1, where Oads removal from the surface is considered to be fast. All chain growth reaction steps, converting a Ci chain plus a C1 into a Ci+1, are considered reversible with rate constants kfCC and kbCC, independent of chain length. Finally, C1 desorbs with rate kmt while chains Ci of at least length 2 desorb with, again chain length independent, rate kt. , resulting in an adsorbed C1, where Oads removal from the surface is considered to be fast. All chain growth reaction steps, converting a Ci chain plus a C1 into a Ci+1, are considered reversible with rate constants kfCC and kbCC, independent of chain length. Finally, C1 desorbs with rate kmt while chains Ci of at least length 2 desorb with, again chain length independent, rate kt. | ||
In this section we will discuss the steady state solutions to the corresponding partial differential equations. In the next section we will apply those to time-dependent solutions relevant to transient kinetics. The advantage of this way to solve the kinetic equations is that no rate controlling step has to be assumed.
A useful theoretical approach developed within computational catalysis is to study the kinetics of a reaction as a function of surface interaction strength. It leads to analyses in terms of the Sabatier principle.9,100,101,139,140 The rate of a catalytic reaction will show a maximum at optimum interaction strength of the surface. Such an analysis is also possible for the complex reaction scheme that corresponds to Scheme 1, when one realizes that the different rate constants will not vary independently with surface strength. This can be implemented in a computational approach using the Brønsted–Evans–Polanyi (BEP) relationship between activation energies and reaction energies of elementary surface reaction steps.7,101,102,141 Such relations have been extensively analyzed using computational quantum-chemical data that provide rules for activation energy change as a function of the adsorption energy of reaction intermediates. Through the scaling laws107 mentioned earlier, this can be related in an approximate way to the adsorption energies of the atoms. It is for instance well understood that as long as the structure of the reactive center and the mechanism of elementary reaction steps do not alter, the changes in activation energy for elementary reactions in which bonds are broken follow closely the energetics of reaction energies, while, because of microscopic reversibility, recombination reactions as the chain growth reaction to a first approximation can be considered independent of changes in reaction energies77,116,142 and hence are rather insensitive to changes in surface reactivity. When one follows such an approach, the dependence of the rate of CO consumption and the chain growth parameter α on the changing adsorption energy of a C-atom as shown in Fig. 9 is found.132
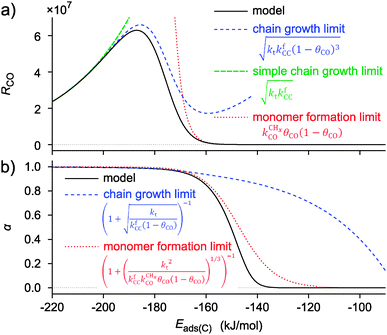 | ||
Fig. 9 Catalyst performance parameters RCO (a) and α (b) as a function of surface reactivity with variation in elementary lumped rate parameters based on BEP type expressions. The interaction energy decreases to the right, as would be the case in a row of the periodic system. Apart from the simulated model curves also the monomer formation and chain growth limits are shown. Kinetic symbols as in Scheme 1. Used parameters: extrapolated activation energies for Eads(C) = 0; E0f = 55 kJ mol−1 (kfCC), E0t = 70 kJ mol−1 (kt), E0d = 270 kJ mol−1 (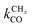 ); respective Brønsted–Evans–Polanyi parameters: βf = 0.0, βt = −0.3, βd = 1.2; respective preexponents; Af = 1013 s−1At = 1017 s−1, Ad = 1013 s−1; kbCC = 0 (adapted from ref. 55). ); respective Brønsted–Evans–Polanyi parameters: βf = 0.0, βt = −0.3, βd = 1.2; respective preexponents; Af = 1013 s−1At = 1017 s−1, Ad = 1013 s−1; kbCC = 0 (adapted from ref. 55). | ||
As expected from the Sabatier principle, the rates of CO consumption show a maximum as a function of the interaction strength of the metal surface. Since we used BEP relations to calculate the curves of Fig. 9, the curves apply only to a situation when there is no change in surface topology.
If one compares the surface coverage to the left and right of the Sabatier maximum in Fig. 9, one finds that for the weakly interacting surfaces to the right of the maximum the surface is covered with CO, while to the right of the Sabatier maximum the surface becomes covered with growing hydrocarbon chains. This implies a change in the rate controlling step. When the surface interaction strength is weak, CO activation has a high activation energy, but the rate of CHx hydrogenation to give methane will be fast. This will suppress the rate of the chain growth reaction. When the surface interaction strength increases, the relative rate of CO dissociation will increase and methane formation becomes suppressed. The increasing rate of chain growth that results will increase the apparent chain growth rate to become faster than the rate of chain growth termination. The latter rate also decreases with increasing M–C interaction strength, because upon product desorption the M–C bond cleaves. The increase in the chain growth parameter α with increasing M–C bond energy as shown in Fig. 9 begins beyond this M–C bond energy. The maximum rate of CO consumption corresponds to the M–C bond energy where the rate constant of the CO to CHx transformation becomes equal to the rate constant of the chain growth reaction. When the M–C bond energy increases further, to the left of the maximum of RCO in Fig. 9, the rate constant of CO dissociation is not only fast compared to the rate of chain growth, but also fast compared to the rate constant of chain growth termination. Then the rate constant of termination becomes limiting to the reaction and the surface becomes covered with growing hydrocarbon chains that inhibit the rate of CO dissociation, so that RCO decreases.
Also shown in Fig. 9 are the approximate solutions to the kinetics that are found when different rate controlling steps are assumed. To the far right of the RCO maximum, the RCO rate can be calculated within the Fischer–Tropsch monomer formation kinetics limit,55 whereas at the RCO maximum and to the left of the RCO maximum, the chain growth limit expression is valid. In eqn (1) and (2) the corresponding expressions for RCO and the chain growth parameter α are given.132,143
Monomer formation limit (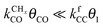 ):
):
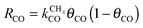 | (1a) |
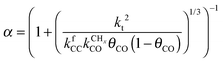 | (1b) |
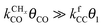 ):
):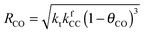 | (2a) |
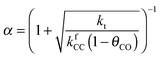 | (2b) |
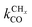 is rate controlling and small compared to kfCC. The chain growth parameter α will be close to one as long as
is rate controlling and small compared to kfCC. The chain growth parameter α will be close to one as long as 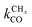 is larger than kmt and kt and methane formation is suppressed. The dependence of α on the surface interaction strength is more shallow than that of the CO consumption rate. Already to the right of the RCO maximum, where the surface remains mainly covered by adsorbed CO, α can be close to one as long as methane production is suppressed.
is larger than kmt and kt and methane formation is suppressed. The dependence of α on the surface interaction strength is more shallow than that of the CO consumption rate. Already to the right of the RCO maximum, where the surface remains mainly covered by adsorbed CO, α can be close to one as long as methane production is suppressed.Within the monomer formation limit the overall free activation energy of the conversion of CO into CHx has to be larger than the activation free energies of chain growth and chain growth termination. At the same time the rate of CO to CHx transformation has to be fast compared to the rate of methane formation from CHx. Thus there is an upper as well as a lower bound to the activation free energy of the CO to CHx transformation. The data presented in Section 3 indicate that CO conversion to CHx has only sufficiently low activation energy, when CO activation occurs on step-edge type sites.
Since within the monomer formation limit the rate of CO consumption is not at its maximum, Fischer–Tropsch catalysts that are empirically found to operate kinetically within this limit are far from their theoretical maximum performance.
Near the RCO maximum, the chain growth limit expression applies, but the decrease in CO surface concentration has to be properly accounted for. The RCO rate depends explicitly on kt and kfCC and α only on their ratio. Both eqn (2a) and (2b) have become independent of 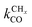 , which now is fast compared to kfCC and kt.
, which now is fast compared to kfCC and kt.
The physical interpretation of the chain growth limit expressions is that the surface becomes covered with growing hydrocarbon chains. The rate of CO consumption becomes controlled by the rate of chain growth termination and the rate constant of chain growth, with the latter being involved since “C1” consumption is also determined by the rate at which it is incorporated into the adsorbed hydrocarbon chain. In the chain growth limit the growing hydrocarbon chains inhibit CO activation. Therefore the dual site model, in which the site of CO activation is different from the location of chain growth, will give substantially higher yield than the single site model.132 In contrast within the monomer formation limit a dual site will not have an advantage, since the surface is mainly covered by CO and the surface coverage with growing hydrocarbon chains is low.
When the surface interaction strength is very large, the C–C bond formation becomes endothermic. Then it is essential to include reversibility of this reaction into the kinetics simulations of the reaction.132 At very high surface interaction strengths, the increasing endothermicity of the chain growth reaction limits overall chain growth and, as a consequence, the chain growth reaction becomes less selective and more methane is produced. The dependence of α on the surface interaction strength is more shallow than that of the CO consumption rate. Already to the right of the RCO maximum α can be close to one as long as methane production is suppressed.
Fig. 10 presents two simulated BEP curves in which a surface with a low barrier of CO activation is compared with a surface with a high activation barrier for CO dissociation. The former can be considered the case where CO dissociates at a step-edge site, and the latter the case where CO dissociates at a terrace. The maximum in RCO shifts to stronger surface interaction energies when dissociation is more difficult. One also observes the substantially lower chain growth probability on the terrace surface. The probability that “CH” generated by CO activation is converted to methane is now substantially increased. This is in line with the experimental observations of decreased activity and increased methane selectivity for small metal particles.123
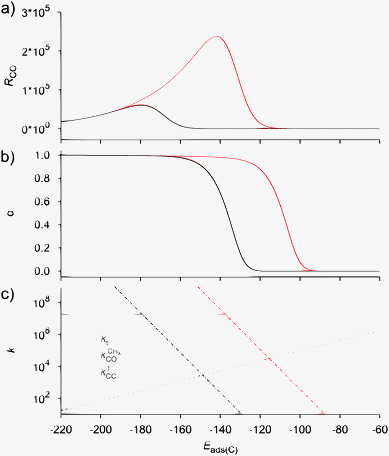 | ||
| Fig. 10 Influence of the CO activation energy E0d on (a) the CO consumption rate RCO and (b) the chain growth parameter α as a function of the adsorption energy of carbon Eads(C). (c) The rate constants (s−1) from the BEP relations as a function of the adsorption energy of carbon Eads(C). Red lines correspond to an initial value (i.e. at Eads(C) = 0) of the CO activation energy E0d of 220 kJ mol−1 and black lines to an initial value of 270 kJ mol−1. Other parameters as in Fig. 9 except that E0t = 85 kJ mol−1 (adapted from ref. 55). | ||
Selective methane formation, as in the Sabatier–Senderens process,144–146 requires rapid CHx to methane formation once CO has been activated. This is favored by surfaces with a high activation energy of CO bond cleavage and weak Cads adsorption energies, typically found far at the right of RCO Fischer–Tropsch maximum of the Sabatier relation curves in Fig. 9 and 10. For such weakly interacting surfaces, the C–O bond cleavage reaction is promoted by intermediate formyl formation. On the other hand, optimum Fischer–Tropsch selectivity requires low methane formation and hence the opposite situation of a very reactive surface with low barrier of CO cleavage and a strong M–C bond. A practical catalyst may contain a mixture of reactive and non-reactive surfaces. Then undesirable methane production will be due to the presence of these non-reactive surfaces.
Comparison of the RCO maxima in Fig. 10a with the changes in rate constants in Fig. 10b shows that the RCO maxima coincide with the crossing of the rate constant 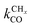 and kfCC, the rate constant of C–C formation (in the simulations of Fig. 10 the reverse of the C–C formation reaction has been ignored for convenience).
and kfCC, the rate constant of C–C formation (in the simulations of Fig. 10 the reverse of the C–C formation reaction has been ignored for convenience).
Fig. 11 schematically illustrates the required relation for high chain growth between CO adsorption equilibria and elementary (lumped) rate constants.
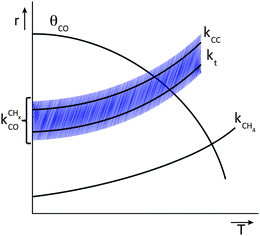 | ||
| Fig. 11 Schematic illustration of the elementary rate relations necessary for high Fischer–Tropsch chain growth according to the carbide mechanism. | ||
The lowest temperature at which the Fischer–Tropsch reaction can happen is determined by the desorption temperature of CO. Only when CO desorbs, vacant sites are available so that C–O bond activation can occur. The condition for low activation energy C–O bond cleavage as well C–C bond formation implies that their activation energies will be low compared to those of methane formation and chain growth termination. The lower temperature will favor chain growth, because then the rate of chain growth termination kt is slow compared to the rate constant of chain growth kfCC and the rate of methane formation kmt remains slow compared to the rate constant 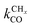 . At the higher temperatures, the surface coverage of CO will rapidly decrease further. The rate constants of methane formation and chain growth termination increase and may cross the more slowly increasing rate constants of CO dissociation and C–C bond formation. Hence, formation of methane will become favored at the higher temperatures far above the CO desorption maximum. Higher pressure will favor chain growth at the higher temperatures because it increases the rate of CHx formation by increasing CO surface coverage.
. At the higher temperatures, the surface coverage of CO will rapidly decrease further. The rate constants of methane formation and chain growth termination increase and may cross the more slowly increasing rate constants of CO dissociation and C–C bond formation. Hence, formation of methane will become favored at the higher temperatures far above the CO desorption maximum. Higher pressure will favor chain growth at the higher temperatures because it increases the rate of CHx formation by increasing CO surface coverage.
Within the Fischer–Tropsch monomer formation limit the CO to CHx transformation rate is slow compared to the rate constant of C–C bond formation, whereas within the chain growth limit the reverse condition holds. A high value of α is possible in both limits. The optimum CO consumption rate is found for a surface of intermediate reactivity where the overall rate constant of CHx formation from CO 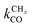 balances the rate of chain growth kfCC.
balances the rate of chain growth kfCC.
An important recent experiment that seemingly contradicts the carbide mechanism is a transient Fischer–Tropsch kinetics study by Schweicher et al.147 They observe an increase in Fischer–Tropsch selectivity when following a transient pulse as the CO surface concentration increases. They observe no correlation with “C” coverage. However, within the monomer formation limit the CO to CHx transformation is slow compared to the rate constant of chain growth. This implies that under the condition of CO shortage the chain growth probability is a strong function of CO pressure and reactive “C1” concentration is very low. Part of the reactive “C1” will be converted to non-reactive carbon under low CO and H2 conditions.
4.2 The CO insertion chain growth mechanism and oxygenate formation
The kinetics of the Fischer–Tropsch reaction based on the CO insertion chain growth mechanism is quite different from that of the carbide mechanism. For this reason we also include here an analysis of CO insertion chain growth kinetics using an analogous approach as in the previous section.133 As we will see, it predicts that the rate of CO consumption has a positive order in CO pressure and that it will also depend on the chain growth rate.The lumped kinetics scheme according to the CO insertion chain growth mechanism is shown in Scheme 2.
 | ||
Scheme 2 Schematic representation of the lumped reaction steps of the growth by CO insertion mechanism, their rate constants, and their dependencies on reactants, where θCO represents adsorbed CO, θi adsorbed non-oxygen containing chains of i carbons, θi,CO adsorbed oxygen containing chains of i + 1 carbons, θv vacant surface sites, Ci desorbed alkanes of length i and Ci,CO desorbed oxygenates with i + 1 carbons. CO adsorbs again to and desorbs from vacant surface sites with rate constants kCOads and kCOdes. Adsorbed CO can still dissociate with rate constant 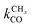 , resulting in an adsorbed C1, where Oads removal from the surface is considered to be fast. All chain growth reaction steps, inserting a CO into a chain Ci resulting in a Ci,CO, are considered reversible with rate constants kf and kb, independent of chain length. Chain growth can proceed after cleavage of the CO bond, with the rate constant kp. Finally, C1 desorbs with rate kmt while chains Ci of at least length 2 desorb with, again chain length independent, rate kt, and oxygen containing chains Ci,CO desorb with rate kt′. , resulting in an adsorbed C1, where Oads removal from the surface is considered to be fast. All chain growth reaction steps, inserting a CO into a chain Ci resulting in a Ci,CO, are considered reversible with rate constants kf and kb, independent of chain length. Chain growth can proceed after cleavage of the CO bond, with the rate constant kp. Finally, C1 desorbs with rate kmt while chains Ci of at least length 2 desorb with, again chain length independent, rate kt, and oxygen containing chains Ci,CO desorb with rate kt′. | ||
Whereas in the carbide scheme the maximum in CO consumption rate is determined by the balance of rates of chain growth kfCC and  , and the latter has to be fast, the conditions for high RCO and α are very different within the CO insertion mechanism. This is illustrated by Fig. 12.
, and the latter has to be fast, the conditions for high RCO and α are very different within the CO insertion mechanism. This is illustrated by Fig. 12.
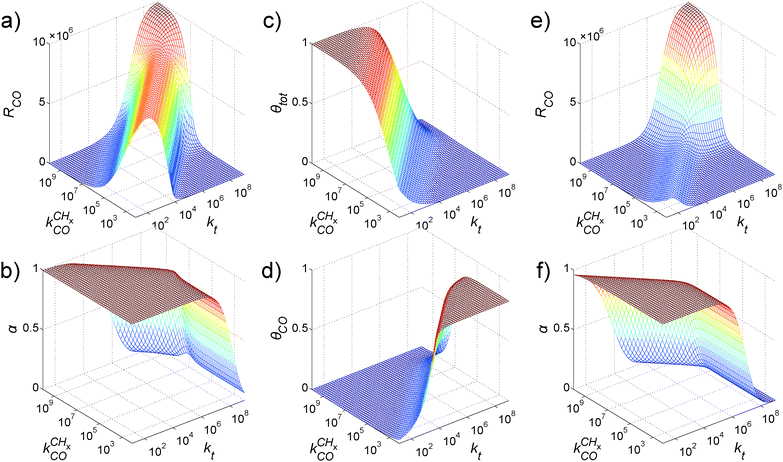 | ||
Fig. 12 Catalyst performance as a function of kt and  for (a–d) the case of high chain growth, i.e., kp = 109 and kf = 109 (kb = 0, kCOadsPCO = 107, kCOdes = 2 × 106), and (e and f) the case of reduced CO insertion, i.e., kf = 107. (a) and (e) The CO consumption rate RCO. (b) and (f) The chain growth parameter α. (c) The surface coverage with growing chains, i.e., for (a–d) the case of high chain growth, i.e., kp = 109 and kf = 109 (kb = 0, kCOadsPCO = 107, kCOdes = 2 × 106), and (e and f) the case of reduced CO insertion, i.e., kf = 107. (a) and (e) The CO consumption rate RCO. (b) and (f) The chain growth parameter α. (c) The surface coverage with growing chains, i.e.,  . (d) The surface coverage with CO θCO (adapted from ref. 133). . (d) The surface coverage with CO θCO (adapted from ref. 133). | ||
Fig. 12 shows that the maximum in the rate of CO consumption RCO now is determined by the values where 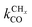 crosses the rate of chain growth termination kt (for simplicity in Fig. 12 the three kt's have been assumed to be equal). Different from the carbide mechanism kinetics, the probability of the rate of CO consumption becomes negatively affected when
crosses the rate of chain growth termination kt (for simplicity in Fig. 12 the three kt's have been assumed to be equal). Different from the carbide mechanism kinetics, the probability of the rate of CO consumption becomes negatively affected when 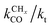 becomes large, because then CO transformation to CHx is so fast that no adsorbed CO is left on the surface for incorporation into the growing chain.
becomes large, because then CO transformation to CHx is so fast that no adsorbed CO is left on the surface for incorporation into the growing chain.
As long as α remains large, the surface coverage is dominated by growing hydrocarbon chains. This, however, depends on the rate of CO insertion kf compared to kt. α will decrease when the ratio of kt and kf becomes too large. Then the coverage by growing hydrocarbon chains is taken over by coverage with “C1” species. When 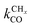 is less than kt the surface becomes covered with CO. Now methane formation competes with methanol formation. Upon increasing the value of
is less than kt the surface becomes covered with CO. Now methane formation competes with methanol formation. Upon increasing the value of 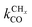 , methane selectivity and the rate of CO consumption increase. When
, methane selectivity and the rate of CO consumption increase. When 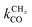 is equal to kt, methane yield and CO consumption reach their Sabatier principle maxima. The surface becomes covered with C1 species and the overall rate becomes controlled by that of “CHx” hydrogenation.
is equal to kt, methane yield and CO consumption reach their Sabatier principle maxima. The surface becomes covered with C1 species and the overall rate becomes controlled by that of “CHx” hydrogenation.
Fig. 12 illustrates that also within the CO insertion mechanism high values of α and CO consumption rate are in principle possible. One condition is that the overall rate constant of CO insertion is fast compared to the rates of chain growth termination as an oxygenate or a hydrocarbon. As we indicated in Section 3, this is in conflict with computational observations that indicate the reverse relation.
The rate of CO dissociation to generate the initial CHx species into which CO (see Fig. 1b) initially inserts has to be slow not only compared to the rate of CO insertion, but also compared to the rate of the termination reactions. This is very different from the condition of relatively fast CO dissociation compared to the rate of methanation within the carbide mechanism. It implies that the Fischer–Tropsch reaction according to the CO insertion mechanism will be substantially less structure dependent than predicted according to the carbide mechanism.
Within the chain growth through the CO insertion mechanism RCO increases strongly with CO pressure133 when α is high. This is because then the CO consumption rate RCO is dominated by the CO insertion rate into the growing chain, which is proportional to the CO coverage. This also explains the large decrease in RCO when comparison is made between cases of high (Fig. 12a) and low values of kf (Fig. 12e). Strong CO pressure dependence occurs especially in the regime of maximum RCO where the rate of CO dissociation 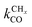 competes with methane formation or rates of termination kt towards hydrocarbon or kt′ towards formation of oxygenate (see Scheme 2).
competes with methane formation or rates of termination kt towards hydrocarbon or kt′ towards formation of oxygenate (see Scheme 2).
This CO pressure dependence is also very different from that of the carbide mechanism. In agreement with experiments within the carbide monomer formation limit RCO decreases with CO pressure,55 and at the RCO maximum remains independent of CO pressure.
The CO insertion chain growth model expression for α(ins) is
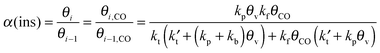 | (3) |
Eqn (3) of α(ins) can be used to identify the conditions for high chain growth according to the CO insertion. We have concluded in Section 3 that the overall rate constant of CO insertion kf is substantially smaller than the rate constant of C–O bond cleavage kp. kp is also larger than the reverse CO insertion reaction constant kb. Then the value of the CO insertion chain growth parameter α reduces to
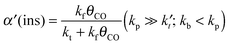 | (4) |
CO insertion being a slow reaction step however does not exclude chain growth termination by insertion of CO that will produce oxygenates within the carbide mechanism. The quantum-chemical data indicate that within the carbide mechanism CO insertion into adsorbed type hydrocarbon chains (that will terminate the reaction) and CH insertion into such adsorbed hydrocarbon species (that will lead to chain growth) compete (see Fig. 3). Consistent with this, microkinetics model simulations111 show that when the apparent rate constant of methane formation from adsorbed “CH” is decreased by an increase in activation energy the chain growth parameter increases but oxygenate formation decreases. This is in contrast to a suggestion by Choi et al.,16 who proposed that methane formation has to be suppressed to increase oxygenate formation. Although this will indeed enhance chain growth, it will come at the cost of oxygenate formation instead.
For oxygenate formation the activation energy for CHx formation from CO and the activation energy for CO insertion have to compete. Also the activation energy of oxygenate desorption has to be lower than the activation energy for C–O bond cleavage after CO insertion. Quantum-chemical results suggest that this may be the case for Rh13,16,22 consistent with experiments.148 Low temperatures favor oxygenate formation on more reactive metals, especially when they have small particles. On such small particles, as we discussed before, CO dissociation that competes with CO insertion is suppressed. An interesting example is the low temperature Fischer–Tropsch reaction on Ru nanometer particles that at 460 K produce 80% oxygenate, which is reduced to less than 10% at 500 K.126
4.3 Summarizing discussion on microkinetics
The dependence of RCO on the rate constants defined within the carbide mechanism, as derived in the previous section, is summarized schematically in Fig. 13a and compared with that of the CO insertion mechanism in Fig. 13b (see also the schematic in Fig. 1).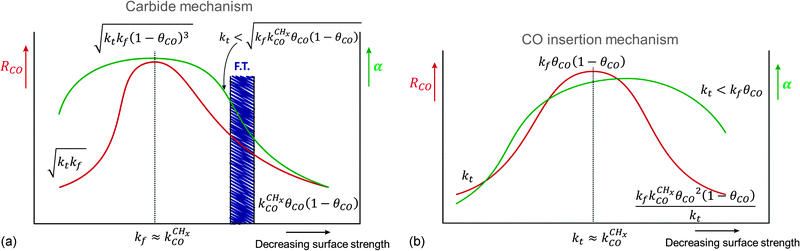 | ||
| Fig. 13 Schematic comparison of elementary rate constant relations between catalyst strength and catalyst performance for (a) the carbide mechanism and (b) the CO insertion mechanism. | ||
Within the CO insertion chain growth mechanism analytical expressions for RCO and α valid at different ratios of elementary rate constants can be derived analogous to eqn (1) and (2). We refer for this to ref. 133. In the schematic of Fig. 13b the predicted dependence of RCO and α as a function of surface reactivity is presented for the CO insertion chain growth mechanism. Also the analytical expressions133 for maximum RCO when α is high and the expression of RCO for a relatively weakly interacting surface are shown. We have argued in the previous subsection that the condition of high α, i.e. that kt is smaller than kfθCO, is not satisfied. For the same reason the rate of CO consumption will be far from its theoretical maximum and significantly less than  .
.
We also presented strong arguments that the carbide mechanism applies within the monomer formation kinetics limit on practical catalysts. The CO consumption rate is rate limited in the activation of CO  . Therefore practical Fischer–Tropsch catalysts are predicted to operate below the maximum in CO consumption. In Fig. 13a this reactivity regime is indicated with the blue area.
. Therefore practical Fischer–Tropsch catalysts are predicted to operate below the maximum in CO consumption. In Fig. 13a this reactivity regime is indicated with the blue area.
An important kinetic argument in favor of the carbide mechanism is the positive order in CO pressure predicted according to the CO insertion mechanism, which is not the experimental observation. Furthermore, we concluded that predicted α values based on quantum-chemical estimates will also be low within the CO insertion mechanism. Whereas agreement with kinetics predictions is no proof for the validity of a particular mechanism at least it has to be consistent with experiments.
The conclusion that the carbide mechanism applies has a major implication for the particle size dependence of the reaction. Since the overall chain growth probability strongly depends on the rate of CO to CHx transformation as well as the rate of CHx hydrogenation to methane, a change in the chemistry of the reactive center that affects the relative rate of CO dissociation will have a major effect on the chain growth probability α. We have discussed that on small particles step edge sites uniquely active for low activation energy CO dissociation may become unstable and hence below a particular particle size Fischer–Tropsch reaction selectivity will change. The selectivity for longer hydrocarbon formation has been experimentally found to decrease for Co. On the other hand the decrease in CO consumption rate on Ru nanoparticles with decreased size has been ascribed only to a change in reactive centers without change in reactivity.78
Transient SSITKA experiments using switching experiments with isotopes are able to distinguish changes in the fraction of reaction centers from the change in the chemistry of the reaction center that changes reaction rate constants.149 The partial differential equations that correspond to kinetics schemes such as Schemes 1 and 2 can also be solved as a function of time and enable one to calculate the residence times of particular products.
For the carbide mechanism Fig. 14 illustrates typical results of such simulations.143 We have studied the residence times τ as a function of different rate parameters, changing each of them independently. Fig. 14 illustrates that whereas there is no change in the methane residence time τmethane with the change in  in the absence of chain growth, it increases when
in the absence of chain growth, it increases when 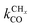 is decreased. The kinetics changes from chain growth limited kinetics when
is decreased. The kinetics changes from chain growth limited kinetics when 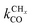 is large to monomer limited kinetics when
is large to monomer limited kinetics when 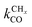 becomes less than kfCC. Also dependence on CO pressure or the elementary rate of chain growth termination can be studied computationally in the same way. As expected τCO will increase with increased adsorption energy of CO, but the effect on the residence time of methane is small. When the rate of hydrocarbon chain termination increases, the chain growth parameter α decreases and the residence time of methane will decrease.
becomes less than kfCC. Also dependence on CO pressure or the elementary rate of chain growth termination can be studied computationally in the same way. As expected τCO will increase with increased adsorption energy of CO, but the effect on the residence time of methane is small. When the rate of hydrocarbon chain termination increases, the chain growth parameter α decreases and the residence time of methane will decrease.
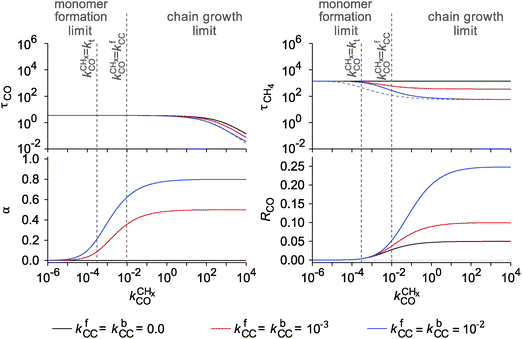 | ||
Fig. 14 Dependence of half-lives for CO (τCO) and methane (τCH4), steady state production (RCO) and chain growth rate (α) on the dissociation rate constant 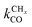 . Values of not mentioned rate constants are kCOadsPCO = 1, kCOdes = 0.2, and kt = 5 × 10−4. Three regimes are discerned, which are separated by the dashed vertical lines at . Values of not mentioned rate constants are kCOadsPCO = 1, kCOdes = 0.2, and kt = 5 × 10−4. Three regimes are discerned, which are separated by the dashed vertical lines at 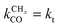 and and 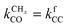 for the blue case, i.e., kfCC = kbCC = 10−2. For this case also the approximations for the blue case, i.e., kfCC = kbCC = 10−2. For this case also the approximations 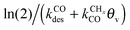 for τCO and ln(2)/(kt + kfCC(θ1 + θt)) for τCH4 are shown (adapted from ref. 143). for τCO and ln(2)/(kt + kfCC(θ1 + θt)) for τCH4 are shown (adapted from ref. 143). | ||
The experimentally observed decrease in τmethane with an increase in particle size is an indication that on the larger particle the monomer limit is not anymore strictly valid and that the experimental RCO has shifted more closely to the maximum in RCO. Consistent with experiments no changes in the residence time of CO occur. It has been argued79 that possibly the increased adsorption energy of CO is responsible for the change in τmethane, but this is not confirmed by the simulations.
This information can be used to analyse available experimental SSITKA data on changes in transient behavior in combination with changes in catalyst performance for a few supported Co and Ru catalysts as a function of catalyst particle size. Data from the Holmen group78–80 are summarized in Table 4. It also includes one set of data that refers to a promoted supported Co catalyst.
| Experimental observation | Model explanation | ||||
|---|---|---|---|---|---|
| τCH4 | τCO | RCO | α | ||
| Effect of decrease in particle size | |||||
| Co (carbon support)79 | Longer | Shorter | Decreases | Decreases | 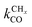 decreases decreases |
| Co (silica support)79 | Shorter | Shorter | Decreases | Decreases | kt increases, decrease in number of sites |
| Ru (alumina support)78 | Constant | Longer | Decreases | Constant | Decrease in number of sites |
| Effect of promotion | |||||
| Co (MnO promoted)80 | Longer | Longer | Increases | Increases | kt decreases, increase in number of sites |
In Table 4 we used four catalyst performance parameters to determine the reasons for the changes in reactivity. The use of transient kinetic data enables one to decouple changes in elementary rate constants from changes in site concentration or surface coverage. The experiments are done in such a way that reaction conditions remain the same, but transient behavior is induced by the isotope change of CO. One notes that for the Co catalysts supported by carbon, the change in the elementary rate constant of CO activation causes a change in reactivity when particle size decreases. However in other cases there is only a change in the number of sites, or there is also a change in the rate of termination. Clearly there is not one unique reason why the reactivity pattern changes for different catalysts.
Another relevant experiment is the measurement of H2/D2 isotope effects in the Fischer–Tropsch reaction. Experimentally it is reported150,151 that when excess methane is produced there is no measurable isotope shift on methane production, whereas there is a substantial effect on C2+ yield. We have argued in the previous sections that excess methane is produced on low-reactive surface sites on which CO activation is hydrogen assisted, but “CHx” conversion to methane is fast. This is consistent with the absence of an isotope effect since isotope replacement by deuterium will only imply a small secondary effect on the overall activation energy of C–O bond cleavage. This situation is different for C2+ production that increases with the chain growth parameter α. A high value of α implies that 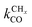 has to be fast compared to the rate of “CHx” transformation to methane. The apparent chain growth rate is a sensitive function of competition between “CHx” insertion and CHx hydrogenation. The faster the CHx hydrogenation, the smaller the chain growth parameter α. The rate of “CHx” to methane transformation will have a large isotope effect, and hence the C2+ yield will be affected.
has to be fast compared to the rate of “CHx” transformation to methane. The apparent chain growth rate is a sensitive function of competition between “CHx” insertion and CHx hydrogenation. The faster the CHx hydrogenation, the smaller the chain growth parameter α. The rate of “CHx” to methane transformation will have a large isotope effect, and hence the C2+ yield will be affected.
5 In perspective
One of the key unresolved questions in fundamental heterogeneous catalysis is understanding and predicting not only the activity of a catalyst, but also its selectivity. While the Sabatier principle, which predicts the volcano curve type dependence of rate versus surface reactivity, can be used to predict the intrinsic rate of a catalytic reaction based on first principle molecular data,3,6,7,9,11 no such general principle for the intrinsic selectivity of a reaction can be given.5,140 The main reason for this absence of a general theory of selectivity in heterogeneous catalysis is that the molecular events that control this are reaction specific. One first needs to unravel the sequence of molecular events that close the catalytic cycle of reactant adsorption and product desorption. Then, when different products are formed in parallel reaction sequences, selective product formation may depend on the relative stability of adsorbed reaction intermediates and the kinetics of individual elementary reaction steps. Heterogeneity of the catalyst surface may further relate different surface sites with the selectivity. This is however only one example of an explanation of catalyst selectivity. Also surface reaction sequences may occur where the relative rate of a consecutive elementary reaction is essential. The Fischer–Tropsch reaction is a prime example of a complex network of surface reactions that illustrates the various features that control selectivity differences. Selectivity of the Fischer–Tropsch reaction depends on the presence of different surface sites, but not because they preferentially stabilize a particular surface intermediate, but rather because at different sites the ratio of essential elementary reaction steps is quite different.A theoretical basis to the mechanistic understanding of selectivity has become available from state of the art quantum-chemical calculations. It provides molecular information on the relative stability of reaction intermediates and their corresponding elementary reaction rates. These data can be used as input to microkinetics simulations, so that predictions can be made of catalyst performance for different proposed reaction mechanisms. In order to kinetically discriminate between different molecular mechanistic models, it is hereby essential to use methods for the solution of the microkinetics model equations that do not invoke any assumption on a particular rate controlling step. This can be done by direct solution of the ordinary differential equations (ODEs) of the corresponding microkinetics models. For the Fischer–Tropsch reaction, we have argued that quantum-chemical molecular data strongly indicate that not the CO insertion chain growth mechanism but the carbide chain growth mechanism is responsible because the chain growth in the Fischer–Tropsch reaction kinetics operates within the so-called monomer formation kinetics limit, in which the activity is controlled by C–O bond activation that is the rate controlling step. This insight is an important attainment for the practical kinetics modeling of Fischer–Tropsch processes. Kinetics models other than those based on the carbide chain growth mechanism have limited predictive value.
An interesting advantage of the possibility to use computed molecular data deduced from quantum-chemical modeling is also that a comparison can be made between the kinetics performance of different reaction centers. Predictive catalysis has thus become available that relates catalyst structure and composition with catalyst performance.
5.1 The selectivity of the Fischer–Tropsch reaction
The Fischer–Tropsch reaction is one of the most complex heterogeneous catalytic reactions that are known. It is a polymerization reaction that uniquely combines formation of its elementary building unit (CHx from CO) with chain growth of long hydrocarbon chains and formation of products of a complex composition. This reflects in a complicated reaction scheme with many different reaction intermediates that interrelate through surface reaction steps. Interestingly we do not only have sequential or parallel reaction steps, but also reaction loops. The latter relates to a new kinetics feature discovered by the use of first principle quantum-chemical hydrocarbon chain growth rate data. In contrast to the widely used assumption of all of current chain growth models of the Fischer–Tropsch reaction, the chain growth reaction is not unidirectional. The chain growth equilibrium constant of adsorbed hydrocarbon chains that vary with one carbon unit varies from exothermic or thermodynamically neutral in favor of chain growth to endothermic for reactive surfaces that stabilize the dissociated state. Because of the latter surface CHx intermediates are not only generated from adsorbed CO, but also through dissociation of growing hydrocarbon chains, which is the reverse of the chain growth reaction. This creates a surface reaction loop with increased residence times of surface CHx intermediates. It provides an explanation for high methane yield with catalysts of high reactivity (see ref. 75) such as W or Mo.Theory indicates that the selectivity of the Fischer–Tropsch reaction depends on the presence of different surface sites, not just because they preferentially stabilize particular intermediates, but rather because at different sites the ratio of essential elementary reaction steps is quite different. One of the most important selectivity issues for the Fischer–Tropsch reaction is for instance the need to suppress methane formation, but formation of long chain hydrocarbons has to be efficient. The surface reaction responsible for methane formation is hydrogenation of adsorbed CHx. This CHx intermediate is formed through reaction sequences in which ultimately a C–O bond of CO is cleaved. The competitive desirable reaction that removes CHx from the surface is insertion of CHx into the growing hydrocarbon chain.
Interestingly the elementary rate constant for CHx insertion into the growing hydrocarbon chain is not strongly dependent on catalyst composition or reaction site structure. One predicts optimal yield of long hydrocarbons when the elementary rate constant of CHx insertion into the growing hydrocarbon chain is of comparable rate as the rate constant of CHx formation. However since the Fischer–Tropsch reaction operates within the monomer formation kinetics limit the rate constant of CHx formation from CO is rate controlling. Hence theory indicates that current Fischer–Tropsch catalysts do not operate under the condition of maximum long hydrocarbon yield. This provides a great challenge for further exploratory work to improve current catalysts. The simulations also indicate that to improve Fischer–Tropsch process yield one condition is to increase the rate of C–O bond cleavage reactions steps that form CHx.
The condition that formation of CHx by decomposition of CO has to be fast, while the removal rate of CHx as methane has to be slow has an important implication for the optimum structure of the catalytic site. This condition is not satisfied on surface terraces but can be satisfied on more highly coordinatively unsaturated surfaces of metals such as Co, Ru and Rh that contain stepped surface edge type sites. This has obviously important consequences for the particle size dependence and structure sensitivity of Fischer–Tropsch active metal particles. It is for instance also the molecular basis for the preference of Ni as a methanation catalyst. This metal has a high barrier for CO activation and CHx is rapidly hydrogenated to give methane.
An important corollary of monomer formation kinetics is that CO is the major adsorbate on surface sites that primarily give methane as well as on surface sites that are selective for chain growth. Then the CO consumption rate does not explicitly depend on the rate of chain growth or chain growth termination. The rate controlling step of the overall conversion rate of CO is the activation of CO to produce adsorbed CHx intermediates and possibly the rate of Oads removal. This simplifies dramatically the kinetic equations for the calculation of the rate of CO consumption.152 There is however an important caveat. Although this leads to the same expressions as for the methanation reaction, to model the Fischer–Tropsch reaction the elementary rate constant of methane production has to be low compared to that of (hydrogen activated) CO bond cleavage. Only then the Fischer–Tropsch reaction will have a high selectivity towards the production of long chain hydrocarbons.
The microkinetics simulations illustrate the subtle role of adsorbed hydrogen in the formation of longer hydrocarbons. The reaction rate generally has a positive order in hydrogen pressure and negative order in CO pressure. Since the overall rate of reaction is controlled by C–O bond activation these reaction orders are consistent with CO as the dominant adsorbed species. The positive order of CO consumption rate in hydrogen pressure is amongst others because the CO adsorption energy is higher than that of dissociatively adsorbed H2. CO adsorption will suppress hydrogen adsorption. Hydrogen is needed for hydrogenation of reaction intermediates and removal of adsorbed oxygen. Hydrogen activated CO dissociation is the dominant path that leads to the formation of methane on surface sites that have high barriers for direct CO bond cleavage. It is not yet clear whether the sites that are responsible for chain growth also require hydrogen assisted C–O bond cleavage or that then direct C–O dissociation already occurs with an activation energy low compared to methane formation from adsorbed CHx. This is an interesting question in need of further investigation. The effect of hydrogen pressure on chain growth selectivity relates to the nature of the partially hydrogenated CHx intermediate that is incorporated into the growing hydrocarbon chain. The chain growth parameter α can have a positive (increased formation of CHx from adsorbed CO) as well as a negative order in hydrogen pressure (increased rate of methane formation or chain growth termination).
Mathematically the surface reaction loop in the Fischer–Tropsch reaction due to reversibility of the hydrocarbon chain growth reaction leads to unexpected behavior of the chain growth parameter α. This is because when the chain growth reaction is reversible two values of chain growth parameter α can be the solution of corresponding kinetics steady state equations. One value of α is larger than one and the other is smaller than one.132 In the case of reversible chain growth, conservation of mass indicates that only the value of chain growth parameter α less than one is physically acceptable. However practical microkinetics simulations have to include cut-off of hydrocarbon chain length beyond a particular chain length. Mathematically this implies deviations in the calculated product distribution near hydrocarbon chain length cut off, which arise from mixing of solutions of the steady state equation corresponding to a value of α higher than one. In the particular case of the Fischer–Tropsch reaction simulations have to include at least hydrocarbon chain lengths longer than 50 carbon atoms. Because of this limitation, it is a great computational challenge to implement lateral effects in dynamic Monte Carlo simulations of the Fischer–Tropsch reaction, because it implies inclusion of a prohibitively large number of reaction steps in such a simulation.
Chemically chain growth value α higher than one occurs typically in conventional oligomerization reactions of limited range with reversible reaction steps. Then one finds differentially from the Fischer–Tropsch product that the longer oligomers will dominate.
This observation may be relevant to the unresolved problems in Fischer–Tropsch catalysis to produce selectively a hydrocarbon distribution within a limited chain length range without coproduction of lighter hydrocarbons. Possibly transient process conditions that limit the reaction time for chain growth153 may lead to such unique selectivity patterns in combination with catalysts that show slightly endothermic surface chain growth thermodynamics.
Alternatively a steady state approach can be used by inorganic engineering of the catalyst so that methane formation is suppressed. Application of high temperature will reduce the chain growth parameter α, but promoters have to be found that suppress methane formation by decreasing the rate of CHx hydrogenation. Interestingly selective ethylene and propylene production without coproduction of methane has been discovered recently by de Jong et al.42 for a promoted supported Fe catalyst at high temperature.
5.2 Improvements in the Fischer–Tropsch microkinetics model
In the microkinetics simulations we have assumed oxygen removal to be fast, which is consistent with indications from quantum-chemical studies. Nonetheless microkinetics simulations should be explored with explicit incorporation of surface oxygen removal. In this context it is interesting that it has been suggested that CO activation and low activation energy O removal can be coupled.31 They suggest end-on activation of CO by a surface hydrogen atom to give the dominant activation path for C–O bond cleavage, because then easily removable OH intermediates are formed on the surface. In case the two reaction steps of CO activation and Oads removal are not coupled, that particular reaction pathway of CO activation would not compete with alternative lower activation paths for C–O bond cleavage. Oxygen removal reactions may also appear essential for better understanding of support effects and particle size dependence. An early explanation of the decrease in the rate of the Fischer–Tropsch reaction beyond a particular size of the metal particle154 has been the suggestion that the smaller nanoparticles become oxidized. Partially oxidized phases of metal particles are often experimentally observed. Changes in the water partial pressure have also been observed to assist as well as suppress the rate of the Fischer–Tropsch reaction.37Furthermore, although we discussed some aspects of the kinetics of oxygenate formation, this topic and more generally the discussion of the detailed selectivity of the Fischer–Tropsch reaction as a function of catalyst composition and structure warrants extensive broadening of the current molecular database on reaction intermediates and elementary reaction steps of the reaction. A question that is essentially open is whether the optimum structure and composition of the reaction center for oxygenate formation versus long chain hydrocarbon formation are different. This may well be the case, since the balance between the rate of C–O bond cleavage and that of CO insertion will be different for the two cases. A guiding principle to optimize oxygenate formation is the search for promoters that change this balance, without promotion of the formation of methane or methanol.
Moreover, the microkinetics simulations do not include readsorption effects. In applied Fischer–Tropsch reaction kinetics models olefin readsorption has been shown to be of particular interest to predict deviations from the hydrocarbon product ASF chain length distribution.52,155 Readsorption effects depend on local concentrations of product around the catalyst particle and are hence intrinsically linked to inclusion of heat and mass transfer effects. The integration of the molecular catalysis approach and microkinetics into overall macroscopic kinetics that includes mass and heat transfer provides an important challenge to computational reactor engineering.156–158
5.3 Future developments in computational catalysis
There is considerable scope for improvement of the first principle microkinetics simulation approach of this Perspective. The microkinetics models used to support our arguments have to be considered idealized, allowing substantial room for further improvement. Quantum-chemical studies indicate that activation barriers of surface reactions can be substantially altered, when comparison is made for reactions in a surface overlayer with few vacancies, compared to the situation on a vacant surface.118,159 This can be accounted for in simulations that do not include explicitly lateral effects, but apply at high surface coverage by using free energy values of ground and transition states calculated under this condition. For instance, the microkinetics simulations of the carbide mechanism did not explicitly include lateral effects, but used a value for the CO adsorption energy adjusted to its value at high CO coverage. Early kinetic Monte Carlo simulations on hydrogenation of ethylene160,161 illustrate the relevance of explicit inclusion of lateral effects in order to model alloying effects properly. We envision that in the coming years more often coverage-dependent free energy changes, but even more importantly reaction path changes, will be explicitly incorporated into microkinetics models.First principle microkinetics simulations are based on molecular data of reaction intermediate stability and corresponding activation free energies. State of the art is the application of quantum-chemical DFT calculations. The accuracy of calculated energies varies typically between 10 and 30 kJ mol−1. This is generally acceptable when one needs to decide between different mechanistic options. However prediction of kinetics as a function of temperature requires accuracy of energies of the order of a few kJ mol−1. Hence there is a great need for the development of more accurate quantum-chemical methods useful to study the large systems relevant to computational catalysis.
Current state of the art catalytic reaction modeling relates catalyst performance with catalyst structure and composition. However an essential ingredient to be predictive in practical catalysis has still to be added. This is to predict the surface phase of a heterogeneous catalytic reaction under reaction conditions. Unfortunately to predict this surface phase is still one of the great challenges in the computational approach to heterogeneous catalysis. To the modeling of the Fischer–Tropsch reaction in particular this is a very important issue.
As especially emphasized by Schulz,47,162 Fischer–Tropsch catalysts may self-organize and become activated in the course of reaction. This may relate to formation of a selective (carbidic) surface phase163 or surface reconstruction effects.49,50
This topic of catalyst surface reconstruction in contact with a reactive medium is expected to be a major field of study in the future, not only for Fischer–Tropsch catalysis, but also more generally in heterogeneous catalysis.
Notwithstanding the great progress in modeling and understanding of heterogeneous catalytic reactions made, a new venue to catalyst modeling is envisioned when the dynamics of atomistic and molecular events on surfaces becomes explicitly considered. On a short time scale molecular dynamics simulations of individual movement of surface atoms or their collective motion will lead to formation of new surface phases, which may have different catalytic reactivity compared to the initial surface state. The use of surface thermodynamics methods to deduce the relative stability of surface phases in equilibrium with a gas atmosphere of particular composition and pressure will increasingly be used to approximate the structure of reacting surfaces.56–58 To study changes of catalyst performance at time scales relevant to catalyst deactivation is still a greater challenge. Nonselective reactions that occur with low probability, as for instance carbon deposition in the Fischer–Tropsch reaction, then become relevant. Also intermediate carbonyl formation that may lead to catalyst sintering then has to be considered. To include such phenomena into the catalyst modeling domain implies a multiscale approach that integrates events over a large range of different length and time scales. With this strategy one joins the great endeavor of current computational science that relates microscopic properties of short time and length scales with macroscopic phenomena at the larger length and longer time scales.
References
- G. A. Somorjai, Introduction to surface chemistry and catalysis, Wiley, New York, 1994 Search PubMed.
- G. Ertl, Reactions at Solid Surfaces, John Wiley & Sons, 2009 Search PubMed.
- T. Bligaard and J. K. Nørskov, Chemical Bonding at Surfaces and Interfaces, Elsevier, Amsterdam, 2008, pp. 255–321 Search PubMed.
- J. M. Thomas and W. J. Thomas, Principles and Practice of Heterogeneous Catalysis, Wiley VCH, 1997 Search PubMed.
- Catalysis: From Principles to Applications, ed. M. Beller, A. Renken and R. A. van Santen, Wiley-VCH, Weinheim, 2012 Search PubMed.
- A. Nilsson and L. G. M. Pettersson, Chemical Bonding at Surfaces and Interfaces, Elsevier, Amsterdam, 2008, pp. 57–142 Search PubMed.
- R. A. van Santen, M. Neurock and S. Shetty, Chem. Rev., 2010, 110, 2005–2048 CrossRef CAS PubMed.
- Computational Methods in Catalysis and Materials Science, ed. R. A. van Santen and P. Sautet, Wiley-VCH, 2009 Search PubMed.
- H. Toulhoat and P. Raybaud, J. Catal., 2003, 216, 63–72 CrossRef CAS.
- A. Groß, Theoretical Surface Science: A Microscopic Perspective, Springer, 2009 Search PubMed.
- M. P. Andersson, F. Abild-Pedersen, I. N. Remediakis, T. Bligaard, G. Jones, J. Engbæk, O. Lytken, S. Horch, J. H. Nielsen and J. Sehested, et al., J. Catal., 2008, 255, 6–19 CrossRef CAS PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 9464–9473 CAS.
- J. Chen and Z.-P. Liu, J. Am. Chem. Soc., 2008, 130, 7929–7937 CrossRef CAS PubMed.
- J. Cheng, X.-Q. Gong, P. Hu, C. M. Lok, P. Ellis and S. French, J. Catal., 2008, 254, 285–295 CrossRef CAS PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, J. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 6082–6086 CAS.
- Y. Choi and P. Liu, J. Am. Chem. Soc., 2009, 131, 13054–13061 CrossRef CAS PubMed.
- I. M. Ciobîcă, G. J. Kramer, Q. Ge, M. Neurock and R. A. van Santen, J. Catal., 2002, 212, 136–144 CrossRef.
- Q. Ge and M. Neurock, J. Phys. Chem. B, 2006, 110, 15368–15380 CrossRef CAS PubMed.
- Q. Ge, M. Neurock, H. A. Wright and N. Srinivasan, J. Phys. Chem. B, 2002, 106, 2826–2829 CrossRef CAS.
- C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. C, 2008, 112, 3840–3848 CAS.
- C.-F. Huo, Y.-W. Li, G. Wang and H. Jiao, J. Am. Chem. Soc., 2009, 131, 14713–14721 CrossRef CAS PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, Top. Catal., 2010, 53, 326–337 CrossRef CAS.
- Z.-P. Liu and P. Hu, J. Chem. Phys., 2001, 114, 8244–8247 CrossRef CAS.
- Z.-P. Liu and P. Hu, J. Am. Chem. Soc., 2002, 124, 11568–11569 CrossRef CAS PubMed.
- J. M. H. Lo and T. Ziegler, J. Phys. Chem. C, 2007, 111, 13149–13162 CAS.
- S. Shetty, I. M. Ciobîcă, E. J. M. Hensen and R. A. van Santen, Chem. Commun., 2011, 47, 9822–9824 RSC.
- P. van Helden, J.-A. van den Berg and I. M. Ciobîcă, Catal. Sci. Technol., 2012, 2, 491–494 CAS.
- M. C. Valero and P. Raybaud, Catal. Lett., 2013, 143, 1–17 CrossRef.
- O. R. Inderwildi, S. J. Jenkins and D. A. King, J. Phys. Chem. C, 2008, 112, 1305–1307 CAS.
- J. W. Mirwald and O. R. Inderwildi, Phys. Chem. Chem. Phys., 2012, 14, 7028–7031 RSC.
- M. Ojeda, R. Nabar, A. U. Nilekar, A. Ishikawa, M. Mavrikakis and E. Iglesia, J. Catal., 2010, 272, 287–297 CrossRef CAS PubMed.
- I. M. Ciobîcă and R. A. van Santen, J. Phys. Chem. B, 2003, 107, 3808–3812 CrossRef.
- S. Shetty, A. P. J. Jansen and R. A. van Santen, J. Am. Chem. Soc., 2009, 131, 12874–12875 CrossRef CAS PubMed.
- R. A. van Santen, A. Koster and T. Koerts, Catal. Lett., 1990, 7, 1–14 CrossRef CAS.
- C. Zheng, Y. Apeloig and R. Hoffmann, J. Am. Chem. Soc., 1988, 110, 749–774 CrossRef CAS.
- M. Zhuo, K. F. Tan, A. Borgna and M. Saeys, J. Phys. Chem. C, 2009, 113, 8357–8365 CAS.
- Fischer-Tropsch Technology, ed. A. P. Steynberg and M. E. Dry, Elsevier, Amsterdam, 2004 Search PubMed.
- F. Fischer and H. Tropsch, Brennst.-Chem., 1926, 7, 97–116 CAS.
- V. Subramani and S. K. Gangwal, Energy Fuels, 2008, 22, 814–839 CrossRef CAS.
- J. W. Niemantsverdriet, A. M. Van der Kraan, W. L. Van Dijk and H. S. Van der Baan, J. Phys. Chem., 1980, 84, 3363–3370 CrossRef CAS.
- M. A. Petersen, J. A. van den Berge and W. J. van Rensburg, J. Phys. Chem. C, 2010, 114, 7863–7879 CAS.
- H. M. T. Galvis, J. H. Bitter, C. B. Khare, M. Ruitenbeek, A. I. Dugulan and K. P. de Jong, Science, 2012, 335, 835–838 CrossRef PubMed.
- M. C. Valero, P. Raybaud and P. Sautet, J. Catal., 2007, 247, 339–355 CrossRef CAS PubMed.
- A. Sanchez, S. Abbet, U. Heiz, W. D. Schneider, H. Häkkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578 CrossRef CAS.
- K. M. Neyman, C. Inntam, V. A. Nasluzov, R. Kosarev and N. Rösch, Appl. Phys. A: Mater. Sci. Process., 2004, 78, 823–828 CrossRef CAS PubMed.
- M. O. Özbek, I. Önal and R. A. van Santen, ChemCatChem, 2013, 5, 443–451 CrossRef.
- H. Schulz, Appl. Catal., A, 1999, 186, 3–12 CrossRef CAS.
- H. Schulz, Top. Catal., 2003, 26, 73–85 CrossRef CAS.
- J. Wilson and C. de Groot, J. Phys. Chem., 1995, 99, 7860–7866 CrossRef CAS.
- I. M. Ciobîcă, R. A. van Santen, P. J. van Berge and J. van de Loosdrecht, Surf. Sci., 2008, 602, 17–27 CrossRef PubMed.
- E. Iglesia, S. C. Reyes, R. J. Madon and S. L. Soled, Adv. Catal., 1993, 39, 221–302 CrossRef CAS.
- J. J. C. Geerlings, J. H. Wilson, G. J. Kramer, H. P. C. E. Kuipers, A. Hoek and H. M. Huisman, Appl. Catal., A, 1999, 186, 27–40 CrossRef CAS.
- H. Pichler and H. Schulz, Chem. Ing. Tech., 1970, 42, 1162–1174 CrossRef CAS.
- I. G. Csizmadia, in Quantum Theory of Chemical Reactions: Vol. III: Chemisorption, Catalysis, Biochemical Reactions, ed. R. Daudel, A. Pullman, L. Salem and A. Veillard, Springer, 1982, pp. 77–84 Search PubMed.
- C. S. Kellner and A. T. Bell, J. Catal., 1981, 67, 175–185 CrossRef CAS.
- M. Scheffler, in Studies in Surface Science and Catalysis, ed. J. Koukal, Elsevier, 1988, vol. 40, pp. 115–122 Search PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- K. Reuter, in Modeling Heterogeneous Catalytic Reactions: From the Molecular Process to the Technical System, ed. O. Deutschmann, Wiley-VCH, Weinberg, 2009 Search PubMed.
- R. J. Gelten, A. P. J. Jansen, R. A. van Santen, J. J. Lukkien, J. P. L. Segers and P. A. J. Hilbers, J. Chem. Phys., 1998, 108, 5921–5934 CrossRef CAS.
- A. T. Bell, Catal. Rev.: Sci. Eng., 1981, 23, 203–322 CAS.
- A. Outi, I. Rautavuoma and H. S. van der Baan, Appl. Catal., 1981, 1, 247–272 CrossRef CAS.
- G. P. van der Laan and A. A. C. M. Beenackers, Ind. Eng. Chem. Res., 1999, 38, 1277–1290 CrossRef CAS.
- F. G. Botes, B. van Dyk and C. McGregor, Ind. Eng. Chem. Res., 2009, 48, 10439–10447 CrossRef CAS.
- B. W. Wojciechowski, Catal. Rev.: Sci. Eng., 1988, 30, 629–702 CAS.
- G. A. Huff and C. N. Satterfield, Ind. Eng. Chem. Process Des. Dev., 1984, 23, 696–705 CAS.
- I. C. Yates and C. N. Satterfield, Energy Fuels, 1991, 5, 168–173 CrossRef CAS.
- C. H. Bartholomew and R. J. Farrauto, Fundamentals of Industrial Catalytic Processes, John Wiley & Sons, Inc., Hoboken, New Jersey, 2nd edn, 2005 Search PubMed.
- P. Biloen and W. M. H. Sachtler, Adv. Catal., 1981, 30, 165–216 CrossRef CAS.
- B. H. Davis, Fuel Process. Technol., 2001, 71, 157–166 CrossRef CAS.
- B. C. Enger and A. Holmen, Catal. Rev.: Sci. Eng., 2012, 54, 437–488 CAS.
- P. M. Maitlis, R. Quyoum, H. C. Long and M. L. Turner, Appl. Catal., A, 1999, 186, 363–374 CrossRef CAS.
- O. R. Inderwildi and S. J. Jenkins, Chem. Soc. Rev., 2008, 37, 2274–2309 RSC.
- N. E. Tsakoumis, M. Rønning, Ø. Borg, E. Rytter and A. Holmen, Catal. Today, 2010, 154, 162–182 CrossRef CAS PubMed.
- R. A. van Santen, I. M. Ciobîcă, E. van Steen and M. M. Ghouri, in Advances in Catalysis, ed. B. C. Gates and H. Knozinger, Academic Press, 2011, vol. 54, pp. 127–187 Search PubMed.
- R. A. van Santen, M. M. Ghouri, S. Shetty and E. J. M. Hensen, Catal. Sci. Technol., 2011, 1, 891–911 CAS.
- M. J. Overett, R. O. Hill and J. R. Moss, Coord. Chem. Rev., 2000, 206–207, 581–605 CrossRef CAS.
- R. A. van Santen, Acc. Chem. Res., 2009, 42, 57–66 CrossRef CAS PubMed.
- J. M. G. Carballo, J. Yang, A. Holmen, S. García-Rodríguez, S. Rojas, M. Ojeda and J. L. G. Fierro, J. Catal., 2011, 284, 102–108 CrossRef CAS PubMed.
- J. P. den Breejen, P. B. Radstake, G. L. Bezemer, J. H. Bitter, V. Frøseth, A. Holmen and K. P. de Jong, J. Am. Chem. Soc., 2009, 131, 7197–7203 CrossRef CAS PubMed.
- J. den Breejen, A. Frey, J. Yang, A. Holmen, M. Schooneveld, F. F. Groot, O. Stephan, J. Bitter and K. Jong, Top. Catal., 2011, 54, 768–777 CrossRef CAS.
- R. C. Brady III and R. Pettit, J. Am. Chem. Soc., 1981, 103, 1287–1289 CrossRef.
- R. C. Brady III and R. Pettit, J. Am. Chem. Soc., 1981, 102, 6181–6182 CrossRef.
- P. M. Maitlis and V. Zanotti, Catal. Lett., 2007, 122, 80–83 CrossRef.
- P. M. Maitlis, H. C. Long, R. Quyoum, M. L. Turner and Z.-Q. Wang, Chem. Commun., 1996, 1–8 RSC.
- B. E. Mann, M. L. Turner, R. Quyoum, N. Marsih and P. M. Maitlis, J. Am. Chem. Soc., 1999, 121, 6497–6498 CrossRef CAS.
- J. Gaube and H. F. Klein, J. Mol. Catal. A, 2008, 283, 60–68 CrossRef CAS PubMed.
- H. Pichler, H. Schulz and F. Hojabri, Brennst.-Chem., 1964, 45, 215 CAS.
- M. P. Anderson, F. Abild-Pedersen, I. N. Remedias, T. Bligaard, G. Jones, J. Engbaek, O. Lytken, S. Horch, J. H. Nielsen, J. Sehested, J. R. Rostrup-Neilsen, J. K. Norskov and I. Chorkendorff, J. Catal., 2008, 255, 6 CrossRef PubMed.
- Y.-H. Zhao, K. Sun, X. Ma, J. Liu, D. Sun, H.-Y. Su and W.-X. Li, Angew. Chem., Int. Ed., 2011, 50, 5335–5338 CrossRef CAS PubMed.
- G. Brodén, T. N. Rhodin, C. Brucker, R. Benbow and Z. Hurych, Surf. Sci., 1976, 59, 593–611 CrossRef.
- T. Engel and G. Ertl, in Advances in Catalysis, ed. H. P. D. D. Eley and B. W. Paul, Academic Press, 1979, vol. 28, pp. 1–78 Search PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2010, 114, 1085–1093 CAS.
- A. Tuxen, S. Carenco, M. Chintapalli, C.-H. Chuang, C. Escudero, E. Pach, P. Jiang, F. Borondics, B. Beberwyck, A. P. Alivisatos, G. Thornton, W.-F. Pong, J. Guo, R. Perez, F. Besenbacher and M. Salmeron, J. Am. Chem. Soc., 2013, 135, 2273–2278 CrossRef CAS PubMed.
- P. Biloen, J. N. Helle, F. G. A. van den Berg and W. M. H. Sachtler, J. Catal., 1983, 81, 450–463 CrossRef CAS.
- P. Biloen, J. W. Helle and W. M. H. Sachtler, J. Catal., 1979, 58, 95–107 CrossRef CAS.
- T. Koerts, M. J. A. G. Deelen and R. A. van Santen, J. Catal., 1992, 138, 101–114 CrossRef CAS.
- T. Koerts and R. A. van Santen, J. Mol. Catal., 1992, 74, 185–191 CrossRef CAS.
- G. A. Beitel, A. Laskov, H. Oosterbeek and E. W. Kuipers, J. Phys. Chem., 1996, 100, 12494–12502 CrossRef CAS.
- G. A. Beitel, C. P. M. de Groot, H. Oosterbeek and J. H. Wilson, J. Phys. Chem. B, 1997, 101, 4035–4043 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- S. Dahl, A. Logadottir, C. J. H. Jacobsen and J. K. Norskov, Appl. Catal., A, 2001, 222, 19–29 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CrossRef CAS.
- R. A. van Santen and M. Neurock, Molecular Heterogeneous Catalysis, Wiley-VCH, 2006 Search PubMed.
- R. Hoffmann, Solids and Surfaces: A Chemist's View of Bonding in Extended Structures, Wiley-VCH, 1st edn, 1989 Search PubMed.
- C. Zheng, Y. Apeloig and R. Hoffmann, J. Am. Chem. Soc., 1988, 110, 749–774 CrossRef CAS.
- E. Shustorovich, Adv. Catal., 1990, 37, 101–163 CrossRef CAS.
- F. Abild-Pedersen, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS.
- R. A. Santen, A. Koster and T. Koerts, Catal. Lett., 1990, 7, 1–14 CrossRef.
- J. Zhang, X. M. Cao, P. Hu, Z. Zhong, A. Borgna and P. Wu, J. Phys. Chem. C, 2011, 115, 22429–22437 CAS.
- I. A. W. Filot, R. A. v. Santen and E. J. M. Hensen, 2013, unpublished.
- M. M. Ghouri and R. A. Santen, 2013, in preparation.
- B. S. Bunnik and G. J. Kramer, J. Catal., 2006, 242, 309–318 CrossRef CAS PubMed.
- I. M. Ciobîcă, F. Frechard, R. A. van Santen, A. W. Kleyn and J. Hafner, J. Phys. Chem. B, 2000, 104, 3364–3369 CrossRef.
- I. M. Ciobîcă and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 6200–6205 CrossRef.
- G. Jones, J. G. Jakobsen, S. S. Shim, J. Kleis, M. P. Andersson, J. Rossmeisl, F. Abild-Pedersen, T. Bligaard, S. Helveg and B. Hinnemann, et al., J. Catal., 2008, 259, 147–160 CrossRef CAS PubMed.
- Z.-P. Liu and P. Hu, J. Am. Chem. Soc., 2003, 125, 1958–1967 CrossRef CAS PubMed.
- S. Shetty, A. P. J. Jansen and R. A. van Santen, J. Phys. Chem. C, 2010, 114, 22630–22635 CAS.
- M. Zhuo, A. Borgna and M. Saeys, J. Catal., 2013, 297, 217–226 CrossRef CAS PubMed.
- H.-J. Li, C.-C. Chang and J.-J. Ho, J. Phys. Chem. C, 2011, 115, 11045–11055 CAS.
- S. Shetty, A. P. J. Jansen and R. A. van Santen, J. Phys. Chem. C, 2008, 112, 14027–14033 CAS.
- M. Mavrikakis, M. Baumer, H. J. Freund and J. K. Nørskov, Catal. Lett., 2002, 81, 153–156 CrossRef CAS.
- S. Eckle, H.-G. Anfang and R. J. r. Behm, J. Phys. Chem. C, 2011, 115, 1361–1367 CAS.
- G. L. Bezemer, J. H. Bitter, H. P. C. E. Kuipers, H. Oosterbeek, J. E. Holewijn, X. Xu, F. Kapteijn, A. J. van Dillen and K. P. de Jong, J. Am. Chem. Soc., 2006, 128, 3956–3964 CrossRef CAS PubMed.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef CAS PubMed.
- R. van Hardeveld and A. van Montfoort, Surf. Sci., 1966, 4, 396–430 CrossRef CAS.
- X.-Y. Quek, Y. Guan, R. A. van Santen and E. J. M. Hensen, ChemCatChem, 2011, 3, 1735–1738 CrossRef CAS.
- G. Lozano-Blanco, J. W. Thybaut, K. Surla, P. Galtier and G. B. Marin, Oil Gas Sci. Technol., 2006, 61, 489–496 CAS.
- G. P. Van der Laan and A. A. C. M. Beenackers, Catal. Rev.: Sci. Eng., 1999, 41, 255–318 CAS.
- C. G. Visconti, E. Tronconi, L. Lietti, P. Forzatti, S. Rossini and R. Zennaro, Top. Catal., 2011, 54, 786–800 CrossRef CAS PubMed.
- Y.-N. Wang, W.-P. Ma, Y.-J. Lu, J. Yang, Y.-Y. Xu, H.-W. Xiang, Y.-W. Li, Y.-L. Zhao and B.-J. Zhang, Fuel, 2003, 82, 195–213 CrossRef CAS.
- R. Zennaro, M. Tagliabue and C. H. Bartholomew, Catal. Today, 2000, 58, 309–319 CrossRef CAS.
- A. J. Markvoort, R. A. Van Santen, P. A. J. Hilbers and E. J. M. Hensen, Angew. Chem., Int. Ed., 2012, 51, 9015–9019 CrossRef CAS PubMed.
- R. A. Santen and A. J. Markvoort, ChemCatChem, 2013 DOI:10.1002/cctc.201300173.
- R. B. Anderson, in Hydrocarbon Synthesis, Hydrogenation and Cyclization, ed. P. H. Emmett, Reinhold Publishing, New York, 1956, vol. IV Search PubMed.
- R. B. Anderson, H. Kölbel and M. Rálek, The Fischer-Tropsch Synthesis, Academic Press, 1984 Search PubMed.
- H. H. Storch, N. Golumbic and R. B. Anderson, The Fischer-Tropsch and Related Syntheses, John Wiley & Sons, New York, 1951 Search PubMed.
- E. Iglesia, S. C. Reyes and R. J. Madon, J. Catal., 1991, 129, 238–256 CrossRef CAS.
- R. J. Madon and E. Iglesia, J. Catal., 1993, 139, 576–590 CrossRef CAS.
- P. Sabatier, La Catalyse en Chimie Organique, Librarie Polytechnique, Paris, 1913 Search PubMed.
- R. A. van Santen and J. W. Niemantsverdriet, Chemical Kinetics and Catalysis, Plenum Press, London, 1995 Search PubMed.
- M. P. Andersson, T. Bligaard, A. Kustov, K. E. Larsen, J. Greeley, T. Johannessen, C. H. Christensen and J. K. Nørskov, J. Catal., 2006, 239, 501–506 CrossRef CAS PubMed.
- Z.-P. Liu and P. Hu, J. Chem. Phys., 2001, 115, 4977 CrossRef CAS.
- R. A. van Santen and A. J. Markvoort, Faraday Discuss., 2013, 162, 267–279 RSC.
- P. Sabatier and J. B. Senderens, C. R. Acad. Sci., Paris, 1902, 134, 514 CAS.
- P. Sabatier and J. B. Senderens, J. Soc. Chem. Ind., 1902, 21, 504 Search PubMed.
- P. Sabatier and J. B. Senderens, J. Chem. Soc., 1905, 88, 401 Search PubMed.
- J. Schweicher, A. Bundhoo, A. Frennet, N. Kruse, D. Helen and F. d. r. C. Meunier, J. Phys. Chem. C, 2010, 114, 2248–2255 CAS.
- W. M. H. Sachtler and M. Ichikawa, J. Phys. Chem., 1986, 90, 4752–4758 CrossRef CAS.
- S. L. Shannon and J. G. Goodwin, Chem. Rev., 1995, 95, 677–695 CrossRef CAS.
- J. Yang, E. Z. Tveten, D. Chen and A. Holmen, Langmuir, 2010, 26, 16558–16567 CrossRef CAS PubMed.
- S. Krishnamoorthy, M. Tu, M. P. Ojeda, D. Pinna and E. Iglesia, J. Catal., 2002, 211, 422–433 CAS.
- R. A. van Santen, A. J. Markvoort, M. M. Ghouri, P. A. J. Hilbers and E. J. M. Hensen, J. Phys. Chem. C, 2013, 117, 4488–4504 CAS.
- F. M. Dautzenberg, J. N. Helle, R. A. van Santen and H. Verbeek, J. Catal., 1977, 50, 8–14 CrossRef CAS.
- E. van Steen, M. Claeys, M. E. Dry, J. van de Loosdrecht, E. L. Viljoen and J. L. Visagie, J. Phys. Chem. B, 2005, 109, 3575–3577 CrossRef CAS PubMed.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS.
- Modeling and Simulation of Heterogeneous Catalytic Reactions, ed. O. Deutschmann, Wiley-VCH, 2011 Search PubMed.
- M. K. Sabbe, M.-F. Reyniers and K. Reuter, Catal. Sci. Technol., 2012, 2, 2010–2024 CAS.
- D. Vervloet, F. Kapteijn, J. Nijenhuis and J. R. van Ommen, Catal. Sci. Technol., 2012, 2, 1221–1233 CAS.
- B. T. Loveless, C. Buda, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2013, 135, 6107–6121 CrossRef CAS PubMed.
- M. Neurock, J. Catal., 2003, 216, 73–88 CrossRef CAS.
- P. A. Sheth, M. Neurock and C. M. Smith, J. Phys. Chem. B, 2005, 109, 12449–12466 CrossRef CAS PubMed.
- H. Schulz, Stud. Surf. Sci. Catal., 2007, 163, 177–199 CrossRef CAS.
- P. Sautet and F. Cinquini, ChemCatChem, 2010, 2, 636–639 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp52506f |
| This journal is © the Owner Societies 2013 |