Hole conductivity in oxygen-excess BaTi_1−xCa_xO_3−x+δ

Abstract

BaTiO₃ containing Ca substituted for Ti as an acceptor dopant, with oxygen vacancies for charge compensation and processed in air, is a p-type semiconductor. The hole conductivity is attributed to uptake of a small amount of oxygen which ionises by means of electron transfer from lattice oxide ions, generating O⁻ ions as the source of p-type semiconductivity. Samples heated in high pressure O₂, up to 80 atm, absorb up to twice the amount expected from the oxygen vacancy concentration. This is attributed to incorporation of superoxide, O₂⁻, ions in oxygen vacancies associated with the Ca²⁺ dopant and is supported by Raman spectroscopy results.

---

Introduction

Barium titanate, BaTiO₃, is the base material for a wide range of commercial electroceramic materials and devices. Depending on the application, BaTiO₃-based ceramics contain a wide variety of dopants in order to modify or optimise properties such as high, or low, resistivity and temperature of the ferroelectric Curie transition. Consequently, a large number of studies on the defect chemistry of BaTiO₃ have been carried out, mainly by equilibrium electrical conductivity (σ) measurements vs. oxygen partial pressure (P_O2) but also by thermogravimetry, Hall effect and Seebeck coefficient measurements.^1–10

A feature of the electrical conductivity of undoped BaTiO₃ and indeed, of many other electroceramic oxides is that, on decreasing P_O2 during equilibrium electrical conductivity measurements, the electrical properties are dominated first by holes (p-type region) with σ ∝ P_O2^1/4, second by oxide ions (electrolytic region) independent of oxygen partial pressure and third by electrons (n-type region) with σ ∝ P_O2^−1/n (n = 4 or 6).^1–10 On doping BaTiO₃ with donor dopants, such as La³⁺ on the Ba sites and Nb⁵⁺ on the Ti sites, the p-type and electrolytic regions are suppressed whereas they are enhanced on doping with acceptor dopants, such as Ca²⁺ on the Ti site.^11,12

In acceptor-doped BaTiO₃ conductivity may, however, be dominated by protons if the materials can absorb water molecules leading to hydroxyl groups () which are the source of subsequent proton conduction. Hence, the electrical properties of Ca-doped BaTiO₃, e.g. BaTi_0.98Ca_0.02O_2.98, are remarkably complex since, depending on processing conditions and atmosphere, three species may contribute to the conductivity: protons, oxygen vacancies, holes.¹³ For oxide ion conduction to predominate, it is necessary to work in dry atmospheres of low P_O2; for proton conduction, wet atmospheres of low P_O2 are necessary; in dry atmospheres of high P_O2, hole conduction predominates.¹³

In the p-type region, where the conductivity is dominated by the presence of extrinsic holes, the conductivity is dependent upon oxygen partial pressure in the surrounding atmosphere since, with increasing P_O2, oxygen molecules may be absorbed at the sample surface and holes created by the idealised process:

½O₂ → O²⁻ + 2h˙ (1)

We have recently found that the hole concentration and associated p-type conductivity can be increased similarly by application of a small dc bias during conductivity measurements and that, on removal of the bias, the conductivity reverts to its original value.^14–18 This effect is observed only with acceptor-doped materials. Oxygen vacancies associated with the acceptor dopants are necessary for O₂ absorption to occur and a source of electrons (leading to hole creation) is required in order for the absorbed oxygen to form anionic species. The only possible source of electrons in high purity BaTiO₃ is lattice O²⁻ ions which ionise. The ionisation process:

O²⁻ → O⁻ + e⁻ (2)

is favoured in situations where O²⁻ ions are underbonded such as when they are coordinated to acceptor dopants such as .

The purpose of this work was to investigate further the electrical properties in the p-type region of acceptor-doped BaTiO₃ in which the oxygen vacancy concentration is controlled by the acceptor content. It was of interest to correlate the electrical properties with the absorption of oxygen by treatment in high oxygen pressures and study the subsequent desorption of oxygen by high sensitivity thermogravimetry. The system chosen for study is BaTiO₃ with Ca doped on the Ti site. Oxygen absorption was achieved by high pressure oxidation, monitored by thermogravimetry and gave the surprising result that the amount of possible oxygen absorption can exceed, by up to a factor of two, the oxygen vacancy concentration. This result leads us to conclude that as well as O⁻ ion formation, superoxide ions, O₂⁻, are created by O₂ absorption at high pressures.

Experimental

Samples of BaTi_1−xCa_xO_3−x (x = 0.005, 0.01, 0.015 and 0.02, labelled as BTC005, BTC01, BTC015 and BTC02, respectively) were prepared by solid state reaction using BaCO₃ (Aldrich 99.98%), TiO₂ (Aldrich 99.99%) and CaCO₃ (Aldrich 99%), which were dried prior to weighing at 180, 800 and 180 °C, respectively. Samples totalling ca. 3 g were mixed with acetone manually in a mortar and pestle, dried and fired in Pt crucibles, initially to decarbonate at 1000 °C for 10 h, and then heated at 1250 and 1350 °C for 12 h to initiate reaction. At this stage, pellets were prepared by uniaxial pressing and heated, together with unpelleted powder, in air at 1425 ∼ 1450 °C for 12 h and cooled slowly inside the furnace. For electrical property measurements, pellets were then coated with electrodes made from Pt paste that was decomposed and hardened by heating to 900 °C for 2 h. Further heat treatments were carried out on both powders and pellets with Pt electrodes attached; these were either reheated to 1300 °C for 1 h and cooled rapidly in liquid nitrogen, or heated to 800 °C under high pressure oxygen, HOP using a Morris furnace and slow-cooled under pressure. Three sets of powder samples: slow-cooled, quenched and HOP were analysed by X-ray powder diffraction, XRD and thermogravimetry, TG.

XRD used a Stoe Stadi P Diffractometer (Darmstadt, Germany), CuKα₁ radiation with linear position-sensitive detector; lattice parameters were determined by least-squares refinement for reflections in the range 20 < 2θ < 80°, using the software WinXPow version 1.06, and an external Si standard.

TG analysis used a Setaram, SETSYS Evolution TGA with a resolution of 0.002 μg. About 60 mg of sample were placed in a Pt crucible and data recorded from room temperature to 1300 °C in N₂ at 10 °C min⁻¹. In addition, a baseline was collected using the same experimental conditions as those for the sample(s). The baseline was accordingly subtracted from the sample data using the software CALISTO.

A Renishaw inVia micro-Raman spectrometer (London, UK) was used to record Raman spectra over the range 100–2000 cm⁻¹; the spectral excitation was provided by an Ar⁺ laser, using the 514.5 nm line. X-ray photoelectron spectroscopy (XPS) used a Perkin Elmer PHI5400 (Waltham, USA) with Al Kα (1486.6 eV) radiation.

For electrical property measurements, slow-cooled pellets (∼0.3 g, ∼1.0 mm thick, ∼6.5 mm diameter, and ∼96.8% pellet density) with electrodes attached were placed into a conductivity jig. Dielectric permittivity as a function of temperature was measured by a LCR, HP 4284A instrument. Impedance data were measured using a Solartron SI 1260 impedance analyzer over the frequency range 0.01 Hz to 10 MHz with an ac measuring voltage of 0.1 V; isothermal stepwise measurements were made on cooling over the range 500 to 200 °C. Conductivities of the HOP-treated samples were measured similarly; isothermal stepwise measurements were made on heating over the range 200 to 400 °C. Impedance data were corrected for overall pellet geometry and blank capacitance of the conductivity jig. Resistance values were obtained from intercepts on the real, Z′ axis. Conductivity and capacitance data are reported in units of Scm⁻¹ and Fcm⁻¹, respectively, that refer to correction for only the overall sample geometry.

Measurements of electrical conductivity as a function of P_O2 in the range 700–850 °C were carried out in a specially-designed cell fitted with a built-in zirconia probe (MicroPoas® by SETNAG), which was fitted next to the sample, to measure P_O2. The desired oxygen partial pressures were obtained from mixtures of Ar–O₂.

Results

Single phase solid solutions of formula BaTi_1−xCa_xO_3−x+δ were prepared by solid state reaction with a final firing at 1425 ∼ 1450 °C for 12 h. Samples were phase-pure by XRD and were indexed on the usual tetragonal unit cell for BaTiO₃. Results were obtained for samples given three sets of post-reaction treatments: quenched from 1300 °C in air, slow-cooled in air from 1450 °C and slow-cooled from 800 °C under high pressure oxygen, HOP, as shown in Fig. 1. For each sample set, lattice parameters and cell volume change linearly with x: a increases, c decreases and cell volume increases. On comparing the three data sets, the quenched samples have the largest lattice parameters and cell volume whereas the samples slow-cooled in air at atmospheric pressure have the smallest values.

Fig. 1 Lattice parameters against composition for three sets of samples.

Thermogravimetric results are shown in Fig. 2 for samples of BTC02, x = 0.02 that were either quenched after heating in N₂ at 1300 °C, or slow-cooled from 800 °C in the HOP furnace. The HOP pressures refer to the pressure at 800 °C; during cooling to room temperature, this gradually reduced to ∼25% of its pressure at 800 °C. For TG measurements, samples were heated and cooled in N₂. The quenched sample showed essentially no weight change on either heating or cooling. For samples given different HOP treatment, weight loss was observed on heating and the amount of weight loss correlated approximately with the maximum oxygen pressure in the HOP furnace prior to slow cool to room temperature under pressure. For all cases, a rapid weight loss occurred between ∼700 °C and 850 °C, followed by a more gradual weight loss up to 1300 °C; small weight changes were apparent on cooling in some cases but these may be associated with base line drift. In each case, it is assumed that the samples had no oxygen excess, i.e. δ = 0 in the formula, BaTi_1−xCa_xO_3−x+δ, at 1300 °C. The initial oxygen contents, δ, after HOP treatment and prior to TG were therefore calculated from the weight losses; these are shown in Table 1. A maximum δ value of 0.02 would be expected if all the oxygen vacancies were filled by monatomic oxide ions.

Fig. 2 TG data in N₂ for samples of x = 0.02 given different heat treatments.

Table 1 Oxygen content (2.98 + δ) for composition x = 0.02 given different high pressure heat treatments

	Quench	5 bar	10 bar	30 bar	80 bar
δ	0	0.027	0.037	0.045	0.046

---

TG data are shown in Fig. 3 for four different compositions subjected to a maximum HOP pressure of 80 bar. All samples lost weight on heating in air; the total weight losses increased approximately linearly with composition. The weight loss profiles are also composition-dependent. For compositions x = 0.005 and 0.01, weight loss commenced above ∼600 °C, increased rapidly up to ∼750 °C and then more slowly up to a maximum temperature of 1300 °C. With increasing x, 0.015 and 0.02, weight loss commenced at increasingly lower temperatures although the high temperature weight loss profile is similar to that of the other compositions. The total weight loss at 1300 °C is converted to values of δ which are summarised in Table 2. In each case, the observed total weight loss is approximately double that expected if all oxygen vacancies are filled by monatomic oxygen species.

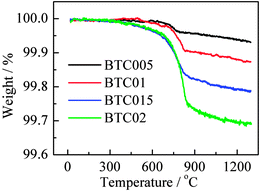Fig. 3 TG data in N₂ for samples of different composition heated to 800 °C in 80 bar O₂.

Table 2 Oxygen content, δ, for samples heated at 800 °C and 80 bar

	BTC005	BTC01	BTC015	BTC02
δ	0.01	0.019	0.031	0.046

---

A selection of typical impedance data is shown in Fig. 4, from which total sample conductivities were obtained. These approximate to, but are slightly less than, the bulk conductivities since there is evidence for a small grain boundary resistance whose magnitude is a small fraction of the total resistance. This is seen by the distortion at low frequency of the main, high frequency impedance arc in (a) and the low frequency shoulder in the Z′′/log f spectrum (d) which does not show a corresponding shoulder in the M′′/log f spectrum (d). Data are shown for one composition, x = 0.02, which was prepared without HOP treatment but was simply slow-cooled to room temperature in air after sintering at 1450 °C. Other samples showed a similar impedance response.

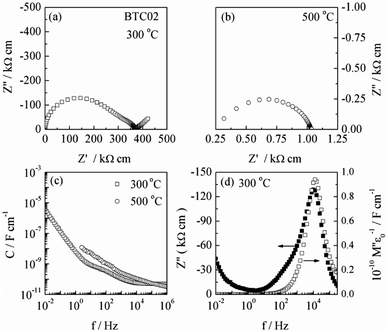Fig. 4 A typical set of impedance data for one composition, x = 0.02, with data shown at 300 and 500 °C: (a and b) impedance complex plane plot, (c) capacitance spectroscopic plot and (d) Z′′/M′′ spectroscopic plots.

Conductivity data for the same composition are shown at 800 °C as a function of P_O2 in Fig. 5. The conductivity increases with P_O2 which indicates an increasing transition from oxide ion conductivity to hole conductivity. The data agree very well with literature data,¹⁹ shown as a solid curve, especially since our total conductivity values, Fig. 4, are slightly less than bulk values.

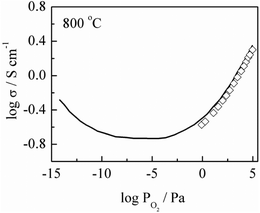Fig. 5 Conductivity as a function of P_O2 at 800 °C for x = 0.02. Solid curve represents literature data for the same composition.¹⁹

Conductivity data are shown in Fig. 6 in Arrhenius format for samples of the same composition, x = 0.02, that had been given HOP treatment to various pressures prior to conductivity measurements. The measurements were made in laboratory air and therefore, no attempt was made to ensure that any excess oxygen introduced during the HOP treatment was preserved during the conductivity measurements, which were made at temperatures in the range 200 to 400 °C. Nevertheless, the Arrhenius plots are essentially linear and show a gradual increase in conductivity with increasing HOP pressure which indicates that most, if not all, of the excess oxygen introduced during HOP treatment, together with an associated increase in hole carrier concentration, was retained during the conductivity measurements.

Fig. 6 Conductivity Arrhenius plots for samples of x = 0.02 after different high pressure heat treatments.

Permittivity data as a function of temperature for different compositions are shown in Fig. 7. Data were recorded at a fixed frequency of 10 kHz; the impedance data, Fig. 4, show that at this frequency and these temperatures, permittivity data were essentially independent of frequency and therefore represent the sample bulk. Permittivities show the expected profile with a maximum representing the Curie temperature, T_c, which decreases rapidly with x, Fig. 7 inset, consistent with literature data for B-site substitution of Ca into BaTiO₃.^16,20,21 This contrasts with the effect of isovalent A-site doping, i.e. Ba_1−xCa_xTiO₃, for which T_c remains approximately constant with x;^16,21,22 Ca is a particularly unusual dopant of BaTiO₃ since it is able to occupy either Ba and/or Ti sites, but with very different effect on the subsequent properties.^{11–13,16,19–22} Here, we deliberately targeted T-site doping and this is confirmed by the T_c results.

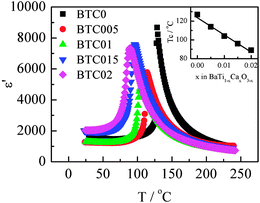Fig. 7 Fixed frequency permittivity data at 10 kHz as a function of temperature for different compositions.

For one composition, x = 0.02, permittivity data for samples given different post-reaction heat treatments are shown in Fig. 8. For samples that were measured immediately after their heat treatment, (a and b), two effects are seen. First, permittivity data (a) show the same T_c value but the value of the permittivity maximum is higher for the quenched sample than for the slow cooled/HOP samples. Second, the dielectric loss, tan δ, data show essentially zero loss for the quenched sample over the range 25–180 °C but increasing loss for the slow cooled and especially, HOP sample. For a quenched sample that was left exposed to laboratory air for a few days, the permittivity profile was significantly different on heating and cooling (c). This is attributed to H₂O molecules which were adsorbed on the surface of the quenched sample which contains oxygen vacancies and were subsequently desorbed prior to the cooling cycle measurements.

Fig. 8 (a) Fixed frequency permittivity of x = 0.02 after different heat treatment conditions, (b) dielectric loss data for the same sample used in (a) and (c) permittivity data after exposure of the sample to laboratory air for several days. Data were recorded at a fixed frequency of 10 kHz.

TG analysis of a quenched sample containing oxygen vacancies is shown in Fig. 9(a). The TG was carried out immediately after the sample was quenched. On heating by TG in air, a significant and rapid increase in weight occurred, especially between ∼350 and ∼450 °C, which was essentially retained on heating (1) the sample to 1250 °C and subsequent cooling (1) to room temperature. However, the weight gained was then lost on a second heating (2) on changing the atmosphere to N₂. This weight loss was not recovered on cooling (2) in N₂. We attribute these changes to uptake/loss of O₂ rather than H₂O.

Fig. 9 TG data for a sample of x = 0.02: (a) quenched from 1300 in air (TG was done first in air and then in N₂ for heating and cooling process); (b) slow cooled in air from 1450 °C (TG was done in N₂).

By contrast, TG data for a sample of x = 0.02, which had been slow cooled in air from 1450 °C, Fig. 9(b), show a gradual weight loss on the TG heating cycle in N₂ over the range 25 to ∼400 °C and a second weight loss between 700 and 800 °C, neither of which were recovered during the cooling cycle of TG in N₂ (not shown). We attribute the initial weight loss to loss of water and the second to loss of O₂.

The Raman spectra of BTC02 after different heat treatments are shown in Fig. 10. All spectra show sharp bands at ∼172 and 309 cm⁻¹ and asymmetric broader bands at ∼255, 518, 720 and 830 cm⁻¹ in agreement with the literature values.²³ In addition, the HOP sample shows an extra peak at ∼1125 cm⁻¹ (inset Fig. 10), but which is largely absent from the quenched sample. The Raman spectrum of KO₂, RbO₂ and CsO₂ shows a peak in the range 1132–1146 cm⁻¹ which is attributed to a fundamental peak of the superoxide, O₂⁻.^24,25 Recently, lithium superoxide-like species in the discharge product of a Li–O₂ battery have been identified by the presence of a peak at ∼1125 cm⁻¹ in the Raman spectra and supported by DFT calculations;²⁶ the O–O stretching frequency in the LiO₂ bulk phase is calculated to be ∼1103 cm⁻¹ by DFT.²⁷ These results, taken together, demonstrate conclusively that the peak at ∼1125 cm⁻¹ in the HOP sample is associated with superoxide ions.

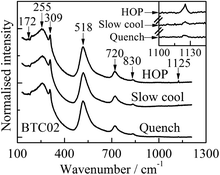Fig. 10 Room temperature Raman spectra for x = 0.02 after different heat treatment conditions. Peak positions, in wavenumbers, are shown.

The XPS spectra of BTC02, Fig. 11, show peaks at ∼528.6 and 531.1 eV, which correspond to the standard O1s peaks and a rather weak shoulder at ∼534.5 eV in the HOP sample which is not seen in the slow cooled and quenched samples. Strongin et al.²⁸ studied by XPS the presence of oxygen species in Li deposited on solid O₂ and assigned the peak at 534.5 eV to the presence of superoxide ions, O₂⁻.

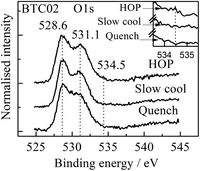Fig. 11 XPS spectra of the O1s core level for x = 0.02 after different heat treatment conditions. Peak positions, in eV, are shown.

Discussion

A range of compositions has been prepared whose properties, in particular lattice parameters and Curie temperatures, vary with Ca content. The T_c data are fully consistent with literature reports^16,20,21 indicating that for these samples, Ca substitutes for Ti on the B sites of the perovskite structure with creation of oxygen vacancies for charge compensation. When, alternatively, Ca substitutes for Ba, T_c shows very little change with Ca content;^16,21,22 permittivity data and the permittivity profiles therefore provide a very sensitive indicator of the doping mechanism. For samples processed under standard conditions involving firing and subsequent cooling in air, the expectation is that the oxygen content in the formula BaTi_1−xCa_xO_3−x would be controlled directly by the calcium content, x.

Stoichiometric BaTiO₃ loses a small amount of oxygen on firing in air above ∼1350 °C;²⁹ the amount of oxygen loss is too small to detect, even by sensitive thermogravimetry, but does have a significant effect on the electrical properties leading to n-type semiconductivity. Our samples with 0.005 ≤ x ≤ 0.02 show no evidence of n-type semiconductivity but instead, are p-type and show an increase in conductivity with increasing P_O2 We see no evidence of n-type semiconductivity since additional oxygen loss would be required, above that associated with the doping mechanism, in order for the samples to be n-type.

The dependence of conductivity on P_O2, Fig. 5, is consistent with a gradual change from oxide ion conductivity to p-type conductivity with increasing oxygen partial pressure, in agreement also with literature results.¹⁹ In order for p-type conductivity to occur, holes must be created and the question arises as to the location of the holes. Frequently in the literature, holes are assigned to the presence of unavoidable acceptor impurities such as Fe^5–7 but there are also cases, in both high purity and doped BaTiO₃, where such an explanation is not consistent with the results. The holes are clearly localised rather than in a conduction band since the materials are low-level hopping semiconductors with high activation energy.

Since it is highly unlikely that the holes could be located on any of the cations, Ba, Ti or Ca, the unavoidable conclusion is that they are located on oxygen as O⁻ ions. With increasing P_O2, the gradual transition from oxide ion conductivity to p-type conductivity is therefore attributed to the absorption of O₂ by the sample, which becomes fully or partially ionised; the source of electrons must be oxide ions in the crystal lattice. It has been argued¹⁶ that oxide ions in the immediate vicinity of the acceptor dopant, Ca, are more susceptible to ionisation since they are significantly underbonded: in the gas phase, the O²⁻ ion is unstable and is preserved in the crystal lattice only by the additional lattice energy associated with formation of O²⁻ ions; oxide ions in the vicinity of acceptor dopants do not experience the same degree of lattice energy stabilisation as those that are fully inside the bulk, undoped lattice and therefore, may be ionised more readily.

On the assumption that monatomic oxygen species can enter the oxygen vacancies in the doped crystal lattice, the maximum oxygen uptake that is achievable with increasing P_O2 should correspond to δ = x in the general formula, BaTi_1−xCa_xO_3−x+δ. TG data show clearly that this limit is exceeded, Tables 1 and 2, and that at the highest oxygen pressures, the value of δ is approximately twice the maximum expected value. The interpretation of this result is that the additional oxygen species are not fully dissociated O⁻ ions but instead, are singly charged, superoxide molecule ions, O₂⁻.

The question then arises as to whether the oxygen vacancies in the crystal lattice are large enough to accommodate a diatomic anion. Our explanation is that the Ca²⁺ acceptor dopant is much larger than the Ti⁴⁺ ion that it replaces in the BaTiO₃ lattice, giving rise to a highly distorted local environment in which the size of the oxygen vacancy associated with Ca²⁺ is significantly enhanced. Ca²⁺ usually shows coordination numbers of 8 or higher in the perovskite structure whereas in the present materials without any oxygen excess, its coordination number is, on average, reduced to 5.

The occurrence of molecule anions on a single anion site in a crystal structure finds precedence in the alkali halide colour centres for which, from spectroscopic evidence, the H⁻ centre has been proposed in which the chlorine molecule ion, Cl₂⁻, is able to occupy a regular anion lattice site. From surface spectroscopic studies on oxide systems there is also evidence that partially ionised oxygen species such as O₂⁻ exist.³⁰

For each superoxide ion that enters the structure, it is necessary also to create one O⁻ ion, giving rise to the general formula:

BaTi_1−xCa_xO_3−x−δ²⁻O_δ⁻(O₂⁻)_δ, 0 ≤ δ ≤ x (3)

From the TG results on the HOP samples, there is, therefore, very strong evidence that incorporation of superoxide ions is responsible for the observed weight changes. Within errors, the maximum observed weight changes agree with what is expected for complete lattice incorporation of O₂⁻ ions in the available oxygen vacancies rather than for selective adsorption at e.g. sample surfaces and grain boundaries.

Conclusively evidence for the incorporation of superoxide ions into the lattice is provided by Raman spectra which showed a clear signal of the O₂⁻ ion in the HOP sample that is largely absent from the quenched sample. Supporting evidence is obtained from XPS spectra which show the presence of a weak shoulder peak in the HOP sample.

The lattice parameter data as a function of x and δ, Fig. 1, show that for all samples, the slow-cooled materials have smaller lattice parameters and cell volumes than either the quenched or HOP samples. We speculate that the slow-cooled samples absorb oxygen but mainly as O⁻ ions whereas superoxide ions are incorporated only after high pressure treatment. It is frequently observed that oxidation of oxygen-deficient samples of various transition metal-containing compounds leads to a contraction in unit cell volume since the associated increase in oxidation state of the transition metal species present leads to stronger and shorter metal–oxygen bonds. In the present case, the initial oxidation is not associated with metal cations but with oxidation of some lattice O²⁻ ions to O⁻ ions; these are smaller than O²⁻ ions and so, a lattice contraction occurs. We therefore attribute the lattice contraction in slow-cooled samples to the absorption of O₂ and the formation of some O⁻ ions. The subsequent increase in lattice parameters and cell volume after HOP treatment is attributed to the incorporation of superoxide ions which are significantly larger than the O⁻ ions.

The thermal stability of oxygen-excess samples appears to be very sensitive to both composition and atmosphere. With increasing Ca content, HOP-treated samples appear to lose mass at increasingly lower temperatures on heating in the TG instrument, Fig. 3.

Samples quenched from high temperature appear to be oxygen-stoichiometric with δ = 0 and show no evidence of additional oxygen loss that could give rise to n-type semiconductivity. On heating quenched samples in air in the TG instrument, however, a small but rapid uptake of O₂ occurs on heating which is retained in air to the highest temperature studied, 1250 °C, Fig. 9. This uptake of O₂ was reversed on reheating in N₂. It is likely, therefore, that samples heat-treated in air and subjected to a standard cool will absorb a small amount of extra oxygen giving enhanced p-type conductivity associated with O⁻ ion formation. This is the first stage of oxygen uptake. In the second stage, the oxygen uptake is greatly increased by HOP treatment in which the absorbed O⁻ ions are effectively converted to O₂⁻ ions.

The increased dielectric loss of slow-cooled and HOP samples compared with quenched samples, Fig. 8(b), can be explained by the increase in hole concentration with increasing P_O2 and therefore, increase in p-type conductivity. This leads to an increase in dielectric loss which is shown most clearly for the HOP sample, Fig. 8(b); it illustrates that the loss data reflect electronic conductivity rather than oxide ion conductivity, which is the main conduction mechanism in the quenched sample, Fig. 5.

Previous work has shown that depending on sample treatment, three species contribute to the conductivity in Ca (acceptor)-doped BaTiO₃: holes, oxide ions and protons.¹³ Although the conditions used here have largely excluded the possibility of proton conduction, there is evidence for H₂O absorption and subsequent loss on TG of samples left exposed to the atmosphere for a few days. This water adsorption also seems to have an effect on the permittivity profile, Fig. 8(c).

Conclusions

With increasing oxygen partial pressure, BaTiO₃ containing Ca²⁺ ions acceptor-doped onto the B site, with oxygen vacancies for charge compensation, shows increasing p-type conductivity. This is attributed to absorption of oxygen by the samples leading to an increase in hole concentration by ionisation of lattice O²⁻ ions to O⁻ ions.

Thermogravimetric analysis shows that the amount of oxygen uptake using high pressure treatment in the range 5–80 bar, is greater than can be accounted for by single atom occupancy of the available oxygen vacancies. The maximum oxygen uptake is essentially twice that expected and it is proposed that the superoxide, O₂⁻ ion is responsible. Creation of the superoxide ion avoids the necessity of providing sufficient energy to dissociate the O₂ molecules and the electron affinity to form these superoxide ions may be sufficiently negative that they are subsequently stabilised, at least at low temperatures, within the perovskite crystal lattice.

Commencing with quenched samples whose oxygen content is given by the formula BaTi_1−xCa_xO_3−x, two stages in oxygen absorption are envisaged and can be summarised ideally as:

For both of these processes, δ is variable, depending on conditions, over the range 0 ≤ δ ≤ x.

In stage 1, oxygen vacancies are filled by dissociated oxygen anions; it is assumed that these are O⁻ ions and for each, one lattice O²⁻ ion ionises to produce a second O⁻ ion. In stage 2, oxygen vacancies are filled by superoxide ions, each of which requires ionisation of a lattice O²⁻ ion to create an O⁻ ion. We have not tested the conditions under which the products of stage 1 can be converted to those of stage 2 by HOP treatment, stage 3.

Extra space is required for the large superoxide to enter the crystal lattice; this is provided by the immediate coordination environment of the Ca²⁺ ion, which locally, causes lattice expansion and has an anion coordination reduced to five, which is much less than usually expected for the large Ca²⁺ ion.

Acknowledgements

We thank: EPSRC; Chinese Scholarship Council, National Nature Science Foundation (51172187), the SPDRF (20116102130002); 111 Program (B08040) of MOE; the Xi'an Science and Technology Foundation (CX1261-2, CX1261-3, XA-AM-201003) and the Doctorate Foundation (CX201208) of China.

References

1. S. A. Long and R. N. Blumenthal, Ti-rich nonstoichiometric BaTiO₃: I, high-temperature electrical conductivity measurements, J. Am. Ceram. Soc., 1971, 54(10), 515–519.
2. S. A. Long and R. N. Blumenthal, Ti-rich nonstoichiometric BaTiO₃: II, analysis of defect structure, J. Am. Ceram. Soc., 1971, 54(11), 577–583.
3. R. J. Panlener and R. N. Blumenthal, Ti-rich nonstoichiometric BaTiO₃: III, high-temperature thermodynamic and X-ray diffraction measurements, J. Am. Ceram. Soc., 1971, 54(12), 610–613.
4. G. J. Conger and H. U. Anderson, Nonstoichiometry in BaTiO₃, J. Am. Ceram. Soc., 1972, 55(10), 539.
5. N. G. Eror and D. M. Smyth, Nonstoichiometric disorder in single-crystalline BaTiO₃ at elevated temperatures, J. Solid State Chem., 1978, 24(3–4), 235–244.
6. N.-H. Chan and D. M. Smyth, Defect chemistry of BaTiO₃, J. Electrochem. Soc., 1976, 123(10), 1584–1585.
7. N. H. Chan, R. K. Sharma and D. M. Smyth, Nonstoichiometry in undoped BaTiO₃, J. Am. Ceram. Soc., 1981, 64(9), 556–562.
8. J. Nowotny and M. Rekas, Electrical properties and defect structure of barium metatitanate within the p-type regime, J. Eur. Ceram. Soc., 1989, 5(3), 173–182.
9. J. Nowotny and M. Rekas, Defect chemistry of BaTiO₃, Solid State Ionics, 1991, 49, 135–154.
10. H.-I. Yoo, C.-R. Song and D.-K. Lee, BaTiO_3–δ: defect structure, electrical conductivity, chemical diffusivity, thermoelectric power, and oxygen nonstoichiometry, J. Electroceram., 2002, 8, 5–36.
11. N.-H. Chan and D. M. Smyth, Defect chemistry of donor-doped BaTiO₃, J. Am. Ceram. Soc., 1984, 67(4), 285–288.
12. N.-H. Chan, R. K. Sharma and D. M. Smyth, Nonstoichiometry in acceptor-doped BaTiO₃, J. Am. Ceram. Soc., 1982, 65(3), 167–170.
13. P. Ren, N. Masó, Y. Liu, L. Ma, H. Fan and A. R. West, Mixed oxide ion and proton conduction and p-type semiconduction in BaTi_0.98Ca_0.02O_2.98 ceramics, J. Mater. Chem. C, 2013, 1(13), 2426–2432.
14. M. Prades, N. Masó, H. Beltrán, E. Cordoncillo and A. R. West, Field enhanced bulk conductivity of BaTiO₃:Mg ceramics, J. Mater. Chem., 2010, 20(25), 5335–5344.
15. H. Beltrán, M. Prades, N. Masó, E. Cordoncillo and A. R. West, Voltage-dependent low-field bulk resistivity of BaTiO₃:Zn ceramics, J. Am. Ceram. Soc., 2010, 93(2), 500–505.
16. N. Masó, M. Prades, H. Beltrán, E. Cordoncillo, D. C. Sinclair and A. R. West, Field enhanced bulk conductivity of acceptor doped BaTi_1−xCa_xO_3−x ceramics, Appl. Phys. Lett., 2010, 97(6), 062907.
17. H. Beltrán, M. Prades, N. Masó, E. Cordoncillo and A. R. West, Enhanced conductivity and non-linear voltage-current characteristics of non-stoichiometric BaTiO₃ ceramics, J. Am. Ceram. Soc., 2011, 94(9), 2951–2962.
18. Q.-L. Zhang, N. Masó, Y. Liu, H. Yang and A. R. West, Voltage-dependent low-field resistivity of CaTiO₃:Zn ceramics, J. Mater. Chem., 2011, 21(34), 12894–12900.
19. Y. H. Han, J. B. Appleby and D. M. Smyth, Calcium as an acceptor impurity in BaTiO₃, J. Am. Ceram. Soc., 1987, 70(2), 96–100.
20. Z. Q. Zhuang, M. P. Harmer and D. M. Smyth, The effect of octahedrally-coordinated calcium on the ferroelectric transition of BaTiO₃, Mater. Res. Bull., 1987, 22(10), 1329–1335.
21. L. Zhang, O. P. Thakur, A. Feteira, G. M. Keith, A. G. Mould, D. C. Sinclair and A. R. West, Comment on the use of calcium as a dopant in X8R BaTiO₃-based ceramics, Appl. Phys. Lett., 2007, 90, 142914.
22. T. Mitsui and W. B. Westphal, Dielectric and X-ray studies of Ca_xBa_1−xTiO₃ and Ca_xSr_1−xTiO₃, Phys. Rev., 1961, 124(5), 1354–1359.
23. J. Pokorný, U. M. Pasha, L. Ben, O. P. Thakur, D. C. Sinclair and I. M. Reaney, Use of Raman spectroscopy to determine the site occupancy of dopants in BaTiO₃, J. Appl. Phys., 2011, 109(11), 114110.
24. F. J. Blunt, P. J. Hendra and J. R. Mackenzie, The laser Raman spectra of salts containing the anions O₂⁻ and O₂²⁻, J. Chem. Soc., Chem. Commun., 1969, 6, 278–279.
25. S. A. Hunter-Saphir and J. A. Creighton, Resonance Raman scattering from the superoxide ion, J. Raman Spectrosc., 1998, 29(5), 417–419.
26. J. Yang, D. Zhai, H.-H. Wang, K. C. Lau, J. A. Schlueter, P. Du, D. J. Myers, Y.-K. Sun, L. A. Curtiss and K. Amine, Evidence for lithium superoxide-like species in the discharge product of a Li–O₂ battery, Phys. Chem. Chem. Phys., 2013, 15(11), 3764–3771.
27. K. C. Lau and L. A. Curtiss, Density functional investigation of the thermodynamic stability of lithium oxide bulk crystalline structures as a function of oxygen pressure, J. Phys. Chem. C, 2011, 115(47), 23625–23633.
28. M. Strongin, S. L. Qiu, J. Chen, C. L. Lin and E. M. McCarron, Question of superoxide in La₂CuO_4+δ, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(10), 7238–7240.
29. H. Beltrán, E. Cordoncillo, P. Escribano, D. C. Sinclair and A. R. West, Oxygen loss, semiconductivity, and positive temperature coefficient of resistance behavior in undoped cation-stoichiometric BaTiO₃ ceramics, J. Appl. Phys., 2005, 98(9), 094102.
30. C.-Y. Yoo, B. A. Boukamp and H. J. M. Bouwmeester, Oxygen surface exchange kinetics of erbia-stabilized bismuth oxide, J. Solid State Electrochem., 2011, 15(2), 231–236.

---