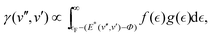Vibrational enhancement of electron emission in CO (a³Π) quenching at a clean metal surface

Abstract

We have combined a Stark decelerator with a molecular beam-surface scattering setup to accurately measure the absolute electron emission yield, γ, of CO (a³Π) quenching at a Au(111) surface with quantum state resolution. We clearly observe an enhanced probability of electron emission when scattering vibrationally excited states of CO from the surface.

---

The radiationless neutralization of ions and de-excitation of metastable atoms in front of clean and adsorbate-covered surfaces has been established as a sensitive probe of the surface's and adsorbate's electronic structure.^1,2 Since metastable atoms do not penetrate into the bulk of the solid, the related method Metastable Quenching Spectroscopy (MQS) provides a complement to other surface spectroscopic methods like Photoelectron Spectroscopy (PES),³ Auger Electron Spectroscopy (AES)⁴ or Electron Energy Loss Spectroscopy (EELS).⁵ Due to their easy production in the laboratory, long lifetimes and high excitation energies, metastable rare gas atoms are normally used as collision partners and correspondingly the underlying quenching mechanisms are well studied. These quenching mechanisms involve Auger emission of electrons either from the metal or from the metastable atom, in some cases preceded by resonant ionization or neutralization.⁶ De-excitation of the metastable molecular species, however, has been explored only to a limited extent, mostly driven by the urge to construct and understand efficient detectors for metastable particles.^7–9 Obviously, models describing the metastable–surface interaction of metastable atoms do not take into account degrees of freedom like vibration, rotation and orientation. The importance of these additional degrees of freedom has been pointed out by experiments performed in recent years, where vibrational degrees of freedom in molecules have coupled strongly with electronic degrees of freedom in metal surfaces.

Our group has previously reported promotion of electron emission during the collision of highly vibrationally excited NO with a Cs-dosed Au(111) surface,^10–12 which exhibits an inverse velocity dependence.¹³ These results are compatible with theoretical models suggesting coupling of molecular vibrations to electron–hole-pairs in the metal. Evidence for these effects has also been found in the direct vibrational excitation of the electronic ground state of CO on Au(111)¹⁴ and for the excitation and de-excitation of the electronic ground state of NO on Au(111).¹⁵ In this work we present the first direct measurement of the absolute electron emission yield, γ, of CO (a³Π) scattered from a Au(111) surface. We further observe an unambiguous increase of electron emission with vibrational excitation, suggesting that in the quenching of electronically excited CO, vibrational excitation leads to effects which cannot be explained by a simple Auger de-excitation model.

For the sake of conducting quantum-state resolved, background-gas free molecule-surface scattering with unprecedented kinetic energy resolution and tunability, we have constructed a new machine which combines a Stark decelerator¹⁶ with a UHV molecular beam-surface scattering chamber. As a detailed description of the apparatus will soon be given in a future publication, we will provide only a concise outline of it here. Carbon monoxide is co-expanded with Xenon by means of a cooled pulsed valve to yield a supersonic beam of 360 m s⁻¹ mean velocity. After being skimmed, the CO is excited by a narrow bandwidth laser at 206 nm to the a³Π₁(v = 0, J = 1) metastable state, from now on referred to as CO*, which has a lifetime of 2.63 ms²⁹ and an electric dipole moment of 1.37 Debye. A switched electric hexapole focuser then deflects the metastables onto the main beam axis of the machine, whereas both Xe and ground-state CO are removed from the beam. Subsequently, velocity tuning of the beam is performed employing a 720.5 mm long Stark decelerator, the operation principle of which has been described in detail before.^16,17 In brief, an array of high voltage electrode pairs is used to create periodic and inhomogeneous electric fields. A molecule in a quantum state whose internal energy increases with electric field strength thus experiences a potential energy hill at each charged electrode pair along the forward direction, while at the same time it is transversally focused. By switching the electrodes at appropriate times between different configurations, kinetic energy can be added to or removed from a narrow slice of the initial kinetic energy distribution. For the experiments described in this communication, we have used the decelerator to slice out the most intense part of the initial CO* beam and guide it at 360 m s⁻¹ towards the surface, yielding a pulse of 25 μs full duration and 28 m s⁻¹ full velocity width when it collides with the surface.

For these experiments, the UHV scattering chamber is maintained at a pressure of 1 × 10⁻¹⁰ mbar with no discernible pressure rise upon switching on the beam. The Au(111) single crystal is regularly cleaned by Ne⁺ sputtering and subsequent annealing, and its purity is observed by Auger electron spectroscopy. In addition, the surface temperature is stabilized to 373 K to limit contamination by any residual gas. A fraction of the molecules can be ionized 21 mm upstream from the surface by a focused laser beam via a (1 + 1) REMPI process at 283 nm, and the ions detected via a chevron MCP detector mounted below the extraction zone, as indicated in Fig. 1. Laser power of 3 mJ per pulse is sufficient to saturate the transition even when the laser is only gently focused. Electrons which are emitted due to the interaction of CO* with the surface are extracted upward where they are detected by a second chevron MCP detector. Numerical simulation of the extraction fields using SIMION¹⁸ suggests 100% extraction efficiency both for CO⁺ and electrons, and a detection efficiency of 90% is assumed at both MCP detectors due to the limited transmission of extraction grids.

Fig. 1 Schematic drawing of the experimental setup near the surface region. The molecular beam pulse passes a horizontal slit of 200 μm width 3 cm upstream from the REMPI laser. Ionized CO molecules are accelerated towards a MCP assembly mounted below the detection zone by applying −1480 V to a grid in front of the MCP detector. Electrons which are emitted due to the interaction of CO* with the surface are extracted upward by a +550 V biased grid where they are detected by a second MCP detector. Electrons originating from the REMPI process are well separated from surface emission electrons due to the time of flight of the molecular beam between the ionization zone and the surface.

The most direct way of sensitively measuring the electron yield, γ, defined as the number of emitted electrons per incident metastable, is to remove part of the metastables from the beam, and divide the number of missing electrons by the number of removed molecules. In our setup, we laser ionize a significant fraction of the incident beam, and the resulting REMPI signal is then directly compared to the dip in the electron emission signal caused by ionized CO* molecules. To improve the contrast in the electron signal, a 200 μm wide slit is introduced 30 mm upstream from the ionization laser. Great care was taken to correct for different MCP gains by normalization to an identical signal prior to the measurement, such that both detectors could be operated at optimum gain without saturation. Three signals are thus obtained: the ion signal produced by the REMPI laser, the electron emission signal with the REMPI laser switched on, and the electron emission signal with the REMPI laser beam blocked. The absolute yield, γ, may then be obtained by subtracting one electron signal from the other, and dividing the corresponding time-integrated time-of-flight spectrum by the integrated and calibrated ion signal.

When taking a closer look at the electron signals, depicted in Fig. 2, the most striking aspects are wings on each side of the depletion signal, which indicates an enhancement of the electron signal. Of course, the laser intensity is reduced on the spatial edges of the laser focus, suggesting that the signal increase is due to molecules which are excited to the short-lived (53 ns lifetime¹⁹) b³Σ⁺(v = 0) state but not ionized and subsequently fall back into different vibrational levels of the a³Π state. This idea was confirmed by varying the power of the REMPI laser, where an enhancement of the electron signal can be seen at low (≈20 μJ per pulse) REMPI laser pulse energies. According to the known Franck–Condon factors of the b³Σ⁺(v = v′) → a³Π(v = v′′) transition,²⁰ one expects to find 75% of all molecules in v′′ ≥ 1 after the CO* has been exposed to this excitation pulse. This is clear evidence of the vibrational enhancement of electron emission in quenching of CO*. We assume no relaxation to the a′³Σ⁺ state, since to our knowledge, no experimental observation of the b → a′ emission exists.

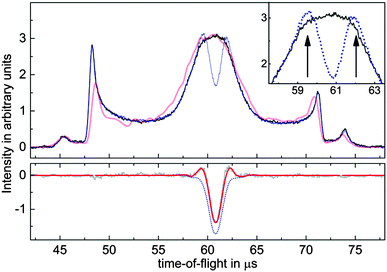Fig. 2 (color online) Time-of-flight measurements of electrons emitted during the scattering of CO* from Au(111). The upper curves show experimental data (solid black) and simulated signals (light red) without REMPI induced depletion of molecules. The inset consists of a zoomed image in part of the center of the pulse. Enhanced wings next to the central dip, indicated by arrows, can be clearly seen in the experimentally observed signal depleted by REMPI (dotted blue). In the lower panel, the experimentally undepleted signal has been subtracted from the depleted trace (gray), and fitted with a simple model (red). The lower dotted blue curve depicts the contribution of depletion, the difference between this curve and the red curve is due to vibrational enhancement of electron emission. The shape of the time-of-flight profile, exhibiting two pronounced side peaks, is caused by the trajectories of molecules in the switched electric fields of the Stark decelerator.²²

Further evidence was found by scanning the frequency of the REMPI laser and recording simultaneously the electron signal originating from the quenching process at the surface and the ion signal from the REMPI process. The REMPI laser was not focused during the scans in order to minimize ionization and hence increase production of vibrationally excited CO* molecules by optical pumping through the b³Σ⁺(v = 0) state. The spectrum displayed in Fig. 3 clearly shows two distinct peaks assigned to the R₃₂(1) and the overlapping P₃₂(1) and R₁₂(1) transitions. Electron emission signal enhancement takes place only at resonances in the REMPI spectrum, corresponding to the simultaneous production of vibrationally excited CO*.

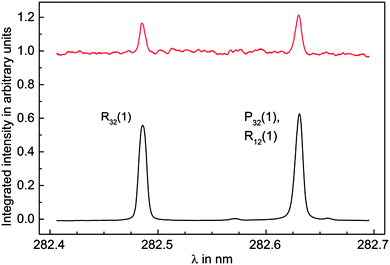Fig. 3 Integrated REMPI (lower black) and electron (upper red) signal while the REMPI laser frequency is scanned over the b³Σ⁺(v = 0) ← a³Π₁(v = 0) transition. The intensity of the unfocused REMPI laser is chosen to be so low that depletion of CO* population is negligible. The electron signal exhibits strong enhancement when the ionization laser is resonant with the R₃₂(1) or both the P₃₂(1) and R₁₂(1) transition, which produces vibrationally excited CO* by optical pumping. Note that the electron signal is scaled to the unenhanced signal.

We have developed a simple model, which allows us to fit the contributions of signal depletion and enhancement to our signal and take into account the observations described above, see Fig. 2. We assume an ionization efficiency ∝I², but saturated ionization within one full width at half maximum (FWHM) of the laser intensity I. Outside the FWHM, we assume a ring of inner radius 0.5 × FWHM and width 1 × FWHM where the remaining molecules are transferred to higher vibrational states, and their signal is multiplied by the enhancement factor ε > 1. The molecular beam is modeled based on numerical trajectory calculations of molecules in the Stark decelerator, which have been shown to provide excellent agreement with even minor details of the experiment.²¹ Using an appropriate choice of input parameters for our molecular beam source, the undepleted and unenhanced electron emission signal is well-reproduced by these simulations, as is apparent from Fig. 2. Combining the 6-dimensional phase space of molecular space and velocity coordinates with the model of our laser, we are able to reproduce our data by adjusting only the two parameters FWHM and ε. Note that the resulting peak shape of the subtracted signal depends very sensitively on both parameters, so it is safe to assume that the resulting values are a local minimum of the fit. As a final result, we obtain values of FWHM = 480 μm and ε = 1.31, meaning that vibrationally excited states of CO a³Π, which make up 75% of the beam, enhance the electron emission by (40 ± 10)%. Subtracting the enhancement contribution from the peak shown in Fig. 2, time-integrating the remaining depletion and dividing by the calibrated and time-integrated ion signal gives a result for the electron emission yield of

γ = 0.13 ± 0.05.

The knowledge of this number provides a powerful tool to determine the molecular beam density of CO* molecules by monitoring the electron emission at the surface. This will greatly aid all quantitative measurements on this system planned in the future. In addition, the comparison to existing studies on metastable atoms reveals several unexpected interesting insights. For the case of metastable rare gas atoms the electron emission mechanism has been well-understood. If the ionization potential of the metastable particle, M*, is higher than the work function of the surface, an electron from the conduction band of the metal is transferred to the half occupied ground state orbital of the metastable (that is the HOMO of M). If the associated energy release, ΔE, meets the condition ΔE ≥ E* – Φ, the electron in the metastable level is ejected in an intra-molecular Auger process. Here, E* denotes the excitation energy of the metastable particle, and Φ the work function of the surface. This mechanism, described in detail by Hagstrum,⁶ is referred to as Auger de-excitation.

Previous studies of electron emission from metal surfaces due to metastable rare gases suggest that, in general, γ increases with the electronic excitation energy of the metastable species,^8,23 even though it depends strongly on the species and surface involved. Whereas the excitation energy of CO a³Π₁ is E* = 6.0 eV, resulting in excess energy for de-excitation of only 0.69 eV for collisions with Au(111), E* for rare gases often used in electron emission experiments is typically above 10 eV. Compared to previously reported results by Schohl et al. for various metastable rare gas species impinging on a gold surface,²³ the value of γ presented here is remarkably high. It is comparable to reported values for Kr ³D₃ (E* = 11.4 eV) of γ = 0.16 and significantly higher than that for Kr ³P₂ (E* = 9.9 eV, γ = 0.059). Despite the fact that these values were obtained for a polycrystalline gold surface which was only heated to 87 °C to remove adsorbates, the nobility of gold and the stability of the Au(111) surface suggest that their results should provide a reasonable benchmark for our measurements. The remarkably high value of γ for CO* as well as the directly observed vibrational enhancement of the quenching probability show that vibrational degrees of freedom play a crucial role in the mechanism of electron emission in CO* quenching.

A dependence of γ on the vibrational level v of the incoming metastable molecule has previously been reported by Zubek⁷ both for CO a³Π and N₂ A³Σ_u⁺ at molybdenum surfaces and was attributed by the author to an Auger de-excitation process. He tried to explain his data by incorporating the Franck–Condon factors for de-excitation to different vibrational levels of the electronic ground state into Hagstrum's model (vide infra). In his data, however, which were recorded at a base pressure of 10⁻⁵ mbar, γ is slightly increased for v = 1 only, and then decreases quickly with higher v, which is in direct contrast to the 40% increase observed in our work. The vibrational dependence was also observed by Borst⁸ for CO and N₂ relaxation on CuBeO and by Furlong et al.⁹ on Hf. In all cases, adsorbate-covered surfaces were used, which might also explain why the absolute value of γ of Borst is almost three orders of magnitude smaller compared to metastable rare gas atoms than in the case of gold. We believe our results to be more accurate and more representative of a metal surface, because any adsorbates are expected to have a high influence on γ since Auger de-excitation is known to be extremely surface sensitive.²⁴

However, the high absolute value of γ, and especially the strong enhancement for vibrationally excited CO*, poses the question whether the simple model for Auger de-excitation can be as easily extended to molecules as has been suggested. This can be seen when calculating the electron yield using the simple model proposed by Zubek:⁷ the electron yield γ for initial and final vibrational states v′′ and v′ is proportional to the density of states which is energetically available for electron emission, i.e.

where ε_F is the Fermi energy, f(ε) the Fermi function at 373 K, and the density of states in the conduction band. The electron yield of each upper vibrational level v′ is then obtained by summing over all lower level contributions weighted by the Franck–Condon factors²⁵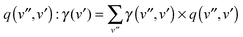. For the case of CO and Au(111), however, this model fails to reproduce the experimental data since it predicts a decrease in γ as v′ is increased. Calculated relative values for γ(v′) are about 80% of γ₀ for v′ = 1–3 and drop to 42% of γ₀ for v′ = 4. This is a simple result of the nature of the Franck–Condon factors in this system; higher values of v′ lead to much higher values of v′′, reducing the available energy for electron ejection.

Conclusions

We have determined the absolute electron emission yield for the CO a³Π₁(v = 0) – Au(111) system to be γ = 0.13 ± 0.05. Within the scope of these measurements, we have observed an enhancement of electron emission signal which is correlated with the REMPI laser being resonant with the b³Σ⁺(v = 0) state, and occurs already at low laser power. This signal enhancement can be attributed to higher vibrational states of CO (a³Π) produced by optical pumping from the REMPI laser. These results led us to conclude that γ(v ≥ 1) is (40 ± 10)% higher than γ(v = 0).

In order to improve our understanding of the process that leads to electron emission, further experiments to investigate the dependence of γ on the exact vibrational quantum state by populating only specific vibrational levels via Franck–Condon pumping or the more sophisticated methods of SEP,²⁶ Pump–Dump–Sweep²⁷ or STIRAP²⁸ are conceivable. In addition, studying the influence of surface temperature, kinetic energy, and orientation of metastable CO might provide further insight.

Acknowledgements

We acknowledge support from Deutsche Forschungsgemeinschaft and the National Science Foundation under grant CHE0724038. AMW also thanks the Alexander von Humboldt Foundation for support under a Humboldt Professorship.

References

1. H. Conrad, G. Ertl, J. Küppers, S. W. Wang, K. Gérard and H. Haberland, Phys. Rev. Lett., 1979, 42, 1082–1086.
2. H. D. Hagstrum, Phys. Rev., 1966, 150, 495–515.
3. K. Siegbahn, Rev. Mod. Phys., 1982, 54, 709–728.
4. C. C. Chang, Surf. Sci., 1971, 25, 53–79.
5. R. F. Egerton, Rep. Prog. Phys., 2009, 72, 016502.
6. H. D. Hagstrum, Phys. Rev., 1954, 96, 336–365.
7. M. Zubek, Chem. Phys. Lett., 1988, 149, 24–28.
8. W. L. Borst, Rev. Sci. Instrum., 1971, 42, 1543–1544.
9. J. M. Furlong and W. R. Newell, Meas. Sci. Technol., 1996, 7, 641–649.
10. J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, Nature, 2005, 433, 503–505.
11. J. D. White, J. Chen, D. Matsiev, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2006, 124, 064702–064713.
12. J. LaRue, T. Schäfer, D. Matsiev, L. Velarde, N. H. Nahler, D. J. Auerbach and A. M. Wodtke, Phys. Chem. Chem. Phys., 2011, 13, 97–99.
13. N. H. Nahler, J. D. White, J. LaRue, D. J. Auerbach and A. M. Wodtke, Science, 2008, 321, 1191–1194.
14. T. Schäfer, N. Bartels, K. Golibrzuch, C. Bartels, H. Kockert, D. J. Auerbach, T. N. Kitsopoulos and A. M. Wodtke, Phys. Chem. Chem. Phys., 2013, 15, 1863–1867.
15. Y. Huang, A. M. Wodtke, H. Hou, C. T. Rettner and D. J. Auerbach, Phys. Rev. Lett., 2000, 84, 2985–2988.
16. H. L. Bethlem, G. Berden and G. Meijer, Phys. Rev. Lett., 1999, 83, 1558–1561.
17. H. L. Bethlem, F. M. H. Crompvoets, R. T. Jongma, S. Y. T. van de Meerakker and G. Meijer, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 053416.
18. D. A. Dahl, Simion 3D Version 6.0, Idaho National Engineering Laboratory, Idaho Falls (USA), 1995.
19. A. J. Smith, R. E. Imhof and F. H. Read, J. Phys. B: At. Mol. Phys., 1973, 6, 1333.
20. C. V. V. Prasad, G. L. Bhale and S. P. Reddy, J. Mol. Spectrosc., 1987, 121, 261–269.
21. S. Y. T. van de Meerakker, N. Vanhaecke, H. L. Bethlem and G. Meijer, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 053409.
22. H. L. Bethlem, G. Berden, A. J. A. van Roij, F. M. H. Crompvoets and G. Meijer, Phys. Rev. Lett., 2000, 84, 5744–5747.
23. S. Schohl, H. A. J. Meijer, M. W. Ruf and H. Hotop, Meas. Sci. Technol., 1992, 3, 544–551.
24. B. Woratschek, W. Sesselman, J. Küppers, G. Ertl and H. Haberland, Surf. Sci., 1987, 180, 187–202.
25. R. W. Nicholls, J. Quant. Spectrosc. Radiat. Transfer, 1962, 2, 433–449.
26. C. Kittrell, E. Abramson, J. L. Kinsey, S. A. McDonald, D. E. Reisner, R. W. Field and D. H. Katayama, J. Chem. Phys., 1981, 75, 2056–2059.
27. N. Bartels, B. C. Krüger, S. Meyer, A. M. Wodtke and T. Schäfer, J. Phys. Chem. Lett., 2013, 2367–2370.
28. U. Gaubatz, P. Rudecki, S. Schiemann and K. Bergmann, J. Chem. Phys., 1990, 92, 5363–5376.
29. J. J. Gilijamse, S. Hoekstra, S. A. Meek, M. Metsälä, S. Y. T. van de Meerakker, G. Meijer and G. C. Groenenboom, J. Chem. Phys., 2007, 127, 221102.

---

Footnote

† Current address: Radboud University Nijmegen, Institute for Molecules and Materials, Heijendaalseweg 135, 6525 AJ Nijmegen, The Netherlands.

---