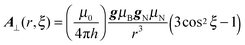An ENDOR and DFT analysis of hindered methyl group rotations in frozen solutions of bis(acetylacetonato)-copper(II)

Abstract

ENDOR spectroscopy and DFT calculations have been used to thoroughly investigate the ligand hyperfine couplings for the bis(acetylacetonato)–copper(II) complex [Cu(acac)₂] in frozen solution. Solutions of [Cu(acac)₂] were prepared under anhydrous conditions, and EPR revealed that the g and ^CuA values were affected by traces of water present in the solvent. The ligand ^HA_i hyperfine couplings were subsequently investigated by CW and pulsed ENDOR spectroscopy. Anisotropic hyperfine couplings to the methine protons (^HA_i = 1.35, −1.62, −2.12 MHz; a_iso = −0.80 MHz) and smaller couplings to the fully averaged methyl group protons (^HA_i = −0.65, 1.658, −0.9 MHz; a_iso = 0.036 MHz) were identified by simulation of the angular selective ENDOR spectra and confirmed by DFT. Since the barrier to methyl group rotation was estimated to be ca. 5 kJ mol⁻¹ by DFT, rapid rotation of these –CH₃ groups, even at 10 K, leads to an averaged value of ^HA_i. However, variable temperature X-band Mims ENDOR revealed an additional set of hyperfine couplings which showed a pronounced temperature dependency. Using CW Q-band ENDOR, these additional couplings were characterised by the hyperfine parameters ^HA_i = 3.45, 2.9, 2.62 MHz, a_iso = 2.99 MHz and assigned to a hindered methyl group rotation. This hindered rotation of a sub-set of methyl groups occurs in 120° jumps, such that a large A_dip and a_iso component is always observed. Whilst the majority of the methyl groups undergo free rotation, a sub-set of methyl groups experience hindered rotation in frozen solution, through proton tunnelling. This hindered rotation appears to be caused by weak outer-sphere solvent interactions with the complex.

---

Introduction

The bis(acetylacetonato)-copper(II) complex [Cu(acac)₂] is one of the most extensively studied d-transition metal compounds by Electron Paramagnetic Resonance (EPR) spectroscopy (Scheme 1).^1–14 This can largely be attributed to its relative simplicity, ease of preparation and favourable stability constant, which collectively facilitate the investigation of this complex in single crystal,^1–4 frozen solution^5–12 and powder (doped Cu–Pd solid solution)¹³ forms. The simple square planar arrangement of [Cu(acac)₂] with four oxygen donors forming the inner coordination sphere, has led to its inclusion in the Peisach and Blumberg ‘truth tables’, correlating trends in g/^CuA with coordination environment for Cu(II) systems.¹⁵ The successful extrapolation of the trends established using small inorganic complexes to more complex, biologically relevant systems, including metalloproteins and metalloenzymes, has also resulted in [Cu(acac)₂] being widely regarded as a standard model complex for such studies. As a result, the complex has been characterised in detail by continuous wave (CW) EPR, so that both the local geometry and electronic structure of the paramagnetic Cu(II) centre are well defined. Furthermore, it often serves as a standard model system to assess the accuracy and validity of estimating the spin Hamiltonian parameters in combined experimental¹⁶ and computational^17–22 methods, ensuring interest in this simple complex continues.

Scheme 1 Structure and coordinate axes for [Cu(acac)₂].

In addition to CW EPR, advanced hyperfine techniques, including ENDOR, ESEEM, and HYSCORE, can also be used to probe the remote ligand nuclei in transition metal complexes, and therefore provide even greater detail on the local geometric and electronic structure compared to EPR alone.^23,24 Structural elucidation of the ligand environment beyond the inner-coordination sphere is of significant importance when considering structure–function relationships of metal complexes.^25,26 With magnetic resonance studies being used increasingly to probe the role of paramagnetic metal ions and complexes within intricate biological systems,^{23,25,27–31} a full appreciation of the level of information provided by these advanced techniques is required. In the same way that the full characterisation of [Cu(acac)₂] on an EPR level has enabled it to serve as a model complex, thereby aiding the interpretation of EPR spectra of more complex systems, a complete ENDOR study of [Cu(acac)₂] would highlight the additional information that can be extracted from the advanced hyperfine techniques.

Whilst EPR studies of [Cu(acac)₂] are extremely numerous, there are surprisingly few detailed ENDOR investigations of this complex.^2,3,32,33 Analysis of the hyperfine tensors of the ligand protons can be found in a comparative single crystal and powder–frozen solution study by Baker et al.,³ and in an earlier frozen solution investigation by Kirste et al.³² A doped Cu/Pd(acac)₂ powder was also used by Henderson et al., in their seminal angular selective ENDOR study.³³ In these papers, intense features observed in the CW ENDOR spectra were attributed to the methine and methyl group protons (the latter were assumed to be rapidly rotating in frozen solution on the EPR timescale). Two pairs of intense lines were thus observed in the ENDOR spectrum at the unique single crystal-type field position when the applied magnetic field was aligned parallel to the molecular z axis (i.e., when the ENDOR spectrum was recorded at the field position corresponding to the m_I = +3/2 (∥) line). Closer analysis of these reported frozen solution ENDOR spectra of Kirste et al.,³² and Baker et al.,³ reveals an additional, less intense pair of lines in the spectral wings. The splitting of these additional lines was surprisingly larger than the methine proton and the fully averaged methyl groups, and these less intense lines were not observed in the single crystal or doped [Cu/Pd(acac)₂] powder samples.^3,32,33 Whilst Baker et al.,³ made no comment on the origin of these lines, Kirste et al.,³² suggested that they may likely stem from a temperature dependence of the methyl group rotation.³² However, no further analysis was done,³² and to date, no other investigations have considered the origin of these additional lines in any detail.

Herein we present a detailed CW EPR and CW/pulsed ENDOR characterisation of [Cu(acac)₂] in frozen solution. Using complementary DFT calculations, we have investigated the anisotropic hyperfine couplings to the ligand protons, and used this information to explore in detail the influence of both freely and hindered rotating methyl groups on the resulting frozen solution ENDOR spectrum. Since [Cu(acac)₂] is widely used as a model complex in paramagnetic resonance studies, it is important that all aspects of the ENDOR spectra of this system, including additional unexplained features that arise from the solvent environment, are fully understood.

Experimental

Materials

[Cu(acac)₂] was purchased from Sigma Aldrich and used without further purification. Reagent grade (amylene stabilised) chloroform, CHCl₃, was purchased from Fisher Scientific and dried over calcium hydride (note that ethanol stabilised solvents should be avoided to ensure the solvent remains completely non-coordinating).⁷ Toluene was purified using an MBraun SPS-800 solvent purification system by being passed through a column of activated alumina. CDCl₃ and d₈-toluene were obtained from Goss Scientific, while D₂O was sourced from Fluorochem. All deuterated solvents were used as received from sealed glass ampoules.

Sample preparation

A 0.03 M solution of [Cu(acac)₂] was prepared by dissolving the complex in chloroform : toluene (1 : 1). This solvent system was chosen to facilitate a higher Cu(II) concentration for ENDOR measurements. Approximately 200 μL of this solution was added to the X-band EPR tube and frozen to 140 K for EPR measurements. Slight differences in the EPR spectra (vide infra) can be detected when the [Cu(acac)₂] sample is dissolved in rigorously anhydrous (‘dry’) solvents, compared to normal ‘bench-top’ solvents. For this reason all ‘dry’ samples were prepared using standard Schlenk techniques whereas for comparative purposes ‘wet’ samples were prepared by exposing this [Cu(acac)₂] solution to a saturated water vapour pressure overnight. The EPR spectra obtained in these two extreme cases (using ‘dry’ and ‘wet’ solvents) were then compared to the spectra obtained using standard bench-top solvents.

Spectroscopic measurements

The X-band continuous wave (CW) EPR spectra were recorded on a Bruker EMX spectrometer operating at 100 kHz field modulation and 10 mW microwave power in a high sensitivity cavity (Bruker ER 4119HS) at 140 K. The Q-band CW EPR/ENDOR spectra were recorded at 10 K on a Bruker ESP 300E series spectrometer equipped with an ESP360 DICE ENDOR unit, operating at 12.5 kHz field modulation in a Q-band ENDOR cavity (Bruker ER 5106 QT-E). The ENDOR spectra were obtained using 8 dB RF power from an ENI A-300 RF amplifier, with 50 or 200 kHz RF modulation depth and 1 mW microwave power. Accurate g values were obtained using an NMR Gaussmeter (Bruker ER 035 M) calibrated using the perylene radical cation in concentrated H₂SO₄ (g = 2.002569).

X-band pulsed ENDOR experiments were performed on a Bruker E580 Elexsys spectrometer (operating at 9.76 GHz) equipped with a liquid-helium cryostat from Oxford Inc. The magnetic field was measured with a Bruker ER035M NMR Gaussmeter. Mims ENDOR experiments were carried out using the following pulse sequence: π/2–τ–π/2–T–π/2–τ–echo. The experiments were performed with mw pulse lengths of t_π/2 = 16 ns and an inter-pulse time τ of 104 ns. An rf π pulse of variable frequency and a length of 25 μs was applied during time T. Computer simulations of the EPR and ENDOR data were performed using the EasySpin programme.³⁴

DFT calculations

DFT calculations of energy and spin Hamiltonian parameters were performed with the hybrid PBE0 functional,³⁵ using the ORCA software developed by Neese.^17–19,36 The ‘Core prop’ (CP)³⁷ basis set, known to provide accurate hyperfine couplings for transition metal compounds, was employed for the copper ion and the EPRII basis set was applied to the ligand atoms.³⁸ DFT calculations were performed on a series of geometry optimised structures of [Cu(acac)₂] in which one methyl group was systematically rotated in 15° intervals whilst the rest of the complex was allowed to relax.

Results and discussion

CW EPR

The X-band CW EPR spectrum for [Cu(acac)₂] dissolved in dry, non-coordinating solvents^6,7,39,40 is shown in Fig. 1a. Experiments showed that a solvent system based on chloroform : toluene (1 : 1), gave the best resolved EPR spectra at low temperatures (140 K). This [Cu(acac)₂] solution was prepared under rigorously anhydrous conditions, using dried and purified solvents (hereafter referred to as the ‘dry’ sample). The resulting spectrum displays approximately axial g and ^CuA symmetry with a large hyperfine splitting observed in the parallel direction, entirely consistent with a d_xy ground state.^41,42 Even at this frequency, all four Cu hyperfine lines can clearly be observed in the parallel direction, and an additional splitting resulting from the lower abundant ⁶⁵Cu isotope is also observed on the low field m_I = +3/2 transition. The spin Hamiltonian parameters, extracted by simulation of the X- and Q-band data (vide infra), are listed in Table 1.

Fig. 1 CW EPR spectra recorded at (a and b) X-band and (c) Q-band frequencies of [Cu(acac)₂] dissolved in (a and c) dried/purified chloroform : toluene (1 : 1) solvent, and (b) after exposure of the solution to water vapour overnight. The corresponding simulations are given in a′, b′, c′. The angular dependency profiles of the Cu hyperfine at X- and Q-band are also shown, highlighting the overshoot features (labelled *) at X-band.

Table 1 Principal g and ^CuA spin Hamiltonian parameters for [Cu(acac)₂]

Solvent^d	g 1	g 2	g 3	A 1	A 2	A 3	Ref.
^Cu A given in MHz.a ±0.003.b ±6 MHz.c ±4 MHz.d The CHCl3 : Tol solvent ratio was 40 : 60. T.W = this work.
Single crystals
	2.053	2.053	2.266	57.0	57.0	479.7	1
	2.050	2.052	2.259	72	79	570.0	2
	2.050	2.056	2.264	47.3	76.0	596.4	3
	2.075	2.075	2.254	—	—	—	4
Frozen solutions
CHCl3 : Tol (wet)	2.053^a	2.058^a	2.272^a	64.1^b	64.1^b	545.1^c	T.W
CHCl3 : Tol (dry)	2.048^a	2.052^a	2.252^a	81.0	58.5	572.1	T.W
CHCl3 : Tol^d	2.052	2.057	2.251	80.9	58.5	579.8	5
CHCl3 : Tol^d	2.043	2.043	2.273	68.1	68.1	545.0	6
CHCl3 : Tol^d	2.033	2.033	2.249	90.2	90.2	581.0	7
CHCl3 : Tol^d	2.036	2.036	2.264	86.9	86.9	436.2	8
Toluene	2.050	2.052	2.253	74.9	51.0	557.6	9
CHCl3	2.0429	2.042	2.285	85.1	85.1	523.7	10
CHCl3	2.0452	2.045	2.285	84.5	84.5	524.6	11
CHCl3	2.051	2.051	2.287	—	—	—	12
Cu–Pd solid solution
	2.048	2.052	2.261	74.9	72.0	563.6	13

---

The above ‘dry’ sample was subsequently exposed to a saturated water vapour environment overnight, to explore the influence of H₂O, which may weakly coordinate to the [Cu(acac)₂] complex, on the EPR spectrum. The resulting spectrum is shown in Fig. 1b. Simulation of this latter spectrum reveals noticeable differences in the g₃ and ^CuA₃ parameters, as compared to Fig. 1a (see Table 1); these differences are consistent with weak H₂O solvation of the [Cu(acac)₂] complex.⁴³ Clearly the quality of the solvent system (i.e., dry versus wet solvents) has a marked influence on the g and ^CuA values. The angular dependency profile of this ‘wet’ sample is also shown in Fig. 1 for completeness. Two turning points at off-axis orientations, referred to as “overshoot” features, are visible on the m_I = −3/2 transition at 332 mT and the m_I = −1/2 transition at 327 mT; both are labelled with an asterisk in Fig. 1. These features arise due to the relatively small g and large ^CuA anisotropy, and can lead to ambiguities in the interpretation of X-band spectra.^5,44,45

It should be noted that an appreciable variation in the reported g and ^CuA values for frozen [Cu(acac)₂] solutions is often found in the literature.^5–12 A selection of these parameters, demonstrating the range of reported values, are listed in Table 1. In many cases, no precautions were taken to use innocently stabilised (i.e. non-coordinating) solvents^6,7 or to ensure strict anhydrous conditions were used for sample preparation. As the above EPR results demonstrate (Fig. 1), this can lead to anomalous spin Hamiltonian parameters. To further illustrate this, the frozen solution EPR spectrum of [Cu(acac)₂] prepared using ‘bench-top’ solvents (chloroform:toluene) is shown in the ESI† (Fig. S1); a mixed EPR spectrum is produced, bearing overlapping features from the ‘dry’ (Fig. 1a) and ‘wet’ (Fig. 1b) [Cu(acac)₂] spectra. Such differences can be easily missed in experimental studies, and therefore care must be taken when preparing the [Cu(acac)₂] solutions for EPR analysis. In fact, the dependence of the g/^CuA values on the [Cu(acac)₂] environment were recently used to determine the interaction of the complex with carbon nanotubes, highlighting the sensitivity of the spin Hamiltonian parameters on the surroundings.¹⁴

The Q-band CW EPR spectrum of the ‘dry’ sample is shown in Fig. 1c, along with the corresponding simulation. The small degree of rhombic distortion in both g/^CuA was confirmed at this higher frequency, although resolution of the individual hyperfine splitting patterns in the parallel direction for the two ^63,65Cu isotopes is lost due to the greater influence of g and ^CuA strain.^46,47 The accompanying angular dependency profile is also given, which clearly demonstrates the increased angular selection and absence of overshoot features at higher microwave frequencies. The pulsed X-band and CW Q-band ENDOR spectra (vide infra) were subsequently recorded using the ‘dry’ [Cu(acac)₂] solution, thereby ensuring no traces of weakly coordinated water could indirectly contribute to artefacts in the ENDOR analysis.

CW & pulsed (Mims) ¹H ENDOR

The variable temperature X-band Mims ENDOR spectra of [Cu(acac)₂] are shown in Fig. 2. The spectra were recorded at the field positions corresponding to g = g_∥ and g = g_⊥. The g_∥ position (283 mT) leads to a ‘single-crystal’ like spectrum, as only one hyperfine transition (m_I = +3/2) is selected (Fig. 2a–d). Hence, each unique ligand nucleus environment is expected to produce a pair of ENDOR lines at this field position, centred on the ¹H nuclear Larmor frequency. Accordingly two intense resonances are observed with hyperfine couplings of 0.85 and 2.0 MHz (labelled with the stick diagram for clarity in Fig. 2a). Analogous couplings have been previously reported in single crystal, powder and frozen solution [Cu(acac)₂] studies and have been assigned to the fully averaged methyl protons and the methine protons, respectively (Table 2).

Fig. 2 X-band Mims ¹H ENDOR spectra of [Cu(acac)₂] dissolved in dry chloroform : toluene (1 : 1) solvent, recorded at the field positions corresponding to g = g_∥ (a–d) and g = g_⊥ (e–h). The spectra were recorded at the following temperatures; (a and e) 10 K, (b and f) 15 K, (c and g) 20 K and (d and f) 25 K. Peaks labelled * arise from the temperature dependent methyl groups undergoing hindered rotation.

Table 2 ¹H principal hyperfine values for [Cu(acac)₂] dissolved in CDCl₃: d₈-toluene. For comparison the ENDOR data for the doped single crystals are also listed

Proton	A 1(x)	A 2(y)	A 3(z)	a iso	β	A dip	Ref.
T.W = this work; the signs of the hyperfine couplings as determined by DFT, were used in the experimental simulations.a A values in MHz (error ±0.1 MHz). ^RH^methyl = averaged rotating –CH3 group; ^HH^methyl = rotationally hindered –CH3 group.b The angle of non-coincidence between the applied field B and the g tensor were defined in Euler angles. For an axial system, α and γ can be treated as ≈0°, hence only β is given in the table.
H^methine	1.977	0.647	−2.624	0.121			3
	−1.56	1.23	−2.17	−0.833			32
	1.35	−1.62	−2.12	−0.797	0°	−1.32	T.W
	1.05	−1.75	−2.36	−1.016			DFT
^HH^methyl	3.45	2.90	2.62	2.99	0°	1.06	T.W
^RH^methyl	−0.65	1.658	−0.90	0.036	0°	−0.94	T.W
	−0.79	−0.68	−0.49	−0.187			DFT

---

However, an additional pair of less intense lines is also observed (at the g = g_∥ position) possessing a larger hyperfine coupling of 2.6 MHz (see Fig. 2a–d, peaks labelled *). The intensity of these particular lines decrease as the temperature increases (from 10 K to 25 K): by comparison, the intensities of the peaks with couplings of 0.85 and 2.0 MHz are temperature independent (Fig. 2a–d). These results agree with the earlier experimental observations of Kirste and Van Willigen.³² Although they provided no definitive explanation to account for this extra pair of lines, they suggested that these lines must stem from a temperature dependence of the methyl group rotation.³² Extra peaks possessing large hyperfine couplings are also observed in the ENDOR spectra of single crystal and doped [Cu/Pd(acac)₂] powders; however in those cases, the extra peaks arise from intermolecular couplings with neighbouring complexes in the stacked crystals. In contrast, the temperature dependent 2.6 MHz coupling observed in Fig. 2, is only observed under dilute frozen solution conditions and so does not arise from intermolecular ligand interactions.

The ENDOR spectra recorded at the perpendicular field position (344 mT, m_I = −3/2) are also shown in Fig. 2e–h. At this field position, a two-dimensional ENDOR pattern is recorded; i.e., two couplings arise from each set of equivalent nuclei. Four dominant pairs of lines are readily observed at 0.49, 0.69, 1.29 and 1.56 MHz in the 10 K ENDOR spectrum (Fig. 2e). As these couplings are all temperature independent (Fig. 2f–h), they can be assigned to the remaining hyperfine components of the methine and averaged methyl group protons. Additional peaks with weak intensities are also identified around 3.3 MHz, which show the same temperature dependence as the 2.6 MHz coupling previously observed in Fig. 2a–d.

Q-band CW ENDOR spectra were also recorded for the [Cu(acac)₂] frozen solution (Fig. 3). Owing to the improved resolution in g anisotropy at the higher frequency, a better resolved angle selective ENDOR study can be performed, facilitating the extraction of the hyperfine tensors (^HA_i) for all ligand protons by simulation. The corresponding ENDOR simulations for the methine and fully rotating methyl groups are shown in Fig. 3 and the hyperfine parameters used in the simulations are listed in Table 2. The largest contribution to the methine coupling was observed along the g = g_∥ direction, since according to the single crystal study,³ the form of this tensor is unusual and the principal direction of this methine proton is almost coincident with the copper g tensor.³ The experimentally derived hyperfine (^HA_i) parameters are very similar to those reported previously for [Cu(acac)₂] (Table 2) and agree well with the theoretical (DFT) calculations described below.

Fig. 3 CW Q-band ¹H ENDOR spectra (recorded at 10 K; 75 kHz RF modulation) of [Cu(acac)₂] dissolved in dry CDCl₃–C₆D₅CD₃ (1 : 1), recorded at different field positions: (a) 1186.2 (b) 1181.9 (c) 1169.0 (d) 1153.5 (e) 1129.2 (f) 1099.4 (g) 1082.3 (h) 1063.7 and (i) 1046.8 mT. Solid line = experimental, dashed line = simulation. Peaks labelled * arise from the largest couplings of the temperature dependent methyl groups undergoing hindered rotation, whereas the peaks labelled # arise from smaller couplings associated with these methyl groups.

In their single crystal ENDOR study, Baker and Raynor³ observed highly resolved hyperfine couplings from the methine protons and from each of the three individual protons in the methyl groups, suggesting that the methyl groups are not rotating (Table 2). In the single crystal state, rotation is prevented by interactions with neighbouring molecules in the crystal. However, in both frozen solution and solid solutions, these interaction forces are greatly reduced. In the latter case, distortions and dislocations in the solid solution are sufficient to partially reduce these interactions. Although Baker and Raynor also reported the ENDOR spectra for a frozen solution, the complete hyperfine tensors were not given (as some components of the hyperfine tensor could not be resolved in the perpendicular field region).³

However, the X- and Q-band ENDOR spectra contain the additional temperature dependent peaks, with large hyperfine couplings (labelled * in Fig. 3). These couplings are more easily seen in the Q-band spectra recorded with a higher radiofrequency modulation, particularly the asymmetric profile of the largest peaks corresponding to a hyperfine coupling of about 3 MHz (Fig. S2, ESI†). Analysis of these peaks by simulation enabled the hyperfine coupling to be extracted (Table 2). These experimental hyperfine couplings, for the methine proton and both the rotationally averaged and hindered methyl groups, are now compared to the couplings derived by DFT.

DFT calculations

A number of papers have described the use of density functional theory (DFT) to calculate the spin Hamiltonian parameters of simple Cu(II) model complexes, including [Cu(acac)₂], in which good agreement between the theoretical and experimental g and ^CuA values have been reported.^{18,19,21,22,48,49} Surprisingly, detailed calculations of the ligand hyperfine tensors have not been reported for [Cu(acac)₂]. Following geometry optimisation of [Cu(acac)₂], the ¹H hyperfine tensors were determined using the ORCA program,³⁶ and the results for the methine and methyl protons are listed in Table 2.

For the methine protons, a slightly larger a_iso value was predicted by DFT (−1.016 MHz) compared to the experimental value (−0.793 MHz), but otherwise the agreement is satisfactory. As expected, this coupling is not affected by rotation of –CH₃ groups. By comparison, the hyperfine tensor for each individual methyl proton (labelled H⁸, H⁹, H¹⁰ in Scheme 1) must be calculated as a function of the methyl groups rotation angle with respect to the Cu–O4 plane. This was performed in 15° intervals from 0° to 120°. The full set of hyperfine values, including appropriate atomic coordinates for all angles, are listed in Tables S1–S3 (ESI†). The averaged hyperfine value for all three protons in the methyl group, averaged over all angles, was calculated in order to estimate the expected isotropic hyperfine coupling assuming a freely rotating methyl group. These averaged DFT values are in excellent agreement with the experimental values extracted by simulation of the ENDOR spectra (Table 2).

According to DFT, a strong angular dependency between the hyperfine couplings and the angle of methyl group rotation exists, with pronounced changes to both anisotropic (^HA_i) and isotropic (a_iso) couplings depending on the angle of rotation (Table S1, ESI†). This explains why three individual sets of hyperfine couplings are observed in the single crystal ENDOR spectra of [Cu(acac)₂].³ This angular dependency can be more easily illustrated by examining the variations in calculated a_iso (rather than A_dip) as a function of the methyl group rotation angle (Fig. 4). For example, for a specific angle of ca. 60°, the a_iso value is largest for H¹⁰ (+2.28 MHz) and smallest for the two remaining protons, H⁹ and H⁸ (−1.22 and −1.42 MHz) (Fig. 4). As the methyl group is rotated through 360°, a large positive a_iso will always exist for one proton, whilst the other two protons will simultaneously possess small negative a_iso values at this particular angle (Fig. 4), with the exception of the angle 0°, 120° and 240° where the couplings are similar. Despite this pronounced angular dependency for each individual proton, an averaged a_iso value of ca. −0.25 MHz is always observed (essentially independent of angle) when the methyl groups undergo free rotation. However, the anisotropic dipolar couplings (A_dip) will similarly be affected by variation in methyl group rotation angle. As a result, if the rotations of these methyl groups are hindered on the EPR timescale, a more complex anisotropic hyperfine pattern will arise in the frozen solution ENDOR spectra. This scenario is in fact responsible for the temperature dependent peaks visible in the ENDOR spectra (vide infra).

Fig. 4 Dependence of the isotropic hyperfine coupling (a_iso) on the angle of rotation of each individual methyl group proton as calculated by DFT. (● = H⁸; ■ = H⁹; ▲ = H¹⁰; ○ = average of H^8–10).

Analysis of the dipolar couplings

The magnitude of the anisotropic (dipolar) hyperfine coupling is expected to be highly dependent on the orientation of the methyl group with respect to the Cu(II) orbitals hosting the unpaired electron as the Cu⋯H distance depends on the orientation of the methyl group. To calculate this dependency, the geometry optimized [Cu(acac)₂] structure was used, with specific reference to a single methyl group proton (labelled H⁸). The position of this proton was varied by rotating the methyl group around an axis defined by the two carbon atoms C5 and C7 (Scheme 1). The distance (r) between the copper atom and H⁸ was then calculated as a function of the clockwise rotation angle, as was the angle between the z-axis (perpendicular to the molecular plane) and the Cu⋯H⁸ axis (ξ). Plots of the Cu⋯H⁸ distance and the angle between the z-axis and the Cu⋯H⁸ axis are shown in Fig. 5. It can be seen that the distance is a minimum (4.4 Å) for a rotation angle of 115°, corresponding to an angle (ξ) of 90° (Fig. 5a), while the distance is maximum (5.0 Å) when the rotation angle is 300° (Fig. 5b).

Fig. 5 (a) Orientation of closest approach between H⁸ and the Cu centre, (b) orientation of furthest distance between H⁸ and the Cu centre, and (c) dependence of the Cu⋯H⁸ distance (r) and the angle between the z-axis and Cu⋯H⁸ axis (ξ) on the methyl rotation angle.

Knowing the distance r and the angle ξ, the theoretical anisotropic contribution to the hyperfine coupling can be easily calculated⁵⁰ using the equation:

The above equation is used to calculate A_dip when the angle θ is employed;^24,50i.e., for an axial system, θ_B represents the angle between the applied field (B) and the g_z direction. It is important to note that for transition metal complexes, where appreciable electron spin delocalisation occurs onto the ligand nuclei, this equation is only approximate, whereas the DFT calculations do include this spin delocalisation in determining the spin Hamiltonian parameters. Nevertheless this equation is instructive in the current case, simply to examine and illustrate the effects of the rotation angle ξ, on the anisotropic ^HA_i values. Since these ξ angles lie in the range 100° to 80° (Fig. 5c), this would equate to a θ_B angle of ca. 90°, which corresponds to the A_⊥ component of the anisotropic hyperfine tensor. The resulting plot of A_⊥ as a function of the methyl group rotation (A_⊥(r,ξ)) is thus given in Fig. 6.

Fig. 6 Dependence of the dipolar hyperfine contribution (A_⊥) to the Cu⋯H⁸ coupling on the methyl rotation angle.

A pronounced angular dependency of A_⊥ as a function of methyl group rotation is clearly observed. Because the angles ξ are all close to 90° (i.e. the methyl protons never extend too far above or below the molecular xy plane), the A_⊥ contribution is always negative, with a maximum value of |A_⊥| corresponding to the closest approach of the copper and hydrogen atoms; i.e., a methyl rotation angle of 115° (Fig. 5a). Although the maximum A_⊥ value for H⁸ occurs at a different rotation angle (115°) compared to its maximum a_iso value (180°; Fig. 4), this difference simply reflects the different mechanisms contributing to the hyperfine interaction for A_⊥ (‘through-space’ interaction) compared to a_iso (‘through-bond’ interaction). The angular difference between the positions of maxima observed for A_⊥ and a_iso ensures that the two contributions combine so that a large ‘overall’ hyperfine coupling will always be experimentally observed for a methyl group undergoing hindered rotation on the EPR timescale, as indeed observed in Fig. 2 and 3.

Hindered methyl group rotation

The temperature dependent ENDOR peaks arising from hindered methyl group rotations are labelled * in Fig. 2. Only the two largest components of the hyperfine tensor for this group are easily observed in the Q-band ENDOR spectra (A₁ = ±2.6 MHz and A₃ = ±3.3 MHz; Fig. 3); the third smaller component is unresolved. According to DFT, the largest anisotropic hyperfine coupling is calculated to be +1.24, +1.76, +3.84 MHz with a_iso = 2.28 MHz for a specific set of coordinates (Table S1, ESI†). These theoretical values, specifically the A₁ and A₂ components, do not give a satisfactory fit to the overall profile of the experimental ENDOR spectra. However, based on the above analysis of A_⊥ and a_iso, with maximum couplings of −1.06 and 2.28 MHz respectively, an estimated range of values for the third experimentally unresolved A₂ component was obtained and tested by simulation. The resulting simulation of the angular selective temperature dependent ENDOR peaks and corresponding couplings are given in Fig. 3 and Table 2 respectively.

The ENDOR data therefore reveals that in frozen solution, a hindered rotation of the methyl groups occurs, producing a highly anisotropic hyperfine pattern (Table 2). For most of the methyl groups, an average of all possible orientations is detected as these groups undergo rapid rotation on the EPR timescale. On the other hand, the hindered rotation of a smaller sub-set of methyl groups must occur in 120° ‘jumps’, such that the largest hyperfine coupling from one proton in the methyl group is always observed in the ENDOR spectra. At this specific rotation angle, the hyperfine couplings from the two remaining protons in the methyl group are also visible in the ENDOR spectra, but they produce smaller hyperfine parameters and therefore are poorly resolved, due to overlapping features from the methine and fully averaged methyl couplings. Some of these smaller hyperfine couplings from the hindered methyl groups are in fact visible in the spectra (as highlighted in Fig. 3).

The rotation of methyl groups in organic radicals, and in some cases complex molecular structures, as studied by EPR, has been well documented.^51–61 At very low temperatures, rotation occurs via quantum tunnelling and for low barrier systems second order shifts are often detected in the ENDOR spectra. Both slow and fast mechanisms of tunnelling can operate. At higher temperatures a transition occurs from the quantum to the classical motional regimes. Owing to the broadened linewidths of the powder ENDOR spectra recorded for [Cu(acac)₂], and the limiting range of measurement temperatures that can be achieved (due to the fast relaxation characteristics of the copper ion), lineshape analysis of the ENDOR spectra was not performed. However, according to the DFT calculations, the barrier to methyl group rotation was found to be ca. 5 kJ mol⁻¹ (Fig. S2, ESI†). This suggests that a tunnelling process must be responsible for the rotation at the low temperatures adopted in the ENDOR measurements (10–25 K), and it is possible that a slow tunnelling mechanism is responsible for the hindered rotations, as opposed to a fast mechanism for the fully averaged methyl groups. The question remains why a fraction of the methyl groups experience hindered rotation (producing an anisotropic hyperfine pattern) whilst the majority undergo free rotation (producing an almost isotropic, averaged hyperfine pattern of small magnitude) in frozen solution. One explanation is based on the solvent. It is known for example that weak outer-sphere solvent interactions can occur in metal complexes bearing the acac ligand. Polar solvents, such as chloroform, can form weak H-bonds with the oxygen atoms of the acac ligand.^39,40 This slight ordering of solvent within the outer-sphere may be just sufficient to prevent the free rotation of methyl groups in close proximity. Owing to the poor solubility of [Cu(acac)₂] in neat toluene, we were unable to test this by measuring the ENDOR spectra of the complex in a non-coordinating solvent. However, recent work from our group⁶² has revealed an enhancement of the peak intensities for these hindered methyl group rotations upon coordination, and subsequent adduct formation, of H-bonding substrates with the [Cu(acac)₂], confirming the role of secondary sphere solvent interactions in –CH₃ rotations.

Conclusion

[Cu(acac)₂] is often used as a simple model complex in EPR studies. As a result it has attracted wide-spread interest over the years, and therefore numerous papers have been published on this system. EPR and ENDOR studies of this complex as a single crystal, solid powder or frozen solution have all been investigated. A range of g and ^CuA values have been reported for the frozen solution case. The current results reveal how traces of water in the solvent can adversely affect the spin Hamiltonian parameters. Therefore care must be taken to ensure rigorously anhydrous conditions are used throughout the sample preparation stages. Furthermore weak hyperfine couplings to the ligand protons are revealed in the ENDOR spectra. These spectra are dominated by the anisotropic hyperfine couplings to the methine protons and the almost isotropic couplings to the methyl protons undergoing rapid rotation on the EPR timescale. All of the anisotropic couplings from the methyl protons are thus averaged under these conditions. A smaller sub-set of methyl groups experiences a temperature dependent hindered rotation; these protons are responsible for the largest couplings identified in the ENDOR spectra. Although these couplings have been reported in the past, they have never been fully analysed. At a specific methyl group rotational angle, the orientation of a single methyl group proton is sufficient to produce a large A_dip and a_iso coupling (even larger than the coupling to the methine proton). By undergoing 120° jumps, this coupling from the hindered methyl group remains visible in the ENDOR spectra. The cause of the hindered rotation is not known, but likely arises from weak outer-sphere interactions between the complex and the polar solvent molecules. Care must therefore be exercised in ENDOR studies employing [Cu(acac)₂] since the environment can affect the dynamics of methyl group rotation, which in turn may produce additional and perhaps unexpected hyperfine couplings in the experimental spectra.

Acknowledgements

EPSRC funding (EP/H023879, EP/K017322) is gratefully acknowledged.

References

1. A. H. Maki and B. R. McGarvey, J. Chem. Phys., 1958, 29, 31–34.
2. S. Kita, M. Hashimoto and M. Iwaizumi, J. Magn. Reson., 1982, 46, 361–373.
3. G. J. Baker and J. B. Raynor, J. Chem. Soc., Dalton Trans., 1986, 2663–2667.
4. B. R. McGarvey, J. Phys. Chem., 1956, 60, 71–76.
5. I. V. Ovchinnikov and V. N. Konstantinov, J. Magn. Reson., 1978, 32, 179–190.
6. S. Antosik, N. M. D. Brown, A. A. McConnell and A. L. Porte, J. Chem. Soc. A, 1969, 545–550.
7. M. D. Wisniewski and B. B. Wayland, J. Chem. Soc. A, 1971, 2727–2728.
8. H. R. Gersmann and J. D. Swalen, J. Chem. Phys., 1962, 36, 3221–3233.
9. H. Yokoi, Inorg. Chem., 1978, 17, 538–542.
10. I. Adato and I. Eliezer, J. Chem. Phys., 1971, 54, 1472–1476.
11. H. A. Kuska, M. T. Rogers and R. E. Drullinger, J. Phys. Chem., 1967, 71, 109–114.
12. R. Wilson and D. Kivelson, J. Chem. Phys., 1966, 44, 4445–4452.
13. L. D. Rollmann and S. I. Chan, J. Chem. Phys., 1969, 50, 3416–3431.
14. S. Cambre, W. Wenseleers and E. Goovaerts, J. Phys. Chem. C, 2009, 113, 13505–13514.
15. J. Peisach and W. E. Blumberg, Arch. Biochem. Biophys., 1974, 165, 691–708.
16. J. Higuchi, M. Yagi and A. Shimizu, Chem. Phys. Lett., 1979, 62, 603–607.
17. F. Neese, J. Chem. Phys., 2001, 115, 11080–11096.
18. F. Neese, J. Phys. Chem. A, 2001, 105, 4290–4299.
19. F. Neese, J. Chem. Phys., 2003, 118, 3939–3948.
20. A. C. Saladino and S. C. Larsen, J. Phys. Chem. A, 2003, 107, 5583–5587.
21. Z. Rinkevicius, K. J. de Almeida and O. Vahtras, J. Chem. Phys., 2008, 129, 064109–064117.
22. C. Remenyi, R. Reviakine, A. V. Arbuznikov, J. Vaara and M. Kaupp, J. Phys. Chem. A, 2004, 108, 5026–5033.
23. C. Calle, A. Sreekanth, M. V. Fedin, J. Forrer, I. Garcia-Rubio, I. A. Gromov, D. Hinderberger, B. Kasumaj, P. Léger, B. Mancosu, G. Mitrikas, M. G. Santangelo, S. Stoll, A. Schweiger, R. Tschaggelar and J. Harmer, Helv. Chim. Acta, 2006, 89, 2495–2521.
24. D. M. Murphy and R. D. Farley, Chem. Soc. Rev., 2006, 35, 249–268.
25. S. Van Doorslaer and E. Vinck, Phys. Chem. Chem. Phys., 2007, 9, 4620–4638.
26. E. Carter and D. M. Murphy, in Spectroscopic Properties of Inorganic and Organometallic Compounds: Techniques, Materials and Applications, ed. J. Yarwood, R. Douthwaite and S. Duckett, RSC Specialist Periodical, 2009, pp. 355–384.
27. M. Ubbink, J. A. R. Worrall, G. W. Canters, E. J. J. Groenen and M. Huber, Annu. Rev. Biophys. Biomol. Struct., 2002, 31, 393–422.
28. T. Prisner, M. Rohrer and F. MacMillan, Annu. Rev. Phys. Chem., 2001, 52, 279–313.
29. W. R. Hagen, Dalton Trans., 2006, 4415–4434.
30. L. Hunsicker-Wang, M. Vogt and V. J. DeRose, in Methods in Enzymology, ed. H. Daniel, Academic Press, 2009, pp. 335–367.
31. Metals in Biology: Applications of High-Resolution EPR to Metalloenzymes, ed. G. Hanson and L. Berliner, Springer, 2010, pp. 1–419.
32. B. Kirste and H. Van Willigen, J. Phys. Chem., 1983, 87, 781–788.
33. T. A. Henderson, G. C. Hurst and R. W. Kreilick, J. Am. Chem. Soc., 1985, 107, 7299–7303.
34. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
35. (a) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. F. Neese, J. Chem. Phys., 2005, 122, 34107.
37. The ORCA basis set ‘CoreProp’ was used. This basis is based on the TurboMole DZ basis developed by Ahlrichs and coworkers and obtained from the basis set library under ftp.chemie.uni-karlsruhe.de/pub/basen.
38. V. Barone, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific Publ. Co., Singapore, 1996.
39. N. D. Yordanov and M. Zdravkova, Polyhedron, 1993, 12, 635–639.
40. T. S. Davis and J. P. Fackler, Inorg. Chem., 1966, 5, 242–245.
41. K. J. de Almeida, T. C. Ramalho, Z. Rinkevicius, O. Vahtras, H. Āgren and A. Cesar, J. Phys. Chem. A, 2011, 115, 1331–1339.
42. R. L. Belford and M. A. Hitchman, Inorg. Chem., 1971, 10, 984–988.
43. Similar perturbations to the g/^CuA values have previously been observed upon ethanol coordination to [Cu(acac)₂].
44. R. P. Bonomo and F. Riggi, Lett. Nuovo Cimento, 1981, 30, 304–310.
45. P. H. Rieger, Electron Spin Resonance: Analysis and Interpretation, RSC, 2007.
46. J. S. Hyde and W. Froncisz, Annu. Rev. Biophys. Bioeng., 1982, 11, 391–417.
47. S. K. Misra, Multifrequency Electron Paramagnetic Resonance: Theory and Applications, Wiley-VCH, 2011.
48. M. Bruschi, L. De Gioia, R. Mitric, V. Bonacic-Koutecky and P. Fantucci, Phys. Chem. Chem. Phys., 2008, 10, 4573–4583.
49. E. D. Hedegård, J. Kongsted and S. P. A. Sauer, J. Chem. Theory Comput., 2011, 7, 4077–4087.
50. D. Attanasio, J. Phys. Chem., 1986, 90, 4952–4957.
51. J. H. Freed, J. Chem. Phys., 1965, 43, 1710–1720.
52. S. F. J. Read and D. H. Whiffen, Mol. Phys., 1967, 12, 159–161.
53. S. Clough and F. Poldy, J. Chem. Phys., 1969, 51, 2076–2079.
54. S. Clough and F. Poldy, J. Phys. C: Solid State Phys., 1973, 6, 1953–1964.
55. S. Clough, J. R. Hill and M. Punkkinen, J. Phys. C: Solid State Phys., 1974, 7, 3413–3417.
56. M. Brustolon, T. Cassol, L. Micheletti and U. Segre, Mol. Phys., 1986, 57, 1005–1014.
57. M. Matsushita, T. Momose and T. Shida, J. Chem. Phys., 1990, 92, 4749–4758.
58. S. Kubota, M. Matsushita, T. Shida, A. Abu-Raqabah, M. C. R. Symons and J. L. Wyatt, Bull. Chem. Soc. Jpn., 1995, 68, 140–145.
59. A. Zecevic, G. R. Eaton, S. S. Eaton and M. Lindgren, Mol. Phys., 1998, 95, 1255–1263.
60. J. R. Harbridge, S. S. Eaton and G. R. Eaton, Appl. Magn. Reson., 2003, 24, 261–276.
61. C. J. Wedges, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204.
62. K. Sharples, E. Carter, J. A. Platts, D. M. Murphy, work in prep.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp52464g

---