 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Guanine binding to gold nanoparticles through nonbonding interactions†
Xi
Zhang
a,
Chang Q.
Sun
b and
Hajime
Hirao
*a
aDivision of Chemistry and Biological Chemistry, School of Physical and Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, Singapore 637371. E-mail: hirao@ntu.edu.sg
bSchool of Electric and Electronic Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639794
First published on 11th October 2013
Abstract
Gold nanoparticles have been widely used as nanocarriers in gene delivery. However, the binding mechanism between gold nanoparticles and DNA bases remains a puzzle. We performed density functional theory calculations with and without dispersion correction on AuN (N = 13, 55, or 147) nanoparticles in high-symmetry cuboctahedral structures to understand the mechanism of their binding with guanine at the under-coordinated sites. Our study verified that: (i) negative charges transfer from the inner area to the surface of a nanoparticle as a result of the surface quantum trapping effect; and (ii) the valence states shift up toward the Fermi level, and thereby participate more actively in the binding to guanine. These effects are more prominent in a smaller nanoparticle, which has a larger surface-to-volume ratio. Additional fragment orbital analysis revealed that: (i) electron donation from the lone-pair orbital of N to the unoccupied orbital of the Au cluster occurs in all complexes; (ii) π back-donation occurs from the polarized Au dyz orbital to the N py-π* orbital when there is no Au⋯H–N hydrogen bond, and, (iii) depending on the configuration, Au⋯H–N hydrogen bonding can also exist, to which the Au occupied orbital and the H–N unoccupied orbital contribute.
1 Introduction
Gold nanoparticles (NPs) are size-tunable materials that function as efficient nanocarriers in the delivery of peptides, proteins, DNA, or RNA.1,2 The reported noncytotoxicity3 and high efficiency of gold NPs2,4 reinforce the expectation that gold NPs should serve as appropriate vehicles for gene delivery. It is well known that gold in bulk is so inert that it has only a low adsorption capacity. Then why and how do gold NPs acquire adsorption ability? Answering this question is of crucial importance for the effective application of gold NPs in gene delivery. In particular, it is necessary to understand the roles of under-coordinated atoms at gold surfaces, the effects of Au d electrons on the interaction with biomolecules such as DNA, and the binding patterns in such interactions.A large proportion of atoms of a gold NP at the surface, edge, defects, or other kinds of boundaries of nanostructures are under-coordinated. In fact, the volume ratio of the surface layer to the entire body, referred to as the surface-to-volume ratio, increases with decreasing size of a NP. The ratio can be 90% for a gold NP with a diameter of 1 nm. A large surface-to-volume ratio has been shown to give rise to the “under-coordination effect” of gold NPs,5,6 which has recently been drawing rapidly increasing attention.7,8 The under-coordination effect exerts considerable influences on the structure, bonding, energy, and behavior of gold NPs.5,9 For example, Au–Au bonds are shortened around the under-coordinated sites,5,10,11 and surface potential energy is elevated in gold NPs.12 Moreover, the energy states and electronic structures of gold NPs differ significantly from those of bulk gold,13,14 which can also be attributed to the under-coordination effect. These under-coordination-induced properties provide tunability in electron conductivity,15 local magnetism,16 and catalytic ability7,8,17 of gold atoms in a nanoisland on substrates, stepped surfaces, nanoporous materials,7 nanoparticles, etc.
In gene delivery, gold–molecule (or –base) interactions, which are ubiquitous in science,18,19 may be effectively exploited. At the molecular level, such interactions involve a bond between Au and, e.g., N of an organic molecule. This bond may not be described as a pure N–Au donor–acceptor bond,19 because back-donation of gold 5d electrons to an organic molecule may also exist.18,20,21
Unconventional N–H⋯Au hydrogen bonding is another interesting structural feature of gold–molecule complexes.22–26 On the basis of computational studies, unconventional hydrogen bonds have been claimed to exist in the complexes of gold with pterin,22 glycine,23 and ammonia,26 whereas such hydrogen bonding was not observed in the complex of gold and PH3.24
Precise characterization of these key structural and electronic factors controlling the properties and interactions of gold NPs should help establish the molecular basis for the effective application of gold NPs in gene delivery. Density functional theory (DFT) has useful roles to play in this endeavor. So far, a few DFT studies have been performed on relatively small and low-symmetry DNA base–gold [AuN (N = 2–20)] complexes.27–32 Kryachko and Remacle investigated the complexes between AuN (N = 2–6) and nucleobases or base pairs.31 Kumar et al. studied the complexes between the adenine–thymine (AT) or the guanine–cytosine (GC) pair and AuN (N = 4, 8).27 Shukla et al.30 studied the interaction between gold nanoclusters AuN (N = 2, 4, 6, 8, 10, 12) and the purine base in guanine (G) and the GC base pair. Martínez29 analyzed the properties of planar and 3-D gold clusters (AuN with N = 2–20) interacting with the adenine–uracil (AU) and GC base pairs.32 Zhang et al. investigated the interaction of G base with AuN (N = 2, 4, 6, 8).33,34 Despite extensive DFT studies, however, the core size of the experimentally synthesized particles usually falls in the range between 1.5 nm (∼Au55) and ∼6 nm,35,36 and clusters tend to adopt a high-symmetry structure (i.e., truncated octahedral, cuboctahedral, icosahedral or decahedral nanocrystal), as corroborated by studies based on the Wulff construction,37 genetic algorithms,38,39 and first-principles methods,40 as well as by experiments.41–43 Clearly, computational studies should be performed on the interactions between larger gold NPs and bases.
In this work, complexes between high-symmetry cuboctahedral NPs with relatively large sizes (Au13, Au55 and Au147) and the guanine (G) nucleobase are studied using DFT. The main goal of this work is to identify the mechanism underlying the binding between G and gold NPs from the perspective of under-coordination effects6 on charge redistribution, local structure relaxation, and electronic properties of gold NPs.9,10 We chose G because it is a well-studied DNA base30,33,34 that therefore allows us to investigate the role of under-coordinated gold in adsorption processes using the reported stable binding patterns.30,31 Moreover, to better characterize the donor–acceptor and H-bonding interactions between the gold NPs and G, we perform fragment orbital analyses of Au13–G and atomic-orbital bond-order analyses of all complexes.
2 Methods
2.1 Structures and principles
Gold NPs in cuboctahedral structures of three “magic sizes”,44i.e., Au13 (2 atomic shells), Au55 (3 atomic shells), and Au147 (4 atomic shells) were considered in this study. The cuboctahedral structure has been proven stable in gold clusters with relatively large sizes that consist of >50 atoms.38,39 The icosahedral structure is also stable in Au13.40 We also examined icosahedral Au13; however, the binding energy (BE) for icosahedral Au13–G was much smaller (28.5 kcal mol−1) than that for cuboctahedral Au13–G (44.9 kcal mol−1). Therefore, we focused mainly on cuboctahedral NPs in studying the size-dependent under-coordination effects and unconventional hydrogen bonding.Fig. 1 illustrates the Au–N bonding sites for the interaction between guanine (N2 or N5) and Au13 NPs. Two configurations were chosen from the most stable binding sites of Au–G complexes.31 Consistent with the reported45 and our previous results,9 the corner atom of Au55 forms a stronger bond with guanine (BE: 35.3 kcal mol−1) than the edge atoms (BE: 24.2 kcal mol−1). Therefore, in the following discussions, we shall focus on the interactions at the most under-coordinated corner atoms. The cross sections of Au55 and Au147 are shown in the figure of Mulliken charges (Fig. 2).
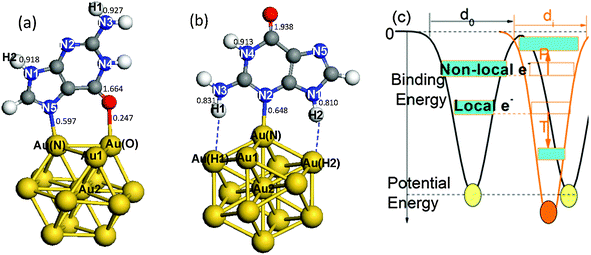 | ||
| Fig. 1 Illustration of the structures and under-coordination effects. Gold atom-shell labels extend from the surface corner toward the center, Au1 and Au2. N atoms in guanine are labeled N1–N5. Two H atoms on N3 and N1 are labeled H1 and H2. (a) The Au13–G1 complex with the gold binding sites labeled Au(N) and Au(O). The binding pattern involves Au(N)–N5 and Au(O)–O bonds. (b) The Au13–G2 complex with the gold binding sites labeled Au(N), Au(H1) and Au(H2). This binding pattern involves a Au(N)–N2 bond and two N–H⋯Au hydrogen bonds. (c) Illustration of under-coordination-induced bond contraction, surface quantum trapping (T), and valence charge polarization (P) at the surface. Values in (a) and (b) are the calculated Mayer bond orders for the Au13–G complexes.48 | ||
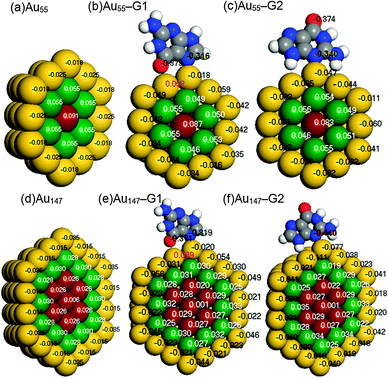 | ||
| Fig. 2 Core–shell separations of Mulliken charges in cross sections of (a) Au55, (b) Au55–G1, (c) Au55–G2, (d) Au147, (e) Au147–G1, and (f) Au147–G2. A negative value (black) means electronic gain and a positive value (white and red) means electronic loss. | ||
Fig. 1c illustrates the under-coordination-induced bond contraction, surface quantum trapping, and charge polarization of gold NPs, as reported in the theme articles.46,47 Our recent study9 demonstrated that the length of the Au–Au interlayer bond contracts from the bulk value of 2.883 Å to 2.694 Å in the outermost two shells of Au NPs. The effective coordination number z is shell-dependent,9,10i.e.
 | (1) |
2.2 Calculation procedures
Spin-unrestricted DFT calculations were performed using the DMol3 code with the double numeric atomic orbital plus polarization basis set.49 A DFT semi-core pseudopotential50 was used to describe the inner electrons while including some degrees of relativistic effects. The Perdew–Wang (PW92) functional51 in the localized density approximation (LDA), the Perdew–Burke–Ernzerhof (PBE) functional52 in the generalized gradient approximation (GGA), and the PBE functional with a dispersion correction based on the Tkatchenko–Scheffler scheme (DC-PBE)53 were used for calculation of the BE. The use of hybrid functionals for the systems considered in this study is prohibitive because of the high demand of the Hartree–Fock exchange energy calculation. Besides, for the studies of high-symmetry noble metal nanoparticles, LDA54,55 and GGA functionals24,45,56,57 have been extensively used. Because the trend in the calculated BE was not altered in a functional-dependent manner, only the PW92 functional was used for calculations of other properties. The threshold for self-consistent field (SCF) iterations was set at 10−6 (Hartree). To overcome the energy fluctuation that is caused by the existence of many energy states near EF in large gold NPs (≥∼Au55), thermal smearing of 0.005 Hartree was applied in the initial optimizations to allow electrons to be smeared out over several orbitals using the finite-temperature Fermi function.58 The smearing was suppressed in the final optimization to obtain integer orbital occupations. No symmetry was imposed on the geometry during geometry optimizations. In the geometry optimization, the convergence tolerances for energy, force, and displacement were set at 10−5 Hartree, 0.002 Hartree per Å, and 0.005 Å, respectively. COSMO59 solvent calculations with the DC-PBE functional were also performed using the dielectric constant of water, i.e., 78.54.In addition to the size effect of gold on the binding to G, the BEs of two different complexes that use N5 and N2 as binding sites of G, denoted as AuN–G1 and AuN–G2, respectively (see Fig. 1), were compared. To gain insight into the nature of the Au–G bonding, additional fragment orbital analysis was performed for the Au13 cluster using Matlab.60 In this analysis, Kohn–Sham molecular orbitals for the complexes (MOs) and fragments (FOs) were obtained by performing non-smeared single-point calculations on the above-obtained optimized geometries of complexes. We expanded the MOs (ψσi), or eigenvectors, in the AuN–G complex in terms of the FOs of isolated AuN and G fragments, instead of using the atomic orbitals for expansion; that is,61
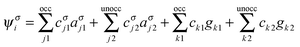 | (2) |
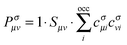 | (3) |
3 Results and discussion
3.1 Size effect: under-coordination induced charge polarization
| BE = E(Au NP) + E(G) − E(Complex) | (4) |
| PW92 | PBE | DC-PBE | DC-PBE (COSMO) | |
|---|---|---|---|---|
| Au13–G1 | 44.9 | 27.7 | 31.3 | 33.5 |
| Au55–G1 | 35.3 | 26.5 | 22.0 | 24.1 |
| Au147–G1 | 32.0 | 20.8 | 21.8 | 24.3 |
| Au13–G2 | 47.2 | 30.3 | 32.4 | 28.2 |
| Au55–G2 | 35.8 | 28.9 | 25.0 | 20.3 |
| Au147–G2 | 24.9 | 16.3 | 18.1 | 13.7 |
| Au13 | Au13–G1 | Au13–G2 | Au55 | Au55–G1 | Au55–G2 | Au147 | Au147–G1 | Au147–G2 | |
|---|---|---|---|---|---|---|---|---|---|
| Q 1 | −0.15 | −0.61 | −0.48 | −0.75 | −1.31 | −1.12 | −1.21 | −1.88 | −1.70 |
| Q NP | 0.00 | −0.45 | −0.33 | 0.00 | −0.43 | −0.31 | 0.00 | −0.43 | −0.31 |
| R NP–G | N/A | 9.06 | 2.21 | N/A | 7.84 | 4.72 | N/A | 7.40 | 3.00 |
| μ | 0.00 | 4.07 | 0.73 | 0.00 | 3.36 | 1.46 | 0.00 | 3.15 | 0.94 |
Table 2 compares the gross Mulliken charges of bare neutral gold NPs, AuN–G1, and AuN–G2. The surface negative charge (Q1) increases upon complexation, as a result of electron donation from G to Au NPs. The gross charge of a gold NP (QNP) is larger in AuN–G1 than in AuN–G2, indicating that the electron donation is more significant in AuN–G1. This also relates to the back-donation of a gold NP as discussed in Section 3.2. Because the complex is neutral, the negative charge of Au NPs (QNP) and positive charge of G (QG) form a dipole (QG = −QNP), with their centers located at
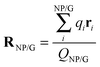 | (5) |
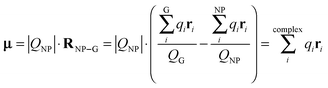 | (6) |
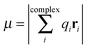 ; however, eqn (6) shows that the two methods are equivalent and give the same value of μ. As can be seen in Table 2, μ of a bare Au NP is zero because of the high symmetry of the NP structure. Moreover, μ for AuN–G1 is much larger than that for AuN–G2. This is attributable to the larger degree of charge transfer in AuN–G1 and partly to its larger RNP–G. The center of QG is near N2 of G, which makes RNP–G in AuN–G1 much larger than in AuN–G2.
; however, eqn (6) shows that the two methods are equivalent and give the same value of μ. As can be seen in Table 2, μ of a bare Au NP is zero because of the high symmetry of the NP structure. Moreover, μ for AuN–G1 is much larger than that for AuN–G2. This is attributable to the larger degree of charge transfer in AuN–G1 and partly to its larger RNP–G. The center of QG is near N2 of G, which makes RNP–G in AuN–G1 much larger than in AuN–G2.
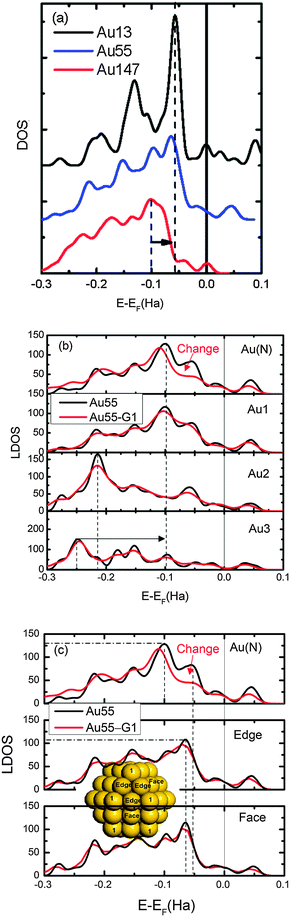 | ||
| Fig. 3 (a) Comparison of normalized DOS of Au13, Au55, and Au147. (b) Comparison of normalized LDOS of Au55 and Au55–G1 (complex) at the bonding gold atom (Au(N)) and corner atoms in different shells as labeled in Fig. 1. (c) Comparison of LDOS at three non-equivalent sites (inset) in the first shell. AuN and Au1 in bare particles are placed at the equivalent positions. Black arrows indicate valence charge polarization and red arrows show the significant change in LDOS upon complex formation. | ||
Thus, the higher stability of a small gold NP–G base complex originates from under-coordination-induced surface charge trapping and valence charge polarization. When a AuN–G complex is formed, there is an electronic density change at the binding gold, which, together with the electron donation from the N pz lone-pair orbital to gold and the surface charge trapping of the gold NP, assists the binding process.
3.2 Site effect: Au–G back-donation of the polarized charge
Further analyses of FOs were performed to characterize the local interactions between bonding gold atoms and G in more detail for two binding patterns, Au13–G1 (N5–Au; O–Au) and Au13–G2 (N5–Au; H⋯Au).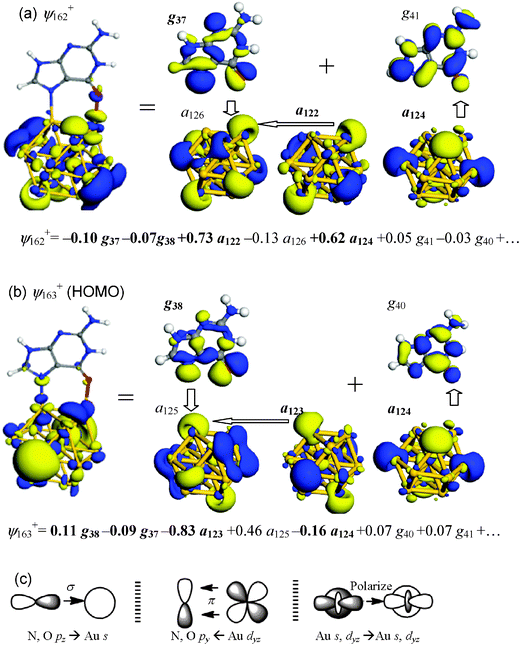 | ||
| Fig. 4 Summary of key MOs and FOs of Au13–G1. (a) ψ162+, which contains Au–O interaction. (b) ψ163+ (HOMO), which contains Au–N interaction. Dominant FO expansion coefficients of the MO are shown underneath each orbital diagram, where occupied FOs are highlighted in boldface. (c) Schematic drawings of key orbital interactions. | ||
Key orbital interactions between Au13 and G in Au13–G1 and expansion coefficients of FOs are summarized in Fig. 4c. The following insights are derived: (i) electrons are donated from the lone-pair orbitals of N and O to the unoccupied Au 6s and 6pz orbitals in the binding process; (ii) back-donation also occurs from the Au dyz to the N and O py orbitals through π orbital interaction; and, (iii) there is charge polarization from the occupied to unoccupied FOs within the Au cluster, enhancing the Au–N and Au–O σ-type interactions.
The nature of Au–G bonding can be understood either from expansion coefficients or from gross populations. Table 3 summarizes the changes in gross populations of frontier FOs upon Au13–G1 formation. Complete data are summarized in the ESI.† A negative value means a loss of electrons from the original state. The populations of orbitals around the HOMO and the lowest-unoccupied MO (LUMO) are seen to undergo significant changes upon the formation of Au13–G1. Consistent with the insights gained from the FO expansion coefficients, the gold NP not only accepts electrons from guanine 2pz-type FOs g37 and g38 into its unoccupied 6s-type a125+, a126+ and dz2-type a127+, but it also donates electrons from its occupied dyz-type FOs a119+ and a124+ to guanine py-type g40, g41 and g43. There is a significant charge loss in occupied Au 6s and 5dz2 FO a123+ (−0.18), whereas there is a gain in unoccupied Au 6s and 5dz2 FO a125+ (0.27), indicating that valence charges are substantially polarized from occupied orbitals to unoccupied orbitals.
| Au13 | G | ||
|---|---|---|---|
| FO | Change | FO | Change |
| a HOMO. b LUMO. | |||
| a 119 + | −0.012 | g 36 | −0.006 |
| a 120 + | −0.008 | g 37 | −0.105 |
| a 121 + | −0.001 | g 38 | −0.070 |
| a 122 + | −0.021 | g 39 a | −0.006 |
| a 123 + | −0.180 | g 40 b | 0.019 |
| a 124 + a | −0.015 | g 41 | 0.018 |
| a 125 + b | 0.270 | g 42 | 0.002 |
| a 126 + | 0.062 | g 43 | 0.012 |
| a 127 + | 0.050 | g 44 | 0.002 |
| a 128 + | 0.004 | g 45 | 0.001 |
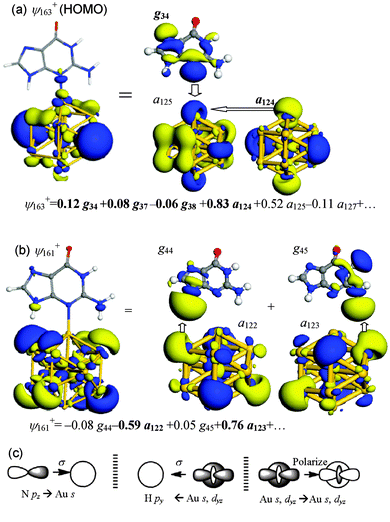 | ||
| Fig. 5 Summary of key MOs and FOs in Au13–G2 of (a) ψ163+ (HOMO), which contains Au–N interaction and (b) ψ161+, which contains Au⋯H–N hydrogen bonds. (c) Schematic drawings of key orbital interactions. | ||
The interactions between Au13 and guanine in Au13–G2 have been summarized in Fig. 5c: (i) electron donation from the N 2pz lone-pair orbital to the unoccupied Au 6s and 6pz orbitals results in the formation of a Au–N bond; (ii) back-donation is enabled because of the Au⋯H–N hydrogen bonding; and (iii) the occupied Au 6s and 5dz2 FOs polarize their charges to the unoccupied Au FOs and make contributions to the Au–N bonding.
Table 4 lists the changes in gross population of each frontier FO upon formation of Au13–G2. Consistent with the mechanism obtained from the FO coefficients, besides the donation from the guanine pz-type FOs, g37 and g38, to the Au 6s-type (a125+) and 5dz2-type (a127+) FOs, there are charge transfers from gold to N–H unoccupied orbitals g42, g44 and g45, which can be characterized as H-bond interactions. Moreover, the occupied a124+ orbital polarizes its charge to the unoccupied a125+ orbital, as can be seen from their respective population changes of −0.200 and 0.322.
| Au13 | G | ||
|---|---|---|---|
| FO | Change | FO | Change |
| a HOMO. b LUMO. | |||
| a 119 + | −0.016 | g 36 | −0.001 |
| a 120 + | −0.003 | g 37 | −0.049 |
| a 121 + | −0.001 | g 38 | −0.025 |
| a 122 + | −0.020 | g 39 a | −0.008 |
| a 123 + | −0.030 | g 40 b | 0.003 |
| a 124 +a | −0.200 | g 41 | 0.005 |
| a 125 +b | 0.322 | g 42 | 0.013 |
| a 126 + | 0.010 | g 43 | 0.008 |
| a 127 + | 0.055 | g 44 | 0.046 |
| a 128 + | 0.001 | g 45 | 0.032 |
Comparing the binding models of Au13–G1 and Au13–G2, one sees that, in both configurations, the guanine pz-type FOs donate electrons to the Au unoccupied FOs and that the Au occupied FOs polarize charges to the unoccupied FOs, while back-donation from Au to G occurs mainly from Au dyz-type FOs into the π-type py-type FOs of G in Au13–G1. The N–H unoccupied FOs accept electrons in the back-donation of Au13–G2, to form a Au⋯H–N hydrogen bond.
| Au13–G1 | Au55–G1 | Au147–G1 | Au13–G2 | Au55–G2 | Au147–G2 | |
|---|---|---|---|---|---|---|
| N–H1 | 0.927 | 0.927 | 0.926 | 0.831 | 0.883 | 0.899 |
| N–H2 | 0.918 | 0.917 | 0.917 | 0.810 | 0.867 | 0.875 |
4 Conclusions
Mysteries behind the binding between gold nanoparticles and guanine arise from their complex geometries, electronic structures, bonding types, surface relaxation, symmetry, environments, etc. Regarding the correlation among under-coordination induced surface quantum trapping, valence charge polarization, back-donation from gold and unconventional H-bonds, this theoretical study makes three important suggestions. First, polarization caused by under-coordination effects of gold NPs results in the activation of valence electrons. Second, the binding mode between a gold NP and guanine is not described as a pure N–Au donor–acceptor interaction; rather, it also contains π- or σ-back-donations from polarized Au valence charges. Third, Au⋯H–N bonding exists that features orbital interaction between a gold σ FO and a N–H σ* FO. The under-coordination-induced surface charge polarization also affects the favorable binding mode.The under-coordination effect at the surface of gold NPs leads to core–shell charge separations. The surface valence charges are polarized toward EF and thus contribute more significantly to the back-donation to a base. It is verified that the smallest Au13 NP undergoes a dramatic valence charge polarization and can form a stable complex with guanine. Furthermore, the FO analysis shows that, besides the electron donation from N to Au, there is back-donation in the formation of Au–G complexes. While Au13 and Au55 prefer the G2 binding mode, Au147 prefers G1 because the valence charge polarization and the back-donation ability are weak. In Au13–G1, back-donation is through the formation of a π bond between Au dyz and N py. In contrast, in Au13–G2, back-donation occurs mainly through two N–H⋯Au hydrogen bonds, from the Au 5dz2 and 6s orbitals to the N–H σ* orbital. This unconventional H bonding leads to intensification of the Au–base interaction, especially in smaller complexes.
Acknowledgements
This work was supported by a Nanyang Assistant Professorship. We thank the High Performance Computing Centre at Nanyang Technological University for computer resources.References
- N. L. Rosi, D. A. Giljohann, C. S. Thaxton, A. K. R. Lytton-Jean, M. S. Han and C. A. Mirkin, Science, 2006, 312(5776), 1027–1030 CrossRef CAS PubMed.
- P. Ghosh, G. Han, M. De, C. K. Kim and V. M. Rotello, Adv. Drug Delivery Rev., 2008, 60(11), 1307–1315 CrossRef CAS PubMed.
- A. M. Alkilany and C. J. Murphy, J. Nanopart. Res., 2010, 12(7), 2313–2333 CrossRef CAS PubMed.
- D. A. Schafer, J. Gelles, M. P. Sheetz and R. Landick, Nature, 1991, 352(6334), 444–448 CrossRef CAS PubMed.
- Q. Jiang, L. H. Liang and D. S. Zhao, J. Phys. Chem. B, 2001, 105(27), 6275–6277 CrossRef CAS.
- C. Q. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(4), 045105 CrossRef.
- T. Fujita, P. Guan, K. McKenna, X. Lang, A. Hirata, L. Zhang, T. Tokunaga, S. Arai, Y. Yamamoto, N. Tanaka, Y. Ishikawa, N. Asao, Y. Yamamoto, J. Erlebacher and M. Chen, Nat. Mater., 2012, 11(9), 775–780 CrossRef CAS PubMed.
- A. S. K. Hashmi, Science, 2012, 338(6113), 1434 CrossRef CAS PubMed.
- X. Zhang, J.-l. Kuo, M. Gu, X. Fan, P. Bai, Q.-G. Song and C. Q. Sun, Nanoscale, 2010, 2(3), 412–417 RSC.
- W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Nat. Mater., 2008, 7(4), 308–313 CrossRef CAS PubMed.
- W. H. Qi, B. Y. Huang and M. P. Wang, J. Comput. Theor. Nanosci., 2009, 6, 635–639 CrossRef CAS PubMed.
- P. Donnadieu, S. Lazar, G. A. Botton, I. Pignot-Paintrand, M. Reynolds and S. Perez, Appl. Phys. Lett., 2009, 94(26), 263116 CrossRef.
- J. N. Crain and D. T. Pierce, Science, 2005, 307(5710), 703–706 CrossRef CAS PubMed.
- K. Schouteden, E. Lijnen, D. A. Muzychenko, A. Ceulemans, L. F. Chibotaru, P. Lievens and C. V. Haesendonck, Nanotechnology, 2009, 20(39), 395401 CrossRef CAS PubMed.
- B. Wang, K. D. Wang, W. Lu, J. L. Yang and J. G. Hou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(20), 205411 CrossRef.
- Y. Yamamoto, T. Miura, M. Suzuki, N. Kawamura, H. Miyagawa, T. Nakamura, K. Kobayashi, T. Teranishi and H. Hori, Phys. Rev. Lett., 2004, 93(11), 116801 CrossRef CAS.
- J. Oliver-Meseguer, J. R. Cabrero-Antonino, I. Domínguez, A. Leyva-Pérez and A. Corma, Science, 2012, 338(6113), 1452–1455 CrossRef CAS PubMed.
- D. Benitez, N. D. Shapiro, E. Tkatchouk, Y. Wang, W. A. Goddard and F. D. Toste, Nat. Chem., 2009, 1(6), 482–486 CrossRef CAS PubMed.
- S. V. Aradhya, M. Frei, M. S. Hybertsen and L. Venkataraman, Nat. Mater., 2012, 11(10), 872–876 CrossRef CAS PubMed.
- X. Xu, S. H. Kim, X. Zhang, A. Das, H. Hirao and S. H. Hong, Organometallics, 2013, 32, 164–171 CrossRef CAS.
- P. Pyykkö, Science, 2000, 290(5489), 64–65 CrossRef.
- R. Vargas and A. Martinez, Phys. Chem. Chem. Phys., 2011, 13(28), 12775–12784 RSC.
- H.-J. Xie, Q.-F. Lei and W.-J. Fang, J. Mol. Model., 2012, 18(2), 645–652 CrossRef CAS PubMed.
- G. Shafai, S. Hong, M. Bertino and T. S. Rahman, J. Phys. Chem. C, 2009, 113(28), 12072–12078 CAS.
- G.-J. Cao, H.-G. Xu, R.-Z. Li and W. Zheng, J. Chem. Phys., 2012, 136(1), 014305–014308 CrossRef PubMed.
- E. S. Kryachko, J. Mol. Struct., 2008, 880(1–3), 23–30 CrossRef CAS PubMed.
- A. Kumar, P. C. Mishra and S. Suhai, J. Phys. Chem. A, 2006, 110(24), 7719–7727 CrossRef CAS PubMed.
- N. K. Jena, K. R. S. Chandrakumar and S. K. Ghosh, J. Phys. Chem. C, 2012, 116(32), 17063–17069 CAS.
- A. Martínez, J. Phys. Chem. C, 2010, 114(49), 21240–21246 Search PubMed.
- M. K. Shukla, M. Dubey, E. Zakar and J. Leszczynski, J. Phys. Chem. C, 2009, 113(10), 3960–3966 CAS.
- E. S. Kryachko and F. Remacle, Nano Lett., 2005, 5(4), 735–739 CrossRef CAS PubMed.
- A. Martínez, J. Phys. Chem. A, 2009, 113(6), 1134–1140 CrossRef PubMed.
- L. Zhang, T. Ren, X. Yang, L. Zhou and X. Li, Int. J. Quantum Chem., 2013, 113(19), 2234–2242 CrossRef CAS.
- L. Zhang, T. Ren, L. Zhou, J. Tian and X. Li, Comput. Theor. Chem., 2013, 1019(0), 1–10 CrossRef CAS PubMed.
- M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802 RSC.
- A. C. Templeton, W. P. Wuelfing and R. W. Murray, Acc. Chem. Res., 1999, 33(1), 27–36 CrossRef PubMed.
- R. Cerf, The Wulff Crystal in Ising and Percolation Models, Springer, 2006 Search PubMed.
- C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Phys. Rev. Lett., 1997, 79(10), 1873 CrossRef CAS.
- K. P. McKenna, Phys. Chem. Chem. Phys., 2009, 11, 4097 RSC.
- Y. Pei, Y. Gao, N. Shao and C. Z. Xiao, J. Am. Chem. Soc., 2009, 131(38), 13619–13621 CrossRef CAS PubMed.
- P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318(5849), 430–433 CrossRef CAS PubMed.
- H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132(24), 8280–8281 CrossRef CAS PubMed.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130(18), 5883–5885 CrossRef CAS PubMed.
- B. Corain, G. Schmid and N. Toshima, Metal Nanoclusters in Catalysis and Materials Science: The Issue of Size, Elsevier B.V., 2008 Search PubMed.
- W. Gao, X. F. Chen, J. C. Li and Q. Jiang, J. Phys. Chem. C, 2009, 114(2), 1148–1153 Search PubMed.
- S. J. Bao, Q. L. Bao, C. M. Li, T. P. Chen, C. Q. Sun, Z. L. Dong, Y. Gan and J. Zhang, Small, 2007, 3(7), 1174–1177 CrossRef CAS PubMed.
- C. Q. Sun, Prog. Mater. Sci., 2009, 54, 179 CrossRef CAS PubMed.
- I. Mayer, Int. J. Quantum Chem., 1986, 29, 477–483 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92(1), 508–517 CrossRef CAS.
- B. Delley, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155125 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102(7), 073005 CrossRef.
- I. L. Garzón, K. Michaelian, M. R. Beltrán, A. Posada-Amarillas, P. Ordejón, E. Artacho, D. Sánchez-Portal and J. M. Soler, Phys. Rev. Lett., 1998, 81(8), 1600–1603 CrossRef.
- A. Mayoral, D. A. Blom, M. M. Mariscal, C. Guiterrez-Wing, J. Aspiazu and M. Jose-Yacaman, Chem. Commun., 2010, 46(46), 8758–8760 RSC.
- Y. Pei, Y. Gao and X. C. Zeng, J. Am. Chem. Soc., 2008, 130(25), 7830–7832 CrossRef CAS PubMed.
- M. R. Beltrán, R. Suárez Raspopov and G. González, Eur. Phys. J. D, 2011, 65(3), 411–420 CrossRef.
- M. Weinert and J. W. Davenport, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13709–13712 CrossRef.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 0(5), 799–805 RSC.
- MATLAB and R2011b, The MathWorks Inc., Natick, MA, 2011 Search PubMed.
- H. Fujimoto, S. Kato, S. Yamabe and K. Fukui, J. Chem. Phys., 1974, 60(2), 572–578 CrossRef CAS.
- A. Staykov, T. Nishimi, K. Yoshizawa and T. Ishihara, J. Phys. Chem. C, 2009, 116(30), 15992–16000 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp52149d |
| This journal is © the Owner Societies 2013 |
