Open Access Article
Open Access ArticlePhotoinduced charge transport over branched conjugation pathways: donor–acceptor substituted 1,1-diphenylethene and 2,3-diphenylbutadiene
Cornelis A.
van Walree
*ab,
Bas C.
van der Wiel
c and
René M.
Williams
d
aFlinders Centre for Nanoscale Science and Technology, School of Chemical and Physical Sciences, Flinders University, GPO Box 2100, Adelaide 5001, Australia
bDepartment of Chemistry, Utrecht University, Sorbonnelaan 16, 3584 CA, Utrecht, The Netherlands. E-mail: c.a.vanwalree@uu.nl
cBELECTRIC OPV GmbH, Landgrabenstrasse 94, 90443, Nürnberg, Germany
dMolecular Photonics Group, Van ‘t Hoff Institute of Molecular Sciences, University of Amsterdam, Science Park 904, 1090 GD Amsterdam, The Netherlands
First published on 9th August 2013
Abstract
Photoinduced charge transport in 1,1-diphenylethene and 2,3-diphenylbutadiene functionalized with an electron donating dimethylamino group and an electron accepting cyano group is reported. UV-spectroscopy reveals that in these compounds, which incorporate a cross-conjugated spacer, a direct charge transfer transition is possible. It is shown by application of the generalized Mulliken–Hush approach that introduction of an additional branching point in the π-electron spacer (i.e., when going from the 1,1-diphenylethene to the 2,3-diphenylbutadiene) leads to only a moderate reduction (68–92%) of the electronic coupling between the ground and the charge separated state. The σ-electron system is however likely to be dominant in the photoinduced charge separation process.
Introduction
Charge transport is the key process in molecular electronics and a variety of optoelectronic phenomena. In organic compounds and materials the feasibility and the rate of the transport are largely determined by the nature of the path over which it occurs.1–3 The effectiveness of a given pathway can be assessed by substitution with electron donating and accepting functionalities at the termini and the subsequent evaluation of the electronic interaction between these entities. Thus, the occurrence of photoinduced charge separation and charge recombination processes in electron donor–acceptor compounds is often diagnostic of the ability of the intervening molecular framework to transmit charges while the dynamics of these processes are indicative of the nature of the electron transport mechanism.4,5Photoinduced charge transfer (CT) in a vast amount of donor-bridge-acceptor compounds has been investigated. The various types of electronic interactions that are inherent to the intervening medium between the donor and the acceptor can be described as resulting from e.g. linear π-conjugation,4,6 σ-interactions,7 homoconjugation,8 and foldamer coupling in helical bridges.9 Photoinduced charge transfer in donor–acceptor substituted compounds with a branched (bifurcated) π-spacer has however received little attention.10–17 Branched π-systems, also referred to as cross-conjugated systems,18 are intriguing since they represent topological two-dimensional conducting systems and incorporate multiple conjugation paths. As such, they can give rise to quantum interference,19–25i.e. the interaction between different conjugation paths. This can manifest itself in two ways, i.e., by communication via a through-bond or a through-space mechanism.26 The availability of multiple conjugation paths is thus of great importance for the development of two-dimensional molecular conduction systems and molecular switches, particularly when radical ions or excited states are involved.27,28 Furthermore, an electron mobility among the highest observed has been reported for an organic field effect transistor based on a cross-conjugated material.29 Donor and/or acceptor substituted branched π-systems are moreover useful for two-photon absorption purposes.30,31
An important and hitherto largely unanswered question is how efficiently charge carriers can be transported over branching points in bifurcated π-systems; the feasibility of charge transport over π-systems containing multiple branching sites has to our knowledge hardly been explored. Here we address these issues with the use of the dimethylamino-cyano functionalized 1,1-diphenylethene DA1 and 2,3-diphenylbutadiene DA2 (Chart 1). In these compounds each olefinic carbon atom bonded to a phenylene group forms the branching point of linear π-systems; the bridge in DA2 is an extension of the one in DA1. The charge transport ability of the branched conduction paths is addressed by considering the absorption and fluorescence properties of DA1 and DA2, which allow the evaluation of the electronic coupling and the communication between the donor and acceptor sites. As such, this study is an extension of our earlier work32,33 on these cross-conjugated systems.
 | ||
| Chart 1 Molecular structures of DA1 and DA2. | ||
Results and discussion
Synthesis
The synthesis of DA1 has been reported previously.33 Donor–acceptor substituted 2,3-diphenylbutadiene DA2 was synthesized starting with a benzoin condensation of 4-N,N-dimethylaminobenzaldehyde and 4-bromobenzaldehyde, giving benzoin 1 (Scheme 1). It is known from the literature that exclusive formation of the benzoin isomer occurs in which the carbonyl group is adjacent to the dimethylaminophenyl fragment.34 Nevertheless, the other possible isomer also would have given benzil 2 in the next step, oxidation by copper(II)sulfate in pyridine. The oxidation was followed by a twofold Wittig reaction with methylenetriphenylphosphorane to obtain disubstituted 2,3-diphenylbutadiene 3. Finally, bromide 3 was converted into DA2 by a palladium-catalyzed reaction with trimethylsilylcyanide.35 | ||
| Scheme 1 Synthesis of DA2. | ||
Molecular structures
Since the molecular geometry can have a strong effect on CT processes,36 the structures of DA1 and DA2 are of interest. Unsubstituted 2,3-diphenylbutadiene was previously found to adopt a somewhat surprising s-gauche conformation in the solid state, with a torsion angle of 55.6° around the butadiene single bond.37,38 MP2 and DFT calculations supported that this compound possesses an s-gauche minimum, and also revealed the presence of an s-trans minimum, which is somewhat (depending on the calculation method up to 1.47 kcal mol−1) higher in energy.38,39The structures of DA1 and DA2 were investigated with 6-311G** DFT/B3LYP calculations. In the optimized structure of DA1 (E = −481![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363.76 kcal mol−1), the torsion angles between the double bond and the aniline and cyanophenyl groups amount to 36.9° and 41.3°, respectively (Fig. 1). These values are close to those found for 1,1-diphenylethene.27 In common with 2,3-diphenylbutadiene, for DA2 two minima were found (Fig. 2). The global minimum is represented by a structure with an s-gauche geometry around the central single bond (torsion angle 55.8°, E = −529
363.76 kcal mol−1), the torsion angles between the double bond and the aniline and cyanophenyl groups amount to 36.9° and 41.3°, respectively (Fig. 1). These values are close to those found for 1,1-diphenylethene.27 In common with 2,3-diphenylbutadiene, for DA2 two minima were found (Fig. 2). The global minimum is represented by a structure with an s-gauche geometry around the central single bond (torsion angle 55.8°, E = −529![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943.14 kcal mol−1), while a minimum with a central torsion angle of 152.2° (E = −529
943.14 kcal mol−1), while a minimum with a central torsion angle of 152.2° (E = −529![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 942.58 kcal mol−1) occurs as well. The limited energy difference between the two conformations indicates that two conformations might be present under ambient conditions, the s-gauche structure being dominant. The s-gauche minimum is further characterized by torsion angles of 31.5° between the aniline moiety and the adjacent double bond, and 33.4° between the cyanophenyl part and the adjacent double bond. The other structure contains torsion angles of 133.5° and 130.0° between the double bonds and the aniline and the cyanophenyl moiety, respectively. The calculated conformations are in agreement with geometries calculated by Limacher and Lüthi.39
942.58 kcal mol−1) occurs as well. The limited energy difference between the two conformations indicates that two conformations might be present under ambient conditions, the s-gauche structure being dominant. The s-gauche minimum is further characterized by torsion angles of 31.5° between the aniline moiety and the adjacent double bond, and 33.4° between the cyanophenyl part and the adjacent double bond. The other structure contains torsion angles of 133.5° and 130.0° between the double bonds and the aniline and the cyanophenyl moiety, respectively. The calculated conformations are in agreement with geometries calculated by Limacher and Lüthi.39
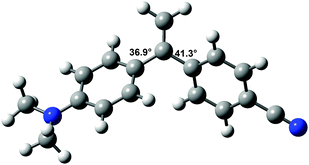 | ||
| Fig. 1 6-311G** DFT/B3LYP calculated structure of DA1. Magnitudes of some torsion angles are indicated. | ||
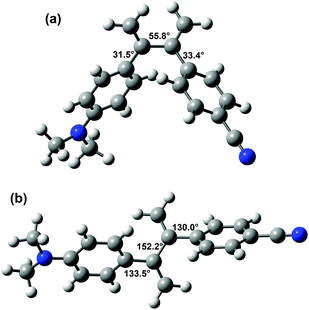 | ||
| Fig. 2 6-311G** DFT/B3LYP calculated structures of DA2 in the s-gauche (a) and s-trans (b) minima. Magnitudes of some torsion angles are indicated. | ||
The lowest energy structure of DA2 is thus different from the s-trans structure that was initially assumed,32 and this might have a bearing on the understanding of the behaviour of the compound. In the butterfly-like s-gauche geometry DA2 possesses a compact structure, whereas in the s-trans conformation the geometry is extended. In fact, in the former geometry the donor and acceptor parts are closer together than in DA1. The N–N distance is 10.9 Å in DA1 and 9.4 Å in s-gaucheDA2 (while it is 13.2 Å in s-transDA2). This is also exemplified by the 6-311G** DFT/B3LYP ground state dipole moments, which are 5.41 and 7.33 D for s-gaucheDA2 and DA1, respectively. The dipole moment of s-transDA2 is 7.98 D.
Absorption and fluorescence spectroscopy
UV spectra of DA1 and DA2 are depicted in Fig. 3, together with spectra of the reference compounds 4-N,N-dimethylaminostyrene and 4-cyanostyrene. The spectra of the donor–acceptor compounds exhibit local cyanophenyl 1La type transitions at 258–265 nm and N,N-dimethylaniline 1La type transitions at 280–298 nm.33 For both DA1 and DA2 a charge transfer (CT) absorption band is present; it appears as a shoulder at the red edge of the dimethylaniline 1La transition. In the difference spectra (Fig. 3b) the CT absorptions are found at 341 and 340 nm for DA1 and DA2, respectively. For DA1 a second CT absorption seems to be present near 310 nm, but the actual maximum may be obscured by the negative absorption at 290 nm. This signal possibly reflects a CT absorption in another conformation.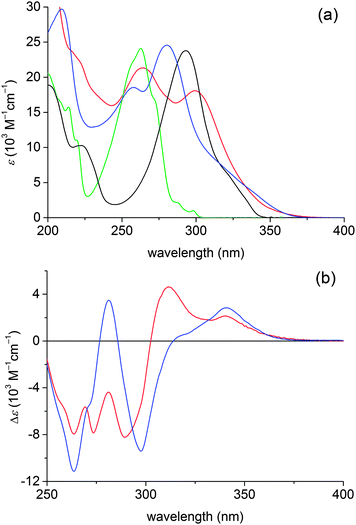 | ||
| Fig. 3 (a) UV spectra of DA1 (blue) and DA2 (red) along with spectra of the reference chromophores 4-N,N-dimethylaminostyrene (black) and 4-cyanostyrene (green) in cyclohexane. (b) UV difference spectra obtained by subtraction of the spectra of the reference chromophores 4-N,N-dimethylaminostyrene and 4-cyanostyrene from the spectra of DA1 (blue) and DA2 (red). | ||
As the stabilization of the CT state by Coulomb attraction between the separate charges depends on the donor–acceptor distance, the minor difference between the CT absorption maxima (341 vs. 340 nm) is not unexpected when the donor–acceptor distance is similar, as is the case for DA1 and s-gaucheDA2. Note however that the behaviour of a CT absorption as a function of chain length also depends on the combination of donor–acceptor strength and the conjugation path,6 and it could be that compounds DA1 and DA2 are in a regime where the energy of the (Franck–Condon) CT state is only weakly dependent on the chain length. This might be in line with the sometimes complex electronic spectra of cross-conjugated systems, which do not always reflect the extent of conjugation.40–42 If the CT absorption of DA2 at 340 nm arises in the s-gauche conformation, then the band near 310 nm could represent the CT absorption in the s-trans conformation.
The presence of CT absorption bands implies that a significant ground state interaction between the donor and acceptor chromophores is present. For DA1 and other compounds with a bridge consisting of a single sp2 hybridized carbon atom this was derived earlier,10,12–14,33 but as far as we are aware DA2 is the first compound for which an interaction over two branching points has been reported.32 As judged from the absorption coefficient of the CT band in the difference spectrum, ε = 2140 M−1 cm−1 and ε = 2800 M−1 cm−1 for DA1 and DA2, respectively, the coupling is moderate. The negative peaks in the wavelength range 290–300 nm and near 263 nm in Fig. 3b suggest that the CT transitions borrow their intensity from the local N,N-dimethylaniline and cyanophenyl 1La transitions.43
Fluorescence spectra of DA1 and DA2 in various solvents are shown in Fig. 4 (tabulated data were reported previously).32 The fluorescence is strongly solvatochromic, revealing that in both compounds a highly dipolar CT excited state is generated upon excitation. The fluorescence maxima can be plotted against the solvent polarity according to the well-known Lippert–Mataga relationship (Fig. 5). Since DA1 and DA2 have substantial ground state dipole moments, the following form is most appropriate:44,45
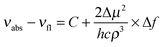 | (1a) |
 | (1b) |
 | ||
| Fig. 4 Fluorescence spectra of DA1 (a) and DA2 (b) in various solvents. Maxima of DA1 are situated at 389.0 (cyclohexane, black), 437.5 (di-n-butyl ether, blue), 465.5 (diethyl ether, red), 525.5 (ethyl acetate, green), 525.5 (THF, cyan) and 605.0 nm (acetonitrile, magenta). Maxima of DA2 are found at 410.5 (cyclohexane, black), 464.0 (di-n-butyl ether, blue), 493.0 (diethyl ether, red), 556.0 (ethyl acetate, green) and 558.0 nm (THF, cyan). In acetonitrile DA2 is non-fluorescent. | ||
 | ||
| Fig. 5 Solvatochromism of DA1 (squares) and DA2 (spheres). | ||
The equal slopes suggest that the emitting species of DA1 and DA2 are homologous; the structure in the excited state must be very similar. DA1 is a fairly rigid molecule in which only rotation along the two phenylene–vinylidene single bonds is possible. DA2 has more conformational freedom, which is of interest since Coulombic attraction between the radical ion sites might induce conformational changes, particularly in nonpolar solvents.47–50 Because of the very similar solvatochromic sensitivities of DA1 and DA2 and the fact that the solvatochromism of DA2 is convincingly described by a single straight line, we tend to think that such conformational changes do not occur. In the excited state DA2 must adopt a structure similar to the s-gauche structure and which bears a strong resemblance to that of DA1. Fast processes (down to the order of 30 ps) reflecting potential conformational changes were not observed in time-resolved fluorescence measurements. If the difference UV-signal near 310 nm corresponds to the CT absorption in the s-trans conformation, the change into the compact conformation must be very fast. Note that in the fluorescence spectra of DA2 in di-n-butyl and di-n-pentyl ether a weak band near 380 nm is visible. In common with the behaviour of 1-(4-N,N-dimethylaminophenyl)-1-phenylethene,33 this signal is assigned to local aniline type fluorescence. Using cavity radii of 4.5 and 4.7 Å (ref. 51) from the solvatochromic fits Δμ values of 16.7 and 17.6 D are calculated for DA1 and DA2, respectively.
As described above, the fluorescence maxima of DA2 are systematically situated below those of DA1 by some 1200 cm−1, meaning that the CT state of DA2 is more stable than that of DA1. In order to rationalize this difference, it is instructive to consider which terms determine the energy of a CT state. According to the expression52,53
| hνfl = ΔG0RIP − λi − λs | (2a) |
 | (2b) |
The first oxidation potentials of DA1 and DA2 were both determined to be 0.65 V vs. SCE by cyclic voltammetry in acetonitrile, while the respective first reduction potentials are −2.16 and −2.13 V vs. SCE, respectively.54 The small differences between the redox potentials of DA1 and DA2 thus account for another portion, albeit small, of the offset of 1200 cm−1 (0.03 eV corresponds to 242 cm−1) in the CT state energies. Therefore, the largest contribution to the onset must arise from a difference in reorganization energy. The solvent reorganization energy is determined by53
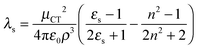 | (3) |
Electronic couplings
In a two-level model, the coupling HDA between the ground state and the CT excited state can be obtained from the generalized Mulliken–Hush expression56 | (4) |
 | (5) |
| f = 4.32 × 10−9εmaxΔν1/2 | (6) |
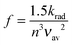 | (7) |
The CT bands of DA1 and DA2 have absorption coefficients εmax of 2800 and 2140 M−1 cm−1, respectively, while the bandwidths are 2000 and 1840 cm−1 (Fig. 3b). Application of eqn (6), (5) and (4) then leads to couplings HDA given in Table 1. Fluorescence data and couplings derived from them are also compiled in this table. In cyclohexane, the couplings obtained from the absorption and fluorescence data are rather similar. This seems to be partly fortuitous, since the differences in oscillator strength are compensated by the difference in absorption and fluorescence energy. Nevertheless, the data are in reasonable agreement. The fluorescence data show that with increasing solvent polarity the couplings decrease. This does not take away that in the most polar solvent considered, THF, the magnitude of the couplings is still substantial, even when two branching points are present. In each solvent the coupling in DA1 is larger than in DA2, but the decrease of HDA when going from one to two branching points is surprisingly modest. The ratio of the couplings varies between 68% in cyclohexane and 92% in THF.
| DA1 | DA2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ν av/103 cm−1 | Φ fl | τ fl/ns | f/10−2 | H DA/cm−1 | ν av/103 cm−1 | Φ fl | τ fl/ns | f/10−2 | H DA/cm−1 | |
| a From absorption spectrum (eqn (6), (5) and (4)); ε was taken from Fig. 3b, absorption band widths are 2000 (DA1) and 1840 (DA2) cm−1. b From radiative decay rates (eqn (7), (5) and (4)). | ||||||||||
| Cyclohexanea | 2.4 | 2290 | 1.7 | 1840 | ||||||
| Cyclohexaneb | 24.76 | 0.087 | 2.2 | 3.33 | 2460 | 23.56 | 0.084 | 4.4 | 1.78 | 1680 |
| Diethyl etherb | 20.58 | 0.19 | 18.5 | 1.46 | 1502 | 19.69 | 0.044 | 6.7 | 1.03 | 1170 |
| THFb | 18.16 | 0.13 | 16.9 | 1.24 | 1300 | 17.30 | 0.062 | 9.0 | 1.22 | 1190 |
The most significant data are presumably those obtained in THF. The couplings in cyclohexane and diethyl ether should be treated with some caution since intensity borrowing from local transitions by the CT transitions occurs in the compounds under investigation.33,43 In particular the radiative decay of the CT states in cyclohexane will be strongly affected by the properties of the locally excited aniline type 1La state, as in this nonpolar solvent these states are close in energy. Hence, couplings in the nonpolar solvents are expected to be too large, and a three state model would be more appropriate.43,58–60 However, in a computational study on multistate effects in the generalized Mulliken–Hush treatment the two state model was shown to be applicable to dimethylaminobenzonitrile, which was considered to be an extreme test case.60 Significant state mixing was shown to have a marginal effect on interstate couplings. Moreover, state energies and the nature of the CT state are similar for DA1 and DA2, so that the amount of intensity borrowing is not too different for the two compounds. The relative differences between DA1 and DA2 are therefore considered to be meaningful.
General discussion and conclusions
There is a significant electronic interaction between donor and acceptor functionalities in the branched π-systems considered here. While it has been established that the cross-conjugation pattern in diphenylethene strongly decreases the donor–acceptor coupling,16 the remaining interaction certainly is substantial and implies that charge transport is well possible in bifurcated π-systems. Moreover, in these types of compounds additional branching points can be inserted at the cost of only a limited extent of donor–acceptor interaction. This suggests molecular wire behaviour, i.e. weak attenuation of the electronic coupling with the distance.4 It is of interest to note that molecular wire behaviour is often observed for systems based on other modes of conjugation than linear π-conjugation.61,62 In this wire-like behaviour, quantum interference can play a significant role,26 but its precise nature in compounds like DA1 and DA2 is difficult to assess. It involves answering the question as to which mechanism underlies the charge transport in the compounds under investigation. Given the structures of the compounds, both through-space and through-bond interactions may be operative. The importance of through-bond interactions is indicated by the observation that HDA is larger for DA1 than for DA2. If only a through-space mechanism would be active, a larger value would have been expected for DA2, which has a shorter donor–acceptor separation.In the through-bond mechanism, effects in both the π- and σ-electron systems may contribute. From a NBO population analysis Limacher and Lüthi revealed a ground state effect on the π-electrons of compound DA2.39 Butler-Ricks et al. showed that in a donor–acceptor substituted diphenylethene the σ-electron system may be dominant in charge transport.16 In this respect it is of interest to compare the behavior of DA1 with that of data for molecules containing an N,N-dimethylaniline donor and a cyanophenyl acceptor separated by a bridge consisting of a single sp3 carbon atom like compound 1C.43,63 The ε-value of the charge transfer absorption in 1C is 2500 M−1 cm−1, which is close to that for DA1. Evaluation of the coupling between the ground and CT states for 1C with the generalized Mulliken–Hush method gives HDA = 2190 cm−1 in diethyl ether (νav = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1, f = 0.031 and Δμ = 17.7 D) and HDA = 1420 cm−1 in ethyl acetate (νav = 20
700 cm−1, f = 0.031 and Δμ = 17.7 D) and HDA = 1420 cm−1 in ethyl acetate (νav = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1, f = 0.014 and Δμ = 17.7 D). The higher HDA values for 1C in comparison to DA1 might be explained by the somewhat shorter donor–acceptor distance in 1C (N–N distance 10.3 Å vs. 10.9 Å) and an increased through-space contribution. More importantly, the small difference between the couplings in DA1 and 1C indicates that the effect of the double bond is minor and that the σ-electron system is dominant in photoinduced charge transfer processes in the cross-conjugated compounds indeed.
900 cm−1, f = 0.014 and Δμ = 17.7 D). The higher HDA values for 1C in comparison to DA1 might be explained by the somewhat shorter donor–acceptor distance in 1C (N–N distance 10.3 Å vs. 10.9 Å) and an increased through-space contribution. More importantly, the small difference between the couplings in DA1 and 1C indicates that the effect of the double bond is minor and that the σ-electron system is dominant in photoinduced charge transfer processes in the cross-conjugated compounds indeed.
In conclusion, it has been shown that charge can be transported efficiently over cross-conjugated pathways incorporating one or two branching points. This reveals that 1,1-diphenylethene and 2,3-diphenylbutadiene systems can participate in 2-dimensional conducting systems, in which charge carriers can be conducted along linear- and cross-conjugated pathways. Herewith it should be realized that DA1 and DA2 are not planar, and that it is difficult to separate through-bond and through-space effects. Moreover, the σ-system is likely to be dominant.
Experimental section
General
Reactions involving organolithium reagents were conducted under nitrogen using standard Schlenk techniques. Starting materials and reagents were obtained from commercial sources and used as received. Solvents generally were distilled before use; dry diethyl ether and toluene were obtained by distillation from sodium-benzophenone. Column chromatography was performed with Acros silica (0.035–0.070 mm, pore diameter ca. 6 nm). For gas chromatography use was made of a Varian 3400 gas chromatograph equipped with an Alltech EC-5 capillary column. NMR spectra were recorded in CDCl3 using a Bruker AC-300 spectrometer (operating at 300 MHz for 1H NMR and 75 MHz for 13C NMR) and are calibrated to TMS as internal standard. IR spectra were taken in ATR mode on neat samples on a Perkin-Elmer Spectrum One FT-IR spectrometer equipped with a Universal ATR Sampling accessory. Melting points were determined on a Mettler FP5/FP51 photoelectric apparatus. Elemental analysis was carried out at Kolbe Microanalytisches Laboratorium, Mülheim an der Ruhr, Germany.UV spectra were collected on Cary 1 or Cary 5 spectrophotometers in spectrophotometric grade solvents. Fluorescence spectra were obtained on a Spex Fluorolog instrument.33 Fluorescence quantum yields64 were determined relative to anthracene (Φfl = 0.27) upon 310 nm excitation. Fluorescence lifetimes were determined using a streak camera system described elsewhere.65 Cyclic voltammetry was conducted using an EG&G PAR model 63A potentiostat/galvanostat in acetonitrile with tetrabutylammonium hexafluorophosphate as a supporting electrolyte. Potentials were calibrated against SCE by recording a voltammogram of internal ferrocene (E1/2 = +0.31 V vs. SCE).
DFT B3LYP/6-311G** calculations were performed with the Gaussian09 package.66 Stationary points were characterized as minima by Hessian calculations.
The synthesis of DA1 has been reported elsewhere.33
A pure sample of 1 was obtained as a white crystalline solid by repeated crystallization from ethanol and methanol. mp 115 °C. NMR: δH(CDCl3) 7.80 (2H, d, 3J 9.09, Ar-H), 7.43 (2H, d, 3J 8.52, Ar-H), 7.22 (2H, d, 3J 8.52, Ar-H,), 6.57 (2H, d, 3J 9.09, Ar-H), 5.80 (1H, d, 3J 6.06, CH(OH)), 4.78 (1H, d, 3J 6.06, OH), 3.03 (6H, s, NMe2); δC(CDCl3) 195.6 (q, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 154.1 (q, C-NMe2), 139.8 (q), 132.2, 131.7, 129.5, 122.4 (q), 120.6 (q), 110.8, 74.6 (COH), 40.1 (NMe2). IR: νmax/cm−1 3389, 2913, 1821, 1648, 1593, 1549, 1485, 1375, 1255, 1196, 1169, 1084, 1013, 976, 949, 808, 755.
O), 154.1 (q, C-NMe2), 139.8 (q), 132.2, 131.7, 129.5, 122.4 (q), 120.6 (q), 110.8, 74.6 (COH), 40.1 (NMe2). IR: νmax/cm−1 3389, 2913, 1821, 1648, 1593, 1549, 1485, 1375, 1255, 1196, 1169, 1084, 1013, 976, 949, 808, 755.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, 250 mL) was refluxed for 21 hours. Water (250 mL) was added to dissolve the copper salts and the resulting slurry was extracted with ether (3 × 350 mL). The combined organic layers were dried on magnesium sulfate, filtered and evaporated under reduced pressure. The crude product (29.85 g) was purified by Kugelrohr distillation at 0.05 mbar, discarding the fractions boiling below 120 °C. Hot ethanol was added to the residue and insoluble impurities were removed by filtration. Recrystallization from ethyl acetate gave 7.13 g (21.5 mmol) of a brown-yellow solid. Purity 96% by GC.
1 v/v, 250 mL) was refluxed for 21 hours. Water (250 mL) was added to dissolve the copper salts and the resulting slurry was extracted with ether (3 × 350 mL). The combined organic layers were dried on magnesium sulfate, filtered and evaporated under reduced pressure. The crude product (29.85 g) was purified by Kugelrohr distillation at 0.05 mbar, discarding the fractions boiling below 120 °C. Hot ethanol was added to the residue and insoluble impurities were removed by filtration. Recrystallization from ethyl acetate gave 7.13 g (21.5 mmol) of a brown-yellow solid. Purity 96% by GC.
Following the same procedure, pure 2 was obtained in 83% yield from the small amount of pure 1. mp 145 °C. NMR: δH(CDCl3) 7.87–7.81 (2 × 2H, 2 × d, Ar-H), 7.62 (2H, d, 3J 8.52, Ar-H), 6.67 (2H, d, 3J 9.36, Ar-H), 3.10 (6H, s, NMe2); δC(CDCl3) 194.5 (q, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 191.8 (q, C
O), 191.8 (q, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 154.7 (q, C-NMe2), 132.7 (q), 132.4, 132.3, 131.4, 129.9 (q), 120.7 (q), 111.2, 40.2 (NMe2). IR: νmax/cm−1: 2915, 1671, 1637, 1580, 1480, 1374, 1230, 1167, 1067, 873, 830, 810, 743.
O), 154.7 (q, C-NMe2), 132.7 (q), 132.4, 132.3, 131.4, 129.9 (q), 120.7 (q), 111.2, 40.2 (NMe2). IR: νmax/cm−1: 2915, 1671, 1637, 1580, 1480, 1374, 1230, 1167, 1067, 873, 830, 810, 743.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v hexane
1 v/v hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ether) to give 0.80 g of a yellow solid containing 66% 3 and 13% triphenylphosphine as the main components (GC). This mixture was used without further purification. NMR: δH(CDCl3) 7.36 (2H, d, 3J 8.52, Ar-H), 7.28 (2H, d, 3J 8.52, Ar-H), 7.26 (2H, d, 3J 8.79, Ar-H), 6.60 (2H, d, 3J 8.79, Ar-H), 5.53 (1H, d, 2J 1.65, C
ether) to give 0.80 g of a yellow solid containing 66% 3 and 13% triphenylphosphine as the main components (GC). This mixture was used without further purification. NMR: δH(CDCl3) 7.36 (2H, d, 3J 8.52, Ar-H), 7.28 (2H, d, 3J 8.52, Ar-H), 7.26 (2H, d, 3J 8.79, Ar-H), 6.60 (2H, d, 3J 8.79, Ar-H), 5.53 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 5.45 (1H, d, 2J 1.65, C
CH), 5.45 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 5.35 (1H, d, 2J 1.65, C
CH), 5.35 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 5.13 (1H, d, 2J 1.65, C
CH), 5.13 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 2.91 (6H, s, NMe2). GC-MS (EI): m/z 329 + 327 (M+), 285, 283, 248, 207–204, 172, 134 (100%), 124, 101, 77.
CH), 2.91 (6H, s, NMe2). GC-MS (EI): m/z 329 + 327 (M+), 285, 283, 248, 207–204, 172, 134 (100%), 124, 101, 77.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v CH2Cl2
1 v/v CH2Cl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHCl3). This was followed by recrystallization from ethanol to yield 0.17 g (0.62 mmol, 39%) of a yellow solid. mp 132 °C. NMR: δH(CDCl3) 7.55–7.45 (2 × 2H, 2 × d, Ar-H), 7.21 (2H, d, 3J 9.06, Ar-H), 6.59 (2H, d, 3J 9.06, Ar-H), 5.64 (1H, d, 2J 1.65, C
CHCl3). This was followed by recrystallization from ethanol to yield 0.17 g (0.62 mmol, 39%) of a yellow solid. mp 132 °C. NMR: δH(CDCl3) 7.55–7.45 (2 × 2H, 2 × d, Ar-H), 7.21 (2H, d, 3J 9.06, Ar-H), 6.59 (2H, d, 3J 9.06, Ar-H), 5.64 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 5.49 (2 × 1H, 2 × d, C
CH), 5.49 (2 × 1H, 2 × d, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 5.15 (1H, d, 2J 1.65, C
CH), 5.15 (1H, d, 2J 1.65, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH), 2.92 (6H, s, NMe2); δC(CDCl3) 150.3 (q, C-NMe2), 149.1 (q, C
CH), 2.92 (6H, s, NMe2); δC(CDCl3) 150.3 (q, C-NMe2), 149.1 (q, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 148.5 (q, C
CH2), 148.5 (q, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 145.1 (q), 132.2, 128.2, 128.0, 127.1 (q), 119.1 (q, CN), 118.2 (C
CH2), 145.1 (q), 132.2, 128.2, 128.0, 127.1 (q), 119.1 (q, CN), 118.2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 113.5 (C
CH2), 113.5 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 112.1, 111.0 (q), 40.5 (NMe2). IR: νmax/cm−1 2888, 2812, 2231, 1610, 1524, 1505, 1362, 1199, 925, 888, 843, 814. Anal. found: C, 83.0; H, 6.6; N, 10.1. Calc. for C19H18N2: C, 83.2; H, 6.6; N, 10.2%.
CH2), 112.1, 111.0 (q), 40.5 (NMe2). IR: νmax/cm−1 2888, 2812, 2231, 1610, 1524, 1505, 1362, 1199, 925, 888, 843, 814. Anal. found: C, 83.0; H, 6.6; N, 10.1. Calc. for C19H18N2: C, 83.2; H, 6.6; N, 10.2%.
References and notes
- M. R. Wasielewksi, Chem. Rev., 1992, 92, 435–461 CrossRef.
- O. Wenger, Acc. Chem. Res., 2011, 44, 25–35 CrossRef CAS.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60–63 CrossRef CAS.
- G. Pourtois, D. Beljonne, J. Cornil, M. A. Ratner and J.-L. Brédas, J. Am. Chem. Soc., 2002, 124, 4436–4447 CrossRef CAS.
- H. Meier, Angew. Chem., Int. Ed., 2005, 44, 2482–2506 CrossRef CAS.
- H. Oevering, M. N. Paddon-Row, M. Heppener, A. E. Oliver, E. Cotsaris, J. W. Verhoeven and N. S. Hush, J. Am. Chem. Soc., 1987, 109, 3258–3269 CrossRef CAS.
- N. Herrero-García, M. Del Rosario Colorado Heras, M. Del Rosario Torres, I. Fernández and J. Osío Barcina, Eur. J. Org. Chem., 2012, 2643–2655 CrossRef.
- M. Wolffs, N. Delsuc, D. Veldman, N. Vân Anh, R. M. Williams, S. C. J. Meskers, R. A. J. Janssen, I. Huc and A. P. H. J. Schenning, J. Am. Chem. Soc., 2009, 131, 4819–4829 CrossRef CAS.
- C. Bosshard, R. Spreiter, P. Günter, R. R. Tykwinski, M. Schreiber and F. Diederich, Adv. Mater., 1996, 8, 231–234 CrossRef CAS.
- C. Eckert, F. Heisel, J. A. Miehé, R. Lapouyade and L. Ducasse, Chem. Phys. Lett., 1988, 153, 357–364 CrossRef CAS.
- C. Maertens, C. Detrembleur, P. Dubois, R. Jérôme, C. Boutton, A. Persoons, T. Kogej and J. L. Brédas, Chem.–Eur. J., 1999, 5, 369–380 CrossRef CAS.
- R. R. Tykwinski, M. Schreiber, V. Gramlich, P. Seiler and F. Diederich, Adv. Mater., 1996, 8, 226–231 CrossRef CAS.
- R. R. Tykwinski, M. Schreiber, R. P. Carlón, F. Diederich and V. Gramlich, Helv. Chim. Acta, 1996, 79, 2249–2281 CrossRef CAS.
- J. N. Wilson, K. I. Hardcastle, M. Josowicz and U. H. F. Bunz, Tetrahedron, 2004, 60, 7157–7167 CrossRef CAS.
- A. Butler Ricks, G. C. Solomon, M. T. Colvin, A. M. Scott, K. Chen, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 15427–15434 CrossRef.
- N. N. P. Moonen, W. C. Pomerantz, R. Gist, C. Boudon, J.-P. Gisselbrecht, T. Kawai, A. Kishioka, M. Gross, M. Irie and F. Diederich, Chem.–Eur. J., 2005, 11, 3325–3341 CrossRef CAS.
- M. Gholami and R. R. Tykwinski, Chem. Rev., 2006, 106, 4997–5027 CrossRef CAS.
- C. Patoux, C. Coudret, J.-P. Launay, C. Joachim and A. Gourdon, Inorg. Chem., 1997, 36, 5037–5049 CrossRef CAS.
- R. Baer and D. Neuhauser, J. Am. Chem. Soc., 2002, 124, 4200–4201 CrossRef CAS.
- A. Cheong, A. E. Roitberg, V. Mujica and M. A. Ratner, J. Photochem. Photobiol., A, 1994, 82, 81–86 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 7788–7789 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17301–17308 CrossRef CAS.
- D. Fracasso, H. Valkenier, J. C. Hummelen, G. C. Solomon and R. C. Chieci, J. Am. Chem. Soc., 2011, 133, 9556–9563 CrossRef CAS.
- C. M. Guédon, H. Valkenier, T. Markussen, K. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305–309 CrossRef.
- M. J. Shephard, M. N. Paddon-Row and K. D. Jordan, J. Am. Chem. Soc., 1994, 116, 5328–5333 CrossRef CAS.
- S. Smolarek, A. Vdovin, A. Rijs, C. A. van Walree, M. A. Zgierski and W. J. Buma, J. Phys. Chem. A, 2011, 115, 9399–9410 CrossRef CAS.
- P. A. Limacher and H. P. Lüthi, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 477–486 CrossRef CAS.
- R. P. Ortiz, A. Facchetti, T. J. Marks, J. Casado, M. Z. Zgierski, M. Kozaki, V. Hernández and J. T. L. Navarrete, Adv. Funct. Mater., 2009, 19, 386–394 CrossRef CAS.
- E. Zojer, D. Beljonne, P. Pacher and J.-L. Bredas, Chem.–Eur. J., 2004, 10, 2668–2680 CrossRef CAS.
- T.-C. Lin, S.-J. Chung, K.-S. Kim, X. Wang, G. S. He, J. Swiatkiewicz, H. E. Pudavar and P. N. Prasad, Adv. Polym. Sci., 2003, 161, 157–193 CrossRef CAS.
- B. C. van der Wiel, R. M. Williams and C. A. van Walree, Org. Biomol. Chem., 2004, 2, 3432–3433 CAS.
- C. A. van Walree, V. E. M. Kaats-Richters, S. J. Veen, B. Wieczorek, J. H. van der Wiel and B. C. van der Wiel, Eur. J. Org. Chem., 2004, 3046–3056 CrossRef CAS.
- J. March, Advanced Organic Chemistry, Wiley, New York, 4th edn, 1992 Search PubMed.
- M. Sundermeier, S. Mutyala, A. Zapf, A. Spanneberg and M. Beller, J. Organomet. Chem., 2003, 684, 50–55 CrossRef CAS.
- R. M. Williams, Photochem. Photobiol. Sci., 2010, 9, 1018–1026 CAS.
- M. Lutz, A. L. Spek, B. C. van der Wiel and C. A. van Walree, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2005, 61, o300–o302 Search PubMed.
- C. A. van Walree, B. C. van der Wiel, L. W. Jenneskens, M. Lutz, A. L. Spek, R. W. A. Havenith and J. H. van Lenthe, Eur. J. Org. Chem., 2007, 4746–4751 CrossRef CAS.
- P. A. Limacher and H. P. Lüthi, J. Phys. Chem. A, 2008, 112, 2913–2919 CrossRef CAS.
- M. Klokkenburg, M. Lutz, A. L. Spek, J. H. van der Maas and C. A. van Walree, Chem.–Eur. J., 2003, 9, 3544–3554 CrossRef CAS.
- N. N. P. Moonen and F. Diederich, Org. Biomol. Chem., 2004, 2, 2263–2265 CAS.
- C. A. Van Walree, B. C. Van der Wiel and J. H. Van Lenthe, Chem. Phys. Lett., 2012, 528, 29–33 CrossRef CAS.
- C. A. van Walree, M. R. Roest, W. Schuddeboom, L. W. Jenneskens, J. W. Verhoeven, J. M. Warman, H. Kooijman and A. L. Spek, J. Am. Chem. Soc., 1996, 118, 8395–8407 CrossRef CAS.
- E. Lippert, Z. Elektrochem., 1957, 61, 962 CAS.
- Note that in our earlier study (ref. 32) when no information on the ground state dipole moment was available, a slightly different expression was used.
- Data were taken from: C. Reichardt, Solvents and Solvent Effects in Organic Chemistry, VCH, Weinheim, 2nd edn, 1988 Search PubMed.
- F. C. de Schryver, N. Boens and J. Put, Adv. Photochem., 1977, 10, 359–465 CrossRef CAS.
- J. W. Verhoeven, Pure Appl. Chem., 1990, 62, 1585–1596 CrossRef CAS.
- F. J. Hoogesteger, C. A. van Walree, L. W. Jenneskens, M. R. Roest, J. W. Verhoeven, W. Schuddeboom, J. J. Piet and J. M. Warman, Chem.–Eur. J., 2000, 6, 2948–2959 CrossRef CAS.
- W. D. Oosterbaan, C. Koper, T. W. Braam, F. J. Hoogesteger, J. J. Piet, B. A. J. Jansen, C. A. van Walree, H. J. van Ramesdonk, M. Goes, J. W. Verhoeven, W. Schuddeboom, J. M. Warman and L. W. Jenneskens, J. Phys. Chem. A, 2003, 107, 3612–3624 CrossRef CAS.
- As documented before (ref. 33), the cavity radius of DA1 was estimated by comparison with related compounds. The radius of DA2 is assumed to be 0.2 Å larger.
- R. A. Marcus, J. Phys. Chem., 1989, 93, 3078–3086 CrossRef CAS.
- J. Cortés, H. Heitele and J. Jortner, J. Phys. Chem., 1994, 98, 2527–2536 CrossRef.
- The peak potentials are given here. Due to the irreversible nature of the reduction process of DA1 and DA2 the half wave potentials can only be approached. Since we are primarily interested in the differences between DA1 and DA2, the peak potentials suffice.
- I. R. Gould, D. Noukakis, L. Gomez-Jahn, R. H. Young, J. L. Goodman and S. Farid, Chem. Phys., 1993, 176, 439–456 CrossRef CAS.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- A. M. Oliver, M. N. Paddon-Row, J. Kroon and J. W. Verhoeven, Chem. Phys. Lett., 1992, 191, 371–377 CrossRef CAS.
- I. R. Gould, R. H. Young, L. J. Mueller, A. C. Albrecht and S. Farid, J. Am. Chem. Soc., 1994, 116, 3147–3148 CrossRef CAS.
- M. Bixon, J. Jortner and J. W. Verhoeven, J. Am. Chem. Soc., 1994, 116, 7349–7355 CrossRef CAS.
- M. Rust, J. Lappe and R. J. Cave, J. Phys. Chem. A, 2002, 106, 3930–3940 CrossRef CAS.
- M. N. Paddon-Row, M. J. Shephard and K. D. Jordan, J. Phys. Chem., 1993, 97, 1743–1745 CrossRef CAS.
- R. W. A. Havenith, C. A. van Walree, A. W. Marsman, J. H. van Lenthe and L. W. Jenneskens, Phys. Chem. Chem. Phys., 2007, 9, 1312–1317 RSC.
- The similarity of a cross-conjugated C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bridge and a bridge consisting of a single sp3 hybridized atom has recently been described: R. Emanuelsson, A. Wallner, E. A. M. Ng, J. R. Smith, D. Nauroozi, S. Ott and H. Ottoson, Angew. Chem., Int. Ed., 2013, 52, 983–987 CrossRef CAS.
C bridge and a bridge consisting of a single sp3 hybridized atom has recently been described: R. Emanuelsson, A. Wallner, E. A. M. Ng, J. R. Smith, D. Nauroozi, S. Ott and H. Ottoson, Angew. Chem., Int. Ed., 2013, 52, 983–987 CrossRef CAS. - D. F. Eaton, Pure Appl. Chem., 1988, 60, 1107–1114 CrossRef CAS.
- X. Y. Lauteslager, I. H. M. van Stokkum, H. J. van Ramesdonk, D. Bebelaar, J. Fraanje, K. Goubitz, H. Schenk, A. M. Brouwer and J. W. Verhoeven, Eur. J. Org. Chem., 2001, 3105–3118 CrossRef CAS.
- M. J. Frisch, et al.Gaussian, 09, Revision. 01, Gaussian Inc., Wallingford, CT, 2010 Search PubMed.
| This journal is © the Owner Societies 2013 |