Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Glassy dynamics of sorbitol solutions at terahertz frequencies
Juraj
Sibik
a,
Evgenyi Y.
Shalaev
b and
J.
Axel Zeitler
*a
aDepartment of Chemical Engineering and Biotechnology, University of Cambridge, New Museums Site, Pembroke Street, Cambridge, CB2 3RA, UK. E-mail: jaz22@cam.ac.uk; Tel: +44 (0)1223 334783
bAllergan Inc., 2525 Dupont Dr., Irvine, CA 92612, USA
First published on 31st May 2013
Abstract
The absorption spectra of D-sorbitol and a range of its concentrated aqueous solutions were studied by terahertz spectroscopy over the temperature interval of 80 K < T < 310 K. It is shown that the slow-down of molecules at around the glass transition temperature, Tg, dramatically influences the thermal dependence of the absorption at terahertz frequencies. Furthermore, two different absorption regimes are revealed below Tg: at temperatures well below Tg, the absorption resembles the coupling of terahertz radiation to the vibrational density of states (VDOS); above these temperatures, between 160 K and Tg, in the sample of pure sorbitol and the sample of a solution of 70 wt% sorbitol in water, another type of absorption is observed at terahertz frequencies. Several possibilities of the physical origin of this absorption are discussed and based on the experimental data this process is tentatively assigned to the Johari–Goldstein β-relaxation processes shifting to lower frequencies at temperatures below Tg leaving behind a spectrum largely dominated by losses into the VDOS.
1 Introduction
Supercooled liquids and glasses and their fascinating physical properties have been the subject of extensive studies for many decades. For example, the preservation of an amorphous structure is a necessary (although not sufficient) requirement for stabilisation of many proteins and other biologically relevant systems.1,2 Dynamic properties of such systems, in particular the relaxation behaviour below the calorimetric glass transition temperature, are key to understanding and predicting their chemical and physical stability. Furthermore, while there are well-established and convenient experimental methods to study relaxation in such systems from around 200 K and above (e.g. isothermal calorimetry and differential scanning calorimetry3), covering the Tg of a large range of materials, it has proven rather difficult to acquire high quality experimental data at lower temperatures using such conventional methods.One of the most commonly used techniques to study molecular dynamics of amorphous systems is dielectric spectroscopy. By implementing different instrument configurations this type of spectroscopy can be used to study the dielectric properties of a material over a broad range of frequency (or time) ranging from μHz to GHz (corresponding to relaxation timescales of days to ps). In these studies the dielectric losses of amorphous systems typically exhibit two main relaxation processes: a primary, α, and a secondary, β, relaxation.4
Using interferometric techniques it was possible to obtain dielectric data of glycerol and sorbitol up to 0.4 THz, revealing a minimum of dielectric losses between the structural relaxation and far-infrared resonances5,6 as predicted by Wong and Angell.7 Despite these recent experimental advances in dielectric spectroscopy, only a limited amount of experimental data of glass-forming liquids in the THz frequency range has been reported to date.8 An infrared spectroscopy study of amorphous solids by Strom covered the frequency range of 3–3000 GHz.9 The experiments showed that absorption in this part of the spectrum can be described by a general power-law, which can be explained in terms of disorder-induced coupling of far-infrared radiation to a density of low frequency Debye modes, also known as the vibrational density of states (VDOS). Optical heterodyne detected optical Kerr effect (OHD-OKE) experiments performed by Fayer's group spanned a broad range of timescales (100 fs to 10 ms) of the orientational dynamics of liquids. The results revealed that, similar to what is observed for liquid crystals, the OHD-OKE signal in supercooled liquids follows a temperature-independent intermediate power law starting at picosecond timescales. Based on this finding the authors hypothesised that, as for liquid crystals, the picosecond orientational dynamics of supercooled liquids is a result of a pseudonematic domain structure.10 In addition to the OHD-OKE experiments scattering techniques such as inelastic light scattering or Raman scattering can also access the terahertz frequency range and provide structural correlation functions. The data obtained by these techniques have played a crucial role in the development of MCT.11
With the advent of terahertz time-domain spectroscopy (THz-TDS) it has become possible to directly access this part of the spectrum experimentally. In comparison to conventional dielectric spectroscopy THz-TDS has some additional advantages such as its nature as a non-contact method as well as the fact that it is straightforward to measure spectral data over a broad temperature range. THz-TDS has been widely employed in studies of crystalline solids and liquids.12 While crystalline solids commonly exhibit universal fingerprints in terahertz spectra due to low energy inter- and intra-molecular vibrations, in liquids one can observe fast relaxational dynamics at (sub-)picosecond timescales.
Nevertheless, apart from a limited number of studies that have reported the optical constants of glasses at room temperature so far only very few studies of amorphous systems using terahertz spectroscopy have been reported in the literature. In the example of carbamazepine Zeitler et al. demonstrated the possibility of using in situ THz-TDS to study both relaxation and crystallisation processes of small organic molecules in the amorphous state.13 It was also demonstrated that the absorption of electromagnetic radiation in glasses follows a universal frequency dependance in the terahertz range14 due to two phenomena: (i) coupling to VDOS and (ii) fluctuating atomic charges in the sample. Using this concept Parrott et al. quantitatively studied the charge distribution and its relationship with short-range and long-range order in sodosilicate glasses.15 Wietzke et al. used THz spectroscopy to study the phenomenon of glass transition in polymers.16 Very recently Zalkovskij et al. studied chalcogenide glasses over a broad frequency range of 0.2–18 THz.17 The broad spectral window achieved in their study allowed them to observe both the well established universal power-law dependance of the absorption coefficient at low THz frequencies14 as well as its breakdown at higher THz frequencies followed by vibrational features.
In the present work we show the results of THz-TDS on D-sorbitol and its aqueous solutions containing 70 and 50 wt% sorbitol over a broad temperature range. D-Sorbitol is a glass-former with a glass transition temperature, Tg = 268 K, that has been well characterised in the past by various experimental techniques6,18–26 and the phase behaviour of sorbitol–water mixtures is known in some detail. In particular, the pure sorbitol melt and the 70 wt% sorbitol–water mixture are known to remain in the glassy state upon cooling, whereas cooling more dilute sorbitol–water mixtures typically results in two-phase systems of hexagonal ice and a freeze-concentrated solution. The dramatic slowdown of structural relaxation during the glass transition significantly decreases the thermal dependence of terahertz absorption.
2 Experimental details
Samples were prepared from D-sorbitol (C6H8(OH)6, 99% purity, Sigma Aldrich) without further purification. We prepared four different samples: (i) 100 wt% water; (ii) a solution of 50 wt% sorbitol and 50 wt% water; (iii) a solution of 70 wt% sorbitol and 30 wt% water; (iv) and an amorphous sample of 100 wt% sorbitol. The solutions were prepared by dissolving sorbitol in deionised water at room temperature. The pure amorphous sorbitol sample was prepared immediately prior to the measurements by melting the crystalline powder of sorbitol at approximately 400 K followed by cooling to room temperature. The aqueous mixtures were prepared a couple of days in advance of the experiment.The terahertz absorption spectra and refractive indices were obtained using THz-TDS as described previously.27 Spectra were acquired in the frequency range of 0.2–2.2 THz and over a temperature range of 80–310 K. The samples were loaded between two polyethylene (PE) windows separated by a PE spacer of 190 ± 3 μm thickness. The PE spacer had a circular aperture of 9 mm in diameter. The windows and sample were screwed to a copper cold finger and attached to a modified continuous flow cryostat (ST-100 FTIR, Janis, Wilmington, MA, USA). The cryostat was operated under vacuum using liquid nitrogen and the temperature was controlled using a temperature controller (Lake Shore Model 331, Westerville, OH, USA). Samples were cooled to 80 K in approximately 30 min and the system was left to equilibrate for 20 min before the measurements commenced. For all subsequent measurements the samples were heated in 10 K intervals and allowed to equilibrate for 15 min at each heating step. The estimated accuracy in temperature control is 1 K due to rather robust metal sample holder.
3 Theory
3.1 Dielectric spectroscopy of glass-forming liquids
As outlined in the Introduction, two main relaxation processes (α and β) are typically detected in the dielectric losses of an amorphous system.The α-relaxation is a structural relaxation process. In a supercooled liquid the relaxation time of the α-process changes from the range of 10−12 s to 102 s when undergoing glass transition. This change is also related with a change in viscosity of the supercooled liquid by more than 10 orders of magnitude.28 The α-relaxation can be explained by cooperatively rearranging regions (CRRs).29–31 The idea is that each unit (not necessarily a molecule) requires surrounding units for orientational motion. Upon cooling the number of units required for such orientational motion increases and causes an increase in the size of CRR. This process slows the rate of motion, thus increasing the relaxation time.
The β-relaxation is often referred to as the Johari–Goldstein (JG) β-relaxation or the slow β-relaxation to distinguish it from fast secondary relaxation that we will discuss later. In contrast to the α-relaxation, the JG β-relaxation, which is observed in both glassy solid state and supercooled liquid, takes place at higher frequencies. The α and JG β-relaxation remain separated at temperatures just above the glass transition temperature, Tg, however, they merge as the system is heated further.32 The JG β-relaxation is commonly observed either as a separate peak or as a high frequency wing of the α-relaxation. In the latter case it is however considered that the JG β-relaxation peak is submerged in the α process.32 Several different mechanisms have been proposed to explain the molecular origin of the JG β-relaxation, two of which are the homogeneous and heterogeneous mechanism. The homogeneous approach says that each molecule contributes to the JG β-relaxation equally by a local libration motion.19 In contrast, the heterogeneous approach is based on clusters of molecules, also called “islands of mobility”, where molecules within the cluster keep certain degrees of freedom while the cluster itself is frozen.33 The dynamics of molecules in the clusters is different from the dynamics of molecules in a bulk material, giving rise to the secondary relaxation. In his original paper Johari discussed that this relaxation process can be explained both in terms of partial reorientations of molecules as well as islands of mobility.33 There is however still an ongoing discussion regarding the exact molecular origin of the JG β-relaxation, which seems to be a universal feature of the amorphous state.34
Several theoretical models have been proposed to explain the dynamics of the amorphous state and a very nice review of the most commonly used theories can be found elsewhere.35 A relatively more recent theoretical framework describing the amorphous state is the mode-coupling theory (MCT).36,37 In MCT the glassy dynamics is accessed by formulating equations of motion for correlation functions of density fluctuations. These correlation functions cannot be solved directly and it is therefore necessary to use approximations to find a solution for them. MCT also predicts two relaxation processes: the α-relaxation, which refers to the same relaxation as observed by dielectric spectroscopy, and the fast β-relaxation. The fast β-relaxation is believed to originate from a rattling movement of molecules in a cage of their neighbouring molecules.37 It has been shown that the fast β-relaxation and the JG β-relaxation are not necessarily of the same origin38,39 and there is a need for more data to address this question. It is important to note that MCT works only above some critical temperature, Tc, which is higher than Tg. In this temperature regime the JG β-relaxation cannot be clearly distinguished from the α-process, which complicates the analysis. Moreover the fast relaxation process described by MCT is not clearly visible as a separate peak in the spectra, it is rather an additional contribution to dielectric losses next to the other processes discussed above.
The commonly used empirical model to fit the complex dielectric spectra obtained by dielectric spectroscopy can be written as a superposition of Havriliak–Negami functions22,40
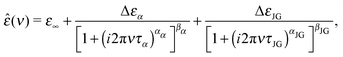 | (1) |
The Havriliak–Negami and Cole–Cole functions are in excellent agreement with the experimental spectra well up to GHz frequencies. However, at 109–1012 Hz frequencies one can also observe a contribution from the fast β-relaxation predicted by MCT and microscopic excitations,36,38 yet these effects are not considered in eqn (1). Alternatively it is possible to use a model predicted by MCT in this frequency range that describes the dielectric and susceptibility spectra more accurately.
3.2 Mode-coupling theory
The MCT describes glassy dynamics as a two step relaxation process expressed by two power laws: the Curie–von Schweidler ν−b law for the high-frequency part of the α-relaxation42 and the critical νa law for fast β-relaxation, which is proposed for higher frequencies compared to the α-relaxation, thus yielding37,41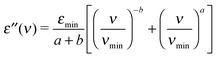 | (2) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/char_e107.gif) = ε′ + iε′′. The critical exponent a and the Curie–von Schweidler exponent b are limited to 0 < a, b < 1.37,41 The fast β-relaxation is explained as a rattling movement of molecules. MCT predicts37,41 a shallow minimum in dielectric losses εmin between α- and fast β-relaxation at frequency νmin. However, the validity of MCT is well established only above what is referred to as the critical temperature, Tc.38,41 The critical temperature is higher than the calorimetric glass transition temperature, Tg, and many studies report a relationship of Tc ≈ 1.2Tg.38
= ε′ + iε′′. The critical exponent a and the Curie–von Schweidler exponent b are limited to 0 < a, b < 1.37,41 The fast β-relaxation is explained as a rattling movement of molecules. MCT predicts37,41 a shallow minimum in dielectric losses εmin between α- and fast β-relaxation at frequency νmin. However, the validity of MCT is well established only above what is referred to as the critical temperature, Tc.38,41 The critical temperature is higher than the calorimetric glass transition temperature, Tg, and many studies report a relationship of Tc ≈ 1.2Tg.38
3.3 Terahertz and infrared spectroscopy of glasses
At THz frequencies one can expect to observe only the high-frequency wing of the relaxation processes that are observed in conventional dielectric spectroscopy. The major contributions to dielectric losses are expected to originate from the MCT fast β-relaxation as well as from the microscopic excitations that are present at high THz frequencies and in the infrared spectra. If we exclude the contribution from α-relaxation in the THz range we can simplify eqn (2) to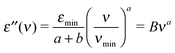 | (3) |
| σ′(ν) = n(ν)α(ν) = Cνq | (4) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) = σ′ + iσ′′, which can also be expressed as the real part of the refractive index n multiplied by the absorption coefficient α. C and q are fitting parameters. Strom reports that in many glasses q ≈ 2 and he suggests that the infrared disorder-induced absorption can be explained through coupling of the radiation to vibrational modes.9 Further explanation based on correlated and uncorrelated charge fluctuations was provided by Taraskin et al.14 Given that σ′ = 2πνε′′ one can interpret q ≈ a + 1 and combine both results into one model.
= σ′ + iσ′′, which can also be expressed as the real part of the refractive index n multiplied by the absorption coefficient α. C and q are fitting parameters. Strom reports that in many glasses q ≈ 2 and he suggests that the infrared disorder-induced absorption can be explained through coupling of the radiation to vibrational modes.9 Further explanation based on correlated and uncorrelated charge fluctuations was provided by Taraskin et al.14 Given that σ′ = 2πνε′′ one can interpret q ≈ a + 1 and combine both results into one model.
There is a good practical reason for using nα as a parameter to describe the results in this paper. In the amorphous state one does not observe any sharp resonances that are characteristic to crystalline materials. The refractive index does not change very much as a function of both frequency and temperature and thus the quantity nα reflects mostly the changes in the absorption coefficient, yet based on eqn (4) it represents a physically more meaningful parameter compared to just using the absorption coefficient. Alternatively, it would be possible to use eqn (1) or eqn (2) as well to describe the spectra observed at THz frequencies, however, these empirical expressions are specifically optimised to fit the broadband spectra that extend over several decades of frequency most of which are barely accessible by THz-TDS.
4 Results and analysis
4.1 Terahertz spectra
Terahertz spectroscopy is a time-domain technique allowing direct access to the absorption coefficient and refractive index, or the complex dielectric function, with no need to use Kramers–Kronig relationship. Fig. 1 shows the absorption coefficient of water, sorbitol and their mixtures. The absorption of liquid water is rather strong and it increases with frequency (Fig. 1a). In comparison, crystalline ice does not exhibit absorption below 1 THz. Above 1.3 THz we can observe an increase in the absorption coefficient, corresponding to the previously reported phonon mode of ice (peak at 3 THz43,44). In this frequency range the spectra of ice show no dependence on temperature below 270 K. The jump in absorption that can be observed in the sample of pure water between temperatures of 270–280 K matches with the melting point of water. At temperatures above its melting point the absorption of liquid water increases continuously with frequency. The spectrum of water is well characterised at THz frequencies and the high absorption in liquid water is attributed to the dielectric relaxation of the strong hydrogen-bonded network.45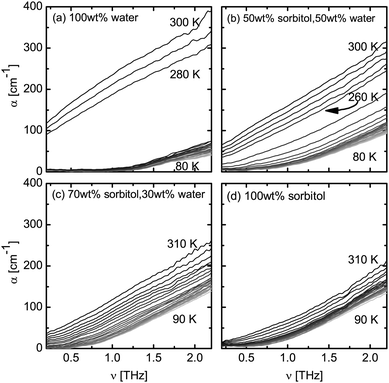 | ||
| Fig. 1 Absorption spectra at temperatures between 80–310 K. The temperature increment between spectra is 10 K for all samples. (a) 100 wt% water, (b) 50 wt% sorbitol–water, (c) 70 wt% sorbitol–water, and (d) 100 wt% sorbitol. | ||
For water–sorbitol mixtures and pure sorbitol an increase in absorption with frequency is observed with temperature over the entire range in the majority of conditions (Fig. 1b–d). As expected, no spectral features are present. Compared to the abrupt increase in absorption that is observed in the case of water, the change in absorption in the completely amorphous samples of pure sorbitol as well as the 70 wt% sorbitol–water mixture is continuous, especially at temperatures above 200 K. However a step change between 260–270 K, albeit less pronounced than in the case of pure water, is observed in the sample of the 50 wt% sorbitol–water mixture (Fig. 1b).
4.2 Temperature dependance of absorption at THz frequencies
A clearer picture of how the absorption changes with temperature emerges in Fig. 2. The plots show the temperature dependence of the absorption coefficient at the frequencies of 0.5, 1.0 and 1.5 THz. In this representation a very clear and sharp melting point can be observed in the water sample (Fig. 2a). The plot also highlights the fact that crystalline ice exhibits minimal (and temperature-independent) losses and that continuously increasing losses are observed in liquid water with temperature. For ice the losses observed at 1.5 THz are higher than zero due to the onset of the phonon mode at this frequency as previously discussed.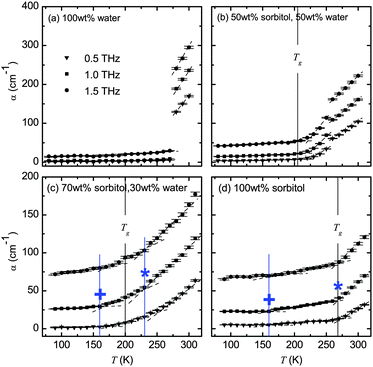 | ||
| Fig. 2 Temperature dependence of absorption over the range of 80–310 K. Dashed lines are plotted to guide the eye and highlight the change in the gradient of absorption with temperature. Vertical lines indicate the calorimetric glass transition temperature Tg as well as the transition from region (i) to (ii), marked by a plus symbol, and the transition from region (ii) to (iii), marked by an asterisk. Note the change in y-scale between the upper and lower plots. The error bars represent standard errors reflecting both the uncertainty in sample thickness and the noise estimate based on the averaging of the time-domain waveforms. | ||
In the case of the completely amorphous samples, i.e. 70 wt% sorbitol–water mixture (Fig. 2c) and pure sorbitol (Fig. 2d), the results can be divided into three distinct temperature ranges: (i) the range where the absorption remains almost constant irrespective of temperature. For both the 70 wt% sorbitol–water mixture and pure amorphous sorbitol this is observed at temperatures up to around 160–175 K. For example, in the former sample the onset is 175 K at 0.5 THz and 1.5 THz, and 160 K at 1 THz. (ii) Above 160–175 K absorption starts to increase with temperature in an approximately linear manner; and (iii) the range where the absorption increases more rapidly. For the 70 wt% sorbitol–water mixture the absorption starts to increase at 225–235 K, which is approximately 30 K above the calorimetric Tg. For pure sorbitol, the absorption starts to increase at around 270 K, which is close to the calorimetric Tg.
The temperatures corresponding to the transition between these regions are added to the phase diagram (Fig. 3). To compare the temperature dependence of the absorption of 70 wt% vs. 100 wt% sorbitol, the α vs. T data are fitted by linear regression, with each region (i) to (iii) treated separately. The gradients of the linear fits are summarised in Table 1. Table 1 shows that the absorption of 70 wt% sorbitol shows stronger temperature dependence than that of 100 wt% sorbitol in all three regions, and the temperature dependence is stronger at higher frequencies (i.e., 1.5 THz > 1 THz > 0.5 THz).
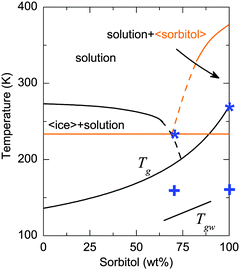 | ||
Fig. 3 Solid–liquid state phase diagram of the sorbitol–water system. The Tg line is constructed by fitting the calorimetric Tg (onset, determined by DSC18,47) to the Gordon–Taylor equation.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) † The plus symbols and the asterisks represent the transition from region (i) to (ii), and from region (ii) to region (iii), respectively, as defined in the text. Note that crystalline sorbitol does not form under the conditions of the experiment of the present study; elements of the phase diagram that include crystalline sorbitol are shown in orange. † The plus symbols and the asterisks represent the transition from region (i) to (ii), and from region (ii) to region (iii), respectively, as defined in the text. Note that crystalline sorbitol does not form under the conditions of the experiment of the present study; elements of the phase diagram that include crystalline sorbitol are shown in orange. | ||
| Sample | (i) | (ii) | (iii) |
|---|---|---|---|
| ν = 0.5 THz | |||
| 70 wt% sorbitol | 0.007 ± 0.009 | 0.132 ± 0.011 | 0.649 ± 0.035 |
| 100 wt% sorbitol | 0.002 ± 0.005 | 0.056 ± 0.004 | 0.468 ± 0.019 |
| ν = 1.0 THz | |||
| 70 wt% sorbitol | 0.032 ± 0.005 | 0.282 ± 0.021 | 0.803 ± 0.045 |
| 100 wt% sorbitol | 0.001 ± 0.006 | 0.125 ± 0.005 | 0.735 ± 0.022 |
| ν = 1.5 THz | |||
| 70 wt% sorbitol | 0.098 ± 0.010 | 0.337 ± 0.056 | 0.926 ± 0.060 |
| 100 wt% sorbitol | 0.054 ± 0.015 | 0.154 ± 0.005 | 0.832 ± 0.028 |
The results for the 50 wt% sorbitol–water mixture (Fig. 2b) show a distinctly different behaviour compared to both pure water and pure sorbitol. Here, both a continuous increase in absorption above 205 K as well as a distinct jump in absorption between 250–260 K are observed. As will be discussed later in more detail this sample is a two phase system where part of the water forms ice crystals. Therefore both the glass transition of the freeze-concentrated solution and the melting of ice crystals can be resolved in our measurements.
4.3 Modelling of terahertz spectra
In principle it should be possible to describe the terahertz data using eqn (4) as this equation combines both the microscopic excitations as well as the MCT fast β-relaxation. However, a more realistic model has to take into account that above Tg one can also expect a contribution from both the α- and the β-relaxation process. Furthermore, the terahertz spectra are obtained only above a cut-off frequency of ν0 > 0. Therefore we modify eqn (4) to| n(ν)α(ν) = A + C(ν − ν0)q. | (5) |
Here, the parameters A and ν0 represent the starting point of our fitting function. The constant A accounts for the fact that the spectra do not start at zero absorption, especially at higher temperatures. Thus it represents the contributions from vibrational and relaxation processes below ν0 that cannot be measured using our setup. For all spectra fitting was performed by using data up to 2.2 THz.
We have not modelled the spectra of the 50 wt% sorbitol–water mixture as the formation of ice crystals complicates the analysis which makes this sample unsuitable in this context. For the 70 wt% sorbitol–water mixture and pure sorbitol sample the selected spectra and their fits are presented in Fig. 4. From the plot it can be seen that eqn (5) fits the data very well over the entire measured temperature range although there are some minor deviations at temperatures below Tg.
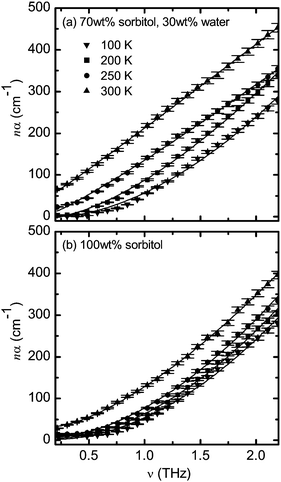 | ||
| Fig. 4 Frequency dependance of nα for (a) the mixture of 70 wt% sorbitol and 30 wt% water and (b) 100 wt% sorbitol at temperatures T = 100, 200, 250, and 300 K. Solid lines represent fits using eqn (5) with ν0 = 0.2 THz. The error bars represent standard errors reflecting both the uncertainty in sample thickness and the noise estimate based on the averaging of the time-domain waveforms. | ||
In Fig. 5 we show the fitting parameters that were obtained from modelling the spectra of the 70 wt% sorbitol–water mixture and the 100 wt% sorbitol sample by eqn (5). Vertical lines mark the calorimetric glass transition temperature Tg. In the case of 100 wt% sorbitol (Fig. 5, right column) all parameters exhibit major changes around Tg. The parameters A and C are almost constant below 160 K, slowly increasing between 160–270 K and then rapidly increasing above 270 K. The exponent q can be similarly split into a constant region, a slowly decreasing region and a quick drop above Tg.
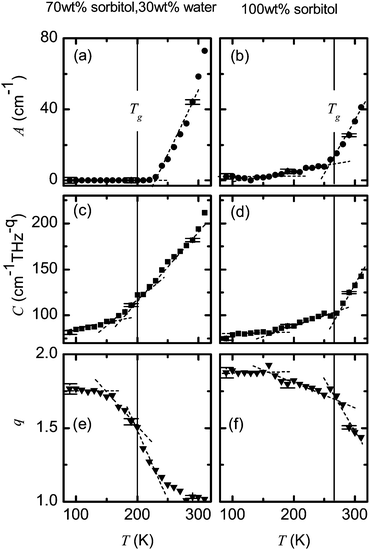 | ||
| Fig. 5 Temperature dependence of fitting parameters A, C and q from eqn (5) for the 70 wt% sorbitol and 30 wt% water mixture (left panel) and 100 wt% sorbitol (right panel). The frequency ν0 was set to 0.2 THz for all fits. Vertical lines indicate the calorimetric glass transition temperature Tg. Dashed lines are drawn to guide the eye. The error bars represent standard errors from non-linear regression. | ||
In the case of the 70 wt% sorbitol–water mixture (Fig. 5, left column) the thermal dependance of parameters is of a similar shape although the absolute values are rather different. Below T = 160 K the parameter A is practically zero; C increases relatively slowly and q is close to 1.8. In the temperature range of 160 K < T < Tg the parameters C and q change more rapidly with temperature compared to the case of pure sorbitol. The parameter A stays constant up to 230 K. For T > 230 K all parameters change smoothly. The exponent q decreases with temperature up to 270 K. At higher temperatures its value stays very close to 1.
5 Discussion
5.1 Glass transition and water crystallisation in aqueous sorbitol solutions
Terahertz radiation interacts strongly with the intermolecular hydrogen-bond network.49 In the general case the dielectric function of a polar liquid contains contributions from dielectric relaxation processes at the lower frequencies and from inter- and intra-molecular vibrational modes at higher frequencies.49 A multi-component Debye model is commonly used to describe the absorption theoretically.Over the past few years water has been studied extensively by terahertz spectroscopy.45 Upon heating the relaxation dynamics in water becomes faster, which leads to stronger absorption.45 This is well in line with the increase of absorption of water upon heating above its melting point as observed in Fig. 2a. The overall thermal dependance of terahertz absorption of water can be split into two regimes: liquid water with high terahertz absorption and crystalline ice with negligible terahertz absorption. As observed in Fig. 2a the transition from ice to liquid is seen as a sharp step that occurs at the melting point.
The primary dielectric relaxation peak in the supercooled state above Tg commonly does not change its amplitude or width significantly but simply shifts to lower frequencies, or longer timescales, upon cooling. Therefore the same explanation as for water can be used to explain the decrease of absorption in sorbitol and its aqueous solutions above Tg at terahertz frequencies: as the sample is cooled the timescales of dielectric relaxation slow down and thus relaxation is observed at lower frequencies. Therefore it is only the high-frequency tail of the primary dielectric relaxation that contributes to the terahertz spectra.
Around Tg the primary dielectric relaxation becomes extremely slow and vanishes completely from terahertz frequencies to lower frequencies. This may also be well explained from the molecular network point of view: it is reasonable to expect that below Tg the lifetime of the hydrogen bonds is significantly longer than in the supercooled liquid above Tg and the interaction between the hydrogen-bond network and terahertz radiation is weakened.
As mentioned earlier, water exhibits strong absorption at terahertz frequencies. It is therefore not surprising that higher values of absorption are observed in the sample of the 70 wt% sorbitol–water mixture compared to pure sorbitol. On the other hand, ice crystals can form upon cooling when the water concentration exceeds a certain limit. Based on the phase diagram in Fig. 3 this is expected to happen for water concentrations in excess of 35% (or sorbitol concentration below 65%), which has been confirmed by previous studies.47 While the sample of the 70 wt% sorbitol–water mixture was confirmed not to contain any ice crystals,50 ice crystals will be present in the case of the 50 wt% mixture.
This ice crystal formation in the 50 wt% water–sorbitol solution can be observed in the DSC data at 260 K (Fig. 6) and was further confirmed by X-ray analysis.51 As a consequence, the sample at the lowest temperatures covered in this study resembles a two-phase system of ice crystals and freeze-concentrated solution. The composition of the maximally freeze-concentrated solution is estimated based on the intersection of two lines in the phase diagram in Fig. 3: the extrapolation of the water liquidus and the glass transition curve. Based on this estimate the freeze-concentrated solution contains approximately 74 wt% sorbitol, and has a Tg = 205 K, which is confirmed experimentally by DSC (Fig. 6) and matches with the continuous increase in absorption observed above 205 K in the terahertz data (Fig. 2b). The distinct jump in the absorption level at 260 K is indicative of the melting of ice crystals in the solution. Above this temperature the additional amount of water that was previously frozen leads to much stronger absorption. Overall the terahertz spectroscopy results are consistent with the DSC data showing the glass transition of the freeze-concentrated solution and ice melting. While the melting effect is pronounced in the terahertz spectra as a sharp step, the glass transition leads to a continuous change.
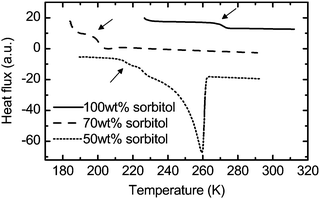 | ||
| Fig. 6 Differential scanning calorimetry results for 100 wt% sorbitol47 (solid line), 70 wt% sorbitol–water47 (dashed line) and 50 wt% sorbitol–water52 (dotted line). The arrows highlight the glass transition. The melting of ice in 50 wt% sorbitol–water leads to a sharp peak at 260 K. No such peak is observed in the case of 70 wt% sorbitol–water, providing further evidence that no ice crystals form in this solution. | ||
5.2 Sub-Tg absorption
Due to the formation of ice crystals in 50% water–sorbitol we limit our discussion of the glassy dynamics to the samples of pure sorbitol and 70% water–sorbitol only. Fig. 2 clearly reveals that the absorption of both amorphous samples can be split into three areas of (i) almost no dependence on temperature below 160 K, (ii) medium dependence on temperature between 160 K and Tg and (iii) high dependence on temperature above Tg. This suggests that while a significant amount of molecular mobility vanishes at Tg, some is preserved even below and ceases only at around 160 K in both cases.It is interesting to note a similarity in the behaviour of the 70 wt% sorbitol–water mixture and pure sorbitol samples at 0.5 and 1 THz, where the absorption starts to increase at around 160–175 K for both, which suggests that the origin of the increase in α might be related to the clusters of sorbitol molecules that remain unaffected by water. One can also note that the absorption of the 70 wt% sorbitol–water mixture is higher than that of pure sorbitol. It is most likely that this is because of the presence of unfrozen water in the 70 wt% sorbitol–water mixture. In the region of 80–160 K the absorption is independent of temperature at 0.5 and 1 THz. Based on the results from dielectric spectroscopy,6 we can conclude that in this temperature range the relaxation processes are too slow to be observed at THz frequencies. The absorption can be understood in terms of coupling of THz radiation to the VDOS of brittle glass. Such coupling is not expected to depend on temperature for frequencies above 10 cm−1 (0.3 THz).9,53
At 1.5 THz, the temperature behaviour of 70 wt% and 100 wt% sorbitol in the 100–170 K temperature range was somewhat different. While the absorption for 100 wt% sorbitol did not change with temperature in this range there was a relatively minor but noticeable increase for the 70 wt% sorbitol sample. We hypothesise that this increase in absorption may be connected with the changes in water coordination numbers as observed in a recent neutron scattering study.50 In particular the Ow–Hw coordination numbers were similar at both 100 and 170 K, and decreased upon heating to 213 and 298 K, which is indicative of changes in hydrogen bonding between water molecules above 170 K. The change in absorption that is observed above 170 K is consistent with the decrease in the O–H coordination numbers. Therefore, it is reasonable to suggest that the change in hydrogen bonding between water molecules may contribute to the increase in absorption that is measured in the 70 wt% sorbitol sample. This casual observation might indicate that lower frequencies (0.5 and 1 THz) are related to Ow–Hw relaxation whereas higher frequency (1.5 THz) reflects Ow–Ow and Hw–Hw coordination numbers. If this observation has any physical significance remains to be seen.
While the lack of temperature induced changes in the absorption below 160 K is expected, an increase in absorption above 160 K is a novel observation that warrants further consideration. It is not immediately obvious why the absorption increases with temperature in the range above 160–175 K (i.e., well below the calorimetric Tg). Several possible reasons are discussed here.
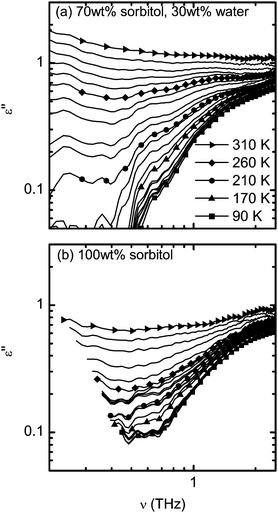
The presence of the microscopical peak at low temperatures is clearly revealed by a logarithmic plot of the dielectric losses in Fig. 7. It can be seen that in both studied samples the dielectric losses below 160 K remain constant and resemble the microscopical peak that is also observed by dielectric spectroscopy and light scattering techniques.5,6,55
A recent study of the Boson peak in sorbitol revealed that its central frequency is around 4.5 meV and that it is decreasing in intensity, but not shifting in frequency, upon cooling.25 Optical photons with 4.5 meV oscillate at approximately 1 THz, a frequency well covered in this study. This further revealed that in the case of sorbitol the Boson peak can be explained in terms of acoustic vibrations.25 If this is true it is reasonable to expect no contribution of the Boson peak to terahertz radiation. The fact that absorption of sorbitol is close to zero up to 0.7 THz at the lowest temperatures (lowest lines in Fig. 1d) is in agreement with these studies and further supports the evidence of a non-optical origin of the Boson peak in the case of sorbitol glass.
In principle intra-molecular mobility could also contribute to terahertz spectra, especially at frequencies above 0.5 THz. A NMR study of polyols revealed that spatially restricted rotational movements of molecules or their subgroups are involved in the JG relaxation.20 The intra-molecular excitations are however expected to be present as sharp peaks with a full width half maximum (FWHM) of 10s of GHz which are clearly not observed in our results. Furthermore, intra-molecular vibrational modes are expected to be present at all temperatures. They typically increase in intensity and the FWHM decreases due to the change in thermal populations of the vibrational states towards ground state transitions at lower temperature. It therefore seems unlikely that these processes can be held responsible for the change in the absorption of sorbitol at around 160 K.
Kubo et al.23 as well as Nakanishi and Nozaki63 have previously observed an intriguingly similar temperature behaviour of dielectric losses in the kHz–GHz frequency range in a sample of sorbitol. The authors suggested that below 140 K the contributions from the JG β-relaxation decrease in intensity in the MHz–GHz regime due to a shift to lower frequencies and in this regime the nearly constant losses become more dominant.63 The conclusion was based on relatively noisy data due to the severe experimental limitations when working at these temperatures and frequencies using conventional dielectric spectroscopy. Nonetheless qualitatively their observations seem to agree with the results presented in this work. In our study we observe a change in absorption at around 160 K, which is reasonably close to 140 K considering the difficulty in determining the onset of the change in both studies. This provides evidence that the JG β-relaxation influences the losses in the terahertz range below Tg and makes it the most favourable explanation of the changes in absorption we observe at around 160 K. A somewhat simplistic, yet reasonable, explanation is thus as follows: at Tg the high-frequency tail due to the α relaxation vanishes from the terahertz spectra due to its shift to lower frequencies, while the tail from the JG β-relaxation remains present down to 160 K. At even lower temperatures it too stops contributing to the terahertz losses, possibly due to a shift of this feature to lower frequencies as well in line with the observations of Kubo et al.23 as well as Nakanishni and Nozaki.63 Although the physical origin of the JG β-relaxation is still disputed, NMR studies have proven that, in the case of polyalcohols, spatially restricted rotational motions of molecules or molecular subgroups play a significant role.20
Lunkenheimer et al. have successfully managed to shift the experimental limitations of dielectric spectroscopy to higher frequencies and reported dielectric losses of sorbitol up to the low THz range.6 The study clearly revealed a fast relaxation process in addition to α- and JG β-relaxation, as predicted by mode coupling theory.36 Nevertheless, due to experimental limitations below the glass transition temperature the study did not fully cover the GHz–THz frequency range where this fast relaxation is found.
One of the previous studies that covered the desired frequency range also well below Tg is a light scattering study of toluene.55 Here Wiedersich et al. showed that the fast relaxation process is also present below Tg and its strength ceases quickly upon cooling. In particular, the authors were able to show that at 50 GHz the susceptibility originating from fast relaxation decreases linearly upon cooling between Tg > T > 7 K.55 The susceptibility spectra show truly similar temperature behaviour as the dielectric losses as shown in Fig. 7. However, the thermal gradient of susceptibility below Tg at 50 GHz remained constant. This is surprising given the fact that dielectric studies also confirmed the presence of the JG β-relaxation in toluene.55 It raises a further question about the origin of the change in the gradient at 160 K observed in our study for pure sorbitol (as seen in Fig. 2). One important aspect that needs to be investigated further is the nature of the inter-molecular forces on the terahertz dynamics, such as whether there is hydrogen-bonding or not, like in the case of toluene. In this context it is important to consider whether light scattering experiments and terahertz spectroscopy are sensitive to exactly the same molecular dynamics or whether the origin of the light-matter interaction is slightly different between the two techniques.
5.3 Power law
As seen in Fig. 4 the real part of conductivity (absorption coefficient multiplied by refractive index) at terahertz frequencies can be well described by a generalised power law. The usage of the power law is not new and we have adopted it primarily from infrared studies9 where it proved to be an excellent fit for the low-THz frequency absorption part of the microscopical peak originating from the VDOS, with an exponent being close to 2 in many reported cases. Despite that, in the liquid phase one may expect the terahertz absorption to be dominated by the Debye relaxation and vibrational relaxation tail. In terms of the dielectric losses the tail will be roughly constant with frequency in the terahertz regime, which is equivalent to the linear frequency dependence that we observe in conductivity, for instance in the case of the 70 wt% sorbitol–water mixture at 310 K (Fig. 7a).This discussion highlights the practicality of using a power law in cases like here where the frequency window that is covered by the measurement technique is too narrow to use full physical models. The distinct changes in the exponent of the power law can then still be assigned to different regimes of absorption at terahertz frequencies. It must however be stated that any discussion can be done only by careful comparison with dielectric, scattering and other broad frequency range studies as the power law itself is too general in order to draw conclusions on the physical origin of the changes on the power law alone. Based on the results from other techniques it is possible to make a physical interpretation of the fitting parameters A, K and q in more detail as follows.
As mentioned earlier, parameter A describes the contribution to the losses present at frequency ν0 = 0.2 THz. In principle, it is possible to regard parameter A as a simplification of the Curie–von Schweidler law using a temperature-dependant constant. Parameter A largely, though not exclusively, covers the high-frequency end of the primary dielectric relaxation. Another contribution may be expected from the JG β-relaxation as well as the fast-β relaxation. Due to the limited frequency range it is not possible to clearly separate their individual contributions. Nevertheless the major change in A at Tg indicates that the major contribution comes from the α-relaxation. A similar result has been observed in amorphous sorbitol by dielectric spectroscopy.6
The parameter C can be understood in analogy to a coupling coefficient of THz radiation to disordered matter. It shows a similar shape of temperature dependance to that of the absorption coefficient α. The values of C can again be split into three representative areas of T < 160 K, 160 K < T < Tg and T > Tg, similar to the response of the absorption coefficient (see Fig. 2, 5c and d).
The exponent q highlights the different absorption regimes in the samples. In Fig. 5e and f it can be seen that in both cases q stays constant and relatively close to 2 below 160 K. Similar q values were reported for other organic glasses below the Tg. For example, q = 1.6 was reported for semi-crystalline PS,9 whereas values of q = 1.9–2.0 are observed for many inorganic glasses.53 This would indicate that in this regime the absorption originates from VDOS as observed by infrared spectroscopy where it is expected that the exponent q does not change with temperature.9
A very interesting result is the change of q at temperatures above 160 K but below the liquid phase. As the temperature approaches Tg the exponent q changes smoothly, showing the highest gradient around Tg. To the best of our knowledge this is the first time a change of q with temperature has been observed for glasses. While in sorbitol the value of q changes only slightly for T < Tg, in the case of the 70 wt% sorbitol–water mixture the decrease is steeper. This means that, firstly, the onset of the decrease in q is irrespective of the presence of water. Thus it is either a property of sorbitol or a genuine property of the glass. Based on our results alone it is not possible to resolve this question. Secondly, water enhances the change in the exponent. As can be seen from the changes in the absorption coefficient (Fig. 2), the samples with water exhibit steeper changes than the pure sorbitol sample in the region around Tg. Thus water enhances the transition into the liquid phase and the parameter q yields steeper changes around Tg in solutions. Thirdly, and most importantly, the change in the THz spectra starts far below Tg. There is no obvious link to the VDOS as such absorption should be independent of temperature at the frequencies covered in this experiment. The change in q is however consistent and exhibits a continuous evolution with temperature. This result therefore opens the question whether the fast β-relaxation plays any role at these temperatures at all.
Upon heating the 70 wt% sorbitol–water mixture further we observe that q reaches a value close to 1 at around 280 K and then remains constant at higher temperatures. At these temperatures the sample is in the liquid phase and the losses originate from the high-frequency tail of the dielectric relaxation as well as vibrational processes. We expect that if the pure sorbitol sample would be heated further towards its melting point, causing a reduction in the viscosity of the supercooled liquid, the value of q would also drop close to 1.
The limitation of eqn (5) lies in the sensitivity to the choice of ν0. Due to the exponent q the model is non-linear in frequency ν0. We would like to emphasise that ν0 is purely used to constrain the fit. As the low-THz frequency low-temperature data can be constant with frequency these spectra cannot be fitted precisely using eqn (5). Strictly speaking the cut-off frequency ν0 could be set to the frequency where the flat spectrum ends and absorption starts to increase. However this point can be hard to determine from the THz spectra or it may actually not lie within the frequency window that is covered by the experiment. We have therefore decided to set ν0 to a constant value of 0.2 THz in all fits in this study. We would like to emphasise that this frequency was chosen based on the low-temperature data where it actually matches with the point where losses start to increase from a constant line. As can be seen in Fig. 4 the model with ν0 = 0.2 THz fits the data very well over the entire temperature range covered in this experiment.
6 Conclusions
In the present work we have studied the dynamics of supercooled liquids and glasses by terahertz spectroscopy. As a model system we have used sorbitol and its aqueous solutions. We have discussed the physical origin of the absorption at terahertz frequencies both above and below Tg. A simple power law model was used to further separate contributions of different physical processes to terahertz absorption. At around the glass transition temperature the primary relaxation vanishes from the terahertz spectra by shifting to lower frequencies, flattening the thermal dependence of the absorption. The results reveal a further change in the absorption of sorbitol and the 70 wt% sorbitol–water mixture at around 160 K, well below Tg in both cases. We argue that such a change might be a signature of the Johari–Goldstein β-relaxation shifting out of the spectral window covered by THz-TDS and leaving behind an absorption spectrum dominated by the VDOS. However, we need to stress that this interpretation is tentative and alternative explanations are possible. In particular the role of the MCT fast β-relaxation remains unclear. Further studies in different glass formers are needed to fully characterise the sub-Tg changes of the low-energy part of the VDOS.The results show that although terahertz spectroscopy only covers one decade in frequency it does not suffer from temperature-dependant variations in experimental accuracy and can easily be used to study dynamics in liquid, supercooled liquid and amorphous solid state. Therefore it is an excellent complementary technique for studies of glassy dynamics at terahertz frequencies over a wide temperature range where experimental data below Tg are still limited and challenging to obtain by other techniques.
Acknowledgements
The authors would like to thank N.K.H. Slater, University of Cambridge, for helpful discussions, T. Narayanan, European Synchrotron Radiation Facility, for X-ray scattering measurements on the 70 wt% sorbitol–water mixture and Bakul Bhatnagar and Raj Suryanarayanan, University of Minnesota, for sharing the DSC data of the 50 wt% sorbitol–water mixture. J.S. would like to acknowledge the EPSRC for funding through a studentship.References
- K. C. Fox, Science, 1995, 267, 1922–1923 CrossRef CAS.
- F. Franks, Biophys. Chem., 2003, 105, 251–261 CrossRef CAS.
- J. Liu, D. R. Rigsbee, C. Stotz and M. J. Pikal, J. Pharm. Sci., 2002, 91, 1853–1862 CrossRef CAS.
- G. P. Johari and C. P. Smyth, J. Chem. Phys., 1972, 56, 4411 CrossRef CAS.
- P. Lunkenheimer, A. Pimenov, M. Dressel, Y. Goncharov, R. Böhmer and A. Loidl, Phys. Rev. Lett., 1996, 77, 318–321 CrossRef CAS.
- S. Kastner, M. Köhler, Y. Goncharov, P. Lunkenheimer and A. Loidl, J. Non-Cryst. Solids, 2011, 357, 510–514 CrossRef CAS.
- J. Wong and C. A. Angell, in Glass: Structure by Spectroscopy, ed. M. Dekker, New York, 1974, p. 750 Search PubMed.
- P. Lunkenheimer and A. Loidl, Phys. Rev. Lett., 2003, 91, 207601 CrossRef CAS.
- U. Strom, J. R. Hendrickson, R. I. Wagner and P. C. Taylor, Solid State Commun., 1974, 15, 1871–1875 CrossRef CAS.
- H. Cang, J. Li, V. N. Novikov and M. D. Fayer, J. Chem. Phys., 2003, 118, 9303–9311 CrossRef CAS.
- T. Franosch, M. Fuchs, W. Gotze, M. R. Mayr and A. P. Singh, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 7153–7176 CrossRef CAS.
- P. Jepsen, D. Cooke and M. Koch, Laser Photonics Rev., 2011, 5, 124–166 CrossRef CAS.
- J. A. Zeitler, P. F. Taday, M. Pepper and T. Rades, J. Pharm. Sci., 2007, 96, 2703–2709 CrossRef CAS.
- S. Taraskin, S. Simdyankin, S. Elliott, J. Neilson and T. Lo, Phys. Rev. Lett., 2006, 97, 055504 CrossRef CAS.
- E. P. J. Parrott, J. A. Zeitler, G. Simon, B. Hehlen, L. F. Gladden, S. N. Taraskin and S. Elliott, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 140203 CrossRef.
- S. Wietzke, C. Jansen, T. Jung, M. Reuter, B. Baudrit, M. Bastian, S. Chatterjee and M. Koch, Opt. Express, 2009, 17, 19006–19014 CrossRef CAS.
- M. Zalkovskij, C. Z. Bisgaard, A. Novitsky, R. Malureanu, D. Savastru, A. Popescu, P. U. Jepsen and A. V. Lavrinenko, Appl. Phys. Lett., 2012, 100, 031901 CrossRef.
- R. A. Talja and Y. H. Roos, Thermochim. Acta, 2001, 380, 109–121 CrossRef CAS.
- N. T. Correia, C. Alvare, J. J. M. Ramos and M. Descamps, J. Phys. Chem. B, 2001, 105, 5663–5669 CrossRef CAS.
- A. Döβ, M. Paluch, H. Sillescu and G. Hinze, Phys. Rev. Lett., 2002, 88, 095701 CrossRef.
- V. N. Novikov and a. P. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 031507 CrossRef CAS.
- G. Power, G. P. Johari and J. K. Vij, J. Chem. Phys., 2003, 119, 435 CrossRef CAS.
- E. Kubo, A. Minoguchi, H. Sotokawa and R. Nozaki, J. Non-Cryst. Solids, 2006, 352, 4724–4728 CrossRef CAS.
- J. J. M. Ramos, H. P. Diogo and S. S. Pinto, J. Chem. Phys., 2007, 126, 144506 CrossRef.
- B. Ruta, G. Baldi, V. M. Giordano, L. Orsingher, S. Rols, F. Scarponi and G. Monaco, J. Chem. Phys., 2010, 133, 041101 CrossRef CAS.
- G. Power, J. K. Vij and G. P. Johari, J. Chem. Phys., 2006, 124, 074509 CrossRef CAS.
- E. P. J. Parrott, J. A. Zeitler, T. Friscic, M. Pepper, W. Jones, G. M. Day and L. F. Gladden, Cryst. Growth Des., 2009, 9, 1452–1460 CAS.
- M. H. Cohen and G. S. Grest, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1077–1098 CrossRef CAS.
- G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139 CrossRef CAS.
- S. Matsouka and X. Quan, Macromolecules, 1991, 24, 2770 CrossRef.
- K. L. Ngai, R. W. Rendell and D. J. Plazek, J. Chem. Phys., 1991, 94, 3018 CrossRef CAS.
- A. Minoguchi, K. Kitai and R. Nozaki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 031501 CrossRef.
- G. P. Johari and M. Goldstein, J. Chem. Phys., 1970, 53, 2372 CrossRef CAS.
- J. K. Vij and G. Power, J. Non-Cryst. Solids, 2011, 357, 783–792 CrossRef CAS.
- A. Cavagna, Phys. Rep., 2009, 476, 51–124 CrossRef CAS.
- W. Götze, J. Phys.: Condens. Matter, 1999, 11, A1 CrossRef.
- W. Götze, Complex Dynamics of Glass-Forming Liquids, Oxford University Press, New York, 2009 Search PubMed.
- L. C. Pardo, P. Lunkenheimer and A. Loidl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 030502 CrossRef CAS.
- P. Lunkenheimer, L. C. Pardo, M. Köhler and A. Loidl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031506 CrossRef CAS.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- W. Götze and L. Sjogren, Rep. Prog. Phys., 1992, 55, 241–376 CrossRef.
- K. Ngai and C. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 2475–2486 CrossRef CAS.
- K. D. Möller and W. G. Rothschild, Far-infrared spectroscopy, Wiley-Interscience, New York, 1974 Search PubMed.
- V. I. Gaiduk and D. S. F. Crothers, J. Mol. Liq., 2006, 128, 145–160 CrossRef CAS.
- C. Rønne, L. Thrane, P. Astrad, A. Wallqvist, K. V. Mikkelsen and S. R. Keiding, J. Chem. Phys., 1997, 107, 5319 CrossRef.
- M. Siniti, Thermochim. Acta, 1999, 325, 171–180 CrossRef CAS.
- S. Ewing, A. Hussain, G. Collins, J. C. Roberts and E. Y. Shalaev, Water Stress in Biological, Chemical, Pharmaceutical and Food Systems, ed. G. Gutiérrez-López and D. Reid, Springer, 2012, in press Search PubMed.
- M. Gordon and J. S. Taylor, J. Appl. Chem., 1952, 2, 493–500 CrossRef CAS.
- U. Møller, D. G. Cooke, K. Tanaka and P. U. Jepsen, J. Opt. Soc. Am. B, 2009, 26, A113 CrossRef.
- S. G. Chou, A. K. Soper, S. Khodadadi, J. E. Curtis, S. Krueger, M. T. Cicerone, A. N. Fitch and E. Y. Shalaev, J. Phys. Chem. B, 2012, 116, 4439–4447 CrossRef CAS.
- T. Narayanan and E. Y. Shalaev, unpublished results.
- B. Bhatnagar, S. Martin, D. Teagarden, E. Shalaev and R. Suryanarayanan, Proceedings of AAPS Annual Meeting and Exposition, New Orleans, LO, USA, 2010 Search PubMed.
- U. Strom and P. C. Taylor, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 5512–5522 CrossRef CAS.
- G. Hinze, D. D. Brace, S. D. Gottke and M. D. Fayer, J. Chem. Phys., 2000, 113, 3723–3733 CrossRef CAS.
- J. Wiedersich, N. V. Surovtsev and E. Rössler, Chem. Phys., 2000, 113, 1143–1153 CAS.
- W. Schirmacher, G. Ruocco and T. Scopigno, Phys. Rev. Lett., 2007, 98, 025501 CrossRef CAS.
- B. Rufflé, D. Parshin, E. Courtens and R. Vacher, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef.
- J. P. Poley, Appl. Sci. Res., Sect. B, 1955, 4, 337–387 CrossRef.
- N. E. Hill, W. E. Vaughan, A. H. Price and M. Davies, in Dielectric Properties and Molecular Behaviour, Von Nostrand Reinhold Co., London, 1969, p. 306 Search PubMed.
- C. J. Reid and M. W. Evans, J. Chem. Phys., 1982, 76, 2576–2584 CrossRef CAS.
- C. J. Reid and J. K. Vij, J. Chem. Phys., 1983, 79, 4624–4628 CrossRef CAS.
- G. P. Johari, J. Non-Cryst. Solids, 2002, 307–310, 114–127 CrossRef CAS.
- M. Nakanishi and R. Nozaki, J. Non-Cryst. Solids, 2010, 356, 733–737 CrossRef CAS.
Footnote |
| † Tg = (w1Tg1 + Kw2Tg2)/(w1 + Kw2) with K as a fitting parameter, where Tg1 = 268 K and Tg2 = 136 K are the glass transition temperatures and w1 and w2 are the weight fractions of sorbitol and water, respectively, and K is a constant. K was determined to be 3.1 ± 0.2. The water liquidus and sorbitol liquidus lines and the eutectic temperature are based on data from ref. 46. The dashed lines represent graphical extrapolation beyond this data. The Tgw line represents the onset of rotational mobility of water molecules.47 The phase diagram is not comprehensive, as it does not reflect the existence of several polymorphic forms of sorbitol and sorbitol hydrate. |
| This journal is © the Owner Societies 2013 |