 Open Access Article
Open Access ArticleIdentifying and characterising the different structural length scales in liquids and glasses: an experimental approach
Philip S.
Salmon
* and
Anita
Zeidler
*
Department of Physics, University of Bath, Bath BA2 7AY, UK. E-mail: p.s.salmon@bath.ac.uk; a.zeidler@bath.ac.uk
First published on 12th August 2013
Abstract
The structure of several network-forming liquids and glasses is considered, where a focus is placed on the detailed information that is made available by using the method of neutron diffraction with isotope substitution (NDIS). In the case of binary network glass-forming materials with the MX2 stoichiometry (e.g. GeO2, GeSe2, ZnCl2), two different length scales at distances greater than the nearest-neighbour distance manifest themselves by peaks in the measured diffraction patterns. The network properties are influenced by a competition between the ordering on these “intermediate” and “extended” length scales, which can be manipulated by changing the chemical identity of the atomic constituents or by varying state parameters such as the temperature and pressure. The extended-range ordering, which describes the decay of the pair-correlation functions at large-r, can be represented by making a pole analysis of the Ornstein–Zernike equations, an approach that can also be used to describe the large-r behaviour of the pair-correlation functions for liquid and amorphous metals where packing constraints are important. The first applications are then described of the NDIS method to measure the detailed structure of aerodynamically-levitated laser-heated droplets of “fragile” glass-forming liquid oxides (CaAl2O4 and CaSiO3) at high-temperatures (∼2000 K) and the structure of a “strong” network-forming glass (GeO2) under pressures ranging from ambient to ∼8 GPa. The high-temperature experiments show structural changes on multiple length scales when the oxides are vitrified. The high-pressure experiment offers insight into the density-driven mechanisms of network collapse in GeO2 glass, and parallels are drawn with the high-pressure behaviour of silica glass. Finally, the hydrogen-bonded network of water is considered, where the first application of the method of oxygen NDIS is used to measure the structures of light versus heavy water and a difference of ≃0.5% is found between the O–D and O–H intra-molecular bond lengths. The experimental data are best matched by using path integral molecular dynamics simulations with a flexible anharmonic water model, and the results support a competing quantum effects model for water in which its structural and dynamical properties are governed by an offset between intra-molecular and inter-molecular quantum contributions.
 Philip S. Salmon | Phil Salmon was born in Romford in the UK, and is presently a Professor of Physics at the University of Bath. He graduated with a BSc from the University of Bristol in 1981, and completed his PhD in 1985 at the same institution under the supervision of Professor Sir John Enderby FRS. After Bristol, he worked at the University of Exeter as a Research Fellow before joining the University of East Anglia as a “New Blood” Lecturer in 1985. He moved to Bath as a Senior Lecturer in 1998. His research is focussed on the atomic-scale structure and dynamics of materials, with a particular interest in liquids and glasses. He has benefited from visiting scientist positions at the Institut Laue-Langevin, the University of Oxford, Kyushu University, and the Université de Montpellier II. |
 Anita Zeidler | Anita Zeidler was born in Lauchhammer in the former Deutsche Demokratische Republik, and is presently a Research Officer at the University of Bath. She graduated with a Chemiediplom from the Philipps-Universität Marburg in 2004, following a year as an exchange student at the University of Cambridge. She completed her PhD in physics at the University of Bath in 2009. She is extensively involved in developing the methods required to measure and interpret the structure of a wide range of materials, including liquids and glasses under extreme high-pressure and high-temperature conditions, and water in its various phases. |
1 Introduction
Disordered networks are at the heart of many materials of significant scientific and technological importance, ranging from the glasses used for optical fibres and lasers,1–6 to water in chemical processes and biological systems.7,8 It is important to know the structure of these materials in order to understand the physical properties of different network types. It is also necessary to know the structure in a first step to manipulating or designing networks in order to make new materials with the required physical and chemical properties as achieved, for example, by the incorporation of additional chemical species or by processing under high-temperature and/or high-pressure conditions.9 The required information is, however, notoriously difficult to access owing to the inherent nature of structural disorder. For instance, an absence of the long-ranged translational periodicity associated with a crystalline phase allows for enhanced flexibility in the bond angles when linking basic structural motifs such as the SiO4 tetrahedra in liquid and glassy silicates.Unravelling the complexity of structurally disordered materials is therefore a challenging problem, and requires a multi-disciplinary approach involving experiment, theory and simulation. From the experimental standpoint, there are several diffraction and spectroscopic techniques for deducing the identity of the local structural motifs,2,6 but it is much more difficult to discern the nature of the ordering at distances greater than the nearest-neighbour distance. For example, in a neutron or X-ray diffraction experiment on a binary system, the intensity measured as a function of the magnitude of the scattering vector k is represented by three overlapping partial structure factors Sαβ(k), which describe the pair-correlations between atoms of chemical species α and β. This overlap extends to the corresponding real-space partial pair-distribution functions gαβ(r), and makes it desirable to devise experiments in order to separate the individual Sαβ(k) functions. Fortunately this is possible because each Sαβ(k) function receives a probe-dependent weighting factor that can be varied, for example, by changing the incident X-ray energy near the absorption edge of an element in an anomalous X-ray scattering (AXS) experiment10 or by substituting the isotope of a given chemical species in a neutron diffraction with isotope substitution (NDIS) experiment.11 Information at the partial structure factor level can therefore be obtained by using AXS,12,13 by mixing the results obtained from X-ray and neutron diffraction experiments,14–16 or by using the NDIS method.17
In the following, the focus is on the contribution that NDIS can play in providing information at the partial structure factor level for liquids and glasses. In particular, by matching carefully designed experiments to suitable instrumentation, it is possible to measure accurate diffraction patterns and hence target specific features in the structure of a system. Recent work includes the development of suitable protocols to measure (i) the structure of single droplets of liquid oxides at high-temperatures (∼2000 K) by using the containerless aerodynamic-levitation with laser-heating method,18,19 (ii) the structure of glass at high-pressures in the range from ambient to ∼8 GPa by employing a Paris-Edinburgh press,20 and (iii) the structure of light versus heavy water by using the method of oxygen NDIS where there is a small contrast between the measured diffraction patterns for different isotopically enriched samples.21–23
The aim of all of these NDIS experiments is to provide benchmark results to test whether the various theoretical schemes, which need to be employed in the development of accurate predictive models for different classes of materials, contain the right ingredients. For example, how best can transferrable potentials be constructed for use in classical molecular dynamics simulations,24–28 and what is the best density functional to use for a given system in first-principles molecular dynamics simulations?29 Unlike other atomistic modelling methods such as reverse Monte Carlo (RMC)30,31 and Empirical Potential Structure Refinement (EPSR),32,33 which use diffraction data to make a three-dimensional structural model, molecular dynamics simulations can explore the dynamical properties of a system and, provided they are suitably constructed, they can be used to predict e.g. the properties of materials under state conditions that extend beyond those for which diffraction data are available. The question as how best to prepare accurate molecular dynamics models of glasses given the use of fast simulated quench-rates is an ongoing source of debate.29,34–36
The manuscript is organized as follows. The essential theory for understanding the diffraction results is given in Section 2 and several different classes of system are then discussed. In Section 3, binary network glass-forming materials such as GeO2, GeSe2 and ZnCl2 are considered where the full set of partial structure factors are now available from NDIS experiments. Two different length scales are found at distances larger than the nearest-neighbour distance and manifest themselves by peaks in the measured diffraction patterns. The so-called first sharp diffraction peak at a scattering vector kFSDP ≃ 1–1.5 Å−1 is associated with ordering on an intermediate range while the principal peak at kPP ≃ 2.0–2.7 Å−1 is associated with ordering on an extended range, which can persist to nanometer distances in real-space. The results show that a competition between the ordering on these length scales influences the relative “fragility”37 of these network glass-forming materials. In Section 4, the structure of liquid and amorphous metals is then considered where packing constraints are important and where the principal peak is an important feature in the measured diffraction patterns. The extended-range ordering, which describes the decay of the measured pair-correlation functions at large-r, can be represented for both network glass-forming and densely-packed metallic systems by making a pole analysis of the Ornstein–Zernike equations.38–40 In Section 5, the structure of fragile glass-forming liquid oxides is investigated by applying the NDIS method to aerodynamically-levitated laser-heated droplets of CaAl2O4 and CaSiO3.18,19 Large structural changes on multiple length scales are observed on vitrification. In Section 6, the first application of the NDIS method to measure the structure of glass in situ at high-pressures is described. In particular, the density-driven mechanisms of structural collapse are investigated in GeO2 glass at pressures up to ∼8 GPa. Similarities with the behaviour of SiO2 glass are discussed, where there is also a density-driven transformation from a tetrahedral to an octahedral glass albeit at much higher pressures. In Section 7, the role of competing quantum effects in water is then deliberated in relation to the results obtained from the first application of the oxygen NDIS method to both light and heavy water. Finally, conclusions are drawn in Section 8 and the future outlook is considered.
2 Diffraction methods
2.1 Outline theory
In a neutron diffraction experiment, the intensity measured as a function of the magnitude of the scattering vector k can be written in terms of the differential scattering cross-section17| dσ/dΩ = F(k) + P(k) | (1) |
 | (2) |
 | (3) |
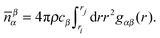 | (4) |
The real-space information corresponding to F(k) is provided by the total pair-distribution function G(r) which is obtained from the Fourier transform relation
 | (5) |
 | (6) |
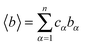 is the mean scattering length.
is the mean scattering length.
For a binary system comprising two chemical species denoted by M and X, it is also instructive to re-write the total structure factor of eqn (2) in terms of the Bhatia–Thornton44 number–number, concentration–concentration and number–concentration partial structure factors, denoted by SNN(k), SCC(k) and SNC(k) respectively, where
| F(k) = 〈b〉2SNN(k) + (bM − bX)2SCC(k) + 2〈b〉(bM − bX)SNC(k) − (cMbM2 + cXbX2). | (7) |
| SNN(k) = cM2SMM(k) +cX2SXX(k) + 2cMcXSMX(k) | (8) |
| SCC(k) = cMcX{1 + cMcX[SMM(k) + SXX(k) − 2SMX(k)]} | (9) |
| SNC(k) = cMcX{cM[SMM(k) − SMX(k)] − cX[SXX(k) − SMX(k)]}. | (10) |
From eqn (7) it follows that if bM = bX the incident neutrons in a diffraction experiment cannot distinguish between the different scattering nuclei and the measured total structure factor gives SNN(k) directly. The Fourier transform of SNN(k), the partial pair-distribution function gNN(r), therefore describes the sites of the scattering nuclei and, since it cannot distinguish between the chemical species that decorate those sites, it gives information on the topological ordering. If 〈b〉 = 0, however, the measured total structure factor gives SCC(k) directly and its Fourier transform, gCC(r), describes the chemical ordering of the M and X atomic species.§ The partial pair-distribution function gCC(r) will show a positive or negative peak at a given distance when there is a preference for like or unlike neighbours, respectively. The Fourier transform of SNC(k), namely the partial pair-distribution function gNC(r), describes the correlation between the sites described by gNN(r) and their occupancy by a given chemical species.
In the case of an X-ray diffraction experiment, eqn (2) remains valid provided the scattering lengths bα are replaced by the k-dependent atomic form factors with dispersion terms fα(k). In order to compensate for this k dependence, the total structure factor is often rewritten as
 | (11) |
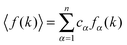 . From eqn (7), it follows that if fM(k) ≃ fX(k) (or bM ≃ bX) then S(k) ≃ SNN(k) i.e. if both chemical species have the same coherent scattering cross-sections then the incident X-rays (or neutrons) will observe the material to be a one component system. The notation SX(k) and SN(k) will be used in order to distinguish between the total structure factors measured by X-ray and neutron diffraction, respectively, and a similar notation will be used to distinguish between their corresponding total pair-distribution functions GX(r) and GN(r). From eqn (6), it follows that in the case of a neutron diffraction experiment
. From eqn (7), it follows that if fM(k) ≃ fX(k) (or bM ≃ bX) then S(k) ≃ SNN(k) i.e. if both chemical species have the same coherent scattering cross-sections then the incident X-rays (or neutrons) will observe the material to be a one component system. The notation SX(k) and SN(k) will be used in order to distinguish between the total structure factors measured by X-ray and neutron diffraction, respectively, and a similar notation will be used to distinguish between their corresponding total pair-distribution functions GX(r) and GN(r). From eqn (6), it follows that in the case of a neutron diffraction experiment| GN(r) − 1 = G(r)/〈b〉2. | (12) |
To unravel the complexity of pair-correlation functions associated with the measurement of F(k) for a liquid or glass, it is necessary to obtain information on the partial structure factors. This can be achieved by using the NDIS method11 where the neutron scattering length of a given chemical species is changed by preparing two or more samples that are identical in every respect, except for the isotopic enrichment of that chemical species. In favourable cases, it is possible to extract the full set of partial structure factors for a binary system directly from the experimental data.11,17 In other cases, the use of difference function methods leads to an elimination of selected partial structure factors, thus simplifying the complexity of pair-correlation functions associated with F(k).17
As an illustration, if the diffraction patterns for an MX2 system are measured for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (≥3) samples that are identical in every respect, except for the isotopic enrichment of one or more of the chemical species, then the equations for the total structure factors can be written in the form
(≥3) samples that are identical in every respect, except for the isotopic enrichment of one or more of the chemical species, then the equations for the total structure factors can be written in the form
| F = WS | (13) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) × 3 weighting factor matrix with elements defined by eqn (2) or (7). The full set of partial structure factors can then be found by using the method of singular value decomposition (SVD) where S = W†F and W† is the Moore–Penrose pseudo-inverse of W, which is equal to the inverse matrix W−1 when
× 3 weighting factor matrix with elements defined by eqn (2) or (7). The full set of partial structure factors can then be found by using the method of singular value decomposition (SVD) where S = W†F and W† is the Moore–Penrose pseudo-inverse of W, which is equal to the inverse matrix W−1 when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3.52,53
= 3.52,53
2.2 Instrumentation and data analysis
Several neutron diffractometers have been designed for work on liquid and amorphous materials, including D4c at the Institut Laue-Langevin,54 SANDALS, GEM and NIMROD at the ISIS pulsed neutron source,55–57 NOMAD at the Spallation Neutron Source,58 and NOVA at the Japan Proton Accelerator Research Complex.59 For NDIS experiments, the diffractometer D4c has a proven track record, combining the necessary attributes of a high detector count-rate over a wide k-range with a low-background signal, an excellent count-rate stability (±0.01% over three days), and an ability to re-measure to within 0.020(1)% the diffraction pattern for different mountings of the same sample.23,54 It was therefore the diffractometer of choice for the majority of NDIS experiments reported herein.The corrections that need to be applied to neutron diffraction data for e.g. container scattering, beam attenuation and multiple scattering are generally straight-forward for experiments made under ambient conditions, although inelasticity corrections are an important exception in cases where the masses of the neutron and scattering nuclei are comparable.17 It is usual, however, for the corrections to become more difficult for the complex sample environments and scattering geometries encountered in experiments made under extreme conditions of high-pressures or high-temperatures.51,60–62 In general, systematic errors that remain in the corrected diffraction patterns can be reduced by using difference function methods where two or more diffraction patterns are subtracted from one another, a technique that can also be used to cancel the worst effects that arise from the inelastic scattering of neutrons by light nuclei.23,63,64
For binary systems, our approach is to solve eqn (13) point-by-point, without an application of the constraints that were used in the first NDIS experiments.65 Uncertainties on the partial structure factors that result from uncertainties on the total structure factors and weighting factor matrix can be assessed by using the SVD method.53 The efficacy of the results can be assessed by checking, for example, that the partial structure factors satisfy the required sum-rule and inequality relations, and that they take physically meaningful k → 0 limiting values.11,44 It follows that it should also be possible to construct 3-dimensional models of non-overlapping atoms that are consistent with the measured partial structure factors by using atomistic modelling methods. The merits of this direct approach, in which confidence is assigned to the results obtained from carefully designed experiments, are briefly discussed in Section 3.2 by reference to the case study of liquid and glassy GeSe2.
3 Network glass-forming materials
3.1 Intermediate versus extended-range ordering
The NDIS method has been used to measure the full set of partial pair-correlation functions for several network glass-forming materials having the MX2 stoichiometry, namely liquid and glassy GeSe2,66–68 liquid and glassy ZnCl2,53,69,73 and glassy GeO2.70,71 The NDIS method has also been combined with X-ray diffraction to measure the Sαβ(k) functions for SiO2 glass.74 In the Angell classification scheme,37 GeO2 and SiO2 are regarded as “strong” glass forming liquids whereas ZnCl2 and GeSe2 have a character that is more intermediate between the “strong” and “fragile” extremes (Fig. 1).75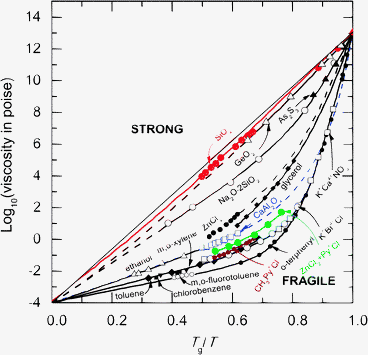 | ||
| Fig. 1 The logarithm of the liquid viscosity η for several glass-forming materials as plotted against Tg/T, where T is the absolute temperature and Tg is the glass transition temperature.37 The fragility index m ≡ d log10η/d(Tg/T)|T=Tg gives the gradient at T = Tg and therefore characterises how steeply the liquid viscosity increases when cooling to form a glass. | ||
The measured Faber–Ziman partial structure factors Sαβ(k) for liquid GeSe2 and for the glasses GeSe2, ZnCl2 and GeO2 are illustrated in Fig. 2. These reciprocal space functions show a so-called first sharp diffraction peak (FSDP) at kFSDP ≃ 1–1.5 Å−1 together with a principal peak at a larger scattering vector kPP ≃ 2.0–2.7 Å−1. The FSDP is associated with intermediate-range order of periodicity given by 2π/kFSDP with a correlation length given by 2π/ΔkFSDP where ΔkFSDP is the full-width at half-maximum.76–78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ¶ The largest contribution to the FSDP arises from M–M correlations, although the M–X and X–X correlations also contribute in the cases of GeO2 and SiO2,71,74 and it is therefore associated with the ordering of M-centred structural units. In comparison, the principal peak is associated with extended-range order having a periodicity of 2π/kPP with a correlation length given by 2π/ΔkPP where ΔkPP is the full-width at half-maximum. The extended-range order derives its name from the observation that it usually persists to distances well beyond the domain of the FSDP.69,80
¶ The largest contribution to the FSDP arises from M–M correlations, although the M–X and X–X correlations also contribute in the cases of GeO2 and SiO2,71,74 and it is therefore associated with the ordering of M-centred structural units. In comparison, the principal peak is associated with extended-range order having a periodicity of 2π/kPP with a correlation length given by 2π/ΔkPP where ΔkPP is the full-width at half-maximum. The extended-range order derives its name from the observation that it usually persists to distances well beyond the domain of the FSDP.69,80
 | ||
| Fig. 2 The measured Faber–Ziman partial structure factors Sαβ(k) for liquid GeSe2,66,67 and for the glasses GeSe2,67,68 ZnCl2 (ref. 53 and 69) and GeO2.70,71 In each panel, the upper (red) curve gives SMM(k), the middle (black) curve gives SXX(k), and the lower (blue) curve gives SMX(k). The statistical uncertainties are represented by the scatter in the data points. In the case of liquid GeSe2, the ratio of the liquid to melting-point temperatures, T/Tmp, is 1.041. The diffraction measurements for the glasses were all made at ≃298 K. Figure from Salmon.72 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
The measured partial pair-distribution functions gαβ(r) for liquid and glassy GeSe2, glassy ZnCl2 and glassy GeO2 are illustrated in Fig. 3. Several of the parameters describing the local structure of these materials and liquid ZnCl2 are listed in Table 1. In each case, the structure is built predominantly from tetrahedral MX4 motifs. Corner-sharing tetrahedra predominate in GeO2 glass, while edge-sharing tetrahedra also appear in ZnCl2 and GeSe2, their numbers being greater for the liquid by comparison with the glass. The appearance of these edge-sharing conformations is consistent with the more fragile characters of ZnCl2 and GeSe2 by comparison with GeO2.75 Homopolar Ge–Ge and Se–Se bonds are also an important feature in liquid and glassy GeSe2. In the case of the glass, the first three peaks in gGeGe(r) correspond with increasing r to the Ge–Ge distances in homopolar bonds, edge-sharing tetrahedra and corner-sharing tetrahedra, respectively.67,68
 | ||
| Fig. 3 The measured partial pair-distribution functions gαβ(r) for liquid GeSe2,66,67 and for the glasses GeSe2,67,68 ZnCl2 (ref. 53 and 69) and GeO2.70,71 In each panel, the dark (black) curve gives gMX(r), the light (red) curve gives gMM(r) and the broken (blue) curve gives gXX(r). In the case of the glasses, the effect in real space of truncating the diffraction pattern at a finite maximum value kmax before Fourier transformation was taken into account by using the procedure described by Salmon and Petri.67 The oscillations at r-values smaller than the distance of closest approach between two atoms have been suppressed for clarity of presentation. Figure from Salmon.72 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) βα for the gαβ(r) functions measured for several liquid and glassy network-forming materials with the MX2 stoichiometry. In the case of liquid and glassy GeSe2, peaks also occur in gGeGe(r) and gSeSe(r) at smaller r-values. The ratio of the X–X distance rXX to the M–X distance rMM is also given where, for regular tetrahedral MX4 units,
βα for the gαβ(r) functions measured for several liquid and glassy network-forming materials with the MX2 stoichiometry. In the case of liquid and glassy GeSe2, peaks also occur in gGeGe(r) and gSeSe(r) at smaller r-values. The ratio of the X–X distance rXX to the M–X distance rMM is also given where, for regular tetrahedral MX4 units,  . The M–X–M bond angle θMXM is calculated from rMX and the M–M distance rMM by using cos(θMXM) = 1 − rMM2/2rMX2. For an MX2 system, the X-atom number density ρX = 2ρ/3 such that, if these atoms are assumed to be hard spheres of radius rX, then their packing fraction ηX = (8/9)ρπrX3. If the X-atoms are also touching in regular MX4 tetrahedra then rXX = 2rX such that the packing fraction can be re-written as
. The M–X–M bond angle θMXM is calculated from rMX and the M–M distance rMM by using cos(θMXM) = 1 − rMM2/2rMX2. For an MX2 system, the X-atom number density ρX = 2ρ/3 such that, if these atoms are assumed to be hard spheres of radius rX, then their packing fraction ηX = (8/9)ρπrX3. If the X-atoms are also touching in regular MX4 tetrahedra then rXX = 2rX such that the packing fraction can be re-written as 
| System | g αβ (r) | r αβ (Å) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) β
α
β
α
|
r XX/rMX | M–X–M (°) | η X | Ref. |
|---|---|---|---|---|---|---|---|
| a For liquid GeSe2, the smallest-r peaks in gGeGe(r) and gSeSe(r) at 2.33(3) and 2.30(2) Å correspond to the Ge–Ge and Se–Se distances in homopolar bonds, respectively. b For glassy GeSe2, the smallest-r peaks in gGeGe(r) at 2.42(2) and 3.02(2) Å correspond to the Ge–Ge distances in homopolar bonds and edge-sharing tetrahedra, respectively, while the smallest-r peak in gSeSe(r) at 2.32(2) Å corresponds to the Se–Se distance in homopolar bonds. c The Ge–Se–Ge angle for edge-sharing tetrahedra as calculated by using the measured value of rGeGe = 3.02(2) Å for this structural conformation. d From a combination of neutron diffraction and RMC modelling. | |||||||
| l-GeSe2 | GeSe | 2.42(2) | 3.5(2) | 1.550(15) | 96(1) | 0.670(17) | 66, 67 |
| GeGea | 3.59(2) | 2.9(3) | |||||
| SeSea | 3.75(2) | 9.6(3) | |||||
| g-GeSe2 | GeSe | 2.36(2) | 3.7(1) | 1.648(16) | 80(1)c, 98(1) | 0.667(17) | 67, 68 |
| GeGeb | 3.57(2) | 3.2(3) | |||||
| SeSeb | 3.89(2) | 9.3(2) | |||||
| l-ZnCl2 | ZnCl | 2.27(2) | 4.2(2) | 1.621(19) | 121(2), 111(3)d | 0.596(16) | 53 |
| ZnZn | 3.96(3), 3.74(5)d | 3.8(2), 4.20(1)d | |||||
| ClCl | 3.68(3) | 10.0(2) | |||||
| g-ZnCl2 | ZnCl | 2.28(1) | 3.9(1) | 1.623(8) | 111(1) | 0.647(9) | 53, 69 |
| ZnZn | 3.75(1) | 4.0(1) | |||||
| ClCl | 3.70(1) | 12.1(2) | |||||
| g-GeO2 | GeO | 1.73(1) | 3.8(1) | 1.636(11) | 132(2) | 0.495(9) | 70, 71 |
| GeGe | 3.16(1) | 4.1(2) | |||||
| OO | 2.83(1) | 6.7(1) | |||||
The X-atom packing fraction ηX, as calculated by assuming spherical X atoms arranged in MX4 tetrahedra, is smaller for GeO2 by comparison with ZnCl2, in keeping with a larger inter-tetrahedral M–X–M bond angle, and in the case of ZnCl2 glass53,81 its magnitude is close to the value of ≃0.64 expected for a random close-packing of hard spheres.82 The high values of ηX for liquid and glassy GeSe2 could be attributed to the relative softness of Se atoms, although the presence of non-tetrahedral motifs such as homopolar bonds will lead to smaller calculated ηX values.72
For MX2 materials, the Bhatia–Thornton pair-correlation functions have proved to be an instructive way of decomposing the structure into its contributions from the topological and chemical ordering.45,72 The measured Bhatia–Thornton partial structure factors SIJ(k) for liquid and glassy GeSe2, glassy ZnCl2 and glassy GeO2 are illustrated in Fig. 4. The FSDP and principal peak appear, to a greater or lesser extent, as features in all of the measured SIJ(k) functions and, for a given material, the FSDP positions are comparable as are the principal peak positions. The principal peak is the dominant feature in SCC(k) and corresponds to chemical ordering (i.e. a preference for M–X nearest-neighbours) in real space. In comparison, SNN(k) is more structured with a ratio of FSDP to principal peak heights that correlates with the system's fragility. For example, the FSDP in SNN(k) is a comparatively large feature for the strong glass-forming material GeO2 but is a comparatively small feature for the more fragile glass-forming material ZnCl2. Hence, there is an interplay between the relative importance of the length scales associated with the intermediate versus extended ranges and, with increasing fragility, it is the extended-range ordering which dominates.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ||
||
 | ||
| Fig. 4 The measured Bhatia–Thornton partial structure factors SIJ(k) for liquid GeSe2,66,67 and for the glasses GeSe2,67,68 ZnCl2 (ref. 53 and 69) and GeO2.70,71 In each panel, the upper (black) curve gives SNN(k), the middle (red) curve gives SCC(k) and the lower (blue) broken curve gives SNC(k). The statistical uncertainties are represented by the scatter in the data points. Figure from Salmon.72 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
The character of the observed extended-range order can be investigated by considering a simple rigid-ion pair-potential model for the interactions between two particles labelled by i and j separated by a distance r as represented by the expression83
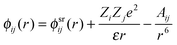 | (14) |
For the rigid-ion model, a simple power-law dependence for the ultimate decay of the pair correlation functions is expected i.e. rhNN(r) → r−5, rhNC(r) → r−7, rhCC(r) → r−9 where hNN(r) ≡ gNN(r) − 1, hNC(r) ≡ gNC(r), hCC(r) ≡ gCC(r).40,85 However, if the dispersion terms are absent in eqn (14), then a pole analysis of the k-space solutions to the Ornstein–Zernike equations following the method of Evans and co-workers38,39 leads, in the case when the system density is high, to the following expressions for the asymptotic decay of the pair-correlation functions40
rhNN(r) → 2|![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) NN|exp(−a0r)cos(a1r − θNN), NN|exp(−a0r)cos(a1r − θNN), | (15) |
rhCC(r) → 2cMcX|![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) CC|exp(−a0r)cos(a1r − θCC), CC|exp(−a0r)cos(a1r − θCC), | (16) |
rhNC(r) → 2|![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) NC|exp(−a0r)cos(a1r − θNC). NC|exp(−a0r)cos(a1r − θNC). | (17) |
The rhIJ(r) are therefore exponentially damped oscillatory functions with a common decay length given by a0−1 and a common wavelength for the oscillations given by 2π/a1.** The ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) IJ are complex numbers with amplitudes related by |
IJ are complex numbers with amplitudes related by |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) NN||
NN||![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) CC| = |
CC| = |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) NC|2 and phases related by θNN + θCC = 2θNC. Eqn (15)–(17) also hold for hard-sphere systems when both the Coulomb and dispersion terms are absent from eqn (14). Thus, although they are derived from a simple theory, eqn (15)–(17) provide a convenient starting point for investigating the extended-range order in liquid and glassy materials.
NC|2 and phases related by θNN + θCC = 2θNC. Eqn (15)–(17) also hold for hard-sphere systems when both the Coulomb and dispersion terms are absent from eqn (14). Thus, although they are derived from a simple theory, eqn (15)–(17) provide a convenient starting point for investigating the extended-range order in liquid and glassy materials.
To illustrate the ordering on an extended length scale in MX2 network glass-forming materials, it is instructive to consider the results for glassy ZnCl2 (ref. 69) since it is a system that is expected to fall within the framework of an ionic interaction model, provided that ion polarisation effects are taken into account.24 The measured real-space functions rhIJ(r) and ln|rhIJ(r)| are plotted in Fig. 5 and show ordering at large-r values which persists to distances far exceeding the correlation length 2π/ΔkFSDP ≃ 12.6 Å estimated from the width of the FSDP in SNN(k). The extended range oscillations in glassy ZnCl2 show exponential decay with a common inverse decay length a0 ≃ 0.19 Å−1 and a periodicity that is governed not by the position of the FSDP but by the position of the principal peak, giving oscillations of wavelength 2π/a1 ≃ 2π/kPP. Indeed, eqn (16) and (17) provide a robust account of the measured rhCC(r) and rhNC(r) functions from large-r to distances as short as ≃5 Å. The relationship between the amplitudes predicted by simple theory does not, however, appear to hold. Similar conclusions are drawn from an analysis of the measured rhIJ(r) functions for GeSe2 and GeO2 glass.72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) †† The presence of extended-range ordering in network glass-forming systems has been confirmed by molecular dynamics simulations using a polarisable ion model to describe the atomic interactions.89
†† The presence of extended-range ordering in network glass-forming systems has been confirmed by molecular dynamics simulations using a polarisable ion model to describe the atomic interactions.89
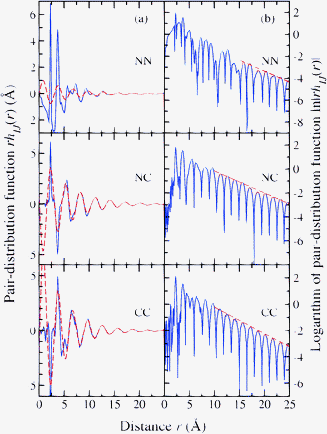 | ||
| Fig. 5 Decay of the Bhatia–Thornton partial pair-distribution functions for glassy ZnCl2 as shown by plotting in column (a) rhIJ(r) versus r (solid (blue) curves) and in column (b) ln|rhIJ(r)| versus r (solid (blue) curves).40 In column (a), the broken (red) curves show fits to the rhIJ(r) functions at large r-values using eqn (15)–(17). In column (b), the broken (red) curves show fits of the repeated maxima at large-r to a straight line (ln|rhIJ(r)| = −a0r + constant) from which the decay length a0−1 can also be found. | ||
For the investigated MX2 network glass-forming materials, the wavelength of the extended range oscillations is comparable to the size of a tetrahedral MX4 motif i.e. 2π/kPP ≃ 4rMX/3 where the latter is the base-to-apex distance in a regular tetrahedron and rMX is the nearest-neighbour M–X distance.72 Although homopolar bonds appear in materials like GeSe2, there is a preference for chemical ordering as manifested by the large principal peak in SCC(k). The tetrahedra therefore pack to give number-density fluctuations, as represented by oscillations at large-r in rhNN(r), that occur on a very similar length scale to the concentration fluctuations, as represented by oscillations at large-r in rhCC(r). The structural motifs also organise on an intermediate length scale via the formation of ring structures, thus providing a modulation of the pair-distribution functions on this length scale that manifests itself by the appearance of an FSDP in reciprocal space.
3.2 Specific issues regarding the structure of GeSe2
The validity of the NDIS results for liquid and glassy GeSe2 has been called into question by some authors.Petkov and Le Messurier90 measured a single X-ray total structure factor SX(k) and constructed an RMC model in which the glass structure is described in terms of a continuous network of corner- and edge-sharing GeSe4 tetrahedra with no homopolar bonds. As discussed in ref. 90, the differences with the NDIS results presented in Section 3.1 could originate, in part, from the use of different sample preparation methods. However, the atomic numbers of Ge and Se are similar such that their atomic form factors are close to one another. From eqn (7) and (11) it follows that, in a conventional X-ray diffraction experiment, the weighting factors for SNN(k), SCC(k) and SNC(k) in the expression for SX(k) are e.g. 1, 0.0036 and −0.12 at k = 0 such that SX(k) ≃ SNN(k). Hence, SX(k) will contain negligible information on the function SCC(k) which describes the chemical ordering i.e. the X-rays cannot distinguish between Ge and Se atoms (Section 2.1). In comparison, the observation by the NDIS method of homopolar bonds in GeSe2 glass is consistent with the findings from Raman, Mössbauer and X-ray emission spectroscopy experiments,67,91,92 and the concentration of homopolar bonds found from the NDIS experiments is in agreement with an estimate based on the law of mass action.67,68
Soper93 has discussed the relatively weak contribution of Ge–Ge correlations to the measured diffraction patterns for GeSe2 glass, using the EPSR method with simple reference pair-potentials‡‡ to model the measured total structure factors. As expected from an SVD analysis,53 the Ge–Ge correlations were found to be most sensitive to the details of the model, and doubt was cast on the reality of structural features such as Ge–Ge homopolar bonds. In comparison, the GeSe2 system has been the subject of extensive first-principles molecular dynamics simulations in which the electronic structure of the material is taken into explicit account, as befits an iono-covalent bonded system in which the electronegativity of the different chemical species is similar.29,95–110 In the work of Drabold and co-workers, features in the NDIS results such as homopolar Ge–Ge and Se–Se bonds and the appearance of an FSDP in SCC(k), were reproduced in the first-principles models.95,96,100 In the work of Massobrio and co-workers, it initially proved difficult to reproduce these features which led inter alia to the use of different functionals for the electron exchange and correlation.97–99,101,103,105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) §§ Nowadays, use of the Becke, Lee, Yang, and Parr (BLYP) functional, which enhances a localised distribution of the valence electrons, is leading to much improved agreement with the NDIS results.29,107–110 These developments have also been accompanied by improvements in the simulated diffusion coefficients of the melt.107,109 Thus, the partial structure factors obtained directly from the measured diffraction data,66–68 as opposed to modelling those data,93 appear to provide the most realistic picture for the structure of liquid and glassy GeSe2.¶¶ All of this is helping to provide a framework for e.g. interpreting 73Ge and 77Se solid state nuclear magnetic resonance spectra for Ge–Se glasses, investigations that also find evidence for broken chemical order in GeSe2.111–114
§§ Nowadays, use of the Becke, Lee, Yang, and Parr (BLYP) functional, which enhances a localised distribution of the valence electrons, is leading to much improved agreement with the NDIS results.29,107–110 These developments have also been accompanied by improvements in the simulated diffusion coefficients of the melt.107,109 Thus, the partial structure factors obtained directly from the measured diffraction data,66–68 as opposed to modelling those data,93 appear to provide the most realistic picture for the structure of liquid and glassy GeSe2.¶¶ All of this is helping to provide a framework for e.g. interpreting 73Ge and 77Se solid state nuclear magnetic resonance spectra for Ge–Se glasses, investigations that also find evidence for broken chemical order in GeSe2.111–114
3.3 Concentration fluctuations on an intermediate length scale
The observation of an FSDP in SCC(k) for several MX2 network glass-forming materials (Fig. 4)45,66 has been a source of controversy because it was not predicted from the investigation of these materials by using classical molecular dynamics simulations or integral-equation calculations.115–118 Also, if these materials can be treated as purely ionic, i.e. as a two-component system of point-like cations and anions, then the charge–charge partial structure factor is given by SZZ(k) = SCC(k)/cMcX such that an FSDP in SCC(k) implies a non-uniformity in the charge distribution on an intermediate length scale.45Extensive first-principles molecular dynamics investigations, in which SCC(k) is calculated from the atomic positions and SZZ(k) is calculated by taking into account the valence-electron density, show that these fluctuations in charge do not occur.29,102 Instead, the absence of charge fluctuations over intermediate range distances provides a constraint on the network properties.102 For example, in chemically ordered systems like SiO2, where the valence state of a given chemical species is invariant, the net charge on a network-forming structural motif is zero so there is no need for concentration fluctuations to occur on an intermediate range. In contrast, for systems like GeSe2 and SiSe2, there is a moderate number of chemical defects which leads to a local variation in the charge on network-forming structural motifs. These motifs must then link to satisfy charge neutrality on the length scale of a few structural motifs, leading to the appearance of concentration fluctuations on this intermediate length scale. In the case of liquid GeSe2, a significant contribution to the FSDP in SCC(k) is likely to arise from short chains of edge-sharing tetrahedra in which the Ge atoms at opposite chain ends are separated from each other by intermediate range distances and where the overall unit has the valence state of a mis-coordinated Ge atom.29,104 Eventually, as the degree of chemical disorder increases and the network structure breaks-up, the FSDP disappears from the total structure factor and vanishes from SCC(k). Thus, the concentration–concentration partial structure factor has proved to be a sensitive probe of the chemical bonding in MX2 systems.
4 Liquid and amorphous metals: extended-range ordering
The measured structure factors of metallic liquids and glasses are usually dominated by a first sharp peak in the range k ≃ 2.2–2.9 Å−1,123,124 which will be referred to as the principal peak in keeping with the description of binary network glass-forming materials given in Section 3. This is illustrated by the measured neutron total structure factors SN(k) shown in Fig. 6 for the liquid alloys Au0.81Si0.19, Au0.72Ge0.28 and Ag0.74Ge0.26 which have compositions at or near to the eutectic.|||| The fragility of glass-forming liquid metals can take a wide range of values,127,128 there being a trend towards less fragile behaviour with increasing number of chemical components.128 The materials generally have densely-packed structures,129 and so-called bulk metallic alloys made by using low cooling-rates have applications as engineering materials.128,130–133 The nature of the structural motifs, their organisation at distances larger than the nearest-neighbour distance, and the relationship between structure and issues such as glass-forming ability, remain the subjects of debate.129,134–136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) *** As in Section 3, we associate extended-range ordering with the principal peak, although the structure in disordered metals at distances beyond the nearest-neighbour is usually called medium-range ordering in the literature on these materials.124,129,134,136
*** As in Section 3, we associate extended-range ordering with the principal peak, although the structure in disordered metals at distances beyond the nearest-neighbour is usually called medium-range ordering in the literature on these materials.124,129,134,136
 | ||
| Fig. 6 The total neutron structure factors SN(k) as measured for liquid Au0.81Si0.19 at 665 K, Au0.72Ge0.28 at 666 K, and Ag0.74Ge0.26 at 976 K (solid dark (black) curves). The line thickness is greater than the size of the vertical error bars at most k values.119 The arrows point to small prepeaks in SN(k) at ≃1.3 and 1.6 Å−1 for the Au–Ge and Ag–Ge alloys, respectively, and the insets show an expanded view of the low-k region for SN(k). The total structure factors SX(k) as measured for the liquid alloys at similar temperatures by using high-energy X-ray diffraction are also shown (solid light (red) curves).120–122 | ||
The asymptotic decay of the measured total pair-distribution functions for a variety of metallic glasses has been interpreted by Ma et al.124 in terms of a self-similar packing of atomic clusters which leads to a fractal network of dimension Df. Specifically, if it is assumed that the clusters show a degree of self-similarity or scale invariance, and that the principal peak position in SX(k) or SN(k) is related to the atomic volume v as calculated from the measured density by using kPP ∝ v−1/Df, then it follows that119,124
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kPP = ln kPP = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a − ln a − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v/Df v/Df | (18) |
| rD′[GN(r) − 1] ≃ A exp(−a0r)cos(a1r − ϕ) | (19) |
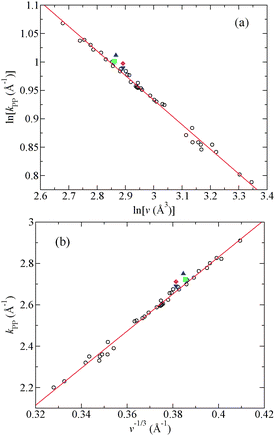 | ||
Fig. 7 Plots of (a) ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kPPvs. ln kPPvs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v and (b) kPPvs. v−1/3 for a selection of metallic glasses and liquids where kPP is the position of the principal peak in a measured total structure factor and v is the atomic volume.119 The open circles show the data points for various glasses taken from Ma et al.124 and the solid (red) curves show straight-line fits. Also shown are the data points for glassy Au0.80Si0.20 ((blue) ▲) and for liquid Au0.81Si0.19 at 665 K ((green) ■), Au0.72Ge0.28 at 666 K ((magenta) ◆) and Ag0.74Ge0.26 at 976 K ((blue) ▼).119,143 Reprinted with permission from Chirawatkul et al.119 Copyright (2011) by the American Physical Society. v and (b) kPPvs. v−1/3 for a selection of metallic glasses and liquids where kPP is the position of the principal peak in a measured total structure factor and v is the atomic volume.119 The open circles show the data points for various glasses taken from Ma et al.124 and the solid (red) curves show straight-line fits. Also shown are the data points for glassy Au0.80Si0.20 ((blue) ▲) and for liquid Au0.81Si0.19 at 665 K ((green) ■), Au0.72Ge0.28 at 666 K ((magenta) ◆) and Ag0.74Ge0.26 at 976 K ((blue) ▼).119,143 Reprinted with permission from Chirawatkul et al.119 Copyright (2011) by the American Physical Society. | ||
It is, however, possible to account for the extended-range ordering associated with the principal peak in liquid and glassy metals without invoking fractal dimensionality.119 For example, the available data for metallic glasses can be equally well fitted by using the relation kPP ∝ v−1/3 as expected for a three-dimensional structure (Fig. 7(b)). Also, the extended-range ordering can be accounted for by making a pole analysis of the Ornstein–Zernike equations, an approach that has been used to describe the asymptotic behaviour of the pair-distribution functions for hard-sphere mixtures.144,145 If the dispersion term is absent from eqn (14) then, irrespective of whether the Coulomb term is absent or present, the asymptotic behaviour of a partial pair-distribution function for sufficiently high particle density is described by the relation38,39
r[gαβ(r) − 1] = 2|![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αβ|exp(−a0r)cos(a1r − θαβ) αβ|exp(−a0r)cos(a1r − θαβ) | (20) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αα||
αα||![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ| = |
ββ| = |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αβ|2 and the phases are related by θαα + θββ = 2θαβ. By using the definition of the total pair-distribution function given by eqn (12) it follows that119
αβ|2 and the phases are related by θαα + θββ = 2θαβ. By using the definition of the total pair-distribution function given by eqn (12) it follows that119r[GN(r) − 1] = 2|![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) |exp(−a0r)cos(a1r − θ) |exp(−a0r)cos(a1r − θ) | (21) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = (cαbα
= (cαbα![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αα1/2 + cβbβ
αα1/2 + cβbβ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ1/2)2/〈b〉2 ≡ |
ββ1/2)2/〈b〉2 ≡ |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) |exp(−iθ),
|exp(−iθ), ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αα = |
αα = |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) αα|exp(−iθαα),
αα|exp(−iθαα), ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ = |
ββ = |![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ββ|exp(−iθββ),
ββ|exp(−iθββ),  and θ is a phase.‡‡‡ The only significant difference between eqn (19) and (21) is the power of r used to weight GN(r) − 1 and, as illustrated in Fig. 8, eqn (21) can be used to account for the measured behaviour of the total pair-distribution functions for several liquid eutectic alloys over a large r-range. A similar conclusion is anticipated for the glassy metals studied by Ma et al.124 given the similarity between the equations obtained from the fractal and Ornstein–Zernike approaches. The fractal approach for describing extended-range ordering in liquid and glassy metals is not, therefore, convincing.
and θ is a phase.‡‡‡ The only significant difference between eqn (19) and (21) is the power of r used to weight GN(r) − 1 and, as illustrated in Fig. 8, eqn (21) can be used to account for the measured behaviour of the total pair-distribution functions for several liquid eutectic alloys over a large r-range. A similar conclusion is anticipated for the glassy metals studied by Ma et al.124 given the similarity between the equations obtained from the fractal and Ornstein–Zernike approaches. The fractal approach for describing extended-range ordering in liquid and glassy metals is not, therefore, convincing.
![Decay of the total pair-distribution functions for liquid (a) Au0.81Si0.19 at 665 K, (b) Au0.72Ge0.28 at 666 K, and (c) Ag0.74Ge0.26 at 976 K. In the left-hand column, the measured functions r[GN(r) − 1] (solid dark (blue) curves) are fitted to eqn (21) at large-r, and for a given liquid alloy the values of a0 and a1 obtained from the fits are comparable to the half-width at half-maximum of the principal peak in SN(k) and to the position kPP of this peak, respectively. In the right-hand column, the solid dark (blue) curves give ln|r[GN(r) − 1]| and the broken (red) curves show fits to the repeated maxima at large-r to a straight line (ln|r[GN(r) − 1]| = −a0r + constant) from which the decay length a0−1 can also be found. Reprinted with permission from Chirawatkul et al.119 Copyright (2011) by the American Physical Society.](/image/article/2013/CP/c3cp51741a/c3cp51741a-f8.gif) | ||
| Fig. 8 Decay of the total pair-distribution functions for liquid (a) Au0.81Si0.19 at 665 K, (b) Au0.72Ge0.28 at 666 K, and (c) Ag0.74Ge0.26 at 976 K. In the left-hand column, the measured functions r[GN(r) − 1] (solid dark (blue) curves) are fitted to eqn (21) at large-r, and for a given liquid alloy the values of a0 and a1 obtained from the fits are comparable to the half-width at half-maximum of the principal peak in SN(k) and to the position kPP of this peak, respectively. In the right-hand column, the solid dark (blue) curves give ln|r[GN(r) − 1]| and the broken (red) curves show fits to the repeated maxima at large-r to a straight line (ln|r[GN(r) − 1]| = −a0r + constant) from which the decay length a0−1 can also be found. Reprinted with permission from Chirawatkul et al.119 Copyright (2011) by the American Physical Society. | ||
5 Liquids at high-temperatures: vitrification of fragile glass-forming systems
Containerless high-temperature levitation methods offer several attractions for investigating liquids.146 For example, contamination of the liquid by reaction with container walls is avoided and crystal formation by heterogeneous nucleation is minimised, allowing liquids to be deeply supercooled. This can extend the number of glass-forming systems and/or the range of glass-forming compositions such that it is possible to make new glasses with novel physical properties.147,148 A disadvantage for the NDIS method is that the samples are small, being roughly spherical with a diameter of ∼8 mm for electromagnetic-levitation experiments149 or 2–4 mm for aerodynamic-levitation experiments.150,151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) §§§ Nevertheless, the NDIS method with electromagnetic levitation has been applied to measure the partial structure factors of liquid Ni36Zr64.152,153 Its isomorphic substitution counterpart has also been combined with electromagnetic levitation to measure the partial structure factors of stable and supercooled liquid Al13(CoxFe1−x)4 (0 ≤ x ≤ 1), where isomorphism was assumed for the transition metals Co and Fe.154
§§§ Nevertheless, the NDIS method with electromagnetic levitation has been applied to measure the partial structure factors of liquid Ni36Zr64.152,153 Its isomorphic substitution counterpart has also been combined with electromagnetic levitation to measure the partial structure factors of stable and supercooled liquid Al13(CoxFe1−x)4 (0 ≤ x ≤ 1), where isomorphism was assumed for the transition metals Co and Fe.154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ¶¶¶ It is only recently, however, that the NDIS method with aerodynamic-levitation and laser-heating has been used to investigate the structure of oxides, where initial investigations have focussed on the fragile glass-forming systems CaAl2O4 (see Fig. 1)18 and CaSiO3.19
¶¶¶ It is only recently, however, that the NDIS method with aerodynamic-levitation and laser-heating has been used to investigate the structure of oxides, where initial investigations have focussed on the fragile glass-forming systems CaAl2O4 (see Fig. 1)18 and CaSiO3.19
Consider the case of CaAl2O4, and let diffraction patterns be measured for three samples that are identical in every respect, except for the isotopic composition of calcium which is of natural isotopic abundance natCa, predominantly the isotope 44Ca, or a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of the two mixCa. Let the corresponding scattering lengths be denoted by bnatCa, b44Ca and bmixCa and the measured total structure factors be represented by natF(k), 44F(k) and mixF(k), respectively.18 In matrix notation,
50 mixture of the two mixCa. Let the corresponding scattering lengths be denoted by bnatCa, b44Ca and bmixCa and the measured total structure factors be represented by natF(k), 44F(k) and mixF(k), respectively.18 In matrix notation,
 | (22) |
| ΔFCaμ(k) = cAlbAl[SCaAl(k) − 1] + cObO[SCaO(k) − 1], | (23) |
| ΔFμμ(k) = cAl2bAl2[SAlAl(k) − 1] + cO2bO2[SOO(k) − 1] + 2cAlcObAlbO[SAlO(k) − 1]. | (24) |
The measured difference functions ΔFCaμ(k) and ΔFμμ(k) for the liquid at 1973(30) K and for the glass at 300(1) K are shown in Fig. 9 and the corresponding real-space functions ΔGCaμ(r) and ΔGμμ(r) are shown in Fig. 10. In the case of the glass, the sample was not levitated but was rested on the nozzle of the levitation device, and improved counting statistics made it possible to extract the Ca–Ca partial structure factor SCaCa(k) and corresponding partial pair-correlation function dCaCa(r) ≡ 4πρr[gCaCa(r) − 1] which are shown in Fig. 11.
 | ||
| Fig. 9 The difference functions ΔFμμ(k) and ΔFCaμ(k) for glassy and liquid CaAl2O4.18 The vertical bars show the statistical errors on the measured data points, and the solid (red) curves show the back Fourier transforms of the corresponding real-space functions shown by the solid (black) curves in Fig. 10. The chained (blue) curves show the molecular dynamics results obtained by using a polarisable-ion model in which anion polarisability and shape-deformation effects are taken into account along with the polarisability of the calcium cations.27,155 | ||
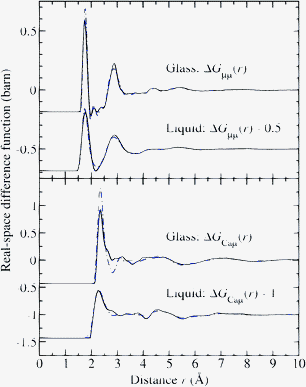 | ||
| Fig. 10 The difference functions ΔGμμ(r) and ΔGCaμ(r) for glassy and liquid CaAl2O4 as obtained by Fourier transforming either the spline-fitted measured (solid (black) curves) or the simulated (chained (blue) curves) reciprocal-space functions shown in Fig. 9. The unphysical small-r oscillations below the distances of closest interatomic approach are omitted for clarity of presentation. | ||
 | ||
| Fig. 11 (a) The measured (points with vertical error bars) and simulated (chained (blue) curve) partial structure factors SCaCa(k) for CaAl2O4 glass.18 The solid (red) curve shows the back Fourier transform of dCaCa(r) given in (b) by the solid (black) curve. (b) The partial pair-correlation function dCaCa(r) as obtained by Fourier transforming the spline-fitted measured (solid (black) curve) or the simulated (broken (red) curve) SCaCa(k) function shown in (a) after applying a Lorch modification function with kmax = 8.5 Å−1. The chained (blue) curve shows the results obtained directly from the molecular dynamics simulation (see the text). Reprinted with permission from Drewitt et al.18 Copyright (2012) by the American Physical Society. | ||
The results were interpreted with the aid of molecular dynamics simulations, using interaction potentials that take into account anion polarisability and shape-deformation effects as well as the polarisability of the calcium cations,27,155 and revealed key structural modifications upon glass formation on multiple length scales. Specifically, there is a reorganisation on quenching that leads to an almost complete breakdown of the AlO5 polyhedra and threefold coordinated oxygen atoms present in the liquid, and to their replacement by a predominantly corner-sharing network of AlO4 tetrahedra with twofold coordinated oxygen atoms in the glass. This process is accompanied by the formation of branched-chains of edge- and face-sharing Ca-centered polyhedra that give cationic ordering on an intermediate length scale, where the measured Ca–O coordination numbers are ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OCa = 6.0(2) for the liquid and
OCa = 6.0(2) for the liquid and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OCa = 6.4(2) for the glass.|||||| The formation of more extensively linked chains of Ca-centred polyhedra on vitrification is also indicated by the joint NDIS and molecular dynamics investigation of CaSiO3 by Skinner et al.19
OCa = 6.4(2) for the glass.|||||| The formation of more extensively linked chains of Ca-centred polyhedra on vitrification is also indicated by the joint NDIS and molecular dynamics investigation of CaSiO3 by Skinner et al.19
Since glasses can explore localities on an energy landscape that are inaccessible to the crystalline state, they are widely used as proxies for the liquid in materials of geophysical interest.158–163 Although this is known to be an approximation,162,163 the extreme experimental conditions make it difficult to assess the extent of associated structural differences. The results for liquid and glassy CaAl2O4 show significant structural re-organization on vitrification in this fragile glass former, a taxonomy that encompasses a range of magma-related liquids.164–166 There is a change not only in the character of the network-forming motifs but also in the nature of the intermediate-ranged cationic ordering. The work therefore cautions against the use of glasses as proxies for investigating the structure of fragile glass-forming liquids that are of geophysical interest.
The NDIS method, or its isomorphic substitution counterpart, has previously been used to investigate the structure of a wide variety of metal-containing multi-component liquids and glasses, allowing a measured total structure factor to be separated either into its contributions from the M–M, M–μ and μ–μ pair-correlations, where M denotes a metal atom and μ denotes the other chemical species,64,167–171 or into difference functions that otherwise simplify the complexity of correlations.172–180 The results obtained by Drewitt et al.18 demonstrate that it is now feasible to use this methodology to study the detailed structure of small oxide samples, including single liquid droplets under high-temperature conditions.
6 Glasses at high-pressures: mechanisms of density-driven network collapse
The structural changes in glasses and liquids induced by high-pressure and/or high-temperature conditions can alter substantially their dynamical and transport properties.6,37,181,182 A notable example is provided by so-called polyamorphic transitions, where the variation of pressure and/or temperature leads to an abrupt transformation between two phases having identical compositions but different densities.6,37,151,181–184 The nature of structural disorder, combined with the experimental difficulties associated with the investigation of materials under extreme conditions,60,185–188 provide severe challenges to unravelling the mechanisms by which these structural transformations occur. Recently, however, Wezka et al.20 have made the first application of the NDIS method to measure the structure of GeO2 glass with a Paris-Edinburgh press at pressures ranging from ambient to ∼8 GPa. Valuable new information was thereby provided on the mechanisms of density-driven network collapse.Let diffraction experiments be made on samples of 70GeO2 and 73GeO2 glass that are identical in every respect, except for their Ge isotope enrichments, such that the total structure factors 70F(k) and 73F(k) are measured, respectively. Then the contribution to the diffraction patterns from the O–O partial structure factor can be eliminated by forming the first-difference function
| ΔFGe(k) ≡ 70F(k) − 73F(k) = 2cGecObO(b70Ge − b73Ge)[SGeO(k) − 1] + cGe2(b70Ge2 − b73Ge2)[SGeGe(k) − 1]. | (25) |
| ΔFO(k) ≡ [b73Ge2 70F(k) − b70Ge2 73F(k)]/(b73Ge2 − b70Ge2) = 2cGecObOb70Geb73Ge(b70Ge + b73Ge)−1 × [SGeO(k) − 1] + cO2bO2[SOO(k) − 1]. | (26) |
The pressure dependence of the measured 70F(k) and 73F(k) functions is shown in Fig. 12, where 73F(k) is dominated by the Bhatia–Thornton number–number partial structure factor SNN(k) because the scattering lengths of oxygen and the isotope 73Ge are similar (see eqn (7)). With increasing density, the position of the FSDP moves to higher k values as the principal peak sharpens. These changes indicate a competition between the intermediate and extended-range ordering which is won by the latter with increasing density, consistent with the transformation from a “strong” low-density to a more “fragile” high-density glass (see Section 3.1).70,72 Similar behaviour is observed in high-pressure X-ray diffraction experiments on GeSe2 glass,191 where SX(k) ≃ SNN(k) because fGe(k) ≃ fSe(k) (Section 3.2).****
 | ||
| Fig. 12 The pressure dependence of the measured total structure factors (a) 70F(k) and (b) 73F(k) for GeO2 glass.20 According to eqn (11), these functions can be re-written as SN(k) ≡ F(k)/〈b〉2 + 1 in which the weighting factors for the Bhatia–Thornton SNN(k), SCC(k) and SNC(k) partial structure factors are (a) 1, 0.3344 and 1.1565 or (b) 1, 0.0137 and −0.2338, respectively, i.e.73F(k) is dominated by SNN(k). Vertical bars give the statistical errors on the measured data points, and the high-pressure data sets have been displaced vertically for clarity of presentation. | ||
The pressure dependence of the measured difference functions ΔFGe(k) and ΔFO(k) for GeO2 glass is shown in Fig. 13. The robustness of the results was thoroughly checked by using the procedures described in ref. 20. The corresponding real-space functions ΔGGe(r) and ΔGO(r) are illustrated in Fig. 14 where the first peak, which is attributable to Ge–O correlations, gives the Ge–O bond distances and coordination numbers shown in Fig. 15. Importantly, the NDIS method allows for the nearest-neighbour Ge–Ge and O–O correlations to be resolved, as manifested by the second peaks in ΔGGe(r) and ΔGO(r), respectively. The corresponding distances are plotted in Fig. 15 along with the O–O coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OO, obtained by assuming minimal overlap with the Ge–O correlations as observed under ambient conditions.71 In Fig. 13–15, the diffraction results are compared to molecular dynamics simulations made using interaction potentials that include dipole-polarisation effects.20,28,36 The potentials were parameterised using ab initio simulations as opposed to experimental results and are therefore largely unbiased in their predictions of the glass structure. In contrast to other models for GeO2 glass under pressure,193–197 the experimental and simulation results are consistent with one another, an agreement that also extends to the pressure dependence of the mean O–Ge–O and Ge–O–Ge bond angles.20
OO, obtained by assuming minimal overlap with the Ge–O correlations as observed under ambient conditions.71 In Fig. 13–15, the diffraction results are compared to molecular dynamics simulations made using interaction potentials that include dipole-polarisation effects.20,28,36 The potentials were parameterised using ab initio simulations as opposed to experimental results and are therefore largely unbiased in their predictions of the glass structure. In contrast to other models for GeO2 glass under pressure,193–197 the experimental and simulation results are consistent with one another, an agreement that also extends to the pressure dependence of the mean O–Ge–O and Ge–O–Ge bond angles.20
![The pressure dependence of the difference functions (a) ΔFGe(k)/barn = 0.124(3)[SGeO(k) − 1] + 0.081(2)[SGeGe(k) − 1] and (b) ΔFO(k)/barn = 0.0875(5)[SGeO(k) − 1] + 0.1497(2)[SOO(k) − 1] for GeO2 glass.20 The vertical bars give the statistical errors on the measured data points, the solid (red) curves give the Fourier transforms of the corresponding real-space functions shown in Fig. 14, and the broken (green) curves give the molecular dynamics results obtained by using transferrable interaction potentials that include dipole-polarisation effects.28,36 The high-pressure data sets have been shifted vertically for clarity of presentation. Figure from Wezka et al.20 © IOP Publishing. Reproduced with permission. All rights reserved.](/image/article/2013/CP/c3cp51741a/c3cp51741a-f13.gif) | ||
| Fig. 13 The pressure dependence of the difference functions (a) ΔFGe(k)/barn = 0.124(3)[SGeO(k) − 1] + 0.081(2)[SGeGe(k) − 1] and (b) ΔFO(k)/barn = 0.0875(5)[SGeO(k) − 1] + 0.1497(2)[SOO(k) − 1] for GeO2 glass.20 The vertical bars give the statistical errors on the measured data points, the solid (red) curves give the Fourier transforms of the corresponding real-space functions shown in Fig. 14, and the broken (green) curves give the molecular dynamics results obtained by using transferrable interaction potentials that include dipole-polarisation effects.28,36 The high-pressure data sets have been shifted vertically for clarity of presentation. Figure from Wezka et al.20 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
![The pressure dependence of the difference functions (a) ΔGGe(r)/barn = 0.124(3)[gGeO(r) − 1] + 0.081(2)[gGeGe(r) − 1] and (b) ΔGO(r)/barn = 0.0875(5)[gGeO(r) − 1] + 0.1497(2)[gOO(r) − 1] (solid (black) curves), as obtained by spline fitting and Fourier transforming the measured reciprocal-space functions shown in Fig. 13, where the chained (red) curves show the oscillations at r-values smaller than the distance of closest approach between two atoms. The broken (green) curves give the molecular dynamics results as obtained by Fourier transforming the simulated functions shown in Fig. 13 after applying the same maximum cutoff kmax as for the neutron diffraction data. The high-pressure data sets have been shifted vertically for clarity of presentation. Figure from Wezka et al.20 © IOP Publishing. Reproduced with permission. All rights reserved.](/image/article/2013/CP/c3cp51741a/c3cp51741a-f14.gif) | ||
| Fig. 14 The pressure dependence of the difference functions (a) ΔGGe(r)/barn = 0.124(3)[gGeO(r) − 1] + 0.081(2)[gGeGe(r) − 1] and (b) ΔGO(r)/barn = 0.0875(5)[gGeO(r) − 1] + 0.1497(2)[gOO(r) − 1] (solid (black) curves), as obtained by spline fitting and Fourier transforming the measured reciprocal-space functions shown in Fig. 13, where the chained (red) curves show the oscillations at r-values smaller than the distance of closest approach between two atoms. The broken (green) curves give the molecular dynamics results as obtained by Fourier transforming the simulated functions shown in Fig. 13 after applying the same maximum cutoff kmax as for the neutron diffraction data. The high-pressure data sets have been shifted vertically for clarity of presentation. Figure from Wezka et al.20 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
 | ||
| Fig. 15 The pressure dependence of the nearest-neighbour (a) Ge–O, O–O and Ge–Ge distances and (b) Ge–O and O–O coordination numbers. The results from the neutron diffraction (■) and molecular dynamics (broken (red) curves) work of Wezka et al.20 are compared to those obtained from the neutron diffraction studies of Drewitt et al.60 ((green) ●) and Salmon et al.61 ((blue) ▲). In (b) the Ge–O coordination numbers from inelastic X-ray scattering experiments189 are also shown ((red) ◇). Figure from Wezka et al.20 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
It is concluded that when the reduced density ρ/ρ0 < 1.16, where ρ0 is the value at ambient pressure, compaction proceeds via a reorganisation of distorted corner-sharing GeO4 tetrahedra in which there is a reduction of the mean Ge–O–Ge bond angle and an increase in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OO. On further densification, GeO4 units are replaced mostly by distorted square pyramidal GeO5 units, where the vacancy at the base of the latter anticipates the eventual formation of octahedral (i.e. square bipyramidal) units. At higher pressures, GeO6 units begin to form when ρ/ρ0 ≳ 1.4 and the fraction of GeO5 units reaches a maximum when ρ/ρ0 = 1.45. Thus when ρ/ρ0 ≳ 1.16, the replacement of tetrahedral GeO4 units proceeds via an interplay between the predominance of distorted square pyramidal GeO5 units versus octahedral GeO6 units.20 This replacement necessitates the formation of threefold coordinated oxygen atoms in order to maintain the glass stoichiometry, and leads to an increase with density in the number of small rings. The increase when ρ/ρ0 > 1.16 in the number of threefold rings (i.e. those containing 3 Ge and 3 O atoms), which are attributed to the D2 band at ≃520 cm−1 in Raman spectra,198,199 is consistent with the measured density dependence of this feature.200–202 A preference is shown for sixfold rings when ρ/ρ0 = 1 and for fourfold rings when ρ/ρ0 = 1.64.
OO. On further densification, GeO4 units are replaced mostly by distorted square pyramidal GeO5 units, where the vacancy at the base of the latter anticipates the eventual formation of octahedral (i.e. square bipyramidal) units. At higher pressures, GeO6 units begin to form when ρ/ρ0 ≳ 1.4 and the fraction of GeO5 units reaches a maximum when ρ/ρ0 = 1.45. Thus when ρ/ρ0 ≳ 1.16, the replacement of tetrahedral GeO4 units proceeds via an interplay between the predominance of distorted square pyramidal GeO5 units versus octahedral GeO6 units.20 This replacement necessitates the formation of threefold coordinated oxygen atoms in order to maintain the glass stoichiometry, and leads to an increase with density in the number of small rings. The increase when ρ/ρ0 > 1.16 in the number of threefold rings (i.e. those containing 3 Ge and 3 O atoms), which are attributed to the D2 band at ≃520 cm−1 in Raman spectra,198,199 is consistent with the measured density dependence of this feature.200–202 A preference is shown for sixfold rings when ρ/ρ0 = 1 and for fourfold rings when ρ/ρ0 = 1.64.
Like GeO2, SiO2 glass also forms under ambient conditions a network of corner-sharing MO4 tetrahedra where the mean inter-tetrahedral M–O–M bond angle is 151° for SiO2 as compared to 132(2)° for GeO2.71,203 With increasing density, SiO2 is also converted from a tetrahedral to an octahedral glass, the changes occurring at higher pressures by comparison to GeO2.200–202 As shown in Fig. 16, the structural changes do, however, occur at similar scaled number densities ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 where
MO3 where ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO is the ambient-pressure bond-length.61 For example, the measured M–O bond lengths and coordination numbers for both GeO2 and SiO2 barely change at low pressures, but then increase once the dimensionless number density ρ
MO is the ambient-pressure bond-length.61 For example, the measured M–O bond lengths and coordination numbers for both GeO2 and SiO2 barely change at low pressures, but then increase once the dimensionless number density ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≳ 0.4. For both glasses, there is also an alteration to the rate of change of the FSDP position kFSDP with increasing density at ρ
MO3 ≳ 0.4. For both glasses, there is also an alteration to the rate of change of the FSDP position kFSDP with increasing density at ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≃ 0.45.
MO3 ≃ 0.45.
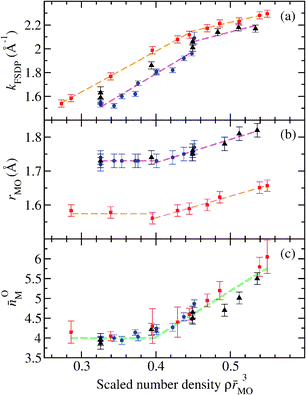 | ||
Fig. 16 The dependence on the scaled number-density ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 of several parameters describing the compressed structures of GeO2 and SiO2 glass, where MO3 of several parameters describing the compressed structures of GeO2 and SiO2 glass, where ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO is the M–O bond length at ambient pressure and M denotes either Ge or Si.61 (a) The position of the first sharp diffraction peak kFSDP in the measured total structure factors, (b) the bond distance rMO as deduced from the position of the first peak in the total pair-distribution functions, and (c) the coordination number MO is the M–O bond length at ambient pressure and M denotes either Ge or Si.61 (a) The position of the first sharp diffraction peak kFSDP in the measured total structure factors, (b) the bond distance rMO as deduced from the position of the first peak in the total pair-distribution functions, and (c) the coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OM. In the expression ρ OM. In the expression ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 the values MO3 the values ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) GeO = 1.73 Å and GeO = 1.73 Å and ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) SiO = 1.60 Å were used.70 The neutron diffraction results for GeO2 were taken from Drewitt et al.60 ((blue) ●) and from Salmon et al.61 ((black) ▲) while the X-ray diffraction results for SiO2 were taken from Benmore et al.190 ((red) ■). The broken straight lines are fits to the data sets at either small or large densities. Figure from Salmon et al.61 © IOP Publishing. Reproduced with permission. All rights reserved. SiO = 1.60 Å were used.70 The neutron diffraction results for GeO2 were taken from Drewitt et al.60 ((blue) ●) and from Salmon et al.61 ((black) ▲) while the X-ray diffraction results for SiO2 were taken from Benmore et al.190 ((red) ■). The broken straight lines are fits to the data sets at either small or large densities. Figure from Salmon et al.61 © IOP Publishing. Reproduced with permission. All rights reserved. | ||
In the case of GeO2 glass, the regime when ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≲ 0.4 is associated with a reorganization of GeO4 units, the regime when 0.4 ≲ ρ
MO3 ≲ 0.4 is associated with a reorganization of GeO4 units, the regime when 0.4 ≲ ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≲ 0.45 corresponds to the replacement of GeO4 units by predominantly GeO5 units, and the regime when ρ
MO3 ≲ 0.45 corresponds to the replacement of GeO4 units by predominantly GeO5 units, and the regime when ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≳ 0.45 corresponds to the appearance of a growing concentration of GeO6 units. According to Fig. 16, similar structural transformations are expected for SiO2 glass. Hence, SiO4 units will be replaced predominantly by SiO5 units in a dimensionless number density regime which corresponds to a pressure range from about 15 to 24 GPa, and appreciable concentrations of SiO6 units will begin to form at pressures in excess of ∼24 GPa. These findings are in broad agreement with the molecular dynamics studies of SiO2 by Liang et al.204 and Wu et al.205 From the experimental perspective, X-ray Raman scattering oxygen K-edge spectra show little change at pressures below 14 GPa and may be interpreted at higher pressures in terms of the formation of SiO5 units.205,206 In addition, the appearance of SiO5 units at pressures above 12 GPa has been suggested on the basis of X-ray Raman scattering silicon L-edge spectra.207
MO3 ≳ 0.45 corresponds to the appearance of a growing concentration of GeO6 units. According to Fig. 16, similar structural transformations are expected for SiO2 glass. Hence, SiO4 units will be replaced predominantly by SiO5 units in a dimensionless number density regime which corresponds to a pressure range from about 15 to 24 GPa, and appreciable concentrations of SiO6 units will begin to form at pressures in excess of ∼24 GPa. These findings are in broad agreement with the molecular dynamics studies of SiO2 by Liang et al.204 and Wu et al.205 From the experimental perspective, X-ray Raman scattering oxygen K-edge spectra show little change at pressures below 14 GPa and may be interpreted at higher pressures in terms of the formation of SiO5 units.205,206 In addition, the appearance of SiO5 units at pressures above 12 GPa has been suggested on the basis of X-ray Raman scattering silicon L-edge spectra.207
The packing fraction of oxygen atoms arranged in regular tetrahedral units is given by  (see Table 1) and, as shown by Fig. 16, the nearest-neigbour bond length
(see Table 1) and, as shown by Fig. 16, the nearest-neigbour bond length ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO changes little between ambient and a scaled number density ρ
MO changes little between ambient and a scaled number density ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≃ 0.4. The latter corresponds to a packing fraction ηO ≃ 0.61, close to the value of ≃0.64 expected for a random close-packing of hard spheres.82 Thus, fivefold coordinated Si or Ge atoms begin to appear only when the oxygen atoms have filled the space that is available to them.††††
MO3 ≃ 0.4. The latter corresponds to a packing fraction ηO ≃ 0.61, close to the value of ≃0.64 expected for a random close-packing of hard spheres.82 Thus, fivefold coordinated Si or Ge atoms begin to appear only when the oxygen atoms have filled the space that is available to them.††††
As discussed in Section 5, glasses are not expected to give an accurate account of the structure of the corresponding liquids, especially for more fragile glass-forming systems. However, since glasses can explore localities on an energy landscape that are inaccessible to the crystalline state, the formation of fivefold coordinated silicon atoms at high pressures is likely to be mirrored in the liquid phases of e.g. compressed high-temperature liquid silicates. These materials are of geophysical relevance since they account for a significant proportion of the Earth's mantle, and structural changes that take place under high-pressure and temperature conditions alter physical properties (e.g. the compressibility, thermal expansivity and viscosity) that govern magma related processes such as volcanic activity and the differentiation and evolution in composition of the planetary interior.208,209 As suggested by molecular dynamics simulations,210,211 the formation of SiO5 species in these liquids is likely to have a substantial impact on the extent of network polymerisation and, thereby, the physical properties of the melt.
7 Quantum effects in the hydrogen bonded network of water
Oxygen is a ubiquitous element,212 playing an essential role in most scientific and technological disciplines, and is often incorporated within a structurally disordered material where examples include molten silicates in planetary science,213 glasses used for lasers and optical communications,5 the insulating oxide layers in silicon-based electronic devices,214 and water in biological processes.7,8 To investigate the possibility of using oxygen as a site specific structural probe in neutron diffraction experiments, the sensitive technique of neutron interferometry215 has recently been applied to measure the coherent scattering length values of the isotopes 17O and 18O relative to oxygen of natural isotopic abundance natO.216 The measured values of b17O = 5.867(4) and b18O = 6.009(5) fm give a factor of ≃6 increase in the scattering length contrast between 18O and natO by comparison with standard tabulations.217,218These results encouraged Zeidler et al.21–23 to make the first application of the method of oxygen NDIS to measure the structure of light (H2O) versus heavy (D2O) water to investigate the role played by nuclear quantum effects, such as zero point energy and tunnelling, on water's hydrogen bonded network. These quantum effects manifest themselves by differences between the structure and dynamics of light versus heavy water which lead to changes in properties such as their melting and boiling points, their temperature of maximum density, and their interaction with biological systems.8,219–222 In addition, techniques such as two-dimensional infra-red spectroscopy commonly require H to be partially substituted by D, and it is therefore important to understand the accompanying effect on the structure and dynamics of water.223,224
Let diffraction experiments be made on light water samples of H2natO and H218O and on heavy water samples of D2natO and D218O. In each case, the neutron and proton/deuteron masses are comparable, which leads to a large contribution to the measured diffraction patterns from inelastic scattering effects, for which there is no exact theory.17,225,226 In experiments on water, it is therefore desirable to minimise the distortion that these unwanted effects have on the measured diffraction patterns, and this can be achieved by using the oxygen NDIS method. For example, in the case of light water it follows from eqn (1) that subtraction of the measured differential scattering cross-sections gives the expression
| ΔFH′(k) ≡ dσ/dΩ|18H − dσ/dΩ|natH = ΔFH(k) + ΔPH(k) | (27) |
| ΔFH(k) = F18H(k) − FnatH(k) = cO2(b18O2 − bnatO2)[SOO(k) − 1] + 2cOcHbH(b18O − bnatO)[SOH(k) − 1]. | (28) |
| ΔFD′(k) ≡ dσ/dΩ|18D − dσ/dΩ|natD = ΔFD(k) + ΔPD(k) | (29) |
| ΔFD(k) = F18D(k) − FnatD(k) = cO2(b18O2 − bnatO2)[SOO(k) − 1] + 2cOcDbD(b18O − bnatO)[SOD(k) − 1] | (30) |
The complexity of correlations associated with a total structure factor can also be simplified by forming the second-difference function
 | (31) |
The measured first-difference functions are shown in Fig. 17(a) and the corresponding real-space functions are shown in Fig. 18(a), where the robustness of these results was thoroughly checked by using the procedures described in ref. 23. The first peak in ΔGD(r) at 0.985(5) Å and the first trough in ΔGH(r) at 0.990(5) Å arise from intra-molecular O–D and O–H correlations and give coordination numbers of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) DO = 1.9(1) and
DO = 1.9(1) and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) HO = 2.0(2). The O–D distance compares with a value of 0.983(8) Å obtained by Powles225 from a re-analysis of neutron diffraction data for liquid heavy water at 294 K, and with a value of 0.985(7) Å as estimated from a pair-distribution function analysis of neutron diffraction data for ice-Ih.228 The difference between the O–D and O–H bond lengths of ≃0.5% compares to ≃0.4% for both the vapour phase of water in its ground vibrational state (where the O–D and O–H distances are 0.9687 and 0.9724 Å, respectively)229 and for ice-Ih at 123 K (where the O–D and O–H distances are 0.983(5) and 0.987(5) Å, respectively).230 All of these values are smaller than the bond-length difference of ∼3% found in the neutron and X-ray diffraction investigation of liquid water by Soper and Benmore231 using the EPSR method, a difference that is much larger than found by any theoretical prediction.21,23 Indeed, in more recent work Soper reports a revised bond-length difference that is a factor of ten smaller.232
HO = 2.0(2). The O–D distance compares with a value of 0.983(8) Å obtained by Powles225 from a re-analysis of neutron diffraction data for liquid heavy water at 294 K, and with a value of 0.985(7) Å as estimated from a pair-distribution function analysis of neutron diffraction data for ice-Ih.228 The difference between the O–D and O–H bond lengths of ≃0.5% compares to ≃0.4% for both the vapour phase of water in its ground vibrational state (where the O–D and O–H distances are 0.9687 and 0.9724 Å, respectively)229 and for ice-Ih at 123 K (where the O–D and O–H distances are 0.983(5) and 0.987(5) Å, respectively).230 All of these values are smaller than the bond-length difference of ∼3% found in the neutron and X-ray diffraction investigation of liquid water by Soper and Benmore231 using the EPSR method, a difference that is much larger than found by any theoretical prediction.21,23 Indeed, in more recent work Soper reports a revised bond-length difference that is a factor of ten smaller.232![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡‡‡‡
‡‡‡‡
![(a) The first-difference functions ΔFD(k)/barn = 0.0059(2)[SOD(k) − 1] + 0.00262(8)[SOO(k) − 1] and ΔFH(k)/barn = −0.0033(1)[SOH(k) − 1] + 0.00263(8)[SOO(k) − 1] and (b) the second-difference function ΔFOX(k) which is constructed by subtracting ΔFH(k) from ΔFD(k) and is equal to SOD(k) (or SOH(k)) if the net quantum effects are sufficiently small (see the text).21,23 In (a) and (b) the vertical bars give the statistical errors on the measured data points and the solid (black) curves give spline fits that were used to generate the corresponding real-space functions shown in Fig. 18. The broken (red) curves show the results obtained from path integral molecular dynamics using the flexible anharmonic TTM3-F model for water.227 Reprinted with permission from Zeidler et al.21 Copyright (2011) by the American Physical Society.](/image/article/2013/CP/c3cp51741a/c3cp51741a-f17.gif) | ||
| Fig. 17 (a) The first-difference functions ΔFD(k)/barn = 0.0059(2)[SOD(k) − 1] + 0.00262(8)[SOO(k) − 1] and ΔFH(k)/barn = −0.0033(1)[SOH(k) − 1] + 0.00263(8)[SOO(k) − 1] and (b) the second-difference function ΔFOX(k) which is constructed by subtracting ΔFH(k) from ΔFD(k) and is equal to SOD(k) (or SOH(k)) if the net quantum effects are sufficiently small (see the text).21,23 In (a) and (b) the vertical bars give the statistical errors on the measured data points and the solid (black) curves give spline fits that were used to generate the corresponding real-space functions shown in Fig. 18. The broken (red) curves show the results obtained from path integral molecular dynamics using the flexible anharmonic TTM3-F model for water.227 Reprinted with permission from Zeidler et al.21 Copyright (2011) by the American Physical Society. | ||
![(a) The first-difference functions ΔGD(r)/barn = 0.0059(2)[gOD(r) − 1] + 0.00262(8)[gOO(r) − 1] and ΔGH(r)/barn = −0.0033(1)[gOH(r) − 1] + 0.00263(8)[gOO(r) − 1]. The O–H correlations in ΔGH(r) have a negative weighting factor because bH < 0. (b) The second-difference function ΔGOX(r) which is equal to gOD(r) (or gOH(r)) if the net quantum effects are sufficiently small (see the text). In (a) and (b) the solid curves were obtained by Fourier transforming the spline fitted data sets presented in Fig. 17 before and after the application of a Lorch modification function. The data obtained from the first procedure were joined with the data obtained from the second procedure after the first peak or trough. The open circles show the results obtained from path integral molecular dynamics using the flexible anharmonic TTM3-F model for water.227 Reprinted with permission from Zeidler et al.21 Copyright (2011) by the American Physical Society.](/image/article/2013/CP/c3cp51741a/c3cp51741a-f18.gif) | ||
| Fig. 18 (a) The first-difference functions ΔGD(r)/barn = 0.0059(2)[gOD(r) − 1] + 0.00262(8)[gOO(r) − 1] and ΔGH(r)/barn = −0.0033(1)[gOH(r) − 1] + 0.00263(8)[gOO(r) − 1]. The O–H correlations in ΔGH(r) have a negative weighting factor because bH < 0. (b) The second-difference function ΔGOX(r) which is equal to gOD(r) (or gOH(r)) if the net quantum effects are sufficiently small (see the text). In (a) and (b) the solid curves were obtained by Fourier transforming the spline fitted data sets presented in Fig. 17 before and after the application of a Lorch modification function. The data obtained from the first procedure were joined with the data obtained from the second procedure after the first peak or trough. The open circles show the results obtained from path integral molecular dynamics using the flexible anharmonic TTM3-F model for water.227 Reprinted with permission from Zeidler et al.21 Copyright (2011) by the American Physical Society. | ||
Isotope effects in water have been investigated by McBride et al.234 by constructing a new model for D2O in which the O–H bond length in the rigid and non-polarisable TIP4PQ/2005 water model was shortened in line with the bond-length difference reported by Zeidler et al.21,23 The isotope shifts found for the melting point temperature of ice-Ih, and for the temperature of maximum density of the liquid, are in good agreement with the experimental results for H2O versus D2O.
The measured second-difference function ΔFOX(k) is shown in Fig. 17(b) and the corresponding real-space function ΔGOX(r) is shown in Fig. 18(b). The first peak in ΔGOX(r) at 0.987(5) Å is attributed to intra-molecular O–X correlations and gives a coordination number ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) XO = 2.0(1). The second peak at 1.83(2) Å corresponds to the inter-molecular O–X hydrogen bond and is at the same position as the inter-molecular O–D peak position in ΔGD(r).
XO = 2.0(1). The second peak at 1.83(2) Å corresponds to the inter-molecular O–X hydrogen bond and is at the same position as the inter-molecular O–D peak position in ΔGD(r).
The first- and second-difference functions were compared21,23 to the results obtained from path integral molecular dynamics simulations235 of light and heavy water using several different models of water, namely the rigid models TIP4P and SPC/E,236,237 the flexible harmonic models SPC/F and qSPC/Fw,238,239 and the flexible anharmonic models q-TIP4P/F and TTM3-F.227,240 These calculations, in which a system of quantum mechanical particles is mapped onto a simulation of classical ring polymers, provide an exact treatment of nuclear quantum fluctuations in the structure of a given potential energy model for water.235 In the cases of rigid or flexible harmonic classical models, the introduction of quantum effects leads, in general, to a large de-structuring of the hydrogen bonded network as shown by (i) a decrease in height of the first peak in gOO(r) which is an indicator of inter-molecular ordering, and (ii) an increase in the number of hydrogen bonds broken.239,241–243 This de-structuring can have dramatic implications for the dynamics with the diffusion coefficient changing by as much as 50%.239,240,244 Replication of the first O–O peak height reduction by using classical models requires an increase of the liquid temperature by ΔT ≃ 35–40 K. By contrast, flexible anharmonic models and a recent first-principles molecular dynamics study predict much smaller changes in the structure of water,220,240 corresponding to ΔT ≃ 5–18 K.
Of the various models, the intra-molecular O–H and O–D bond length difference of 0.0054 Å or ≃0.5% found using the TTM3-F model is in excellent agreement with the new diffraction data, and the comparison in Fig. 18(a) shows that theory and experiment are essentially superposed in the region where the intra-molecular correlations dominate. The TTM3-F model gives inter-molecular O–D and O–H peak positions both equal to 1.84 Å, with weighted peak positions 〈rOX〉 = ∫dr r gOX(r)/∫dr gOX(r) (where X denotes D or H) both equal to 1.91 Å i.e. the average length of a hydrogen bond barely changes between light and heavy water. The TTM3-F model reproduces accurately the O–H stretching region of the infra-red absorption spectrum of liquid water,227 and when quantum effects are included the diffusion coefficient Dqm = 0.95 × 0.237 = 0.225 Å2 ps−1 is in excellent accord with the measured value of 0.229 Å2 ps−1.227,240
As discussed by Zeidler et al.,21,23 the quantitative agreement found between the oxygen NDIS experimental results and the path integral molecular dynamics results for the TTM3-F model supports the proposal of “competing quantum effects” in liquid water.220,240 In this hypothesis inter-molecular zero point energy and tunnelling weaken the hydrogen bond network, as previously predicted,239,241–243 but quantum fluctuations in the anharmonic intra-molecular O–H bond increase its length and hence the dipole moment of each water molecule. This higher dipole acts, in turn, to increase the binding between molecules and hence the net effect of quantum fluctuations is smaller than originally suggested from rigid water simulations. It can be shown that, for a selection of water models, the extent of cancellation is strongly related to Δr = rOH − rOD, the change observed in the intra-molecular bond length on substituting H for D in the path integral simulations.21,23 The largest values of Δr correspond to flexible anharmonic models which show a much smaller change upon including quantum effects in (i) the O–O peak height, (ii) the number of hydrogen bonds broken, and (iii) the diffusion coefficient. In the case of the TTM3-F model, the cancellation between opposing quantum effects is large, leading to a small fall in the O–O peak height of 0.03 and a ratio of quantum to classical diffusion coefficients of 0.95. These changes are much smaller than for rigid models which cannot exhibit any competition between intra-molecular and inter-molecular quantum contributions. Support for the proposal of competing quantum effects also comes from calculations of the isotope fractionation ratio i.e. the equilibrium D/H ratio for the liquid versus the vapour phases of water.245 In this case, the flexible anharmonic q-TIP4P/F water model predicts the correct magnitude for the isotope fractionation ratio, but the TTM3-F water model overestimates the extent of the intra-molecular versus inter-molecular competition.
A large cancellation of competing quantum effects is fortuitous for experimental methods that exploit H/D isotope substitution such as the method of neutron diffraction with H/D isotope substitution,94,246–248 two-dimensional infra-red spectroscopy223,224 and nuclear magnetic resonance spectroscopy.249 This is because when these methods are used to study systems involving either light or heavy water at 300 K the structural environments probed, as well as the quantum contribution to the dynamics, are likely to be similar.
8 Conclusions and outlook
The results presented in this Perspective demonstrate that, by matching carefully designed experiments with suitable neutron diffraction instrumentation, it is possible to use NDIS to probe the detailed structure of liquids and glasses on multiple length scales. Moreover, it is now possible to apply the NDIS method even when the samples are small, as in high-pressure Paris-Edinburgh press experiments20 and in high-temperature aerodynamic-levitation experiments,18 or when the neutron scattering length contrast is small, as in experiments on water using oxygen isotope substitution.21–23 The different length scales that were discussed are associated with e.g. (i) intermediate versus extended-range ordering in network glass-forming systems, where there is a competition that affects the relative fragility of a material; (ii) changes in the local structural motifs on vitrification in the fragile glass-former CaAl2O4, which are accompanied by the development of extended branched-chains of Ca-centred polyhedra; and (iii) intra-molecular versus inter-molecular ordering in liquid water, where there is a competition between the associated quantum effects.The results obtained from carefully performed NDIS experiments play an important role in helping to assess e.g. the accuracy of various theoretical schemes that are employed to make atomistic models for different classes of disordered materials. This is illustrated by (i) first-principles investigations of liquid and glassy chalcogenide materials at ambient pressure, where the progression from use in self-consistent calculations of the local density approximation (LDA) to a generalised gradient approximation using the Becke–Lee–Yang–Parr (BLYP) functional to describe the electron exchange and correlation, has led to models that are in better agreement with the NDIS and other experimental results;29,66–68,107–110,250 (ii) classical molecular dynamics simulations of network-forming oxide glasses, where the parameterisation of a polarisable ion model for GeO2 using ab initio results has led to transferrable potentials that can be used to accurately predict, for the first time, the material properties under high-pressure conditions;20,28,36 and (iii) path integral molecular dynamics investigations of liquid water, where flexible anharmonic models best account for the measured difference between the intra-molecular O–H and O–D bond distances in light and heavy water,21,23 thus giving support to the hypothesis of competing intra-molecular versus inter-molecular quantum effects.220,240 Once the correct theoretical scheme has been established, these simulations can be used to enrich the information about a material that can be extracted, and they can also be used to predict the changes in material properties that occur when e.g. new chemical species are added or the state conditions are varied.
In summary, the NDIS method can be used to investigate the coordination environment of a growing number of chemical species under a variety of different sample conditions. This is enabling an increased exploitation of the neutron's attributes as a structural probe to study a broad range of disordered materials having scientific and/or technological significance. The development of new high counting-rate instrumentation at central neutron scattering facilities for diffraction studies of liquid and glassy materials, which can often be adapted for making a pair-distribution function analysis of the structure of crystalline or nano-crystalline materials, will continue to offer new opportunities for the NDIS method to provide benchmark experimental results.
Acknowledgements
We would particularly like to thank Henry Fischer at the Institut Laue-Langevin (ILL, Grenoble) for his help and advice with many of the NDIS experiments reported in this manuscript. Special thanks also go to Adrian Barnes (Bristol), Wilson Crichton (ESRF), Gabriel Cuello (ILL), Louis Hennet (Orlèans) and Stefan Klotz (Paris) for their contributions to the experimental work; and to Sandro Jahn (Potsdam), Sébastien Le Roux (Strasbourg), Tom Markland (Stanford), Dario Marrocchelli (Dublin), Carlo Massobrio (Strasbourg), Alfredo Pasquarello (Lausanne) and Mark Wilson (Oxford) for their contributions on the molecular dynamics front. Pierre Chieux (ILL), John Enderby (Bristol), Bob Evans (Bristol), Paul Madden (Oxford) and Shin'ichi Takeda (Kyushu) have all offered sound advice over the years. Much of the NDIS work described in this Perspective has benefitted immensely from the contributions made by past and present group members, including Ian Penfold, Chris Benmore (Argonne National Laboratory), Ingrid Petri, Takeshi Usuki (Yamagata), Richard Martin (Aston), James Drewitt (Edinburgh), Prae Chirawatkul (Synchrotron Light Research Institute, Thailand), Dean Whittaker (JET, Culham), Kamil Wezka and Harry Bone. We also thank James Drewitt for his help in preparing Fig. 1. The support of the EPSRC (Grant Ref.: EP/J009741/1) and ILL is gratefully acknowledged.References
- N. E. Cusack, The Physics of Structurally Disordered Matter, Hilger, Bristol, 1987 Search PubMed.
- S. R. Elliott, Physics of Amorphous Materials, Longman, Harlow, 2nd edn, 1990 Search PubMed.
- A. Feltz, Amorphous Inorganic Materials and Glasses, VCH, Weinheim, 1993 Search PubMed.
- CRC Handbook of Laser Science and Technology (Suppl. 2), ed. M. J. Weber, CRC Press, Boca Raton, FL, 1995 Search PubMed.
- M. Yamane and Y. Asahara, Glasses for Photonics, Cambridge University Press, Cambridge, 2000 Search PubMed.
- G. N. Greaves and S. Sen, Adv. Phys., 2007, 56, 1 CrossRef CAS.
- F. Franks, Water: A Matrix of Life, Royal Society of Chemistry, Cambridge, 2nd edn, 2000 Search PubMed.
- F. Paesani and G. A. Voth, J. Phys. Chem. B, 2009, 113, 5702 CrossRef CAS.
- P. S. Salmon, Nat. Mater., 2002, 1, 87 CrossRef CAS.
- P. Bondot, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1974, 30, 470 CrossRef CAS.
- J. E. Enderby, D. M. North and P. A. Egelstaff, Philos. Mag., 1966, 14, 961 CrossRef CAS.
- S. Ramos, A. C. Barnes, G. W. Neilson and M. J. Capitan, Chem. Phys., 2000, 258, 171 CrossRef CAS.
- S. Hosokawa, W.-C. Pilgrim, J.-F. Bérar and S. Kohara, Phys. Status Solidi A, 2011, 208, 2544 CrossRef CAS.
- A. C. Barnes, S. B. Lague, M. A. Hamilton, H. E. Fischer, A. N. Fitch and E. Dooryhee, J. Phys.: Condens. Matter, 1998, 10, L645 CrossRef CAS.
- D. L. Price, M.-L. Saboungi and A. C. Barnes, Phys. Rev. Lett., 1998, 81, 3207 CrossRef CAS.
- S. Sampath, C. J. Benmore, K. M. Lantzky, J. Neuefeind, K. Leinenweber, D. L. Price and J. L. Yarger, Phys. Rev. Lett., 2003, 90, 115502 CrossRef CAS.
- H. E. Fischer, A. C. Barnes and P. S. Salmon, Rep. Prog. Phys., 2006, 69, 233 CrossRef CAS.
- J. W. E. Drewitt, L. Hennet, A. Zeidler, S. Jahn, P. S. Salmon, D. R. Neuville and H. E. Fischer, Phys. Rev. Lett., 2012, 109, 235501 CrossRef.
- L. B. Skinner, C. J. Benmore, J. K. R. Weber, S. Tumber, L. Lazareva, J. Neuefeind, L. Santodonato, J. Du and J. B. Parise, J. Phys. Chem. B, 2012, 116, 13439 CrossRef CAS.
- K. Wezka, P. S. Salmon, A. Zeidler, D. A. J. Whittaker, J. W. E. Drewitt, S. Klotz, H. E. Fischer and D. Marrocchelli, J. Phys.: Condens. Matter, 2012, 24, 502101 CrossRef.
- A. Zeidler, P. S. Salmon, H. E. Fischer, J. C. Neuefeind, J. M. Simonson, H. Lemmel, H. Rauch and T. E. Markland, Phys. Rev. Lett., 2011, 107, 145501 CrossRef.
- A. Zeidler, P. S. Salmon, H. E. Fischer, J. C. Neuefeind, J. M. Simonson, H. Lemmel, H. Rauch and T. E. Markland, Phys. Rev. Lett., 2012, 108, 259604 CrossRef.
- A. Zeidler, P. S. Salmon, H. E. Fischer, J. C. Neuefeind, J. M. Simonson and T. E. Markland, J. Phys.: Condens. Matter, 2012, 24, 284126 CrossRef.
- M. Wilson and P. A. Madden, J. Phys.: Condens. Matter, 1993, 5, 6833 CrossRef CAS.
- P. A. Madden and M. Wilson, Chem. Soc. Rev., 1996, 25, 339 RSC.
- F. Hutchinson, A. J. Rowley, M. K. Walters, M. Wilson, P. A. Madden, J. C. Wasse and P. S. Salmon, J. Chem. Phys., 1999, 111, 2028 CrossRef CAS.
- S. Jahn and P. A. Madden, Phys. Earth Planet. Inter., 2007, 162, 129 CrossRef CAS.
- D. Marrocchelli, M. Salanne, P. A. Madden, C. Simon and P. Turq, Mol. Phys., 2009, 107, 443 CrossRef CAS.
- C. Massobrio, Lect. Notes Phys., 2010, 795, 343 CrossRef CAS.
- R. L. McGreevy and L. Pusztai, Mol. Simul., 1988, 1, 359 CrossRef.
- R. L. McGreevy, J. Phys.: Condens. Matter, 2001, 13, R877 CrossRef CAS.
- A. K. Soper, Chem. Phys., 1996, 202, 295 CrossRef CAS.
- A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- Y. Liang, C. R. Miranda and S. Scandolo, High–Pressure Res.: Appl. Geophys., 2008, 28, 35 CrossRef CAS.
- C. Massobrio, M. Celino, P. S. Salmon, R. A. Martin, M. Micoulaut and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174201 CrossRef.
- D. Marrocchelli, M. Salanne and P. A. Madden, J. Phys.: Condens. Matter, 2010, 22, 152102 CrossRef.
- C. A. Angell, Science, 1995, 267, 1924 CAS.
- R. Evans, R. J. F. Leote de Carvalho, J. R. Henderson and D. C. Hoyle, J. Chem. Phys., 1994, 100, 591 CrossRef CAS.
- R. J. F. Leote de Carvalho and R. Evans, Mol. Phys., 1994, 83, 619 CrossRef.
- P. S. Salmon, J. Phys.: Condens. Matter, 2006, 18, 11443 CrossRef CAS.
- T. E. Faber and J. M. Ziman, Philos. Mag., 1965, 11, 153 CrossRef CAS.
- E. Lorch, J. Phys. C: Solid State Phys., 1969, 2, 229 Search PubMed.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714 CrossRef CAS.
- A. B. Bhatia and D. E. Thornton, Phys. Rev. B: Solid State, 1970, 2, 3004 CrossRef.
- P. S. Salmon, Proc. R. Soc. London, Ser. A, 1992, 437, 591 CrossRef CAS.
- J. Blétry, Z. Naturforsch., A: Phys. Phys. Chem. Kosmophys., 1976, 31, 960 Search PubMed.
- A. B. Bhatia and V. K. Ratti, Phys. Chem. Liq., 1977, 6, 201 CrossRef CAS.
- M. Maret, P. Chieux, J. M. Dubois and A. Pasturel, J. Phys.: Condens. Matter, 1991, 3, 2801 CrossRef CAS.
- V. Bitrián, J. Trullàs and M. Silbert, Physica B, 2008, 403, 4249 CrossRef.
- H. Ruppersberg and H. Egger, J. Chem. Phys., 1975, 63, 4095 CrossRef CAS.
- A. Zeidler, J. W. E. Drewitt, P. S. Salmon, A. C. Barnes, W. A. Crichton, S. Klotz, H. E. Fischer, C. J. Benmore, S. Ramos and A. C. Hannon, J. Phys.: Condens. Matter, 2009, 21, 474217 CrossRef.
- K. F. Ludwig Jr, W. K. Warburton, L. Wilson and A. I. Bienenstock, J. Chem. Phys., 1987, 87, 604 CrossRef.
- A. Zeidler, P. S. Salmon, R. A. Martin, T. Usuki, P. E. Mason, G. J. Cuello, S. Kohara and H. E. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104208 CrossRef.
- H. E. Fischer, G. J. Cuello, P. Palleau, D. Feltin, A. C. Barnes, Y. S. Badyal and J. M. Simonson, Appl. Phys. A: Solid Surf., 2002, 74, S160 CrossRef CAS.
- A. K. Soper, in Advanced Neutron Sources - Inst. Phys. Conf. Ser., ed. D. K. Hyer, Institute of Physics, Bristol, 1989, vol. 97, p. 353 Search PubMed.
- A. C. Hannon, Nucl. Instrum. Methods Phys. Res., Sect. A, 2005, 551, 88 CrossRef CAS.
- D. T. Bowron, A. K. Soper, K. Jones, S. Ansell, S. Birch, J. Norris, L. Perrott, D. Riedel, N. J. Rhodes, S. R. Wakefield, A. Botti, M.-A. Ricci, F. Grazzi and M. Zoppi, Rev. Sci. Instrum., 2010, 81, 033905 CrossRef CAS.
- J. Neuefeind, K. K. Chipley, C. A. Tulk, J. M. Simonson and M. J. Winokur, Physica B, 2006, 385–386, 1066 CrossRef CAS.
- T. Hattori, Y. Katayama, A. Machida, T. Otomo and K. Suzuya, J. Phys.: Conf. Ser., 2010, 215, 012024 CrossRef.
- J. W. E. Drewitt, P. S. Salmon, A. C. Barnes, S. Klotz, H. E. Fischer and W. A. Crichton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 014202 CrossRef.
- P. S. Salmon, J. W. E. Drewitt, D. A. J. Whittaker, A. Zeidler, K. Wezka, C. L. Bull, M. G. Tucker, M. C. Wilding, M. Guthrie and D. Marrocchelli, J. Phys.: Condens. Matter, 2012, 24, 415102 CrossRef.
- A. Zeidler, J. Appl. Crystallogr., 2012, 45, 122 CrossRef CAS.
- A. K. Soper, G. W. Neilson, J. E. Enderby and R. A. Howe, J. Phys. C: Solid State Phys., 1977, 10, 1793 CrossRef CAS.
- P. S. Salmon, S. Xin and H. E. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6115 CrossRef CAS.
- F. G. Edwards, J. E. Enderby, R. A. Howe and D. I. Page, J. Phys. C: Solid State Phys., 1975, 8, 3483 CrossRef CAS.
- (a) I. T. Penfold and P. S. Salmon, Phys. Rev. Lett., 1991, 67, 97 CrossRef CAS; (b) I. T. Penfold and P. S. Salmon, Phys. Rev. Lett., 1992, 68, 253 CrossRef.
- P. S. Salmon and I. Petri, J. Phys.: Condens. Matter, 2003, 15, S1509 CrossRef CAS.
- I. Petri, P. S. Salmon and H. E. Fischer, Phys. Rev. Lett., 2000, 84, 2413 CrossRef CAS.
- P. S. Salmon, R. A. Martin, P. E. Mason and G. J. Cuello, Nature, 2005, 435, 75 CrossRef CAS.
- P. S. Salmon, A. C. Barnes, R. A. Martin and C. J. Cuello, Phys. Rev. Lett., 2006, 96, 235502 CrossRef.
- P. S. Salmon, A. C. Barnes, R. A. Martin and G. J. Cuello, J. Phys.: Condens. Matter, 2007, 19, 415110 CrossRef.
- P. S. Salmon, J. Phys.: Condens. Matter, 2007, 19, 455208 CrossRef.
- S. Biggin and J. E. Enderby, J. Phys. C: Solid State Phys., 1981, 14, 3129 CrossRef CAS.
- Q. Mei, C. J. Benmore, S. Sen, R. Sharma and J. L. Yarger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 144204 CrossRef.
- M. Wilson and P. S. Salmon, Phys. Rev. Lett., 2009, 103, 157801 CrossRef.
- S. C. Moss and D. L. Price, in Physics of Disordered Materials, ed. D. Adler, H. Fritzsche and S. R. Ovshinsky, Plenum, New York, 1985, p. 77 Search PubMed.
- S. R. Elliott, Nature, 1991, 354, 445 CrossRef CAS.
- P. S. Salmon, Proc. R. Soc. London, Ser. A, 1994, 445, 351 CrossRef CAS.
- P. S. Salmon, J. Non-Cryst. Solids, 2007, 353, 2959 CrossRef CAS.
- P. S. Salmon, J. Phys.: Condens. Matter, 2005, 17, S3537 CrossRef CAS.
- J. A. E. Desa, A. C. Wright, J. Wong and R. N. Sinclair, J. Non-Cryst. Solids, 1982, 51, 57 CrossRef CAS.
- A. V. Anikeenko and N. N. Medvedev, Phys. Rev. Lett., 2007, 98, 235504 CrossRef CAS.
- M. J. L. Sangster and M. Dixon, Adv. Phys., 1976, 25, 247 CrossRef CAS.
- N. C. Pyper, in Adv. Solid State Chem., ed. C. R. A. Catlow, JAI Press, London, 1991, vol. 2, p. 223 Search PubMed.
- R. Kjellander and B. Forsberg, J. Phys. A: Math. Gen., 2005, 38, 5405 CrossRef CAS.
- V. A. Levashov, S. J. L. Billinge and M. F. Thorpe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024111 CrossRef.
- J. K. Christie, S. N. Taraskin and S. R. Elliott, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 134207 CrossRef.
- J. K. Christie, S. N. Taraskin and S. R. Elliott, J. Phys.: Condens. Matter, 2004, 16, S5109 CrossRef CAS.
- M. Wilson, Phys. Chem. Chem. Phys., 2012, 14, 12701 RSC.
- V. Petkov and D. Le Messurier, J. Phys.: Condens. Matter, 2010, 22, 115402 CrossRef CAS.
- S. B. Mamedov, N. D. Aksenov, L. L. Makarov and Y. F. Batrakov, J. Non-Cryst. Solids, 1996, 195, 272 CrossRef CAS.
- P. Boolchand and W. J. Bresser, Philos. Mag. B, 2000, 80, 1757 CrossRef CAS.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 415108 CrossRef.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS.
- M. Cobb, D. A. Drabold and R. L. Cappelletti, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 12162 CrossRef CAS.
- M. Cobb and D. A. Drabold, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 3054 CrossRef CAS.
- C. Massobrio, A. Pasquarello and R. Car, Phys. Rev. Lett., 1998, 80, 2342 CrossRef CAS.
- C. Massobrio, A. Pasquarello and R. Car, J. Am. Chem. Soc., 1999, 121, 2943 CrossRef CAS.
- C. Massobrio, A. Pasquarello and R. Car, Comput. Mater. Sci., 2000, 17, 115 CrossRef CAS.
- X. Zhang and D. A. Drabold, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15695 CrossRef CAS.
- C. Massobrio, A. Pasquarello and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 144205 CrossRef.
- C. Massobrio, M. Celino and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174202 CrossRef.
- C. Massobrio and A. Pasquarello, J. Phys.: Condens. Matter, 2007, 19, 415111 CrossRef.
- C. Massobrio and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 014206 CrossRef.
- C. Massobrio and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144207 CrossRef.
- M. Wilson, B. K. Sharma and C. Massobrio, J. Chem. Phys., 2008, 128, 244505 CrossRef.
- M. Micoulaut, R. Vuilleumier and C. Massobrio, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214205 CrossRef.
- C. Massobrio, M. Micoulaut and P. S. Salmon, Solid State Sci., 2010, 12, 199 CrossRef CAS.
- M. Micoulaut, S. Le Roux and C. Massobrio, J. Chem. Phys., 2012, 136, 224504 CrossRef.
- A. Bouzid and C. Massobrio, J. Chem. Phys., 2012, 137, 046101 CrossRef.
- E. L. Gjersing, S. Sen and B. G. Aitken, J. Phys. Chem. C, 2010, 114, 8601 CAS.
- S. Sen and Z. Gan, J. Non-Cryst. Solids, 2010, 356, 1519 CrossRef CAS.
- M. Kibalchenko, J. R. Yates, C. Massobrio and A. Pasquarello, J. Phys. Chem. C, 2011, 115, 7755 CAS.
- T. G. Edwards, S. Sen and E. L. Gjersing, J. Non-Cryst. Solids, 2012, 358, 609 CrossRef CAS.
- P. Vashishta, R. K. Kalia, G. A. Antonio and I. Ebbsjö, Phys. Rev. Lett., 1989, 62, 1651 CrossRef CAS.
- P. Vashishta, R. K. Kalia and I. Ebbsjö, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 6034 CrossRef CAS.
- H. Iyetomi, P. Vashishta and R. K. Kalia, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1726 CrossRef.
- P. Vashishta, R. K. Kalia, J. P. Rino and I. Ebbsjö, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 12197 CrossRef CAS.
- P. Chirawatkul, A. Zeidler, P. S. Salmon, S. Takeda, Y. Kawakita, T. Usuki and H. E. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 014203 CrossRef.
- H. Fujii, S. Tahara, Y. Kato, S. Kohara, M. Itou, Y. Kawakita and S. Takeda, J. Non-Cryst. Solids, 2007, 353, 2094 CrossRef CAS.
- S. Takeda, H. Fujii, Y. Kawakita, Y. Kato, S. Fujita, Y. Yokota and S. Kohara, Mater. Sci. Eng., A, 2007, 449–451, 590 CrossRef.
- S. Takeda, H. Fujii, Y. Kawakita, S. Tahara, S. Nakashima, S. Kohara and M. Itou, J. Alloys Compd., 2008, 452, 149 CrossRef CAS.
- I. Egry and D. Holland-Moritz, Eur. Phys. J.: Spec. Top., 2011, 196, 131 CrossRef.
- D. Ma, A. D. Stoica and X.-L. Wang, Nat. Mater., 2009, 8, 30 CrossRef CAS.
- W. Klement Jr, R. H. Willens and P. Duwez, Nature, 1960, 187, 869 CrossRef.
- H. S. Chen and D. Turnbull, J. Appl. Phys., 1967, 38, 3646 CrossRef CAS.
- V. N. Novikov and A. P. Sokolov, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064203 CrossRef.
- W. H. Wang, Prog. Mater. Sci., 2007, 52, 540 CrossRef CAS.
- D. B. Miracle, Nat. Mater., 2004, 3, 697 CrossRef CAS.
- W. L. Johnson, JOM, 2002, 54, 40 CrossRef CAS.
- J. F. Löffler, Intermetallics, 2003, 11, 529 CrossRef.
- A. Inoue and A. Takeuchi, Acta Mater., 2011, 59, 2243 CrossRef CAS.
- E. Axinte, Mater. Des., 2012, 35, 518 CrossRef CAS.
- H. W. Sheng, W. K. Luo, F. M. Alamgir, J. M. Bai and E. Ma, Nature, 2006, 439, 419 CrossRef CAS.
- P. F. Guan, T. Fujita, A. Hirata, Y. H. Liu and M. W. Chen, Phys. Rev. Lett., 2012, 108, 175501 CrossRef CAS.
- L. Yang, G. Q. Guo, L. Y. Chen, C. L. Huang, T. Ge, D. Chen, P. K. Liaw, K. Saksl, Y. Ren, Q. S. Zeng, B. LaQua, F. G. Chen and J. Z. Jiang, Phys. Rev. Lett., 2012, 109, 105502 CrossRef CAS.
- P. A. Egelstaff, N. H. March and N. C. McGill, Can. J. Phys., 1974, 52, 1651 CAS.
- J. Chihara, J. Phys. F: Met. Phys., 1987, 17, 295 CrossRef CAS.
- S. Takeda, M. Inui, S. Tamaki, K. Maruyama and Y. Waseda, J. Phys. Soc. Jpn., 1994, 63, 1794 CrossRef CAS.
- S. Takeda, Y. Kawakita, M. Inui, K. Maruyama, S. Tamaki and Y. Waseda, J. Non-Cryst. Solids, 1996, 205–207, 365 CrossRef CAS.
- P. S. Salmon, I. Petri, P. H. K. de Jong, P. Verkerk, H. E. Fischer and W. S. Howells, J. Phys.: Condens. Matter, 2004, 16, 195 CrossRef CAS.
- T. Freltoft, J. K. Kjems and S. K. Sinha, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 269 CrossRef CAS.
- P. Mangin, G. Marchal, C. Mourey and C. Janot, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 3047 CrossRef CAS.
- C. Grodon, M. Dijkstra, R. Evans and R. Roth, Mol. Phys., 2005, 103, 3009 CrossRef CAS.
- P. Hopkins and M. Schmidt, J. Phys.: Condens. Matter, 2010, 22, 325108 CrossRef.
- D. L. Price, High-Temperature Levitated Materials, Cambridge University Press, Cambridge, 2010 Search PubMed.
- J. K. R. Weber, J. J. Felten, B. Cho and P. C. Nordine, Nature, 1998, 393, 769 CrossRef CAS.
- L. B. Skinner, A. C. Barnes and W. Crichton, J. Phys.: Condens. Matter, 2006, 18, L407 CrossRef CAS.
- D. Holland-Moritz, T. Schenk, P. Convert, T. Hansen and D. M. Herlach, Meas. Sci. Technol., 2005, 16, 372 CrossRef CAS.
- L. Hennet, I. Pozdnyakova, A. Bytchkov, V. Cristiglio, P. Palleau, H. E. Fischer, G. J. Cuello, M. Johnson, P. Melin, D. Zanghi, S. Brassamin, J.-F. Brun, D. L. Price and M.-L. Saboungi, Rev. Sci. Instrum., 2006, 77, 053903 CrossRef.
- (a) A. C. Barnes, L. B. Skinner, P. S. Salmon, A. Bytchkov, I. Pozdnyakova, T. O. Farmer and H. E. Fischer, Phys. Rev. Lett., 2009, 103, 225702 CrossRef; (b) A. C. Barnes, L. B. Skinner, P. S. Salmon, A. Bytchkov, I. Pozdnyakova, T. O. Farmer and H. E. Fischer, Phys. Rev. Lett., 2011, 106, 119602 CrossRef.
- T. Voigtmann, A. Meyer, D. Holland-Moritz, S. Stüber, T. Hansen and T. Unruh, Europhys. Lett., 2008, 82, 66001 CrossRef.
- D. Holland-Moritz, S. Stüber, H. Hartmann, T. Unruh, T. Hansen and A. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 064204 CrossRef.
- T. Schenk, V. Simonet, D. Holland-Moritz, R. Bellissent, T. Hansen, P. Convert and D. M. Herlach, Europhys. Lett., 2004, 65, 34 CrossRef CAS.
- J. E. Drewitt, S. Jahn, V. Cristiglio, A. Bytchkov, M. Leydier, S. Brassamin, H. E. Fischer and L. Hennet, J. Phys.: Condens. Matter, 2011, 23, 155101 CrossRef.
- J. Akola, S. Kohara, K. Ohara, A. Fujiwara, Y. Watanabe, A. Masuno, T. Usuki, T. Kubo, A. Nakahira, K. Nitta, T. Uruga, J. K. R. Weber and C. J. Benmore, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10129, DOI:10.1073/pnas.1300908110.
- D. Iuga, C. Morais, Z. Gan, D. R. Neuville, L. Cormier and D. Massiot, J. Am. Chem. Soc., 2005, 127, 11540 CrossRef CAS.
- S. Y. Park and S. K. Lee, Geochim. Cosmochim. Acta, 2012, 80, 125 CrossRef CAS.
- J. F. Stebbins and D. Sykes, Am. Mineral., 1990, 75, 943 CAS.
- G. S. Henderson, Can. Mineral., 2005, 43, 1921 CrossRef CAS.
- W. E. Jackson, F. Farges, M. Yeager, P. A. Mabrouk, S. Rossano, G. A. Waychunas, E. I. Solomon and G. E. Brown Jr, Geochim. Cosmochim. Acta, 2005, 69, 4315 CrossRef CAS.
- G. S. Henderson, G. Calas and J. F. Stebbins, Elements, 2006, 2, 269 CrossRef CAS.
- J. F. Stebbins, E. V. Dubinsky, K. Kanehashi and K. E. Kelsey, Geochim. Cosmochim. Acta, 2008, 72, 910 CrossRef CAS.
- D. Giordano and D. B. Dingwell, J. Phys.: Condens. Matter, 2003, 15, S945 CrossRef CAS.
- D. Giordano and J. K. Russell, J. Phys.: Condens. Matter, 2007, 19, 205148 CrossRef.
- D. Giordano, J. K. Russell and D. B. Dingwell, Earth Planet. Sci. Lett., 2008, 271, 123 CrossRef CAS.
- C. J. Benmore and P. S. Salmon, Phys. Rev. Lett., 1994, 73, 264 CrossRef CAS.
- J. Liu and P. S. Salmon, Europhys. Lett., 1997, 39, 521 CrossRef CAS.
- P. S. Salmon and S. Xin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064202 CrossRef.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, Phys. Rev. Lett., 2003, 90, 185501 CrossRef.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, J. Phys.: Condens. Matter, 2003, 15, 8235 CrossRef CAS.
- I. T. Penfold and P. S. Salmon, Phys. Rev. Lett., 1990, 64, 2164 CrossRef CAS.
- S. A. van der Aart, P. Verkerk, A. C. Barnes, P. S. Salmon, R. Winter, H. Fischer, L. A. de Graaf and W. van der Lugt, Physica B, 1998, 241–243, 961 Search PubMed.
- J. C. Wasse and P. S. Salmon, J. Phys.: Condens. Matter, 1999, 11, 1381 CrossRef CAS.
- J. C. Wasse, P. S. Salmon and R. G. Delaplane, J. Phys.: Condens. Matter, 2000, 12, 9539 CrossRef CAS.
- J. C. Wasse, I. Petri and P. S. Salmon, J. Phys.: Condens. Matter, 2001, 13, 6165 CrossRef CAS.
- R. A. Martin, P. S. Salmon, C. J. Benmore, H. E. Fischer and G. J. Cuello, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054203 CrossRef.
- R. A. Martin, P. S. Salmon, H. E. Fischer and G. J. Cuello, J. Non-Cryst. Solids, 2004, 345–346, 208 CrossRef.
- S. Xin, J. Liu and P. S. Salmon, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 064207 CrossRef.
- K. Wezka, A. Zeidler, P. S. Salmon, P. Kidkhunthod, A. C. Barnes and H. E. Fischer, J. Non-Cryst. Solids, 2011, 357, 2511 CrossRef CAS.
- V. V. Brazhkin and A. G. Lyapin, J. Phys.: Condens. Matter, 2003, 15, 6059 CrossRef CAS.
- M. C. Wilding, M. Wilson and P. F. McMillan, Chem. Soc. Rev., 2006, 35, 964 RSC.
- G. N. Greaves, M. C. Wilding, S. Fearn, D. Langstaff, F. Kargl, S. Cox, Q. Vu Van, O. Majérus, C. J. Benmore, R. Weber, C. M. Martin and L. Hennet, Science, 2008, 322, 566 CrossRef CAS.
- D. Daisenberger, T. Deschamps, B. Champagnon, M. Mezouar, R. Q. Cabrera, M. Wilson and P. F. McMillan, J. Phys. Chem. B, 2011, 115, 14246 CrossRef CAS.
- M. Guthrie, C. A. Tulk, C. J. Benmore, J. Xu, J. L. Yarger, D. D. Klug, J. S. Tse, H.-K. Mao and R. J. Hemley, Phys. Rev. Lett., 2004, 93, 115502 CrossRef CAS.
- M. Wilding, M. Guthrie, C. L. Bull, M. G. Tucker and P. F. McMillan, J. Phys.: Condens. Matter, 2008, 20, 244122 CrossRef.
- E. Soignard, C. J. Benmore and J. L. Yarger, Rev. Sci. Instrum., 2010, 81, 035110 CrossRef.
- S. Klotz, Techniques in High Pressure Neutron Scattering, CRC Press, Boca Raton, 2013 Search PubMed.
- G. Lelong, L. Cormier, G. Ferlat, V. Giordano, G. S. Henderson, A. Shukla and G. Calas, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134202 CrossRef.
- C. J. Benmore, E. Soignard, S. A. Amin, M. Guthrie, S. D. Shastri, P. L. Lee and J. L. Yarger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054105 CrossRef.
- Q. Mei, C. J. Benmore, R. T. Hart, E. Bychkov, P. S. Salmon, C. D. Martin, F. M. Michel, S. M. Antao, P. J. Chupas, P. L. Lee, S. D. Shastri, J. B. Parise, K. Leinenweber, S. Amin and J. L. Yarger, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 014203 CrossRef.
- M. Guthrie, C. A. Tulk, J. Molaison and A. M. dos Santos, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184205 CrossRef.
- M. Micoulaut, J. Phys.: Condens. Matter, 2004, 16, L131 CrossRef CAS.
- M. Micoulaut, Y. Guissani and B. Guillot, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2006, 73, 031504 CrossRef CAS.
- K. V. Shanavas, N. Garg and S. M. Sharma, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094120 CrossRef.
- T. Li, S. Huang and J. Zhu, Chem. Phys. Lett., 2009, 471, 253 CrossRef CAS.
- X. F. Zhu and L. F. Chen, Physica B, 2009, 404, 4178 CrossRef CAS.
- L. Giacomazzi, P. Umari and A. Pasquarello, Phys. Rev. Lett., 2005, 95, 075505 CrossRef.
- L. Giacomazzi, P. Umari and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155208 CrossRef.
- D. J. Durben and G. H. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 2355 CrossRef CAS.
- C. H. Polsky, K. H. Smith and G. H. Wolf, J. Non-Cryst. Solids, 1999, 248, 159 CrossRef CAS.
- M. Micoulaut, L. Cormier and G. S. Henderson, J. Phys.: Condens. Matter, 2006, 18, R753 CrossRef CAS.
- M. G. Tucker, D. A. Keen, M. T. Dove and K. Trachenko, J. Phys.: Condens. Matter, 2005, 17, S67 CrossRef CAS.
- Y. Liang, C. R. Miranda and S. Scandolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 024205 CrossRef.
- M. Wu, Y. Liang, J.-Z. Jiang and J. S. Tse, Sci. Rep., 2012, 2, 398 Search PubMed.
- J.-F. Lin, H. Fukui, D. Prendergast, T. Okuchi, Y. Q. Cai, N. Hiraoka, C.-S. Yoo, A. Trave, P. Eng, H. Y. Hu and P. Chow, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 012201 CrossRef.
- H. Fukui, M. Kanzaki, N. Hiraoka and Y. Q. Cai, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 012203 CrossRef.
- J.-P. Poirier, Introduction to the Physics of the Earth's Interior, Cambridge University Press, Cambridge, 2nd edn, 2000 Search PubMed.
- D. L. Anderson, New Theory of the Earth, Cambridge University Press, Cambridge, 2007 Search PubMed.
- C. A. Angell, P. A. Cheeseman and S. Tamaddon, Science, 1982, 218, 885 CAS.
- J. D. Kubicki and A. C. Lasaga, Phys. Chem. Miner., 1991, 17, 661 CrossRef CAS.
- N. Lane, Oxygen: The Molecule that Made the World, Oxford University Press, Oxford, 2002 Search PubMed.
- M. Mookherjee, L. Stixrude and B. Karki, Nature, 2008, 452, 983 CrossRef CAS.
- A. Pasquarello, M. S. Hybertsen and R. Car, Nature, 1998, 396, 58 CrossRef CAS.
- H. Rauch and S. A. Werner, Neutron Interferometry: Lessons in Experimental Quantum Mechanics, Clarendon Press, Oxford, 2000 Search PubMed.
- H. E. Fischer, J. M. Simonson, J. C. Neuefeind, H. Lemmel, H. Rauch, A. Zeidler and P. S. Salmon, J. Phys.: Condens. Matter, 2012, 24, 505105 CrossRef.
- L. Koester, H. Rauch and E. Seymann, At. Data Nucl. Data Tables, 1991, 49, 65 CrossRef CAS.
- V. F. Sears, Neutron News, 1992, 3, 26 CrossRef.
- B. Tomberli, C. J. Benmore, P. A. Egelstaff, J. Neuefeind and V. Honkimäki, J. Phys.: Condens. Matter, 2000, 12, 2597 CrossRef CAS.
- B. Chen, I. Ivanov, M. L. Klein and M. Parrinello, Phys. Rev. Lett., 2003, 91, 215503 CrossRef.
- R. T. Hart, C. J. Benmore, J. Neuefeind, S. Kohara, B. Tomberli and P. A. Egelstaff, Phys. Rev. Lett., 2005, 94, 047801 CrossRef CAS.
- J. A. Morrone and R. Car, Phys. Rev. Lett., 2008, 101, 017801 CrossRef.
- J. D. Eaves, J. J. Loparo, C. J. Fecko, S. T. Roberts, A. Tokmakoff and P. L. Geissler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13019 CrossRef CAS.
- J. J. Loparo, S. T. Roberts and A. Tokmakoff, J. Chem. Phys., 2006, 125, 194522 CrossRef.
- J. G. Powles, Mol. Phys., 1981, 42, 757 CrossRef CAS.
- A. K. Soper, Mol. Phys., 2009, 107, 1667 CrossRef CAS.
- G. S. Fanourgakis and S. S. Xantheas, J. Chem. Phys., 2008, 128, 074506 CrossRef.
- M. A. Floriano, D. D. Klug, E. Whalley, E. C. Svensson, V. F. Sears and E. D. Hallman, Nature, 1987, 329, 821 CrossRef CAS.
- R. L. Cook, F. C. De Lucia and P. Helminger, J. Mol. Spectrosc., 1974, 53, 62 CrossRef CAS.
- W. F. Kuhs and M. S. Lehmann, in Water Science Reviews 2, ed. F. Franks, Cambridge University Press, Cambridge, 1986, p. 1 Search PubMed.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2008, 101, 065502 CrossRef CAS.
- A. K. Soper, ISRN Phys. Chem., 2013, 279463 CAS.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2012, 108, 259603 CrossRef CAS.
- C. McBride, J. L. Aragones, E. G. Noya and C. Vega, Phys. Chem. Chem. Phys., 2012, 14, 15199 RSC.
- M. Parrinello and A. Rahman, J. Chem. Phys., 1984, 80, 860 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269 CrossRef CAS.
- K. Toukan and A. Rahman, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 2643 CrossRef CAS.
- F. Paesani, W. Zhang, D. A. Case, T. E. Cheatham III and G. A. Voth, J. Chem. Phys., 2006, 125, 184507 CrossRef.
- S. Habershon, T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2009, 131, 024501 CrossRef.
- R. A. Kuharski and P. J. Rossky, J. Chem. Phys., 1985, 82, 5164 CrossRef CAS.
- A. Wallqvist and B. J. Berne, Chem. Phys. Lett., 1985, 117, 214 CrossRef CAS.
- L. Hernández de la Peña and P. G. Kusalik, J. Chem. Phys., 2004, 121, 5992 CrossRef.
- L. Hernández de la Peña and P. G. Kusalik, J. Chem. Phys., 2006, 125, 054512 CrossRef.
- T. E. Markland and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7988 CrossRef CAS.
- A. K. Soper, Chem. Phys., 2000, 258, 121 CrossRef CAS.
- A. K. Soper and M. A. Ricci, Phys. Rev. Lett., 2000, 84, 2881 CrossRef CAS.
- J. C. Dore, M. Garawi and M.-C. Bellissent-Funel, Mol. Phys., 2004, 102, 2015 CrossRef CAS.
- X. Cui, S. Mao, M. Liu, H. Yuan and Y. Du, Langmuir, 2008, 24, 10771 CrossRef CAS.
- S. Le Roux, A. Zeidler, P. S. Salmon, M. Boero, M. Micoulaut and C. Massobrio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 134203 CrossRef.
Footnotes |
| † The mathematical validity of the Lorch function has been called into question by Soper and Barney.43 However, a rigorous derivation, which also gives an analytical expression for the real-space manifestation of this function, is given in ref. 40. |
| ‡ The Bhatia–Thornton formalism can be generalised to systems containing more than two chemical species.46–49 |
| § The neutron scattering lengths for several isotopes take negative values. It is therefore possible in a neutron diffraction experiment to measure SCC(k) directly.50 |
| ¶ The periodicity associated with the FSDP can be discerned in the r-space functions measured for several network glass-forming systems.78,79 |
| || The appearance of ordering on both the intermediate and extended length scales is sometimes unappreciated for prototypical network glass-forming systems such as SiO2 and GeO2 because the principal peak is usually small or absent in the measured neutron or X-ray diffraction patterns. However, as shown by the measured partial structure factors for SiO2 and GeO2 glass,71,74 the suppression of this feature simply reflects the fact that the weighting factors in eqn (2) lead to a cancellation of the principal peaks in SMM(k) and SXX(k) with the principal trough in SMX(k). |
| ** For low densities, the rhIJ(r) functions show simple exponential decay with a common decay length. The crossover from pure exponential to exponentially damped oscillatory decay defines a line in the density–temperature plane known either as the Fisher–Widom line or as the Kirkwood line, depending on the mechanism by which crossover occurs.38–40 |
| †† Exponentially damped oscillatory rhIJ(r) functions for network glasses will not be reproduced by models based on crystalline systems since the ordering in rhIJ(r) will persist to arbitrarily large distances,86 even when a large positional disorder is applied to the atomic coordinates.87,88 |
| ‡‡ The reference pair-potentials used to produce EPSR models usually comprise a Lennard-Jones term, a Coulomb term to represent charged atom interactions, and often an additional repulsive exponential term aimed at softening the Lennard-Jones repulsive core.33,93,94 |
| §§ The work in ref. 95, 96 and 100 used an electronic-structure scheme within the local density approximation (LDA) for the exchange and correlation energy which does not evolve self-consistently with the atomic motion, together with a minimal basis set. Several of the features in the resultant models are consistent with experiment67 but are not reproduced when using fully self-consistent LDA calculations. This is attributed, in the latter, to an underestimate in the ionic character of the bonding.97–99,101 |
| ¶¶ When using the EPSR method to extract partial structure factors, it is possible to weight the results either towards those obtained from the reference rigid-ion pair-potential model, such that the extracted pair-correlation functions are essentially those of this starting model, or towards the experimental data, such that the extracted pair-correlation functions contain more information from the experimental results.33 It is therefore possible to bias the results towards those expected from the starting model. |
| |||| The formation of metallic glasses was first reported for the Au–Si system near the eutectic composition.125,126 |
| *** In principle, liquid and glassy metals should be treated as a mixture of ions and valence electrons such that the structure, for example, of a single component system is described in terms of ion–ion SII(k), ion–valence electron SIe(k), and valence electron–valence electron See(k) partial structure factors.137 Since neutrons scatter from nuclei whereas X-rays scatter from electrons, it is possible in some materials like liquid Li to extract SII(k) and SIe(k) along with the valence electron form factor.138–141 |
| ††† Eqn (19) was assumed by Ma et al.124 to be valid for both neutron and X-ray diffraction data. |
| ‡‡‡ It is necessary to assume that the weighting factors for the r[gαβ(r) − 1] terms are independent of r if eqn (21) is also to apply to X-ray diffraction data. In general these weighting factors are, however, related to Fourier transforms of the atomic form factors f(k) and will therefore be r-dependent.119 |
| §§§ In the case of aerodynamic-levitation experiments, a large fraction of the sample volume is shielded from an incident neutron or X-ray beam by the nozzle of the levitation device.150 |
| ¶¶¶ In the isomorphic substitution method, different elements with contrasting scattering lengths are substituted for one another. It is assumed that these elements have identical coordination environments. |
|||||| These Ca–O coordination numbers were obtained by integrating over the first peak in the relevant ΔGCaμ(r) function up to a cut-off value rcut = 3 Å (eqn (4)). For the glass, a reduced coordination number of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OCa = 5.1(2) is obtained by shortening rcut to 2.79 Å, in accord with new results obtained from work using density functional theory and reverse Monte Carlo modelling.156 In the latter work, the fraction of oxygen atoms in the glass that form triclusters, where one oxygen atom is shared by three AlO4 tetrahedra, was found to be ∼14.5% from the models, somewhat larger than the fraction of ∼5% found from nuclear magnetic resonance experiments157 and the estimate of 2(2)% from the NDIS work.18 OCa = 5.1(2) is obtained by shortening rcut to 2.79 Å, in accord with new results obtained from work using density functional theory and reverse Monte Carlo modelling.156 In the latter work, the fraction of oxygen atoms in the glass that form triclusters, where one oxygen atom is shared by three AlO4 tetrahedra, was found to be ∼14.5% from the models, somewhat larger than the fraction of ∼5% found from nuclear magnetic resonance experiments157 and the estimate of 2(2)% from the NDIS work.18 |
| **** The principal peak in the measured neutron diffraction pattern for liquid ammonia also sharpens with increasing density as packing constraints become more important.192 The extended-range ordering for this system is described by using eqn (21). |
†††† Since the volume of a regular tetrahedron  and the number density of tetrahedral units for SiO2 or GeO2 at low pressures ρtet = ρ/3, the packing fraction for tetrahedral units is and the number density of tetrahedral units for SiO2 or GeO2 at low pressures ρtet = ρ/3, the packing fraction for tetrahedral units is  . The appearance of fivefold coordinated Si or Ge atoms at ρ . The appearance of fivefold coordinated Si or Ge atoms at ρ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) MO3 ≃ 0.4 therefore coincides with a packing fraction for tetrahedral units of ≃0.62. MO3 ≃ 0.4 therefore coincides with a packing fraction for tetrahedral units of ≃0.62. |
| ‡‡‡‡ In ref. 232 the EPSR method was used with the TIP4P-2005 reference potential model for water in order to improve agreement with X-ray diffraction data for the first inter-molecular O–O peak (A. K. Soper, private communication). The sensitivity of the EPSR method to the choice of reference potential is discussed elsewhere.22,23,94,233 |
| This journal is © the Owner Societies 2013 |
