The dissociation of glycolate—astrochemical and prebiotic relevance

Abstract

On the basis of mass spectrometric experiments and quantum chemical calculations, including detailed kinetic and dynamics calculations, we report the unimolecular dissociation of an isolated glycolate anion. The dominating processes are: loss of formaldehyde; loss of carbon monoxide; loss of carbon dioxide; and loss of a hydrogen molecule, with the latter having the lowest energetic threshold. At higher energies, CO loss is the dominating reaction. The loss of CO may be followed by a second CO loss, leading to the H⁻H₂O complex in close mechanistic relationship to the Nibbering reaction. The results provide valuable insights into possible mechanisms for interstellar and prebiotic formation of glycolate via the reverse of the unimolecular dissociation reactions. We propose that the addition of the complex of OH⁻ and CO to CH₂O is the most feasible route to gas phase synthesis of glycolate, since all species are abundant in interstellar space.

---

Introduction

Among the large number of organic molecules that are plausibly involved in the first prebiotic reactions, glycolic acid (HOCH₂COOH), being the smallest α-hydroxy carboxylic acid is of special interest. This interest results from the fact that the molecule not only is involved in present biological processes, in particular since the conversion of glycolic acid leads to the simplest α-amino acid, glycine, but also was very likely present on the early Earth.

The hypothesis that animate matter originates from inanimate matter through a spontaneous and gradual increase in molecular complexity was first formulated in 1924 by Alexander Oparin,¹ and is referred to as chemical evolution. The underlying so-called chemical continuity principle states that there is a gradual increase in complexity during this part of evolution. The process started already when atoms combined to form small inorganic and organic molecules that in turn formed larger organic molecules. Eventually, macromolecules formed and molecular complexes were built and became involved in metabolic networks—which in turn lead to cellular life. After the formation of the first unicellular living organisms, one may say that chemical evolution turned into biological evolution.

Prebiotic organic compounds on the early Earth can be divided into two groups depending on whether they were of terrestrial or extraterrestrial origin.² Terrestrial sources include endogenous organic synthesis driven by different energy sources (UV radiation, electric discharge, hydrothermal energy) and have been subject to laboratory simulations. Extraterrestrial sources of organic material include cosmic dust, meteorites and comets, and are subject to direct examination because these objects continue to deliver organic molecules to Earth.

Glycolic acid (alongside with formic and lactic acid, glycine and alanine) is one of the dominant products in electric discharge syntheses in strongly reducing atmospheres (mixtures of CH₄, NH₃ or N₂, and H₂O, with or without H₂).³ In mildly reducing and non-reducing atmospheres, the yields of hydroxy acids (as well as amino acids) are low.³ If such conditions were prevailing, one should consider extraterrestrial objects as more likely primary sources of organic compounds. Glycolic acid has been detected in the Murchison meteorite.^4,5 It is one of the most studied meteorites due to its large mass (>100 kg), the fact that it was an observed fall, and that it belongs to a group of meteorites called carbonaceous chondrites, which are rich in organic compounds. The formation of complex organic molecules in interstellar space has been considered to occur mainly in the gas phase by bimolecular radical or cationic reactions, since reactions without significant activation energies are essential for efficient synthesis under the extremely low pressures and temperatures encountered in typical molecular clouds.⁶ Interestingly, the existence of glycolic acid or glycine in the much-studied giant molecular cloud Sgr B(N) has not yet been confirmed,^7,8 although related compounds have been detected including acetaldehyde,⁹ acetic acid,¹⁰ glycolaldehyde,¹¹ and methyl formate.¹² More recently, it has been realized that gas-grain processes also should be considered to explain the pre-comet or pre-meteor formation of organic molecules.¹³ In this respect it is relevant that laboratory studies show that glycolic acid is efficiently formed by UV radiation of organic ices.^14,15 In addition to gas-grain and radical and cationic bimolecular reactions, it is also necessary to include anionic reactions. Traditionally, there has been little interest in this topic,¹⁶ but recent observations of organic anions¹⁷ in giant molecular clouds have challenged this view. For this reason it is also pertinent to look for plausible anionic routes to key prebiotic molecules. In the present study, we have investigated the deprotonated form of glycolic acid, the glycolate ion, in order to elucidate the energetics and mechanisms of its unimolecular dissociation.

Direct investigation of the gas phase reactions that may lead to a given target molecule is complicated, even for a small molecule such as a glycolate anion, since the number of potential combination of reactants leading to this molecule is large. Studying the reverse reaction may in many cases be a more rewarding strategy—an approach that is analogous to the retrosynthetic analysis¹⁸ used in modern organic synthesis; consequently, the spontaneous dissociation of the molecule of interest can be studied to obtain insight into the reverse synthetic pathways to the molecule. We are aware of three previous studies of the unimolecular dissociation of the glycolate anion.^19–21 Very recently, a partial computational study on some possible dissociation mechanisms has also been published.²² Despite that these studies contain useful details and provide some chemical insight, none of them is comprehensive, and the mass spectra presented in the two experimental publications are widely different. The purpose of our contribution is therefore to clarify the unimolecular chemistry, the associated mechanistic features, and the energetics in order to provide a full and consistent picture. Based on this, our second goal is to identify likely reactions for the interstellar synthesis of glycolic acid.

Experimental methods

Low-energy collisional activation mass spectrometry

The experiments were conducted using a three-sector mass spectrometer with quadrupole/hexapole/time-of-flight (QHT) geometry (QTOF 2, Micromass/Waters, Manchester, U.K.) equipped with an electrospray ionization (ESI) source operated in the negative ion mode. Glycolic acid solution was purchased from Sigma-Aldrich, and no further purification was done. Solutions were prepared by diluting the glycolic acid with 1 : 1 (by weight) water–methanol down to a concentration of 50 μg ml⁻¹. The solution was injected at a rate of 0.01 ml min⁻¹ into the electrospray ionization (ESI) source via a syringe pump. Collisionally induced dissociation (CID) experiments were performed at two different pressures for mass selected deprotonated glycolic acid (m/z = 75). Argon was used as the collision gas at nominal pressures set to 4.8 × 10⁻³ mbar and 6.4 × 10⁻⁴ mbar for the high and low pressure experiment, respectively. The gas inlet was controlled by a leak valve.

In addition, energy-resolved CID mass spectra were obtained by varying the central electrical potential difference between the quadrupole and hexapole units. The correspondence between the potential readout and the actual value has been calibrated, and is known to be accurate within 0.1 V. By plotting and analyzing the breakdown curves—the relative abundance of each fragment ion as a function of the center-of-mass energy E_CM (i.e., the fraction of E_lab that is available for inelastic scattering, E_CM = E_lab [M/(M + m)], where M is the mass of the neutral collision gas molecule and m is the mass of the parent ion) was obtained. Attempts to estimate the threshold energies, E₀, for the most abundant fragment ions were done by a deconvolution procedure of the energy-resolved, collision-induced, dissociation cross-sections.^23,24

Quantum-chemical calculations

Gaussian 09, the most recent version of the Gaussian program suite, was used for most quantum-chemical calculations.²⁵ Initial geometry optimizations were performed using B3LYP/6-31G(2df,p). The results of frequency calculations (N.B. specifically monitoring the number of imaginary frequencies) were used to identify the nature of the stationary points (minimum or first-order saddle points). Intrinsic reaction path calculations (IRC) were employed for all transition state geometries to verify that they actually connect the presupposed minima. To obtain more accurate estimates of the thermochemical quantities we took advantage of the G4 (Gaussian-4 theory) compound method,²⁶ for which geometry optimization is performed at a moderate level of theory, B3LYP/6-31G(2df,p). Then the equilibrium structures obtained are subject to a sequence of single point energy calculations; CCSD(T) calculations are performed with a moderate-sized basis set as are MP4 calculations with a relatively large basis set. Finally, the results of the calculations are combined using an extrapolation scheme, also including zero point vibrational energy corrections, to approximate the energies of more expensive calculations; final energies are estimated to be accurate within ±10 kJ mol⁻¹.

Multireference quantum chemical methods are often essential in addressing questions of energetics and even geometries of molecular species with multiconfigurational structures. Methylene (CH₂) and closely related species, such as the hydroxymethyl anion and the radical of present relevance, have a long and controversial history in quantum chemistry,²⁷ and are generally only reliably described using multireference methods. Second-order Generalized van Vleck perturbation theory (GVVPT2)²⁸ is a particularly robust variant of multireference perturbation theory²⁹ that can be used to describe whole potential energy surfaces, including those of excited electronic states. GVVPT2 has been used in this study to provide additional insight into the electronic structures of the hydroxymethyl anion and the neutral radical. Although GVVPT2 also supports incomplete model spaces, complete model spaces of the CASSCF variety were used in this study. Specifically, a 10 electron, 9 orbital CASSCF was used to describe the anion; this generated an active space of 2699 configuration state functions (CSFs) in ¹A′ symmetry. The augmented cc-pVTZ single particle basis set (aug-cc-pVTZ) was used for all calculations.³⁰ All single and double excitations related to any one of the reference CSFs were included in the description of the external space; this resulted in a space spanned by 875, 039, 238 spin- and space-adapted CSFs. Geometry optimizations were performed using an energy-based algorithm to a precision of 2 × 10⁻⁴ a.u. in coordinates and 4 × 10⁻⁸ a.u. in energy. GVVPT2 and CASSCF calculations were performed using a local electronic structure package, referred to as UNDMOL.³¹

Selected CCSD(T)/aug-cc-pV(TQ)Z//CCSD(T)/aug-cc-pVTZ calculations, where aug-cc-pV(TQ)Z denotes basis set extrapolation after the extrapolation scheme of Helgaker et al.,³² were performed using Molpro 2012.1,^33–38 to corroborate the G4 and GVVPT2 predictions.

Product distribution of the most important first generation dissociations as a function of effective temperature after the collision cell was calculated using a master equation model with a simplified potential energy surface, as shown in the ESI.† Microcanonical rate coefficients for the loose transition states were calculated using inverse Laplace transform of Langevin capture rates; for the tight transition states, RRKM theory with rovibrational data from the quantum chemical calculations was used. In the simulations, 1 mbar of Ar was used as bath gas, but the calculated product distributions showed only minimal pressure dependence. The product distribution calculations were performed using MESMER 1.0.³⁹

Results and discussion

Mass spectra

Fig. 1 shows two CID mass spectra of deprotonated glycolic acid, recorded under different experimental conditions. Five fragment peaks are detected and the relative intensities depend on the gas pressure and the collision energy: (elemental composition of the neutral loss indicated)—at m/z 73 (–H₂), m/z 47 (–CO), m/z 45 (–COH₂), m/z 31 (–CO₂), m/z 19 (–C₂O₂) and m/z 17 (–C₂O₂H₂).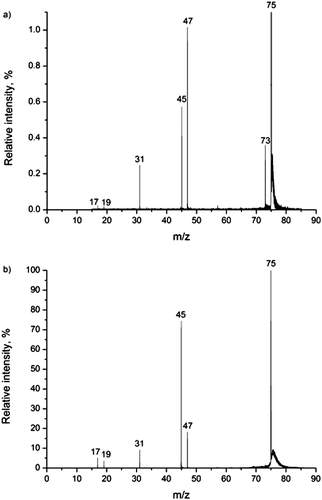

Fig. 1 CID mass spectrum of the glycolate anion (m/z 75); (a) at highest collision gas (Ar) pressure, nominally p = 4.8 × 10⁻³ mbar, and lowest energy (E_lab = 7 eV); and (b) at lowest pressure, nominally p = 6.4 × 10⁻⁴ mbar, and highest energy (E_lab = 15 eV).

The H₂ loss results from a 1,2-elimination mechanism, as reported by Baker and Gabryelski on the basis of the mass shifts observed in their isotopic labelling experiments.¹⁹ The fact that H₂ loss is only evident in our CID mass spectra recorded at relatively high pressure and low collision energy is indicative of a process requiring multiple low energy activating collisions, i.e. slow heating of the ions. This is also consistent with the fact that the peak resulting from H₂ loss is the most abundant one in the mass spectra of Baker and Gabryelski, while it is not seen in the spectra reported by Bialecki et al.²⁰ In the former case, the experiments were conducted using an ion trap under slow heating conditions, while in the latter case the experiments were done using a triple quadrupole mass spectrometer under near single collision conditions at relatively high collision energy (E_lab = 20 eV, Ar collision gas). In addition to H₂ loss, CO loss (giving rise to m/z 47) is the only other major fragmentation that can be inferred from the CID spectra from the ion trap experiment, indicating also a relatively low energy threshold for this process. In the spectra obtained under higher energy single collision conditions, both seen in Fig. 1a and in agreement with the observation by Bialecki et al., the peak at m/z 45, hardly seen in the spectra of Baker and Gabryelski, dominates. Bialecki et al. attribute this to the hydroxycarbonyl ion, as discussed in more detail by Sheldon and Bowie,⁴⁰ a signature peak in CID mass spectra of α-hydroxy carboxylic acids,^41–43 as carefully demonstrated by isotopic labelling and quantum chemical calculations.²⁰ In the case of the glycolate ion, this is most likely due to loss of formaldehyde, although sequential CO + H₂ loss cannot be ruled out.

The remaining product ions (m/z 19 and 17) have the elemental compositions H₃O⁻ and OH⁻, respectively—although the corresponding fragmentation reactions are not necessarily trivial.

The peak at m/z 31, corresponding to CO₂ loss, is seen in both spectra. We note that this peak is neither seen in the ion trap spectra of Baker and Gabryelski nor the triple quadrupole spectra of Bialecki et al.

The peak at m/z 19 is seen in the spectrum presented by Bialecki et al., but was not commented on by them.²⁰ The mass range of the ion trap used in the experiments by Baker and Gabryelski was not set wide enough to include the low mass region. Interestingly, a peak at m/z 35, probably due to OH⁻·H₂O, was observed but not commented on. The H₃O⁻ ion (m/z 19) differs in mass from the precursor ion by 56 Da, and is most likely generated by the consecutive losses of two CO molecules from glycolate. The existence of H₃O⁻ was first reported in 1982 by Paulson and Henchman,⁴⁴ when it was observed as a product ion in the reaction OH⁻·H₂O + H₂ → H₃O⁻ + H₂O in a tandem mass spectrometry experiment. In 1983, Kleingeld and Nibbering generated H₃O⁻ in a FT-ICR mass spectrometer by the reaction between OH⁻ and formaldehyde, resulting from dehydrogenation. The results of the experiments in the presence of D₂O provided a further understanding of both the structure of the H₃O⁻ ion and the mechanism of its formation. These experiments showed that the hydrogen atoms in H₃O⁻ are not equivalent, and the ion structure is best described as a water-solvated hydride ion, H⁻·H₂O.⁴⁵ The formation reaction was summarized as follows⁴⁵

OH⁻ + H₂CO ⇌ [OH⁻,H₂CO] ⇌ [H₂O,HCO⁻] → [H⁻,H₂O] + CO, (1)

and proceeds through formation of a collision complex [OH⁻·H₂CO], which is followed by proton transfer. The complex formed upon the proton transfer [H₂O·HCO⁻] is not likely to dissociate into H₂O + HCO⁻ since water is more acidic than formaldehyde. The intermediates of this reaction have the formula CH₃O₂⁻, which is identical to the m/z 45 ion formed by CO loss from the glycolate anion; a fact that both hints at the origin of the m/z 19 seen in our experiments and the mode of formation. It was shown by de Lange and Nibbering that collision-induced dissociation of H₃O⁻ ion results exclusively in formation of OH⁻ by elimination of H₂,⁴⁶ thereby also connecting the OH⁻ (m/z 17) observed in our experiments to the same reaction chain.

Further evidence about the kinetics and energetics of the dissociation of glycolate was obtained from energy resolved CID (Fig. 2). Inspection shows that the onset of m/z 47 is slightly lower than for m/z 45, but m/z 47 quickly becomes more intense. Both ions have onset in the region E_CM = 2.5–3 eV. Attempts to accurately determine the energetic thresholds by applying the program L-CID, developed by Chen and co-workers,²⁴ failed due to the complexity of the dissociation reactions (N.B. L-CID is most reliable for one or two fragmentation reactions).

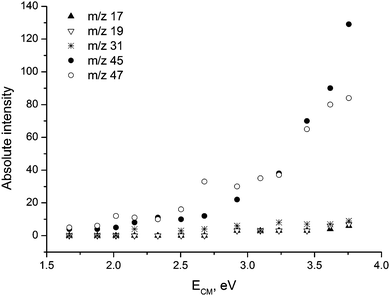Fig. 2 Energy-resolved CID cross section (arbitrary intensity units) for the various dissociation routes. The experimental data were obtained under near single collision conditions with p = 6.4 × 10⁻⁵ mbar.

Isomers

The glycolate anion may exist in several isomeric forms. Starting from glycolic acid, deprotonation may occur from three different sites: each of the two non-equivalent hydroxyl groups and the alpha carbon. For each deprotonated form there exist a number of different conformers. The ten most stable isomers, according to our computational modelling, are summarized in Fig. 3. Starting geometries were generated by systematically rotating around the rotatable bonds in a molecule by taking advantage of this functionality provided by OpenBabel.⁴⁷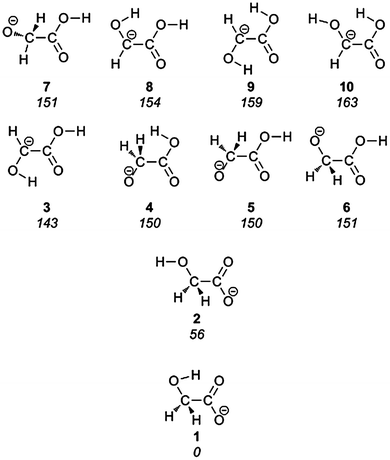

Fig. 3 The lowest energy forms of the glycolate anion, with relative energies in kJ mol⁻¹ given in italics.

Isomerization

According to the results of our quantum chemical survey, the majority of the dissociation reactions occur from the immediate precursors 4 and 5. However, the most stable isomer, 1, corresponds to deprotonation of the carboxylic group. For that reason, the dissociation processes are induced by isomerization leading from 1 to 4 or 5 involving successive intramolecular proton transfer and bond rotations. The energy diagram describing the relevant isomerization reactions is shown in Fig. 4. Proton transfer from the hydroxymethyl group to the carboxylate group of isomer 1 gives rise to intermediate isomer 7. Continuing, the subsequent steps are: C–C bond rotation giving isomer 5; and, in order to reach 4, a final rotation around the C–O bond is required. These details are in accordance with previous studies.^48,49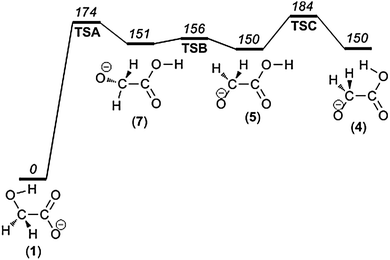

Fig. 4 Potential energy diagram for the isomerization reactions prior to the dissociation processes.

Loss of H₂CO and CO₂

Loss of formaldehyde (H₂CO) results in (C, O₂, H)⁻ (m/z 45). As mentioned above, the corresponding peak in the mass spectrum is diagnostic of α-hydroxy carboxylic acids and the product ion has been proposed to be the hydroxycarbonyl anion.²⁰ On the basis of our calculations, we present a mechanism (see Fig. 5) that in broad terms is in agreement with earlier mechanistic proposals.^20,43 It involves isomer 5 as the first intermediate, which rearranges into the ion–neutral complex [OCOH⁻, CH₂O] (26). The direct dissociation of this complex leads to the hydroxycarbonyl anion (11) plus formaldehyde, for which the reverse process is barrierless. The calculations predict an energetic threshold for OCOH⁻ + CH₂O of E_crit = 265 kJ mol⁻¹.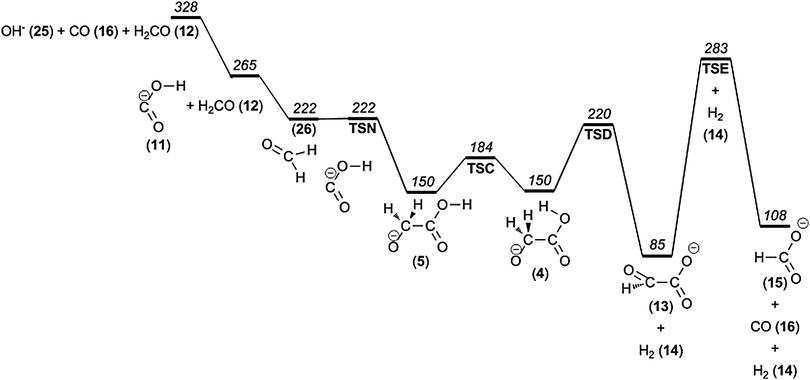

Fig. 5 Potential energy diagram illustrating formaldehyde and hydrogen molecule loss from glycolate anions.

In contrast to larger α-hydroxy acids, glycolate is unique by lacking β-hydrogens, thereby making the alternative elimination of formic acid from the complex more difficult.⁴³ More importantly, however, is the fact that formic acid is much more acidic than formaldehyde, thereby effectively blocking this pathway.

The hydroxycarbonyl ion (COOH⁻) and formate (HCOO⁻) are the two isomeric anions resulting from deprotonation of formic acid. When formic acid reacts with OH⁻ in the gas phase, both ions are produced, but in a ratio of 11 : 1 in favour of the formate ion.⁵⁰ Our quantum chemical calculations predict that the formate ion is 145 kJ mol⁻¹ more stable than the hydroxycarbonyl ion. The rearrangement of the hydroxycarbonyl ion to formate, COOH⁻ → HCOO⁻, is, in spite of this, unfavourable under low energy CID conditions, since it requires overcoming an additional barrier of 122 kJ mol⁻¹ (Fig. 6).

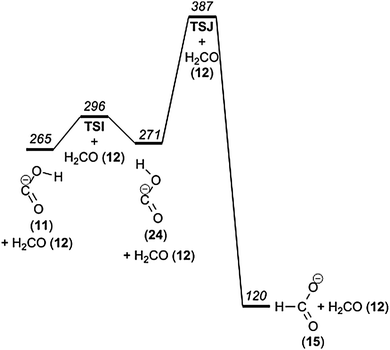Fig. 6 Potential energy diagram of the interconversion of formate and hydroxycarbonyl ions.

It should also be mentioned that glycolate isomers 4, 5, 6 and 7 are of nearly the same relative energy (150 kJ mol⁻¹) and are also potential direct precursors for formaldehyde plus hydroxycarbonyl anions. Isomer 4 is the least preferable since, during its dissociation, the hydroxycarbonyl anion is not formed in its most stable form (with dihedral angle φ(O–C–O–H) = 0°) but instead in a form with φ(O–C–O–H) = 180°, which is 5 kJ mol⁻¹ higher in energy (at the G4 level of theory). The dissociation of the remaining isomers 5, 6, and 7, on the other hand, gives the most stable conformer of the hydroxycarbonyl anion, 11 directly (at 265 kJ mol⁻¹).

Loss of carbon dioxide, giving either ⁻CH₂OH or CH₃O⁻ at m/z 31, is evident from the mass spectra presented in Fig. 1; and it appears from Fig. 2 that this process has a critical energy similar to the other major fragmentations. We have investigated alternative reaction pathways by which the CO₂ loss may occur. Starting from the most stable isomer of glycolate, 1, we first investigated the direct dissociation leading to ⁻CH₂OH (29) + CO₂ at 309 kJ mol⁻¹ (Fig. 7), which at first sight appears to be feasible. According to the calculations, the reverse reaction is barrierless. To our knowledge, the hydroxymethyl anion has not been observed, and its existence has been seriously questioned by Bowie on the basis of MP2 calculations.⁵¹ For this reason we conducted high level calculations to investigate the electronic structure of this species in greatest possible detail, including the use of multiconfigurational methods. B3LYP/6-31G(2df,p), B3LYP/6-311++G(d,p) and GVVPT2/aug-cc-pVTZ predict it to have a potential energy minimum, with all methods giving very similar geometries (bond lengths within 0.01 Å). The vertical electron detachment energies (CCSD(T)/aug-cc-pVTZ//GVVPT2/aug-cc-pVTZ and GVVPT2/aug-cc-pVTZ) are 66 and 48 kJ mol⁻¹, respectively. However, it turns out that the structure of the ˙CH₂OH radical is very different from that of the anion. As a result, the corresponding adiabatic detachment energy is −4 and −17 kJ mol⁻¹, meaning that the anion is inherently unstable towards spontaneous electron loss. In our experiments, in which we register product ions several milliseconds after fragmentation, it seems unlikely that any ions of the CH₂OH⁻ structure will survive the flight all the way to the ToF mass analyzer. We also investigated the lowest-lying triplet electronic state of the ⁻CH₂OH anion, which is 55 kJ mol⁻¹ and 51 kJ mol⁻¹ higher in energy than the singlet at CCSD(T)/aug-cc-pVTZ//GVVPT2/aug-cc-pVTZ and GVVPT2/aug-cc-pVTZ levels of theory, respectively.

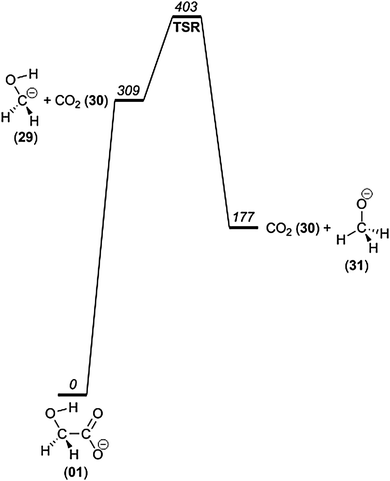Fig. 7 Potential energy diagram of the direct loss of CO₂ from 1 and the isomerization to CH₃O⁻.

The electronic adiabatic detachment energy computed with CCSD(T)/aug-cc-pV(TQ)Z//CCSD(T)/aug-cc-pVTZ is −22 kJ mol⁻¹ and the vertical detachment energy is 63 kJ mol⁻¹. When zero point energies are included, the ADE (adiabatic detachment energy) becomes −17 kJ mol⁻¹. The calculations were performed using Molpro version 2012.1,^33,34 with unrestricted coupled cluster wave functions^37,38,52 for the radical. Vertical detachment energies of 64 kJ mol⁻¹ and 63 kJ mol⁻¹ were obtained.

According to our G4 computational modelling, the methoxy anion, CH₃O⁻ (31), is 132 kJ mol⁻¹ lower in potential energy than the isomeric (putative, at best short-lived) hydroxymethyl anion (29), but a considerable isomerization barrier of 94 kJ mol⁻¹ separates them (Fig. 7). In order to reach the products CH₃O⁻ + CO₂ but avoid this barrier, rearrangement mechanisms requiring hydrogen rearrangements prior to dissociation were considered. During the dissociation leading to formaldehyde loss, we had already noted the intermediacy of a key [OCOH⁻, CH₂O] complex, which may exist in several forms of similar energy (26–28, Fig. 8). It turns out that this complex may dissociate after intracomplex hydride transfer:

[OCOH⁻,CH₂O] (28) → TSQ → CH₃O⁻ (31) + CO₂. (2)

These features are illustrated in Fig. 8, and the transition state geometry is shown in Fig. 9. According to our calculations, this rearrangement mechanism, having an intracomplex hydride transfer as the limiting step, has a significant barrier of E_crit = 300 kJ mol⁻¹, leading to the products at 177 kJ mol⁻¹ (confirmed by IRC calculations). However, the nature of the transition state led us to consider an alternative outcome, namely that the same transition state geometry (TSQ) could serve as a link to the even more stable products, i.e.

[OCOH⁻,CH₂O] (28) → TSQ → [CH₃O⁻,CO₂] → HCO₂⁻ (15) + CH₂O. (3)

This would require a situation where the transient product complex [CH₃O⁻,CO₂] would be sufficiently long-lived and that the relative geometric requirements would allow for back-transfer of the hydride to the CO₂ unit, but this time to the central carbon atom giving formate as the ultimate ionic product. The interesting hydroxycarbonyl–formate dichotomy has previously been discussed by Sheldon and Bowie,⁴⁰ and the present results provide a catalytic mechanism for the isomerization. The formate–formaldehyde product pair has a potential energy of 120 kJ mol⁻¹, and we now see that this also would correspond to an alternative mechanism for the formaldehyde loss already discussed. In order to provide better insight into this interesting possibility, we performed Born Oppenheimer molecular dynamics calculations. A total of 150 trajectories were calculated for which we varied the initial conditions by picking 50 samples of a Boltzmann ensemble for each of three temperatures (Table 1).

Table 1 Number of different reactive trajectories out of 50 for each temperature

	300 K	600 K	900 K	Total
CH3O^−, CO2	26	26	30	82
CH2O, HCO2^−	20	17	11	48

---

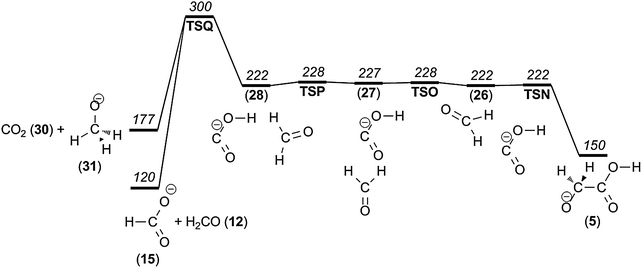Fig. 8 Potential energy diagram of the process leading to both CH₃O⁻ and HCO₂⁻.

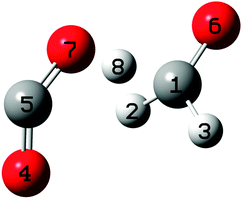Fig. 9 Transition state geometry, TSQ.

It turned out that the majority of trajectories (82 out of 150) produced the methoxy anion–carbon dioxide product pairs, but a total of 48 trajectories led to the formation of the formate anion–formaldehyde product pair. The statistically small sample neither allows for definitive conclusions about product distribution nor the effect of temperature. A priori it would appear to be reasonable that higher internal energies at TSQ would discriminate against back-transfer of the hydride and thereby this formaldehyde loss mechanism. Separate calculations show that the hydride transfer from CH₃O⁻ to CO₂ is barrierless.

Loss of H₂

At high pressure and low collision energy we observe a peak m/z 73, which corresponds to an ion resulting from the loss of a hydrogen molecule. According to our computations, the two hydrogen atoms are released from adjacent atoms, a 1,2-elimination (cf.Fig. 5). This finding is in agreement with experiments on isotope-labeled glycolate.¹⁹ The low energetic threshold for this reaction of 220 kJ mol⁻¹ is in good agreement with the appearance of the m/z 73 ion in CID mass spectra obtained by slow heating of the ions (see above). Furthermore, the unfavourably tight transition state structure TSD also explains the disappearance of this reaction channel at slightly higher energies when processes with looser transition states emerge, as evident from the CID experiments conducted at low pressure/high energy; see further discussion of the reaction kinetics in the Discussion and Conclusion section. It should also be mentioned that the alternative 1,4-elimination of H₂ from 9 has a considerably higher barrier at 310 kJ mol⁻¹.

The product of the hydrogen molecule elimination – glyoxylate (13) – could in principle fragment further by eliminating carbon monoxide, thereby forming the formate ion and contributing to the m/z 45 peak. However, our calculations indicate that the barrier to carbon monoxide elimination from the glyoxylate anion is prohibitively high, being 18 kJ mol⁻¹ higher in energy than the barrier for the formaldehyde elimination from the glycolate anion (see Fig. 5) as well as requiring an extremely tight transition state geometry (TSE). For this reason we do not consider that this consecutive H₂ + CO loss mechanism contributes to the m/z 45 signal to any significant degree, in contrast to a previous proposition.⁵³

Loss of CO

The peak at m/z 47 in the CID mass spectra corresponds to the neutral loss of CO. On the basis of experiments with isotopically labelled glycolic acid, Baker and Gabryelski found that the major source of CO is from the carboxylate group.¹⁹ Their reaction mechanism involves nucleophilic attack of a carboxylate oxygen on the α-carbon followed by C–C bond cleavage. The intermediate ion formed in that process finally eliminates CO.

On the basis of our computational investigation, we suggest a mechanism that has these essential features but is somewhat more complex. The first step is proton transfer accompanied by conformeric rotation, which leads from the most stable glycolate isomer 1 to isomer 5 (Fig. 3). After that, nucleophilic attack of the hydroxyl group at the α-carbon takes place. This process (viaTSF at 247 kJ mol⁻¹) results in irreversible OH insertion into the C–C bond, which eventually leads to the elimination of CO (see Fig. 6).

We also investigated the possibility of further fragmentation of the product hydroxymethanolate ion (18) by hydrogen molecule elimination as an additional source of the m/z 45 product ion. We find that the barrier for vicinal elimination of a hydrogen molecule leading to the formation of formate anion (15) is more than 50 kJ mol⁻¹ higher (Fig. 10) than the barrier for formaldehyde elimination giving COOH⁻ (11) (Fig. 6). The barrier for geminal elimination leading to the formation of hydroxycarbonyl anion is even higher. Together with the results of the calculations on the consecutive loss of a hydrogen molecule followed by the carbon monoxide elimination mentioned in the previous section, we consider formaldehyde elimination as the major source of the m/z 45 product ion and that the product ion has the hydroxycarbonyl ion (11) geometry rather than that of the formate ion (15).

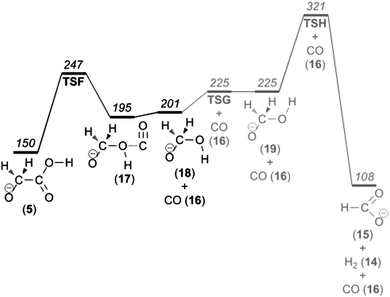Fig. 10 Potential energy diagram illustrating carbon monoxide loss from the glycolate anion.

Second CO loss

We propose that the m/z 47 product ion, hydroxymethanolate, may dissociate further and give rise to the peak at m/z 19. The loss of 28 mass units corresponds to a second consecutive CO elimination; the elemental composition of the product ion is H₃O⁻.

The mechanism for this process, based on the results of our computations, consists of 3 steps. First, the elongation of the C–O bond to the hydroxyl group leads to the transfer of the hydroxyl group towards the hydrogen atoms of the hydroxymethyl group. In concert with this, a proton is transferred from the emerging formaldehyde moiety to the emerging hydroxide. Second, the resulting intermediate (20) is then subject to conformeric rotation around one of the O–H bonds of the water molecule. The rearrangement in the last of the three steps can be understood as hydride transfer from the formyl ion to the water molecule, which results in elimination of CO and formation of H₃O⁻ (23) (Fig. 11). These reaction steps are essentially identical to those occurring in the direct reaction between OH⁻ and CH₂O, the Nibbering reaction, eqn (1).

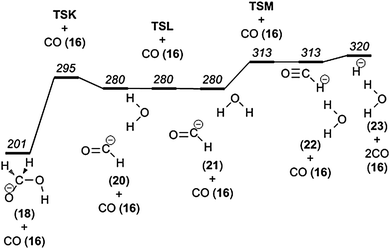Fig. 11 Potential energy diagram illustrating carbon monoxide loss from the hydroxymethanolate anion.

Dissociation of H₃O⁻

Paulson and Henchman reported the first observation of the H₃O⁻ ion and also estimated the ion binding energies with respect to two different dissociation reactions⁴⁴ – the one which corresponds to H⁻ + H₂O products was found to be 72 ± 5 kJ mol⁻¹, and the other which corresponds to OH⁻ + H₂ products was found to be 29 ± 5 kJ mol⁻¹. Later it was shown by de Lange and Nibbering⁴⁶ that upon collisional activation the dissociation follows only the lowest energy pathway and OH⁻ is the only product ion of H₃O⁻ collision-induced dissociation. A number of ab initio calculations by Chałasinśki, Kendall, and Simons,⁵⁴ by Ortiz,⁵⁵ and by Xantheas and Dunning,⁵⁶ and also more recent measurements by Miller et al.⁵⁷ are in a good agreement with the results quoted above.

On the basis of the experimental observations and quantum chemical computational modelling, we present a consistent model for the unimolecular decomposition of glycolate anions (m/z 75). The lowest energy processes and estimated minimum energy requirements are:

HOCH₂CO₂⁻ → HCOCO₂⁻ + H₂ Very tight TS 220 kJ mol⁻¹, (4)

HOCH₂CO₂⁻ → HOCH₂O⁻ + CO Tight TS 247 kJ mol⁻¹, (5)

HOCH₂CO₂⁻ → OCOH⁻ + CH₂O Loose TS 265 kJ mol⁻¹, (6)

HOCH₂CO₂⁻ → HCO₂⁻ + CH₂O Tight TS 300 kJ mol⁻¹, (7)

HOCH₂CO₂⁻ → CH₃O⁻ + CO₂ Tight TS 300 kJ mol⁻¹, (8)

HOCH₂CO₂⁻ → HOH⋯H⁻ + 2CO Tight, then loose TS 320 kJ mol⁻¹, (9)

While H₂ elimination (eqn (4)) has the lowest energetic threshold, the more favourable transition states for the loss of CO and in particular for the loss of CH₂O make the latter two processes dominate at the energies probed in our experiments. In order to check the consistency of our reaction model against experimental observations, we simulated the reaction kinetics using the quantum chemical data (without modifications) at various pressures. As evident from Fig. 12, the kinetic simulations reproduce the experimental results well by showing that H₂ loss dominates at low internal energies and CO₂ becomes the most important reaction at high internal energies. In the broad intermediate energy range CO loss and CH₂O loss predominate.

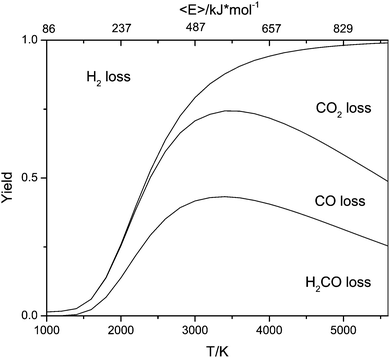Fig. 12 Calculated branching ratios for the first generation fragmentation reactions calculated using a master equation model based on a simplified potential energy surface shown in the ESI.† The glycolate anion was allowed to dissociate directly to give H₂COH⁻ plus CO₂ or to isomerize to 5, which could in turn dissociate to 11 and 12, 13 and 14 or isomerize to 17 and then dissociate to 18 plus CO. Microcanonical rate coefficients were calculated using RRKM theory for the tight transition states and inverse Laplace transformation of Langevin capture rates for the loose transition states. Isomerization reactions were treated as reversible, while all dissociations were treated as final sinks.

In a homogenous gas at low pressure and temperature, typical conditions found in the interstellar medium, only barrierless bimolecular reactions will be of interest in accounting for the synthesis of larger molecules from smaller. Herbst¹⁶ considered the presence of anionic molecules in the interstellar medium based on radiative attachment of electrons, and estimated that their maximum abundance would be of the order of 1% of the neutral species. Noticeable cross sections for the production of H⁻, and somewhat lower for O⁻ and OH⁻, have been measured for electron collisions with water in the gas phase.⁵⁸

H₂O + e⁻ → H⁻ + OH, (10)

This leads us to propose the following series of reactions in an atmosphere of CO, H₂O, CH₂O, etc., based on the reverse of CO loss observed for glycolate:

H⁻ + H₂O → OH⁻ + H₂, (11)

OH⁻ + H₂ + M → [H⁻,H₂O] (23) + M, (12)

OH⁻ + CH₂O → [H⁻,H₂O] (23) + CO, (13)

[H⁻,H₂O] + CO ⇌ [OH⁻,H₂CO]*, (14)

[OH⁻,H₂CO]* + CO ⇌ ⁻OCH₂COOH (5), (15)

Although this scenario is reasonable, the significant barriers of reaction 15 (Fig. 10) has the consequence that the overall reaction is inefficient at the low temperatures typical of giant molecular clouds. Alternatively, we consider a route corresponding to the reverse of the reaction described in Fig. 5, i.e.

OH⁻ + CO → COOH⁻ (11), (16)

COOH⁻ + CH₂O ⇌ [⁻OCH₂COOH]*, (17)

[⁻OCH₂COOH]* + M → ⁻OCH₂COOH (5) + M, (18)

[⁻OCH₂COOH]* → OCHCOO⁻ (13) + H₂. (19)

These reaction schemes represent potential synthetic pathways towards glycolate and glyoxolate in atmospheres containing abundant prebiotic and interstellar molecules at relatively high pressures for collisional stabilization of the energetic intermediate (reaction 18). However, at concentrations of 10⁴–10⁷ molecules per cm³, characteristic of giant molecular clouds, these reactions are not likely to be significant.

Conclusions

The unimolecular dissociation characteristics of the glycolate ion have been probed by mass spectrometry, and simulated by kinetic master equation model calculations in conjunction with a detailed survey of the relevant parts of the potential energy surfaces using high-level quantum chemical methods. Good consistency between the model calculations and the experimental observations is reported. The most significant reactions are loss of CO and loss of CH₂O. Loss of CO₂ and H₂, respectively, is also reported but are of minor importance. Interestingly, it was found that there is direct competition between the methoxy anion/carbon dioxide and the formate anion/formaldehyde product pairs in the sense that both product pairs are accessible from the same transition state so that the product distribution is determined by the detailed dynamics in the post-TS region of the potential energy surface. In addition, the CO loss may be followed by a second CO loss at higher energies leading to H₃O⁻ and subsequently to OH⁻. The reverse of the unimolecular dissociation reactions with regard to possible synthetic pathways to glyoxylic acid in the gas phase via anionic mechanisms is discussed briefly. While such reaction pathways from simpler molecules appear likely under ambient conditions, it is concluded that under the conditions typically found in giant molecular clouds formation of glycolate by these reactions is not likely.

Acknowledgements

This work was supported by the Norwegian Research Council by the Grant No. 179568/V30 to the Centre of Theoretical and Computational Chemistry through their Centre of Excellence program and the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K).

References

1. A. I. Oparin, Proishkhozhddenie Zhisni, Moskowski Rabocii, 1924.
2. P. Ehrenfreund, W. Irvine, L. Becker, J. Blank, J. R. Brucato, L. Colangeli, S. Derenne, D. Despois, A. Dutrey, H. Fraaije, A. Lazcano, T. Owen and F. Robert, Rep. Prog. Phys., 2002, 65, 1427.
3. S. Miller, Origins Life Evol. Biospheres, 1996, 26, 201–202.
4. E. T. Peltzer and J. L. Bada, Nature, 1978, 272, 443–444.
5. J. R. Cronin, S. Pizzarello and D. P. Cruikshank, in Meteorites and the early solar system, ed. J. F. Kerridge and M. S. Matthews, University of Arizona Press, Tucson, 1988, pp. 819–857.
6. E. Herbst, Chem. Soc. Rev., 2001, 30, 168–176.
7. Y.-J. Kuan, S. B. Charnley, H.-C. Huang, W.-L. Tseng and Z. Kisiel, Astrophys. J., 2003, 593, 848.
8. L. Majumdar, A. Das, S. K. Chakrabarti and S. Chakrabarti, Res. Astron. Astrophys., 2012, 12, 1613.
9. C. A. Gottlieb, in Molecules in the Galactic Environment, ed. L. E. S. M. A. Gordon, 1973, p. 181.
10. D. M. Mehringer, L. E. Snyder, Y. Miao and F. J. Lovas, Astrophys. J., Lett., 1997, 480, L71.
11. J. M. Hollis, F. J. Lovas and P. R. Jewell, Astrophys. J., Lett., 2000, 540, L107.
12. R. D. C. Brown, J. G. Crofts, P. D. Godfrey, F. F. Gardner, B. J. Robinson and J. B. Whiteoak, Astrophys. J., 1975, 197, L29–L31.
13. R. T. Garrod, S. L. W. Weaver and E. Herbst, Astrophys. J., 2008, 682, 283.
14. G. M. M. Caro and W. A. Schutte, Astron. Astrophys., 2003, 412, 121–132.
15. M. Nuevo, J. H. Bredehöft, U. J. Meierhenrich, L. d'Hendecourt and W. H. P. Thiemann, Astrobiology, 2010, 10, 245–256.
16. E. Herbst, Nature, 1981, 289, 656–657.
17. M. C. McCarthy, C. A. Gottlieb, H. Gupta and P. Thaddeus, Astrophys. J., Lett., 2006, 652, L141.
18. E. J. Corey, Angew. Chem., Int. Ed. Engl., 1991, 30, 455–465.
19. M. Baker and W. Gabryelski, Int. J. Mass Spectrom., 2007, 262, 128–135.
20. J. B. Bialecki, F. U. Axe and A. B. Attygalle, J. Mass Spectrom., 2009, 44, 252–259.
21. L. E. Greene, J. S. Grossert and R. L. White, J. Mass Spectrom., 2013, 48, 312–320.
22. H. Zhu, H. Cao and T. Li, Comput. Theor. Chem., 2013, 1008, 32–38.
23. M. T. Rodgers, K. M. Ervin and P. B. Armentrout, J. Chem. Phys., 1997, 106, 4499–4508.
24. S. Narancic, A. Bach and P. Chen, J. Phys. Chem. A, 2007, 111, 7006–7013.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Wallingford, CT, 2009.
26. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
27. H. F. Schaefer, III, Science, 1986, 231, 1100–1107.
28. Y. G. Khait, J. Song and M. R. Hoffmann, J. Chem. Phys., 2002, 117, 4133–4145.
29. M. R. Hoffmann, D. Datta, S. Das, D. Mukherjee, A. Szabados, Z. Rolik and P. R. Surjan, J. Chem. Phys., 2009, 131, 204104.
30. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
31. W. Jiang, Y. G. Khait and M. R. Hoffmann, J. Phys. Chem. A, 2009, 113, 4374–4380.
32. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
33. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
34. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, Cardiff, UK, 2012.
35. C. Hampel, K. A. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1–12.
36. M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326.
37. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219–5227.
38. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106–3107.
39. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
40. J. C. Sheldon and J. H. Bowie, J. Am. Chem. Soc., 1990, 112, 2424–2425.
41. J. L. Kerwin and J. J. Torvik, Anal. Biochem., 1996, 237, 56–64.
42. M. K. Moe, M. B. Strøm, E. Jensen and M. Claeys, Rapid Commun. Mass Spectrom., 2004, 18, 1731–1740.
43. M. L. Bandu, T. Grubbs, M. Kater and H. Desaire, Int. J. Mass Spectrom., 2006, 251, 40–46.
44. J. F. Paulson and M. J. Henchman, Bull. Am. Phys. Soc., 1982, 27, 108.
45. J. C. Kleingeld and N. M. M. Nibbering, Int. J. Mass Spectrom. Ion Phys., 1983, 49, 311–318.
46. W. de Lange and N. M. M. Nibbering, Int. J. Mass Spectrom. Ion Processes, 1987, 80, 201–209.
47. N. O'Boyle, M. Banck, C. James, C. Morley, T. Vandermeersch and G. Hutchison, J. Cheminf., 2011, 3, 33.
48. A. Fernandez-Ramos, J. Rodriguez-Otero and M. A. Rios, J. Chem. Phys., 1997, 107, 2407–2414.
49. Z. Smedarchina, A. Fernandez-Ramos and M. A. Rios, J. Chem. Phys., 1997, 106, 3956–3964.
50. P. C. Burgers, J. L. Holmes and J. E. Szulejko, Int. J. Mass Spectrom. Ion Processes, 1984, 57, 159–166.
51. K. M. Downard, J. C. Sheldon, J. H. Bowie, D. E. Lewis and R. N. Hayes, J. Am. Chem. Soc., 1989, 111, 8112–8115.
52. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219–5227.
53. J. Sultan and W. Gabryelski, Anal. Chem., 2006, 78, 2905–2917.
54. G. Chałasinśki, R. A. Kendall and J. Simons, J. Chem. Phys., 1987, 87, 2965–2975.
55. J. V. Ortiz, J. Chem. Phys., 1989, 91, 7024–7029.
56. S. S. Xantheas and T. H. Dunning, J. Phys. Chem., 1992, 96, 7505–7506.
57. T. M. Miller, A. A. Viggiano, A. E. S. Miller, R. A. Morris, M. Henchman, J. F. Paulson and J. M. Van Doren, J. Chem. Phys., 1994, 100, 5706–5714.
58. Y. Itikawa and N. Mason, J. Phys. Chem. Ref. Data, 2005, 34, 1–22.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized molecular geometries and energies. See DOI: 10.1039/c3cp51638e

---