Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulation of ultrafast photodynamics of pyrrole with a multiconfigurational Ehrenfest method
Kenichiro Saita,
Michael G. D. Nix and
Dmitrii V. Shalashilin
School of Chemistry, University of Leeds, Leeds LS2 9JT, UK. E-mail: K.Saita@leeds.ac.uk; M.G.Nix@leeds.ac.uk; D.Shalashilin@leeds.ac.uk
First published on 6th August 2013
Abstract
We report the first results of ab initio multiconfigurational Ehrenfest simulations of pyrrole photodynamics. We note that, in addition to the two intersections of 11A2 and 11B1 states with the ground state 11A1, which are known to be responsible for N–H bond fission, another intersection between the 12A2 and 12B1 states of the resulting molecular radical becomes important after the departure of the H atom. This intersection, which is effectively between the two lowest electronic states of the pyrrolyl radical, may play a significant role in explaining the branching ratio between the two states observed experimentally. The exchange of population between the two states of pyrrolyl occurs on a longer scale than that of N–H bond fission.
1. Introduction
Heteroaromatic molecules such as pyrrole, imidazole, and phenol have been the focus of experimental and theoretical attention due to the role their derivatives play as the chromophores of nucleobases and aromatic amino acids. The mechanisms of their photochemistry have been studied experimentally1,2 and theoretically,3–10 where it was suggested that the N–H/O–H bond fission was an important channel in the photodissociation dynamics. The role of the 1πσ* states in this process has been emphasized11–23 wherein a number of total kinetic energy release (TKER) spectra for various bond fission reactions were reported.In particular, the photodissociation of pyrrole (C4NH5) has been investigated24,25 and has proven to be an interesting case, prototypical of many heteroaromatic systems in which low energy heteroatom centred πσ* states occur in the singlet manifold. These states result from the close degeneracy of the 3s Rydberg orbital of the heteroatom with the repulsive σ* orbital of the heteroatom to substituent bond, which leads to strong mixing. Where the substituent is simply H, N–H bond fission is the primary decay mechanism for pyrrole molecules excited to this πσ* state. Experimental evidence for this dissociation has been reported26 wherein H atoms were detected with a centre-of-mass frame energy of 18 kcal mol−1 and a strong anisotropy, indicating prompt dissociation (within the molecular rotation period). Further evidence from ion-imaging1 and hydrogen (Rydberg) atom photofragment translational spectroscopy (HRAPTS)24 supported these initial findings. Additional details from the high resolution HRAPTS data showed several notable features, including direct (Herzberg–Teller allowed) excitation to the 1A2 electronic state, with the preservation of the H–T active vibrations in the product radical, apparently showing strong vibrational adiabaticity during the dissociation. Theoretical work by Sobolewski and Domcke3,4 showed the existence of conical intersections in the decay channel, which are by now well known and opened the possibility of electronic population branching during the dissociation. Despite sufficient total energy to access both the 2A2 and 2B1 states of pyrrolyl, the interpretation of the HRAPTS data is that population was only observed in the lowest (X2A2) electronic state of the radical. The peaks in the TKER spectrum were assigned to various vibrational states of this ground electronic state of the pyrrolyl radical.
Time resolved studies have also been performed27,28 albeit in the region of the stronger1 ππ* absorption, and place an upper bound on the timescale for N–H fission of ∼200 fs, although direct dissociation on the 1πσ* state is expected to be much faster. Previously, quantum dynamics calculations1,5,6 have been performed on a limited dimensionality model PES and have predicted rapid dissociation and significant population of the 2B1 state of pyrrolyl, in contrast to the experimental data.
In this article we report the results of our simulations of the nonadiabatic dynamics of pyrrole with the help of the multiconfigurational Ehrenfest (MCE) method. In this approach, the nonadiabatic dynamics are represented by a trajectory which is “shared” between several electronic states. In the MCE29–32 method, Ehrenfest trajectories are dressed with Gaussian wave packets which serve as a basis for exact quantum propagation of the nuclear wave packet. They carry and exchange quantum amplitudes, which makes MCE fully quantum in principle. However, as has been explained in our previous work, with time the Ehrenfest trajectories start running away from each other and the quality of the basis deteriorates. As a result, the quantum coupling between Gaussians decreases, although this can be corrected, in principle, by increasing the number of basis trajectories. Nevertheless even without full, long time quantum coupling between the amplitudes of trajectories, many features of the dynamics can be understood (at least qualitatively) on the basis of the analysis of an ensemble of almost independent Ehrenfest trajectories. This analysis provides a semi-classical approximation to the exact quantum dynamics of the nuclei, whilst still retaining a fully quantum description of electronically nonadiabatic processes. An important feature of the ab initio MCE method described in ref. 30 is that it is a direct dynamics which, similar to other ab initio techniques, calculates electronic potential energy surfaces “on the fly” and does not require any a priori information about the PESs. This is similar in spirit to other existing methods such as the ab initio multiple spawning33–36 and ab initio variational Gaussians.37,38 These alternative quantum direct dynamics methods differ from MCE and from each other only in the precise way the trajectories are guided.
The availability of “on-the-fly” ab initio Ehrenfest quantum dynamics allows a more complete analysis of the dissociation of pyrrole. By including all nuclear degrees of freedom in our numerical experiment, we do not bias the simulation by the choice of dimensions to a model, hence allowing any nuclear coordinate to influence the dynamics. The current simulation provides evidence that the population of the 2B1 state is low and thus confirms the original assignment of the HRAPTS data. We notice that after partial departure of the H-atom, the two electronic states 2A2 and 2B1 are still coupled via an intersection between the potential energy surfaces of the pyrrolyl radical, which is nearly isolated. This intersection is reached by the pyrrolyl vibrational motion, and as a result the population of the higher 2B1 state resulting from rapid nonadiabatic dynamics of the N–H bond fission leaks to the lower 2A2 state via longer time dynamics at this final intersection. A possible role for this feature has been proposed in ref. 5 but a multidimensional simulation allows one to see it very naturally. Previously, such a conical intersection between two lowest electronic states of pyrrolyl has been found in ref. 39 and our current simulation suggests that it may play an important role in the nonadiabatic dynamics of pyrrole, which to the best of our knowledge has never been considered before.
2. Theory
Our multiconfigurational Ehrenfest approach to nonadiabatic dynamics is described in ref. 29–32. In particular see ref. 30 for ab initio MCE. In this article we only sketch briefly the main concept. The exact molecular wave function at time t can be expanded as a sum of N Ehrenfest wavepackets with amplitude Dk(t)
 | (1) |
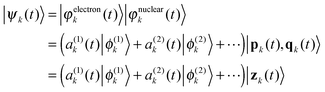 | (2) |
 , which is a product of 3D frozen Gaussians for each atom j included in the quantum dynamics simulation. Often a frozen Gaussian is called a coherent state |z(t)〉 and labelled with a single complex vector
, which is a product of 3D frozen Gaussians for each atom j included in the quantum dynamics simulation. Often a frozen Gaussian is called a coherent state |z(t)〉 and labelled with a single complex vector| z3D = (γ1/2q3D + iγ−1/2ℏ−1p3D)/21/2 | (3) |
 , with the amplitudes
, with the amplitudes  of ne electronic states. A single configuration (2) is not flexible enough to describe accurately the quantum dynamics and it is well accepted that the standard Ehrenfest method is often unsuitable for accurate nonadiabatic dynamics. However the Ehrenfest configurations can be used as a basis function for a multiconfigurational approach and the wavefunction (1) can be converged to the exact result.27,28
of ne electronic states. A single configuration (2) is not flexible enough to describe accurately the quantum dynamics and it is well accepted that the standard Ehrenfest method is often unsuitable for accurate nonadiabatic dynamics. However the Ehrenfest configurations can be used as a basis function for a multiconfigurational approach and the wavefunction (1) can be converged to the exact result.27,28
The evolution of the wave function is described by the motion of Ehrenfest configurations (z,a) and time dependence of their amplitudes D. The equations of motion for the Ehrenfest trajectories follow from the Hellmann–Feynman theorem.40 They can be written in the form of Newton's second law, ṗ = F and ![[q with combining dot above]](https://www.rsc.org/images/entities/b_char_0071_0307.gif) = p/m, where
= p/m, where
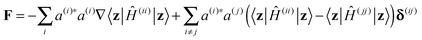 | (4) |
 where
where  , the equations for the amplitudes take the form
, the equations for the amplitudes take the form
 | (5) |
Δ(lj) = ![[q with combining dot above]](https://www.rsc.org/images/entities/b_char_0071_0307.gif) δ(lj)(q) δ(lj)(q)
| (6) |
The quantum coupled equations for the amplitudes Dk(t) in (1) are as follows:
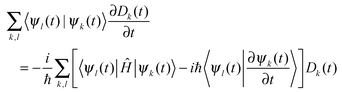 | (7) |
 | (8) |
 | (9) |
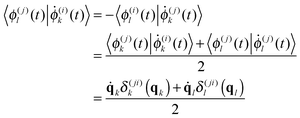 | (10) |
The adiabatic potential energy surfaces V(jj), their derivatives and the NACME vectors can easily be calculated using MOLPRO41 or any other electronic structure package.
3. Computational details
3.1 Initial sampling
The initial conditions for the Ehrenfest trajectories are based on projection of a ground state zero-point nuclear eigenfunction onto the S1 surface, allowing excitation at all energies. Therefore, the simulated wavepackets contain a broader spread of total energies than is accessible in the experiments.24 Initial conditions for the trajectories were generated from a vibrational Wigner distribution42 of the v = 0 vibrational state of the S0 electronic state
 | (11) |
3.2 The level of electronic structure theory
In this study, Dunning's cc-pVDZ (correlation-constant polarized valence double zeta) basis set44 was employed on all atoms. In order to describe the low-lying πσ* states (11A2 and 11B1 states), one additional diffuse s function, one additional set of p functions and one additional set of d functions were added to the nitrogen atom, and one additional diffuse s function and one additional set of p functions were added to the dissociative hydrogen atom. The exponents of these orbitals were taken from the diffuse functions of Dunning's aug-cc-pVDZ basis set.44 The necessary energy, gradient and NACME data for the S0, S1 and S2 states were computed on the fly at the CASSCF level via interface with MOLPRO 2010.1.41 The complete active space consisted of seven orbitals (three ring π orbitals and two corresponding π* orbitals, one σ orbital and a corresponding σ* orbital) with eight electrons, and state averaging was performed over four states (SA4-CAS(8,7)-SCF). This level of theory is required to realistically represent the multiconfigurational nature of the electronic states as the N–H bond is extended and to allow analytic calculation of the non-adiabatic coupling between states, particularly near points of degeneracy. This level of theory generally reproduces the lowest three PESs for pyrrole, although the minimum in the S1 surface due to the 3s Rydberg character of the 1πσ* state is somewhat overestimated, leading to some artificial trapping of the wavepackets in this region. However, as in this study we will discuss the dynamics of the dissociative surfaces, the artificially deep well around the Franck–Condon region has little impact on the dynamics, once the dissociative part of the potential is accessed. Calculation of the electronic surfaces and conical intersection in pyrrolyl used identical methodology, save for the absence of the dissociative H atom and its single electron. Furthermore, only three states exist at low energies, leading to the SA3-CAS(7,7)-SCF calculation. For consistency, the same cc-pVDZ basis set, with additional basis functions applied to the N atom, was used in these calculations.4. Results and discussion
Tables 1 and 2 show the orbitals which are taken into account in the active space of the CASSCF calculation, and the primary electron configurations of the lowest three electronic states at the equilibrium geometry (rNH = 0.996 Å) and in the region H-atom dissociated (rNH = 5 Å). The equilibrium geometry of pyrrole has C2v symmetry. Fig. 1(a) illustrates the one-dimensional potential energy cuts of the low-lying electronic states as a function of the N–H stretching coordinate with a fixed molecular framework. As discussed in ref. 6 the CASSCF method underestimates the vertical excitation energies45–49 so that the lines are plotted with an offset of 0.8 eV in order to compare with the CASSCF surfaces corrected by the MRCI method (plotted as dotted curves).6 The 11A2 and 11B1 curves calculated by the pure CASSCF method are in good agreement with those by the CASSCF/MRCI in the Franck–Condon region. Fig. 1(b) shows another 1D cut of the potential energy surfaces as a function of the N–H distance with a relaxed molecular skeleton. In the dissociative region the Ehrenfest trajectories of basis CSs tend to propagate in the vicinity of this minimum energy path region rather than the “frozen” PESs shown in Fig. 1(a). The states 11A1, 11A2, 11B1, 21A1 and 21B1 are depicted by blue, red, green, orange and black lines. However, in our simulation, molecules no longer keep their symmetry and the states should be labelled as 11A, 21A, 31A, and 41A under C1 symmetry, or with adiabatic labels: S0, S1, S2, and S3. Therefore Fig. 1 also indicates the S0, S1, S2, and S3 states, with dashed, solid, dotted and dash-dotted lines respectively. In all figures in this article the adiabatic states and their populations are represented by the line type (solid, dashed, etc.) and the colour of the line represents the diabatic states, although of course the latter convention is not entirely rigorous because diabatic states are not unique. The potential energy curves depicted in Fig. 1(b) show “step” at rNH = 1.45 Å due to the state-averaging over four electronic states, 11A1, 11A2, 11B1, 21A1 (for rNH < 1.45 Å) and 11A1, 11A2, 11B1, 21B1 (for rNH > 1.45 Å). When the character of the fourth state changes, the CASSCF optimised orbitals and the CI coefficients change. As a result the calculated energies change slightly as well. However, the fourth electronic excited state is indispensable to reproduce the order of the 3 lower states (11A1, 11A2, 11B1) involved in the dynamics and the dissociative character of 1πσ* states. The averaging over more than five states is not converged in the right order, at this level of theory (CAS(8,7)-SCF/(aug-)cc-pVDZ). The step is clearly visible under the C2v symmetry, but it becomes much smoother if the symmetry is lowered. The actual trajectories never reach close proximity of C2v geometry and they are never affected by “steps”. For this study, the interesting dynamics occurs after passing the two first intersections of the 11A2 and 11B1 states with the state 11A1, and after the departure of the H atom, at rNH > 2.0 Å. The “step” therefore hardly affects these dynamics. Besides, the N–H cleavage is mostly coupled with the out-of-plane motions of the pyrrolyl ring, which are not under the C2v symmetry. Hence this level of electronic structure calculation is acceptable.
|
|||||||
|---|---|---|---|---|---|---|---|
| σ (9a1) | π (1b1) | π (2b1) | π (1a2) | σ* (10a1) | π* (3b1) | π* (2a2) | |
| 11A1 (S0) | 2 | 2 | 2 | 2 | 0 | 0 | 0 |
| 11A2 (S1) | 2 | 2 | 2 | 1 | 1 | 0 | 0 |
| 11B1 (S2) | 2 | 2 | 1 | 2 | 1 | 0 | 0 |
|
|||||||
|---|---|---|---|---|---|---|---|
| π (1b1) | σ (9a1) | π (2b1) | π (1a2) | σ* (10a1) | π* (3b1) | π* (2a2) | |
| 11A2 (S0) | 2 | 2 | 2 | 1 | 1 | 0 | 0 |
| 11B1 (S1) | 2 | 2 | 1 | 2 | 1 | 0 | 0 |
| 11A1 (S2) | 2 | 1 | 2 | 2 | 1 | 0 | 0 |
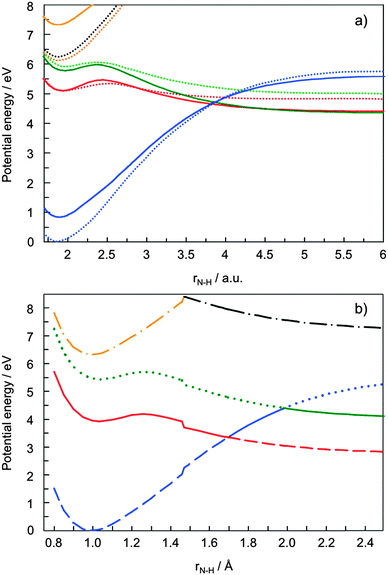 | ||
| Fig. 1 (a) One-dimensional potential energy curves of the low-lying electronic states as a function of the NH stretching coordinate. In this figure only the NH bond length was stretched and the molecular frame was frozen. The curves calculated at the SA5-CAS(8,7)-SCF/(aug-)cc-pVDZ level are plotted as solid lines with an offset of 0.8 eV. The 11A1, 11A2, 11B1, and 21A1 states are shown in blue, red, green, and orange, respectively. The dotted lines are from ref. 6. The line colours of the dotted lines correspond to those of the solid lines. The actual dynamics occurs far away from the geometry shown in this figure. (b) Low-lying electronic states 11A1, 11A2, 11B1, 21A1 and 21B1 of pyrrole under C2v symmetry shown in blue, red, green, orange and black, respectively. The adiabatic states S0, S1, S2, and S3 are represented by dashed, solid, dotted, and dash-dotted lines. | ||
In the region of rNH > 2.0 Å, the 11A1 state is no longer the electronic ground state. It finally correlates with the S2 state, making 11A2 and 11B1 states the ground (S0) and the first excited (S1) states respectively. The S0 and S1 states correspond to the πσ* states and the S2 state is the σσ* state. All these surfaces lead to the dissociation of a pyrrole molecule into a pyrrolyl radical and an H atom.
A typical trajectory is depicted in Fig. 2. Fig. 2(a) shows the time evolution of the adiabatic (solid, dashed and dotted lines) and diabatic (labelled with colours) potential energies. Fig. 2(b) depicts the amplitude |d|2, which represents the populations of electronic states. The symmetry of the system is not restricted under C2v so that the electronic states should be labelled as S0, S1, S2; however, these states are strongly correlated with the 11A1, 11A2, 11B1 states of the equilibrium geometry which has C2v symmetry. In different regions, S0, S1, S2 correspond to different character states 11A1, 11A2, 11B1, which is reflected by the changes in the line colours. At 12.7 fs, the trajectory reaches the S1–S0 conical intersection, and almost all the population is transferred from the 1A2-like state into the 1A1-like state, remaining on the S1 adiabatic surface. This is in apparent contrast to the behaviour determined from the HRAPTS experiment, where the S0 (2A2) state of the radical appears to be populated exclusively. The molecular geometry at the intersection point is determined by a combination of the ν24(b1) and ν16(b2) normal modes. The trajectory goes through the second conical intersection between the S2–S1 (1B1–1A1) states at 17.0 fs. Then, roughly 80% of the population of the 1A1-like state rapidly moves into the 1B1-like state, again remaining on the S1 surface. The geometry at this second intersection point corresponds to a combination of the ν10(a2) and ν16(b2) normal modes. The N–H bond length, shown in Fig. 2(c), is now 1.939 Å, which is twice the equilibrium bond length, so that the pyrrole molecule has essentially already dissociated into the pyrrolyl radical and the hydrogen atom. After passing this conical intersection, the population of S2, which is now in the 1A1-like state, becomes almost constant (|d|2 ∼ 0.23). On the other hand, the lowest two S0 and S1 states (11A2-like and 11B1-like states of pyrrole) are still coupled. At ∼55 fs, there is a drastic population transfer between the 1A2-like and 1B1-like state (finally populating the S0 adiabat) due to another conical intersection, at which the ν9(a2), ν20(b1) and some a1-symmetry (ν3, ν4, ν7, ν8, etc.) vibrational modes of the pyrrolyl radical are involved. There are several more significant population exchanges between the S1–S0 states of the system (the D1–D0 states of the pyrrolyl radical) when the pyrrolyl radical reaches the vicinity of the conical intersection again at 125 and 136 fs.
 | ||
| Fig. 2 (a) Evolution of the potential energies of the S0, S1, and S2 states (solid, dashed and dotted lines) as a function of time during a typical trajectory. The line colours reflect the correlation of adiabatic states with states 11A1, 11A2, and 11B1. These correlations change at the moment of passing in the vicinity of the various intersections, indicated by colour changes. (b) The Ehrenfest populations |d|2 of the electronic states S0, S1, and S2 (dashed, solid and dotted lines) along a typical Ehrenfest trajectory. The changes in the line colour reflect the changing correlations with the states 11A1, 11A2, and 11B1, as the trajectory passes through various conical intersections. (c) N–H bond distance as a function of time and its derivative (effectively equivalent to the velocity of dissociating hydrogen atom) along the trajectory shown. | ||
All dissociative Ehrenfest trajectories show similar behaviour. As can be seen from Fig. 2(c) the N–H bond breaks very quickly (within a few tens of femtoseconds) in the vicinity of the intersections around r(N–H) = 2 Å, shown in Fig. 1. During the H atom departure, the pyrrolyl radical remains in a mixture of two electronic states (with the major component of the population in the S1 state), which are populated by the dissociative wavepacket as it crosses the initial conical intersections in the r(N–H) coordinate. However, the average population of the S1 state (1B1-like state of pyrrole) decreases, which is reflected by the fact that any given trajectory spends very little time in this state. Most of the time, the Ehrenfest amplitude of the S1 state is close to zero and if this state is populated, the trajectory quickly returns to the lower state S0 (1A2-like state of pyrrole). The energy present in the pyrrolyl system is sufficient to allow population of the upper electronic (2B1) state, yet population of this state is dynamically disfavoured. There appears to be strong coupling between this state and the ground state, such that a statistical population distribution is eventually established and the excess energy tends to be present as nuclear motion (kinetic energy of the wavepacket) on the ground state.
A more traditional way to represent dynamics would simply be to plot the time dependent population of the adiabatic states averaged over all Ehrenfest trajectories, which is shown in Fig. 3. The figure clearly demonstrates two processes. First, the fission of the N–H bond occurs on the time scale of less than 20 fs. Then, the two states of pyrrolyl exchange amplitude and the population of the excited (2B1) state is transferred to the ground state over a much longer time scale of hundreds of fs. On this time scale the energy is also exchanged between pyrrolyl and hydrogen atom translation motion. Frames 3(a) and (b) show the time dependent population of the electronic states averaged over 3 propagating “bits” obtained for two different choices of the parameter γ in eqn (3), which is the width of the Gaussian Coherent State. For the frame (a), γ = 1 a.u. for all atoms. For the frame (b), the choice suggested in ref. 50 has been employed. Fully converged quantum calculations would be independent of γ. Fig. 3 indicates that the result depends on the choice of the width parameter only slightly.
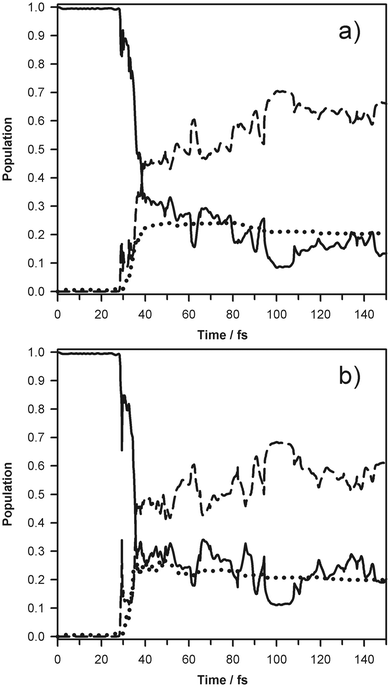 | ||
| Fig. 3 Time evolution of populations of the states with different Gaussian Coherent State basis sets. Broken, solid, and dotted lines represent the S0, S1, and S2 states, respectively. Frame (a) is for γH/mH = 5.443 × 10−4 bohr−2 emu−1, γC/mC = 4.570 × 10−5 bohr−2 emu−1, γN/mN = 3.919 × 10−5 bohr−2 emu−1, which corresponds to γ = 1 a.u. for all atoms. Frame (b) is for γH/mH = 5.062 × 10−3 bohr−2 emu−1, γC/mC = 2.076 × 10−3 bohr−2 emu−1, γN/mN = 1.488 × 10−3 bohr−2 emu−1, which was suggested in ref. 50. | ||
The electronic structure of isolated pyrrolyl can give an idea about the electronic structure of pyrrole with strongly elongated N–H bonds. The intersection between the two electronic states of pyrrolyl has been identified previously in ref. 39 and our dynamics calculations also imply its existence. To confirm this, a conical intersection search has been performed at the same level of theory used for the electronic structure in the dynamics calculations. By optimizing both the D0 (2A2) minimum and the intersection point, an intrinsic coordinate could be constructed by linear interpolation of the multidimensional coordinate space. By calculation of the state-averaged electronic potentials along this coordinate, the form of the potential and the energetic location of the intersection were established and are displayed in Fig. 4. The intersection is found to occur ∼0.45 eV above the D0 minimum and is essentially isoenergetic with the D1 (2B1) minimum. This D1 state is therefore coupled at its minimum to the lower state. Due to the presence of this ‘photochemical funnel’, the final population of the electronically excited state is low and the assignment of the strong TKER peaks at around this energy to the high vibrational states of the electronic ground state (X2A2) rather than to the low vibrational states of the higher electronic state 2B1 of pyrrolyl is placed on a more solid theoretical footing.
 | ||
| Fig. 4 (a) Cuts through the PESs of the pyrrolyl radical, showing the lowest three states at the SA3-CAS(7,6)-SCF level with (aug)-cc-pVDZ basis. The unit of the intrinsic coordinate is defined as linear displacement of the D0 minimum from the D0/D1 CI geometries (see text). The ground state has a minimum of 2A2 character, but the D1 state is intersected at its minimum and there is thus no minimum with 2B1 character. The states 2A2, 2B2 and 2A1 of pyrrolyl correlate with 1A2, 1B2 and 1A1 of pyrrole with strongly elongated N–H bonds, as the removal of the H atom does not alter the C2v symmetry. (b) D0 minimum and (c) D0/D1 intersection geometries are shown for reference. | ||
Fig. 5 demonstrates the time dependence of the quantum coupling coefficients D in the wave function (1) for one of the three bundles of 10 Ehrenfest trajectories run in the current simulation. Again frames (a) and (b) represent the result for two different choices of the CS width parameter γ, chosen as γ = 1 a.u. for all atoms (a) and according to the recipe of ref. 50. In both cases quantum coupling is taken into account up to approximately 50 fs. After that, the amplitudes of Ehrenfest trajectories become constant, which indicates that the trajectories have diverged. The CSs, which dress the trajectories, no longer overlap and are therefore no longer coupled. Thus, on the time scale of more than ∼50 fs, the current calculation is only semiclassical, although this has been shown previously to be a good approximation. The time scale of the fully quantum part of the simulation increases with the increase in the size of the trajectory basis. Many more configurations and their trajectories are required for a fully quantum MCE simulation.
 | ||
| Fig. 5 Time dependence plots of the coefficient D. Frame (a) is for γH/mH = 5.443 × 10−4 bohr−2 emu−1, γC/mC = 4.570 × 10−5 bohr−2 emu−1, γN/mN = 3.919 × 10−5 bohr−2 emu−1, which corresponds to γ = 1 a.u. for all atoms. Frame (b) is for γH/mH = 5.062 × 10−3 bohr−2 emu−1, γC/mC = 2.076 × 10−3 bohr−2 emu−1, γN/mN = 1.488 × 10−3 bohr−2 emu−1, which was suggested in ref. 50. Quantum coupling is initially strong and lessens as the trajectories separate. Beyond 50 fs, the amplitudes are constant and the simulation becomes effectively semi-classical. | ||
“On-the-fly” dynamics is computationally expensive. In this particular case we use the SA4-CAS(8,7)-SCF level of electronic structure calculation with the partially augmented cc-pVDZ basis, which requires ∼1600 seconds of CPU time for one time step (in this study the time step was set to 0.1 fs) propagation on an Intel(R) Xeon(R) 5130 processor (2.0 GHz). The advantage of our ab initio MCE approach in its current implementation is that it is a “post-processing” technique. More Ehrenfest trajectories can be run independently and stored. Eqn (7) for their amplitudes D can be run separately after a sufficient number of Ehrenfest trajectories are accumulated. This attractive feature follows from the linear approximation (9) and (10) of the matrix elements. The linear approximation is justified by the fact that in many dimensions only the CSs which are very close to each other overlap and are coupled. In future, the approximation (9) and (10) can be improved by involving more information about the potential energy and its gradient in the neighbouring points of the trajectory. We are currently running more Ehrenfest trajectories and accumulating more data in order to extend the temporal range of the fully quantum part of the simulation and to improve the statistics, which perhaps will allow us to reproduce the translational energy distribution observed in ref. 51. However, even the limited statistics of the current simulation reveals important information about the dissociation dynamics of pyrrole, due to the full dimensionality approach used to simulate the nuclear dynamics.
Thus, we are able to draw strong conclusions about the role of the various conical intersections in the dissociation dynamics of the pyrrole and the subsequent internal dynamics of the nascent pyrrolyl radicals and provide an interpretation for the observation that only the ground (2A2) state of pyrrolyl appears to be populated at long times in the HRAPTS experiments.
The HRAPTS data indicate exclusive population of the 2A2 state of pyrrolyl, following N–H bond fission, suggesting that the coupling at the 1A2/1A1 and 1A1/1B1 intersections which lie along the dissociation coordinate is minimal and that the dissociative wavepacket remains largely on the diabatic 1A2 state. Previous (limited dimensionality) dynamics simulations have predicted population of both the 2A2 and 2B1 states, in conflict with observation. Our full dimensionality simulation indicates significant coupling at both intersections, yielding a population of ∼0.8 in the 1B1 state after 25 fs (Fig. 3), in agreement with previous dynamics calculations. However, in contrast to the limited dimensionality models, our simulation shows further strong coupling between the D1 (2B1) and D0 (2A2) states of nearly isolated pyrrolyl, during the dissociation. This leads to decay of the 2B1 population on the timescale of a few hundred fs and predicts exclusive 2A2 population on the ns timescale, as observed experimentally. A possible role of this intersection has been proposed in ref. 5 but a multidimensional simulation allows one to demonstrate its importance very naturally.
It is perhaps interesting to consider the timescale of the experiment more carefully. The nascent H atoms show a kinetic energy distribution which is determined by the final pyrrolyl product state distribution. That distribution is only established after a few hundred fs, when the H atom is rather distant (5–7 Å) from the pyrrolyl fragment. Despite the use of nanosecond laser pulses to dissociate the pyrrole, the H atoms depart within 20–30 fs of photon absorption. At this time, the pyrrolyl population is largely on the S1 (2B2) surface. One might therefore expect the HRAPTS data to represent a measure of the state of the system after this short time evolution, where after the departure of the H atom the KE distribution is unaffected by the internal dynamics of the pyrrolyl. This appears not to be the case, suggesting that the wavefunctions of the H atom and the partner radical remain coupled even at large spatial separations, as might be expected if H atom is strongly delocalized by preparation of the wave packet and its dynamics.
5. Conclusions
The availability of “on-the-fly” Ehrenfest quantum dynamics allows a more complete analysis of the dissociation of pyrrole than has previously been possible. By including all degrees of freedom in our numerical experiment we do not bias the simulation by the choice of dimensions to a model, hence allowing any and all nuclear coordinates to influence the dynamics. Although the current simulation has been performed mostly semiclassically and has not yet been converged on a fully quantum level, it provides clear evidence that the eventual population of the 2B1 state of pyrrole is low and thus lends strength to the assignments in the original HRAPTS experiments. It appears that taking into account a large number of degrees of freedom naturally captures the dynamics occurring as a result of several conical intersections, which is harder to see by low dimensionality models or imply from the experimental data alone. It shows that after N–H bond fission the internal dynamics of the pyrrolyl radical ensures coupling between its two lowest electronic states and affects their branching ratio by leaking the population from the upper state to the lower one on the timescale of a few hundred fs. Counterintuitively, the HRAPTS experiment seems sensitive to the final product state distribution, rather than the energy partitioning at the moment of classical dissociation.Acknowledgements
KS and DS acknowledge the support of EPSRC grant EP/I014500/1.References
- J. Wei, J. Riedel, A. Kuczmann, F. Renth and F. Temps, Faraday Discuss., 2004, 127, 267–282 RSC.
- C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernandez and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239 CrossRef CAS PubMed.
- A. L. Sobolewski and W. Domcke, Chem. Phys., 2000, 259, 181–191 CrossRef CAS.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- Z. Lan, A. Dupays, V. Vallet, S. Mahapatra and W. Domcke, J. Photochem. Photobiol., A, 2007, 190, 177–189 CrossRef CAS PubMed.
- V. Vallet, Z. G. Lan, S. Mahapatra, A. L. Sobolewski and W. Domcke, J. Chem. Phys., 2005, 123, 144307 CrossRef PubMed.
- M. Barbatti, J. Pittner, M. Pederzoli, U. Werner, R. Mitric, V. Bonacic-Koutecky and H. Lischka, Chem. Phys., 2010, 375, 26–34 CrossRef CAS PubMed.
- V. Vallet, Z. Lan, S. Mahapatra, A. L. Sobolewski and W. Domcke, Faraday Discuss., 2004, 127, 283–293 RSC.
- Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 224315 CrossRef PubMed.
- S. Mahapatra, Acc. Chem. Res., 2009, 42, 1004–1015 CrossRef CAS PubMed.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G. D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706 CrossRef CAS PubMed.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238 RSC.
- A. L. Devine, B. Cronin, M. G. D. Nix and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 184302 CrossRef PubMed.
- A. L. Devine, M. G. D. Nix, R. N. Dixon and M. N. R. Ashfold, J. Phys. Chem. A, 2008, 112, 9563–9574 CrossRef CAS PubMed.
- G. A. King, A. L. Devine, M. G. D. Nix, D. E. Kelly and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2008, 10, 6417–6429 RSC.
- G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, J. Chem. Phys., 2010, 132, 064305 CrossRef PubMed.
- M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, J. Chem. Phys., 2007, 126 Search PubMed.
- M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 2610–2618 RSC.
- M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125 Search PubMed.
- M. G. D. Nix, A. L. Devine, R. N. Dixon and M. N. R. Ashfold, Chem. Phys. Lett., 2008, 463, 305–308 CrossRef CAS PubMed.
- A. G. Sage, M. G. D. Nix and M. N. R. Ashfold, Chem. Phys., 2008, 347, 300–308 CrossRef CAS PubMed.
- A. J. van den Brom, M. Kapelios, T. N. Kitsopoulos, N. H. Nahler, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2005, 7, 892–899 RSC.
- B. Cronin, M. G. D. Nix, R. H. Qadiri and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2004, 6, 5031–5041 RSC.
- B. Cronin, A. L. Devine, M. G. D. Nix and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2006, 8, 3440–3445 RSC.
- D. A. Blank, S. W. North and Y. T. Lee, Chem. Phys., 1994, 187, 35–47 CrossRef CAS.
- H. Yu, N. L. Evans, V. G. Stavros and S. Ullrich, Phys. Chem. Chem. Phys., 2012, 14, 6266–6272 RSC.
- R. Montero, A. P. Conde, V. Ovejas, M. Fernandez-Fernandez, F. Castano, J. R. V. d. Aldana and A. Longarte, J. Chem. Phys., 2012, 137, 064317 CrossRef PubMed.
- K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- D. V. Shalashilin, Faraday Discuss., 2011, 153, 105–116 RSC.
- D. V. Shalashilin, J. Chem. Phys., 2010, 132, 244111 CrossRef PubMed.
- D. V. Shalashilin, J. Chem. Phys., 2009, 130, 244101 CrossRef PubMed.
- B. G. Levine and T. J. Martinez, J. Phys. Chem. A, 2009, 113, 12815–12824 CrossRef CAS PubMed.
- T. J. Martinez, M. Ben-Nun and R. D. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef CAS.
- B. G. Levine, J. D. Coe, A. M. Virshup and T. J. Martinez, Chem. Phys., 2008, 347, 3–16 CrossRef CAS PubMed.
- M. Ben-Nun and T. J. Martinez, Chem. Phys., 2000, 259, 237–248 CrossRef CAS.
- D. Mendive-Tapia, B. Lasorne, G. A. Worth, M. J. Bearpark and M. A. Robb, Phys. Chem. Chem. Phys., 2010, 12, 15725–15733 RSC.
- G. A. Worth, M. A. Robb and B. Lasorne, Mol. Phys., 2008, 106, 2077–2091 CrossRef CAS.
- A. J. Gianola, T. Ichino, R. L. Hoenigman, S. Kato, V. M. Bierbaum and W. C. Lineberger, J. Phys. Chem. A, 2004, 108, 10326–10335 CrossRef CAS.
- N. L. Doltsinis and D. Marx, J. Theor. Comput. Chem., 2002, 01, 319–349 CrossRef CAS.
- P. J. K. H.-J. Werner, G. Knizia, F. R. Manby, M. Schütz, et al., http://www.molpro.net, 2010.
- R. C. Brown and E. J. Heller, J. Chem. Phys., 1981, 75, 186–188 CrossRef CAS.
- A. Kirrander and D. V. Shalashilin, Phys. Rev. A, 2011, 84, 13 Search PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- H. Nakano, T. Tsuneda, T. Hashimoto and K. Hirao, J. Chem. Phys., 1996, 104, 2312–2320 CrossRef CAS.
- O. Christiansen, J. Gauss, J. F. Stanton and P. Jorgensen, J. Chem. Phys., 1999, 111, 525–537 CrossRef.
- B. O. Roos, P. A. Malmqvist, V. Molina, L. Serrano-Andres and M. Merchan, J. Chem. Phys., 2002, 116, 7526–7536 CrossRef CAS.
- P. Celani and H. J. Werner, J. Chem. Phys., 2003, 119, 5044–5057 CrossRef CAS.
- M. Pastore, C. Angeli and R. Cimiraglia, Chem. Phys. Lett., 2006, 422, 522–528 CrossRef CAS PubMed.
- A. L. Thompson, C. Punwong and T. J. Martínez, Chem. Phys, 2010, 370, 70–77 CrossRef CAS PubMed.
- G. M. Roberts, C. A. Williams, H. Yu, A. S. Chatterley, J. D. Young, S. Ullrich and V. G. Stavros, Faraday Discuss. 10.1039/c2fd20140b.
| This journal is © the Owner Societies 2013 |