C₇₂: gaudiene, a hollow and aromatic all-carbon molecule

Abstract

A new allotropic form of carbon is proposed. The molecular structure of a cavernous C₇₂ molecule has been optimized at the density functional theory level. The structure belonging to the O_h point group was found to be a minimum on the potential energy surface. Current-density calculations show that the gaudiene molecule with formally 72 π electrons sustains strong diatropic currents when exposed to an external magnetic field.

---

The discovery of the fullerene molecules C₆₀ and C₇₀ was reported in 1985.¹ Since then, many fullerenes of different size and shape have been fabricated with carbon nanotubes as the tallest member.² Fullerenes and carbon nanotubes are considered as the third allotropic form of carbon, with diamond and graphite as the first two. More recently, the fourth carbon allotrope, namely graphene which consists of a graphite monolayer, was discovered.³ The discovery of fullerenes and graphene shows the incredible flexibility of carbon. The usefulness of the novel carbon structures has led to an intense research activity in the field. Fullerenes and carbon nanotube-based carbon structures have been proposed as basic building blocks for a variety of interesting nanotechnological applications.⁴ Fullerenes and graphene are not the only possibilities to construct novel all-carbon materials. The carbon nanofoam is considered as the fifth carbon allotrope.⁵ Human imagination and creativity have led to predictions of molecular structures of other carbon allotropes, the building blocks of which one has tried to synthesize.^6–12

Here, a new carbon allotrope is proposed. It is named gaudiene, because its structure is inspired from the work of the Spanish architect Antoni Gaudi, which is shown in the graphical abstract.¹³ Gaudiene has structural similarities to fullerenes as it is also an almost spherical all-carbon molecule. Gaudiene consists of 72 carbon atoms and has O_h symmetry. Gaudiene may be considered as the sixth carbon allotrope, because of its novel carbon structure. It does not consist of any five-membered or six-membered carbon rings but of completely new building blocks for three-dimensional carbon structures. Gaudiene is not merely an interesting molecule, it also opens the avenue to the construction of a new class of carbon based molecules and materials.

The molecular structure of gaudiene was optimized at the density functional theory (DFT) level using the Becke–Perdew generalized gradient approximation (GGA) functional (BP86) in combination with the Karlsruhe split-valence polarization (SVP) basis sets.^14–17 The harmonic frequencies of the vibrational spectrum calculated at the BP86/SVP level were all real.¹⁸ The molecular structure reported in the ESI† was optimized at the DFT level using Becke's three-parameter functional (B3LYP) and the new Karlsruhe triple-ζ quality basis sets augmented with polarization functions (def2-TZVP).^19–21 The DFT calculations were performed using Turbomole.^22,23

The gaudiene structure with O_h symmetry consists of six four-sided rings having four carbons on each side with alternating triple and single bonds. The four-sided rings are surrounded on each side by hexadehydro[12]annulene rings, which are known to form antiaromatic molecules.^25,26 The eight hexadehydro[12]annulene rings have single bonds that alternate with double and triple bonds. Thus, gaudiene has 24 C≡C, 12 C=C, and 48 C–C bonds, whose lengths are R(C≡C) = 122.0 pm, R(C=C) = 141.9 pm, and R(C–C) = 140.2 pm. The molecular structure is shown in Fig. 1.

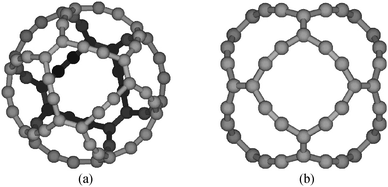Fig. 1 The molecular structure of gaudiene from two different views. The pictures are made with MOLDEN.²⁴

Gaudiene is a stable molecule with an energy gap of 1.81 eV between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) calculated at the B3LYP level. HOMO and LUMO belong to the t_1u and a_1g irreducible representations, respectively. Gaudiene is 12.6 kcal mol⁻¹ per carbon atom less stable than fullerenes (Fig. 2).

Fig. 2 The energy levels of the frontal orbitals calculated at the B3LYP level.

B3LYP calculations of the nuclear magnetic resonance (NMR) shielding constants show that gaudiene has two different carbons with magnetic shieldings of 31.9 ppm and 44.7 ppm, which correspond to ¹³C NMR chemical shifts of 151.5 ppm and 138.7 ppm relatively to tetramethylsilane (TMS), respectively. For C₆₀, the experimental signal in the ¹³C NMR spectrum appears at 142.68 ppm.²⁷

The aromatic character of fullerenes has been a matter of debate ever since the remark by Kroto et al.¹ that C₆₀ appears to be aromatic. Since then, various studies of the aromaticity of C₆₀ have been reported.^28–35 The established opinion is that C₆₀ is nonaromatic. Aromaticity studies are challenged by the elusive nature of the property. An unambiguous definition of aromaticity is unsettled even though or because the aromaticity concept is very old. A common denominator is that planar aromatic molecules that fulfil Hückel's (4n + 2)π electron rule sustain a net diatropic ring current when they are exposed to external magnetic fields. A similar electron-counting rule holds for the aromaticity of fullerenes and other cavernous approximately spherical molecules.^32,34 The magic numbers for spherical aromaticity is obtained by considering that the potential housing the valence electrons is infinitely thin and spherical. The aufbau principle then yields magic numbers of 2(n + 1)² including 72 for n = 5, which is the formal number of π electrons of gaudiene. Current-density calculations on C₆₀ and C₆₀¹⁰⁺ showed that fullerenes are nonaromatic, whereas C₆₀¹⁰⁺ with 50 π electrons is a spherical aromatic molecule with strong diatropic shell currents.³⁴ Spherical aromatic molecules sustain diatropic shell currents on the inside and the outside of the molecular integument. The current flow does not follow the chemical bonds of the molecule. The calculations showed that the magnetically induced currents circulate perpendicularly to the applied magnetic field on the molecular surface of the fullerenes. For C₆₀, the paratropic current on the inside of the molecular frame cancels the diatropic current outside it, whereas for C₆₀¹⁰⁺ the shell current is uniformly diatropic.³⁴

The magnetically induced current density of gaudiene has been studied at the BP86/SVP and B3LYP/def2-TZVP levels to assess its aromatic character. The current density or actually the susceptibility of the magnetically induced current density (in nA T⁻¹) was obtained using our gauge-including magnetically induced current (GIMIC) method,^37–39 which yields gauge-independent current densities, because gauge including atomic orbitals (GIAOs) are employed in the calculations.⁴⁰ Explicit values for the current strengths are obtained by numerical integration of the current density passing chemical bonds or selected planes through the molecule.³⁹

The magnetic field is applied in the z direction along the symmetry axis that passes at the center of the four-sided rings in Fig. 1b. The integration plane begins at the symmetry axis and cuts through half of the molecule. The integration plane extends radially passing at the center of, e.g., the C≡C and C=C bonds obliquely upwards (Fig. 1b). The integrated strength of the current density that passes the plane is 44.3 nA T⁻¹. The net current strength calculated at the B3LYP/def2-TZVP level consists of a diatropic contribution of 56.7 nA T⁻¹ and the paratropic contribution is −12.4 nA T⁻¹. In Fig. 3, the solid line shows the profile of the current density as a function of the radial distance (R) from the symmetry axis of the molecule. Integration of the current-density profile with respect to R yields the radial current-density function, which is proportional to the curve shown with the dashed line. The curves in Fig. 3 show that paratropic currents flow on the inside of the C≡C bonds. Diatropic currents dominate outside the C≡C bonds. The minimum of the current-profile function at about 3 bohr (160 pm) and the minimum of the function at 3.6 bohr (190 pm) for the integrated current strength are just inside the first C≡C bond at a distance of 4.3 bohr (228 pm) from the symmetry axis. The strong diatropic contributions in the interval of 4–8 bohr originate from the region between the C≡C and C=C bonds (Fig. 1b), which corresponds to the hexadehydro[12]annulene ring. The maximum is due a current flow between the two double bonds of the hexadehydro[12]annulene. The current passes almost 100 pm from the C≡C bond. A minimum is seen in the curve for the current profile when the radial distance approaches the C=C bond indicating the presence of some paratropic current contributions inside the double bond. The C=C bond lies at a distance of 8.6 bohr (457 pm) from the symmetry axis. The peak maximum at 9.9 bohr (520 pm) originates from the diatropic current density outside the C=C bond.

Fig. 3 The solid line shows the strength of the magnetically induced current density (in nA T⁻¹ bohr⁻¹) for gaudiene as a function of the radial distance (in bohr), 1 bohr = 52.9177 pm. The shape of the integrated current density is shown with the dashed line. The vertical line at 8.86 bohr (469 pm) indicates the radial position of the outermost carbons. The graph is made using GNUPLOT.³⁶

The large net current strength of 44.3 nA T⁻¹ shows that gaudiene is an aromatic molecule. The ring-current strength is almost four times larger than the benzene value of 11.8 nA T⁻¹ calculated at the same level.⁴¹ Even though gaudiene has 72 π electrons and fulfills the 2(n + 1)² rule for spherical aromaticity it cannot be considered to be a spherical aromatic molecule, because the magnetically induced currents mainly follow the chemical bonds. The holes in the molecule are too large to render significant through-space transport of the currents feasible.

Gaudiene might also open the avenue to novel materials with interesting properties. The synthesis of three-dimensional zeolite-like structures consisting of cross-linked gaudiene molecules might be feasible. The porous all-carbon material would be very light and might possess interesting properties due to the regular cavities. Fullerenes with hexaethynylbenzene (C₁₈H₆)⁴² as basic building blocks might also be a possibility to construct novel all-carbon structures.

Interesting hydrocarbons can be obtained by partially saturating the triple bond to double bonds or by saturating all multiple bonds of gaudiene. The partially hydrogenated gaudiene, with the chemical formula C₇₂H₄₈, may be an interesting starting point for gaudiene-based chemistry. The hydrogenation of the triple bonds of C₇₂ forming double bonds breaks the symmetry yielding a slightly distorted nonsymmetric but almost spherical molecule. Current-density calculations show that C₇₂H₄₈ is nonaromatic. The π orbitals of the C≡C bonds that are perpendicular to the molecular surface are saturated implying that the π conjugation along the molecular surface is interrupted at the hydrogenated triple bonds. The current-density calculations yielded a net current strength of −2.0 nA T⁻¹ at the BP86/SVP level. The net current strength consists of diatropic and paratropic contributions of 59.9 nA T⁻¹ and −61.9 nA T⁻¹, respectively. The hydrogenated gaudiene (C₇₂H₄₈) is though a very stable molecule with a HOMO–LUMO gap of 2.83 eV at the BP86/SVP level. Preliminary calculations indicate that the fully hydrogenated gaudiene (C₇₂H₁₂₀) is a hollow hydrocarbon with a large HOMO–LUMO gap of more than 6 eV at the BP86/SVP level.

This research has been supported by the Academy of Finland through its Computational Science Research Programme (LASTU). We thank Magnus Ehrnrooth foundation for financial support. CSC – the Finnish IT Center for Science – is acknowledged for computer time.

References

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. S. Iijima, Nature, 1991, 354, 56–58.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
4. M. Meyyappan and D. Srivastava, Handbook of Nanoscience, Engineering, and Technology, CRC Press, Boca Raton Fl, 2003, ch. 18, pp. 1–26.
5. A. Rode, S. Hyde, E. Gamaly, R. Elliman, D. McKenzie and S. Bulcock, Appl. Phys. A, 1999, 69, S755–S758.
6. R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699.
7. D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804.
8. F. Diederich and M. Kivala, Adv. Mater., 2010, 22, 803–812.
9. A. N. Enyashin and A. L. Ivanovskii, Phys. Status Solidi B, 2011, 248, 1879–1883.
10. L. Zoppi, J. S. Siegel and K. K. Baldridge, WIREs Comput. Mol. Sci., 2013, 3, 1–12.
11. S. Zhang, Y. Zhang, S. Huang and C. Wang, Nanoscale, 2012, 4, 2839–2842.
12. Y. S. Wang, P. F. Yuan, M. Li, W. F. Jiang, Q. Sun and Y. Jia, J. Solid State Chem., 2013, 197, 323–328.
13. Origamic Chemistry: the molecular structure of the gaudiene molecule was constructed by scrutinizing a photograph taken at the Gaudi museum in Barcelona. The structure was reconstructed as a family project by folding paper at the kitchen table.
14. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
15. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
16. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
17. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
18. P. Deglmann and F. Furche, Chem. Phys. Lett., 2002, 362, 511–518.
19. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
20. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
21. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
22. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
23. TURBOMOLE V6.4 2012, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
24. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.
25. J. A. Pople and K. G. Untch, J. Am. Chem. Soc., 1966, 88, 4811–4815.
26. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 2008, 10, 6630–6634.
27. R. Taylor, G. J. Langley, A. G. Avent, T. J. S. Dennis, H. W. Kroto and D. R. M. Walton, J. Chem. Soc., Perkin Trans. 2, 1993, 1029–1036.
28. P. W. Fowler, D. J. Collins and S. J. Austin, J. Chem. Soc., Perkin Trans. 2, 1993, 275–277.
29. M. Saunders, H. A. Jimenez-Vazquez, R. J. Cross, S. Mroczkowski, D. I. Freedberg and F. A. L. Anet, Nature, 1994, 367, 256–258.
30. A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2000, 39, 3915–3917.
31. M. Bühl, Chem.–Eur. J., 1998, 4, 734–739.
32. M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1183.
33. R. Taylor, Phys. Chem. Chem. Phys., 2004, 6, 328–331.
34. M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846.
35. Z. Chen and R. B. King, Chem. Rev., 2005, 105, 3613–3642.
36. http://www.gnuplot.info/ .
37. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
38. S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123.
39. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
40. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
41. H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676.
42. S. Taubert, J. Jusélius, D. Sundholm, W. Klopper and H. Fliegl, J. Phys. Chem. A, 2008, 112, 13584–13592.

---

Footnote

† Electronic supplementary information (ESI) available: The Cartesian coordinates (in bohr) of gaudiene. See DOI: 10.1039/c3cp51042e

---