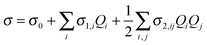Fullerene C₇₀ characterization by ¹³C NMR and the importance of the solvent and dynamics in spectral simulations

Abstract

The nuclear magnetic resonance (NMR) spectroscopy combined with theoretical calculations is an important tool for fullerene identification. However, the accuracy of available theoretical methods is often not adequate. Therefore, in this work, different computational aspects needed to simulate realistically chemical shifts in the C₇₀ molecule are investigated by density functional theory (DFT) calculations. The importance of the functional choice, basis set, solvent, and molecular motions was assessed. The solvent was simulated using the implicit conductor-like polarized continuum model. The molecular motions were included via anharmonic corrections and averaging of snapshots obtained from classical and first-principles molecular dynamics (MD) simulations. Comparison to experiment revealed that density functional calculations typically overestimate the ¹³C NMR chemical shifts. Hybrid functionals, such as BHandH and BHandHLYP, and long-range corrected functionals, such as wB97xd and CAM-B3LYP, give the best results. While the solvent has a minor effect (chemical shift changes by ∼1 ppm), the vibrational and dynamical effects are surprisingly large, causing changes up to 9 ppm. Consideration of the latter was also necessary to explain the observed temperature dependence. While the dynamical corrections for MD performed in vacuum were overestimated, inclusion of the solvent in simulations provided more realistic results. The study thus points out the importance of an appropriate solvent model and a complex approach to the modelling, balancing the static, dynamic and environmental factors.

---

Introduction

Since the initial discovery of C₆₀ by Kroto et al.¹ the fullerene science has evolved into a rich multidisciplinary field. Fullerenes and their derivatives have been intensively studied as materials for solar cells, quantum computing, memory devices, magnetic storage devices, molecular containers, MRI contrast agents, and other applications.^2,3 The fullerene cage structures have been rationalized by the isolated-pentagon rule (IPR).⁴ The number of the possible isomers of C_n grows with n. For example, the C₆₀ fullerene has one isomer, C₈₀ has seven isomers, and for C₈₄, 24 IPR isomers have been predicted to exist. In spite of the similarity of different fullerenes and their isomers, owing to their high molecular symmetry, they can be in many cases distinguished according to the number and intensity of spectral lines in ¹³C nuclear magnetic resonance (NMR) spectra. The NMR spectroscopy, hand in hand with theoretical interpretation of the experimental NMR spectra, is thus an important analytical tool in fullerene chemistry.

Identification of fullerenes can be significantly enhanced by calculations of fullerene structures and ¹³C NMR parameters, typically based on the density functional theory (DFT).^5–11 In a review by Heine,¹² however, typical accuracy of ¹³C NMR DFT calculations was estimated to be 2 ppm, which may not be sufficient for larger fullerenes with a denser spacing (<1 ppm) of spectral lines.

To assess the reliability of commonly used methods for calculations of the ¹³C chemical shift we use the C₇₀ fullerene as a convenient model. It contains five different symmetry-equivalent carbon types (assigned as C_a–C_e in Fig. 1) which cover the range of ∼130–150 ppm spanning to a large part typical fullerene ¹³C chemical shifts.¹³ The performance of various density functionals and basis set convergence are analyzed.

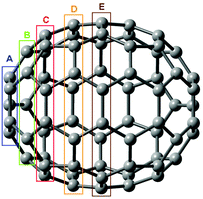Fig. 1 Symmetry equivalent carbon types in C₇₀.

In the next stage, we assess the effects of dynamics, temperature, and solvent on the calculated ¹³C NMR chemical shifts. The effects of solvent are approximated using the conductor-like polarized continuum model (CPCM).¹⁴ Several approaches of involving the molecular motion in the computations are explored: averaging snapshots obtained from classical molecular dynamics (MD) and the first-principles molecular dynamics (FPMD) trajectories, and a quantum averaging of anharmonic vibrational corrections.^15,16

Methods

DFT calculations

The static DFT calculations and the first-principles MD were performed using the Turbomole 6.3.1 (ref. 17) and Gaussian 09, Revision A.02 (ref. 18) program packages. Classical MD was run using the Tinker program suite.^19,20 The geometry was optimized using several DFT functionals (BP86,^21,22 B3LYP,²³ and wB97xd²⁴) and the Ahlrichs-type basis sets (def2-SVP, def2-TZVP, and def2-QZVP).^25,26

The nuclear magnetic shielding was calculated with GGA (HCTH,²⁷ BLYP,^21,28 OLYP,^28,29 BP86,^21,22 PBEPBE,³⁰ OPBE,^29,30 SV5LYP^28,31,32), meta GGA (M06L³³), hybrid (B1LYP,³⁴ B3LYP,²³ O3LYP,³⁵ X3LYP,³⁶ BHandH/Gaussian09,¹⁸ BHandHLYP,¹⁸ and B98³⁷), meta GGA hybrid (M06HF³⁸), and range-separated hybrid (CAM-B3LYP,³⁹ wB97xd²⁴) functionals. The list thus enables us to compare the GGA and hybrid functionals, different exchange potentials (e.g. in B1LYP, B3LYP, O3LYP, X3LYP) and various degrees of the involvement of the HF exchange (e.g. BLYP with 0% exchange, B3LYP (20%), and BHandHLYP (50%)). Because common functionals may suffer from unphysical long-range behavior of the non-Coulomb part of exchange, the effect of long-range corrections was also taken into account by involving the CAM-B3LYP³⁹ and wB97xd²⁴ functionals.

The basis set convergence was investigated using the IGLO-II,⁴⁰ IGLO-III,⁴⁰ and IGLO-IV^41,42 basis sets optimized for calculations of NMR parameters. A set of Jensen's polarization-consistent basis sets, pcS-n, was also tested.⁴³

Calculated isotropic nuclear shielding (σ) was converted to chemical shift (δ) using tetramethylsilane (TMS) as a reference and C₆₀ as a secondary reference, according to formula

δ_i = σ(C₆₀) − σ_i(C₇₀) + δ(C_60,TMS)

where σ_i is a signal of C₇₀ carbon and δ(C_60,TMS) = 143.15 ppm.⁴⁴

Solvent modelling

Effects of solvent were approximated using the conductor-like polarized continuum model (CPCM)¹⁴ as implemented in Gaussian 09,¹⁸ using standard parameters for 1,1,2-trichloroethane. Note that 1,1,2,2-tetrachloroethane was used instead in ref. 44, not supported by Gaussian 09, but with a very similar dielectric constant (7.19 for 1,1,2-trichloroethane and 8.42 for 1,1,2,2-tetrachloroethane).

Quantum vibrational averaging

The nuclear potential of C₇₀ was expanded to a Taylor series up to fourth powers of all normal mode coordinates Q_i.⁴⁵ Only cubic and semi-diagonal normal mode quartic constants (with two or more identical indices) were considered, as these can be obtained by a single normal mode numerical differentiation of harmonic force fields.⁴⁶ The anharmonic force field was calculated at the Hartree–Fock (HF) level using the 6-31G basis set, while the shielding derivatives were obtained at the BP86/IGLO-II level. Gaussian 09¹⁸ was used for the Hessian computations for geometries displaced in normal modes. Program S4⁴⁷ interfaced to Gaussian was used for the anharmonic vibrational averaging.

One of the limitations of anharmonic vibrational corrections performed here is the necessity to use Hartree–Fock approximation which overestimates harmonic frequencies by about 10%.^48,49 While DFT provides typically better harmonic frequencies deviating from experiment by only a few percents,^50–53 it was not affordable for such extensive calculations on C₇₀. We do not suppose that the relatively small frequency error of the HF method would significantly change the anharmonic corrections added in a perturbation way only.

For vibrational ground state ψ_n isotropic nuclear magnetic shielding was calculated as

σ_n = 〈ψ_n|σ|ψ_n〉

where

The σ₁ and σ₂ are the first and second normal mode isotropic shielding derivatives obtained numerically with a differentiation step of 0.2 Å. This parameter was found to be optimal for many systems including fullerenes before.⁵⁴ Within the second-order degeneracy-corrected perturbational (PT2) scheme⁴⁶ the wave function is expanded in the harmonic oscillator basis.¹⁶

Alternatively, the vibrational configuration interaction (VCI) was used for vibrationally averaged shieldings, where the Hamiltonian was diagonalized in the harmonic oscillator basis functions (|l〉, up to doubly excited states) limited by an interaction parameter

|〈l|V|n〉/(E_n − E_l)| ≤ 0.1

where n is a fundamental vibration or the ground state.

A third approximation tried was based on the harmonic oscillator limit for energies⁵⁵ and provided temperature-corrected shielding (TCS) as

σ = σ₀ + 0.25σ_iiexp(−ω_i/kT)[1 − exp(−ω_i/kT)]⁻¹

Although the anharmonic methods should be in principle equivalent, they differ because of the approximations used and the vast number of harmonic oscillator (HO) states that should be considered for C₇₀. The PT2 method provides correction for a large number of HO states but may fail for large anharmonic effects and Fermi resonances. The resonances are better represented in VCI, where, however, a smaller number of the states can be considered. Neither the VCI nor PT2 implementation involves the temperature effects involved in TCS, where, however, simplified anharmonic energy and property surfaces are supposed. Therefore, we used all three methods to get a feeling of the significance of the anharmonic vibrational averaging of the chemical shift.

Molecular dynamics

The BP86/def-TZVP optimized structure of C₇₀ was minimized using the Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) procedure in Tinker. The minimized geometry was evolved for 1 ns. The classical MD trajectories with the MM3 force field⁵⁶ were obtained using the modified Beeman algorithm with a 1 fs integration time step at constant temperature T = 300 K. The MM3 force field was modified for the C₇₀ carbon atoms as described in the ESI.† Chemical shifts were calculated for 40 snapshots at the BHandHLYP/IGLO-III level and averaged. To minimize systematic error, the dynamical correction was calculated as a difference between the average and the shielding calculated for MM3-minimized geometry.

First-principles molecular dynamics

FPMD simulations were performed on the BP86/def-SVP Born–Oppenheimer potential energy surface. The leapfrog Verlet algorithm as implemented in the Turbomole code¹⁷ was used to update the coordinates. To avoid problems due to the limited numerical precision in the density optimization and the force calculation, the thresholds for energy and CPHF equations convergence were tightened to 10⁻⁸ a.u. A denser numerical grid denoted as “m5” was used. The time step was 80 a.u. (1.93 fs). To achieve a better sampling of the configuration space we ran several microcanonical (NVE ensemble) dynamics trajectories 1.2 ps long. The initial velocities were randomly distributed and corresponded to the temperature of 300 K. A total of four MD trajectories of 1.2 ps were produced for the averaging of snapshots. The initial 0.2 ps part of each trajectory was discarded as an equilibration phase, and then 16 equidistant snapshots of each trajectory (64 in total) were taken for the ¹³C NMR calculations (BHandHLYP/IGLO-III) and averaging. To verify the time-correlation of the data the block-averaging method was used.⁵⁷ The mean errors of average were found in the interval of ±0.2 to ±0.25 ppm for the NMR shielding of different carbons, which after subtraction from the C₆₀ reference give a statistical error of ±0.35 ppm in the dynamical corrections for shielding. The dynamical corrections were obtained as differences between the average and result for the BP86/def-SVP optimized structure.

NMR experiment

Fullerenes (C₆₀ and C₇₀) were purchased from Sigma. ¹³C NMR spectra of C₇₀ were recorded in deuterated ortho-dichlorobenzene (ODCB) using a Bruker Advance II™ 600 and 500 MHz spectrometer equipped with a cryoprobe. The spectra were measured at several temperatures (278, 298, 318, 338, 358 and 378 K). A small amount of C₆₀ was detected (at 142.86 ppm) in the sample of C₇₀. The chemical shifts were referenced to tetramethylsilane (TMS).

Results and discussion

Basis set convergence

We used optimized BP86/def-TZVP C₇₀ structure⁵⁸ to investigate the effect of the basis set and DFT functional on the ¹³C NMR chemical shifts in C₇₀ calculated for the molecule at rest in vacuo. The BP86/def-TZVP level previously provided results in an excellent agreement with the experimental structural parameters for the C₆₀ molecule.^58,59

Table 1 lists the ¹³C chemical shifts for C₇₀ calculated using the different IGLO-n type basis sets. The IGLO-III results appear converged within 0.2 ppm as compared to the IGLO-IV basis set, which can be considered to be near the basis set limit. Corrections beyond IGLO-IV can be expected to lie below 0.2 ppm.⁶⁰ Hence the error of the IGLO-III basis set calculations with respect to the basis set limit can be estimated with safe margins to be within 0.4 ppm. With a conservative error estimate of 0.4 ppm for ¹³C shifts the IGLO-III basis set provides a good compromise between the accuracy and the computational cost. IGLO-IV is recommended if higher accuracy is needed.

Table 1 Basis set convergence of ¹³C chemical shifts (in ppm) for C₇₀^a

Carbon	IGLO-II	IGLO-III	IGLO-IV
a Chemical shifts were calculated for BP86/def-TZVP optimized geometry. The BP86 functional was used for ^13C chemical shifts.
Ca	153.3	154.4	154.2
Cb	148.7	149.6	149.5
Cc	150.0	151.2	151.0
Cd	147.4	148.1	148.0
Ce	130.7	130.5	130.5

---

Following the suggestion of a referee, the basis set convergence was also tested on the set of Jensen's polarization consistent pcS-n basis sets⁴³ known to provide accurate nuclear shieldings.⁶¹ The convergence of ¹³C nuclear shieldings in C₆₀ obtained with pcS-n (n = 0, 1, 2, 3) can be seen in Fig. S1 (ESI†). Table S1 (ESI†) lists the ¹³C chemical shifts for C₇₀ calculated using different pcS-n (n = 0, 1, 2) basis sets. It is apparent that the IGLO-n basis sets provided faster convergence than pcS-n.

Performance of various density functionals

The results obtained using the selected DFT functionals are summarized in Table 2, where the calculated ¹³C shifts as well as their root-mean-square deviations (RMSD) from the experimental values are collected. The results in Table 2 are ordered according to the RMSD. Typically, the DFT calculations overestimate the experimental ¹³C NMR chemical shift by several ppm. Obviously, the effects of solvent and temperature are not included at this stage, and we can compare only the main trends exhibited by the functionals.

Table 2 Performance of DFT functionals for ¹³C chemical shifts (in ppm) in C₇₀ with the root-mean-square deviation (RMSD) from experiment

Functional	Ca	Cb	Cc	Cd	Ce	RMSD^a (RMSD^b)
a Ref. 13. b This work. c Values using B3LYP/6-31G* taken from ref. 10. Calculations were performed for BP86/def-TZVP optimized geometry and with the IGLO-III basis set.
wB97xd	150.6	147.3	147.9	145.8	132.3	0.4 (0.4)
CAMB3LYP	151.8	148.0	149.0	146.7	132.5	0.6 (0.7)
M06L	152.8	148.0	149.7	146.6	130.8	0.7 (0.7)
OPBE	152.9	148.4	149.9	147.1	129.9	0.8 (0.8)
BHandHLYP	152.7	148.6	149.9	147.0	132.7	0.8 (0.9)
BHandH	152.8	148.8	150.1	147.1	132.1	0.9 (0.9)
O3LYP	153.2	148.7	150.3	147.4	131.1	0.9 (1.0)
HCTH	153.3	148.6	150.3	147.4	130.5	0.9 (1.0)
OLYP	153.5	148.8	150.4	147.5	130.5	1.0 (1.0)
B98	153.6	149.2	150.7	147.8	131.6	1.1 (1.1)
B1LYP	153.7	149.2	150.7	147.8	132.0	1.1 (1.2)
X3LYP	153.8	149.3	150.8	147.9	131.8	1.1 (1.2)
B3LYP	153.8	149.3	150.9	147.9	131.7	1.1 (1.2)
PBEPBE	154.2	149.5	151.1	148.0	130.4	1.2 (1.3)
BLYP	154.8	150.0	151.5	148.5	131.0	1.4 (1.5)
SV5LYP	154.8	150.1	151.6	148.5	129.7	1.4 (1.5)
M06HF	155.5	152.3	151.0	148.5	132.7	1.7 (1.8)
BP86	155.6	150.8	152.4	149.4	131.9	1.7 (1.8)
Exp.^a	150.8	147.8	148.3	144.4	130.8	—
Exp.^b	150.3	147.1	147.8	145.0	130.5	—
B3LYP^c	151.2	147.0	148.2	146.3	132.1	0.5 (0.5)

---

Nevertheless, for the gas-phase C₇₀ molecule at rest it appears that the long-range corrected functionals CAM-B3LYP and wB97xd as well as the hybrid functionals with 50% of exact-exchange admixture BHandH and BHandHLYP perform the best, while the non-hybrid GGA functionals give a worse agreement with the experiment. The OPBE functional, provides results of the same accuracy as BHandHLYP with much smaller CPU cost. The good performance of the OPBE^62,63 as well as “half-and-half” functionals for NMR parameters has been noticed elsewhere.^{58,59,64–67} A good performance is provided also by the M06L pure DFT functional of Truhlar and Zhao.³³ Combining different exchange functionals with the LYP correlation along the B1LYP, B3LYP, X3LYP, and O3LYP series shows rather marginal dependence of the performance on the exchange functional. Increasing the exact exchange admixture in the functional generally lowers the calculated ¹³C chemical shifts, bringing them closer to the experimental ones, as seen in Fig. 2. A decrease of the RMSD with increasing exact-exchange admixture is observed for relative carbon shifts (C signals relative to C_e) in Fig. 2. Noticeably, if one looks at relative ¹³C NMR chemical shifts in Table S2 (ESI†) instead of the absolute ones in Table 2 the relative performance is somewhat altered especially for larger RMDS values.

Fig. 2 The effect of increasing exact-exchange admixture in DFT functionals on calculated ¹³C chemical shifts. RMSD (solid line) stands for root mean square deviations from the experimental values.¹³ RMSD^r (dashed line) is calculated for relative ¹³C shifts (C–C_e).

We did not include the multiplicative Kohn–Sham methods⁶⁸ denoted also as the optimized-effective potential (OEP) methods, often leading to improvements in calculations of magnetic resonance properties.^69–75However, less significant improvement for carbon only containing compounds was observed.⁷⁶

If the larger IGLO-IV basis set was used in the calculations shown in Table 2 (not affordable presently), most RMSDs should improve, as the DFT calculated ¹³C chemical shifts would lower by about 0.1–0.2 ppm, mostly towards the experimental values. We do not expect this rather small basis set effect to alter the performance of the DFT functionals, as shown in Table 2.

The solvent effect

As seen in Table 3, the inclusion of the solvent within the CPCM implicit solvent model moderately decreases the calculated ¹³C shifts by 0.5–1.0 ppm towards the experimental values. Note that the new experiment performed in this work in ODCB solvent (ε = 9.93) provided almost identical results to the previous experiments done in 1,1,2,2-tetrachloroethane (see Table 1). This suggests a limited dependence of the ¹³C NMR chemical shifts on the kind of solvent for this non-polar molecule. A closer look at Table 3 reveals that the BHandH and OLYP functionals decrease calculated shifts towards experimental results (RMSD drop of ∼0.1 ppm), while including the effects of solvent slightly increases the RMSD error at the wB97xd level, from 0.4 to 0.5.

Table 3 Vacuum vs. solvent chemical shifts (in ppm) calculated in C₇₀^a

	Exp.	BHandH		OLYP		wB97xd
		Vac.	Solv.	Vac.	Solv.	Vac.	Solv.
a The BP86/def-TZVP or BP86/def-TZVP/CPCM geometry was used. Implicit solvent with parameters for 1,1,2-trichloroethane and the IGLO-III basis set for shielding calculations were employed. RMSD is the root-mean-square deviation from experimental values in ref. 13. RMSD^r is calculated for relative chemical shifts (C–Ce).
Ca	150.8	152.8	152.3	153.5	153.2	150.6	150.2
Cb	147.8	148.8	148.2	148.8	148.4	147.3	146.7
Cc	148.3	150.1	149.6	150.4	150.1	147.9	147.5
Cd	144.4	147.1	146.9	147.5	147.4	145.8	145.5
Ce	130.8	132.1	131.8	130.5	130.3	132.3	132.0
RMSD		0.8	0.7	1.0	0.9	0.4	0.5
RMSD^r		0.4	0.4	1.3	1.3	0.8	0.9

---

Equilibrium geometry effect

The effect of the equilibrium geometry on the calculated ¹³C shifts for C₇₀ is illustrated in Table 4. While improving the basis set from def-TZVP towards def2-QZVP, the shift decreases towards the experiment in a uniform way, by about 1 ppm, when comparing the def-TZVP and def2-QZVP structures.

Table 4 Calculated (BHandH/IGLO-III) ¹³C chemical shift (in ppm) for C₇₀ using geometries optimized at different computational levels

Structure	Ca	Cb	Cc	Cd	Ce	RMSD (RMSD^r)
a The BP86 functional was used. b The def2-TZVP basis set was used. RMSD is the root-mean-square deviation from experimental values ref. 13, RMSD^r is calculated for relative chemical shifts (C–Ce).
def-SVP^a	152.2	148.2	149.5	146.5	131.6	0.6 (0.4)
def-TZVP^a	152.8	148.8	150.1	147.1	132.1	0.8 (0.4)
def2-TZVP^a	151.9	147.9	149.3	146.5	131.2	0.5 (0.5)
def2-QZVP^a	151.9	147.8	149.2	146.4	131.2	0.5 (0.5)
BP86^b	152.8	148.8	150.1	147.1	132.1	0.8 (0.4)
B3LYP^b	151.9	147.8	149.0	146.5	131.2	0.5 (0.5)
B97d^b	155.1	151.0	152.3	149.7	134.6	1.9 (0.4)
Exp.	150.8	147.8	148.3	144.4	130.8

---

Changing the DFT functional used for the optimization leads to substantially larger shift changes (obtained at the BHandHLYP/IGLO-III level), and they can both improve or worsen the results, as seen in Table 4. The B3LYP structure provides chemical shifts closer to experiment, while the B97d structure largely overestimates the shifts. If relative chemical shifts are compared to experimental results in Table 4via RMSD^r (obtained from C signals relative to C_e), the B3LYP functional provides worse agreement than BP86 and B97d.

The seemingly good performance of, e.g. the B3LYP/def2-TZVP structure as compared to our default level BP86/def-TZVP is presumably due to error cancellation, as seen in Fig. 3, where the C–C distances in C₆₀ calculated at different levels are compared to the experimental ones. The B3LYP/def2-TZVP or BHandHLYP/def2-TZVP levels provide worse calculated C–C distances than our default level for structure optimization BP86/def-TZVP. The BP86/def-TZVP level appears to provide reliable molecular structures also for endohedral helium fullerenes.^58,59

Fig. 3 Calculated bond lengths in optimized C₆₀ obtained using the BP86 functional and different basis sets (on the right) and density functionals in combination with the def2-TZVP basis set (on the left). Experimental results are obtained from ref. 77. The C–C bonds are displayed on the top.

The molecular motions and ¹³C chemical shifts

The results summarizing different strategies for accounting of the temperature and dynamics are summarized in Table 5, as corrections to individual carbon nuclear magnetic shieldings, i.e. differences between dynamically/vibrationally averaged and optimized-structure nuclear shieldings. Averaged distances and spatial fluctuations of carbon atoms derived from the simulations are detailed in Table S3 (ESI†).

Table 5 Dynamical effects on ¹³C nuclear magnetic shieldings (ppm) presented as difference between vibrationally averaged and minimum structure results

Method	Ca	Cb	Cc	Cd	Ce	C60
a Potential HF/6-31G//level for NMR BP86/IGLO-II. b Potential MM3//level for NMR BP86/IGLO-II. c Potential BP86/def-SVP//level for NMR BHandHLYP/IGLO-III.
PT2^a	−4.6	−4.5	−4.6	−4.5	−4.5	—
VCI^a	−5.0	−5.0	−5.1	−5.5	−6.3	—
TCS^a	−7.3	−7.2	−7.3	−7.9	−9.2	—
MD^b	−6.0	−3.8	−5.0	−5.7	2.1	−3.4
FPMD^c	−1.4	−2.0	−2.3	−2.4	−5.8	−1.4
FPMD/COSMO^c	−1.3	−1.2	−1.2	−1.5	−1.7	−1.2

---

The changes caused by the molecular motions for the gas-phase C₇₀ molecule can be assigned as deshielding and are relatively large, up to ca. −9 ppm, very much depending on the method. The positive (shielding) contribution result for C_e in the MD line in Table 5 may be an artifact caused by the inaccurate force field. The vibrational averaging in PT2 approximation gives nearly uniform deshielding of about −4.5 ppm for all carbon types, while the TCS, classical MD, and FPMD approaches show relatively more variable effects. The corrections for carbon C_e are significantly different from the other carbon types. The geometric fluctuations of atoms C_a–C_e around the equilibrium position are rather uniform (Table S4, ESI†), hence we infer that the differential dynamical contributions for C_a–C_e in FPMD originate from the fluctuations in the electronic structure.

For the C₆₀ reference, dynamical correction to ¹³C nuclear magnetic shielding about −3 to −2 ppm was obtained using different methods comparable with that of −2.5 ppm mentioned previously.⁷⁸ If anomalous contribution for atom C_e in C₇₀ is excluded then the “dynamical” contribution for C₆₀ represents approximately 70% of average C₇₀ values (MD, FPMD). The vibrational (PT2, VCI, TCS) contributions to the ¹³C NMR chemical shifts in C₇₀ are likely to be similar as in C₆₀. Therefore, the usage of C₆₀ as the secondary reference will partly cancel the dynamical corrections.

If the best DFT results in Table 2 are added to the dynamical corrections in Table 5 (taken with opposite sign to turn the nuclear magnetic shielding into the chemical shift), the agreement with the experiment is not improved. However, when the FPMD simulations are performed in the solvent, the dynamical corrections (Table 5) for the ¹³C nuclear magnetic shielding are still deshielding but now considerably smaller in absolute size and more uniform (−1.2 to −1.7 ppm) than those obtained for FPMD simulation in vacuo. A detailed look reveals that the solvent damps the molecular motions. This is documented in Table S2 (ESI†) on the average deviations from equilibrium positions.

The different contributions to the total ¹³C NMR chemical shifts in C₇₀ discussed above are summarized in Fig. 4. The inclusion of solvent and basis set correction decreases the gas phase shifts and thus improve the agreement with experiment.

Fig. 4 Importance of various effects on calculated ¹³C chemical shifts in C₇₀. BHandHLYP stands for shifts obtained by the vacuum BHandHLYP/IGLO-III calculation, “solvent” denotes the BHandHLYP/IGLO-III/CPCM model, and the other bars are related to the involvement of vacuum and solvent FPMD dynamics. All data are corrected for the estimated basis set error calculated from difference between the IGLO-IV and IGLO-III results in Table 1 (all results comprise the previous enhancements, e.g. the “dynamic” = BHandHLYP shifts in vacuum + solvent contribution + basis set correction + dynamic contribution). The experiment is taken from ref. 13.

The contributions due to molecular motions (FPMD is shown as example in Fig. 4) are mostly positive, and shift the values away from the experimental ones. If the FPMD simulations could be run longer, an improvement of a couple of tenths of ppm could be expected due to somewhat large statistical error (mean error of the average, see the Methods section) obtained, ±0.35 ppm for the dynamical corrections to the ¹³C chemical shift. The total calculated ¹³C shifts corrected for the basis set error and dynamical solvent are again closer to the experimental ones. However, the inclusion of the dynamical corrections including solvent does not bring any significant improvement over the static molecule in vacuo results, because they are small in size, relatively uniform, and largely cancelled by the dynamical effect of the reference C₆₀ compound.

The temperature dependence

Vibrational averaging obtained using the TCS method also enables the estimation of the temperature dependence of the carbon chemical shifts in C₇₀. Results for 273 K and 373 K calculated using two different computational levels are shown in Table S4 (ESI†). The calculated and experimental changes (related to value for carbon C_e) are shown in Fig. 5. The temperature dependence appears to be relatively uniform for all carbons at both levels, ∼0.6–0.9 ppm per 100 K. Experimental dependence can be seen in Fig. S2 (ESI†). The correlation between experimental and theoretical results is clear. However, the observed change is about 5 times smaller than in theory. This can be partially attributed to the missing solvent effects in the TCS calculations, which, however, could not be included due to the computational time limits.

Fig. 5 Temperature effect on NMR shifts in C₇₀. Plot shows comparison of experimental and theoretical (BP86/IGLO-II//HF/6-31G) differences in relative shieldings caused by temperature (Δ = 100 K). The shift is referenced to C_e.

Conclusions

To estimate the accuracy of available theoretical procedures, ¹³C NMR chemical shifts in the C₇₀ fullerene were modelled using various density functionals and basis sets. The effects of solvent, dynamics, and temperature on the ¹³C shifts in the theoretical simulations were discussed. Reasonable ¹³C chemical shift values within several ppm from the experimental results could be obtained already by the usual calculations of a gas-phase molecule at rest. With hybrid or long-range corrected functionals the calculated chemical shifts were overestimated by about 2 ppm. The largest errors, up to 5 ppm, were found for the GGA functionals, such as BP86. The basis set effects on the ¹³C shifts calculated for the IGLO-II to IGLO-IV series are moderate; the errors using the IGLO-III basis set are estimated within 0.4 ppm of the basis set limit, or 0.2 ppm from IGLO-IV results. Improving the basis set size in the structure optimization resulted in changes a few tenths of ppm on the ¹³C NMR chemical shifts, whereas changing the functional had a larger impact of several ppm.

Inclusion of the implicit solvent effects caused a decrease of the calculated ¹³C chemical shifts towards the experimental values by about 1 ppm. The effect of molecular motions on the ¹³C NMR chemical shift in gas-phase C₇₀ caused relatively large deshielding contributions of about 2–9 ppm, depending on the method used for averaging. These changes were strongly damped if the solvent was considered in simulation, leading to a deshielding contribution of about 1.2–1.7 ppm only. For the chemical shifts, the changes were largely cancelled by the motional contributions from the C₆₀ reference.

Acknowledgements

This work was supported by the Grant Agency of the Czech Republic (203/09/0237, 13-03978S, P208/10/P356, P208/11/0105), Ministry of Education (LH11033), and Czech Academy of Sciences (M200551205).

Notes and references

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. L. Dunsch and S. Yang, Phys. Chem. Chem. Phys., 2007, 9, 3067–3081.
3. X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760.
4. P. W. Fowler and D. E. Manolopoulos, An Atlas of Fullerenes, Dover Publications, Dover, 2006.
5. G. Y. Sun and M. Kertesz, J. Phys. Chem. A, 2002, 106, 6381–6386.
6. G. Sun and M. Kertesz, Chem. Phys., 2002, 276, 107–114.
7. G. Sun and M. Kertesz, J. Phys. Chem. A, 2001, 105, 5212–5220.
8. G. Sun and M. Kertesz, New J. Chem., 2000, 24, 741–743.
9. G. Sun and M. Kertesz, J. Phys. Chem. A, 2001, 105, 5468–5472.
10. G. Sun and M. Kertesz, J. Phys. Chem. A, 2000, 104, 7398–7403.
11. G. Sun and M. Kertesz, Chem. Phys. Lett., 2000, 328, 387–395.
12. T. Heine, in Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 2004, pp. 409–419.
13. F. Diederich and R. L. Whetten, Acc. Chem. Res., 1992, 25, 119–126.
14. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
15. B. C. Mort and J. Autschbach, J. Phys. Chem. A, 2005, 109, 8617–8623.
16. M. Dračínský, J. Kaminský and P. Bouř, J. Chem. Phys., 2009, 130, 094106.
17. R. Ahlrichs, M. Bar, H.-P. Baron, R. Bauernschmitt, S. Bocker, M. Ehrig, K. Eichkorn, S. Elliot, F. Furche, F. Haase, M. Haser, H. Horn, C. Huber, U. Huniar, M. Kattannek, C. Kolmel, M. Koolwitz, K. May, C. Ochsenfeld, H. Ohm, A. Schafer, U. Schneider, O. Treutler, M. von Arnim, F. Weigend, P. Weis and H. Weiss, TURBOMOLE V6.3.1 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
18. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Wallingford CT, 2009.
19. J. W. Ponder, Tinker – Software Tools for Molecular Design, St. Louis, 2009.
20. P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947.
21. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
22. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
24. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
25. A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
26. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
27. F. A. Hamprecht, A. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264–6271.
28. C. Lee, W. Yang and R. G. Paar, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. J. C. Slater, The Self-Consistent Field for Molecular and Solids, Quantum Theory of Molecular and Solids, McGraw-Hill, New York, 1974, vol. 4.
32. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
33. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118.
34. A. D. Becke, J. Chem. Phys., 1993, 104, 1040–1046.
35. A. J. Cohen and N. C. Handy, Mol. Phys., 2001, 99, 607–615.
36. X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677.
37. H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624–9631.
38. H. Zhao and D. G. Truhlar, J. Phys. Chem., 2006, 110, 5121–5129.
39. T. Yanai, D. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
40. W. Kutzelnigg, U. Fleischer and M. Schindler, The IGLO-Method: Ab Initio Calculation and Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities, Springer-Verlag, Heidelberg, 1990.
41. S. Huzinaga, Approximate Atomic Functions, University of Alberta, Edmonton, 1971.
42. W. Kutzelnigg, U. Fleischer and M. Schindler, NMR – Basic Principles and Progress, Springer-Verlag, Heidelberg, 1990.
43. F. Jensen, J. Chem. Theory Comput., 2008, 4, 719–727.
44. A. G. Avent, D. Dubois, A. Penicaud and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1997, 1907.
45. D. Papoušek and M. R. Aliev, Molecular Vibrational/Rotational Spectra, Academia, Prague, 1982.
46. P. Daněček and P. Bouř, J. Comput. Chem., 2007, 28, 1617–1624.
47. P. Bouř, S4 program for anharmonic molecular vibrations, Academy of Sciences, Prague, 2012.
48. J. A. Pople, H. B. Schlegel, R. Krishnan, D. J. DeFrees, J. S. Binkley, M. J. Frisch, R. A. Whiteside, R. F. Hout and W. J. Hehre, Int. J. Quantum Chem., Quantum Biol. Symp., 1981, 15, 269.
49. R. F. Hout, B. A. Levi and W. J. Hehre, J. Comput. Chem., 1982, 3, 234.
50. P. A. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
51. G. Rauhut and P. Pulay, J. Phys. Chem., 1995, 99, 3093.
52. B. G. Johnson, P. M. W. Gill and J. A. Pople, J. Chem. Phys., 1993, 98, 5612.
53. R. H. Hertwig and W. Koch, J. Comput. Chem., 1995, 16, 576.
54. M. Dračínský and P. Bouř, J. Comput. Chem., 2012, 33, 1080–1089.
55. B. C. Mort and J. Autschbach, J. Phys. Chem., 2005, 109, 8617.
56. N. L. Allinger, Y. H. Yuh and J.-H. Lii, J. Am. Chem. Soc., 1989, 111, 8551–8566.
57. F. Jensen, Introduction to Computational Chemistry, Willey-VCH, Weinheim, 2nd edn, 2007.
58. M. Straka and J. Vaara, J. Phys. Chem. A, 2006, 110, 12338–12341.
59. P. Štěpánek, P. Bouř and M. Straka, Chem. Phys. Lett., 2010, 500, 54–58.
60. A. A. Auer, J. Gauss and J. F. Stanton, J. Chem. Phys., 2003, 118, 10407.
61. T. Kupka, M. Stachow, M. Nieradka, J. Kaminský, T. Pluta and S. P. A. Sauer, Magn. Reson. Chem., 2011, 49, 231–236.
62. A. Wu, Y. Zhang, X. Xu and Y. Yan, J. Comput. Chem., 2007, 28, 2431–2442.
63. Y. Zhang, A. Wu, X. Xu and Y. Yan, Chem. Phys. Lett., 2006, 421, 383–388.
64. T. Kupka, M. Stachow, M. Nieradka, J. Kaminský and T. Pluta, J. Chem. Theory Comput., 2010, 6, 1580–1589.
65. T. Kupka, M. Nieradka, M. Stachow, T. Pluta, P. Nowak, H. Kjaer, J. Kongsted and J. Kaminský, J. Phys. Chem. A, 2012, 116, 3728–3738.
66. M. Straka, P. Lantto and J. Vaara, J. Phys. Chem. A, 2008, 112, 2658–2668.
67. S. Standara, P. Kulhánek, P. Bouř, R. Marek, J. Horníček and M. Straka, Theor. Chem. Acc., 2011, 129, 677–684.
68. Q. Zhao, R. C. Morrison and R. G. Parr, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 2138.
69. P. J. Wilson and D. J. Tozer, Chem. Phys. Lett., 2001, 337, 341–348.
70. M. J. Allen, T. W. Keal and D. J. Tozer, Chem. Phys. Lett., 2003, 380, 70–77.
71. A. M. Teale and D. J. Tozer, Chem. Phys. Lett., 2004, 383, 109–114.
72. A. V. Arbuznikov and M. Kaupp, Chem. Phys. Lett., 2004, 386, 8–16.
73. A. V. Arbuznikov and M. Kaupp, Chem. Phys. Lett., 2004, 391, 16–21.
74. A. J. Cohen, Q. Wu and W. Yang, Chem. Phys. Lett., 2004, 399, 84–88.
75. P. J. Wilson and D. J. Tozer, J. Mol. Struct., 2002, 602–603, 191–197.
76. A. M. Teale, O. B. Lutnaes, T. Helgaker, D. J. Tozer and J. Gauss, J. Chem. Phys., 2013, 138, 024111.
77. K. Hedberg, L. Hedberg, D. S. Bethune, C. A. Brown, H. C. Dorn, R. D. Johnson and V. M. De, Science, 1991, 254, 410–412.
78. T. Heine, K. Vietze and G. Seifert, Magn. Reson. Chem., 2004, 42, S199–S201.

---

Footnote

† Electronic supplementary information (ESI) available: Modified MM3 fullerene parameters, performance of DFT functionals for ¹³C chemical shifts, calculated data for TCS, the effect of temperature on the experimental ¹³C NMR signal. See DOI: 10.1039/c3cp50657f

---