Emission enhancement and lifetime modification of phosphorescence on silver nanoparticle aggregates

Abstract

Silver nanoparticle aggregates have been shown to support very large enhancements of fluorescence intensity from organic dye molecules coupled with an extreme reduction in observed fluorescence lifetimes. Here we show that for the same type of aggregates, similar enhancement factors (∼75× in intensity and ∼3400× in lifetime compared to the native radiative lifetime) are observed for a ruthenium-based phosphorescent dye (when taking into account the effect of charge and the excitation/emission wavelengths). Additionally, the inherently long native phosphorescence lifetimes practically enable more detailed analyses of the distribution of lifetimes (compared with the case with fluorescence decays). It was thus possible to unambiguously observe the deviation from mono-exponential decay which we attribute to emission from a distribution of fluorophores with different lifetimes, as we could expect from a random aggregation process. We believe that combining phosphorescent dyes with plasmonic structures, even down to the single dye level, will offer a convenient approach to better characterize plasmonic systems in detail.

---

Introduction

The high local fields generated around noble metal nanostructures when illuminated close to their plasmon resonance can modify the interaction of nearby molecules with light.^1–4 This effect leads to diverse phenomena such as surface-enhanced Raman scattering (SERS)⁵ and surface-enhanced fluorescence (SEF).⁶ In the case of SEF, both the measured fluorescence intensity and the radiative decay rate⁷ can be enhanced. Most of the literature on SEF involves the use of organic fluorophores^8–11 or quantum dots,^12–14 for which the radiative emission is fully allowed. These dyes have characteristic radiative lifetimes in the ns range.

However, there is also a second large family of dyes, the phosphorescent dyes, that finds growing applications in collecting solar light-energy¹⁵ and lighting.¹⁶ In these dyes, the decay from the excited triplet state to the ground singlet state is partially disallowed, resulting in characteristic radiative lifetimes in the μs range or longer.

Although there have been some studies on the interaction of phosphorescent dyes with plasmonic structures, most of these focus on specific applications. These include metal enhanced rare-earth ion luminescence applied to OLEDs,^17–21 enhancement of organic solar cells with plasmonic nanoparticles,^22,23 and enhanced excitation of phosphorescent dyes related to photodynamic therapy.^24–26 However, only a few examples in the literature look into the basic behaviour of the triplet transition as compared to the normal singlet transition.^27–29 Surprisingly, although theory predicts that lifetime modifications similar to that for fluorescence should occur in the case the triplet transition is dipolar in nature (and even larger lifetime modifications in the case it is quadrupolar in nature³⁰), experimental results so far have observed much weaker modification of phosphorescence lifetimes compared to fluorescence lifetimes.

One possible reason for this discrepancy is the relatively low QY of the phosphorescent dyes used. Under these conditions, the relatively fast intrinsic non-radiative decay would lead to a decrease in the relative contribution of the metal-induced radiative and non-radiative decay modifications. To overcome this problem, a system where the dyes experience very high field enhancements can be used, where the intrinsic non-radiative rates will become negligible compared to the metal-induced radiative and non-radiative rates.

We have recently shown^31,32 that silver nanoparticle (Ag-NP) aggregates can act as efficient plasmonic structures, which lead to more than two orders of magnitude enhancement in the average fluorescence intensity and concomitantly more than two orders of magnitude shortening of the lifetime. We attributed these high enhancement levels to emission from dyes which were close to the hot spots in the aggregates, and which experienced very high local fields. Here we report the results on the intensity enhancement and lifetime modification of a ruthenium-complex-based phosphorescent dye in the same Ag-NP aggregate system. By comparing the result for the phosphorescent dye with our previously reported results (on Atto655) and with new results on a methylene blue (MB)-based fluorescent dye, we show that the experimental results for both fluorescence and phosphorescence are indeed similar in nature. Once we established that the effects of plasmonic field enhancement are similar for both fluorescent and phosphorescent dyes, we exploited the intrinsically small native radiative rate of phosphorescent dyes to better characterize our plasmonic system. As the native lifetime, and even the plasmonically modified lifetime of phosphorescent dyes are much longer than those of the fluorescent dyes, they are all far from the limit of detection that arises from the instrument response function (IRF). We could therefore show that there is a distribution of decay rates from the different emitting dyes, as one would expect for such a randomly aggregated nanoparticle system.

Experimental section

Reagents

DNA labeled with three different dyes (mono-carboxy derivative of Ru(bpy)₃, Atto-MB and Atto-655), and non-labeled control have the following sequence: 5′-dye-TGGAAGTTAGATTGGGATCATAGCGTCAT-3′. These oligonucleotides were custom synthesized by IBA GmbH (Göttingen, Germany). All other chemicals were purchased from Sigma-Aldrich.

Nanoparticle synthesis

EDTA-coated Ag nanoparticles were synthesized according to a modified literature procedure³³ – in brief, 500 ml of a 0.16 mM EDTA solution containing 4 mM NaOH was heated to boiling under stirring. 5 ml of 26 mM AgNO₃ solution was added in 4 aliquots of 1.25 ml, and the solution was held at boiling for 20 min under continuous stirring.

Measurement of fluorescence/phosphorescence

Fluorescence/phosphorescence was measured using a Tecan Safire II fluorescence plate reader equipped with a Quad4™ monochromator.

Enhanced luminescence measurements

For measurements, as-synthesized Ag-nanoparticles were diluted in 6 mM phosphate buffer, pH = 7.1, to a concentration equivalent to 1.6 O.D. (at the peak of the plasmon absorption, 410 nm). 40 μl of 2.5 nM dye-DNA diluted in water was mixed with 40 μl of 100 μM spermine in 10 mM Tris buffer (pH = 7.4), and then 120 μl of the diluted Ag nanoparticles were added. Final concentration of dye-labeled DNA was 500 pM.

Calculation of the quantum yields of dyes

The calculation of quantum yield for the different dyes was done in a similar fashion to that previously reported by us.³² We used sulforhodamine 101 dye in ethanol as the reference dye (assuming a QY of 0.95³⁴). All fluorescent emission measurements for QY calculation were carried out on a Cary Eclipse fluorescence spectrometer (Varian, USA).

Time-resolved fluorescence

Fluorescence decay curves were measured using a time-correlated single photon counting (TCSPC) set-up, as described elsewhere.³⁵ Samples were excited with vertically polarized 460 nm pulses of <0.2 ps duration at a repetition rate of 3.8 MHz. The intensity of the laser output was approximately 1 mW, but the excitation intensity was adjusted further by using neutral density filters to obtain a count-rate below 30 000 per second. The excitation spot diameter was approximately 1 mm. The instrument response function (∼140 ps FWHM) was obtained with pinacyanol iodide in methanol, with ∼6 ps fluorescence lifetime.³⁶ Fluorescence was collected through a vertical or horizontal polarizer, in 10 repeated sequences of 10 s per sequence for each polarization. Fluorescence was detected through a 500 nm long-pass filter, in combination with different interference filters (10–15 nm FWHM) at three detection wavelengths, namely 522, 611, and 657 nm. Individual photons were detected using a microchannel plate photomultiplier, and arrival times were stored in 4096 channels of a multichannel analyzer, the channel time spacing of which was 2 ps, resulting in a 8 ns time window. Fitting was done using the commercial software Fluofit (PicoQuant, Germany).

Theoretical background

In the interaction of fluorescent molecules with plasmons, the observed change in fluorescence (which can be enhancement or quenching) originates from a modification of both the absorption and emission processes. The probability of absorption is proportional to the square of the electric field amplitude, and it can be shown¹ that after averaging for random orientation the absorption enhancement factor is equal to the local field intensity enhancement factor, which we will denote as M_loc. This in all cases will enhance the fluorescence. A second effect is the modification of the radiative decay rate in the proximity of the nanostructure. We will denote the modified rate as γ^M_r. This effect, depending on the orientation of the molecule, can be an increase or a decrease in the decay rate. The third effect is an additional non-radiative decay channel into the metal, which will have a rate γ^M_nr. These last two processes lead to a modified emission quantum yield (QY_M), as defined in eqn (1).where γ⁰_nr is the non-radiative rate in the absence of the metal. Depending on the exact rates in any given system, the QY can be either higher or lower than the original quantum yield of the dye QY₀. The observed combined enhancement factor (EF) of the fluorescence intensity would then be the combination of the modification of the absorption process and that of the emission process, eqn (3):

SEF EF = M_locQY_M/QY₀ (3)

This combination of the excitation enhancement with the quantum yield modification will ultimately determine if fluorescence enhancement or quenching is observed. However one limitation of directly comparing enhancement factors between experiments with different fluorophores is that dyes with different quantum yields give different enhancement factors for a specific plasmonic structure. We have previously suggested³¹ the use of a figure of merit (FoM) that allows easier comparison between experiments, eqn (4):

SEF FoM = M_locQY_M (4)

For structures with very strong modification of the radiative or non-radiative rate, the contribution of the intrinsic non-radiative rate in the denominator of eqn (1) becomes negligible. Under these conditions, the FoM is independent of the characteristics of the dye used.

One interesting property of the radiative and non-radiative rate modification according to the generalized Mie theory is that they are proportional to the native radiative rate (γ_rad) of the emitter.¹ Therefore, for systems which emit phosphorescence instead of fluorescence the radiative rate in free space is much slower than the fluorescence, but the modification factor for a fixed plasmonic structure should be the same.

Results and discussion

To test whether fluorescence and phosphorescence are modified in a similar manner, as theory would suggest, we have used co-aggregation of dye-labeled DNA (29 nucleotides) with silver nanoparticles (34 nm diameter) (see Fig. 1). Full details of the system, such as the effect of DNA sequence on the enhancement factor, can be found in our previous publications.^31,32 It is important to note that the particle to particle distance (previously measured to be ∼2 nm) was shown not to be dependent on the dye used, as for all dyes the average plasmon peak of the aggregates was at the same wavelength (∼670 nm). For this system we have previously shown (for the dye Atto655) that for excitation and emission wavelengths close to the peak of the aggregate plasmon, high enhancement (∼150×) together with very high modification of the radiative lifetime (∼1000× faster than the natural decay rate (τ_d) of 6 ns) occurs.³¹ We have additionally shown in our previous publication that this should correspond to a dye at a distance of about 1–2 nm from the surface. At distances less than 1 nm, the non-radiative part would dominate over the radiative part, and at distances larger than about 2 nm, we should not observe such intense modification of the lifetime. Although experimentally more complex than systems with single particles, using nanoparticle aggregates is expected to provide field enhancement and lifetime modification larger than the native non-radiative rate, which for low QY dyes such as ruthenium dyes is hard to achieve with single particles. The results of our measurements on intensity enhancement of the Ru-based phosphorescent dye and of two other fluorescent dyes (Atto655 and MB), which we use for comparison, are summarized in Table 1. The full time-dependent enhancement data for the ruthenium dye are provided in the ESI.† Although the enhancement for Atto655 for excitation at 650 nm was previously reported in ref. 31, we have remeasured it with the current batch of silver nanoparticle aggregates to verify and validate the reproducibility of our results.

Fig. 1 Spermine induced co-aggregation of dye-labeled DNA and Ag nanoparticles.

Table 1 Observed enhancement factors for different dyes

	460EX/640EM		650EX/690EM
	EF	FoM	EF	FoM	QY0 (%)
EX – excitation wavelength, EM – emission wavelength, ND – not detectable, EF – enhancement factor, FoM – figure of merit. The relative uncertainty in the QY determination is approximately 15–20% in all cases.
Atto655	45 ± 10	5.7 ± 1.6	150 ± 10	19 ± 4	12.7
MB	ND	ND	1000 ± 100	11 ± 3	1.1
Ru dye	75 ± 8	1.7 ± 0.4	ND	ND	2.3

---

Using excitation and emission close to the peak wavelengths of absorption and emission of the ruthenium dye (460 nm and 640 nm respectively, see Fig. 2), we observe an intensity enhancement factor of 75×. In order to compare it to our previously reported result with Atto655, which is an organic dye with natural radiative lifetimes on the ns time scale, we have to recall that the observed enhancement depends on the overlap of the excitation and emission wavelength with the plasmon response of the aggregate, and is inversely proportional to the intrinsic QY₀ of the dyes. Although we have previously demonstrated that Atto655 shows an average enhancement of the fluorescence of 150×, this result was for excitation and emission wavelengths which both overlapped very well with the average plasmon peak of the aggregates (650 nm and 690 nm). However, for the ruthenium dye, the maximum absorbance peak (and therefore the excitation wavelength used) is around 460 nm, which is significantly shifted from the average plasmon peak measured by UV-VIS spectroscopy (see Fig. 2). Experimental determination of the average enhancement of Atto655 at the excitation and emission wavelengths used for the ruthenium dye yielded an enhancement of only 45×, which taking into account the measured QY₀ (12.7%) leads to a figure of merit (FoM) of 5.0. For the ruthenium dye with a QY₀ of 2.3%, we get a FoM of 1.7. We attribute the difference between the FoMs for the fluorescent dye and the ruthenium dye to the difference in charge (Atto655 is neutral while the ruthenium dye is positive). We have previously shown experimentally³² that these charge differences can lead to a factor of 2 difference in SEF, probably because the positively charged molecules tend to be physically closer to the negatively charged silver surface. To further validate this hypothesis, we also measured a positively charged fluorescent dye, methylene blue. This dye has a similar excitation and emission wavelength to Atto655, and therefore 650 nm excitation and 690 emission wavelengths were used. Under these conditions, Atto655 has a FoM of 19, while for the positively charged MB, the FoM was only 11. Thus, we observe for the phosphorescent Ru-based dye an enhancement very similar to what we would expect from a fluorescent dye with a similar QY. This is the first result, to the best of our knowledge, directly comparing the enhanced phosphorescence of organic dyes and metal complexes in a system with high plasmonic enhancement. We attribute the failure of previous studies to observe these effects to the fact that most other studies used films of single particles. For single particles, SEF is observed at distances at which the plasmon related radiative and non-radiative rates are ∼10× larger than the intrinsic radiative rate. However because most metal complexes have a QY of only a few percent, the contribution of the non-plasmon related non-radiative rate can be significant in such systems, and easy comparison of dyes with different initial QY is not possible.

Fig. 2 UV-Vis absorbance of the silver nanoparticle aggregate (solid line) and normalized excitation (triangles) and emission (diamonds) of the Ru-dye.

One of the difficulties in measuring lifetimes in systems with high plasmonic enhancement is that lifetime modification can easily reach 3 orders of magnitude as compared to the intrinsic radiative lifetime, which makes the exact measurement of lifetimes of single organic dyes very difficult, as these can fall below the detection limit of TCSPC systems. In our previous work we have shown using streak-camera measurements on a large population of aggregates a lifetime reduction of 1000× compared to the unmodified lifetime for the dye Atto655. The lifetime measurement on the ruthenium dye is simpler, as even with 3–4 orders of magnitude reduction we expect a lifetime well within the measurement range of TCSPC systems.

In order to determine the modification of the lifetime, we first determined the natural radiative rate for this ruthenium derivative, as the data for this specific derivative are not available in the literature. Previous work estimated the value for the radiative lifetime of the parent compound Ru(bpy)₃ to be 10 μs.³⁷ Other reports have shown that carboxy ethyl derivatives, which are chemically similar to the carboxy methyl derivatives that we have been using, have a very similar radiative rate to Ru(bpy)₃.³⁸ We have measured the QY₀ and lifetime of the ruthenium dye in deoxygenated water (unattached to DNA, as not to be affected by contact quenching by the nucleobases) to be 3.3% and 400 ns respectively, giving a natural radiative lifetime of 12 μs.

When measuring the lifetime of the dye in aggregates, we find that it cannot be well fitted to a single exponential decay (Table 2 and Fig. 3b). This is expected, as not all dyes are located at the same location and experience the same field enhancement. In our previous experiments with organic dyes we could not observe this distribution, as the average measured lifetime was very close to the resolution limit of our experimental equipment. Fig. 3 shows 3 different models used to fit the lifetime data for Ru-DNA in silver nanoparticle aggregates. The fitting parameters are summarized in Table 2.

Table 2 Luminescence decay fitting parameters

	A1	T1 (ns)	A2	T2 (ns)	FWHM (ns)	Red χ^2
1 exp	1780	2.0				2.34
2 exp	1134	3.5	980	0.7		1.10
Gauss	3346	0.8			5.2	1.11

---

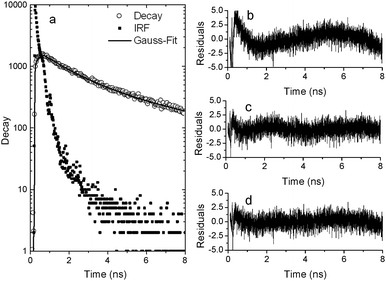Fig. 3 Luminescence decay measurement of Ru-dye in Ag nanoparticle aggregates: (a) data with IRF and Gaussian fit. (b)–(d) Residuals for de-convolution of the measured decay using (b) single exponent fit, (c) double exponent fit and (d) Gaussian lifetime distribution.

The lifetime distribution of the ruthenium derivative could be fitted by a double exponent with a long component of 3.5 ns and a short component of 0.7 ns (Fig. 3b). The long component is about 3400× shorter than the intrinsic radiative lifetime. This is a higher change in lifetime than the ∼1000× change we previously measured for Atto655. We attribute this higher number to the fact that the positively charged ruthenium dye would tend to be positioned closer to the surface than the zwitterionic Atto655 dye. To support this hypothesis we again performed a comparison with the positively charged organic dye MB. The intrinsic radiative lifetime of this dye can be calculated based on literature values (QY₀ and measured lifetime of 0.02 and 345 ps, respectively³⁹) to be 17 ns. Thus, the 6.7 ps lifetime we measured for MB in silver nanoparticle aggregates (see ESI†) yields a similar factor for the change in lifetime, −2500×, to that for the ruthenium derivative.

It is important to note that we use the mathematically fitted double exponent as a convenient way to derive a long component to compare to previous results with organic dyes. Although we got an adequate fit with a double exponential decay (Fig. 3c), but not with a single exponential decay (Fig. 3b), the data could also be fitted with a Gaussian distribution (Fig. 3d) with a similar goodness of fit. Based on the fact that our system is generated by random aggregation, we expect the dyes to be positioned at random points along the aggregate, resulting in a distribution of lifetimes rather than a single decay. Therefore we do not find a physical basis to have separate distinct populations of fluorophores in our system, and we see the results as supporting our claim that the light we detect originates from a rather wide distribution of fluorophores with different lifetimes located at different positions in the aggregates.

Conclusion

We have shown experimentally that the intensity and lifetime modification in silver nanoaggregates for phosphorescence from an Ru-metal complex based dye are similar to those of fluorescent dyes, as theory predicts, once corrected for the effect of excitation/emission wavelengths and dye charge. However, as the intrinsic lifetime for phosphorescence is much longer than that for fluorescence, even after 3 orders of magnitude of reduction in lifetime, we could still measure decay rates in the nanosecond range. This allowed us to show that the light emitted by the dyes comes from a large distribution of dyes which sit at different positions in the aggregate, as we would expect from such a randomly aggregated nanoparticle system. Although we have demonstrated this effect in ensemble measurements, the fact that even under very high modification of the lifetime phosphorescent dyes have decay rates which can be measured accurately using TCSPC systems, can in the future be used in single molecule measurements with plasmonic structures to get high-temporal resolution photon statistics which is not possible with fluorescent dyes.

Notes and references

1. E. C. Le Ru and P. G. Etchegoin, Principles of Surface-Enhanced Raman Spectroscopy, Elsevier, Amsterdam, 2009.
2. R. Aroca, Surface enhanced vibrational spectroscopy, Wiley, Hoboken, NJ, 2006.
3. H. Metiu, Prog. Surf. Sci., 1984, 17, 153–320.
4. M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826.
5. P. L. Stiles, J. A. Dieringer, N. C. Shah and R. P. Van Duyne, Annu. Rev. Anal. Chem., 2008, 1, 601–626.
6. E. Fort and S. Grésillon, J. Phys. D: Appl. Phys., 2008, 41, 013001.
7. J. R. Lakowicz, Anal. Biochem., 2001, 298, 1–24.
8. R. Bardhan, N. K. Grady, J. R. Cole, A. Joshi and N. J. Halas, ACS Nano, 2009, 3, 744–752.
9. A. Kinkhabwala, Z. F. Yu, S. H. Fan, Y. Avlasevich, K. Mullen and W. E. Moerner, Nat. Photonics, 2009, 3, 654–657.
10. S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402.
11. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
12. K. T. Shimizu, W. K. Woo, B. R. Fisher, H. J. Eisler and M. G. Bawendi, Phys. Rev. Lett., 2002, 89, 117401.
13. O. Kulakovich, N. Strekal, A. Yaroshevich, S. Maskevich, S. Gaponenko, I. Nabiev, U. Woggon and M. Artemyev, Nano Lett., 2002, 2, 1449–1452.
14. K. Ray, R. Badugu and J. R. Lakowicz, J. Am. Chem. Soc., 2006, 128, 8998–8999.
15. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663.
16. H. Yersin, Highly Efficient OLEDs with Phosphorescent Materials, Wiley, 2007.
17. Y. Wang, X. Zhou, T. Wang and J. Zhou, Mater. Lett., 2008, 62, 3582–3584.
18. S. T. Selvan, T. Hayakawa and M. Nogami, J. Phys. Chem. B, 1999, 103, 7064–7067.
19. H. Mertens and A. Polman, Appl. Phys. Lett., 2006, 89, 211107.
20. D. A. Weitz, S. Garoff, C. D. Hanson, T. J. Gramila and J. I. Gersten, Opt. Lett., 1982, 7, 89–91.
21. S. Pan and L. J. Rothberg, J. Am. Chem. Soc., 2005, 127, 6087–6094.
22. S. S. Kim, S. I. Na, J. Jo, D. Y. Kim and Y. C. Nah, Appl. Phys. Lett., 2008, 93, 073307.
23. J.-L. Wu, F.-C. Chen, Y.-S. Hsiao, F.-C. Chien, P. Chen, C.-H. Kuo, M. H. Huang and C.-S. Hsu, ACS Nano, 2011, 5, 959–967.
24. Y. X. Zhang, K. Aslan, S. N. Malyn and C. D. Geddes, Chem. Phys. Lett., 2006, 427, 432–437.
25. Y. X. Zhang, K. Aslan, M. J. R. Previte and C. D. Geddes, J. Fluoresc., 2007, 17, 345–349.
26. Y. Zhang, K. Aslan, M. J. R. Previte and C. D. Geddes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1798–1802.
27. F. D. Stefani, K. Vasilev, N. Bocchio, F. Gaul, A. Pomozzi and M. Kreiter, New J. Phys., 2007, 9, 21.
28. D. Chaudhuri, D. Li, E. Sigmund, H. Wettach, S. Hoeger and J. M. Lupton, Chem. Commun., 2012, 48, 6675–6677.
29. J. C. Ostrowski, A. Mikhailovsky, D. A. Bussian, M. A. Summers, S. K. Buratto and G. C. Bazan, Adv. Funct. Mater., 2006, 16, 1221–1227.
30. A. M. Kern and O. J. F. Martin, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 022501.
31. R. Gill, L. Tian, W. R. C. Somerville, E. C. Le Ru, H. Van Amerongen and V. Subramaniam, J. Phys. Chem. C, 2012, 116, 16687–16693.
32. R. Gill and E. C. Le Ru, Phys. Chem. Chem. Phys., 2011, 13, 16366–16372.
33. S. M. Heard, F. Grieser, C. G. Barraclough and J. V. Sanders, J. Colloid Interface Sci., 1983, 93, 545–555.
34. R. Velapoldi and H. Tønnesen, J. Fluoresc., 2004, 14, 465–472.
35. O. J. G. Somsen, L. B. Keukens, M. N. de Keijzer, A. van Hoek and H. van Amerongen, ChemPhysChem, 2005, 6, 1622–1627.
36. B. van Oort, A. Amunts, J. W. Borst, A. van Hoek, N. Nelson, H. van Amerongen and R. Croce, Biophys. J., 2008, 95, 5851–5861.
37. A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. Vonzelewsky, Coord. Chem. Rev., 1988, 84, 85–277.
38. Y. Hou, P. Xie, K. Wu, J. Wang, B. Zhang and Y. Cao, Sol. Energy Mater. Sol. Cells, 2001, 70, 131–139.
39. S. J. Atherton and A. Harriman, J. Am. Chem. Soc., 1993, 115, 1816–1822.

---

Footnote

† Electronic supplementary information (ESI) available: Luminescence enhancement of the Ru-dye with time and lifetime of MB in Ag nanoparticle aggregates. See DOI: 10.1039/c3cp50407g

---