Experimental evidence for surface freezing in supercooled n-alkane nanodroplets†
Viraj P.
Modak
a,
Harshad
Pathak
a,
Mitchell
Thayer
b,
Sherwin J.
Singer
b and
Barbara E.
Wyslouzil
*ab
aWilliam G. Lowrie Department of Chemical and Biomolecular Engineering, The Ohio State University, Columbus, Ohio 43210, USA. E-mail: wyslouzil.1@osu.edu
bDepartment of Chemistry and Biochemistry, The Ohio State University, Columbus, Ohio 43210, USA
First published on 5th March 2013
Abstract
Intermediate chain length (16 ≤ i ≤ 50) n-alkanes are known to surface freeze at temperatures that are up to three degrees higher than the equilibrium melting point [B. M. Ocko et al., Phys. Rev. E, 1997, 55, 3164–3182]. Our recent experimental results suggest that highly supercooled nanodroplets of n-octane and n-nonane also surface freeze, and subsequently bulk crystallization occurs. The data yield surface and bulk nucleation rates on the order of ∼1015 cm−2 s−1 and ∼1022 cm−3 s−1, respectively, at temperatures between 180 K and 200 K. Molecular dynamics simulations at the united atom level were used to follow the freezing of a supercooled n-octane drop and show that an ordered monolayer develops on the surface of the droplet almost immediately, and the rest of the droplet then freezes in a layer-by-layer manner.
I. Introduction
Freezing, or crystallization from the melt, is a fundamental physical process1 that plays a central role in semiconductor processing, chemical separations, pharmaceutical production and purification, material science and metallurgy.2 During freezing, the solid appears from the disordered liquid with a (periodic) structure that is generally accompanied by a change in density.3 For droplets and other systems with free surfaces, the location of the first critical nuclei – whether throughout the volume,4 or near/at the free surface5,6 – is an ongoing controversy that has important implications in atmospheric aerosol science.7–9 With current experimental techniques, it is challenging to differentiate between volume-based and surface-initiated nucleation.7 Hence, experiments that provide convincing evidence supporting surface nucleation are important to advance our understanding of when this nucleation pathway controls the phase transition.In contrast to water and most other substances, where surfaces pre-melt at temperatures below the bulk melting temperature Tm,10–14 surface tension and X-ray reflectivity measurements have established that the intermediate chain length n-alkanes15,16 (16 ≤ i ≤ 50) form a dense frozen surface monolayer at temperatures that are up to 3 K above the bulk melting point. The surface monolayer is always in equilibrium with the bulk liquid and formation occurs via a first order phase transition.17,18 Freezing studies of n-alkane (14 ≤ i ≤ 17) microdroplets in an electrodynamic balance19 also suggest that for the odd alkanes, an ordered monolayer is generated at the surface of the sub-cooled droplets that then serves as the site for freezing of the entire droplet. Surprisingly, the even alkanes did not exhibit this behavior.20 In neither experiments have the rates of surface nucleation been measured.
In this paper we report on our experiments that suggest even the short chain n-alkanes, n-octane and n-nonane freeze at the surface of super-cooled liquid droplets prior to the initiation of bulk freezing. This is an interesting result both because nucleation driven by surface organization is a fundamentally interesting phenomenon that blurs the line between the ideal concepts of homogeneous and heterogeneous nucleation, and because prior experimental reports15–17,21–26 had concluded that the surface freezing effect is confined to longer chain-like molecules and to temperatures above or near the equilibrium melting temperature Tm. Even for these well studied materials, the physical reasons for this phenomenon are still a subject of debate.27–29 Since the n-alkanes are the building blocks of materials as diverse as lipids, surfactants, and polymers, understanding the behavior of the simpler, constituent molecules, including their ability to self assemble and form layered structures, should enhance our ability to predict the behavior of the more complex molecules. The strong anisotropy and conformational flexibility of n-alkanes also means that understanding their microscopic nucleation physics is challenging. The availability of reasonable intermolecular potentials for these molecules, however, makes these problems amenable to a combined experimental and theoretical attack.30
In our experiments we create liquid droplets in highly non-equilibrium states by first forming and then rapidly cooling nanodroplets in a continuous flow supersonic Laval nozzle. We characterize the flow using axially resolved static pressure measurements,31–33 and study the droplets using spatially resolved small angle X-ray34–39 scattering (SAXS) and infrared spectroscopy.40–42 Together, these measurements enable us to accurately characterize the thermodynamic state of the condensate, the size and number densities of the liquid droplets or frozen particles, and the kinetics of their evolution from vapor to liquid to solid. Since there are reasonable theoretical models for the interaction potentials for n-alkanes30,43–45 we complement our experiments with molecular simulation studies at the united atom level to both develop molecular level insight into homogeneous liquid–solid nucleation and to strengthen our interpretation of the experimental results.
The paper is organized as follows. We first briefly describe the experimental and data analysis methods in Section II. We then describe our approach for the molecular dynamics simulations along with the simulation parameters in Section III. We present our results along with their interpretation in Section IV.
II. Experimental methods and analysis
As a condensible-carrier gas mixture flows through a supersonic nozzle, the flow accelerates, and the pressure and temperature drop rapidly, establishing an effective cooling rate of ∼105 K s−1. If the partial pressure of condensible is high enough, the supersaturation increases to the point that particles form via homogeneous vapor–liquid nucleation. The particles then grow rapidly, releasing heat to the flowing gas mixture. The combined effect of heat release and vapor depletion quenches vapor–liquid nucleation after ∼10 μs, resulting in a relatively monodisperse liquid aerosol. Once most of the vapor condenses, the pressure and temperature inside the nozzle start to decrease again, at a rate that is in rough agreement with the expected isentropic expansion. If the temperature drops far enough, a second phase transition is initiated and the droplets freeze.The heat released by a phase transition can be detected by observing an increase in temperature or pressure of the gas mixture over that expected for an isentropic expansion of the same mixture. The degree of deviation depends on the ratio of condensible to carrier gas and the latent heat associated with the phase transition. In particular, the heat released during (liquid) condensation is significantly higher than that released during freezing, and consequently the pressure, temperature, and density deviations associated with condensation are significantly larger than those associated with freezing. The phase transitions can also be followed by observing the appearance and evolution of the aerosol using small angle X-ray scattering (SAXS), or by determining the distribution of condensible between the phases using IR spectroscopy.
Our experiments are conducted in two Laval nozzles (rectangular cross section) that are machined from aluminum. Both nozzles have an expansion rates of d(A(z)/A*)/dz = 0.078 cm−1, where z is the distance downstream of the nozzle throat and A(z)/A* is the area at position z scaled by the area of the throat. The windows in the sidewalls are matched to the experiments. Nozzle C3 has CaF2 windows and is used for the pressure trace and IR spectroscopy experiments, while nozzle C2 has thin mica windows and is used for the SAXS experiments. Since the flow is continuous, long signal integration times are possible. The integrated data analysis approach described in Section II.D accurately characterizes the velocity at every position and, thus, the evolution of the aerosol is also available as a function of time.
The setup of the system required to maintain steady flow is described in detail in previous work.34,35 To summarize briefly, the carrier gas is supplied by high-pressure liquid Ar or liquid N2 Dewars, connected to inline electrical heaters and MKS mass flow controllers. The condensible component is added using a vaporizer, and the condensible flow rate is measured using a balance. The vapor–carrier gas mixture flows through a heat exchanger, and then enters the plenum and a flow straightener where we accurately measure the stagnation temperature and pressure of the expansion. The flow then passes through the nozzle and is discharged to the atmosphere by two rotary vane vacuum pumps. The methods used to characterize the flowing gas mixture and the condensate, are described below.
A. Pressure trace measurements
In this technique we measure the pressure profiles p(z) along the length of the nozzle using a thin static pressure probe. Two measurements are made: the dry trace where only the non-condensible carrier gas flows through the nozzle and the wet trace where the condensible-carrier gas mixture flows through the nozzle. The dry trace provides the effective area ratio of the nozzle. We derive initial estimates for the remaining flow variables, temperature T, density ρ, velocity u, and the mass fraction of condensate g, by assuming that the effective area ratio of the nozzle is not affected by condensation and solving the equations32 that describe the conservation of mass, momentum and energy in the flow together with the ideal gas law for the gas mixture. A more sophisticated and self consistent analysis method – that relaxes the assumption regarding the area ratio and incorporates information about the distribution of condensible between vapor, liquid and solid – requires the results of FTIR and SAXS measurements. The final iterative and self-consistent data analysis method used in this work is described in Section II.D.B. Small angle X-ray scattering
To characterize and follow the evolution of the aerosol size distribution, SAXS spectra are measured as a function of position in the nozzle. The experiments are conducted at the Advanced Photon Source, Argonne National Labs, Argonne, IL using the 12-ID_C beam line. A 0.2 mm × 0.2 mm X-ray beam with a wavelength λ of 0.1 nm and wavelength spread Δλ/λ of 10−4 passes through the nozzle perpendicular to the flow. The nozzle and the plenum are mounted on a sliding plate that is moved relative to the X-ray beam to make position resolved measurements. The procedures used to calibrate the range in the scattering vector q and place the spectra on an absolute intensity scale are described by Manka et al.46 Here q = (4π/λ)sin(θ/2) where θ is the scattering angle.We fit scattering from a Schulz distribution of polydisperse spheres to the spectra to determine the mean particle size 〈r〉, distribution width σ, and the intensity as q tends to zero, I0. If the condensate is all one phase, i.e. all liquid or solid, the number density N of the aerosol is given by:
 | (1) |
| Z = (〈r〉/σ)2 − 1 |
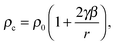 | (2) |
From N, 〈r〉 and Z, we calculate the volume fraction of condensate ϕ
 | (3) |
ci = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) iϕi, iϕi, | (4) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i is the molar density of the condensed alkane in phase i (solid or liquid), and the mass fraction of condensate
i is the molar density of the condensed alkane in phase i (solid or liquid), and the mass fraction of condensate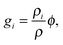 | (5) |
If the aerosol contains both frozen and unfrozen particles it is difficult to obtain the mass fraction of condensate from SAXS alone because we cannot accurately determine the scattering length density of the aerosol, and, thus, the number density N, a priori.
C. Fourier transformed infrared spectroscopy
FTIR absorption spectroscopy experiments determine the distribution of the condensible between the vapor, liquid, and solid phases. As illustrated in Fig. 2 of ref. 41, the beam from the FTIR (Perkin Elmer 100) is guided through the nozzle perpendicular to the flow and back to the detector using 6 plane mirrors and 2 focusing mirrors with a 20 cm focal length. The beam width is ∼4 mm at the focal point in the center of the nozzle and, as in the SAXS experiments, the nozzle and the plenum are moved relative to the IR beam to make position resolved measurements.In an FTIR measurement, we determine the spectrum of the carrier gas-condensible mixture Is, as well as that of carrier gas alone Ie, for wavenumbers between 900 cm−1 and 4000 cm−1 with 1 cm−1 resolution. The absorbance A,
 | (6) |
D. Integrated data analysis
The first step in the integrated data analysis is to determine the offset between the physical throat, the minimum geometrical cross sectional area, and the effective throat, the minimum in the flow area, where the difference arises due to boundary layer formation along the nozzle walls. To determine the offset, we measure the pressure at the physical throat using a 0.34 mm diameter hole in the nozzle block and compare it to the pressure measured by the static pressure probe. In the current experiments the actual throat is ∼1.1 mm downstream of the physical throat and all measurements made with respect to the physical throat (SAXS, FTIR) are corrected to align with the actual throat.If there is only a single phase transition, i.e. vapor to liquid, the next step is to use the initial estimates of T and ρ derived from the pressure trace measurements to analyze the SAXS data and determine an improved estimate of g. We then solve the equations that describe supersonic flow with a phase transition using p and g as the known variables, thereby relaxing the assumption regarding the stability of the boundary layers to condensation. Using the improved values of T and ρ we reanalyze the SAXS data and iterate until the solution converges.
If there is more than one phase transition, i.e. if freezing occurs, we rely on position resolved FTIR measurements to determine the mass fraction of condensible in the liquid gl, and solid gs phases. The values of gl, gs and p, are then used to rerun the analysis and generate new estimates for the other flow variables. The procedure is repeated until the values converge.
E. Chemicals
The n-nonane (ChemSampCo, purity > 99%) and n-octane (Sigma Aldrich, purity > 99%) were not purified further. The carrier gas was N2 or Ar. The thermophysical properties of the substances used in the data analysis, with the exception of liquid compressibility, are those reported by Ghosh et al.35 The liquid compressibility for n-nonane, 7.0 × 10−10 Pa−1, was derived from pressure–volume data published by National Institute of Standards and Technology (NIST).47III. Molecular modeling
We conduct Molecular Dynamics (MD) simulations to follow the freezing of supercooled n-octane droplet using the GROMACS code.48 The molecular interactions are described by a united atom model45 where the –CH3 and –CH2– groups are treated as single entities with identical interaction parameters. The bonded and non-bonded interactions parameters between the united atoms are those specified by Yi and Rutledge.30 The equations governing the interactions and the corresponding interaction parameters are summarized below.The bond stretching potential between two united atoms is given by
 | (7) |
The bond angle vibration potential is given by
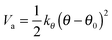 | (8) |
We use the Ryckaert–Bellemans function to represent the dihedral potential:
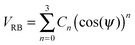 | (9) |
The non-bonded potential is given by a 6–12 Lennard-Jones model
 | (10) |
Finally we use a twin-range cutoff scheme to truncate the potentials since the cutoff distance strongly influences the physical properties including density and the surface tension.49,50 The short-range and long-range cutoffs were 1.0 nm and 2.4 nm, respectively, and long-range interactions were calculated every 5 time steps. The long range cutoff has minor effect on the simulation of bulk systems. For example, we found the bulk freezing temperature with the usual truncation of Lennard-Jones interactions at 1.0 nm was between 213 K and 214 K, near perfect agreement with 212 ± 2 K reported by Yi and Rutledge30 using similar methods. Upon introduction of the long range cutoff, the bulk melting temperature shifted very slightly to 216 ± 1 K. In contrast to the bulk, we found that choice of truncation length for the dispersion interaction could affect the preferred shape of droplets. Experimenting with different values of the outer cutoff, we found that the energy dependence of the droplet shape was converged for an outer cutoff set at 2.4 nm.
To start the simulations, we formed a crystal containing 3840 n-octane molecules and placed it in box with dimensions 20 nm3. Periodic boundary conditions were employed for numerical efficiency to enable the use of the efficient link-cell algorithm, but the periodic replicas of droplets were separated by a distance greater than the range of the interaction potential. We melted the crystal by setting the system temperature to 300 K and running for 1.7 ns to ensure complete melting. We then re-equilibrated the system temperature at 230 K, still well above the melting temperature. Finally, we quenched the temperature to 190 K and followed the droplet for 135 ns as it froze. During the droplet simulation, the angular momentum51,52 drifted away from an initial value of zero and was quenched every nanosecond.
IV. Results and discussion
A. Experiments
Two sets of experiments were conducted and the experimental conditions are summarized in Table 1. In the first set of experiments, nitrogen was the carrier gas and n-nonane the condensible. Under these conditions freezing did not occur because the droplet temperatures were always higher than the melting temperature of n-nonane, or the degree of supercooling was too low to initiate freezing on the timescale of the experiment. The purpose of these experiments was to develop and prove the accuracy of the quantitative FTIR analysis method for the simple case of vapor–liquid condensation before extending the approach to the more complicated case where vapor, liquid, and solid are all present. The second set of experiments was conducted with argon as the carrier gas and n-octane or n-nonane as the condensible. In both cases, the droplet temperature at the nozzle exit was well below Tm, and all of the experimental techniques detect freezing.| Carrier gas | Condensible | p 0 (Pa) | T 0 (K) | p v0 (Pa) | T on (K) (v → l) | p on (Pa) (v → l) | T exit (K) |
|---|---|---|---|---|---|---|---|
| a The onset of condensation is defined as that point in the flow where the temperature of the condensing flow deviates from the expected isentropic expansion by 0.5 K. | |||||||
| Nitrogen | n-Nonane | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
308.16 | 322 | 196.2 | 60 | 202.8 |
| 489 | 204.6 | 103 | 219.7 | ||||
| 625 | 209.3 | 137 | 229.8 | ||||
| Argon | n-Octane | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
308.16 | 209 | 180.2 | 51 | 178.8 |
| n-Nonane | 328.16 | 196 | 195.6 | 49 | 171.2 | ||
 | ||
| Fig. 1 (a) The temperatures of the condensing flow, Tflow (solid lines), the expected isentropic temperature profile, Tisentrope (long dashed lines), and the aerosol droplets Tdrop (open circles) as a function of position. The black short dashed line corresponds to the equilibrium melting temperature of n-nonane. (b) The mean particle radius as a function of position measured by SAXS. | ||
For either set of conditions in Fig. 1(a), the temperature of the gas mixture initially follows the isentropic temperature profile dropping well below the equilibrium melting point of the bulk solid. Eventually, however, the vapor condenses, forming particles that are significantly warmer than the surrounding gas mixture. The dramatic increase in the temperature of the gas mixture reflects the latent heat release due to the vapor–liquid phase transition. As illustrated in Fig. 1(b), the location where the temperature profile deviates from that expected for the corresponding isentropic expansion, is the location where we first observe particles using SAXS. The particles continue to grow rapidly as they move through the nozzle, and even near the nozzle exit the droplet temperature is still slightly higher than that of the gas mixture. The results for pv0 = 489 Pa are similar, and are illustrated in Fig. S1 of the ESI.†
For the experiment at the highest value of pv0, the droplet temperatures are all distinctly higher than Tm and the droplets cannot be frozen. For the experiment at pv0 = 489 Pa, Fig. S1 (ESI†), droplet temperatures are slightly above the melting point near the nozzle exit and hence are assumed to be liquid. For the lowest pv0, both Tflow and Tdrop are well below Tm throughout the expansion. A number of experimental and theoretical studies, however, report that direct nucleation of the solid from the vapor is not favored, even when the solid is the most stable phase under the prevailing experimental conditions.54–58 Hence, even when Tdrop is below Tm near the onset of condensation, the initial fragments of the new phase are assumed to be liquid. We will use spectroscopy to confirm our hypothesis that the particles formed are indeed liquid under all conditions in the three n-nonane–N2 experiments. To do so we turn to FTIR.
To analyze the FTIR data, we assume that the measured absorbance can be described by a linear combination of the normalized absorptivity of each phase present i.e.
 | (11) |
 | (12) |
 | (13) |
To determine the normalized absorptivity of the vapor εv, we measure the absorbance downstream of the throat prior to condensation and normalize it by the concentration of the vapor using
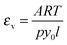 | (14) |
 | ||
| Fig. 2 (a) The integrated absorptivities measured in the current work agree well with the correlation established by Klingbeil et al.60 Here i is the number of carbon atoms in the alkane. (b) The normalized absorptivities of n-octane vapor and n-nonane vapor from supersonic nozzle FTIR measurements. The difference in the curves near 2926 cm−1 and 2855 cm−1 is consistent with the presence of an extra CH2 group in n-nonane relative to n-octane. (c) The normalized absortivities of n-nonane liquid from direct transmission measurements and aerosol measurements. The wavenumber ranges for C–H stretching vibrations are62 as follows; CH3: asymmetric stretch 2962 ± 10, symmetric stretch 2872 ± 10; CH2: asymmetric stretch 2926 ± 10, symmetric stretch 2855 ± 10. | ||
We cannot directly compare our data to those published by the NIST59 since the NIST spectra are saturated in the region of interest, i.e. for wavenumbers ν between 2800 cm−1 and 3000 cm−1. We can, however, compare the integrated normalized absorptivities for these species with those reported in the literature. In particular, Klingbeil et al.60 calculated the integrated normalized absorptivities of several gaseous n-alkanes including n-pentane, n-heptane and n-dodecane. Although their data are at much higher temperatures, 298 K to 773 K, and over such a wide range spectral shape does depend on T, the integrated normalized absorptivities are independent of temperature. As illustrated in Fig. 2(a), Klingbeil et al.60 found that the integrated absorptivities for the n-alkane vapors vary linearly with i, and our points line up well with his correlation. In particular, the correlation predicts values of 6.43 × 105 m mol−1 and 5.80 × 105 m mol−1 for n-nonane and n-octane, respectively, and our measurements are 6.46 × 105 m mol−1 for n-nonane and 5.64 × 105 m mol−1 for n-octane.
To determine the normalized absorptivity of the liquid aerosol εl for n-nonane, we first determined the mass fractions of condensate and vapor as a function of position by combining the results from PTM and SAXS as described in Section II.D. We then took one FTIR spectrum near the nozzle exit from each n-nonane in N2 condensation experiment, and subtracted the vapor contribution from the measured absorption spectra based on the results of the integrated analysis approach described in Section II.D. We then normalized the resultant spectra by the liquid molar concentration obtained from the integrated analysis, i.e.,
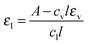 | (15) |
To further confirm that our approach is reasonable we made a direct transmission measurement using a 6 μm thick film of a 15 mol% solution of n-nonane in carbon tetrachloride (CCl4). Fig. 2(c) compares the aerosol εl to the direct transmission measurement. Although there are some differences between the two spectra, the overall shape, location, and intensity of the peaks is very close. We do not expect the spectra to be identical because the absorbance spectrum for an aerosol differs from that of the same material in the bulk phase.61 When the particles are much smaller than the wavelength of light,
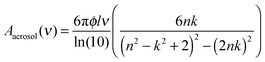 | (16) |
 | (17) |
We then determined the fraction of vapor condensed as a function of position using eqn (11) and the experimental values of εv and εl. A typical fit is shown in Fig. 3(a) and the agreement between the observed and fitted spectrum is very good, i.e. R2 = 0.99.
 | ||
| Fig. 3 (a) The observed normalized aerosol absorptivity 49 mm downstream of the throat for the experiment conducted with pv0 = 625 Pa is well fit by eqn (11). The material balance for this particular position deviates from 1.0 by only ∼1.4%. (b) The values of gi/g∞ obtained from the integrated analysis based on PTM and SAXS are compared to those obtained by FTIR. The lower plot illustrates the material balance obtained from fitting FTIR spectra, where M.B. = (gl + gv)/g∞. | ||
Finally Fig. 3(b) summarizes the position resolved mass fractions of vapor and liquid derived from FTIR and compares these to the values of gi/g∞ obtained from the integrated data analysis described in Section II.D. The overall agreement between the two approaches is excellent, and, furthermore, the FTIR measurements are always within 5% of mass balance. Thus, given an appropriate normalized absorptivity for the solid aerosol εs, it should be possible to extend this approach to three phases.
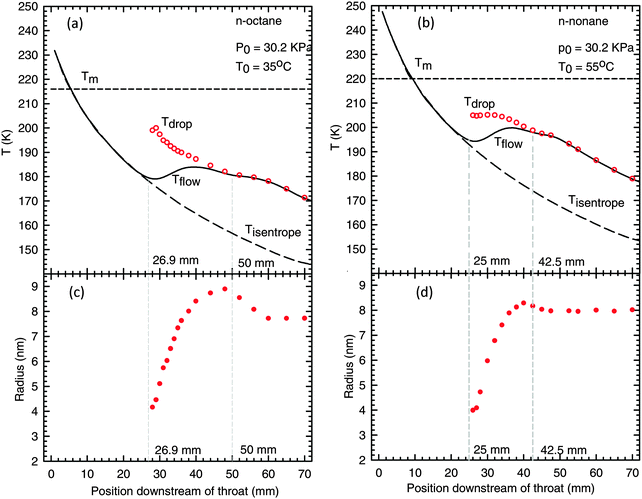 | ||
| Fig. 4 Top: the mixture and particle temperatures as a function of position downstream of the throat for (a) n-octane and (b) n-nonane. The long dashed and solid lines represent the temperature profiles for an isentropic expansion and the condensing flow, respectively. The short dashed lines correspond to the equilibrium melting temperatures. The open circles represent the temperature of droplets. Bottom: the mean particle radius determined from SAXS for (c) n-octane and (d) n-nonane. | ||
For n-nonane, the ∼2.5% decrease in particle size is less than the ∼5% decrease expected based on a simple volume balance and a ∼16% increase in the density of the solid over that of the liquid. This difference is consistent with droplets that are simultaneously freezing and growing. In contrast, the 12% decrease in particle size for n-octane is far larger than the 4% decrease expected based on the ∼14% increase in density. Although it is not the focus of this paper, we note that the decrease in particle size is accompanied by an increase in the particle number density so that the mass fraction of condensate does not decrease, i.e. net droplet evaporation is not detected. Two possibilities for increasing the particle number density include a second nucleation burst or particle break-up. Determining which process dominates is the subject of further investigation.
To further elucidate the sequence of transitions from vapor to liquid to solid, we need to determine the fraction of the three phases as a function of position using FTIR spectroscopy. To do so we must first establish the normalized absorptivity for liquid n-octane εl, and the normalized absorptivities for the n-octane and n-nonane solids, εs.
For n-octane we do not have an experiment where the aerosol was unfrozen at the nozzle exit. To obtain a normalized absorptivity spectrum for the liquid, we therefore analyzed the spectrum measured 34 mm downstream of the throat. At this position the droplets are sub-cooled by only ∼16 K and are, therefore, unlikely to be frozen. Here, the SAXS data give gl/g∞ = 0.4. To confirm that the spectrum derived this way is reasonable, we compared it to a direct transmission measurement at 298 K made with a 6 μm thick film of a 16.7 mol% solution of n-octane in carbon tetrachloride. As illustrated in Fig. 5, the two n-octane spectra are very similar and the overall shape, intensity, and peak locations agree quite well. The normalized aerosol liquid absorptivity εl for n-octane is noisier than that for n-nonane in Fig. 2(c) both because the concentration of condensate at this point is much lower than in the n-nonane experiments and because we did not have multiple spectra to over which to average.
 | ||
| Fig. 5 Normalized absorptivity of n-octane liquid from direct transmission measurements and aerosol measurements. | ||
To obtain the normalized solid absorptivity εs we assume that at the exit, the condensible exists only in the solid and vapor states. This assumption is reasonable because, as illustrated in Fig. 4, the average particle radius does not change near the exit of the nozzle and the temperatures at the nozzle exit are ∼40 K to ∼50 K below Tm. The solid–vapor distribution can therefore be determined from the SAXS data and we can obtain εs using
 | (18) |
 | ||
| Fig. 6 Normalized aerosol absorptivities for solid n-octane and n-nonane. These spectra are determined assuming that the aerosol is entirely frozen near the exit of the nozzle. | ||
Using the normalized absorptivities εv, εl, and εs, we determined g/g∞ for each phase by fitting the intermediate spectra using a least squares approach without imposing material balance constraints during the fit. Fig. 7 illustrates the derived distribution of the condensible between the vapor, liquid and solid states, as well as the material balances. Initially gv/g∞ = 1, and as condensation begins, gv/g∞ decreases monotonically until it attains the constant value that is determined from the integrated PTM/SAXS analysis. In contrast, gl/g∞ starts at zero, increases to reach a maximum, and then decreases to zero at the nozzle exit. Finally, gs/g∞ starts at zero, increasing slowly shortly after the appearance of the liquid, and then more rapidly, before reaching a constant value near the nozzle exit. Although mass balance was not imposed, it is always satisfied to within 5%.
 | ||
| Fig. 7 The distribution of the condensible between the vapor, liquid and solid phases as determined by FTIR for n-octane and n-nonane, together with the material balance. The trends observed are as expected, i.e. the condensible is initially all in the vapor phase, the initial condensate is liquid, and as the solid phase grows in the concentration of the liquid phase approaches zero. Here mass balance, M.B. = (gl + gv + gs)/g∞. | ||
One interesting aspect of the FTIR results is that spectroscopy first detects the solid phase well upstream of the position inferred from the PTM and SAXS experiments. Based on the temperature profiles and the change in particle size, n-octane and n-nonane freezing appeared to start ∼50 mm and ∼42.5 mm downstream of the throat, respectively. In contrast, FTIR experiments suggest the solid phase first appears ∼37 mm and ∼32 mm downstream of the throat, respectively.
To investigate the kinetics of the liquid to solid phase transition, we used the velocity of the flow to convert from position to time. Fig. 8 illustrates the fraction of the aerosol that is solid Fs as a function of time, where Fs = gs/(gs + gl) and t = 0 corresponds to the throat.
 | ||
| Fig. 8 The fraction of solid alkane present in the condensate as a function of time. The symbols are based on the FTIR measurements. The red dashed lines represent the fraction of solid corresponding to a monolayer of alkane on surface of every droplet. The black dashed lines represent the fits used to determine the freezing rates. The presence of a kink in the experimental data suggests that freezing occurs as a two step process that we interpret as surface ordering followed by bulk freezing. | ||
Here we initially see a slow increase in the solid mass fraction before the expected rapid increase begins. Furthermore, the rapid increase starts at the same time (location) as the second heat release is observed to start in the PTM and the droplet shrinkage measured by SAXS begins. We interpret this two-stage behavior as the development of a frozen monolayer on the surface of the droplets prior to crystallization in the remainder of the droplet. PTM does not easily detect the heat release due to surface ordering since the latent heat of fusion is significantly smaller than the latent heat of condensation, and the droplets are still growing slowly. Likewise, droplet growth makes it difficult for SAXS to detect any potential changes in particle size associated with surface freezing.
As illustrated in Fig. 8, n-octane and n-nonane both exhibit distinctly different nucleation behavior than we observed in our recent work46 on ice nucleation from supercooled water nanodroplets, where we found that the fraction of solid Fs, i.e. ice, in the condensed water was well described by the expected functional form
| Fs = 1 − exp(−B(t − t0)), | (19) |
Table 2 summarizes the fit parameters BS, t0S, BV and t0V derived by fitting the Fs data to a two-step crystallization process. Table 2 also reports the freezing rates derived from the fits, assuming surface nucleation is followed by bulk nucleation. We provide nucleation rates for crystallization of the droplet interior based on two possible mechanisms for the bulk crystallization process. First, we give the rate supposing that crystal nuclei are formed anywhere in the droplet below the (already frozen) surface layer. The bulk nucleation rates so calculated for the alkanes are comparable to those we observed for water. Second, we report a “heterogeneous” nucleation rate, i.e. the rate associated with nucleation in the interior of the droplet catalyzed by the presence of the surface layer. Following Weidinger et al.,19 the “heterogeneous” rates are calculated supposing that nuclei for bulk nucleation form in the layer immediately below the surface frozen layer. The heterogeneous rates reported here are 12 orders of magnitude higher than the heterogeneous nucleation rates reported by Weidinger et al.19 This difference is consistent with the fact our droplets are much smaller and are subjected to a much higher degree of supercooling than the micron sized droplets used by Weidinger et al. Ultimately, both these models for crystallization of the interior are likely to be oversimplifications, as discussed below.
Although the data by themselves offer quite a compelling case in favor of surface nucleation, to strengthen our interpretation of the experimental results we turned to molecular dynamics simulations.
B. Molecular dynamics simulations
Fig. 9 illustrates snapshots of the n-octane droplets at intermediate times in a 135 ns run at 190 K. Within the first few nanoseconds, the intermolecular distances and intramolecular coordinates relax from their initial state characteristic of 230 K to values characteristic of 190 K. Also, within a few nanoseconds the surface freezes with a single layer of molecules aligned perpendicular to the bulk liquid. As shown in Fig. 10, these processes are reflected by a steep drop in the Lennard-Jones cohesive energy of the droplet, as well as by a drop in the dihedral energy as alkane chain links are able to assume trans configurations. The average angle-bending potential hardly changes, and the bond stretching potential actually rises, indicating that the bonds are somewhat stretched in the ordered state. This is followed by a time period where we observe just a single ordered layer on the surface. Subsequently the droplet starts to freeze inward from the surface frozen layer to the center in a layer-by-layer manner. Two major events of this type are visible in the configurations shown in Fig. 9, and the energy curves of Fig. 10: formation of a second frozen layer after 25 ns, and a third frozen layer after 85 ns. The implication of these results is that a surface frozen layer appears virtually instantaneously as soon as the droplet temperature dips below the surface freezing temperature, while “bulk” freezing appears to proceed by heterogeneous nucleation at a previously frozen surface. | ||
| Fig. 9 Droplet profiles at various stages in a 250 ns run. These snapshots do not fully convey the degree of chain freezing because the chains do not appear ordered unless they are viewed from the proper angle. For example, at 15 ns the droplet surface is uniformly covered by a solid layer, even though only a fraction of the surface appears ordered in the figure. Rotation of the viewing angle brings some regions into alignment and moves other regions out of alignment. | ||
 | ||
| Fig. 10 Lennard-Jones, dihedral potential, angle-bending, and bond-stretching contributions to the potential energy of the droplet as a function of time. The initial decrease is due to short range relaxation as the configuration initially equilibrated at 230 K is quenched to 190 K, and surface freezing. Two steps in the potential energy at roughly 25 and 85 ns track the layer-by-layer freezing of the droplet from the exterior surface. | ||
V. Summary and conclusions
We followed the freezing of highly supercooled n-octane and n-nonane nanodroplets generated in a supersonic nozzle apparatus. We characterized the flow by combining the results of static pressure measurements and SAXS or FTIR. SAXS also characterized the particle size distribution, whereas FTIR absorption measurements determined the distribution of the condensable between the vapor, liquid and solid states. The presence of two bumps in the temperature profile of the condensing flow was the first indication of multiple phase transitions. SAXS measurements showed that particles grew rapidly from 4 nm to ∼9 nm before distinctly decreasing in size. This size decrease mirrored the 2nd heat addition and served as independent evidence of freezing. Both PTM and SAXS detected onset of freezing at about the same position downstream of the throat.In contrast to PTM and SAXS, FTIR first detected the presence of solid at a position distinctly further upstream. Furthermore, a distinct kink in the fraction of solid versus time curve suggested that freezing occurred as a two-step process that we interpret as the development of an ordered surface monolayer followed by freezing of the rest of the droplet. Analyzing the time dependence of the fraction of solid let us determine the nucleation kinetics of freezing. The surface nucleation rates Js for the outer layer of n-octane and n-nonane droplets were 3.2 × 10+15 cm−2 s−1 and 6.5 × 10+15 cm−2 s−1, respectively. Interpreting our data for crystallization of the interior as a volume nucleation rate, we find Jv = 2.6 × 10+22 cm−3 s−1 for n-octane and Jv = 3.3 × 10+22 cm−3 s−1 for n-nonane, comparable to the bulk nucleation rate determined for water droplets of comparable size.46 Alternatively interpreting the data for the interior with a heterogeneous nucleation model, the nucleation rates are 9.0 × 10+22 for both n-octane and n-nonane. Our values are about 12 orders of magnitude higher than those reported by Weidinger et al.,19 consistent with the current experiments using much smaller droplets that are far more highly supercooled.
We complemented the experimental work by conducting MD simulations in order to support our claim of surface-based nucleation. We simulated an n-octane droplet with 3840 molecules at 190 K and described the molecular interactions using a united atom model.50 We found that upon cooling a liquid droplet to below the surface melting temperature, a monolayer developed on the surface of the droplet within a few nanoseconds. This structure persisted for tens of nanoseconds before layer-by-layer freezing of the entire droplet began. This behavior was also reflected in the different contributions to the potential energy of the droplet with respect to time. The freezing mechanism suggested by our droplet simulation does not follow either of the two simple models used to interpret the data in Table 2. Nucleation by layer-by-layer freezing is distinctly heterogeneous, in that the successive freezing steps always begin in the fluid immediately under the last frozen layer. However, the heterogeneous mechanism developed by Weidinger et al.,19 and utilized in Table 2 assumes that the rate-determining step is nucleation of the layer beneath the surface. However, in the simulation, crystallization of the second layer beneath the surface took longer to nucleate than the first layer below the surface. Therefore, extensive simulation and further theoretical development, as well as further experiments, are required to fully understand the mechanism of alkane crystallization in the presence of a free surface.
Acknowledgements
This work was supported by the National Science Foundation under Grants No. CHE-0911144, CHE-1213959 and CHE-0616872. Use of the Advanced Photon source at Argonne National Labs was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE AC02 06CH11357. We thank H. Laksmono, A. Manka, D. Bergmann, K. Mullick, A. Bhabhe, J. Wölk, G. Wilemski, S. Seifert and R. Winnans for their help in the SAXS experiments. Resources provided by the Ohio Supercomputer Center are gratefully acknowledged for making the calculations reported in this work possible.References
- K. F. Kelton, Solid State Phys., 1991, 45, 75–177 CrossRef CAS.
- G. Arkenbout, Melt Crystallization Technology, CRC Press, 1995 Search PubMed.
- D. W. Oxtoby, Acc. Chem. Res., 1998, 31, 91–97 CrossRef CAS.
- D. Duft and T. Leisner, Atmos. Chem. Phys., 2004, 4, 1997–2000 CrossRef CAS.
- A. Tabazadeh, Y. S. Djikaev and H. Reiss, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15873–15878 CrossRef CAS.
- L. Vrbka and P. Jungwirth, J. Phys. Chem. B, 2006, 110, 18126–18129 CrossRef CAS.
- O. F. Sigurbjornsson and R. Signorell, Phys. Rev. E, 2008, 77, 051601 CrossRef.
- T. Kuhn, M. E. Earle, A. F. Khalizov and J. J. Sloan, Atmos. Chem. Phys., 2011, 11, 2853–2861 CrossRef CAS.
- J. E. Kay, V. Tsemekhman, B. Larson, M. Baker and B. Swanson, Atmos. Chem. Phys., 2003, 3, 1439–1443 CrossRef CAS.
- J. W. M. Frenken and J. F. Vanderveen, Phys. Rev. Lett., 1985, 54, 134–137 CrossRef CAS.
- D. M. Zhu and J. G. Dash, Phys. Rev. Lett., 1986, 57, 2959–2962 CrossRef CAS.
- D. M. Zhu and J. G. Dash, Phys. Rev. Lett., 1988, 60, 432–435 CrossRef CAS.
- J. Krim, J. P. Coulomb and J. Bouzidi, Phys. Rev. Lett., 1987, 58, 583–586 CrossRef CAS.
- M. Elbaum and M. Schick, Phys. Rev. Lett., 1991, 66, 1713–1716 CrossRef CAS.
- J. C. Earnshaw and C. J. Hughes, Phys. Rev. A, 1992, 46, R4494–R4496 CrossRef CAS.
- E. Sloutskin, X. Z. Wu, T. B. Peterson, O. Gang, B. M. Ocko, E. B. Sirota and M. Deutsch, Phys. Rev. E, 2003, 68, 031605 CrossRef CAS.
- P. Lang, J. Phys.: Condens. Matter, 2004, 16, R699–R720 CrossRef CAS.
- E. Sloutskin, C. D. Bain, B. M. Ocko and M. Deutsch, Faraday Discuss., 2005, 129, 339–352 RSC.
- I. Weidinger, J. Klein, P. Stockel, H. Baumgartel and T. Leisner, J. Phys. Chem. B, 2003, 107, 3636–3643 CrossRef CAS.
- T. Leisner, personal communication, 08/2012.
- X. Z. Wu, E. B. Sirota, S. K. Sinha, B. M. Ocko and M. Deutsch, Phys. Rev. Lett., 1993, 70, 958–961 CrossRef CAS.
- M. Deutsch, X. Z. Wu, E. B. Sirota, S. K. Sinha, B. M. Ocko and O. M. Magnussen, Europhys. Lett., 1995, 30, 283–288 CrossRef CAS.
- B. M. Ocko, X. Z. Wu, E. B. Sirota, S. K. Sinha, O. Gang and M. Deutsch, Phys. Rev. E, 1997, 55, 3164–3182 CrossRef CAS.
- O. Gang, X. Z. Wu, B. M. Ocko, E. B. Sirota and M. Deutsch, Phys. Rev. E, 1998, 58, 6086–6100 CrossRef CAS.
- H. Kraack, E. B. Sirota and M. Deutsch, J. Chem. Phys., 2000, 112, 6873–6885 CrossRef CAS.
- E. Sloutskin, O. Gang, H. Kraack, A. Doerr, E. B. Sirota, B. M. Ocko and M. Deutsch, Phys. Rev. E, 2003, 68, 031606 CrossRef CAS.
- A. V. Tkachenko and Y. Rabin, Phys. Rev. Lett., 1996, 76, 2527–2530 CrossRef CAS.
- A. Tkachenko and Y. Rabin, Phys. Rev. Lett., 1997, 79, 532 CrossRef CAS.
- E. B. Sirota, X. Z. Wu, B. M. Ocko and M. Deutsch, Phys. Rev. Lett., 1997, 79, 531 CrossRef CAS.
- P. Yi and G. C. Rutledge, J. Chem. Phys., 2009, 131, 134902 CrossRef.
- M. Gharibeh, Y. Kim, U. Dieregsweiler, B. E. Wyslouzil, D. Ghosh and R. Strey, J. Chem. Phys., 2005, 122, 094512 CrossRef.
- C. H. Heath, K. Streletzky, B. E. Wyslouzil, J. Wolk and R. Strey, J. Chem. Phys., 2002, 117, 6176–6185 CrossRef CAS.
- B. E. Wyslouzil, C. H. Heath, J. L. Cheung and G. Wilemski, J. Chem. Phys., 2000, 113, 7317–7329 CrossRef CAS.
- D. Ghosh, A. Manka, R. Strey, S. Seifert, R. E. Winans and B. E. Wyslouzil, J. Chem. Phys., 2008, 129, 124302 CrossRef.
- D. Ghosh, D. Bergmann, R. Scwering, J. Wölk, R. Strey, S. Tanimura and B. E. Wyslouzil, J. Chem. Phys., 2010, 132, 024307 CrossRef.
- B. E. Wyslouzil, G. Wilemski, R. Strey, S. Seifert and R. E. Winans, Phys. Chem. Chem. Phys., 2007, 9, 5353–5358 RSC.
- B. E. Wyslouzil, G. Wilemski, R. Strey, S. Seifert and R. E. Winans, Phys. Chem. Chem. Phys., 2008, 10, 7327–7328 CAS.
- S. Tanimura, U. M. Dieregsweiler and B. E. Wyslouzil, J. Chem. Phys., 2010, 133, 174305 CrossRef.
- S. Tanimura, U. M. Dieregsweiler and B. E. Wyslouzil, J. Chem. Phys., 2010, 133, 199901 CrossRef.
- S. Tanimura, B. E. Wyslouzil, M. S. Zahniser, J. H. Shorter, D. D. Nelson and B. McManus, J. Chem. Phys., 2007, 127, 034305 CrossRef.
- H. Laksmono, S. Tanimura, H. C. Allen, G. Wilemski, M. S. Zahniser, J. H. Shorter, D. D. Nelson, J. B. McManus and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2011, 13, 5855–5871 RSC.
- S. Tanimura, B. E. Wyslouzil and G. Wilemski, J. Chem. Phys., 2010, 132, 144301 CrossRef.
- W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11125–11136 CrossRef.
- W. Paul, D. Y. Yoon and G. D. Smith, J. Chem. Phys., 1995, 103, 1702–1709 CrossRef CAS.
- A. Manka, H. Pathak, S. Tanimura, J. Woelk, R. Strey and B. E. Wyslouzil, Phys. Chem. Chem. Phys., 2012, 14, 4505–4516 RSC.
- NIST Standard Reference Database 23, Reference Fluid Thermodynamic and Transport Properties – REFPROP, 2002.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- E. M. Blokhuis, D. Bedeaux, C. D. Holcomb and J. A. Zollweg, Mol. Phys., 1995, 85, 665–669 CrossRef CAS.
- M. Mecke, J. Winkelmann and J. Fischer, J. Chem. Phys., 1997, 107, 9264–9270 CrossRef CAS.
- S. C. Harvey, R. K. Z. Tan and T. E. Cheatham, J. Comput. Chem., 1998, 19, 726–740 CrossRef CAS.
- P. Hunenberger, Adv. Polym. Sci., 2005, 173, 105–149 CrossRef.
- T. E. Daubert and R. P. Danner, Physical and Thermodynamic Properties of Pure Chemicals: Data Compilation, Hemisphere Pub. Corp, New York, 1989 Search PubMed.
- B. Chen, H. Kim, S. J. Keasler and R. B. Nellas, J. Phys. Chem. B, 2008, 112, 4067–4078 CrossRef CAS.
- T. Kovacs, F. C. Meldrum and H. K. Christenson, J. Phys. Chem. Lett., 2012, 3, 1602–1606 CrossRef CAS.
- J. F. Lutsko and G. Nicolis, Phys. Rev. Lett., 2006, 96, 046102 CrossRef.
- J. R. Savage and A. D. Dinsmore, Phys. Rev. Lett., 2009, 102, 198302 CrossRef CAS.
- J. A. van Meel, A. J. Page, R. P. Sear and D. Frenkel, J. Chem. Phys., 2008, 129, 204505 CrossRef CAS.
- NIST Chemistry WebBook, http://webbook.nist.gov/chemistry/.
- A. E. Klingbeil, J. B. Jeffries and R. K. Hanson, J. Quant. Spectrosc. Radiat. Transfer, 2007, 107, 407–420 CrossRef CAS.
- R. Signorell and J. Reid, Fundamentals and Applications in Aerosol Spectroscopy, CRC Press, 2010 Search PubMed.
- B. Smith, Infrared Spectral Interpretation: A Systematic Approach, CRC Press, 1998 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp44490b |
| This journal is © the Owner Societies 2013 |





