Benchmark quantum-chemical calculations on a complete set of rotameric families of the DNA sugar–phosphate backbone and their comparison with modern density functional theory

Abstract

The DNA sugar–phosphate backbone has a substantial influence on the DNA structural dynamics. Structural biology and bioinformatics studies revealed that the DNA backbone in experimental structures samples a wide range of distinct conformational substates, known as rotameric DNA backbone conformational families. Their correct description is essential for methods used to model nucleic acids and is known to be the Achilles heel of force field computations. In this study we report the benchmark database of MP2 calculations extrapolated to the complete basis set of atomic orbitals with aug-cc-pVTZ and aug-cc-pVQZ basis sets, MP2(T,Q), augmented by ΔCCSD(T)/aug-cc-pVDZ corrections. The calculations are performed in the gas phase as well as using a COSMO solvent model. This study includes a complete set of 18 established and biochemically most important families of DNA backbone conformations and several other salient conformations that we identified in experimental structures. We utilize an electronically sufficiently complete DNA sugar–phosphate–sugar (SPS) backbone model system truncated to prevent undesired intramolecular interactions. The calculations are then compared with other QM methods. The BLYP and TPSS functionals supplemented with Grimme's D3(BJ) dispersion term provide the best tradeoff between computational demands and accuracy and can be recommended for preliminary conformational searches as well as calculations on large model systems. Among the tested methods, the best agreement with the benchmark database has been obtained for the double-hybrid DSD-BLYP functional in combination with a quadruple-ζ basis set, which is, however, computationally very demanding. The new hybrid density functionals PW6B95-D3 and MPW1B95-D3 yield outstanding results and even slightly outperform the computationally more demanding PWPB95 double-hybrid functional. B3LYP-D3 is somewhat less accurate compared to the other hybrids. Extrapolated MP2(D,T) calculations are not as accurate as the less demanding DFT-D3 methods. Preliminary force field tests using several charge sets reveal an almost order of magnitude larger deviations from the reference QM data compared to modern DFT-D3, underlining the challenges facing force field simulations of nucleic acids. As expected, inclusion of the solvent environment approximated by a continuum approach has a large impact on the relative stabilities of different backbone substates and is important when comparing the QM data with structural bioinformatics and other experimental data.

---

Introduction

Nucleic acids, essential biomacromolecules of cellular life, have numerous functions many of which are still not fully appreciated or are completely unknown. While the primary and the most crucial role of a 2′-deoxyribonucleic acid (DNA) is to preserve, protect and transfer inherited genetic information, the pool of biological functions for which ribonucleic acid (RNA) is accountable is much larger and by far still not exhaustively explored. The independent monomeric units of nucleic acids are called nucleotides and consist of three chemically diverse compounds: an aromatic nucleobase of monocyclic pyrimidine (C, T, U) or a polycyclic purine (A, G) frame, a five-membered sugar moiety, and a negatively charged phosphate group, which imparts a nucleotide with acidic properties. While a nucleobase is linked to C1′ via a glycosidic bond, the phosphate group is covalently attached to the sugar's O5′ through the bridging phosphodiester linkage. The principal difference between DNA and RNA is that DNA nucleotides incorporate 2′-deoxyribose sugar, while RNA incorporate ribose. The nucleotides are merged together by esterification reaction between a C3′ hydroxyl group of one nucleotide and a phosphate group of another to form a directional linear chain. Due to the intrinsic asymmetry of nucleotides a polynucleotide thread has two distinguishable terminals labeled 5′ and 3′. Labeling of nucleotides within a sequence goes from 5′ to 3′, i.e. the first nucleotide is at the 5′end, while the last one at the 3′ end. A polynucleotide chain is thus formed of two elements, a sequence-independent and chemically monotonous sugar–phosphate backbone and an ordered succession of nucleobases attached to sugar rings, which determines specific structural and interaction properties of a given molecule. The major part of the striking structural diversity of RNA is due to the H-bond capability of the C2′ hydroxyl group of a ribose. Also the DNA show considerable structural variability, ranging from local variability of B-DNA to non-canonical structures and higher-order structures in chromatin.¹ The structure and dynamics of nucleic acids result from a delicate balance of numerous energy contributions. Even though it has been often assumed that the sugar–phosphate backbone plays a rather passive role and the main role was ascribed to nucleobases,^2,3 it is now obvious that its intrinsic backbone conformational preferences belong to the most important factors in structuring nucleic acids.⁴ Considering the high number of consecutive single bonds in the sugar–phosphate backbone allowing a substantial freedom for dihedral rotations, systematic exploration of the backbone conformational space is difficult. Nevertheless, to fully comprehend the nucleic acids structure, conformational behavior of the sugar–phosphate backbone needs to be understood.

The conformational space of a phosphodiester DNA sugar–phosphate backbone is defined by six torsion angles α, β, γ, δ, ε, and ζ (Fig. 1).¹ The α torsion is defined as O3′(n − 1)–P–O5′–C5′, β as P–O5′–C5′–C4′, γ as O5′–C5′–C4′–C3′, δ as C5′–C4′–C3′–O3′, ε as C4′–C3′–O3′–P(n + 1), and ζ as C3′–O3′–P(n + 1)–O5′(n + 1), where (n + 1) denotes atoms of the subsequent nucleotide. It is customary to describe the backbone torsional angles of ∼60° as gauche+ (g+), of ∼300° as gauche− (g−), and of ∼180° as trans (t). The DNA conformation is further affected by puckering of the 2′-deoxyribose sugar ring. This is described by five internal torsions τ₀–τ₄, which can be replaced by only two internal degrees of freedom called the pseudorotation phase angle (P) and the pucker amplitude (τ_max).^1,5 The sugar conformations are commonly expressed using suffixes X′-endo and X′-exo, where X′ is one of the sugar ring embedded atoms. The former indicates that the given atom is displaced on the same side of the ring as the C5′ atom, while the latter means that the given atom is displaced on the opposite side. While C2′-endo (P ∼ 162°) is typical for canonical B DNA structure, the C3′-endo (P ∼ 18°) pucker is characteristic of the A DNA double helix. The inherent flexibility of the five-membered ring is an important aspect in understanding the structural properties of furanose sugar moieties.

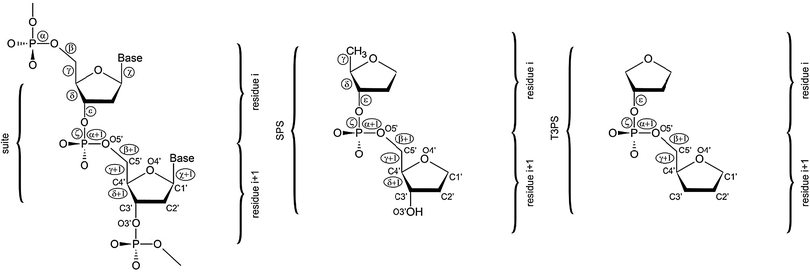Fig. 1 A dinucleotide unit consists of two nucleic acids residues i and i + 1, and is defined from phosphate to phosphate. Its conformation is therefore described by 12 torsion backbone angles (α to ζ + 1). A suite unit spans also two nucleotides, but it goes only from sugar to sugar, consisting thus of the following seven torsion angles: δ, ε, ζ, α + 1, β + 1, γ + 1, δ + 1.⁸⁸ Orientation of the nucleobase attached to C1′ is defined by the χ torsion angle (left). The SPS (sugar–phosphate–sugar) model system used in the present work (center) is derived from the suite unit by cutting off the nucleobases. The T3PS model system (right) suggested by Mackerell in ref. 17.

DNA double helix exists in three main conformations: B DNA, A DNA and Z DNA.¹ The sugar pucker in B DNA is typically in the C2′-endo conformation, though with broad distribution. The B form backbone has two major conformers: BI and BII.⁶ These two arrangements are related to the variability of the ε and ζ torsion angles, which pass from (∼180°, ∼300°) in BI to (∼300°, ∼180°) in BII. DNA can adopt other structures, such as single-stranded hairpins,⁷ triple helices,⁸ three- and four-way junctions,^9,10 four-stranded G-quadruplexes (G-DNA),¹¹ i-DNA quadruplexes,¹² or parallel helices.¹³ Well studied and biochemically relevant are mainly G-DNA molecules which often show unusual but recurrent backbone conformations, some of which are considered in our study.

The contemporary quantum chemistry (QM) methods allow reliable characterization of the nucleic acids sugar–phosphate backbone in model systems.^14–23 Quantum chemistry is not only important to characterize the intrinsic backbone features at the very basic level,^14,17,24 but is also essential in reparameterization of classical molecular mechanics torsional parameters.^25–29 The CHARMM force field³⁰ dihedral parameters of individual furanose conformations were recently developed³¹ by fitting to over 1700 quantum mechanical conformational energies. The last degree of freedom of a nucleotide is represented by the rotation around a glycosidic bond and is characterized by the torsion angle χ. There are two populated substates of χ torsion named (high) anti (χ ∼ 250° in DNA) and syn (χ ∼ 60°).

Since the anionic and highly flexible sugar–phosphate backbone is a rather challenging task for QM techniques, careful selection of methods and sets of basis functions is imperative to obtain reliable results. Accurate calculations can, for small systems, be acquired using high-level reference (benchmark) methods like coupled clusters (CC).³² Benchmark computations play a similar role as reference experiments and are indispensable for understanding the basic physical chemistry features of the studied systems as well as for parameterization and verification of other computational methods.^33–47 However, extensive characterization of the complex potential energy surface of the nucleic acids backbone and studies of larger fragments of nucleic acids require the use of more efficient QM methods. The present-day density functionals supplemented with empirical dispersion corrections^48–50 often yield outstanding results for a fraction of time and thus appear to be a promising way to study the nucleic acids backbone.

In our previous study¹⁴ we introduced the so-called SPSOM and SPM model compounds to study electronic structure and energetics of selected DNA backbone α/γ conformational substates. Subsequently we reported benchmark QM computations²⁴ followed by testing of other methods on 22 individual DNA backbone conformations, covering three distinct conformational space regions (families), namely the canonical B DNA region with α/γ ∼ g−/g+, a native g+/t substate occurring in the stem–loop junction of a parallel stranded human telomeric sequence G-DNA and an essentially pathological g+/t conformation, which has been populated in explicit solvent simulations with older versions of the Cornell et al. force field.²⁶ Note that the two α/γ g+/t substates differ in combination of the remaining backbone dihedrals and thus represent distinct conformational families. An essentially similar approach was adopted also in the work of Mackerell¹⁷ where three canonical A, BI, and BII conformations of DNA were studied using a so-called T3PS model system. It should be noted that two-sugar SPSOM and T3PS models are similar but not identical to the SPS model we use in the present work.

The common attribute of the above-mentioned studies is QM analysis of backbone conformations pertaining to only several families or Taylor expansion-like torsional scans around canonical values. However, while the relative energies ordering of conformers within a given family is usually well reproduced by the majority of methods, energetical comparison between different families is more difficult. Therefore, in this study, we provide reference QM data for essentially all known DNA backbone families. These include the complete set of the 18 most significant DNA backbone families identified by structural bioinformatics⁵¹ as well as several additional experimental geometries we confidently found in specific non-canonical DNA forms which were not classified in the preceding bioinformatics study. Our conformation set is highly diverse and samples all naturally populated conformational domains. The calculations are done in the gas phase as well as using a COSMO continuum solvent model. The calculations are compared with a set of modern DFT functionals, while we also comment on preliminary testing of the MM force field.

Methods

Geometrical optimizations

The structures derived as explained below have been partially optimized using the local meta-GGA functional TPSS⁵² and by applying the new D3 London dispersion correction with Becke–Johnson damping,^49,53 abbreviated as TPSS-D3. To preserve the experimentally determined conformations, constraints on six consecutive backbone torsion angles (δ, ε, ζ, α + 1, β + 1, γ + 1, δ + 1) have been imposed (Fig. 1, center and Table 1). Note that without such constraints, it would be impossible to keep the desired rotameric family.^4,14,24 The conformations were optimized separately in the gas phase and using the COSMO solvent model^54,55 (see below).

Table 1 Standard conformations (families) of repeating units of DNA. Data were analyzed at the “suite” level, i.e. from δ to δ + 1 torsions plus both glycosidic torsions χ and χ + 1. Average values of the individual torsions for each class are given, as well as symbolic names of the classes adopted in our study (“Label”), conformational class tags used in ref. 51 (“#”), the number of individual dinucleotide units of each class in the database (“N”) and short detailed annotations (“Description”). Our numerical ordering of the symbolic names (C1–C18) follows the conformational frequency of occurrence (N). All the bioinformatics data are taken from ref. 51

Label	#	Description	N	δ	ε	ζ	α + 1	β + 1	γ + 1	δ + 1	χ	χ + 1
C1	54	BI	1942	136	184	262	302	179	45	138	251	260
C2	96	BII	539	143	245	172	297	142	46	141	269	259
C3	50	BI, C1′-exo δ + 1	392	130	181	265	301	177	49	122	247	244
C4	8	A DNA	329	82	205	285	294	172	55	83	201	202
C5	86	BII variation in complexes	314	140	201	216	314	156	46	140	261	253
C6	32	BI-to-A, O4′-endo δ + 1	266	130	183	267	297	171	51	106	250	239
C7	41	A-to-B, >C3′-endo δ, C2′-endo δ + 1	215	86	194	281	301	179	55	142	214	251
C8	13	A DNA, BI-like χ	196	89	204	281	291	164	53	85	243	246
C9	116	BI, α + 1/γ + 1 crank, α/γ normal	158	139	195	245	32	196	296	150	252	253
C10	19	A DNA, α + 1/γ + 1 crank (t/t)	65	82	195	291	149	194	182	87	204	188
C11	124	Z, R-Y ZI	49	96	242	292	210	233	54	144	63	205
C12	123	Z, Y-R	21	147	264	76	66	186	179	95	205	61
C13	109	BII-to-A, >C3′-endo, δ + 1	20	139	211	187	300	131	55	85	270	209
C14	121	mismatches, B, anti/syn	19	91	214	280	295	176	56	139	238	67
C15	126	Z, R-Y ZII	18	95	187	63	169	162	44	144	58	213
C16	119	5′-mismatches, BI, α/γ crank (g+/g−)	11	145	190	281	303	167	50	136	71	265
C17	110	BII-to-A, C2′-/C3′, α + 1/γ + 1 crank, high β + 1	9	146	257	186	60	224	196	90	260	200
C18	122	mismatches, B, anti/syn α + 1/γ + 1 crank (g+/g−)	8	137	196	225	33	187	295	145	257	70

---

A large all-electron Gaussian basis set def2-TZVPPD⁵⁶ has been used in the optimizations. This basis set is based on the Karlsruhe segmented contracted basis set of a triple-ζ valence quality (def2-TZVPP)^57,58 and is augmented with a small number of moderately diffuse functions (D) important for weakly bound electrons in negatively charged molecules. It should be noted, however, that application of large flexible basis sets with diffuse functions especially in combination with HF exchange excluded functionals might result in positive HOMO orbital energies, which would describe unbound electrons.^59–64 Due to the anionic character of the SPS model system (charge = −1) converged wave functions were validated by manual inspection. All calculations employ the resolution of the identity (RI) approximation.^65,66 The numerical quadrature multiple grid m4 for the integration of the exchange–correlation contribution has been used. The convergence threshold of the SCF density matrix has been tightened to 10⁻⁷ a.u. as compared to the default value of 10⁻⁶ a.u. Taking advantage of the efficient and robust optimization algorithms of the Gaussian03⁶⁷ software package and the superior scalability of the Turbomole 6.3 code,⁶⁸ we have developed a scheme whereby the electronic energy gradients calculated by Turbomole are passed to Gaussian to execute the energetically downhill geometry alteration. The modified coordinates are then passed back to Turbomole and serve as a new input structure for the subsequent optimization cycle. This iterative procedure repeats until imposed convergence criteria are met.

The COSMO continuum solvation model^54,55 was used for a dielectric constant of 78.5 corresponding to the water environment. The atomic van der Waals radii for the molecular cavity construction in COSMO were taken as their defaults in Turbomole 6.3 (i.e., in Å for H: 1.3, C: 2.0, O: 1.72, P: 2.11).

Single point calculations

Energies of the optimized backbone conformers were calculated using several QM methods and sets of basis functions, both in the gas phase and continuum COSMO solvent^54,55 (with the exception of ΔCCSD(T) corrections, which were calculated in the gas phase only).

MP2/CBS calculations we carried out using the Halkier et al. extrapolation scheme^69,70 with augmented correlation consistent Dunning's basis sets^71,72 (aug-cc-pVXZ, where X = D, T or Q) to obtain MP2 energies at the complete basis set limit (CBS). Even though extrapolation to CBS effectively eliminates both intramolecular basis set superposition (BSSE) and incompleteness (BSIE) errors to a large extent, some residual BSSE/BSIE depreciating the results are likely to remain.^42,73 The Hartree–Fock (HF) and the MP2 correlation components are evaluated separately by solving the following equations:

E^HF_X = E^HF_CBS + Ae^−δX

E^Corr_X = E^Corr_CBS + BX⁻³

where X is the cardinal angular momentum quantum number of the respective basis set (X = 2 for aug-cc-pVDZ, X = 3 for aug-cc-pVTZ, and X = 4 for aug-cc-pVQZ) and δ, A and B are parameters. While δ = 1.43 and 1.54 for (D,T) and (T,Q) extrapolations, respectively, was taken from the literature,⁷⁰A and B are system-dependent coefficients which are to be determined via solution of the given linear equations. E^Corr_CBS and E^HF_CBS are the correlation and HF components of the total electronic energy at the basis set limit, respectively. Analogously E^Corr_CBS and E^HF_CBS are corresponding terms obtained using the aug-cc-pVXZ set of basis functions.

In our preceding study we suggested that the ΔCCSD(T) correction is not needed for calculations of different conformers of the DNA backbone.²⁴ However, as in the present paper we substantially extend the spectrum of the calculated DNA backbone conformers, we augmented the Halkier et al. MP2/CBS extrapolation scheme (dubbed as MP2(D,T) or MP2(T,Q) herein) by ΔCCSD(T) correction calculated in a smaller basis set. We refer this composite method as CBS(T) to indicate that the CBS extrapolation has been carried out only at the MP2 level. The most accurate approach in our study is the MP2(T,Q) + ΔCCSD(T)/aug-cc-pVDZ level, which we refer to as “Higher Level CBS(T)” abbreviated as CBS(T)^HL. This is the level we selected to be the reference against which the remaining techniques were benchmarked. We have also carried out ΔCCSD(T) calculations with a smaller 6-31+G(d) basis set, and thus CBS(T)^LL abbreviation in our paper stands for the “Lower Level CBS(T)” method of MP2(D,T) + ΔCCSD(T)/6-31+G(d) quality, which has been used (and labeled CBS(T)) in our preceding study.²⁴ Since solvation does not significantly affect the magnitude of ΔCCSD(T) corrections CBS(T)/COSMO energies were evaluated using MP2/CBS calculated in COSMO and gas phase ΔCCSD(T) corrections. The MP2 and CCSD(T) calculations were done using Turbomole 6.3⁶⁸ and Molpro 2012.1.⁷⁴

Two GGAs, two meta-GGA, three hybrid, and two double-hybrid functionals were tested in the present study. The GGA level of theory comprises BLYP,^75,76 and the reparameterized variant of PBE,⁷⁷ revPBE.⁷⁸ From the meta-GGA methods the original TPSS⁵² along with its recalibrated version oTPSS⁷⁹ were assessed. The group of investigated global hybrids, which take a portion of HF exchange into account, consists of B3LYP^76,80 and two thermochemistry oriented functionals, PW6B95⁸¹ and MPW1B95.⁸² The tested double-hybrids are PWPB95³⁵ and DSD-BLYP.⁸³ The former one developed by Grimme's group³⁵ contains a mixture of reparameterized Perdew–Wang and Fock (50%) exchange, Becke95 correlation, and 26.9% of spin-opposite scaled perturbative correlation (SOS-PT2). The latter suggested by Kozuch et al.⁸³ is basically identical to the B2PLYP double hybrid functional of Grimme,⁸⁴ but adds a spin-component-scaled perturbative contribution (SCS-PT2). Both SOS- and SCS-PT2 corrections were calculated on the converged Khon–Sham molecular orbitals without frozen core approximation. With the exception of B3LYP and TPSS, which were considered primarily due to their widespread usage, the above functionals were selected based on their outstanding score at the respective Jacob's ladder rung in the thorough benchmark study of Goerigk and Grimme.³⁴

With the exception of double-hybrid calculations where a large quadruple-ζ aug-cc-pVQZ basis set was used for both SCF and PT2 runs, all single point computations were carried out with the def2-TZVPPD set of basis functions. To accelerate SCF calculations of (meta-)GGA density functionals, RI approximation has been employed and corresponding auxiliary basis functions for Coulomb-fitting were used.^65,66 While in (meta-)GGA and double-hybrid single point calculations only the numerical quadrature m4 and m5 grid has been utilized, respectively, for hybrid functionals both m4 and m5 grids were tested to appraise the effect of a denser integration grid on the relative energies and computational time. SCF convergence criteria have been tightened to 10⁻⁷ a.u., as in the geometry minimization (vide supra). All remaining computational parameters were kept at their defaults. The DFT calculations were either carried out with the modified version of Turbomole 5.9 or with the original version of Turbomole 6.3.⁶⁸

Molecular mechanics calculations

The molecular mechanics (MM) energies were calculated using the non-polarizable Cornell et al. force field⁸⁵ including the parmbsc0 torsional potential revision.²⁶ The energies were evaluated for four different sets of partial charges (see below) both in the gas phase and solvent environment approximated by the Poisson–Boltzmann model (MM-PBSA). Prior to evaluation of the MM energies, TPSS-D3 optimized model systems were relaxed using the respective force field except for the fixed backbone torsions, i.e. the force field energies were derived using the force field geometries. The relaxation was carried out to the default tolerances using the steepest descent technique for the first 250 iterations, followed by the conjugate gradient method. No cutoff was applied. To keep the backbone dihedrals at the values given in Table 1 and to obtain geometries equivalent to those minimized by TPSS-D3, tight restraints with a penalty function of 3000 kcal mol⁻¹ have been imposed.

Since our SPS model system (see below) does not belong to standard residues for which the AMBER library contains pre-computed partial charges we derived four sets of charges as follows:

(1) We adopted the pre-computed AMBER partial charges and based on chemical intuition manually adjusted the non-standard ones (e.g. at the artificial 5′ backbone termination, etc.) considering the symmetries in order to keep the total charge −1. This partial charges set is labeled the “AMBER” set.

(2) We derived the restrained electrostatic potential (RESP) charges⁸⁶ fitted to the HF/6-31G(d) potential of the gas phase (for MM calculations) and COSMO (for MM-PBSA calculations) TPSS-D3 optimized BI DNA SPS conformation using the default settings, i.e. two-stage procedure with the restrains of 0.0005 and 0.001. This approach is (in the gas phase) basically equivalent to the one utilized for deriving the original AMBER charges, but the calculation is performed for the SPS model. This partial charges set is labeled the “RESP” set.

(3) We derived the restrained electrostatic potential (RESP) charges⁸⁶ fitted to the HF/6-31G(d) potential of the gas phase TPSS-D3 optimized BI DNA SPS conformation using the modified grid procedure, namely we used an extended grid spacing with 10 layers having a grid density of 17 points per Ų and ten times stronger force constants of restraints compared to AMBER defaults, i.e. 0.005 and 0.01 at the first and the second stage of the fit, respectively. This partial charges set is labeled the “Mod.RESP” set. Only gas phase charges were derived.

(4) We derived the restrained multimolecular (multiconformational) electrostatic potential (RESP) charges⁸⁶ fitted to a set of HF/6-31G(d) potentials of the 18 gas phase TPSS-D3 optimized DNA SPS backbone conformations using the above-mentioned modified procedure. This multimolecular partial charges set is labeled the “Mod.RESP-MM” set. The purpose of the multimolecular fit was to reduce bias due to the choice of just a one single geometry in the fit. Only gas phase charges were derived.

All charges are available in ESI† (Table S2). All force field calculations were performed with the AMBER 12.0 suite of programs.⁸⁷ The MM-PBSA calculations were carried out using MM-PBSA script; Delphi v4 was used for the numerical solution of the Poisson–Boltzmann equation.

DNA backbone model system

There are two main issues of model system selection that need to be addressed when making QM computations on a DNA backbone. First, a truncation is inevitable. Even though a larger model system might give the impression to better mimic the real DNA backbone there are many obstacles associated with it. Clearly, a too large model system might preclude application of accurate and computationally demanding QM methods. However, there is yet another problem well documented in our earlier studies,^14,24 namely, larger model systems have so complex potential energy surfaces (PES) that it is often becoming virtually impossible to get them conformationally under control. Due to the lack of native environment, e.g. a solvent, a nearby strand, etc., large model systems are prone to adopt non-native conformations with non-native intramolecular interactions. Moreover, the anionic nature of the phosphate group would complicate computations where two or more phosphates are present. The second issue is whether the model system should include nucleobase/nucleobases. Although retaining of nucleobases (or substituting them for simpler analogues) makes the model system electronically more complete, inherent backbone conformational preferences become partially obscured by the nucleobase interactions.²⁴ For all the reasons noted above there is no perfect model for QM studies of the nucleic acids backbone and some compromise needs to be made. The model should be as small as possible to prevent spurious interactions to obtain an unbiased picture of the PES and to be analyzable by high-level QM methods, but sufficiently large to represent the actual physico–chemical nature of the DNA backbone.

In our preceding studies we have used a model abbreviated as SPSOM, i.e., Sugar–Phosphate–Sugar capped on both ends with methoxy (–O–Methyl) groups.^14,24 However, in the present study we decided to utilize a slightly reduced model system labeled the SPS model (Fig. 1, center). The core of the SPSOM model, i.e. the sugar–phosphate–sugar backbone tract, is retained. However, to prevent spurious energy-biasing C2′H⋯O5′ interactions discussed in ref. 14 and 24 we replaced the original 5′ terminal methoxy group with a hydrogen atom. Since we are interested in the intervening backbone torsions, such substitution does not have a significant impact on the results. Note that neither of these termini can be considered as biochemically fully relevant. Similar modification has been done at the 3′ end. While the SPSOM model terminates with a methyl group linked to O3′, the SPS model has a hydroxyl group at its 3′ end. We regard both 5′/3′ terminal modifications as insignificant for relative energy evaluations while they enable us to carry out unbiased analysis of the PES corresponding to a given backbone conformational family. As we stated elsewhere,^14,24 further reduction of the model would break the hyperconjugation network along the phosphodiester linkage and alter the electronic structure. We thus regard the SPS model system to be simple enough to be treatable by high-level techniques and still sufficiently complete to mimic the real DNA sugar–phosphate backbone at the same time. There is another efficient two-sugar DNA backbone model system similar to SPS suggested by Mackerell¹⁷ and called T3PS (Tetrahydrofuran with 3′-Phosphate with a capping Sugar). In T3PS the 5′-methyl group and the 3′-hydroxyl group are substituted for hydrogens (Fig. 1, right). Although this further reduction has only a marginal impact on the rather complex electronic topology we decided to retain C5′ and O3′ atoms since their positions define δ torsion we fix during minimization. We nevertheless consider both SPS and T3PS models as interchangeable for the purpose of benchmark studies and we do not expect any substantial differences between SPS and T3PS models from an energetical point of view. The T3PS model was successfully used, e.g. for extensive one-dimensional PES scans of backbone torsions excluding δ coupled to the sugar pucker and subsequent correlation with crystallographic probability distributions.¹⁷ The scans were done using the MP2 method with the cc-pVTZ basis set and unlike the approach adopted in the present study the systematic conformational exploration focused on canonical regions and their vicinities. Both studies nevertheless complement each other, for example, our work provides accuracy assessment of the earlier calculations. Our study is the first QM study directly taking into consideration multi-dimensional correlation among different backbone dihedrals while the preceding study provides scans across the potential energy surface.

Derivation of representative DNA backbone conformations

In the present work we utilize the concept of “suite” (Fig. 1).⁸⁸ A suite is a structural subset of a dinucleotide going from sugar to sugar, containing thus only seven backbone torsion angles (δ, ε, ζ, α + 1, β + 1, γ + 1, δ + 1, see Fig. 1). A suite is a physically meaningful description of a backbone-repeating unit since it is centered around the phosphorus atom. Although the current work is based on the suite structural unit including only the backbone torsion angles, the original DNA bioinformatics analysis considered also the two glycosidic angles χ and χ + 1 that were shown to play an important role in classifying the local conformations of DNA.⁵¹

Most of the structures analyzed in our study come from the preceding bioinformatics analysis of the local conformation space of DNA.⁵¹ The clustering analysis⁵¹ is based on the data consisting of dinucleotide units from 415 duplex crystal structures resolved with the resolution of 1.9 Å or better augmented by additional 58 structures with unusual topologies (G-quadruplexes, i-motifs, three- and four-way junctions, etc.). The final analysis considered a set of 4571 individual dinucleotides that were classified into 18 distinct families⁵¹ (Table 1).

Each conformational class is thus characterized by a vector consisting of average values of its backbone and glycosidic torsions (Table 1). For each class, an exemplar dinucleotide with values of suite's backbone torsion angles as close as possible to the average values was identified (ESI,† Table S1), for details see ref. 51. Subsequently, these 18 exemplar dinucleotides have been manually pruned to obtain our SPS (sugar–phosphate–sugar) model systems and all the backbone torsions (i.e. δ to δ + 1) were then adjusted exactly to the values given in Table 1. The coordinates of each system were then used as the input for consecutive constrained geometry optimizations.

Additional conformations

While the bioinformatics cluster analysis is well suited to identify frequent backbone conformations, it is susceptible to miss some rare, yet biologically significant rotamers. We thus extended our set of 18 average conformations (Table 1) by six auxiliary structures, which have specific non-canonical combinations of backbone dihedrals (Table 2). Three conformations are from antiparallel oxytricha nova telomeric G-DNA⁸⁹ (PDB ID: 3NZ7) as we analyzed elsewhere⁹⁰ and three structures were found in an intercalated four-stranded DNA⁹¹ (PDB ID: 191D). Regarding the G-DNA structure, we added the SPS model of an outer tetrad dinucleotide (T8-G9, chain B) with α(g+)/γ(t) dihedral combination (A1 conformation) and of two inner tetrad dinucleotides (G2–G3, chain B and G10–G11, chain A), which have α(g+)/γ(g−) (A2) and α(g−)/γ(g−) (A3), respectively. Moreover, the latter α/γ combination of A3 has also an unusually high β of ∼260°. All of these combinations are also tightly coupled with specific glycosidic torsions and pucker values. To reproduce the experimentally observed G-DNA backbone conformations by simulation force fields is not easy.⁹⁰ In the case of i-DNA, we derived SPS out of chain B successive dinucleotides, namely C5–C6 (A4), C6–C7 (A5), and C7–T8 (A6). Note that none of the six auxiliary conformations can be assigned to any of the 18 established DNA backbone families (Table 1) despite being likely essential to non-canonical DNA structures formation. The gas phase and solvent stabilities of the auxiliary systems were assessed only at the MP2(T,Q) level and we did not use them for benchmarking of the DFT-D methods, as we believe the 18 standard families provide sufficient data for this purpose. Adding these geometries into the database would be straightforward. However, since force field calculations are more prone to fail for non-canonical backbone conformations, we computed MM and MM-PBSA energies of A1–A6 structures using the force field (vide supra) and validated them against the QM results. Note that when tuning the force field through the dihedral terms, we use formally intramolecular terms to effectively include incorrect or missing intermolecular contributions, which may limit transferability of the torsion potentials for different backbone families.

Table 2 Auxiliary backbone conformations of outer (A1) and inner (A2 and A3) tetrads of antiparallel telomeric G-DNA (PDB ID: 3NZ7) and of chain B successive dinucleotides (A4–A6) of i-DNA (PDB ID: 191D)

Label	Description	δ	ε	ζ	α + 1	β + 1	γ + 1	δ + 1	χ	χ + 1
A1	G-DNA, outer tetrad	144	202	68	77	205	192	147	241	71
A2	G-DNA, inner tetrad	135	193	218	56	168	288	148	247	67
A3		139	201	289	302	258	295	150	238	65
A4	i-DNA	140	219	293	171	139	175	113	246	240
A5		113	206	285	157	145	175	82	240	242
A6		82	200	67	67	175	45	151	242	220

---

Results and discussion

The single point calculations were done on geometries optimized using the TPSS-D3/Def2-TZVPPD method either in the gas phase or in the continuum COSMO solvent model. Since the most flexible torsional degrees of freedom of the SPS model were frozen at their initial values (see Methods and Table 1), there are only marginal structural differences between the experimental and the minimized geometries. The optimized structures were manually inspected for the presence of spurious interactions originating from artificial termini of the SPS model. No such unnatural contacts have been observed so the calculated energies reflect purely intrinsic backbone rotameric preferences and native interactions. The set of optimized SPS geometries is available in the ESI† and can be used for benchmark purposes.

GGA and meta-GGA functionals

The computationally least demanding (meta-)GGA group comprises four tested density functionals: BLYP and revPBE (GGA), and TPSS with its reparameterized version oTPSS (meta-GGA). As anticipated both variants of the kinetic energy density-dependent group perform slightly better than pure GGAs as compared to the reference CBS(T)^HL level. The rather outstanding results of the TPSS functional with MAD being only 0.17 kcal mol⁻¹ for both gas phase and COSMO environments (Tables 3 and 4), respectively, might be partially attributed to the fact that the geometries were minimized at the same level of theory (TPSS-D3/def2-TZVPPD), i.e. the single point calculations were done on the true minima of the TPSS-D3 PES. While the empirically revised variant oTPSS yields negligibly worse results compared to the original TPSS functional in the gas phase with MAD of 0.21 kcal mol⁻¹, it slightly improves on TPSS for COSMO calculations with MAD as low as 0.13 kcal mol⁻¹ (Tables 3 and 4). Note that our finding is slightly in contrary to the benchmark study of Goerigk and Grimme,³⁴ where oTPSS clearly outperforms TPSS in the gas phase. It is therefore evident that the electronic structure of the sugar–phosphate backbone represents a good test for density functionals. Still, both methods exhibit very good performance with a maximum deviation of ∼0.4–0.5 kcal mol⁻¹.

Table 3 Gas phase relative energies (kcal mol⁻¹) compared to reference CBS(T)^HL data (in bold) with the canonical BI DNA conformation (structure C1, in bold) taken as the reference. For hybrid functionals values in parentheses refer to the sparse integration grid (m4). Statistical descriptors VAR, |MAX.DEV|, and MAD refer to variance (kcal² mol⁻²), the absolute value of maximum deviation (kcal mol⁻¹), and mean absolute deviation (kcal mol⁻¹) compared to the CBS(T)^HL relative energies, respectively. Values in square brackets in the “Label” column correspond to the number of identified conformations, i.e. refer to the “N” column in Table 1. The conformations are ordered according to their gas phase stability in the benchmark computations

Label	BLYP	revPBE	TPSS	oTPSS	B3LYP	PW6B95	MPW1B95	PWPB95	DSD-BLYP	MP2(D,T)	MP2(T,Q)	CBS(T)^LL	CBS(T)^HL
C16 [11]	−0.17	−0.05	0.13	0.14	−0.14 (−0.16)	0.02 (−0.01)	0.01 (−0.03)	−0.03	−0.11	−0.34	−0.24	−0.28	−0.14
C1 [1942]	0.00	0.00	0.00	0.00	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00	0.00	0.00	0.00	0.00	0.00
C7 [215]	0.23	0.19	0.51	0.47	0.32 (0.31)	0.57 (0.54)	0.54 (0.50)	0.57	0.38	0.33	0.38	0.26	0.34
C14 [19]	0.21	0.12	0.47	0.35	0.11 (0.10)	0.60 (0.57)	0.65 (0.61)	0.73	0.48	0.82	0.69	0.70	0.56
C3 [392]	0.80	0.74	0.88	0.88	0.92 (0.92)	1.04 (1.03)	1.06 (1.05)	1.05	0.98	1.05	1.03	0.96	0.93
C11 [49]	0.39	0.30	0.69	0.49	0.25 (0.24)	0.67 (0.62)	0.65 (0.59)	0.82	0.89	1.47	1.31	1.21	0.99
C4 [329]	1.00	0.62	1.32	1.07	0.63 (0.63)	1.05 (1.02)	1.02 (0.99)	1.20	1.03	1.48	1.36	1.26	1.13
C6 [266]	1.48	1.42	1.61	1.61	1.65 (1.64)	1.84 (1.83)	1.86 (1.86)	1.86	1.74	1.83	1.79	1.67	1.63
C8 [196]	1.36	1.16	1.74	1.59	1.34 (1.33)	2.19 (2.17)	2.16 (2.15)	2.23	1.69	1.93	1.91	1.73	1.67
C15 [18]	2.61	2.60	2.89	2.89	2.80 (2.79)	3.23 (3.21)	3.26 (3.24)	3.29	3.00	3.36	3.21	3.18	3.03
C2 [539]	3.15	3.01	3.24	3.11	3.02 (3.01)	3.49 (3.45)	3.51 (3.48)	3.50	3.19	3.38	3.23	3.30	3.20
C5 [314]	3.51	3.67	3.62	3.56	3.44 (3.43)	3.76 (3.75)	3.80 (3.78)	3.88	3.66	3.86	3.72	3.85	3.74
C12 [21]	4.73	4.22	4.78	4.69	4.86 (4.85)	5.25 (5.21)	5.22 (5.18)	5.25	5.03	4.99	5.02	4.85	4.90
C13 [20]	5.22	4.73	5.32	5.02	4.93 (4.93)	5.30 (5.24)	5.28 (5.22)	5.43	5.28	5.72	5.45	5.50	5.24
C10 [65]	5.14	4.88	5.53	5.47	4.96 (4.96)	5.67 (5.66)	5.66 (5.65)	5.91	5.59	6.36	6.05	6.05	5.63
C18 [8]	5.29	5.35	5.42	5.47	5.40 (5.39)	5.64 (5.62)	5.69 (5.67)	5.76	5.79	6.19	5.91	6.03	5.69
C9 [158]	6.72	6.83	6.88	6.90	6.95 (6.94)	7.17 (7.15)	7.22 (7.20)	7.36	7.45	7.83	7.64	7.70	7.42
C17 [9]	9.62	8.87	9.58	9.37	9.58 (9.57)	9.94 (9.92)	9.96 (9.94)	10.10	10.02	10.48	10.12	10.17	9.82
VAR	0.11	0.25	0.04	0.07	0.13 (0.13)	0.05 (0.05)	0.05 (0.05)	0.06	0.01	0.14	0.04	0.04	0.00
|MAX.DEV|	0.70	0.95	0.54	0.52	0.74 (0.75)	0.52 (0.50)	0.49 (0.48)	0.56	0.20	0.74	0.43	0.43	0.00
MAD	0.26	0.43	0.17	0.21	0.28 (0.29)	0.18 (0.17)	0.18 (0.17)	0.21	0.07	0.31	0.18	0.17	0.00

---

Table 4 COSMO relative energies (kcal mol⁻¹) compared to reference CBS(T)^HL data (in bold) with the canonical BI DNA conformation (structure C1, in bold) taken as the reference. For hybrid functionals values in parentheses refer to the sparse integration grid (m4). Statistical descriptors VAR, |MAX.DEV|, and MAD refer to variance (kcal² mol⁻²), the absolute value of maximum deviation (kcal mol⁻¹), and mean absolute deviation (kcal mol⁻¹) compared to the CBS(T)^HL relative energies, respectively. Values in square brackets in the “Label” column correspond to the number of identified conformations, i.e. refer to the “N” column in Table 1. The conformations are ordered according to their COSMO stability in the benchmark computations

Label	BLYP	revPBE	TPSS	oTPSS	B3LYP	PW6B95	MPW1B95	PWPB95	DSD-BLYP	MP2(D,T)	MP2(T,Q)	CBS(T)^LL	CBS(T)^HL
C16 [11]	−1.26	−1.07	−0.97	−0.93	−1.21 (−1.22)	−1.08 (−1.08)	−1.09 (−1.09)	−1.13	−1.19	−1.42	−1.30	−1.36	−1.21
C12 [21]	−0.59	−0.78	−0.52	−0.53	−0.57 (−0.58)	−0.25 (−0.26)	−0.25 (−0.26)	−0.23	−0.46	−0.43	−0.46	−0.57	−0.58
C7 [215]	−0.06	−0.12	0.12	0.11	−0.03 (−0.04)	0.03 (0.05)	−0.01 (0.01)	0.02	−0.04	−0.13	−0.06	−0.20	−0.11
C1 [1942]	0.00	0.00	0.00	0.00	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)	0.00	0.00	0.00	0.00	0.00	0.00
C6 [266]	0.26	0.06	0.24	0.18	0.24 (0.24)	0.30 (0.33)	0.31 (0.34)	0.32	0.26	0.30	0.28	0.14	0.12
C8 [196]	0.28	0.18	0.53	0.39	0.11 (0.11)	0.77 (0.78)	0.76 (0.77)	0.79	0.33	0.53	0.53	0.33	0.29
C3 [392]	0.37	0.22	0.36	0.32	0.40 (0.40)	0.43 (0.45)	0.43 (0.45)	0.43	0.42	0.46	0.45	0.38	0.35
C14 [19]	0.24	0.17	0.40	0.31	0.07 (0.06)	0.41 (0.42)	0.45 (0.46)	0.52	0.36	0.65	0.54	0.54	0.42
C4 [329]	0.62	0.57	0.90	0.80	0.32 (0.32)	0.67 (0.68)	0.69 (0.70)	0.81	0.63	1.05	0.95	0.83	0.72
C18 [8]	2.38	2.26	2.37	2.25	2.10 (2.09)	2.30 (2.33)	2.34 (2.37)	2.37	2.36	2.73	2.43	2.57	2.21
C10 [65]	2.89	2.74	3.14	3.08	2.45 (2.45)	3.10 (3.13)	3.14 (3.18)	3.21	2.81	3.43	3.17	3.12	2.74
C9 [158]	2.92	2.85	2.94	2.78	2.69 (2.68)	2.89 (2.91)	2.92 (2.94)	3.00	3.04	3.39	3.16	3.26	2.94
C2 [539]	3.25	3.04	3.33	3.08	2.97 (2.96)	3.41 (3.39)	3.44 (3.43)	3.43	3.13	3.29	3.14	3.22	3.11
C17 [9]	3.59	2.94	3.48	3.14	3.20 (3.20)	3.54 (3.55)	3.57 (3.58)	3.65	3.48	3.86	3.48	3.55	3.18
C5 [314]	3.49	3.55	3.53	3.41	3.26 (3.25)	3.47 (3.51)	3.50 (3.55)	3.56	3.39	3.50	3.38	3.49	3.40
C11 [49]	3.30	3.18	3.56	3.38	3.15 (3.14)	3.48 (3.46)	3.50 (3.49)	3.59	3.71	4.17	3.99	3.91	3.68
C15 [18]	3.64	3.70	3.91	3.92	3.45 (3.44)	3.96 (4.00)	4.08 (4.12)	4.08	3.85	4.55	4.31	4.36	4.13
C13 [20]	4.91	4.44	4.96	4.57	4.45 (4.46)	4.83 (4.80)	4.84 (4.81)	4.95	4.75	5.14	4.91	4.92	4.70
VAR	0.04	0.05	0.04	0.03	0.08 (0.08)	0.05 (0.05)	0.05 (0.06)	0.07	0.02	0.14	0.04	0.04	0.00
|MAX.DEV|	0.50	0.50	0.40	0.34	0.69 (0.69)	0.47 (0.48)	0.47 (0.48)	0.50	0.30	0.69	0.43	0.38	0.00
MAD	0.16	0.17	0.17	0.13	0.21 (0.22)	0.18 (0.19)	0.18 (0.19)	0.21	0.10	0.32	0.18	0.17	0.00

---

As far as the GGA functionals are concerned, BLYP provides energies closer to the reference data than the revPBE functional with the maximum deviation below 1 kcal mol⁻¹ for both gas phase and solvent (Tables 3 and 4). Even though accuracy of the tested (meta-)GGAs is inferior to more elaborated hybrid and double-hybrid functionals (see below), their simpler exchange–correlation evaluation and the possibility of taking advantage of the RI approximation render them computationally noticeably more feasible. For that reason (o)TPSS and BLYP functionals with the def2-TZVPPD basis set and accompanied with the D3(BJ) dispersion correction represent a viable compromise between accuracy and computational demand. These methods can be recommended especially for preliminary conformational searches and calculations on much larger DNA model systems including several nucleotides.

Hybrid functionals

Another group of a higher Jacob's ladder rung incorporating a portion of an exact HF exchange interaction consists of three tested hybrid functionals: B3LYP, PW6B95 and MPW1B95. The PW6B95 and MPW1B95 functionals supplemented with the D3 term yield energies in tight accordance with the CBS(T)^HL benchmark. Both functionals have maximum and mean absolute deviations as low as ∼0.5 and ∼0.2 kcal mol⁻¹ (Tables 3 and 4), respectively, which renders them to be the methods of choice for calculations of electronic energies of the sugar–phosphate backbone. The performance of the B3LYP functional is somewhat inferior, with the maximum deviation being ∼0.7 kcal mol⁻¹ for both environments. The essential role of the dispersion correction is illustrated for the B3LYP functional (Table 5). While the maximum and mean absolute deviation for dispersion-corrected B3LYP in the gas phase is equal to 0.74 and 0.28 kcal mol⁻¹, respectively, pure (i.e., without the dispersion correction) B3LYP deviates markedly from the reference CBS(T)^HL energies with respective deviations being as high as 2.55 and 1.20 kcal mol⁻¹. The noticeable improvement upon D3 correction holds also for the COSMO environment.

Table 5 Performance of the B3LYP functional integrated using the m5 grid with and without D3(BJ) dispersion correction for the gas phase and the COSMO environment. Statistical descriptors VAR, |MAX.DEV|, and MAD refer to variance (kcal² mol⁻²), the absolute value of maximum deviation (kcal mol⁻¹), and mean absolute deviation (kcal mol⁻¹) compared to the CBS(T)^HL

Method	Environment	VAR	|MAX.DEV|	MAD
B3LYP	Gas phase	1.79	2.55	1.20
B3LYP-D3(BJ)		0.13	0.74	0.28
B3LYP	COSMO	1.25	2.00	1.00
B3LYP-D3(BJ)		0.08	0.69	0.21

---

While B3LYP appears to be insensitive to the size of the integration grid (difference between m5 and m4 grids being lower than 0.02 kcal mol⁻¹) in line with preceding studies,⁹² PW6B95 and MPW1B95 show slightly stronger grid size dependence. The relative energies calculated using the sparser m4 integration grid (Tables 3 and 4, values in parentheses) differ from the reference ones (m5) by less than 0.10 kcal mol⁻¹ for both PW6B95 and MPW1B95. Taking into account that the acceleration of a computation when a numerical quadrature grid is pruned from 590 (m5) to 434 (m4) spherical grid points is no more than ∼2% of the wall computational time, we encourage to use the denser m5 integration grid for all hybrid functionals. Even though from the current results the m5 grid might seem to be unnecessary, the magnitude of the numerical error is conformation-dependent and thus it cannot be guaranteed to be insignificant over the whole potential energy surface.

Double hybrid functionals, MP2/CBS and CBS(T)^LL

The last set of the most accurate and computationally challenging methods embraces PWPB95 and DSD-BLYP double hybrid functionals, extrapolated MP2(D,T) and MP2(T,Q) methods and composite CBS(T)^LL. Both double hybrids show a great correlation with the reference CBS(T)^HL gas phase results, with the maximum deviations of 0.56 and 0.20 kcal mol⁻¹ (Tables 3 and 4) for PWPB95 and DSD-BLYP, respectively. The mean absolute deviations of 0.21 and 0.07 kcal mol⁻¹ rank them among the most accurate methods within the current study. Especially the DSD-BLYP functional shows an astonishing agreement with the CBS(T)^HL and is the clear winner of this benchmark. Even though high computational costs prohibit its practical and widespread usage for systems of similar size as the SPS model and larger, D3 correction term complemented DSD-BLYP with the large quadruple-ζ basis set is the method of choice when highly accurate energies are demanded. Contrary to that PWPB95 can be superseded by considerably faster and equally accurate (o)TPSS meta-GGAs or PW6B95/MPW1B95 hybrids and thus its application seems to be rather ineffective for sugar–phosphate backbone model systems.

Although the MP2(D,T) performs rather well as it reaches chemical accuracy with maximum deviation of ∼0.7 kcal mol⁻¹ (Tables 3 and 4), it yields energies slightly inferior to the majority of DFT-D3 methods and is approximately of B3LYP-D3 quality. Note, however, that conclusions of our foregoing study²⁴ about the quality of MP2(D,T) are not in contradiction with the present findings. The difference between the preceding and present study reflects the tremendous improvement in DFT methodology, as the most advanced functionals and D3 dispersion correction were not used in the earlier study. When replacing MP2(D,T) by MP2(T,Q), both the maximum and mean absolute deviations of gas phase energies decrease approximately by a half to 0.43 kcal mol⁻¹ and 0.18 kcal mol⁻¹, respectively. As can be evidenced from both gas phase and COSMO results (Tables 3 and 4), performance of MP2(T,Q) is comparable to the CBS(T)^LL and thus enlargement of the one-electron space by considering the quadruple-ζ basis set effectively compensates for missing higher order excitations covered by the ΔCCSD(T) term.

CCSD(T) corrections

The ΔCCSD(T) calculations were carried out using the 6-31+G(d) and aug-cc-pVDZ basis sets (Table 6). There are two main conclusions that follow from the evaluated corrections. Firstly, the ΔCCSD(T) corrections are, to a good approximation, conformation-independent, in line with our earlier preliminary study.²⁴ The average relative values of the ΔCCSD(T) term, i.e. ΔΔCCSD(T), using the 6-31+G(d) and aug-cc-pVDZ basis sets are equal to 0.16 kcal mol⁻¹ and 0.18 kcal mol⁻¹ (Table 6), respectively. Note, that unlike the previous study²⁴ the current diverse benchmark set effectively covers the whole presently known biologically sampled DNA backbone conformational space, so that significance of the present results is markedly higher. Secondly, we show that ΔCCSD(T) energies are rather invariant to the number of basis functions, at least when going from 6-31+G(d) to aug-cc-pVDZ with the average difference below ∼0.05 kcal mol⁻¹ (Table 6). Thus, when ΔCCSD(T) corrections are required, the 6-31+G(d) basis set seems to be sufficient. It obviously cannot be ruled out that a larger basis set could still affect the results, but we consider this unlikely due to the evident insensitivity of the sugar–phosphate backbone energetics to the higher-order correlation correction, contrasting studies of molecular clusters.³⁷

Table 6 Relative ΔCCSD(T) gas phase corrections (kcal mol⁻¹) for 6-31+G(d) (BS1) and aug-cc-pVDZ (BS2) basis sets, C1 structure taken as the reference. The ΔΔ row denotes the absolute value of the difference between the first two lines, i.e. the basis set dependence of the ΔCCSD(T) corrections

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	C14	C15	C16	C17	C18
BS1	0.00	0.07	0.08	0.22	0.01	0.16	0.07	0.22	0.13	0.31	0.26	0.14	0.22	0.11	0.19	0.06	0.31	0.16
BS2	0.00	0.03	0.10	0.23	0.02	0.16	0.07	0.23	0.22	0.43	0.31	0.12	0.21	0.12	0.18	0.09	0.30	0.22
ΔΔ	0.00	0.04	0.02	0.01	0.01	0.00	0.02	0.01	0.09	0.12	0.05	0.02	0.01	0.01	0.01	0.03	0.01	0.06

---

The assessed performance of the tested methods is visualized in Fig. 2 and 3 for gas phase and COSMO results, respectively. As expected the quality of the density functionals as measured against CBS(T)^HL energies follows in general the Jacob's ladder scheme, i.e. GGA < meta-GGA < hybrids < double-hybrids. The B3LYP and PWPB95 slightly stick out as their performance corresponds rather to the respective lower-lying ladder rung. More specifically, while B3LYP and BLYP functionals are of similar quality, computational demands of the latter functional are significantly lower. The same holds for the PWPB95, which is substantially more demanding than comparably accurate PW6B95 and MPW1B95 hybrid functionals. Even though both B3LYP and PWPB95 yield reliable results with maximum deviation below 1 kcal mol⁻¹, computational inefficiency argues against their usage for comparison of the sugar–phosphate backbone conformational energies. We thus recommend to use BLYP and (o)TPSS functionals supplemented with D3(BJ) dispersion correction for fast exploratory calculations of the sugar–phosphate backbone model. When accurate relative energies are needed, e.g. for force field fitting purposes, we encourage applying PW6B95 and MPW1B95 hybrids supplied with the D3 term instead of the inferior MP2(D,T) level. In case higher precision is needed DSD-BLYP surpasses extrapolated MP2(T,Q) and CBS(T)^LL data as it provides closer agreement with the CBS(T)^HL at comparable time (vide infra) and hardware requirements. Similar trends can be observed also for COSMO calculations.

Fig. 2 Variance (black, kcal² mol⁻²), maximum (red, kcal mol⁻¹) and average (blue, kcal mol⁻¹) deviations of tested methods compared to the reference CBS(T)^HL gas phase results.

Fig. 3 Variance (black, kcal² mol⁻²), maximum (red, kcal mol⁻¹) and average (blue, kcal mol⁻¹) deviations of tested methods compared to the reference CBS(T)^HL COSMO results.

Calculations time demands

For DFT-D3 and MP2 methods a rough comparison of computational time demands is given in Table 7. Timing of the different methods differs by almost three orders of magnitude. CCSD(T) requirements are not included as the calculations were carried out on different computational architecture and thus unambiguous comparison cannot be done. The efficiency of the more accurate DSD-BLYP surpasses MP2(T,Q) and similarly the new D3-corrected hybrid functionals PW6B96 and MPW1B95 are clearly more efficient than MP2(D,T).

Table 7 Computational time ratios of selected DFT-D3 and MP2 methods as compared to the least demanding revPBE. Values for hybrid functionals correspond to the denser m5 integration grid. Basis sets labeled DZ, TZ1, TZ2, and QZ refer sequentially to aug-cc-pVDZ, def2-TZVPPD, aug-cc-pVTZ, and aug-cc-pVQZ. Contribution decomposition to SCF + PT2 (double-hybrids) or to different basis sets (MP2/CBS) is given in the parentheses. All calculations were carried out using Intel Xeon E5 CPUs at 2.00 GHz

Method	revPBE	BLYP	TPSS	oTPSS	B3LYP	MPW1B95	PW6B95	DSD-BLYP	PWPB95	MP2(D,T)	MP2(T,Q)
Basis set	TZ1	TZ1	TZ1	TZ1	TZ1	TZ1	TZ1	QZ	QZ	DZ and TZ2	TZ2 and QZ
Ratio	1.0	1.2	1.5	1.5	19.1	20.3	20.4	561.1 (557.6 + 3.5)	606.3 (602.9 + 3.4)	61.0 (5.6 + 55.4)	619.7 (55.4 + 564.3)

---

Molecular mechanics calculations

Molecular mechanics calculations were carried out both in the gas phase and solvent environment approximated by the Poisson–Boltzmann model using four different partial charges sets labeled AMBER, RESP, Mod.RESP, and Mod.RESP-MM (Table 8). The AMBER charge set was obtained by truncation and simple neutralization from the original force field. It is the worst set in the gas phase with maximum and mean absolute deviations being 8.76 kcal mol⁻¹ and 3.62 kcal mol⁻¹. However, it surprisingly outperforms the remaining charge sets for MM-PBSA calculations with the respective deviations from the benchmark being 4.66 kcal mol⁻¹ and 1.35 kcal mol⁻¹. Even though rough agreement with CBS(T)^HL for solvent was anticipated, the deviation of the gas phase energies is astonishing. The other three sets directly acquired by the standard and tightened RESP procedure for the SPS model (vide supra) provide comparable agreement with the CBS(T)^HL reference data with the maximum and mean absolute deviations ∼4 kcal mol⁻¹ and ∼1.5 kcal mol⁻¹. Considering CBS(T)^HL/COSMO energies, which span a rather narrow range of ∼6 kcal mol⁻¹ width, it is obvious that MM calculations with neither charge set satisfactorily reproduce the fine energy differences between distinct DNA backbone rotamers. Although it cannot be ruled out that the differences can be in future reduced by further tuning of the force field torsional parameters,^25,27–29 we suggest that a substantial part of the discrepancy is due to inherently neglected conformational polarization effects, which are known to be more pronounced in anionic systems. That would mean the uncertainty is inherent to the fixed-charge force field models. As emphasized elsewhere, the capability of refinements on pair-additive force fields with constant point atomic charges via tuning of the formally intramolecular torsional parameters is certainly not unlimited.⁹³ Considering that polar medium partially screens out electrostatic interactions, it might be anticipated that gas phase MM relative energies would be more sensitive to partial charges adjustments compared to MM-PBSA calculations. However, the present results give evidence that also MM-PBSA energies are highly responsive to charge variations. The performance of the non-polarizable force field is in our test substantially inferior to the QM methods and errors of the magnitude seen in our study are likely to affect DNA molecular dynamics simulations.^25,27–29

Table 8 Relative MM and reference CBS(T)^HL energies (kcal mol⁻¹) for the gas phase and the solvent environment. “Solvent” stands for MM-PBSA and COSMO for MM and QM calculations, respectively. Statistical descriptors VAR, |MAX.DEV|, and MAD refer to variance (kcal² mol⁻²), the absolute value of maximum deviation (kcal mol⁻¹), and mean absolute deviation (kcal mol⁻¹) compared to the CBS(T)^HL energies, respectively

Gas phase						Solvent
Label	AMBER	RESP	Mod.RESP	Mod.RESP-MM	CBS(T)^HL	Label	AMBER	RESP	Mod.RESP	Mod.RESP-MM	CBS(T)^HL
C16	−0.10	−0.04	0.49	0.11	−0.14	C16	−1.03	−0.79	−1.19	−0.25	−1.21
C1	0.00	0.00	0.00	0.00	0.00	C12	1.19	1.30	1.24	1.42	−0.58
C7	4.54	1.34	1.46	1.43	0.34	C7	−0.48	−0.44	0.41	0.30	−0.11
C14	5.20	1.91	1.49	1.74	0.56	C1	0.00	0.00	0.00	0.00	0.00
C3	1.02	−0.04	0.09	0.16	0.93	C6	−0.32	−0.03	0.34	0.04	0.12
C11	9.44	4.58	2.40	3.69	0.99	C8	1.37	1.62	2.16	2.52	0.29
C4	8.75	1.54	1.37	1.82	1.13	C3	0.16	0.04	−0.03	0.39	0.35
C6	1.47	0.36	0.66	−0.34	1.63	C14	0.46	0.65	0.55	1.10	0.42
C8	8.45	1.97	1.86	2.18	1.67	C4	1.74	0.74	1.68	1.69	0.72
C15	6.05	6.20	5.87	5.02	3.03	C18	3.23	4.73	3.88	4.73	2.21
C2	5.81	4.51	3.89	3.58	3.20	C10	5.52	6.47	7.05	7.28	2.74
C5	5.10	5.10	5.08	4.84	3.74	C9	4.08	5.15	5.05	5.76	2.94
C12	9.28	5.09	6.25	5.71	4.90	C2	4.05	4.00	3.66	4.07	3.11
C13	8.11	6.05	5.91	5.59	5.24	C17	7.84	7.86	7.35	8.16	3.18
C10	5.56	2.92	2.21	3.10	5.63	C5	4.55	4.66	4.40	4.94	3.40
C18	14.45	8.40	10.22	9.18	5.69	C11	6.51	5.94	5.50	6.44	3.68
C9	7.32	4.52	4.52	4.97	7.42	C15	2.34	2.53	2.62	3.20	4.13
C17	16.25	11.36	12.86	11.80	9.82	C13	6.33	6.11	6.40	6.12	4.70
VAR	22.23	3.43	4.04	2.93	0.00	VAR	3.15	3.81	3.60	5.00	0.00
|MAX.DEV|	8.76	3.59	4.53	3.49		|MAX.DEV|	4.66	4.68	4.31	4.98
MAD	3.62	1.51	1.59	1.43		MAD	1.35	1.48	1.46	1.76

---

Relative energies distribution

The distribution of the gas phase and COSMO CBS(T)^HL relative energies is plotted in Fig. 4. Note that energy distribution calculated in COSMO solvent is appreciably narrower than in the gas phase, which likely reflects the real conformational preferences.

Fig. 4 CBS(T)^HL relative energies (kcal mol⁻¹, with respect to C1 structure) histogram for gas phase (black) and COSMO (red) environment with fitted normal distributions. Bin width equals 1.0 kcal mol⁻¹.

As explained in detail elsewhere,⁴ the individual backbone geometries seen in the X-ray structures are affected by various kinds of data and refinement errors. Thus, many individual observed backbone conformations might be inaccurate or even entirely incorrect. This is the reason why the structures need to be processed by structural bioinformatics, which through statistical methods identifies real conformational families. Many individual backbone geometries then occur as outliers, which cannot be assigned to the established families. Some of them may still represent real structures missed by the bioinformatics due to their infrequent occurrence. On the other side, it cannot be ruled out that some families based on clusters with small numbers of the individual occurrences may be misleading. Definitely, some biologically relevant backbone conformations are missing in the current C1–C18 set, e.g. conformations emerging in structures difficult to crystalize or those, whose frequency of occurrence is too low to be statistically significant. Some examples are the additional auxiliary conformations A1–A6 discussed below. Nevertheless, the selected 18 conformations derived as described above are biologically significant and represent a wide range of real backbone substates of DNA. Since the database analysis was based on structures with 1.9 Å and better resolution, we do not anticipate that it contains any irrelevant or markedly unstable backbone substates. Nevertheless, one of the initial goals of our study was to try to identify potentially incorrect geometries, based on their unfavorable energies. However, we found out that such a task is rather complex and we decided to postpone it to some future studies. The reason is that the energy pattern in our dataset is pretty complex and the energies do not include the overall contexts in which the backbone substates occur. Therefore, it is impossible to establish any straightforward criteria that would unambiguously tag potentially incorrect geometries.

Biomolecular structures should in general sample geometries on a fine energetical scale of several kcal mol⁻¹. Thus, the existence of high-energy biologically significant DNA backbone conformations is not likely. Therefore, rather narrow distribution of conformational energies is expected, which is exactly what is observed when the backbone model systems are put in the continuum solvent. While the most unstable conformation in the gas phase (C17) is ∼9.8 kcal mol⁻¹ above canonical BI DNA, in the solvent environment it is only ∼3.2 kcal mol⁻¹ less stable than the reference. Note also the asymmetric relationship between structure and energy. While the existence of uncommon backbone substates of comparable intrinsic stability to the BI DNA conformation cannot be ruled out, it is much less likely to have a frequently occurring conformation to be intrinsically markedly unstable. Whereas all commonly populated substates (the number of identified dinucleotide steps N > 100, Table 1) are below ∼3.5 kcal mol⁻¹ in COSMO solvent, the BI conformation with α + 1/γ + 1 crankshaft motion (C9, N = 158) is more than twice less stable than canonical BI DNA in the gas phase (7.4 kcal mol⁻¹, Table 3). This substate is identified by structural bioinformatics without any doubt, so it is a very real structure. Based on the gas phase calculations only, i.e. without the solvent correction, the C9 conformation might be incorrectly regarded as too unstable to be adopted in DNA. Despite the fact that the average difference between the gas phase and COSMO CBS(T)^HL relative energies is equal to ∼2 kcal mol⁻¹ in absolute value, in the case of C17, C12, and C9 conformers the difference is 6.6, 5.5, and 4.5 kcal mol⁻¹ at the CBS(T)^HL level of theory, respectively. Also conformational energy ordering is dramatically changed upon inclusion of the continuum solvent (Tables 3 and 4). It is thus evident that inclusion of solvation effects, at least in an approximate continuum fashion, is essential when predictions about stability and conformational preferences of nucleic acids are made. Gas phase data cannot be used to discriminate unstable geometries of the backbone. In COSMO solvent, none of the geometries is unstable enough to be identified as suspicious.

It should be noted that in our dataset each rotameric family is represented just by a single geometry. It is possible that when investigating the PES around the calculated structures, more stable structures could be found. This is more likely to happen for rotameric families, where the bioinformatics clustering has been based on a smaller number of the individual occurrences. Therefore, from the biochemical point of view the energy ordering in the present study should be taken only as approximate. In addition, stability of the given backbone rotamer inside a particular DNA context may be decisively affected by its compatibility with the overall DNA architecture and interactions with DNA parts not included in the computations. Still, on average, more populated clusters tend also to be more stable intrinsically.

Auxiliary conformations

Since the 18 members set of DNA conformations apparently lacks statistically insignificant, yet biologically highly relevant backbone conformations, we also considered six auxiliary systems (A1–A6) we have identified in high resolution experimental structures and which are sufficiently dissimilar to any of the 18 identified conformers, although we did not calculate the CCSD(T) corrections. The MP2(T,Q) and MM energies evaluated in the gas phase and solvent medium are listed in Table 9. Note the rather big average difference between gas phase and solvent MP2(T,Q) relative energies amounting to ∼3.3 kcal mol⁻¹ (Table 9). This finding underlines the effect of the solvent environment, which reshuffles the predicted intrinsic conformational preferences.

Table 9 Relative MP2(T,Q) and MM energies (kcal mol⁻¹) of the auxiliary (A) conformations for the gas phase and the solvent environment compared to BI DNA (C1, in bold). “Solvent” stands for MM-PBSA and COSMO for MM and MP2(T,Q) calculations, respectively. Statistical descriptors VAR, |MAX.DEV|, and MAD refer to variance (kcal² mol⁻²), the absolute value of maximum deviation (kcal mol⁻¹), and mean absolute deviation (kcal mol⁻¹) compared to the MP2(T,Q) energies, respectively

Gas phase						Solvent
System	AMBER	RESP	Mod.RESP	Mod.RESP-MM	MP2(T,Q)	System	AMBER	RESP	Mod.RESP	Mod.RESP-MM	MP2(T,Q)
C1	0.00	0.00	0.00	0.00	0.00	C1	0.00	0.00	0.00	0.00	0.00
A1	6.63	6.32	7.08	6.78	3.64	A1	2.85	3.71	3.42	4.03	−0.26
A2	3.61	1.44	0.60	1.40	2.93	A2	3.05	3.97	2.94	4.06	0.69
A3	4.76	1.44	1.05	1.97	3.40	A3	3.04	3.77	3.70	4.10	−0.52
A4	12.57	9.79	11.37	10.57	7.41	A4	5.21	5.47	4.76	5.87	1.96
A5	12.98	7.72	9.97	8.57	5.84	A5	5.90	6.32	6.77	6.98	3.14
A6	2.54	4.11	3.62	3.57	0.92	A6	−0.24	0.42	0.73	0.99	−0.41
VAR	15.24	5.44	10.47	6.45	0.00	VAR	7.68	11.33	9.78	13.83	0.00
|MAX.DEV|	7.14	3.19	4.13	3.16		|MAX.DEV|	3.56	4.29	4.22	4.62
MAD	3.16	2.26	3.15	2.44		MAD	2.53	3.17	2.95	3.57

---

The MP2(T,Q) results show that highly non-canonical backbone substates are energetically quite feasible. It is well known that non-canonical backbone conformations may be particularly difficult for force fields.^90,94 This is in line with our MM calculations (Table 9), where the mean absolute deviations for the four partial charge sets are slightly below 3.0 kcal mol⁻¹, while for the most frequent DNA conformations (C1–C9 with N > 100, see Table 1) it is below 1.0 kcal mol⁻¹. Just as for the main set of backbone conformers, the “truncated” AMBER charges give worse results in the gas phase, but outperform sets of charges derived directly for our SPS model system in continuum solvent calculations. Note that the multimolecular RESP does not improve the agreement (Table 9). The MM-PBSA destabilization of the A1, A4, and A5 conformations may be partially due to the γ torsion, which is close to the trans region and is intentionally penalized by the parmbsc0 force field, in order to prevent B-DNA degradation.²⁶ It has been shown that the γ(t) penalty of parmbsc0 may be excessive in some other contexts.⁹⁵ We have to conclude that the simple point charge model has difficulties in describing the DNA backbone in a balanced manner, which do not seem to be easily resolvable. Note that when tuning the force field through the dihedral terms, we use formally intramolecular terms to effectively include incorrect or missing intermolecular contributions, which may limit transferability of the torsion potentials for different backbone families.

Note that while the 18 conformational families (structures C1–C18) are represented by exemplar geometries that are close to the respective cluster centers,⁵¹ the additional auxiliary geometries were just taken from some of the available X-ray structures without any bioinformatics processing. That is why we do not mix the two datasets. From the biochemical point of view, however, the A1–A6 geometries are by no means less significant. They were missed by the bioinformatics analysis only because of an insufficient number of i-DNA and antiparallel G-DNA X-ray structures with sufficient resolution in the database. The performance of density functionals with respect to MP2(T,Q) for the A1–A6 set is very similar to data for the C1–C18 data set (data not shown), so we suggest that the C1–C18 database is representative enough for benchmarking other computational methods.

Conclusions

The DNA sugar–phosphate backbone poses a challenging task even for present-day quantum chemistry methods. The ability to predict DNA backbone conformational preferences and the knowledge of backbone energetics are important for comprehension of the DNA structure and dynamics. It is also crucial for empirical force field calibration, as the sugar–phosphate backbone description represents one of the main obstacles in molecular modeling of nucleic acids. To gain insight into the intrinsic energetics of the DNA backbone and to address the performance of modern dispersion corrected DFT, SPS (sugar–phosphate–sugar, Fig. 1) models of 22 diverse backbone conformations sampling the complete presently known naturally populated DNA torsional space were studied both in the gas phase and continuum solvent. While 18 DNA backbone conformational families are taken from the bioinformatics literature,⁵¹ 6 additional conformations are suggested by us based on the inspection of X-ray structures of noncanonical DNA. The main results can be summarized as follows.

We provide a benchmark database of accurate structure–energy data for the DNA backbone, which can be used for assessment of other theoretical methods. The most accurate data are based on MP2/CBS extrapolation with aug-cc-pVTZ and aug-cc-pVQZ basis sets (MP2(T,Q)) supplemented by CCSD(T) correction with the aug-cc-pVDZ basis set (known in the literature as CBS(T) or estimated CCSD(T)/CBS level).

We propose a new simplified SPS (sugar–phosphate–sugar) model system that remediates spurious interactions biasing calculations with the previously used SPSOM (sugar–phosphate–sugar capped with methoxy groups at the 3′ and 5′ ends) model,²⁴ while still being sufficiently electronically complete. The SPS model is conceptually similar to the T3PS model system used by some other groups¹⁷ and discussed above (see Fig. 1).

The latest dispersion-corrected DFT methods are capable of achieving semi-quantitative or even quantitative accuracy for the conformational preference of the DNA backbone. The BLYP, TPSS, and oTPSS functionals augmented with the Grimme's D3 dispersion correction damped by the Becke–Johnson (BJ) method yield very good results close to the reference data. These methods could be recommended for preliminary calculations or geometry optimizations of the sugar–phosphate models and for computations on larger model systems. PW6B95 and MPW1B95 D3-corrected hybrids can be used to obtain even a higher accuracy, as these functionals provide already better results than MP2(D,T) CBS computation. The B3LYP-D3 method provides energies slightly inferior to the other tested methods. B3LYP shows clear integration grid size independence. Even though the PW6B95 and MPW1B95 results are approximately invariant to integration grid density we recommend to generally use the m5 grid for (double-)hybrid functionals. The expensive PWPB95 double-hybrid functional provides energies of comparable quality with PW6B95 and MPW1B96 hybrids and thus appears to be rather inefficient for backbone energies evaluations. Contrary to that the DSD-BLYP double-hybrid yields the most accurate energies as compared to the reference CBS(T)^HL data, however, high computational requirements make its common usage less attractive. Proof of an approximate basis set independence of ΔCCSD(T) corrections when going from 6-31+G(d) to aug-cc-pVDZ is given.

We demonstrate that force field calculations with constant point atomic charges are much less accurate than modern DFT-D3 methods and struggle to reproduce QM relative energies, especially when highly non-canonical backbone conformations are taken into account. In fact, the maximum deviations of MM relative energies are comparable to the energy range spanned by the different biochemically relevant backbone conformations. It confirms that the description of the backbone is a major limitation of MM modeling of nucleic acids. We tested several charge distributions but we were so far unable to substantially reduce the spread of the MM deviations from the reference data.

Finally we stress the importance of inclusion of the solvent environment, which modifies energetical ordering of backbone conformers and reduces the energy difference between the different rotamers. Obviously, both gas phase and condensed phase computations are valid, the latter, however, should be preferred if any suggestions regarding nucleic acids are made based on QM computations.

Acknowledgements

This work was supported by a research grant from the Grant Agency of the Czech Republic P208/11/1822. Institutional funding was provided by the Ministry of Education, Youth and Sports of the Czech Republic: This work was supported by the project “CEITEC – Central European Institute of Technology” (CZ.1.05/1.1.00/02.0068) from European Regional Development Fund, MSM6046137302, by “RCPTM – Regional Centre of Advanced Technologies and Materials” (CZ.1.05/2.1.00/03.0058) from European Regional Development Fund, and “RCPTM-TEAM” (CZ.1.07/2.3.00/20.0017, M.O., P.B., M.Z., P.J.) from the Operational Program Education for Competitiveness – European Social Fund. The present study was also financially supported by the South Moravian Centre for International Mobility within the framework of the “Brno PhD Talent” scholarship program.

References

1. S. Neidle, Principles of Nucleic Acid Structure, Elsevier, 2008.
2. C. R. Calladine and H. R. Drew, J. Mol. Biol., 1984, 178, 773–781.
3. R. E. Dickerson, Sci. Am., 1983, 249, 94–111.
4. J. Sponer, A. Mladek, J. E. Sponer, D. Svozil, M. Zgarbova, P. Banas, P. Jurecka and M. Otyepka, Phys. Chem. Chem. Phys., 2012, 14, 15257–15277.
5. C. Altona and M. Sundaralingam, J. Am. Chem. Soc., 1972, 94, 8205–8212.
6. A. V. Fratini, M. L. Kopka, H. R. Drew and R. E. Dickerson, J. Biol. Chem., 1982, 257, 4686–4707.
7. L. P. M. Orbons, G. A. Vandermarel, J. H. Vanboom and C. Altona, Nucleic Acids Res., 1986, 14, 4187–4196.
8. A. Jain, G. Wang and K. M. Vasquez, Biochimie, 2008, 90, 1117–1130.
9. F. A. Hays, J. Watson and P. S. Ho, J. Biol. Chem., 2003, 278, 49663–49666.
10. F. Stuhmeier, J. B. Welch, A. I. H. Murchie, D. M. J. Lilley and R. M. Clegg, Biochemistry, 1997, 36, 13530–13538.
11. S. Burge, G. N. Parkinson, P. Hazel, A. K. Todd and S. Neidle, Nucleic Acids Res., 2006, 34, 5402–5415.
12. K. Gehring, J. L. Leroy and M. Gueron, Nature, 1993, 363, 561–565.
13. K. Rippe and T. M. Jovin, Methods Enzymol., 1992, 211, 199–220.
14. D. Svozil, J. E. Sponer, I. Marchan, A. Perez, T. E. Cheatham III, F. Forti, F. J. Luque, M. Orozco and J. Sponer, J. Phys. Chem. B, 2008, 112, 8188–8197.
15. N. Foloppe and A. D. MacKerell, J. Phys. Chem. B, 1999, 103, 10955–10964.
16. N. Foloppe, L. Nilsson and A. D. MacKerell, Biopolymers, 2001, 61, 61–76.
17. A. D. MacKerell, J. Phys. Chem. B, 2009, 113, 3235–3244.
18. F. F. Wang, L. D. Gong and D. X. Zhao, THEOCHEM, 2009, 909, 49–56.
19. G. V. Palamarchuk, O. V. Shishkin, L. Gorb and J. Leszczynski, J. Biomol. Struct. Dyn., 2009, 26, 653–661.
20. V. I. Poltev, V. M. Anisimov, V. I. Danilov, T. Van Mourik, A. Deriabina, E. Gonzalez, M. Padua, D. Garcia, F. Rivas and N. Polteva, Int. J. Quantum Chem., 2010, 110, 2548–2559.
21. O. V. Shishkin, L. Gorb, O. A. Zhikol and J. Leszczynski, J. Biomol. Struct. Dyn., 2004, 22, 227–243.
22. O. V. Shishkin, L. Gorb, O. A. Zhikol and J. Leszczynski, J. Biomol. Struct. Dyn., 2004, 21, 537–553.
23. C. D. M. Churchill and S. D. Wetmore, Phys. Chem. Chem. Phys., 2011, 13, 16373–16383.
24. A. Mladek, J. E. Sponer, P. Jurecka, P. Banas, M. Otyepka, D. Svozil and J. Sponer, J. Chem. Theory Comput., 2010, 6, 3817–3835.
25. H. Ode, Y. Matsuo, S. Neya and T. Hoshino, J. Comput. Chem., 2008, 29, 2531–2542.
26. A. Perez, I. Marchan, D. Svozil, J. Sponer, T. E. Cheatham III, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829.
27. I. Yildirim, H. A. Stern, S. D. Kennedy, J. D. Tubbs and D. H. Turner, J. Chem. Theory Comput., 2010, 6, 1520–1531.
28. M. Zgarbova, F. J. Luque, J. Sponer, M. Otyepka and P. Jurecka, J. Chem. Theory Comput., 2012, 8, 3232–3242.
29. M. Zgarbova, M. Otyepka, J. Sponer, A. Mladek, P. Banas, T. E. Cheatham III and P. Jurecka, J. Chem. Theory Comput., 2011, 7, 2886–2902.
30. O. Guvench, S. N. Greene, G. Kamath, J. W. Brady, R. M. Venable, R. W. Pastor and A. D. Mackerell, J. Comput. Chem., 2008, 29, 2543–2564.
31. E. Hatcher, O. Guvench and A. D. MacKerell, J. Phys. Chem. B, 2009, 113, 12466–12476.
32. R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352.
33. K. L. Copeland, J. A. Anderson, A. R. Farley, J. R. Cox and G. S. Tschumper, J. Phys. Chem. B, 2008, 112, 14291–14295.
34. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
35. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
36. E. G. Hohenstein and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 878–886.
37. P. Jurecka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993.
38. M. S. Marshall, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2011, 135, 194102–194111.
39. J. Rezac, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438.
40. L. R. Rutledge and S. D. Wetmore, Can. J. Chem., 2010, 88, 815–830.
41. M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200–10207.
42. J. Sponer, P. Jurecka and P. Hobza, J. Am. Chem. Soc., 2004, 126, 10142–10151.
43. J. Sponer, P. Jurecka, I. Marchan, F. J. Luque, M. Orozco and P. Hobza, Chem.–Eur. J., 2006, 12, 2854–2865.
44. J. Sponer, M. Zgarbova, P. Jurecka, K. E. Riley, J. E. Sponer and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1166–1179.
45. S. Tsuzuki, M. Mikami and S. Yamada, J. Am. Chem. Soc., 2007, 129, 8656–8662.
46. J. Yang and M. P. Waller, J. Chem. Inf. Model., 2012, 52, 3255–3262.
47. Y. Zhao, N. Gonzalez-Garcia and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012–2018.
48. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154122.
50. P. Jurecka, J. Cerny, P. Hobza and D. R. Salahub, J. Comput. Chem., 2007, 28, 555–569.
51. D. Svozil, J. Kalina, M. Omelka and B. Schneider, Nucleic Acids Res., 2008, 36, 3690–3706.
52. V. N. Staroverov, G. E. Scuseria, J. M. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
53. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
54. A. Klamt, WIRES-Comput. Mol. Sci., 2011, 1, 699–709.
55. A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
56. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105–134115.
57. A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
58. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
59. F. Jensen, J. Chem. Theory Comput., 2010, 6, 2726–2735.
60. K. D. Sen, Chem. Phys. Lett., 1980, 74, 201–202.
61. H. B. Shore, J. H. Rose and E. Zaremba, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 15, 2858–2861.
62. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2005, 122, 184107–184113.
63. L. A. Cole and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 1265–1271.
64. Y. F. Guo and M. A. Whitehead, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 28–34.
65. K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–289.
66. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Rob, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Wallingford, 2003.
68. R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169.
69. A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
70. A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446.
71. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
72. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
73. J. Sponer, K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595–2610.
74. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIRES-Comput. Mol. Sci., 2012, 2, 242–253.
75. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
76. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
77. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
78. Y. K. Zhang and W. T. Yang, Phys. Rev. Lett., 1998, 80, 890–890.
79. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126.
80. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
81. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
82. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918.
83. S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808.
84. S. Grimme, J. Chem. Phys., 2006, 124, 034108–034123.
85. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
86. C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
87. D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Goetz, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cuii, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, AMBER 12, University of California, San Francisco, 2012.
88. L. J. W. Murray, W. B. Arendall, D. C. Richardson and J. S. Richardson, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13904–13909.
89. N. H. Campbell, D. L. Smith, A. P. Reszka, S. Neidle and D. O'Hagan, Org. Biomol. Chem., 2011, 9, 1328–1331.
90. M. Krepl, M. Zgarbova, P. Stadlbauer, M. Otyepka, P. Banas, J. Koca, T. E. Cheatham III, P. Jurecka and J. Sponer, J. Chem. Theory Comput., 2012, 8, 2506–2520.
91. C. H. Kang, I. Berger, C. Lockshin, R. Ratliff, R. Moyzis and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 11636–11640.
92. S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2010, 6, 395–404.
93. J. Sponer, X. Cang and T. E. Cheatham III, Methods, 2012, 57, 25–39.
94. P. Banas, D. Hollas, M. Zgarbova, P. Jurecka, M. Orozco, T. E. Cheatham III, J. Sponer and M. Otyepka, J. Chem. Theory Comput., 2010, 6, 3836–3849.
95. E. Fadrna, N. Spackova, J. Sarzynska, J. Koca, M. Orozco, T. E. Cheatham III, T. Kulinski and J. Sponer, J. Chem. Theory Comput., 2009, 5, 2514–2530.

---

Footnote

† Electronic supplementary information (ESI) available: List of exemplar dinucleotides, coordinates of the optimized SPS models, list of atomic charges used for MM calculations. See DOI: 10.1039/c3cp44383c

---