 Open Access Article
Open Access ArticleSymmetrisation schemes for global optimisation of atomic clusters
Mark T.
Oakley
a,
Roy L.
Johnston
a and
David J.
Wales
*b
aSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
bUniversity Chemical Laboratories, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: dw34@cam.ac.uk
First published on 14th January 2013
Abstract
Locating the global minima of atomic and molecular clusters can be a difficult optimisation problem. Here we report benchmarks for procedures that exploit approximate symmetry. This strategy was implemented in the GMIN program following a theoretical analysis, which explained why high-symmetry structures are more likely to have particularly high or particularly low energy. The analysis, and the corresponding algorithms, allow for approximate point group symmetry, and can be combined with basin-hopping and genetic algorithms. We report results for 38-, 75-, and 98-atom Lennard-Jones clusters, which are all multiple-funnel systems. Exploiting approximate symmetry reduces the mean time taken to locate the global minimum by up to two orders of magnitude, with smaller improvements in efficiency for LJ55 and LJ74, which correspond to simpler single-funnel energy landscapes.
1 Introduction
Locating the global minima of molecules with many degrees of freedom is one of the fundamental problems in computational chemistry. The optimisation of atomic or molecular clusters is a widely studied problem in this class. Clusters bound by the Lennard-Jones (LJ) potential represent a physically important set of systems, which have served as useful examples for benchmarking global optimisation algorithms. The LJ potential takes the form | (1) |
A wide range of global optimisation algorithms have been applied to Lennard-Jones clusters. These include basin-hopping,1–4 genetic algorithms,5–11 particle swarm optimisation,12,13 a random tunnelling algorithm,14 hierarchical global optimisation,15 immune algorithms,16 and dynamic lattice searching.17–21 Most of the clusters with fewer than 1000 particles have global minimum structures that comprise an icosahedral core surrounded by an incomplete shell of atoms. For the smaller Lennard-Jones clusters, these are relatively easy to locate with any reasonable method that includes the basin-hopping principle of steps between local minima.2,22,23 However, there are a few cases where the global minima are much more difficult to find with an unbiased search algorithm. These structures include a truncated octahedron for LJ38,24 tetrahedral symmetry for LJ98,3 and Marks decahedra for LJ75–7724 and LJ102–104,25 and the difficulty is due to the multiple-funnel nature of the corresponding energy landscapes.26–28 The funnel containing the icosahedral minima contains the majority of low-lying local minima, and is favoured by entropy, whereas the funnel containing the global minimum contains relatively few minima, and is separated from the structures based on icosahedral packing by a large potential energy barrier.26,29 These examples also provide useful benchmarks for sampling global thermodynamics in systems with broken ergodicity,27,30–32 and for rare event dynamics.33–38
In all of these difficult cases, the global minimum is more symmetrical than the icosahedral-based structures. It has been noted that structures with high (approximate) symmetry are expected to lie at the extremes of the potential energy distribution for local minima.28,39,40 A principle of maximum symmetry therefore exists, namely that global minima are likely to have higher (approximate) symmetry measures, as explained in Section 2. Procedures to exploit this observation were programmed in the GMIN global optimisation code by one of us (DJW) some years ago, but the methodology has not been described before. In the present report we explain how these tools are formulated and report benchmark results for several LJ clusters with multiple funnel landscapes.
The use of symmetry improves the performance of several stochastic search algorithms,13,41,42 either by choosing high-symmetry starting points for the search or by later imposition of symmetry. The best previous published results for optimisation of Lennard-Jones clusters involve particle swarm optimisation with symmetrical structures used to initialise the search.13 Lattice-based searches have also proved to be effective,8,9,19–21,43,44 so long as a lattice that supports the true global minimum structure is included in the analysis. The core orbits approach described in the present contribution does not assume any particular point group symmetry, but instead searches for approximate symmetry operations in a general way. It is therefore a symmetry-biased basin-hopping procedure, but accounts for approximate symmetry and is not biased towards any particular point group. Exploiting this general symmetry bias, which is justified by the principle of maximum symmetry (described in Section 2), greatly improves the efficiency of global optimisation for the cases considered. We show that this procedure performs well when combined with both basin-hopping and with a ‘Lamarckian’ genetic algorithm, where the fundamental steps are also between local minima.
2 The principle of maximum symmetry
Inspection of the point group symmetries for entries in the Cambridge Cluster Database45 supports the notion that global minima often have a significant number of symmetry elements. However, the symmetries identified in complex systems are usually only approximate.46–48 To explain the appearance of near-symmetry in low energy structures we must therefore look beyond previous results for balanced geometries49,50 and the epikernel principle proposed for systems subject to Jahn–Teller effects.51,52 Although a rigorous theory is not yet available, arguments based on an idealised analysis of contributions to the total potential energy remain strongly suggestive. Here we write the total energy as a sum over contributions from a many-body expansion, involving single atom, pairwise and three-body terms, etc. Where quantum mechanical states approach degeneracy we would write separate series for every term in the appropriate Hamiltonian matrix.Exact geometrical symmetry leads to exact duplications in the contributions to the total energy, while approximate symmetry leads to approximate duplications. These approximate duplications immediately provide a means to quantify the notion of near-symmetry. If the terms in the many-body expansion were drawn randomly from the same probability distribution then geometrical symmetry would be manifested as correlation. For alternative structures the distribution will actually vary. However, we would still expect the variance of the sum, which gives the total energy, to be larger when symmetry or near-symmetry is present. Symmetrical structures are then more likely to have particularly high or particularly low energy. Conversely, low-lying structures are more likely to exhibit symmetry.
More formally, denote the mean and variance of a variable, X, drawn from a probability distribution, p(X), as μ and σ2. The variance of a sum of N such variables, Xi, is then53
 | (2) |
 | (3) |
This analysis, and the empirical observations of symmetry in the Cambridge Cluster Database,45 provide the motivation for combining a symmetry bias with global optimisation. The present results, which demonstrate significant improvements in efficiency for difficult cases, without bias towards a particular point group, could be regarded as justification for the procedure. In fact, methods to quantify continuous symmetry measures have been used by Avnir and coworkers,54–59 and correlations have been found for a variety of physical properties.60,61
3 Exploiting approximate symmetry
Here we describe the procedures coded in GMIN62 to treat approximate symmetry using a core orbits (CO) analysis. An overview of this methodology, which was employed for most of the benchmarks, is provided first, followed by the details required for implementation. An alternative approach based on the continuous symmetry measures defined by Avnir and coworkers is then described briefly in Section 3.3. This scheme is also coded in GMIN.3.1 Overview of the core orbits symmetrisation
The basic approach used for most of the benchmarks reported in Tables 1 and 2 involves identification of the point group for a subcomponent (core) of the cluster, denoted![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core. We then analyse the complete structure in terms of orbits of
core. We then analyse the complete structure in terms of orbits of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core. The orbits of a point group are sets of symmetry equivalent objects, atoms in the current context, which map only amongst themselves under all operations of the group. The possible dimensions of these orbits correspond to the dimensions of subgroups of the point group, dimension hcore, which must therefore be integer divisors of hcore. The symmetry analysis used here as a global optimisation tool, involves the identification of orbits of
core. The orbits of a point group are sets of symmetry equivalent objects, atoms in the current context, which map only amongst themselves under all operations of the group. The possible dimensions of these orbits correspond to the dimensions of subgroups of the point group, dimension hcore, which must therefore be integer divisors of hcore. The symmetry analysis used here as a global optimisation tool, involves the identification of orbits of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core for atoms that lie outside the core region. The incomplete orbits that are not fully occupied by atoms are identified. Permutations of atoms outside the core to fill in the incomplete orbits are then considered as additional symmetry-based moves, which are followed by local minimisation in the usual basin-hopping framework. No symmetry constraints are imposed during the minimisations. This approach is therefore related to lattice-based approaches,8,9,17–21,43,44 but with sites defined by incomplete orbits of
core for atoms that lie outside the core region. The incomplete orbits that are not fully occupied by atoms are identified. Permutations of atoms outside the core to fill in the incomplete orbits are then considered as additional symmetry-based moves, which are followed by local minimisation in the usual basin-hopping framework. No symmetry constraints are imposed during the minimisations. This approach is therefore related to lattice-based approaches,8,9,17–21,43,44 but with sites defined by incomplete orbits of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core, which change throughout a run depending upon the current configuration.
core, which change throughout a run depending upon the current configuration.
| Sample size | Cluster size | Method | Mean first encounter time | ||
|---|---|---|---|---|---|
| Energy evaluations | Minimisations | cpu time/s | |||
| 100 | 38 | None | 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 493 |
1271 | 4.4 |
| 100 | 38 | CO symmetrisation | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 655 655 |
142 | 0.5 |
| 100 | 38 | CSM symmetrisation | 4369 | 34 | 0.2 |
| 100 | 55 | None | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 733 |
92 | 0.6 |
| 100 | 55 | CO symmetrisation | 9356 | 103 | 0.5 |
| 100 | 74 | None | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 569 |
329 | 3.5 |
| 100 | 74 | CO symmetrisation | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
281 | 2.2 |
| 10 | 75 | None | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345 345 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 178 |
596.3 |
| 20 | 75 | None | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177 177 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050 |
682.8 |
| 50 | 75 | None | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 315 315![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 542 |
54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 684 684 |
612.1 |
| 100 | 75 | None | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 648 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
688.7 |
| 10 | 75 | CO symmetrisation | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 272 272 |
343 | 3.9 |
| 20 | 75 | CO symmetrisation | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
377 | 4.6 |
| 50 | 75 | CO symmetrisation | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 640 |
322 | 4.2 |
| 100 | 75 | CO symmetrisation | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229 229 |
338 | 4.2 |
| 10 | 98 | None | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 702 702![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 521 |
677.7 |
| 20 | 98 | None | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825 825![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 389 389 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079 079 |
1070.9 |
| 50 | 98 | None | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 211 |
1193.9 |
| 100 | 98 | None | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 387 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 301 |
1314.3 |
| 10 | 98 | CO symmetrisation | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 905 |
385 | 11.4 |
| 20 | 98 | CO symmetrisation | 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 004 004 |
435 | 13.3 |
| 50 | 98 | CO symmetrisation | 108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 276 |
564 | 18.2 |
| 100 | 98 | CO symmetrisation | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753 753 |
563 | 18.5 |
| Cluster size | Symmetry method | Population | Mean first encounter time | ||
|---|---|---|---|---|---|
| Energy evaluations | Minimisations | cpu time/s | |||
| 38 | None | 20 | 404![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825 825 |
2885 | 16.5 |
| 38 | CO | 10 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 365 365 |
105 | 1.1 |
| 55 | None | 20 | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 059 |
329 | 2.9 |
| 55 | CO | 10 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 329 329 |
45 | 0.9 |
| 74 | None | 50 | 329![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 254 |
2561 | 36.1 |
| 74 | CO | 50 | 590![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 346 346 |
2218 | 76.5 |
| 75 | None | 100 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 515 515![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985 985![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 966 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 254![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 742 742 |
176![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 760.8 760.8 |
| 75 | CO | 5 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
296 | 11.3 |
| 98 | None | 100 | 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859 859 |
773![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645.2 645.2 |
| 98 | CO | 5 | 178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 651 651 |
555 | 33.6 |
This CO symmetry analysis involves four principal steps, which are summarised in Fig. 1, and outlined below. Full details are supplied in Section 3.2.
 | ||
| Fig. 1 Summary of the four principal steps involved in the core orbits symmetrisation scheme. | ||
An iterative procedure with a distance-dependent weighting to dampen the contributions of more distant atoms is applied first. The atoms are then sorted according to their distance from XCC, and the largest difference between successive values is located. The origin is translated to the centre of coordinates for the Xcore atoms in this core set before the gap. A full orbit analysis is then performed based on this new origin using the radial distances.
![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) , which is used in step (3) to define incomplete orbits.
, which is used in step (3) to define incomplete orbits.
![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) are applied to all the atoms outside the core to generate new orbits. Incomplete orbits, where one or more of the sites are not occupied by atoms, are identified for use in step (4).
are applied to all the atoms outside the core to generate new orbits. Incomplete orbits, where one or more of the sites are not occupied by atoms, are identified for use in step (4).
The core orbits symmetrisation analysis was conducted at intervals of Nsym basin-hopping steps. In fact, choosing Nsym = 1 proved to be the most efficient strategy for the clusters considered in the present work. In this case, each basin-hopping step is preceded by a set of quenches based on symmetrised structures. Random Cartesian displacements were employed in the basin-hopping moves, leaving core atoms unperturbed. If symmetry elements were diagnosed for the initial minimum, the Cartesian displacements were symmetrised to preserve the corresponding point group. Since the energy minimisation does not involve any constraints the core can change during these steps. The non-core atoms are perturbed in the basin-hopping moves and are unconstrained during minimisation, so the core can also change if a different set of core atoms is identified in the next step.
3.2 Details of the core orbits implementation
Here we provide details of the core orbits symmetrisation scheme. Readers who are more interested in the applications than in implementing the procedure can skip to Section 3.3. | (4) |
 | (5) |
The origin was then redefined using the centre of coordinates for the subset of atoms with increasing radii up to the largest radial gap. This analysis exploits the fact that atoms belonging to a particular orbit of the point group must lie at the same distance from the centre of coordinates. We denote the distance of atom α from XCC by dα. If the largest gap between sorted distances dα occurred between entries β and β + 1 then we set
 | (6) |
The point group symmetry will generally decrease as more orbits are included and Ncore increases. If no point group symmetry was detected then symmetrised moves were not attempted. Otherwise we focused on the group ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core, order hcore, for the largest number of core atoms, Ncore, that produced a point group beyond C1. The system was translated again so that the centre of coordinates for this core lay at the origin. All symmetry operations were then obtained in matrix form from the generators of
core, order hcore, for the largest number of core atoms, Ncore, that produced a point group beyond C1. The system was translated again so that the centre of coordinates for this core lay at the origin. All symmetry operations were then obtained in matrix form from the generators of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core.
core.
A significant improvement in performance was obtained by refining the 3 × 3 matrices, s, that specified the mapping of coordinates corresponding to point group operations. For each such matrix we calculated the action of S3Ncore on the current vector of coordinates, X, a column vector with 3Ncore elements corresponding to the Cartesian coordinates of atom 1, X1, then X2 corresponding to atom 2, etc.S3Ncore is the 3Ncore × 3Ncore matrix with Ncore copies of s along the diagonal, and zero entries elsewhere, so that
 | (7) |
 | (8) |
 | (9) |
 | (10) |
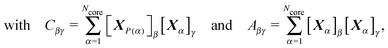 | (11) |
A similar procedure can be applied for all the group operations, but in practice it proved sufficient to ‘purify’ the generator operations according to the above least squares problem. New symmetry operations were identified by comparing the elements for each product matrix with those already known. At least one pair of corresponding matrix elements had to differ by a parameter δm for two operations to be considered distinct. All the point group operations were checked for consistency with the cutoff conditions for the Ncore atoms. The preservation or disappearance of the hcore symmetry operations was then tested for orbits outside the core in order of increasing atomic distance from XCC. This check was terminated if only the identity operation remained, and symmetry operations detected for the complete system were recorded. Any orbits that retained all the symmetry operations of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) core were added to the core, and Ncore adjusted accordingly. Symmetry operations preserved for the complete structure were used in subsequent geometry perturbations to produce symmetry-adapted steps, as described below.
core were added to the core, and Ncore adjusted accordingly. Symmetry operations preserved for the complete structure were used in subsequent geometry perturbations to produce symmetry-adapted steps, as described below.
Two more tolerance parameters were used to define the disappearance of symmetry operations for orbits outside the original Ncore atoms. The largest deviation between atomic positions corresponding to each site before and after the symmetry operation was found, and divided by the distance of this site from the centre of coordinates. If this ratio exceeded the dimensionless cutoff δ4 the symmetry operation was deemed to have been lost. Parameter δ5 is a distance threshold used to identify unoccupied sites in incomplete orbits of the point group. The transformed coordinates for each symmetry operation were compared with the original positions for each orbit outside the core. If a transformed position did not lie within a distance δ5 of any original position then this position was considered a missing site for the corresponding orbit. A distance check was performed to prevent missing sites appearing closer than δ5, and a further check caused the procedure to terminate if the number of missing sites reached 120 (the largest possible orbit size commonly encountered).
If symmetry elements were identified for the full structure, these were combined with the ones that were last lost when an orbit was added to make a set ![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) . If there were more than 50 such operations then we just considered the last ones to be lost and used them to generate the operations for a group,
. If there were more than 50 such operations then we just considered the last ones to be lost and used them to generate the operations for a group, ![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) . The symmetry operations of
. The symmetry operations of ![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) were used to define orbits in the next phase.
were used to define orbits in the next phase.
![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) to each floater atom to generate the corresponding orbit, removing duplicate sites according to the threshold parameter δ5. If the next floater lay in an orbit generated from a previous floater, it was skipped. New orbits should be guaranteed in this way because we check that each floater does not lie in any previous new orbits and we know it does not lie in any of the core sites.
to each floater atom to generate the corresponding orbit, removing duplicate sites according to the threshold parameter δ5. If the next floater lay in an orbit generated from a previous floater, it was skipped. New orbits should be guaranteed in this way because we check that each floater does not lie in any previous new orbits and we know it does not lie in any of the core sites.
If a newly generated orbit with dimension greater than one lay completely within the non-core set of atoms defined by the original structure, we moved these atoms to the core. If all the atoms ended up in the core we returned to the normal step-taking procedure and perturbed the coordinates of each atom in the usual way.
In the final phase of the symmetrisation scheme, starting point geometries for quenches were proposed by distributing the Nfloat atoms in configurations where any subset of the Norbits orbits generated from the floaters was precisely filled. To enumerate these possibilities we performed a convolution over the new orbits using a procedure analogous to the Beyer–Swinehart direct count algorithm for vibrational densities of states.64,65 Here a modification was required to prevent each orbit being occupied more than once in a given state, and the enumeration could terminate if we reach the maximum number of quenches allowed per symmetry analysis, defined by the input parameter Qmax.
To explain the orbit enumeration algorithm we consider r(i), the number of arrangements for i floater atoms that completely fill subsets of the Nfloat orbits. To calculate r(Nfloat) we also need to keep track of the occupation patterns for all states r(i) with i ≤ Nfloat. Let P(i,m,j) be one or zero, according to whether orbit j is occupied or not for state m, corresponding to a possible occupation pattern for i floater atoms. We also require sj, the size of orbit j, and  . The elements of r(i) and P(i,m,j) are initialised to zero for 1 ≤ i ≤ Nfloat, 1 ≤ m ≤ mmax, and 1 ≤ j ≤ Norbits. The parameter mmax specifies a maximum number of states to save for each number of floaters, to prevent memory overflow. We set σ1 = 0 and execute the following steps:
. The elements of r(i) and P(i,m,j) are initialised to zero for 1 ≤ i ≤ Nfloat, 1 ≤ m ≤ mmax, and 1 ≤ j ≤ Norbits. The parameter mmax specifies a maximum number of states to save for each number of floaters, to prevent memory overflow. We set σ1 = 0 and execute the following steps:
Quenches were then conducted for the configurations corresponding to the r(Nfloat) arrangements of floaters identified, up to a maximum of Qmax, and the lowest minimum encountered was recorded. The symmetry analysis was performed in this fashion every Nsym basin-hopping steps, before a modified coordinate perturbation and quench.
The standard step-taking scheme for basin-hopping in GMIN simply involves a perturbation to each Cartesian coordinate using a displacement chosen with uniform probability from the interval dmax × [−0.5,0.5]. The maximum displacement, dmax, is adjusted at regular intervals according to the number of steps accepted and rejected over the last interval and the target acceptance ratio. In the symmetrisation framework the core atoms identified in the most recent symmetry analysis were not perturbed. Furthermore, if symmetry operations were identified for the current structure then the perturbations were chosen to preserve these operations. The permutation P(α) for each atom α was identified for every symmetry operation. The initial random step, ΔX, was then symmetrised using the projection operator for the totally symmetric irreducible representation of the appropriate point group:
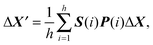 | (12) |
3.3 An alternative symmetrisation scheme
The alternative symmetrisation scheme coded in GMIN is based on the continuous symmetry measure (CSM) of Avnir and coworkers.54–59 The CSM for a given point group![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) , denoted S(
, denoted S(![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) ), is based on the distance from the current configuration to the closest geometry with symmetry
), is based on the distance from the current configuration to the closest geometry with symmetry ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) . The distance is calculated in 3N-dimensional space and defines the CSM as
. The distance is calculated in 3N-dimensional space and defines the CSM as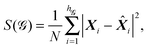 | (13) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0058_0302.gif) i are the points in the closest configuration with point group
i are the points in the closest configuration with point group ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) . The coordinates are initially scaled so that the largest distance from the origin is one, and hence 0 ≤ S(
. The coordinates are initially scaled so that the largest distance from the origin is one, and hence 0 ≤ S(![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) ) ≤ 1. Locating the points corresponding to the closest configuration can be achieved via a folding and unfolding procedure,54,56 or using an approach where the action of all the operations of
) ≤ 1. Locating the points corresponding to the closest configuration can be achieved via a folding and unfolding procedure,54,56 or using an approach where the action of all the operations of ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) on X are considered.66 The latter formulation was employed in the present work, as summarised below. Further details are given in the Appendix.
on X are considered.66 The latter formulation was employed in the present work, as summarised below. Further details are given in the Appendix.
![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) , are applied to the initial configuration, X, to obtain images, Yi. For each operation i, the permutation of atoms, P3N(i) that minimises the distance between X and Yi is obtained using the shortest augmenting path algorithm.67
, are applied to the initial configuration, X, to obtain images, Yi. For each operation i, the permutation of atoms, P3N(i) that minimises the distance between X and Yi is obtained using the shortest augmenting path algorithm.67
The CSM procedure is included here since it produced the fastest mean first encounter time for global optimisation of LJ38. However, the efficiency decreases rapidly with system size, probably because some atoms collapse towards the centre of coordinates or to the principal rotation axis in our current implementation. This collapse takes the system into higher symmetry regions of configuration space that are also higher in energy (see Section 2) and less likely to be productive for global optimisation. Further refinement of the CSM symmetrisation procedure may be possible in future work. For example, a hybrid method might combine the identification of approximate symmetry in a core of atoms, described in Section 3.1, with construction of the closest configuration for a given point group using the CSM. The core orbits scheme achieves symmetrised steps in configuration space by identifying and filling in incomplete orbits outside the core, while the CSM employs a folding and unfolding procedure. Exploiting these complementary approaches might therefore be productive.
4 Results
We have tested the performance of the symmetrisation routines in conjunction with the basin-hopping (BH) algorithm1,22,23 and the Birmingham Cluster Genetic Algorithm (GA).68 Both of these algorithms are implemented in the GMIN global optimisation program.62 The basin-hopping procedures in GMIN provide a variety of different step-taking and accept/reject strategies. In each case the overall procedure involves hops between local minima obtained following geometry optimisation after each structural perturbation.2 The minimisation step enables large moves in configuration space to be proposed and accepted, and effectively removes downhill barriers from the potential energy surface. Occupation probability distributions for structures corresponding to different morphologies are also broadened, which is important for multi-funnel potential energy landscapes.29,69 Similarly, the ‘Lamarckian’ genetic algorithm performs a local minimisation on all offspring and mutant structures before the selection step.We have evaluated the performance of the symmetrisation algorithms for three Lennard-Jones clusters with nonicosahedral global minima: LJ38, LJ75 and LJ98 (Fig. 2–4). We have also tested the symmetrisation algorithm on some clusters with global minima based on icosahedral packing. LJ55 is an interesting case because the Mackay icosahedron70 corresponds to a ‘magic number’ for a variety of clusters, and represents an easy global optimisation target. The global minimum for LJ74 is an icosahedral core surrounded by a incomplete shell of atoms, and is included as an example of a ‘typical’ Lennard-Jones cluster in this size range.
 | ||
| Fig. 2 Structures of the global minimum and lowest minimum based on icosahedral packing for LJ38. Atoms are coloured by distance from the centre of the cluster from dark (core) to light (surface). Atoms in the same orbit are the same shade. | ||
 | ||
| Fig. 3 Structures of the global minimum and lowest minimum based on icosahedral packing for LJ75. Atoms are coloured by distance from the centre of the cluster from dark (core) to light (surface). Atoms in the same orbit are the same shade. | ||
 | ||
| Fig. 4 Structures of the global minimum and lowest minimum based on icosahedral packing for LJ98. Atoms are coloured by distance from the centre of the cluster from dark (core) to light (surface). Atoms in the same orbit are the same shade. | ||
The performance of the search algorithms is measured by the mean time to the first encounter of the global minimum. Both search algorithms employ operators to restart searches that appear to have stagnated. These restarts ensure that, given enough time, all searches eventually find the global minimum. For most of the benchmarks, the mean times for the first encounter of the global minimum are recorded over 100 independent searches from random starting positions. When these clusters are analysed using the genetic algorithm without symmetrisation, the mean first encounter times are long enough that it is impractical to wait for 100 searches to complete. In these cases, we performed 25 searches capped at 5000 generations and calculated the mean first encounter time as the total time taken in all searches divided by the number of times the global minimum was found. Each optimisation run was performed on a single core of an Intel Xeon E5405 CPU with a clock speed of 2.0 GHz. We also report run times in terms of the number of minimisations and energy/gradient evaluations, both of which are independent of the processor used.
4.1 Basin-hopping
The basin-hopping algorithms in GMIN include an operator that restarts the search with a new random structure if there has been no improvement to the energy of the system after a fixed number of steps.71 This procedure is specified by the NEWRESTART keyword in GMIN. A larger value for this parameter produces more extensive local exploration of single funnels, whereas more frequent restarts favour the exploration of new regions of configurational space. The configuration of the lowest minimum encountered since the last reseeding is added to a cyclic taboo list,72 which is used to avoid revisiting regions that have recently been searched.71 This procedure is controlled by the AVOID keyword in GMIN, which specifies the length of the taboo list and the distance threshold, which triggers reseeding if the current minimum is too close to any member of the list. The metric employed here was the Euclidean distance in 3N-dimensional space, minimised with respect to overall translation, rotation, and permutation-inversion operations. This distance optimisation involves a shortest augmenting path algorithm, as described elsewhere.67 Standard procedures to move weakly bound or surface atoms1 were also employed; example input and output files will be made available from the Cambridge Cluster Database45 to ensure that our benchmarks are reproducible.For each test system we present results for the mean first-encounter time (MFET) averaged over 100 randomised starting points, where the atoms were randomly dispersed throughout a sphere of radius 3σ. The MFET exhibits a small dependence on the radius of this container, which should be accounted for in comparing different approaches. The initial coordinates will be included together with the other GMIN input and output files on the GMIN website, to facilitate future comparisons.
All BH runs were continued until the global minimum was encountered, to provide proper statistics. For LJ75 and LJ98Table 1 includes results for the mean first encounter time averaged over the first 10, 20 and 50 starting points. The averages exhibit significant fluctuations for sample sizes of 10 and 20, and could be somewhat misleading, particularly for the runs that do not use symmetrised moves. The values obtained for 100 random starting points are probably sufficient to produce useful statistics for comparison between different methods, while the results for a sample size of 50 provide a reasonable guide. The discussions below will focus on the averages obtained over 100 runs.
The truncated octahedral global minimum LJ38 is the easiest of the examples involving multiple-funnel potential energy landscapes. Without the use of symmetrisation, BH requires 1271 minimisations to find the global minimum, which corresponds to 4.4 s of cpu time (Table 1). Using the core orbits symmetrisation approach reduces this effort to 142 minimisations in 0.5 s, while the CSM symmetrised moves lower these values to 34 minimisations and 0.2 s. However, this system is the only one of the three multi-funnel landscapes considered where the CSM approach is competitive. We aim to investigate the CSM framework further in future work.
The basin-hopping results starting from random geometries without symmetrised moves involve a factor of 60 fewer steps than reported elsewhere for basin-hopping schemes.73 The origin of this discrepancy presumably lies within the details of the different implementations. The mean number of local minimisations without symmetrised moves is about the same as for a basin-hopping framework based on molecular dynamics moves with feedback and escape steps.11 The mean number of function calls reported in the latter work is about 774![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, while the number of energy/gradient evaluations in the present work is about 185
000, while the number of energy/gradient evaluations in the present work is about 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Table 1). These results are likely to reflect the performance of the minimisation algorithms employed. Using order parameters based on common neighbour analysis74 can improve on unbiased basin-hopping by about a factor of four for LJ38. Differences in performance of less than an order of magnitude are probably not very significant, since additional tuning for specific systems can usually produce improvements on this scale. However, combining some of these approaches with symmetrised moves might result in still faster hybrid schemes.
000 (Table 1). These results are likely to reflect the performance of the minimisation algorithms employed. Using order parameters based on common neighbour analysis74 can improve on unbiased basin-hopping by about a factor of four for LJ38. Differences in performance of less than an order of magnitude are probably not very significant, since additional tuning for specific systems can usually produce improvements on this scale. However, combining some of these approaches with symmetrised moves might result in still faster hybrid schemes.
Without symmetrised steps it requires an average of 6.2 × 104 minimisations, corresponding to 902.6 s of cpu time, to locate the decahedral global minimum of LJ75. Reseeding the search if there is no improvement in the energy after around 70 basin-hopping steps is the optimum strategy here. Using symmetrisation reduces the mean first encounter time by over two orders of magnitude to 4.2 s. The global minimum of LJ98 with tetrahedral symmetry requires a similar computational effort without symmetrisation, requiring an average of 4.8 × 104 basin-hopping steps, corresponding to 1314.3 s of cpu time. The optimal value for the minimum reseeding interval is about 100 BH steps. With symmetrisation, the mean first encounter time is 18.5 s, which is a 70-fold improvement. These mean first encounter times for LJ75 and LJ98 with symmetrised moves correspond to much smaller minimum reseeding intervals of 5 and 10 BH steps, respectively. In general, we would expect this parameter to scale roughly with the average number of BH steps required to locate the global minimum.
For LJ55 the global minimum is located rapidly whether symmetrisation is used or not. When using symmetrisation the optimal value for the NEWRESTART parameter is around 60 within the GMIN setup employed. The mean first encounter times are comparable to the 100 to 200 basin-hopping steps required by other optimisation algorithms.2,11,13 For LJ74 the mean first encounter times are optimised for NEWRESTART values of around 75 and 90 BH steps with and without symmetrisation, respectively. Symmetrisation produces a speedup of about 50% in this case, which is much less significant than for the multiple-funnel landscapes corresponding to LJ38, LJ75 and LJ98.
The use of symmetrisation generally provides between one and two orders of magnitude increase in efficiency for the multifunnel cases and can provide a modest improvement for simpler landscapes. A longer interval between possible reseeding operations works best if symmetrised moves are not used. If the global minimum is not known in advance then a larger value for this parameter is probably advisable.
4.2 Genetic algorithm
The GA considered here uses one of two versions of the Deaven–Ho cut and splice method to generate offspring.5 The first, as used in previous optimisations of Lennard-Jones clusters,11,75 is to cut along a plane passing through the centre of the cluster and splice two equally sized fragments. In the second, the plane does not have to pass through the centre of the cluster, allowing splicing between two unevenly-sized spherical caps. The second strategy is optimal for all searches except for the non-symmetrised searches on LJ38. Mutants are constructed by duplicating an existing parent or offspring structure and displacing each Cartesian coordinate of every atom by a distance <dmax.The genetic algorithm is elitist, with the parent structures remaining in the population until they are replaced by more stable offspring or mutant structures. Thus, the fitness of the worst member of the population always improves or remains the same after every generation. A duplicate predator is employed to maintain the diversity of the population.76 If a generation of the GA leads to no improvement in the mean energy of the population the search has stagnated. When this situation occurs, a new population of random structures is generated and a new epoch begins. No information is transferred from one epoch to the next and each epoch is effectively an independent search. The efficiency of the GA is affected by the size of the population. We have performed searches with population sizes of 5, 10, 20, 50 and 100 individuals and the optimum population for each search is shown in Table 2.
The fastest published optimisations of LJ38 with a genetic algorithm took 2000 energy minimisations.75 Our non-symmetrised GA requires an average of 2884 minimisations to locate the global minimum, which is comparable to these results. Symmetrisation of the GA reduces the required search time by a factor of approximately ten (Table 2). The global minimum of LJ55 is rapidly located without any symmetrisation, requiring 324 minimisations. This result is improved to 45 minimisations when symmetrisation is used. For both of these clusters, the time needed for the symmetrised GA is similar to that for symmetrised basin-hopping. For LJ74, symmetrisation leads to little change in the number of energy minimisations required to locate the global minimum. Of the clusters in this study, this is the only one where the symmetrised GA is substantially slower than symmetrised BH.
The global minimum of LJ75 is known to be relatively difficult to locate with a GA,11 and we only find it in one of the 25 runs of the non-symmetrised GA. This result represents one hit in 2000 independent epochs of the GA requiring a total of 49 hours of cpu time. Hartke's evolutionary algorithm,7 which employs the concept of niches to maintain the population diversity, is the most successful algorithm of this class for LJ75. The niches are based on the surface coverage for two-dimensional projections of the cluster structure. This method tends to add clusters with different symmetries into the population, which is clearly advantageous for this system. When symmetrisation is included in the GA, the mean first encounter time drops to 11.3 s, which is about three times longer than the symmetrised basin-hopping result. The fastest searches for LJ75 are obtained with a population size of five. However, the mean first encounter time is not very sensitive to the population size and searches with 100 members are slower by a factor of less than two.
Without symmetrisation, the GA performs better on optimisation of LJ98 than for LJ75, but still only locates the global minimum in 12/25 searches. This result corresponds to one hit in every 77 epochs, requiring an average of 5 hours of cpu time. With symmetrisation, the mean first encounter times are similar to the results for symmetrised basin-hopping. As with LJ75, the fastest searches were obtained with a population size of five, but searches with larger populations are not much slower.
The fastest published optimisation of the high-symmetry Lennard-Jones clusters of which we are aware was obtained by the CALYPSO particle swarm optimisation algorithm.13 The benchmarks presented here represent a small improvement over CALYPSO for the optimisation of LJ38 (600 minimisations), and a larger improvement for the optimisation of LJ75 (2900 minimisations). Both the symmetrised basin-hopping and genetic algorithms locate the global minimum of LJ98 with an average run time well under a minute without failures, whereas CALYPSO only found this structure in 3/10 reported attempts.13
5 Conclusions
The use of approximate symmetry substantially improves the efficiency of global optimisation for the atomic clusters we have considered with multifunnel potential energy surfaces.26–28 Here we have exploited the principle of maximum symmetry28,39,40 to bias the searches towards geometries with a higher symmetry measure, defined in terms of a cluster core. This theory is outlined in Section 2, and explains why symmetrised moves provide a more productive way to explore the configuration space. The bias is general, and not specific to a particular point group for the core orbits procedure, which corresponds to most of the benchmarks we have presented. This approach involves a number of additional parameters, mostly related to geometrical cutoffs, but these are likely to be relatively transferable between related systems.For LJ38, symmetrisation reduces the time required to find the global minimum by more than a factor of ten. For LJ75 and LJ98 basin-hopping searches that do not use the symmetrisation algorithm require an average of around 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 50
000 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps for 100 random starting points, and searches using the GA take much longer. When symmetrisation is used, the global minima of both clusters are located about 85 and 180 times faster for LJ98 and LJ75, respectively, corresponding to 563 and 338 BH steps, on average. For clusters with simpler energy landscapes, such as LJ55 and LJ74, symmetrisation provides more modest improvements in run time. In systems with global minima that have no exact symmetry elements the likely speedup will depend on the complexity of the underlying landscape, and the degree of approximate symmetry. Further tests will be needed to gauge these effects in future work, but our results for LJ74 suggest that the core orbits procedure will generally be beneficial, even for global minima without any formal symmetry.
000 steps for 100 random starting points, and searches using the GA take much longer. When symmetrisation is used, the global minima of both clusters are located about 85 and 180 times faster for LJ98 and LJ75, respectively, corresponding to 563 and 338 BH steps, on average. For clusters with simpler energy landscapes, such as LJ55 and LJ74, symmetrisation provides more modest improvements in run time. In systems with global minima that have no exact symmetry elements the likely speedup will depend on the complexity of the underlying landscape, and the degree of approximate symmetry. Further tests will be needed to gauge these effects in future work, but our results for LJ74 suggest that the core orbits procedure will generally be beneficial, even for global minima without any formal symmetry.
The performance of symmetrised basin-hopping and the symmetrised GA are comparable, and both locate the nonicosahedral global minima significantly faster than other unbiased algorithms. We would expect the same improvement for basin-hopping variants that include the critical minimisation phase, but employ alternative step-taking or accept/reject procedures.11,43,73,77–81
Appendix: details of the CSM-based symmetrisation approach
CSM step (1)
For a given target point group,![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) , dimension h
, dimension h![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) , we first construct the images of the 3N-dimensional scaled coordinate vector, Y(i) = S3N(i)X, for each point group operation, i. Matrix representations of the operations were programmed as data for all the standard point groups. For each image vector Y(i) the shortest augmenting path algorithm was then applied to find the permutation that minimised the distance to X,67 which we can represent by the matrix P3N(i).
, we first construct the images of the 3N-dimensional scaled coordinate vector, Y(i) = S3N(i)X, for each point group operation, i. Matrix representations of the operations were programmed as data for all the standard point groups. For each image vector Y(i) the shortest augmenting path algorithm was then applied to find the permutation that minimised the distance to X,67 which we can represent by the matrix P3N(i). ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0058_0302.gif) i was then calculated as
i was then calculated as | (14) |
![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) is the dimension of group
is the dimension of group ![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) . In fact, the shape measure S(
. In fact, the shape measure S(![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) ) will only agree with the distance calculated from the folding/unfolding procedure54,56 for a particular subset of the possible permutations.66 The unrestricted permutational minimisation of the distance to X for each operation was employed in the present work in the absence of an efficient scheme for constrained optimisation. This approach is sufficient to provide more symmetrical candidate structures for global optimisation. However, it did not prove to be competitive with the core orbits approach for the larger clusters considered in the present work.
) will only agree with the distance calculated from the folding/unfolding procedure54,56 for a particular subset of the possible permutations.66 The unrestricted permutational minimisation of the distance to X for each operation was employed in the present work in the absence of an efficient scheme for constrained optimisation. This approach is sufficient to provide more symmetrical candidate structures for global optimisation. However, it did not prove to be competitive with the core orbits approach for the larger clusters considered in the present work.
CSM step (2)
Fixing the permutations, P3N(i), the CSM was then minimised with respect to the orientation of the original configuration, X, treating the N atoms as a rigid body. Angle-axis coordinates were used to describe the orientation of X, and analytic first derivatives with respect to the three angular variables were employed. Here we exploited the same framework described in our recent investigations of coarse-grained models that treat decorated rigid bodies within the angle-axis framework.82,83 Minimisation in this three-dimensional space was achieved with a modified version of the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm,84,85 which is the same technique employed for all the other geometry optimisations in the present work. Our implementation therefore uses point group operations referred to a fixed reference frame, and rotates the coordinates X to minimise S(![[capital G, script]](https://www.rsc.org/images/entities/i_char_e112.gif) ), rather than transforming the operations themselves.
), rather than transforming the operations themselves.
CSM step (3)
The CSM value that results from the optimisation described above corresponds to a local minimum with respect to the orientation of the initial configuration for a fixed set of permutation matrices, P3N(i). To find the lowest possible CSM we implemented a separate basin-hopping procedure, taking steps in the angle-axis variables that define the orientation of the initial configuration, X. The optimal permutations were recalculated after these displacements, and the CSM minimised again in this three-dimensional space. Here we accepted downhill moves only3 for a maximum number of basin-hopping steps, terminating if the CSM fell below a value of 10−6.CSM step (4)
The rotation matrix, c, corresponding to the orientation of X with the lowest CSM value was then used to construct an average geometry as | (15) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0058_0302.gif) , was then rescaled to undo the distance normalisation used to define the CSM, and taken as the starting point for a fixed number of basin-hopping steps, NCSM, in the full Cartesian coordinate space, accepting only downhill moves in energy.3 This phase of local optimisation of the energy serves to relax the structure specified by
, was then rescaled to undo the distance normalisation used to define the CSM, and taken as the starting point for a fixed number of basin-hopping steps, NCSM, in the full Cartesian coordinate space, accepting only downhill moves in energy.3 This phase of local optimisation of the energy serves to relax the structure specified by ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0058_0302.gif) , which may correspond to a high energy configuration. Local relaxation is required because the averaging procedure that minimises the CSM and defines
, which may correspond to a high energy configuration. Local relaxation is required because the averaging procedure that minimises the CSM and defines ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0058_0302.gif) allows atoms to collapse towards the principal rotation axis, or to the origin, which can result in unphysically small interatomic distances. The lowest minimum obtained at the end of this phase specifies the proposed move for the CSM symmetrisation procedure implemented in the present work.
allows atoms to collapse towards the principal rotation axis, or to the origin, which can result in unphysically small interatomic distances. The lowest minimum obtained at the end of this phase specifies the proposed move for the CSM symmetrisation procedure implemented in the present work.
The collapse of atoms towards symmetry axes or the origin in the above procedure arises when points do not occur in sets that match the dimensions of orbits of the chosen point group. Our averaging procedure then results in orbits of dimension one. Nevertheless, CSM symmetrisation provides the most efficient scheme for the LJ38 cluster (using point group Ci). For the larger systems considered we have not yet been able to locate effective parameters, and the CSM results are not competitive. It may be necessary to implement a constrained permutational optimisation, and change the averaging to avoid collapse of atoms from incomplete orbits, for the CSM symmetrisation to prove effective in larger systems.
Acknowledgements
We acknowledge the Engineering and Physical Sciences Research Council, UK (EPSRC) for funding under Programme Grant EP/I001352/1. The calculations described in this paper were performed using the University of Birmingham's BlueBEAR HPC service, which was purchased through HEFCE SRIF-3 funds (see http://www.bear.bham.ac.uk). DJW is grateful to Prof. John Stanton for his original help with the point group symmetry routines and to Prof. Stefan Goedecker for helping to clarify the performance of algorithms described in previous work.11,73References
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS.
- R. H. Leary and J. P. K. Doye, Phys. Rev. E, 1999, 60, R6320–R6322 CrossRef CAS.
- R. H. Leary, J. Global Opt., 2000, 18, 367–383 CrossRef.
- D. M. Deaven, N. Tit, J. R. Morris and K. M. Ho, Chem. Phys. Lett., 1996, 256, 195–200 CrossRef CAS.
- M. D. Wolf and U. Landman, J. Phys. Chem. A, 1998, 102, 6129–6137 CrossRef CAS.
- B. Hartke, J. Comput. Chem., 1999, 20, 1752–1759 CrossRef CAS.
- D. Romero, C. Barrón and S. Gómez, Comput. Phys. Commun., 1999, 123, 87–96 CrossRef CAS.
- Y. Xiang, H. Jiang, W. Cai and X. Shao, J. Phys. Chem. A, 2004, 108, 3586–3592 CrossRef CAS.
- X. Shao, Y. Xiang and W. Cai, Chem. Phys., 2004, 305, 69–75 CrossRef CAS.
- S. E. Schönborn, S. Goedecker, S. Roy and A. R. Oganov, J. Chem. Phys., 2009, 130, 144108 CrossRef.
- S. T. Call, D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 1177–1186 CrossRef CAS.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef.
- H. Jiang, W. Cai and X. Shao, Phys. Chem. Chem. Phys., 2002, 4, 4782–4788 RSC.
- S. V. Krivov, Phys. Rev. E, 2002, 66, 025701 CrossRef.
- X. Shao, L. Cheng and W. Cai, J. Chem. Phys., 2004, 120, 11401–11406 CrossRef CAS.
- X. Shao, L. Cheng and W. Cai, J. Comput. Chem., 2004, 25, 1693–1698 CrossRef CAS.
- X. Yang, W. Cai and X. Shao, J. Comput. Chem., 2007, 28, 1427–1433 CrossRef CAS.
- L. Cheng, W. Cai and X. Shao, ChemPhysChem, 2007, 8, 569–577 CrossRef CAS.
- X. Shao, X. Yang and W. Cai, J. Comput. Chem., 2008, 29, 1772–1779 CrossRef CAS.
- X. Wu, W. Cai and X. Shao, Chem. Phys., 2009, 363, 72–77 CrossRef CAS.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611 CrossRef CAS.
- Z. Li and H. A. Scheraga, THEOCHEM, 1988, 179, 333 CrossRef.
- J. P. K. Doye, D. J. Wales and R. S. Berry, J. Chem. Phys., 1995, 103, 4234–4249 CrossRef CAS.
- J. P. K. Doye and D. J. Wales, Chem. Phys. Lett., 1995, 247, 339–347 CAS.
- D. J. Wales, M. A. Miller and T. R. Walsh, Nature, 1998, 394, 758–760 CrossRef CAS.
- J. P. K. Doye, M. A. Miller and D. J. Wales, J. Chem. Phys., 1999, 110, 6896–6906 CrossRef CAS.
- D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, 2003 Search PubMed.
- J. P. K. Doye, D. J. Wales and M. A. Miller, J. Chem. Phys., 1998, 109, 8143–8153 CrossRef CAS.
- J. P. Neirotti, F. Calvo, D. L. Freeman and J. D. Doll, THEOCHEM, 2000, 112, 10340–10349 CAS.
- F. Calvo, J. P. Neirotti, D. L. Freeman and J. D. Doll, J. Chem. Phys., 2000, 112, 10350–10357 CrossRef CAS.
- D. D. Frantz, J. Chem. Phys., 2001, 115, 6136–6157 CrossRef CAS.
- M. A. Miller, J. P. K. Doye and D. J. Wales, J. Chem. Phys., 1999, 110, 328–334 CrossRef CAS.
- D. J. Wales, Mol. Phys., 2002, 100, 3285–3305 CrossRef CAS.
- D. J. Wales, Mol. Phys., 2004, 102, 891–908 CrossRef CAS.
- G. Adjanor, M. Athenes and F. Calvo, Eur. Phys. J. B, 2006, 53, 47–60 CrossRef CAS.
- F. Calvo, Phys. Rev. E, 2010, 82, 046703 CrossRef CAS.
- M. Picciani, M. Athenes, J. Kurchan and J. Tailleur, J. Chem. Phys., 2011, 135, 034108 CrossRef.
- D. J. Wales, Chem. Phys. Lett., 1998, 285, 330–336 CrossRef CAS.
- D. J. Wales, Chem. Phys. Lett., 1998, 294, 262 CrossRef CAS.
- S. E. Wheeler, P. v. R. Schleyer and H. F. Schaefer, J. Chem. Phys., 2007, 126, 104104 CrossRef.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef.
- L. Cheng, Y. Feng, J. Yang and J. Yang, J. Chem. Phys., 2009, 130, 214112 CrossRef.
- X. Lai, R. Xu and W. Huang, Sci. China: Chem., 2011, 54, 985–991 CrossRef CAS.
- D. J. Wales, J. P. K. Doye, A. Dullweber, M. P. Hodges, F. Y. Naumkin, F. Calvo, J. Hernández-Rojas and T. F. Middleton, The Cambridge Cluster Database, URL http://www-wales.ch.cam.ac.uk/CCD.html, 2001.
- S.-J. Chen and K. A. Dill, J. Chem. Phys., 1996, 104, 5964 CrossRef CAS.
- M. E. Kellman, J. Chem. Phys., 1996, 105, 2500 CrossRef CAS.
- K. Yue and K. Dill, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 146 CrossRef CAS.
- J. Leech, Mathematical Gazette, 1957, 41, 81 CrossRef.
- D. J. Wales, J. Am. Chem. Soc., 1990, 112, 7908–7915 CrossRef CAS.
- A. Ceulemans, D. Beyens and L. G. Vanquickenborne, J. Am. Chem. Soc., 1984, 106, 5824 CrossRef CAS.
- A. Ceulemans and L. G. Vanquickenborne, Struct. Bonding, 1989, 71, 125 CrossRef CAS.
- J. Pitman, Probability, Springer-Verlag, New York, 1993 Search PubMed.
- H. Zabrodsky, S. Peleg and D. Avnir, J. Am. Chem. Soc., 1992, 114, 7843 CrossRef CAS.
- P. W. Fowler, Nature, 1992, 360, 626 CrossRef.
- H. Zabrodsky, S. Peleg and D. Avnir, J. Am. Chem. Soc., 1993, 115, 8278 CrossRef CAS.
- H. Zabrodsky, S. Peleg and D. Avnir, J. Am. Chem. Soc., 1993, 115, 11656 CrossRef CAS.
- H. Zabrodsky and D. Avnir, J. Am. Chem. Soc., 1995, 117, 462 CrossRef CAS.
- O. Katzenelson, H. Zabrodsky Hel-Or and D. Avnir, Chem.–Eur. J., 1996, 2, 174 CrossRef CAS.
- V. Buch, E. Gershgoren, H. Zabrodsky Hel-Or and D. Avnir, Chem. Phys. Lett., 1995, 247, 149 CrossRef CAS.
- D. R. Kanis, J. S. Wong, T. J. Marks, M. A. Ratner, H. Zabrodsky, S. Keinan and D. Avnir, J. Phys. Chem., 1995, 99, 11061 CrossRef CAS.
- D. J. Wales, GMIN: A program for finding global minima and calculating thermodynamic properties from basin-sampling, http://www-wales.ch.cam.ac.uk/GMIN/.
- J. F. Stanton, J. Gauss, J. D. Watts, W. J. Lauderdale and R. J. Bartlett, Int. J. Quantum Chem., 1992, 44, 879–894 CrossRef.
- T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- S. E. Stein and B. S. Rabinovitch, J. Chem. Phys., 1973, 58, 2438 CrossRef CAS.
- M. Pinsky, C. Dryzun, D. Casanova, P. Alemany and D. Avnir, J. Comput. Chem., 2008, 29, 2712–2721 CrossRef CAS.
- D. J. Wales and J. M. Carr, J. Chem. Theory Comput., 2012, 8, 5020–5034 CrossRef CAS.
- R. L. Johnston, Dalton Trans., 2003, 4193–4207 RSC.
- J. P. K. Doye and D. J. Wales, Phys. Rev. Lett., 1998, 80, 1357–1360 CrossRef CAS.
- A. L. Mackay, Acta Crystallogr., 1962, 15, 916 CrossRef CAS.
- D. J. Wales and T. Head-Gordon, J. Phys. Chem. B, 2012, 116, 8394–8411 CrossRef CAS.
- D. Cvijovic and J. Klinowski, Science, 1995, 267, 664–666 CAS.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS.
- G. Rossi and R. Ferrando, J. Phys.: Condens. Matter, 2009, 21, 084208 CrossRef CAS.
- V. A. Froltsov and K. Reuter, Chem. Phys. Lett., 2009, 473, 363–366 CrossRef CAS.
- G. A. Cox, T. V. Mortimer-Jones, R. P. Taylor and R. L. Johnston, Theor. Chem. Acc., 2004, 112, 163–178 CrossRef CAS.
- U. H. E. Hansmann and L. T. Wille, Phys. Rev. Lett., 2002, 88, 068105 CrossRef.
- M. Iwamatsu and Y. Okabe, Chem. Phys. Lett., 2004, 399, 396–400 CrossRef CAS.
- S. Shanker and P. Bandyopadhyay, J. Phys. Chem. A, 2011, 115, 11866–11875 CrossRef CAS.
- S. Kazachenko and A. J. Thakkar, Chem. Phys. Lett., 2009, 476, 120–124 CrossRef CAS.
- S. Roy, S. Goedecker, M. J. Field and E. Penev, J. Phys. Chem. B, 2009, 113, 7315–7321 CrossRef CAS.
- D. J. Wales, Philos. Trans. R. Soc., A, 2005, 363, 357–377 CrossRef CAS.
- D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 1970–1976 RSC.
- J. Nocedal, Mathematics of Computation, 1980, 35, 773–782 CrossRef.
- D. C. Liu and J. Nocedal, Math. Prog., 1989, 45, 503–528 CrossRef.
| This journal is © the Owner Societies 2013 |

