 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Water formation at low temperatures by surface O2 hydrogenation III: Monte Carlo simulation
Thanja Lamberts*ab, Herma M. Cuppenb, Sergio Ioppolo†a and Harold Linnartza
aRaymond and Beverly Sackler Laboratory for Astrophysics, Leiden Observatory, University of Leiden, P.O. Box 9513, NL 2300 RA Leiden, The Netherlands. E-mail: lamberts@strw.leidenuniv.nl
bFaculty of Science, Radboud University Nijmegen, IMM, P.O. Box 9010, NL 6500 GL Nijmegen, The Netherlands
First published on 14th March 2013
Abstract
Water is the most abundant molecule found in interstellar icy mantles. In space it is thought to be efficiently formed on the surfaces of dust grains through successive hydrogenation of O, O2 and O3. The underlying physico-chemical mechanisms have been studied experimentally in the past decade and in this paper we extend this work theoretically, using Continuous-Time Random-Walk Monte Carlo simulations to disentangle the different processes at play during hydrogenation of molecular oxygen. CTRW-MC offers a kinetic approach to compare simulated surface abundances of different species to the experimental values. For this purpose, the results of four key experiments—sequential hydrogenation as well as co-deposition experiments at 15 and 25 K—are selected that serve as a reference throughout the modeling stage. The aim is to reproduce all four experiments with a single set of parameters. Input for the simulations consists of binding energies as well as reaction barriers (activation energies). In order to understand the influence of the parameters separately, we vary a single process rate at a time. Our main findings are: (i) The key reactions for the hydrogenation route starting from O2 are H + O2, H + HO2, OH + OH, H + H2O2, H + OH. (ii) The relatively high experimental abundance of H2O2 is due to its slow destruction. (iii) The large consumption of O2 at a temperature of 25 K is due to a high hydrogen diffusion rate. (iv) The diffusion of radicals plays an important role in the full reaction network. The resulting set of ‘best fit’ parameters is presented and discussed for use in future astrochemical modeling.
1 Introduction
Water is an important species in molecular astrophysics and a prerequisite for life on Earth; it controls much of the gas–grain chemical interplay in space and is vital to the formation of more complex molecules as star-formation progresses. For this reason, understanding its fundamental properties is vital to disseminating our knowledge of chemical evolution through star and planet formation, and ultimately of the origin of life itself. Yet it has been a perennial question how water forms under the harsh conditions that govern chemistry in the interstellar medium and which physical and chemical processes are most important.In dense cold regions of the interstellar medium gas-phase formation routes for H2O and subsequent freeze-out mechanisms cannot explain the large ice abundances observed. Therefore, it is expected that water is formed on surfaces of cold icy dust grains that act as catalytic sites for molecule formation. Indeed water has been identified as the main component of interstellar ices.1 The first reaction scheme for a grain surface formation route of H2O was theoretically proposed in 1982 by Tielens and Hagen.2 This scheme focussed on the hydrogenation of atomic oxygen, molecular oxygen and ozone. At that time, only gas-phase data were available to estimate surface reaction rates. In 2007 Cuppen and Herbst showed in a theoretical study that the solid-state reaction H + OH → H2O likely dominates water formation under diffuse cloud conditions, whereas H2 + OH → H2O + H is prominent in dark molecular clouds.3
To test the surface hydrogenation of O, O2 and O3, the proposed reaction routes have been experimentally verified in the past decade.4–11 These experiments provide a more detailed understanding of the reaction network involved in water formation, extending the originally proposed network2 to that depicted in Fig. 1. In particular, water formation at low temperatures by surface O2 hydrogenation has been studied in depth. Ioppolo et al. (part I, ref. 8) and Cuppen et al. (part II, ref. 9) explored the dependency on a variety of experimental conditions, such as temperature, thickness, H-atom flux, etc. Different experiments have been performed and constraints on several reaction rates could be determined.
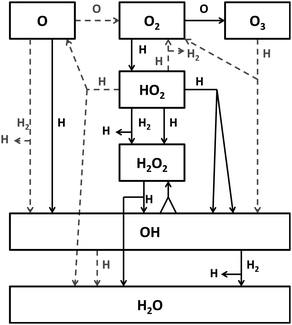 | ||
| Fig. 1 A schematic representation of the extended reaction network as obtained in Cuppen et al.9 Black, straight lines indicate reactions for which the influence of the barrier is studied here. Grey, dashed lines indicate reactions that are kept constant for all simulations. | ||
The WISH key programme of the space telescope Herschel has recently made observations of gas phase water and species related to its chemistry in prestellar cores and young stellar objects at different evolutionary stages. Hot gas containing O(I),12 O2,13 cold H2O,14 HO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and H2O2
15 and H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 as well as OH, OH+, H2O+ and H3O+ have been observed in this context.17 The identification of these molecules is fully consistent with the solid state network (Fig. 1) has been derived experimentally.
16 as well as OH, OH+, H2O+ and H3O+ have been observed in this context.17 The identification of these molecules is fully consistent with the solid state network (Fig. 1) has been derived experimentally.
These experimental results are extended here to Continuous-Time Random-Walk Monte Carlo (CTRW-MC) simulations to disentangle specific reaction mechanisms and to derive more accurate reaction barriers by comparing laboratory surface abundances with those obtained by simulations. These barriers can then be used as an input for astrochemical models in order to meet observational constraints. We show here that through systematical variation of the many input parameters it is possible to extract information concerning key reactions within the full network.
The manuscript is organized in the following way. Section 2 summarizes the key experiments that have been described previously and that are used here as reference for the simulations. Section 3 provides the details of the applied CTRW-MC method and in Section 4 the results are presented and extensively discussed. We conclude with recommendations for future studies and astrochemical considerations in Section 5 as well as with a short summary in Section 6.
2 Experimental observations
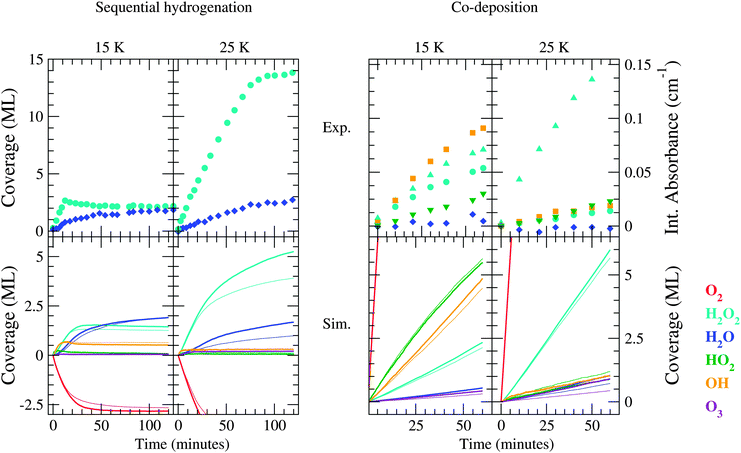
This section briefly summarizes the previous experimental work that is used here as a starting point. For a detailed description of the used setup, procedures and results we refer to ref. 8, 9 and 18. Two types of experiments have been performed: sequential hydrogenation of O2 ice and co-deposition experiments of O2 molecules and H atoms.During sequential hydrogenation experiments, an O2 ice, several monolayers (ML) thick, is first prepared at 15 K and subsequently exposed to hydrogen atoms at various constant ice temperatures. This allows the study of final and stable products of O2 hydrogenation, i.e., H2O2 and H2O (Fig. 1). Quantitative information concerning the surface abundances is obtained by dividing the integrated absorption of a selected infrared band (cm−1) over the so-called band strength (ML cm−1) as described in ref. 8. In Part I we showed that during sequential hydrogenation experiments the initial formation rates of H2O2 and H2O are temperature and thickness independent. The final yield, however, does depend on these parameters. Furthermore, due to the competition between reaction of atomic hydrogen with solid oxygen and hydrogen diffusion into the ice, the penetration depth of H atoms was found to span up to 16 ML at 25 K.8 We will elaborate on this topic in Section 4.3.
During co-deposition experiments, O2 molecules and H atoms are released onto the cold substrate at the same time and therefore are adsorbed simultaneously. Different stages of the hydrogenation route, i.e., various reactive intermediates, become experimentally accessible by changing the stoichiometric ratios of O2 and H9 (Fig. 1). Due to lacking band strengths for the unstable matrix-isolated reactive intermediates, a quantitative study is not trivial. However, quantification of a single species using the ratio between abundances at different temperatures and/or H/O2 ratio can be easily performed.9
Four of the aforementioned experiments are selected for further comparison to simulated results: sequential hydrogenation and co-deposition experiments both at 15 and 25 K, as listed in Table 1. In the following, 15 and 25 K are defined as ‘low’ and ‘high’ temperature. These four experiments are considered to be representative of the different experimentally observed features. In Fig. 2 the measured surface abundances and integrated absorbances are depicted for the selected sequential hydrogenation and co-deposition experiments. In the following, we consistently separate the discussion between these two types. Important features that need to be reproduced by the MC simulations are summarized below.
| Type | T (K) | H/O2 | H flux (cm−2 s−1) | |
|---|---|---|---|---|
| 1 | Seq. hydr. | 15 | — | 2.5 × 1013 |
| 2 | Seq. hydr. | 25 | — | 2.5 × 1013 |
| 3 | Co-dep. | 15 | 1 | 2.5 × 1013 |
| 4 | Co-dep. | 25 | 1 | 2.5 × 1013 |
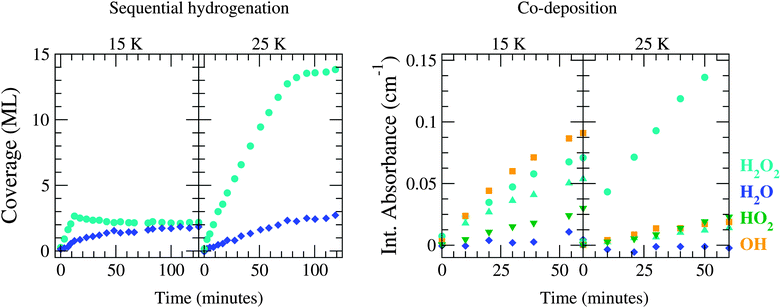 | ||
| Fig. 2 Evolution of the experimental surface abundance of H2O2 (light blue), H2O (dark blue), HO2 (green) and OH (orange) as a function of time for a sequential hydrogenation simulation (left) and a co-deposition simulation (right) at 15 and 25 K. | ||
Sequential hydrogenation:
• evolution of the H2O2 abundance in time with a sharp transition between the initial (T-independent) linear and final steady state (T-dependent) regime,
• increase of the final H2O2 production by a factor of ∼7 between 15 and 25 K, and
• similar behaviour of the H2O abundance for both temperatures.
Co-deposition:
• linearly increasing behaviour of all abundances with time at texp < 60 min,
• decrease of HO2 and OH abundances between 15 and 25 K,
• increase of H2O2 abundance between 15 and 25 K,
• low to zero production of H2O, and
• constant ratio of OH/H2O2 for 15 K and for 25 K.
It should be noted that the uncertainty of the band strengths is estimated to be within 50% and this affects the accuracy with which the experimental surface abundances can be determined.
3 The Monte Carlo method
This section describes the general Continuous-Time Random-Walk Monte Carlo method used for the simulations, discussing sequentially the simulation of O2 deposition, the hydrogenation of O2 ice and the different parameters used for a co-deposition simulation. Subsequently, distinct details of the program are addressed. For a more detailed overview the reader is referred to ref. 19. The present results are obtained with the program described in ref. 3, which has been extended to account for the specific characteristics needed here. The reproducibility of the simulations is monitored by performing each of the standard simulations (see below) three times using different seeds. Standard deviations have typical values of <5% for abundant species (e.g., O2, H2O2), <10% for less abundant species (e.g., OH) and <40% for O3.3.1 Deposition of an O2 surface
During the deposition phase the O2 ice is formed starting from a bare surface; the surface used to mimic the experimental gold substrate has a smooth topology and is 2.5% of that depicted in Fig. 1(c) from ref. 20. The simulation then starts by the addition of an O2 molecule to the surface. This occurs at time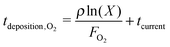 | (1) |
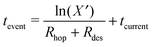 | (2) |
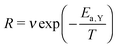 | (3) |
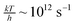 . This factor can be seen as a trial frequency for attempting a new event.
. This factor can be seen as a trial frequency for attempting a new event.The total binding energy, Etot,bind, for each molecule to a site is calculated by additive contributions of its neighbours. Table 2 shows the single binding energy values, E, used throughout this paper. Each species in the lattice has 6 neighbours and 12 nearest neighbours. Nearest neighbours add a contribution of E and next-nearest neighbours of E/8. The latter takes into account the difference in distance of a factor 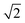 and makes use of a distance dependency of [r−6]. The neighbour below the particle adds a double contribution (2E), mimicking longer range interactions from the bulk ice layer. Binding energies are typically obtained from desorption barriers determined through so-called Temperature Programmed Desorption (TPD) experiments. These experiments can be reproduced with Monte Carlo simulations when an average number of 0.8 lateral nearest neighbours is taken into account. The single binding energy value, E, is then obtained by dividing the desorption energy by a factor of 3.8.21 Note that an order of magnitude difference is applied in binding energy to atoms and small molecules (H, H2 and O) and H2O like molecules (all the rest). For example, the binding energy of a hydrogen atom binding to a flat surface of O2 molecules corresponds to the number of neighbours times the contribution: 1·2·66 + 4·2·66/8 = 198 K. Binding to a surface of H2 molecules yields 19.8 K.
and makes use of a distance dependency of [r−6]. The neighbour below the particle adds a double contribution (2E), mimicking longer range interactions from the bulk ice layer. Binding energies are typically obtained from desorption barriers determined through so-called Temperature Programmed Desorption (TPD) experiments. These experiments can be reproduced with Monte Carlo simulations when an average number of 0.8 lateral nearest neighbours is taken into account. The single binding energy value, E, is then obtained by dividing the desorption energy by a factor of 3.8.21 Note that an order of magnitude difference is applied in binding energy to atoms and small molecules (H, H2 and O) and H2O like molecules (all the rest). For example, the binding energy of a hydrogen atom binding to a flat surface of O2 molecules corresponds to the number of neighbours times the contribution: 1·2·66 + 4·2·66/8 = 198 K. Binding to a surface of H2 molecules yields 19.8 K.
| Species | E (K) |
|---|---|
| H | 66 |
| H2 | 53 |
| O2 | 240 |
| OH | 105 |
| HO2 | 630 |
| H2O2 | 1370 |
| H2O | 1260 |
| O | 260 |
| O3 | 630 |
The barrier for hopping from site i to j is given by
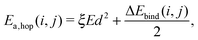 | (4) |
The barrier for desorption is determined only by Etot,bind. Note that the single binding energy value of OH is much smaller than that of H2O. This will be briefly discussed in Section 4.2.3, where the low binding energy is associated with a high diffusion rate.
A total of 10 ML of O2 is eventually simulated to deposit on top of the bare surface. This results in a smooth ice surface according to the definition from ref. 20. In order to compare the results of the different sequential hydrogenation simulations, the same oxygen surface is used for all simulations, except for those that investigate the influence of surface roughness and thickness.
3.2 Sequential hydrogenation
After deposition of O2 molecules, the surface is exposed to H atoms and H2 molecules in a similar manner as before, except that now also reactions can occur and new species are formed. The flux of H atoms and H2 molecules is set to S·2.5 × 1013 particles cm−2 s−1 for both species, where the sticking coefficient S equals 0.2. The reaction rates are calculated by using reaction activation energies (or reaction barriers) in eqn (3) and are listed in Table 3. The reaction rates represent the competition between different reactions and therefore the ratio between the rates is used for future reference. Temperature independent reactions are those that have a low to zero barrier. The temperature dependence for the remaining reactions arises from a combination of thermally activated processes and tunneling, i.e., reactions always occur at a higher rate for higher temperatures, not entirely according to eqn (3), but rather scaling the rates by an arbitrary factor to account for tunneling. Note that tunneling is thus not explicitly included.| Reaction | Ra (s−1) | Rhigh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (s−1) b (s−1) | Rlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (s−1) b (s−1) |
|---|---|---|---|
| NOTE: rates indicated in ITALICS should be used with care, see text.a Standard values used throughout the paper.b Values used to test the effect of the reaction barrier on the overall performance.c Total rate of 1.0 × 1012 s−1 for H + HO2. Individual channels are corrected for their branching ratios.d Total rate of 4.2 × 10−6 or 1.2 × 102 s−1 for 15 and 25 K, respectively. Individual channels are corrected for their branching ratios. | |||
| Temperature-independent reactions | |||
| H + H → H2 | 1.0 × 1012 | ||
| H + O2 → HO2 | 1.1 × 105 | 6.1 × 106 | 2.1 × 103 |
| H + HO2 → products | 1.0 × 1012 | ||
| OH + OHc | 56% | 91% | |
| H2O2c | 35% | 0% | |
| H2 + O2c | 2.0% | 2.0% | |
| H2O + Oc | 7.0% | 7.0% | |
| H + O → OH | 1.0 × 1012 | ||
| O + O → O2 | 1.0 × 1012 | ||
| H + O3 → O2 + OH | 1.1 × 105 | ||
| H + OH → H2O | 1.1 × 105 | 1.0 × 1012 | 2.6 |
| Reaction | 15 K | 25 K | 15 K | 25 K | 15 K | 25 K |
|---|---|---|---|---|---|---|
| Temperature-dependent reactions | ||||||
| H + H2O2 → H2O + OH | 6.9 × 10−12 | 1.9 × 10−10 | 2.6 | 1.4 × 101 | 1.1 × 10−17 | 7.9 × 10−16 |
| H2 + O → OH + H | 2.3 × 10−80 | 1.0 × 10−43 | ||||
| H2 + HO2 → H2O2 + H | 1.7 × 10−133 | 1.4 × 10−75 | 1.1 × 10−17 | 4.2 × 10−6 | ||
| H2 + OH → H2O + H | 3.3 × 10−3 | 1.2 × 102 | 2.1 × 103 | 4.6 × 103 | 6.9 × 10−12 | 5.8 × 10−11 |
| OH + OH → products | 4.2 × 10−6 | 1.2 × 102 | 2.1 × 103 | 1.1 × 105 | 8.8 × 10−15 | 1.4 × 10−9 |
| H2O2d | 100% | 100% | 90% | 90% | 75% | 75% |
| H2O + Od | 0% | 0% | 10% | 10% | 25% | 25% |
| O + O2 → O3 | 3.3 × 10−3 | 2.1 × 103 | 1.0 × 1012 | 1.0 × 1012 | 6.9 × 10−12 | 1.3 × 10−2 |
Although many reactions leave the products with a large excess energy, this energy is thought to be efficiently dissipated into the ice surface on picosecond timescales, which we conclude from preliminary Molecular Dynamics simulations. Furthermore, in the laboratory the He cryostat provides a suitable dissipation path, while in the interstellar medium the time scales allow thermalization. Since the amount of energy remaining in the molecule does not seem to correlate with the amount of initial excess energy, we include an arbitrary, small excess energy of only 100 K for each reaction product in our model. This excess energy can be applied to overcome barriers for reaction, desorption and/or diffusion. In this way, a chemical desorption mechanism, like the one proposed in Garrod et al., is implicitly included.23 A more accurate implementation of the excess energy, for instance an energy dependence on the exothermicity of a specific reaction, is a subject of future studies. Diffusion reduces the excess energy by an arbitrary factor of 1.6 for each hop. Furthermore, after 10−8 s, the local temperature of the excited species is set back to the temperature of the surface. This is based on the assumption that a molecule on the surface will be thermalized after 10 ns. This rather subjective choice of time scale does not affect the outcome of the simulations, since we find that hot species either react immediately to form a new molecule or remain in their initial configuration for times much longer than 10−8 s.
The rates listed in Table 3 are explicitly for thermalized reactions only. Consider a hydrogen atom at room temperature (300 K) that lands atop the O2 surface with a temperature of 15 K. We assume that half of the energy (½ × (300 + 15)) is immediately dissipated into the surface, leaving the atom with a local temperature of 157.5 K. This energy is dissipated either slowly through hopping or through an immediate step function after 10−8 s. All reactions that take place before thermalization have a much higher probability of occurrence, according to eqn (3). This is indeed the case for all reactions with a barrier. The thermalization effect is most pronounced at early times during the simulation, when the surface is not yet filled with molecules, preventing fast reactions. Take for example a surface where H2O has already formed; hydrogen atoms landing on a site next to H2O are forced to hop in order to meet a reaction partner, thereby losing their energy. The effect is much stronger at 15 K, where the competition between the different processes is small, mainly because the rates are less close to the trial frequency. For instance, for the reaction H + H2O2 → H2O + OH, the difference between the hot mechanism and the thermalized reaction is a factor of 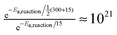 . Reactions that occur easily in the experiment are therefore not necessarily accessible under conditions resembling the darker regions of the interstellar medium.
. Reactions that occur easily in the experiment are therefore not necessarily accessible under conditions resembling the darker regions of the interstellar medium.
Finally, in this paper we only consider physisorbed hydrogen atoms, both on the surface as well as trapped in pores. The solid phase interactions are incorporated indirectly through positioning of the hydrogen atoms on the surface and accounting for the binding energy at a specific lattice site. If a species has more neighbours, the cumulative binding energy increases. Furthermore, the effect of the surroundings on the reaction itself is included in the barrier. In this way, a stabilizing effect through for instance hydrogen bonding of a neighboring species is not included explicitly as is the case when real potentials are used. Rather, a change to the activation energy is applied. In Section 4.2.7 we will briefly talk about the possibility of explicitly incorporating solid state effects involving H atoms.
3.3 Co-deposition
During a co-deposition simulation, H, H2 and O2 all settle on the bare (‘gold’) surface simultaneously, after which their possible events are determined and evaluated again using the Arrhenius behaviour. Reactions can thus take place from the start. The individual deposition rate of O2, H and H2 is set to be 2.5 × 1013, 5 × 1012 and 5 × 1012 particles cm−2 s−1, respectively, assuming again a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between H and H2. The sticking coefficient S is thus already accounted for in the fluxes: SH(2)/SO2 = 0.2.
1 ratio between H and H2. The sticking coefficient S is thus already accounted for in the fluxes: SH(2)/SO2 = 0.2.3.4 Size and ice morphology
We use a lattice-gas model, where the lattice surface consists of 50 × 50 sites. This is large enough to overcome the finite size limit, which is set by the rate of atomic hydrogen desorption, as outlined in ref. 19. Larger lattices would result in computationally too expensive simulations. We performed one simulation using standard parameters (see below) on a surface of 100 × 100 sites as a check and found no difference with respect to the smaller surface.Although experimental surfaces are probably amorphous, the adsorption sites will be clearly defined and likely distributed with some kind of order in terms of the number of neighbours. A lattice-gas model can thus be seen as a grid of potential wells, and the process results in a change of the occupancy of the lattice sites. The largest advantage of using a lattice-gas model is the reduction of computational costs as result of working with a predefined event table. Since the molecules are confined to a lattice, only a fixed amount of processes can occur and large time scales can be simulated. The disadvantage is that the level of molecular detail is limited and some mechanisms are not included. These types of models have, however, demonstrated how powerful they can be in mimicking ice chemistry, covering hours of simulated time.24,25
To account for the penetration of H atoms observed experimentally, small species (i.e., H, H2, OH and O) are allowed to diffuse to interstitial sites in the oxygen ice. For this purpose each monolayer in the ice is represented by two fields in the matrix that holds the ice; one can hold all species present in the simulations, the other contains mainly small species. The diffusion takes place only when an O2 or a HO2 molecule is atop the final position, since penetration in water-like structures has not been observed experimentally. Larger species can be present in the intermediate layer, though, as a result of the positioning of reaction products.
4 Results and discussion
In this section we present and discuss Monte Carlo simulations of the four experiments listed in Table 1. The reaction input parameters for these simulations are given in Table 3. The second column indicates the settings used for the so-called standard simulations (R). These are based on ab initio barriers, experimental constraints or other models and represent the starting point for optimization. Subsequently, for each reaction with a barrier, this activation energy Ea is either increased or decreased, after which the effect of the reaction on the final result is studied. The reaction rates are listed in the third and fourth columns of Table 3. Note that while changing a rate, all other parameters are kept constant. Decreasing or increasing the reaction rates in a systematic way forms the core of this paper and is described in Section 4.2. The final goal is to see whether these variations bring us closer to the experimental results, while simultaneously providing insight into the underlying molecular mechanism. Furthermore, we hope to obtain information on the sensitivity of the system on a specific reaction, i.e., information on the error bar of the barrier. Besides studying the chemistry itself, we also investigate the effect of the diffusion barrier of H and O2 as well as the effect of the interstitial positioning.We first discuss the standard simulations and how the different input parameters affect the production of various species. The simulations are then compared with the experimental results by using the time evolution of the surface abundances of the molecular species, i.e., comparing the simulated trends to the experimental findings shown in Fig. 2. For the sequential hydrogenation experiments, the observations are not only based on the absolute abundances, but also take into account the ratio between H2O and H2O2 as well as trends in the time evolution. For the co-deposition experiments, accurate band strengths are not available. Therefore, the approximation is made that each hydroxyl group contributes equally strongly to the OH-stretching and bending vibrations, which allows for an estimation of the relative band strengths and therefore relative abundances. To strengthen this analysis, we performed simulations for selected sets of parameters for a H/O2 ratio of 2. In this way, we can compare the molecular abundances between different experiments using infrared features. Furthermore, the OH/H2O2 ratio is studied, following the conclusion from ref. 9 that their abundances are correlated for separately 15 and 25 K. To study the temperature dependence, experiments and simulations are compared at 15 and 25 K. Finally, the effect of the ice structure and the experimentally observed penetration depth is discussed.
4.1 Standard simulations
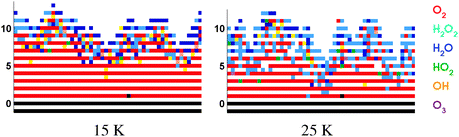 | ||
| Fig. 3 A cross section of the simulated ice mantle for a hydrogenation simulation of predeposited solid O2 at 15 K (left) and 25 K (right). Standard values are used for the reaction rates. O2 is represented by red, H2O2 by light blue, H2O by dark blue, HO2 by green, OH by orange and O3 by violet. On the vertical axis the number of monolayers (ML) is given. | ||
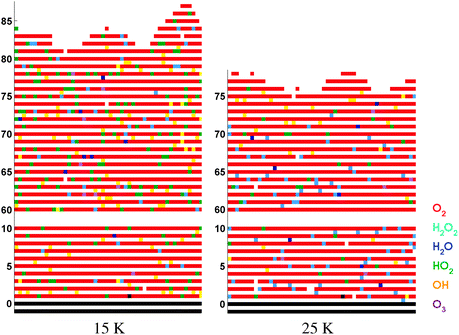 | ||
| Fig. 4 Similar to Fig. 3 for co-deposition simulations. For reasons of clarity, the center 50 ML of the matrix are omitted from the surface. | ||
For the co-deposition simulations (Fig. 4), the resulting ice mantle consists mainly of O2 with other species embedded in the O2 matrix. The top 5 ML of the matrix have a different composition than the lower layers because the hydrogen atoms landing on the surface can still penetrate some of the ice and induce further reactions. The main difference between the 15 and 25 K ice mantles is in the amount of HO2 and OH versus H2O2. At 25 K most of the small species have reacted further as a result of the higher mobility of H and OH. Finally, the total mantle thickness for a higher temperature is smaller as a result of the higher O2 desorption probability. The thermal desorption value of pure O2 ice has been experimentally determined as 31 K.26,27
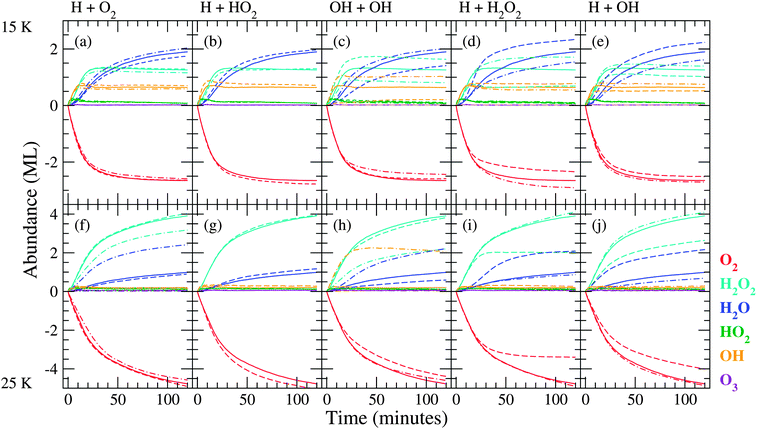 | ||
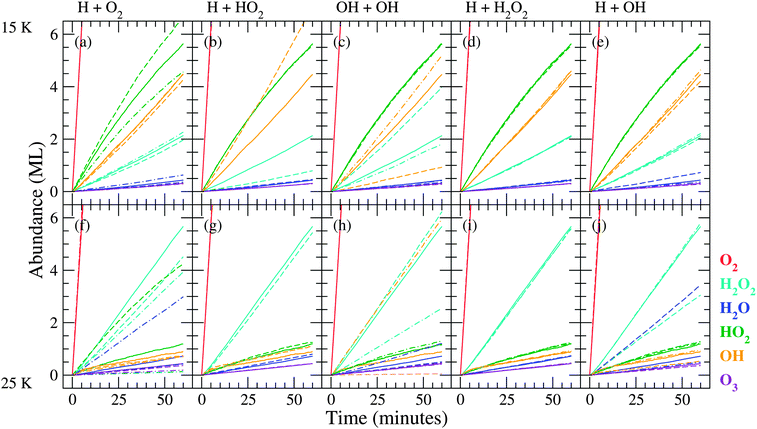
| Fig. 5 Evolution of the surface abundance of O2 (red), H2O2 (light blue), H2O (dark blue), HO2 (green), OH (orange) and O3 (violet) as a function of time for a hydrogenation simulation of predeposited solid O2 for the five key reactions at 15 K ((a)–(e)) and 25 K ((f)–(j)). Solid curves represent simulation results with the standard value, dashed curves with lower barrier (higher rate), and dash-dotted curves with higher barrier (lower rate). | ||
 | ||
| Fig. 6 As for Fig. 5, but applied to the co-deposition simulations. | ||
From these figures we can conclude that the trends in the time evolution of water and hydrogen peroxide surface abundances are in good qualitative agreement with the experimental data. Like for the experimental results (Fig. 2), the initial increase in H2O2 abundance is similar at low and high temperature and there is a clear transition between the linear increase and final steady state behaviour for sequential hydrogenation simulations. The slight decrease before reaching the steady state for the H2O2 signal at 15 K is also reproduced by the standard model. The experimental transition is sharper than the simulated one and the level of the steady state at 25 K is much higher (14 ML vs. 4 ML). The H2O production at 15 and 25 K follows roughly the same behaviour and the curve shape agrees with the experimental one as well. The H2O abundance is slightly higher for lower temperature, and as a result the H2O/H2O2 ratio is overestimated. During experiments, the surface abundance of O3 stays below the detection limit, and this is in agreement with the low value of the simulated abundances.
The molecular time evolution for the co-deposition simulations is plotted as a solid curve in Fig. 6. The final O2 thickness is of the order of 80 ML, which is beyond the dynamic range of the panels (see also Fig. 4). At later times some O2 is observed experimentally only at 15 K for H-atom rich conditions. The simulations confirm this trend, since the final O2 abundance at 15 K is higher than at 25 K. The abundance of most species increases linearly over time except for HO2 which slowly levels off. These abundances are compared to the linear experimental regime (t < 60 minutes) where H2O2 and OH have not yet reached steady state. H2O and O3 remain below the IR detection limit in the experiments and simulated abundances are correspondingly low. From the comparison of the bending and stretching vibration modes it seems that the simulations overproduce the intermediate species HO2 for both temperatures. This can partially be explained by the hydrogen diffusion rate incorporated in the standard simulations. A higher mobility would allow hydrogen to scan both a larger surface area and bulk volume, hence allowing for the reaction H + HO2 to take place more often. The dependence of the molecular surface abundances on both temperature and H/O2 ratio is summarized in Table 4. Comparison with the experimental data is also shown and for H2O2 a good agreement is found. The arrows show the influence of increasing temperature or H/O2 ratio on the amount of species formed. Indeed, the HO2 and OH production decreases at higher temperature, whereas for H2O2 it increases. The OH/H2O2 ratio stays equal throughout a single simulation, in accordance with the experiments. From the above, it appears that the main inconsistencies are caused by radical species. The dynamics of these species is not fully understood, but one should also keep in mind the experimental error bars involved in this analysis, as stated in Section 2.
| T = 15 K → 25 K | T = 15 K → 25 K | T = 15 K | T = 25 K | |||||
|---|---|---|---|---|---|---|---|---|
| H/O2 = 1 | H/O2 = 2 | H/O2 = 1 → 2 | H/O2 = 1 → 2 | |||||
| Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | |
| Arrows indicate the effect on the molecular surface abundances for an increase in temperature (column two and three) or H/O2 ratio (last two columns). A double arrow represents a large increase (up) or decrease (down), a single arrow a small increase (decrease) and a hyphen no change. | ||||||||
| H2O2 bulk | ↑↑ | ↑ | ↑↑ | ↑ | ↑ | ↑ | — | ↑ |
| H2O2 isolated | ↓ | ↓ | ↓↓ | ↓ | ↓ | — | ↓ | ↓ |
| HO2 isolated | ↓ | ↓↓ | ↑ | ↓↓ | ↓ | ↓ | ↓ | ↓ |
| OH isolated | ↓↓ | ↓↓ | ↓↓ | ↓↓ | ↓ | ↑ | ↓ | ↓ |
4.2 Key reactions
The investigation of the reaction rates is done by varying one reaction barrier at a time with respect to the standard values as indicated in Table 3. Fig. 5 and 6 show the resulting time evolution of the surface abundances. The procedure adopted is as follows: if the difference between a given simulation and the standard simulation is larger than the derived standard deviation, it is considered to be a strong effect. The reactions that exhibit the largest effect upon changing their corresponding barriers are:| H + O2 → HO2 | (R1) |
| H + HO2 → products | (R2) |
| OH + OH → products | (R3) |
| H + H2O2 → H2O + OH | (R4) |
| H + OH → H2O. | (R5) |
The implications of these reactions, along with those of reactions with H2, are discussed in the sections below. For reasons of brevity, we will comment only on features that distinctly differ from those in the standard simulations.
In general, an increase in the rate results in a different competition between the first reaction in the scheme (Fig. 1), H + O2, and the follow-up reactions. For a higher rate, more HO2 and subsequently more H2O2 is formed. Therefore, less hydrogen atoms are available for other reactions and the formation yields of those products indeed decrease. The lower rate results in more reactions that occur ‘deeper’ in the reaction network, enhancing for instance H + OH → H2O.
Since the O2 molecules in the pre-deposited oxygen layers probably have some preferred orientation (local crystallinity), the H atoms approach them under the same angle when penetrating the ice. This is reflected by a certain barrier. For co-deposition experiments, the angle dependence is of less physical importance since the oxygen beam provides O2 molecules with a range of different orientations at the surface. This means that there are more molecules available for a reaction pathway with a lower barrier. Since in the Monte Carlo simulations the ice geometry is not explicitly taken into account, the barrier can be lowered for co-deposition simulations.
The back reaction
| HO2 → H + O2 | (R6) |
| H + HO2 → OH + OH | (R2a) |
| H + HO2 → H2O2 | (R2b) |
| H + HO2 → H2 + O2 | (R2c) |
| H + HO2 → H2O + O | (R2d) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 H2O2 is only being indirectly formed by the consecutive reaction of OH + OH → H2O2.
7 H2O2 is only being indirectly formed by the consecutive reaction of OH + OH → H2O2.The latter branching ratio leads to a more open ice structure for the sequential simulations; the regularity of the O2 matrix is destroyed. This is because HO2 will split into two species which will take up interstitial space and distort the ice structure. Two OH radicals can then react again with H2O2, which forms additional pores. A more open ice structure allows H atoms to penetrate deeper in the ice layers and thus more reactions can take place.
In the co-deposition experiments the changed branching ratio is reflected in the OH/H2O2 ratio at 15 K. At 25 K most of the formed OH immediately reacts with H2O2 and little to no difference is observed in the final abundances. In the experiments approximately 3 times more OH is formed than H2O2 at low temperature. In the simulations, this is a factor 2 for the standard simulations and 9 for the changed branching ratio. The real branching ratio is therefore probably in between the two adopted values. This value can only be quantitatively constrained in combination with the reaction rate of OH + OH → H2O2, which is discussed in the following subsection.
4.2.3.1 Branching ratio. The competing reactions,
| OH + OH → H2O2 | (R3a) |
| OH + OH → H2O + O, | (R3b) |
The results from the simulations are trivial in the sense that an increase in the fraction of reaction (R3b) results in an increase of the H2O and O3 and a decrease in the H2O2 abundance for all parameter settings.
Using a non-zero contribution of reaction (R3b), we are able to correctly reproduce the trend in H2O abundance at 25 K for sequential hydrogenation, in particular the initial rise. Based on the small abundance of O3 found in the experiments, we expect that reaction (R3a) is strongly favoured, which is reflected by a branching ratio of (R3a)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (R3b) = 90
(R3b) = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.
10.
4.2.3.2 Diffusion and reaction. Since OH is formed through the same reaction as H2O2 but can still be detected in the ice, there must exist a mechanism that prohibits recombination to peroxide.
Experimentally, OH is only observed during co-deposition where it eventually freezes out in the O2 matrix. When two OH radicals are formed from the reaction H + HO2 the excess energy of the reaction allows the radicals to move away from each other on the surface just before thermalizing and subsequently freezing out in the matrix. Diffusion of thermalized OH at a later stage is not expected. If (R3) takes place, it immediately follows reaction (R2). This makes the two reactions hard to constrain separately.
To model the possibility of two products separating upon reaction is non-trivial, due to the lack of directionality in our simulations, i.e., a high diffusion rate allows fast hopping in all directions, both back and forth. This would allow two species to separate quickly, followed by a fast recombination as a result of hopping back. To prevent recombination, we introduce a relatively high diffusion rate and, contrary to current gas-phase studies, an effective barrier for the reaction OH + OH → H2O2. Different barrier heights are used for the reactions at 15 and 25 K in order to reproduce the experimental features.
The rate of this reaction has a strong effect on the appearance of the ice in the sequential simulations. For a high rate, H2O2 is formed both at the surface and deep in the ice and a small amount of OH resides in the top layers. For a low rate, a layer of H2O covers the surface and OH occupies a large fraction of interstitial positions in the top layers of the matrix. For both the sequential and co-deposition simulations the OH/H2O2 ratio decreases with increasing reaction rate. The decrease in OH also has an effect on the final H2O yield which decreases as well.
The intermediate reaction rate employed in the standard simulations reproduces the experiments best, since the high rate reproduces the sequential simulations but overproduces H2O2 in the co-deposition simulations and the low rate overproduces OH in the sequential simulations but is in better agreement with the co-deposition experiment. As mentioned above, the exact rate can only be determined considering multiple input parameters, of which the OH diffusion and the H + HO2 branching ratio are the most important.
Note, however, that OH diffusion inside the pre-deposited O2 matrix is not likely. Therefore, in reality the OH fragments formed during sequential hydrogenation will react and the H2O2 abundance correspondingly increases whereas the H2O abundance decreases. Indeed, this corresponds with a scenario where the H2O/H2O2 fraction gets closer to the experimental value.
In general the H2O/H2O2 ratio increases with increasing rate. In the sequential simulations this mainly occurs at later times, at the expense of H2O2, of which the abundance declines in time. By increasing the H + H2O2 reaction rate, more H atoms are consumed in this reaction on top of the surface; less of the initial O2 is thus affected upon hydrogenation. A decrease in the rate allows for the build-up of hydrogen peroxide and therefore a more correct ratio with respect to H2O at 15 K. However, the leveling off of the peroxide signal occurs at later times, contrary to the sharp transition observed experimentally.
For the co-deposition simulations, H2O is predominantly formed through (R2d) and (R3b) and the change in H + H2O2 reaction rate only has an effect upon significant decrease of the barrier. The latter, however, results in an overestimation of H2O.
Additional simulations are performed to focus only on the H + H2O2 reaction. A surface consisting only of H2O2 molecules (20 K) is used, on top of which H and H2 (300 K) are deposited. Using a reaction barrier of 1000 K indeed results in a reasonable correspondence to the hydrogenation experiment performed in ref. 9. However, on closer inspection of the dynamics, it becomes clear that all reactions between hydrogen and peroxide occur through the hot mechanism. We therefore expect this reaction to be rather inefficient in the dense interstellar medium.
An increase in rate leads to a higher water production. At the same time, the production of H2O2 goes down since less OH is available for its formation. The low and intermediate rate results appear to be in better agreement with the selected experiments since the H2O/H2O2 ratio is better reproduced.
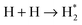 | (R7) |
The reaction H2 + HO2 has a large barrier33 and is even endothermic, therefore it is not expected to proceed at these low temperatures. However, co-deposition experiments with the same H fluence but with ten times higher H2 fluence show an increase in H2O2 and decrease in HO2 in agreement with the proposed reaction. Also in ref. 11 an observed isotope effect between hydrogenation and deuteration of ozone suggested this reaction to occur under laboratory conditions. It was therefore hypothesized that the excess energy from the reaction H + O2 can be used to overcome both the reaction barrier and the endothermicity of the H2 + HO2 reaction since the total reaction H + H2 + O2 → H2O2 + H is exothermic.
In the simulations this reaction is included with a high barrier, and as a result the reaction does not contribute to the H2O2 production. If the activation energy is substantially lowered, a small increase in the H2O2 is observed for the co-deposition simulation at 25 K. The current simulations cannot constrain the value of the reaction barrier.
The reaction H2 + OH has a gas-phase barrier of 2700 K.34 Gas-phase experiments indicate that tunneling starts to play a role for OH + H2 for temperatures below 250 K.35 Recently, Oba et al. performed solid state experiments, confirming a dependency of the reaction rate on effective mass.36 The reaction rate at 15–25 K should therefore be substantially raised through tunneling. In the present simulations the reaction only plays a minor role in the water production regardless of the barrier for reaction. Even in the low barrier case, the H2O formation rate is only slightly changed by this reaction. However, upon closer inspection of the different contributions to the H2O formation rate, one notices that the fraction of water that is produced through H2 + OH increases with reaction rate. The contribution of H + OH declines at the same time, resulting in a zero net effect.
| O + OH → HO2 | (R8) |
| OH + H2O2 → H2O + HO2 | (R9) |
| HO2 + HO2 → H2O2 + O2 | (R10) |
| HO2 + OH → H2O + O2 | (R11) |
| HO2 + O2 → O2 + HO2 | (R12) |
| OH + H2O → H2O + OH. | (R13) |
Adding the first reaction, (R8), to the scheme with zero barrier has a negligible effect, since it accounts at most for 3% of the total HO2 budget as a result of the low O production.
Concerning reaction (R9), Vakhtin et al. (2003) reported an empirical relation with a negative barrier in the gas-phase at relatively low temperatures (96–296 K).37 This would render the reaction effectively barrierless for our purpose. However, a kinetic isotope effect was previously found, suggesting in fact the presence of an activation energy.38 Liquid-phase studies of this reaction indicate that the reaction rate can be decreased by as much as a factor of 1840 with respect to the gas phase.39,40 The presence of water can thus have a large effect on the probability for this reaction to occur. Moreover, a mechanism involving a reorientation into a five-membered prereactive complex was predicted,39,40 but efficient reorientation is not likely in the solid state. Therefore, we exclude reaction (R9) from our simulations. Test runs were performed by using various settings and unequivocally poor reproductions of the experimental results were found through overproduction of water.
Reactions (R10) to (R13) should be considered part of the same train of thought, namely that hydrogen atoms are not all physisorbed but some are trapped in a chemical bond with for instance O2. These complexes or molecules can then continue to react with other species. Only incorporating reaction (R10) (with Ea = 0 K41) has little effect, except for co-deposition at 15 K, where the OH/H2O2 ratio changes to a large extent. This can be easily overcome through changing the branching ratio of (R2). Incorporating also reaction (R11) (with Ea = 0 K) results in a heavy overproduction of water. Reactions (R12) and (R13) allow for a type of proton exchange and may be considered as an alternative to hydrogen diffusion. Since these are reactions that go back and forth, they strongly increase the computational costs for barriers below 2500 K. Preliminary results show a decreased penetration depth for both temperatures as well as underproduction of H2O2. We postpone this concept for the time being and continue using our assumption of physisorbed hydrogen atoms diffusing on and through the ice.
4.3 Penetration depth
In Section 4.2.4 we mentioned that the standard simulations cannot reproduce the large experimental surface abundance of H2O2, 14 ML, at 25 K for sequential hydrogenation. This large abundance can accumulate in time through different mechanisms, for instance: (1) replenishing of the top layers by O2 mobility and (2) competition between reaction and diffusion of H atoms. Several control experiments have been performed and it was established in Part I that the most likely scenario is the second mechanism, where hydrogen atoms can either react with a partner (initially O2) or diffuse deeper into the ice. The extent to which the atoms enter the icy mantle is called penetration depth. The reaction H + O2 is (close to) barrierless and temperature independent. Diffusion, however, is enhanced with increasing temperature and hydrogen atoms are thus able to reach deeper layers in the ice at higher temperature. In Fig. 7 a summary of the study on diffusive effects and penetration depth is presented, depicting the influence of initial ice thickness, availability of interstitial positions, the diffusion parameter ξ and the diffusion and positioning of H and O2 in the ice.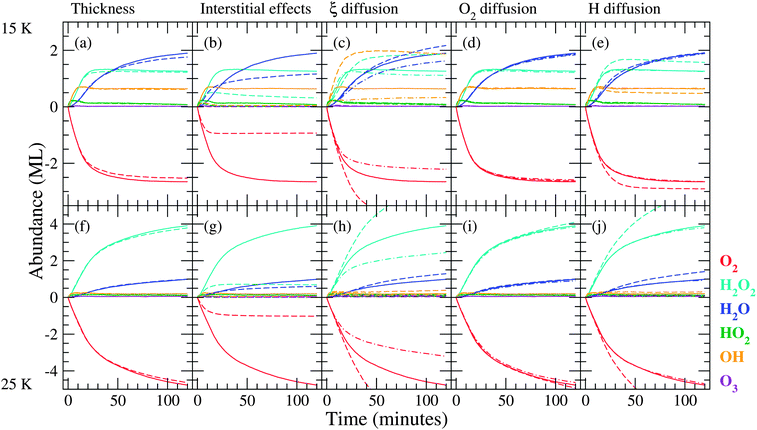 | ||
| Fig. 7 As for Fig. 5, but investigating different parameters relating to penetration depth. Solid curves represent simulation results with standard values. Dashed curves in panel (a) represent standard values applied to a 16 ML surface, and in panel (b) easy access to interstitial positions was switched off. In panel (c) dashed curves represent a low ξ value (eqn (4)) and dashed-dotted curves a high value. In panels (d) and (e) dashed curves represent a lower barrier of diffusion and dashed-dotted curves represent easier access to interstitial positions for O2 and H, respectively. Panels (f)–(j) give the 25 K situation. | ||
The effect of the surface itself is discussed first. Increasing the initial surface roughness allows a higher production of both water and hydrogen peroxide, simply as a result of a larger surface area available for hydrogenation. Starting from a more porous ice, i.e., 10% pores in the standard surface, there is no significant effect on the penetration. The most probable explanation is that during the course of the simulation, pores are created as a result of products that continue to react further. A possibility for the low simulated use-up of O2 could be the initial ice thickness, since the final experimental H2O2 abundance is 14 ML which is more than our initial surface thickness (10 ML). This is illustrated in Fig. 7(a) and (f), and no dependence on ice thickness can be concluded. The fact that the ice thickness does not change abundances significantly is a sign of a lacking penetration mechanism. After all, if hydrogen atoms penetrate deeply into the matrix, a large O2 reservoir would allow for more reactions to occur. The lack of this observation urges further investigation of diffusive effects with the purpose of understanding how we can increase the consumption of O2.
First of all, in the standard simulations there is already a mechanism included to account for some form of penetration, namely the availability of interstitial positions for small species, in particular hydrogen atoms. If this penetration mechanism is switched off, hydrogenation only occurs in the top layer of the ice and the final abundances drop to unrealistically low values as shown in Fig. 7(b) and (g). Furthermore, the shape of the H2O2 curves changes and the sharp transition from linear growth to steady state is no longer present. Also, OH cannot be properly produced since it needs a second lattice site upon production.
The parameter ξ in eqn (4) is used to determine the ease with which molecules can diffuse, which regulates the diffusion both on the surface and into the bulk. A value higher than for the standard simulations decreases the diffusion rate, which leads to a low penetration depth since molecules are not formed deep in the ice and the top layers therefore easily block further reactions. A value of ξ lower than for the standard simulations increases the diffusion rate; this allows for more HO2 production deeper in the ice. The abundance of stable species increases and that of the intermediates decreases as they are more accessible. A high diffusion rate, however, overestimates the abundance of OH and H2O for the sequential simulations and changes the OH evolution in the co-deposition simulations (not shown) so that it no longer follows the same trend as H2O2. Therefore, we conclude that the intermediate diffusion rate reproduces the experiments best.
This brings us back to the two possible scenarios suggested in the experimental paper.8 A higher O2 mobility is obtained through a lower barrier of O2 diffusion or by easier access to interstitial positions. From Fig. 7(d) and (i) it is clear that both have no effect. Therefore, the second scenario was tested by varying the H mobility as depicted in Fig. 7(e) and (j). A lower barrier results in a steeper increase in the abundances of H2O and H2O2 at 25 K and reproduces the transition between the initial rise and subsequent steady state behaviour at 15 K. Since this leads to a higher penetration depth at 25 K, we conclude that fast hydrogen diffusion could be a key feature in reproducing the competition between the reaction H + O2 and diffusion into the ice, confirming the suggestions made in ref. 8.
5 Recommendations for future studies
We have gained insight into the surface processes linked to the formation of water ice by simulating previous experimental results with Continuous-Time Random-Walk Monte Carlo simulations and explicitly taking into account relevant surface effects. A systematic approach to varying reaction barriers is applied here to obtain a best fit model and characterize the sensitivity of the full reaction network to the various reactions. With this model, experimental trends are reproduced and specific reaction barriers have been obtained as given in Table 5. These rates are compared to literature values and recommended for future use in astrochemical models. Below, we describe the best fit found by using our simulations and we highlight some astrochemical considerations.| Reaction | Ra (s−1) | Lit. Ea (K) |
|---|---|---|
| NOTE: the hydrogen diffusion barrier used was 53 K instead of the value listed in Table 3.a This work.b A value of 8.3 × 105 is used for the co-deposition simulations.c Reaction practically does not take place in our simulations.d See Section 4.2.3. | ||
| Temperature independent reactions | ||
| H + H → H2 | 1 × 1012 | — |
| H + O2 → HO2 | 1.1 × 105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b | ∼028,43 |
| H + HO2 → products | 1 × 1012 | T indep.29 |
| OH + OH | 56% | |
| H2O2 | 35% | |
| H2 + O2 | 2% | |
| H2O + O | 7% | |
| H + O → OH | 1 × 1012 | — |
| O + O → O2 | 1 × 1012![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c | — |
| H + O3 → O2 + OH | 1.1 × 105 | 45044 |
| H + OH → H2O | 1.1 × 105 | ∼043 |
5.1 Best fit
The activation energies given in Table 5 are largely similar to those of the standard simulations, except for:• the reaction barrier for the reaction H + O2 in the case of co-deposition simulations,
• the branching ratio of the reaction OH + OH, which is set to (R3a)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (R3b) = 90
(R3b) = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10,
10,
• the binding energy of hydrogen atoms to the surface, E, lowered to 53 K.
Key reactions are indicated in boldface in Table 5. In Fig. 8 the surface abundances as obtained by the best fit simulation are plotted versus time and can be compared to both the standard simulations and the experimental trends.
 | ||
| Fig. 8 Evolution of the surface abundance of O2 (red), H2O2 (light blue), H2O (dark blue), HO2 (green), OH (orange) and O3 (violet) as a function of time for a sequential hydrogenation simulation (left) and a co-deposition simulation (right) at 15 and 25 K compared to the experimental values. The thin lines represent the standard simulations, whereas the thick lines represent the simulation connected to the best fit parameters of Table 5. Note that the experimental surface abundances for the co-deposition simulations are in units of integrated absorbance, due to a lack of available band strengths for matrix isolated species. | ||
In general, a clear agreement between experimental and simulated data can be observed. Prominent is the reproduction of the H2O2 abundance evolution where the shape of the curves for sequential hydrogenation is correct as well as the overall behaviour under influence of a change in temperature. Moreover, with the ‘best fit’ settings the H2O production is roughly similar at 15 and 25 K, as it should be. Note that water does remain slightly overproduced at low temperature, likely due to the dynamics of the OH radical (diffusion versus a barrier for (R3)). Furthermore, the best fit settings are used to test once more the influence of the initial ice thickness. With these improved settings, indeed a small increase in H2O2 abundance is found at 25 K using a 16 ML thick surface, indicating an enhancement of hydrogen penetration.
Considering the co-deposition simulations, the ‘best fit’ runs are performed with parameters equal to those for sequential hydrogenation, except for the rate of the reaction of H + O2. As mentioned in Section 4.2.1, the angle dependence of this reaction is less of a restriction during co-deposition and a lower barrier for this reaction is better at reproducing the HO2 abundances. The overproduction of HO2 decreases slightly and the production of H2O2 increases with respect to the standard simulations. Moreover, the production of O3 is enhanced, which is in agreement with the experimental results, judging by Fig. 5.3 from ref. 9. Furthermore, the branching ratio of the reaction H + HO2 is found to be within the following range: (R2a):(R2b):(R2c):(R2d) = (56–65):(35–26):(2):(7). The effect of changing this translates into a changed OH/H2O2 ratio for co-deposition at 15 K while no change is observed for co-deposition at 25 K or sequential hydrogenation simulations. Note that the uncertainty in the dynamics of the OH radical can also affect the time evolution of the abundance of this species. The comparison made in Table 4 between different temperatures and H/O2 ratio remains unchanged.
Finally, we tried to reproduce the sequential hydrogenation study from Miyauchi et al. (2008) using the best fit parameters combined with experimental conditions mentioned in ref. 6. We corrected for the different band strengths used as well as the systematic shift in temperature reading of 2 K (compare Fig. 2.6 in ref. 24 and Fig. 3 in ref. 42). Our simulations confirm their experimentally observed trends to within 50%, in terms of H2O and H2O2 abundance as well as evolving trends in time.
5.2 Astrochemical considerations
Monte Carlo simulations have the potential to bridge the difference in conditions (time constraints, abundances and fluxes) between experiments and the interstellar medium by investigating surface reaction mechanisms under first laboratory, and then interstellar medium conditions.For instance, a high hydrogen diffusion rate in O2 ice is necessary to reproduce the large penetration depth observed experimentally. However, the penetration depth is a bulk effect, which is largely absent under astrochemical conditions. A pure O2 ice is not likely to be present in space and diffusion will be restricted mainly to the surface layers. In this work the goal is to understand the physico-chemical principles, and therefore the penetration depth is an effect that does need to be investigated.
Penetration depth plays a somehow less important role in the co-deposition simulations and since most features are correctly reproduced, we are confident that this set of parameters can be used in astrochemically relevant simulations to reproduce observations of water in different regions of the interstellar medium. This will also be the topic of a future study in which the influence of directionality in a hot diffusion mechanism will be incorporated.
Another important difference between experiments and astronomical observations is the abundance of formed solid H2O2 with respect to H2O. Starting from O2, a high abundance of H2O2 is found. Here we show that a relatively slow destruction of H2O2 explains the high accumulation of this species. Fig. 2 in ref. 9 indicates that a high and more interstellar relevant H/O2 ratio in co-deposition experiments is in favor of water formation. A more detailed study of the role of the H2O2 surface destruction channel (R4) within the whole reaction network under interstellar conditions is highly needed. Du et al. used a gas–grain model to reproduce the observed gas-phase abundance of H2O2 in ρ Oph A using a low barrier of 92 K for the surface reaction (R4).46 They found a very high gas-phase H2O2 abundance for a range of physical conditions which can be explained by the lack of gas-phase destructive mechanisms. Moreover, the abundance of surface H2O2 as obtained in their model is affected by the height of the barrier of reaction (R4).47 Increasing the barrier for reaction (R4) to our values would result in higher solid H2O2 abundances, further strengthening their and our suggestion to investigate the surface formation and destruction of H2O2 under interstellar relevant conditions in more depth.
The unknown diffusive behaviour of radical species, such as OH and H, is key to predict water formation under conditions relevant to the interstellar medium. However, experiments investigating diffusion are scarce due to the non-trivial competition with the high reaction probabilities involved. In the present study the two most relevant species in this respect are OH and H. The first because the experimental detection in co-deposition experiments poses a challenge as reaction (R4) was initially thought to occur barrierless. Furthermore, the diffusion of hydrogen on a surface was studied experimentally only by Katz et al. in 1999 and barriers found on carbon and silicate surfaces are not necessarily applicable to icy grains as well.48,49 Although the H diffusion is not fully constrained, it is a key parameter for our simulations as we extensively discussed in Section 4.3.
Finally, for astrochemical applications, the reactions with H2, here discussed in Section 4.2.6, are actually relevant to dark cloud conditions.3 Since molecular hydrogen possesses a rather strong intramolecular bond, barriers are typically high and tunneling is required to increase the rate of reaction with other ice species. This tunneling should scale with the so-called effective mass of the total system, since the system needs to be considered as a whole as outlined in ref. 36. This is by no means trivial and depends strongly on the binding of the molecule with the surface as well as on the evolution of the effective mass with reaction coordinate.50 Also here further dedicated experimental research as well as (theoretical) modeling to study reactions with H2 is needed for a deeper understanding of the full reaction scheme.
5.3 Practical use of the best fit parameters
In our Monte Carlo simulations the competition between different processes for a single species is explicitly taken into account. This is not easy to implement in classic rate equation models. However, in the interstellar medium, ice chemistry is limited by diffusion of surface species. Especially in dark molecular clouds, species on the surface are thermalized before engaging in reactions. Therefore, reactions with high rates (either due to a low activation energy or the result of tunneling) will dominate.Here we find a number of key reactions for the O2 + H route, as summarized in Table 5. When implementing these reaction rates in (astrochemical) models, the rates and activation energies given in Table 5 need to be considered in such a way that (i) the ratio between two reaction rates corresponds to the ratio found here and (ii) the rates are scaled according to the prefactor being used that amounts here to 1 × 1012 s−1.
6 Conclusions
Solid state hydrogenation reactions of O2 ice have been simulated with a Continuous-Time Random-Walk Monte Carlo method, explicitly taking into account the recent findings of a number of experimental studies. A strategy of systematically varying the different processes at play in the simulations, and comparing the outcome with experimental values, allows us to derive the key processes. In this way, we can gain insight into the actual processes taking place. Our model consists of a combination of reaction barriers (or activation energies) and binding energies for all species present in the reaction network (Fig. 1). In order to probe the large parameter space, we selected four previously performed different experiments. These are sequential hydrogenation and co-deposition experiments at 15 and 25 K that are all reproduced with a single set of parameters. The best fit model reproduces experimentally observed trends using the binding energies given in Table 2, complemented with the reaction barriers given in Table 5. From an extensive set of simulations of the selected laboratory data, we conclude the following:• the key reactions for the reaction route starting from O2 are (R1) H + O2, (R2) H + HO2, (R3) OH + OH, (R4) H + H2O2 and (R5) H + OH,
• a relatively slow destruction of H2O2 explains the high accumulation of this species,
• a high hydrogen diffusion rate is necessary to reproduce the large penetration depth of H into the O2 ice observed experimentally, and
• the diffusive behaviour of radical species, such as OH and H, is a key parameter.
Acknowledgements
We thank Gleb Fedoseev, Carina Arasa and Xander Tielens for helpful and stimulating discussions. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA) and grant 614.001.008 from the Netherlands Organisation for Scientific Research (NWO) within the Dutch Astrochemistry Network and a Vici Grant, and by the European Community's Seventh Framework Programme FP7/2007-2013 under grant agreement 238358 (LASSIE). H.M.C. acknowledges financial support by the European Research Council (ERC-2010-StG, Grant Agreement No. 259510-KISMOL). Support for S.I. from the Niels Stenson Fellowship and the Marie Curie Fellowship (FP7-PEOPLE-2011-IOP-300957) is gratefully acknowledged.References
- E. L. Gibb, D. C. B. Whittet, W. A. Schutte, A. C. A. Boogert, J. E. Chiar, P. Ehrenfreund, P. A. Gerakines, J. V. Keane, A. G. G. M. Tielens, E. F. van Dishoeck and O. Kerkhof, Astrophys. J., 2000, 536, 347–356 CrossRef.
- A. G. G. M. Tielens and W. Hagen, Astron. Astrophys., 1982, 114, 245–260 CAS.
- H. M. Cuppen and E. Herbst, Astrophys. J., 2007, 668, 294–309 CrossRef CAS.
- K. Hiraoka, T. Miyagoshi, T. Takayama, K. Yamamoto and Y. Kihara, Astrophys. J., 1998, 498, 710–715 CrossRef CAS.
- F. Dulieu, L. Amiaud, E. Congiu, J.-H. Fillion, E. Matar, A. Momeni, V. Pirronello and J. L. Lemaire, Astron. Astrophys, 2010, 512, A30 CrossRef.
- N. Miyauchi, H. Hidaka, T. Chigai, A. Nagaoka, N. Watanabe and A. Kouchi, Chem. Phys. Lett., 2008, 456, 27–30 CrossRef CAS.
- Y. Oba, N. Miyauchi, H. Hidaka, T. Chigai, N. Watanabe and A. Kouchi, Astrophys. J., 2009, 701, 464–470 CrossRef CAS.
- S. Ioppolo, H. M. Cuppen, C. Romanzin, E. F. van Dishoeck and H. Linnartz, Phys. Chem. Chem. Phys., 2010, 12, 12065–12076 RSC.
- H. M. Cuppen, S. Ioppolo, C. Romanzin and H. Linnartz, Phys. Chem. Chem. Phys., 2010, 12, 12077–12088 RSC.
- H. Mokrane, H. Chaabouni, M. Accolla, E. Congiu, F. Dulieu, M. Chehrouri and J. L. Lemaire, Astrophys. J., Lett., 2009, 705, L195–L198 CrossRef CAS.
- C. Romanzin, S. Ioppolo, H. M. Cuppen, E. F. van Dishoeck and H. Linnartz, J. Chem. Phys., 2011, 134, 084504 CrossRef CAS.
- J.-P. Baluteau, P. Cox, J. Cernicharo, D. Pequignot, E. Caux, T. Lim, B. Swinyard, G. White, M. Kessler, T. Prusti, M. Barlow, P. E. Clegg, R. J. Emery, I. Furniss, W. Glencross, C. Gry, M. Joubert, R. Liseau, B. Nisini, P. Saraceno, G. Serra, C. Armand, M. Burgdorf, A. Digiorgio, S. Molinari, M. Price, D. Texier, S. Sidher and N. Trams, Astron. Astrophys., 1997, 322, L33–L36 CAS.
- B. Larsson, R. Liseau, L. Pagani, P. Bergman, P. Bernath, N. Biver, J. H. Black, R. S. Booth, V. Buat, J. Crovisier, C. L. Curry, M. Dahlgren, P. J. Encrenaz, E. Falgarone, P. A. Feldman, M. Fich, H. G. Florén, M. Fredrixon, U. Frisk, G. F. Gahm, M. Gerin, M. Hagström, J. Harju, T. Hasegawa, Å. Hjalmarson, L. E. B. Johansson, K. Justtanont, A. Klotz, E. Kyrölä, S. Kwok, A. Lecacheux, T. Liljeström, E. J. Llewellyn, S. Lundin, G. Mégie, G. F. Mitchell, D. Murtagh, L. H. Nordh, L.-Å. Nyman, M. Olberg, A. O. H. Olofsson, G. Olofsson, H. Olofsson, G. Persson, R. Plume, H. Rickman, I. Ristorcelli, G. Rydbeck, A. A. Sandqvist, F. V. Schéele, G. Serra, S. Torchinsky, N. F. Tothill, K. Volk, T. Wiklind, C. D. Wilson, A. Winnberg and G. Witt, Astron. Astrophys., 2007, 466, 999–1003 CrossRef CAS.
- M. R. Hogerheijde, E. A. Bergin, C. Brinch, L. I. Cleeves, J. K. J. Fogel, G. A. Blake, C. Dominik, D. C. Lis, G. Melnick, D. Neufeld, O. Panić, J. C. Pearson, L. Kristensen, U. A. Yildiz and E. F. van Dishoeck, Science, 2011, 334, 338–340 CrossRef CAS.
- B. Parise, P. Bergman and F. Du, Astron. Astrophys., 2012, 541, L11 CrossRef.
- P. Bergman, B. Parise, R. Liseau, B. Larsson, H. Olofsson, K. M. Menten and R. Güsten, Astron. Astrophys, 2011, 531, L8 CrossRef.
- E. F. van Dishoeck, L. E. Kristensen, A. O. Benz, E. A. Bergin, P. Caselli, J. Cernicharo, F. Herpin, M. R. Hogerheijde, D. Johnstone, R. Liseau, B. Nisini, R. Shipman, M. Tafalla, F. van der Tak, F. Wyrowski, Y. Aikawa, R. Bachiller, A. Baudry, M. Benedettini, P. Bjerkeli, G. A. Blake, S. Bontemps, J. Braine, C. Brinch, S. Bruderer, L. Chavarría, C. Codella, F. Daniel, T. de Graauw, E. Deul, A. M. di Giorgio, C. Dominik, S. D. Doty, M. L. Dubernet, P. Encrenaz, H. Feuchtgruber, M. Fich, W. Frieswijk, A. Fuente, T. Giannini, J. R. Goicoechea, F. P. Helmich, G. J. Herczeg, T. Jacq, J. K. Jørgensen, A. Karska, M. J. Kaufman, E. Keto, B. Larsson, B. Lefloch, D. Lis, M. Marseille, C. McCoey, G. Melnick, D. Neufeld, M. Olberg, L. Pagani, O. Panić, B. Parise, J. C. Pearson, R. Plume, C. Risacher, D. Salter, J. Santiago-García, P. Saraceno, P. Stäuber, T. A. van Kempen, R. Visser, S. Viti, M. Walmsley, S. F. Wampfler and U. A. Yildiz, Publ. Astron. Soc. Pac., 2011, 123, 138–170 CrossRef.
- S. Ioppolo, H. M. Cuppen, C. Romanzin, E. F. van Dishoeck and H. Linnartz, Astrophys. J., 2008, 686, 1474–1479 CrossRef CAS.
- Q. Chang, H. M. Cuppen and E. Herbst, Astron. Astrophys., 2005, 434, 599–611 CrossRef CAS.
- H. M. Cuppen and E. Herbst, Mon. Not. R. Astron. Soc., 2005, 361, 565–576 CrossRef CAS.
- H. M. Cuppen, personal communication.
- H. C. Kang and W. H. Weinberg, J. Chem. Phys., 1989, 90, 2824–2830 CrossRef CAS.
- R. T. Garrod, V. Wakelam and E. Herbst, Astron. Astrophys., 2007, 467, 1103–1115 CrossRef CAS.
- G. W. Fuchs, H. M. Cuppen, S. Ioppolo, C. Romanzin, S. E. Bisschop, S. Andersson, E. F. van Dishoeck and H. Linnartz, Astron. Astrophys., 2009, 505, 629–639 CrossRef CAS.
- S. Cazaux, V. Cobut, M. Marseille, M. Spaans and P. Caselli, Astron. Astrophys., 2010, 522, A74 CrossRef.
- G. W. Fuchs, K. Acharyya, S. E. Bisschop, K. I. Öberg, F. A. van Broekhuizen, H. J. Fraser, S. Schlemmer, E. F. van Dishoeck and H. Linnartz, Faraday Discuss., 2006, 133, 311–345 RSC.
- K. Acharyya, G. W. Fuchs, H. J. Fraser, E. F. van Dishoeck and H. Linnartz, Astron. Astrophys., 2007, 466, 1005–1012 CrossRef CAS.
- S. Walch and R. Duchovic, J. Chem. Phys., 1991, 94, 7068–7075 CrossRef CAS.
- L. F. Keyser, J. Phys. Chem., 1986, 90, 2994–3003 CrossRef CAS.
- S. H. Mousavipour and V. Saheb, Bull. Chem. Soc. Jpn., 2007, 80, 1901–1913 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys, 2004, 4, 1461–1738 CrossRef CAS.
- K. Koussa, M. Bahri, N. Jaïdane and Z. Ben Lakhdar, THEOCHEM, 2006, 770, 149–156 CrossRef.
- W. Tsang and R. F. Hampson, J. Phys. Chem. Ref. Data, 1986, 15, 1087–1279 CrossRef CAS.
- M. Yang, D. H. Zhang, M. A. Collins and S. Lee, J. Chem. Phys., 2001, 115, 174–178 CrossRef CAS.
- V. L. Orkin, S. N. P. G. A. Kozlov and M. J. Kurylo, J. Phys. Chem. A, 2006, 110, 6978–6985 CrossRef CAS.
- Y. Oba, N. Watanabe, T. Hama, K. Huwahata, H. Hidaka and A. Kouchi, Astrophys. J., 2012, 749, 67 CrossRef.
- A. B. Vakhtin, D. C. McCabe, A. R. Ravishankara and S. R. Leone, J. Phys. Chem. A, 2003, 107, 10642–10647 CrossRef CAS.
- G. L. Vaghjiani, A. R. Ravishankara and N. Cohen, J. Phys. Chem., 1989, 93, 7833–7837 CrossRef CAS.
- F. Atadinç, H. Günaydin, A. S. Özen and V. Aviyente, Int. J. Chem. Kinet., 2005, 37, 502–514 CrossRef.
- R. J. Buszek, M. Torrent-Sucarrat, J. M. Anglada and J. S. Francisco, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS.
- C. C. Kircher and S. P. Sander, J. Phys. Chem., 1984, 88, 2082–2091 CrossRef CAS.
- N. Watanabe, H. Hidaka and A. Kouchi, Astrochemistry – From Laboratory Studies to Astronomical Observations, 2006, pp. 122–127 Search PubMed.
- S. R. Sellevåg, Y. Georgievskii and J. A. Miller, J. Phys. Chem. A, 2008, 112, 5085–5095 CrossRef.
- J. H. Lee, J. V. Michael, W. A. Payne and L. J. Stief, J. Chem. Phys., 1978, 69, 350–354 CrossRef CAS.
- D. L. Baulch, C. J. Cobos, R. A. Cox, C. Esser, P. Frank, T. Just, J. A. Kerr, M. J. Pilling, J. Troe, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 1992, 21, 411–734 CrossRef CAS.
- F. Du, B. Parise and P. Bergman, Astron. Astrophys., 2012, 538, A91 CrossRef.
- F. Du, B. Parise and P. Bergman, Astron. Astrophys., 2012, 544, C4 CrossRef.
- N. Katz, I. Furman, O. Biham, V. Pirronello and G. Vidali, Astrophys. J., 1999, 522, 305–312 CrossRef CAS.
- E. Matar, E. Congiu, F. Dulieu, A. Momeni and J. L. Lemaire, Astron. Astrophys., 2008, 492, L17–L20 CrossRef CAS.
- R. P. Bell, The tunnel effect in chemistry, Chapman and Hall, London, 1980 Search PubMed.
Footnote |
| † Current address: Division of Geological and Planetary Sciences, California Institute of Technology, 1200 E. California Blvd., Pasadena, California 91125, USA. |
| This journal is © the Owner Societies 2013 |
