π-Electron ring-currents and bond-currents in [10,5]-Coronene and related structures conforming to the ‘Annulene-Within-an-Annulene’ model

Abstract

A series of hypothetical conjugated structures is defined; the series is called the p-Coronenes and the first four members of it are shown to respect the ‘Annulene-Within-an-Annulene’ (AWA) model when tested by means of Hückel–London–Pople–McWeeny (HLPM) π-electron ring-current and bond-current calculations. The first member of this series, 5-Coronene, is also a member of the regular [r,s]-Coronene series, where it is known as [10,5]-Coronene. It is shown that, as p is varied (with p always odd, and with p > 3) through the values 5, 7, 9, 11, etc., the resulting structures alternate between a ‘[4n + 2]-Annulene-Within-a-[4m]-Annulene’ (if (p − 1) is divisible by 4) and a ‘[4n]-Annulene-Within-a-[4m + 2]-Annulene’ (if (p − 1) is not divisible by 4). It is therefore claimed that the p-Coronenes constitute an ideal series for testing the AWA model. It is also remarked that each member of the p-Coronene series has only four Kekulé structures, and that the ‘spokes’ or ‘transverse’ bonds connecting the central [p(p − 3)]-membered ring to the outer [p(p − 1)]-membered periphery always have a Pauling bond-order of zero, ensuring that the outer and inner rings are ‘decoupled’; such bonds also bear zero bond-current, by symmetry. It is argued that the former property of these transverse bonds, rather than the latter, determines that the p-Coronenes obey the AWA rule—which is in fact an exception, rather than a ‘rule’ per se. The paper concludes by explicitly stating our philosophy that a conceptually simple model depending on no subjective (or any other) parameters whatsoever can give intuitive chemical insight for certain systems equal to that available from far-more complex methods such as ab initio calculations—what Coulson once famously called ‘primitive patterns of understanding’.

---

Introduction

[10,5]-Coronene (the hypothetical structure whose carbon–carbon connectivity is labelled (I) in Fig. 1) was expressly conceived by Bochvar et al.¹ and, much later, adopted by Monaco et al.,² because both sets of authors required a planar, conjugated, ‘super-ring’³ system with [4n + 2] carbon atoms (where, in this case, n = 2) in its central ring and with [4m] carbon atoms (with, here, m = 5) on its periphery. It therefore constitutes a paradigm for testing the π-electron ring-currents and bond-currents in a well-defined ‘[4n + 2]-annulene-within-a-[4m]-annulene’ in the more-general context of the ‘Annulene-Within-an-Annulene’ (AWA) model (which, though sometimes called ‘the AWA rule’, is in fact a ‘rule’ in which most cases are found to be exceptions).^2,4–9 Bochvar et al. unambiguously defined the structure as follows:¹ ‘It is assumed that the C₃₀H₁₀ molecule is planar and has D_10h-symmetry.’ A further notable aspect of (I) is that, if all carbon–carbon bonds are taken to be of equal length, such an idealised [10,5]-Coronene is geometrically planar.^1,2 This is because two adjacent regular pentagons on the perimeter (each with interior angle 108°) tessellate exactly, in the plane, with the central regular decagon of the same side-length (with interior angle 144°), as the sum of the angles at any internal carbon atom in (I) is 108° + 108° + 144° = 360°. Bochvar et al.¹ initially introduced this hypothetical structure, and considered its geometrical and π-electron properties, some forty years ago.¹

Fig. 1 The carbon–carbon connectivities of [10,5]-Coronene (also known here as 5-Coronene) ((I)) and three larger p-Coronenes, ((II)–(IV)), with p = 7, 9 and 11, respectively.

By means of the following three approaches, Monaco et al.² have shown that [10,5]-Coronene (I) conforms to the AWA model:^4–9

(a) Ab initio ‘ipso-centric’ current-density maps;^2,5–7,10

(b) ‘Pseudo-π’ calculations;¹¹

(c) Simple Hückel considerations.¹²

From each of the above, Monaco et al.² concluded that there is a paramagnetic (clockwise) π-electron current flowing around the [4m]-membered perimeter of [10,5]-Coronene (I), and a net π-electron current circulating in the diamagnetic (anti-clockwise) direction around the bonds of its [4n + 2]-membered inner-ring.² This finding is unusual because most ‘super-ring’³ conjugated systems seem to violate the AWA model^4–9 when its predictions are confronted with the results of ab initio ipso-centric calculations of the type frequently presented by Fowler et al.^5–7,10 In our own work, we have been applying the Hückel¹²–London¹³–Pople¹⁴–McWeeny¹⁵ (HLPM) ‘topological’ approach^16–18 and have, thereby, likewise concluded^8,9—though from these HLPM criteria^16–18—that the AWA model^4–9 is not respected by the majority of such structures so far investigated.

We draw attention here to the fact that [10,5]-Coronene (I) is merely the first of a homologous series of hypothetical conjugated structures that may be formed by joining a number, 2p, of p-sided regular polygons in such a manner that they join back onto themselves. The first four members of the series that we are here calling the ‘p-Coronenes’ are shown in Fig. 1: they are (I)—referred to, when considered as a member of this series, as ‘5-Coronene’—and 7-Coronene (II), 9-Coronene (III), and 11-Coronene (IV). We further demonstrate that these p-Coronenes form an ideal series for testing the AWA model^4–9 and, in view of the esteem in which the original London approach¹³ is still held,^6,10,19,20 we investigate the magnetic properties of (I)–(IV) by applying the HLPM formalism^12–18 to calculate π-electron ring-currents and bond-currents in these structures. These more-simplistic calculations agree with the conclusions of Monaco et al.²—based, in the main, on more-sophisticated methods of calculation—that the bond currents in [10,5]-Coronene (I) are in accord with the qualitative predictions of the AWA model^4–9 and we extend this conclusion to the other structures, ((II)–(IV)), of the p-Coronene series that are here investigated.^21,22

The p-Coronenes

By considering, in the general case, the internal-angle sum in the central ring, we have verified that, on purely geometrical grounds—though this is not taking into account, of course, any considerations about potential molecular strain, if these structures were actually extant molecules—such p-Coronenes tessellate, forming a structure that has

(a) An outer perimeter of length p(p − 1);

(b) A central ring of length p(p − 3)—which, however, is a regular [p(p − 3)]-gon only in the case where p = 5 (that is to say, only in the case of [10,5]-Coronene).¹

Furthermore, we have proved (inductively) that the following rules apply:

(a) If (p − 1) is divisible by 4, then

(i) the periphery will be of the ‘[4m]’ type

(with m = ¼p(p − 1)), and

(ii) the central ring will be of the ‘[4n + 2]’ type

(with n = ¼{(p − 1)(p − 2) − 4}).

(p = 5 (structure (I)) and p = 9 (structure (III)) are examples of this.)

(b) If (p − 1) is NOT divisible by 4, then exactly the opposite is true:

(i) the periphery will be of length [4m + 2]

(with m = ¼(p + 1)(p − 2)) and

(ii) the central ring will be of length [4n]

(with n = ¼p(p − 3)).

(p = 7 (structure (II)) and p = 11 (structure (IV)) are like this.)

It will be seen, therefore, that this p-Coronene series has, in the present context, the very pertinent property that, as p is varied (with p always odd, and with p > 3) through the values 5, 7, 9, 11, etc., the resulting structures alternate between a ‘[4n + 2]-Annulene-Within-a-[4m]-Annulene’ (if (p − 1) is divisible by 4) and a ‘[4n]-Annulene-Within-a-[4m + 2]-Annulene’ (if (p − 1) is not divisible by 4).

In addition, there is one other singular feature of this series, which is highly relevant for our purposes. Monaco et al.² observed that [10,5]-Coronene (I) has only four Kekulé structures. These comprise the two ways in which the bonds in the outer perimeter may alternate, single and double, and, for each of these two ways for the outer ring, there are two ways in which the perimeter of the central ring may likewise be depicted with alternating single- and double-bonds. What Bochvar et al.¹ have called the ‘transverse’ bonds and Balaban et al.⁷ have dubbed the ‘spokes’ bonds (that is, those bonds that symmetrically connect the outer perimeter to the inner ring) are formally ‘single’ in any Kekulé structure that can be devised for the system as a whole. Another way of succinctly indicating this property is to note that these spokes⁷/transverse¹ bonds have zero⁷ Pauling bond-order.²³ It can be shown by induction that this is indeed the case for this entire series of p-Coronenes. In other words, the outer and inner rings of the structures in this series are always what Fowler et al.^2,5–7 have previously described as ‘decoupled’. (As an example, the four Kekulé structures for 7-Coronene (structure (II)) are explicitly illustrated in Fig. 2.)

Fig. 2 The four Kekulé structures in structure (II) (7-Coronene).

We therefore submit that the p-Coronenes¹ constitute an ideal series for testing the AWA model,^4–9 in that the inner and outer rings are ‘decoupled’,^2,5–7 and, as the series is traversed, with p successively talking on the values 5, 7, 9, 11, etc., ‘[4n + 2]-within-[4m]’ systems alternate with ones that are ‘[4n]-within-[4m + 2]’.

Calculations

HLPM^12–15 π-electron ring-currents²⁴ were calculated as described in ref. 16–18, by application of the equationwhere J_i is the ring-current intensity in the ith ring of the conjugated system and J_benzene is the corresponding ring-current intensity calculated, by the same method, for benzene (which has a numerical value, in these units, of (1/9)).¹⁵ It is immediately seen, therefore, that the HLPM ring-currents—being, as they are, expressed as a ratio ((J_i/J_benzene))—are entirely dimensionless quantities, devoid of any units; the same is true of the bond currents that are derivable from these ring currents. The calculation is based on an arbitrary spanning-tree^15,25,26 and the summations in the above equation are over what McWeeny, in his classic paper,¹⁵ referred to as ‘circuit-completing bonds’. β is the standard Hückel resonance-integral,¹²P_(μ) is the ordinary ‘field-free’ Coulson bond-order,¹² and the quantities β[small pi, Greek, macron]_(μ)(μ) and β[small pi, Greek, macron]_(μ)(ν) are what McWeeny¹⁵ defined as (respectively) the self- and mutual imaginary bond-bond polarisabilities of circuit-completing bonds μ and ν (likewise in the absence of a magnetic field). It is important for the philosophy of our approach to emphasise that all these quantities may be calculated solely from a knowledge of the molecular graph^25,27 of the conjugated system in question, and the eigenvalues and eigenvectors of its vertex adjacency-matrix,^25,28 which are latent in the structure and which are pre-determined as soon as the carbon-atom adjacencies are specified.¹⁶ It is also vital to note that P_(μ), β[small pi, Greek, macron]_(μ)(μ) and β[small pi, Greek, macron]_(μ)(ν) are calculable solely from knowledge of that molecular graph,^25,27,28without recourse to any parameters. Details of their explicit definition are to be found in the appendix of ref. 25 (which also corrects some typographical errors in McWeeny's original paper¹⁵). S_(μ) is the signed (algebraical) area of the μth circuit (i.e., the enclosed area formed when the μth circuit-completing bond, only, is inserted into the spanning tree on which the calculation is being based^15,16,25,29). These areas are to be counted positive if the arrow on the μth circuit-completing bond (which bears an arbitrarily assigned direction) points in the anti-clockwise sense around the circuit that it completes (the μth circuit), and are to be counted negative if that arrow points in the clockwise sense around the circuit that the μth circuit-completing bond completes.^16,29 The quantities Cⁱ_(μ) are likewise purely topological in nature and take on the values 0, +1 or −1 according to whether (respectively) (a) the ith ring does not lie within the μth circuit, (b) the ith ring lies within the circuit completed by the μth circuit-completing bond and that circuit-completing bond is directed in the anti-clockwise sense around the circuit (the μth one) that it completes, (c) the ith ring lies within the μth circuit but the μth circuit-completing bond points in the clockwise direction around the μth circuit. For detailed examples and more explanation of how the method is applied in practice the reader is referred to ref. 15, 16, 25, 29 and 34.

It is important to specify the assumptions that have been made about ring areas. Strictly, our ‘topological’ approach^16–18 prescribes that the areas of all rings should be taken as the areas of regular polygons of the appropriate number of sides (of unit length). Whilst there is no difficulty in implementing this policy for the p-sided polygons on the peripheries of structures (I)–(IV), this assumption is not realistic for the (irregular¹) polygon that forms the central ring in structures (II)–(IV); this is because the areas when the central polygons are considered as if they were regular polygons are all much larger than the actual geometrical areas that the central rings are calculated to have if the tessellated polygons are to be arranged as they are in Fig. 1. Therefore, in the calculations presented in Table 1, (a) that on [10,5]-Coronene ((I)) is genuinely a ‘topological’ HLPM result (because the geometrical requirements determine that the central ring in (I) is, in any case, a regular polygon^1,2), but (b) the others (for structures (II)–(IV)) are not purely topological. Our computations on (II)–(IV) should therefore properly be described as being HLPM calculations^12–16 with the peripheral polygons being taken as regular polygons but with the central polygon having the actual geometrical area that the arrangement of the peripheral polygons (Fig. 1) requires. These central-ring areas were calculated by elementary trigonometry. The values for these geometrical areas of those central rings are as follows (expressed as a ratio to the ring area of a standard benzene-hexagon), with the quantity in brackets being the area of a regular polygon of the corresponding number of sides (of unit length):

Structure (I):	2.961502364	(2.961502364)
Structure (II):	17.05800409	(23.91258503)
Structure (III):	55.11474128	(89.21449168)
Structure (IV):	134.7276998	(237.0931674)

Table 1 π-Electron ring-currents and bond-currents in structures (I)–(IV) based on calculated geometrical areas for the central rings and areas of the appropriate regular-polygons for the surrounding, peripheral rings

No. of sides, p, in the rings on the periphery	Length, p(p − 1), of the outer perimeter	Size, p(p − 3), of the inner ring	Ring current in the outer rings	Ring current in the central ring	Bond current around the outer perimeter	Bond current around the central ring	Is this compliant with the Annulene-Within-an-Annulene model?
5 (structure (I))	20 ([4m])	10 ([4n + 2])	−1.57	−0.16	1.57 (paramagnetic direction)	1.41 (diamagnetic direction)	Yes
7 (structure (II))	42 ([4m + 2])	28 ([4n])	4.01	3.27	4.01 (diamagnetic direction)	0.74 (paramagnetic direction)	Yes
9 (structure (III))	72 ([4m])	54 ([4n + 2])	−1.16	3.59	1.16 (paramagnetic direction)	4.75 (diamagnetic direction)	Yes
11 (structure (IV))	110 ([4m + 2])	88 ([4n])	8.91	8.75	8.91 (diamagnetic direction)	0.16 (paramagnetic direction)	Yes

---

It can be seen that these central-ring areas grow very rapidly, as the series is progressed.

Calculations were initially carried out in single precision and were, in the first instance, based on un-branched spanning-trees²⁵—in order to be able to take the usual advantage of McWeeny's original unitary-transformation,¹⁵ which requires the ring-current calculation to be founded on a spanning tree that represents a semi-Hamiltonian path²⁵ through the molecular graph under study. This policy, however, gave rise to considerable, and unacceptable, instability in the ring-current intensities calculated for the ten symmetrically-equivalent five-membered rings in [10,5]-Coronene (I). We therefore sought to correct this by repeating the calculations, but this time basing them on branched spanning-trees, for which circuit areas^15,16 are usually smaller; in such cases, the more-general unitary-transformation proposed by Gayoso and Boucekkine²⁶ had to be invoked in order to be able to effect the ring-current calculations. Still, however, there was instability, with the independently calculated ring-current in each of the symmetrically equivalent five-membered rings not converging to the same values when rounded to three places of decimals. It was only when we combined

(a) using double-precision in the computational manipulations and

(b) basing the calculations on a branched spanning-tree

that we finally obtained values of ring-current intensities in all ten of the symmetrically equivalent peripheral pentagonal rings that were identical when corrected to three decimal-places, the accuracy to which, in the past,^8,9,16–18 we have routinely quoted our calculated HLPM ring-currents and bond-currents. Because round-off errors could also potentially arise from the very large circuit-areas that are encountered in the case of structures (II)–(IV)—even when a branched spanning-tree^25,26,29 is used—we judge that it is appropriate in those cases to limit quotation of bond- and ring-currents to only two places of decimals; for consistency, therefore, the corresponding data for structure (I) ([10,5]-Coronene) are likewise quoted to only two decimal-places, even though, in this case, we would have been confident in expressing our results to three decimal-places. (Furthermore, these calculations on [10,5]-Coronene, reported in the first row of Tables 1 and 2, have since been independently verified by Professor P. W. Fowler.³⁰)

Table 2 ‘Topological’ π-electron ring-currents and bond-currents in structures (I)–(IV), where the areas of all polygons—including, even, the central one—are considered to be those appropriate to regular polygons with the corresponding number of sides

No. of sides, p, in the rings on the periphery	Length, p(p − 1), of the outer perimeter	Size, p(p − 3), of the inner ring	Ring current in the outer rings	Ring current in the central ring	Bond current around the outer perimeter	Bond current around the central ring	Is this compliant with the Annulene-Within-an-Annulene model?
a Note that the ‘topological’ ring- and bond-currents for [10,5]-Coronene ((I))—and only for (I)—are the same as the corresponding ‘geometric’ ring- and bond-currents displayed in Table 1 (because, uniquely in this series,^1 the central ring in (I) is in any case required by the geometry of the situation to be a regular polygon^1). The data for structure (I) therefore represent π-electron ring-currents and bond-currents that are, at the same time, both ‘topological’ and ‘geometrical’ in nature. The data in this Table for (II)–(IV), however, represent what may be regarded as purely ‘topological’ calculations.
5^a (structure (I))	20 ([4m])	10 ([4n + 2])	−1.57	−0.16	1.57 (paramagnetic direction)	1.41 (diamagnetic direction)	Yes
7 (structure (II))	42 ([4m + 2])	28 ([4n])	4.80	3.66	4.80 (diamagnetic direction)	1.14 (paramagnetic direction)	Yes
9 (structure (III))	72 ([4m])	54 ([4n + 2])	−1.44	6.03	1.44 (paramagnetic direction)	7.47 (diamagnetic direction)	Yes
11 (structure (IV))	110 ([4m + 2])	88 ([4n])	13.36	12.79	13.36 (diamagnetic direction)	0.57 (paramagnetic direction)	Yes

---

Results and discussion

The results are summarised in Table 1. It should be emphasised that the set of ring currents and the set of bond currents for each structure are consistent with each other and are connected by a common compliance with the microscopic analogy of Kirchhoff's first law (‘Conservation of Currents at a Junction’) for macroscopic electrical-networks.^25,29,31,32 As is implied from eqn (1), ring currents are expressed as a ratio to the corresponding value calculated, by the same method, for benzene and the same goes for the bond currents that are derived from these ring currents. All currents are, accordingly, dimensionless quantities, as was already noted in the section entitled ‘Calculations’.

We discuss the results with reference to the specific example of [10,5]-Coronene ((I)). It is seen from Table 1 that the ring-current intensities in the peripheral five-membered rings are −1.57 (that is, paramagnetic) and the ring-current intensity calculated for the central decagonal ring is also paramagnetic, at −0.16. Because the outer periphery is formed by bonds in the five-membered rings that are unshared with any other ring, the direction of current flow around the periphery is seen to be paramagnetic (that is, clockwise), with an intensity of 1.57—in qualitative accord with the AWA model,^4–9 as this outer periphery is of length 20; (4m, with m = 5).

The situation with the central ten-membered ring is as follows: the bonds in that ring form a part of the peripheral pentagonal rings and, consequently, those rings would provide a current of intensity of 1.57 in what is, from the point of view of the central ring, the anti-clockwise (diamagnetic) direction. But these bonds are also a part of the central, decagonal ring around which there is a ring-current of −0.16. This would therefore make a contribution of 0.16 in the clockwise (paramagnetic) direction around the central ten-membered ring. The overall effect of this electronic competition between the outer rings and the inner ring, therefore, is that those bonds in the central, decagonal ring (each of which is shared with a peripheral pentagonal ring) have a net current of (1.57 − 0.16) = 1.41 in the anti-clockwise (diamagnetic) direction, so far as the central ring is concerned. Thus, despite the paramagnetic ring-current calculated for the decagonal ring, the actual π-electron flow around the central ten-membered ring—a [4n + 2]-ring, with n = 2—is in the anti-clockwise (diamagnetic) direction. This is entirely in accord with the qualitative predictions of the AWA model.^4–9 Finally, we note that the bond current in the spokes bonds⁷/transverse bonds¹ in (I) are all zero, by symmetry—as they are in (II)–(IV) and, indeed, in all subsequent p-Coronenes.

A similar analysis to the above may be given for the peripheral and central rings of structures (II)–(IV) and the results are summarised in the last three rows of Table 1. In every case, the ‘Annulene-Within-an-Annulene’ model^4–9 is seen to be respected.

Conclusions

Monaco et al.² showed that [10,5]-Coronene (I) conforms to the qualitative AWA rule^4–9 when tested by means of calculated ab initio ipso-centric π-electron current-density maps,^5–7,10 ‘pseudo-π’ calculations,¹¹ and simple Hückel¹² considerations. Our present investigation, in which the AWA model^4–9 was tested by means of the more rudimentary but intuitive HLPM approach,^12–15 has come to the same conclusion. Structures (II)–(IV) also comply with the AWA rule,^4–9 though we emphasise again that our calculations in the case of these three structures are not purely topological, for we incorporated actual, calculated, geometrical ring-areas for the central rings, which (as discussed in ref. 1) are not regular polygons in the case of (II)–(IV). In view of the very large ring-areas involved in these calculations, we did have sufficient curiosity to investigate the influence of the various assumptions that we have made about ring areas by repeating all these calculations using purely ‘topological’ ring-areas (those given in brackets in the section labelled ‘Calculations’)—that is, assuming that the central rings in (II)–(IV) have the area of a regular polygon with the same number of sides; the results are given in Table 2. Although the ring-current values were of course quantitatively different when this assumption was invoked, the conclusion was that all four structures did still qualitatively conform with the provisions of the AWA rule.^4–9,33

The question remains to be asked: why is the AWA model^4–9 respected in case of the p-Coronenes, defined here, but usually seems to fail spectacularly for the majority of ‘super-ring’³ systems?^5–10,34 Following Fowler et al.,^2,5–7,35 we suggest that the answer may possibly lie in the fact that, in most ‘super-ring’³ structures,^5–10 the spokes bonds⁷/transverse¹ bonds connecting the outer perimeters to the inner rings are ‘double’ bonds in some Kekulé structures that represent the systems as a whole, and ‘single’ in others. In other words, there is what Fowler et al.^2,5–7 call ‘coupling’ between the outer perimeter and the inner ring and, hence, the bonds in question generally have non-zero⁷ Pauling bond-orders.²³ We have already pointed out, however, in the section headed ‘Calculations’, that, in the p-Coronene series, the inner ring and the outer perimeter are always ‘decoupled’ in this sense because there are only ever four Kekulé structures—all illustrated, in the case of 7-Coronene ((II)), in Fig. 2—and in none of these four Kekulé structures are the spokes⁷/transverse¹ bonds represented as anything other than ‘single’ bonds. The central ring and the outer periphery—connected, as they are, by transverse¹ bonds that all have zero⁷ Pauling bond-order²³—are thus always ‘decoupled’^2,5–7 in the p-Coronene series. We therefore concur that the reason that the members of the p-Coronene series that we have examined respect the AWA rule,^4–9 whereas most super-ring³ structures do not,^5–10,34 is that, in the p-Coronene series, the ‘decoupling’ just described is always extant, whereas, in most ‘super-ring’³ systems, it is not.^{5–10,34–36}

The AWA-rule seems generally (and often indiscriminately) to be invoked by physical organic chemists apparently unaware of the relevance in this context of the intricacies of Graph Theory, Kekulé structures, and Molecular Orbital Theory—such as have been gone into here. In short, it should perhaps be emphasised more strongly than is usually the case that the original AWA model⁴ does in fact represent an exception, rather than a general rule.^2,5–9 In other words, we submit that the so-called ‘AWA rule’ is, in truth, a misnomer.

In conclusion, the Editor has invited us explicitly to spell out in detail why we favour using the HLPM^12–15 ‘topological’ formalism^16–18 to complement ostensibly more justifiable ab initio approaches, such as ref. 5–7, 10, 11, 21 and 24, and many others. Our philosophy here (and elsewhere^8,9,16–18) is that a conceptually simple model that depends on no subjective (or any other) parameters can give intuitive chemical insight for certain systems equal to that available from far-more complex methods such as ab initio calculations—what Coulson once famously called ‘primitive patterns of understanding’.³⁸

Our whole aim here has been to demonstrate how we can tie down when the AWA concept^2,4–9 is and is not expected to work on the basis of a model that needs absolutely no subjective—or, indeed, any other—parameters whatsoever, and that requires no more, as a starting-point, than a mere knowledge of the carbon–carbon σ-bond connectivity of the conjugated system under study (i.e., its ‘molecular graph’²⁷) and the areas of its constituent rings. In the case of the one structure ([10,5]-Coronene) of the general series defined and presented here that has been treated by a more-sophisticated method,² we have shown that qualitative agreement regarding that structure's compliance with the AWA model can be achieved between the simple and intuitive HLPM^12–15 ‘topological’ formalism^16–18 and an ostensibly more-refined calculation, effected by means of an ab initio approach.² Furthermore, another advantage of the HLPM ‘topological’ method^12–18 is that, although it is crude, it is capable of yielding quantitative ring-current and bond-current intensities (quoted in Tables 1 and 2 to two decimal-places) rather than pictorial current-density diagrams.²

As argued, once this molecular graph and these ring areas are established, the results and conclusions of an HLPM calculation depend on no parameters whatsoever. When investigating ring currents in polycyclic conjugated systems, it should be borne in mind that using more-sophisticated models, even though they may be labelled ‘ab initio’, does involve a choice of numerical values for parameters. To see this one need only glance, for example, at the section headed ‘Computational Details’ (page 848) of ref. 21b or that labelled ‘Ab Initio Calculations’ (page 7448) of the paper by Monaco et al.² (which was the starting point for the present investigation). It is clear that such methods—though, of course, properly classified as ‘ab initio’—do nevertheless need extensive ‘parameterisation’.

We therefore offer the HLPM approach for consideration as a vehicle that offers the Chemist an intuitive, parameter-independent appreciation—entirely complementary to, and not in any way intending to be competing with, ab initio calculations—of what happens to conjugated structures, such as those considered here, when they are in the presence of an external magnetic-field.

Acknowledgements

We should like to thank Professor P. W. Fowler, FRS, for stimulating discussions at the conference ‘Computers in Scientific Discovery 6’, held at Portorož, Slovenia, August 21st–25th, 2012, and for very helpfully carrying out an independent check of our calculations on [10,5]-Coronene ((I)), which agreed with the data for this structure reported in the first row of Tables 1 and 2. A referee made useful suggestions about emphasising the special character of our newly defined p-Coronenes and increasing the vehemence of our conclusions concerning deficiencies in the universal generality of the AWA ‘rule’.

Notes and references

1. (a) D. A. Bochvar, E. G. Gal'pern and N. P. Gambaryan, Izv. Akad. Nauk SSSR, Ser. Khim., 1970, 3, 435–437 . An English translation is available from: Consultants Bureau, A Division of Plenum Publishing Corporation, 227 West 17th Street, New York, NY 10011, U.S.A., via the website http://www.springerlink.com/content/l5np5207n8q10240/; (b) In the nomenclature introduced by Bochvar et al.,^1a what Monaco et al.² called ‘[10,5]-Coronene’ is named ‘Coronene-10,5’. The original authors^1a pointed out that this structure could be ‘…considered as two rings symmetrically connected by ten transverse bonds: an inner ten-membered ring for which Hückel's criterion is satisfied, and an outer 20-membered ring not satisfying Hückel's criterion.’ According to Bochvar et al.,^1a a structure is denoted as ‘Coronene-n,m’ if n is the number of vertices in what those authors call^1a the ‘framed polygon’ (that is, the central ring) and m is the number of vertices in what they term (in the English translation^1a from the original Russian) the ‘framing polygon’—by which appears to be meant, not the grand polygon serving as the outer perimeter (as might initially be thought from the above expression), but the number of vertices in each polygon that forms a part of the periphery. Thus, in the case of Coronene-10,5, a ten-membered central-ring (hence the ‘10’) is tessellated with surrounding pentagons (hence the ‘5’). Furthermore, Bochvar et al.^1a explicitly state that they are dealing only with what they call ‘regular Coronenes-n,m’, defined as being those that exhibit a regular polygon at their centres. (What Bochvar et al.¹ called ‘Coronene-n,m’ we are, from here on, calling ‘Coronene-r,s’, in order to avoid potential confusion with our use of the symbols ‘n’ and ‘m’ to have other meanings in this paper; on the terminology of Monaco et al.², the Coronene-r,s is called ‘[r,s]-Coronene’—the nomenclature that we adopt here.) It is easy to verify the assertion of Bochvar et al.^1a that, for such regular Coronenes-r,s, the following simple relationholds: . These authors pointed out^1a that only four regular [r,s]-Coronenes are actually realisable in practice—namely [3,12]-, [4,8]-, [6,6]- and [10,5]-Coronenes. ([6,6]-Coronene does, of course, represent the carbon-atom connectivity of the extant benzenoid hydrocarbon Coronene itself.) In this paper, we are dealing only with entities in which a number, 2p, of regular polygons, each with p sides, are joined together as in Fig. 1 and for which (a) p is odd and (b) p > 3. It is straightforward to show that the only value of p that simultaneously satisfies these two conditions, as well as the above relation requiring, in this case, that 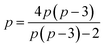, is in fact p = 5. Hence, [10,5]-Coronene or Coronene-10,5 is the only member of the series that we are studying here in which the central ring is a regular polygon. A final point should be noted: in regular [r,s]-Coronenes, each surrounding polygon on the periphery shares just one edge with the central ring; in the extension to the more-general series considered here, in which 2p regular polygons (p odd and p > 3), each with p sides, are joined in a closed form as in Fig. 1, each such regular polygon on the periphery shares (1/2)(p − 3) edges with the polygon—in general, a non-regular one—that constitutes the central ring. In order to avoid potential confusion between these two generally different series, therefore, we shall refer to our series defined here—the first four members of which are illustrated in Fig. 1—as the ‘p-Coronenes’. What is called ‘[10,5]-Coronene’ in the [r,s]-Coronene series^1,2 is thus coincident with what would be called ‘5-Coronene’ in the p-Coronene series. That, however, is the only structure that these two series have in common.
2. G. Monaco, R. Viglione, R. Zanassi and P. W. Fowler, J. Phys. Chem. A, 2006, 110, 7447–7452.
3. (a) I. Gutman and S. J. Cyvin, Introduction to the Theory of Benzenoid Hydrocarbons, Springer Verlag, Berlin (West), Heidelberg, 1989, pp. 105–106; (b) J.-I. Aihara, J. Phys. Chem. A, 2008, 112, 4382–4385.
4. (a) W. E. Barth and R. G. Lawton, J. Am. Chem. Soc., 1966, 88, 380–381; (b) W. E. Barth and R. G. Lawton, J. Am. Chem. Soc., 1971, 93, 1730–1745; (c) R. Benshafrut, E. Shabtai, M. Rabinowitz and L. T. Scott, Eur. J. Org. Chem., 2000, 6, 1091–1106.
5. (a) E. Steiner, P. W. Fowler, L. W. Jenneskens and A. Acocella, Chem. Commun., 2001, 659–660; (b) E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
6. A. Acocella, R. W. A. Havenith, E. Steiner, P. W. Fowler and L. W. Jenneskens, Chem. Phys. Lett., 2002, 363, 64–72.
7. A. T. Balaban, D. E. Bean and P. W. Fowler, Acta Chim. Slov., 2010, 57, 507–512.
8. T. K. Dickens and R. B. Mallion, Chem. Phys. Lett., 2011, 517, 98–102.
9. T. K. Dickens and R. B. Mallion, J. Phys. Chem. A, 2011, 115, 13877–13884.
10. (a) P. W. Fowler, E. Steiner, A. Acocella, L. W. Jenneskens and R. W. A. Havenith, J. Chem. Soc., Perkin Trans. 2, 2001, 1058–1065; (b) S. Fias, P. W. Fowler, J. L. Delgado, U. Hahn and P. Bultinck, Chem.–Eur. J., 2008, 14, 3093–3099.
11. P. W. Fowler and E. Steiner, Chem. Phys. Lett., 2002, 364, 259–266.
12. (a) C. A. Coulson, B. O'Leary and R. B. Mallion, Hückel Theory for Organic Chemists, Academic Press, London, 1978; (b) K. Yates, Hückel Molecular Orbital Theory, Academic Press, New York, 1978.
13. (a) F. London, J. Phys. Radium, 1937, 8, 397–409; (b) F. London, C. R. Hebd. Seances Acad. Sci., 1937, 205, 28–30; (c) F. London, J. Chem. Phys., 1937, 5, 837–838.
14. J. A. Pople, Mol. Phys., 1958, 1, 175–180.
15. R. McWeeny, Mol. Phys., 1958, 1, 311–321.
16. R. B. Mallion, Croat. Chem. Acta, 2008, 81, 227–246.
17. A. T. Balaban, T. K. Dickens, I. Gutman and R. B. Mallion, Croat. Chem. Acta, 2010, 83, 209–215.
18. T. K. Dickens and R. B. Mallion, J. Phys. Chem. A, 2011, 115, 351–356.
19. J.-I. Aihara, R. Sekine and T. Ishada, J. Phys. Chem. A, 2011, 115, 9314–9321.
20. P. W. Fowler and W. Myrvold, J. Phys. Chem. A, 2011, 115, 13191–13200.
21. (a) A referee has suggested that mention ought to be made here of chemical prototypes of these structures (albeit, for the most part, heterocyclic ones), such as tetraoxy[8]circulenes and the so-called ‘sulflowers’, which have recently been synthesised;^21b–f; (b) G. V. Baryshnikov, B. F. Minaev, M. Pittwlkow, C. B. Nielsen and R. Salcedo, J. Mol. Model., 2013, 19, 847–850; (c) S. Radenković, I. Gutman and P. Bultinck, J. Phys. Chem. A, 2012, 116, 9421–9430; (d) B. Napolion, F. Hagelberg, M.-J. Huang, J. D. Watts, T. M. Simeon, D. Vereen, W. L. Walters and Q. L. Williams, J. Phys. Chem. A, 2011, 115, 8682–8690; (e) S. S. Bukalov, L. A. Leites, K. A. Lyssenko, R. R. Aysin, A. A. Korlyukov, J. V. Zubavichus, K. Y. Chernichenko, E. S. Balenkova, V. G. Nenajdenko and M. Y. Antipin, J. Phys. Chem. A, 2008, 112, 10949–10961; (f) B. Hajgató and M. S. Deleuze, Chem. Phys. Lett., 2012, 553, 6–10.
22. (a) A referee has suggested making reference to the way in which hetero-cyclic systems would be considered by our HLPM approach. As a result of the pioneering work of Veillard^22b—these days, however, seldom cited—which elegantly extended and generalised the McWeeny formalism,¹⁵ it is indeed possible to accommodate hetero-cycles in calculations of this sort. In fact, many years ago, one of the present authors did consider sulphur and nitrogen hetero-cycles and published the results—as ref. 22c and d, below—but the task does involve introducing at least two subjective parameters, namely, modifying the diagonal elements in the Hückel matrix corresponding to the hetero-atoms and modifying the off-diagonal elements for bonds in which the hetero-atoms in the conjugated system participate; (b) A. Veillard, J. Chim. Phys. Phys.-Chim. Biol., 1962, 59, 1056–1066; (c) R. B. Mallion, J. Chem. Soc., Perkin Trans. 2, 1973, 235–237; (d) R. B. Mallion, Biochimie, 1974, 56, 187–188.
23. (a) If, in a conjugated system having a total of K Kekulé structures, K_ij denotes the number of Kekulé structures in which there is a double bond between the carbon atoms i and j, then the Pauling bond-order,^23bP_ij, of the bond between those carbon atoms is given by^23c the ratio P_ij = K_ij/K; (b) L. Pauling, L. O. Brockway and J. Y. Beach, J. Am. Chem. Soc., 1935, 57, 2705–2709; (c) S. J. Cyvin and I. Gutman, Lecture Notes in Chemistry 46, Kekulé Structures in Benzenoid Hydrocarbons, Springer-Verlag, Berlin (West), Heidelberg, 1988, p. 5.
24. (a) Referees have commented that it would in principle be possible to ‘test’ the relative magnitudes of ring- and bond-currents calculated by means of our ‘topological’ HLPM approach (from eqn (1), specified in ‘Calculations’) by comparing them with those (necessarily expressed relative to benzene) in similar structures recently computed in an ab initio fashion via density-functional theory and other sophisticated methods by Sundholm et al.^23b,c However, in addition to the difficulty that the two studies do not appear to have any structures in common that would currently enable a comparison of this sort to be effected, such a consideration is outside the scope (and the essentially very simple message) of the present investigation. Such a potential comparison—with calculations based on the approach of Sundholm et al. and, indeed, with currents evaluated from a plethora of other ab initio methods that are, these days, available—is, nevertheless, a possible line of enquiry for the future; (b) H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676; (c) S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123.
25. R. B. Mallion, Proc. R. Soc. London, Ser. A, 1974/1975, 341, 429–449.
26. J. Gayoso and A. Boucekkine, C. R. Seances Acad. Sci., Ser. C, 1971, 272, 184–187.
27. N. Trinajstić, Chemical Applications of Graph Theory, CRC Press, Boca Raton, Florida, USA, 1st edn, 1983, ch. 3, pp. 21–30.
28. D. Janežić, A. Miličević, S. Nikolić and N. Trinajstić, Graph Theoretical Matrices in Chemistry, in Mathematical Chemistry Monographs MCM 3, ed. I. Gutman and B. Furtula, Faculty of Science, University of Kragujevac, Serbia, 2007, pp. 17–18.
29. (a) R. B. Mallion, Mol. Phys., 1973, 25, 1415–1432; (b) C. W. Haigh and R. B. Mallion, Croat. Chem. Acta, 1989, 62, 1–26; (c) J. A. N. F. Gomes and R. B. Mallion, The concept of ‘ring currents’, in Concepts in Chemistry, ed. D. H. Rouvray, Research Studies Press Limited, Taunton, Somerset, England, United Kingdom, 1997, John Wiley & Sons, Inc., New York, 1997, ch. 7, pp. 205–253; (d) J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1383.
30. P. W. Fowler, personal correspondence, October 4th, 2012.
31. (a) G. A. G. Bennett, Electricity and Modern Physics, Edward Arnold (Publishers) Ltd., London, 1968, pp. 31–32; (b) S.M.P. Advanced Mathematics Book [Metric], ed. H. M. Cundy, Cambridge University Press, London, New York, 1970, p. 911.
32. T. K. Dickens, J. A. N. F. Gomes and R. B. Mallion, J. Chem. Theory Comput., 2011, 7, 3661–3674.
33. It may be noted in passing that this finding is in accord with the spirit of a recent statement made by Fowler and Myrvold,²⁰ in the context of ‘conjugation-circuit’ approaches³² to ring- and bond-current calculation, when they commented that the ‘…relative insensitivity…’ of such calculations to ‘…directly contradictory assumptions about the influence of circuit area on bond current…’ is ‘…surprising’.
34. T. K. Dickens and R. B. Mallion, Croat. Chem. Acta , submitted.
35. P. W. Fowler, personal discussions with the authors at the conference ‘Computers in Scientific Discovery’, held at Portorož, Slovenia, August 21st–25th, 2012.
36. (a) It should be noted that when we state that there is ‘a lack of coupling’ in the p-Coronene series between the outer perimeter and the central ring we mean (with Fowler et al.^2,5–7) that the spokes⁷/transverse¹ bonds are always ‘single’ in all four of the Kekulé structures that may devised for each of these systems, and so these latter bonds have zero⁷ Pauling bond-order.²³ We have further pointed out that, solely on the grounds of symmetry, those spokes/transverse bonds also support zero bond-current. This is because these bonds are shared by adjacent peripheral rings which bear ring currents of identical intensity; these ring-currents therefore annul each other in these spokes⁷/transverse¹ bonds that the two neighbouring p-membered rings share, because contributions from internal boundaries cancel—cf. Stokes's Theorem.¹⁵ These two properties of the transverse¹/spokes⁷ bonds—(a) their being fixated as single bonds in all Kekulé structures, and, thereby, having zero Pauling bond-order,²³ and (b) their carrying zero bond-current (by symmetry)—are, however, entirely distinct. Following Fowler et al.,^2,5–7,35 we suggest that it is the former ((a)), and not the latter ((b)), which is responsible for the fact that (I)–(IV) obey the AWA rule.^4–9 As a counter-example to any suggestion otherwise we cite the case of Coronene (‘regular’ [6,6]-Coronene¹) itself (structure 1 of ref. 7–9): the spokes⁷/transverse¹ bonds in that conjugated system likewise bear zero bond-current by symmetry, but those bonds are ‘double’ in some of the 20 Kekulé structures,⁷ and ‘single’ in others; they thus have a non-zero Pauling bond-order²³ (of 0.407)⁷ and so the 18-membered perimeter and the six-membered inner-ring in Coronene are ‘coupled’, in the sense that Fowler et al.^2,5–7 introduced that term—and in the sense in which we are also using the term, here. As is well known (e.g.ref. 7–9 and 37), Coronene itself violates the AWA rule. On the other hand, the fact that the spokes bonds⁷/transverse bonds¹ have zero Pauling bond-order²³ in a given conjugated system does not seem inevitably to guarantee compliance with the AWA rule. A counter-example to any suggestion otherwise is to be found amongst the non-alternant isomers of Coronene that are labelled 16, 17, and 18 in ref. 7 and 9; each of these has only four Kekulé structures⁷ and 16–18 thus possess transverse¹ bonds of zero Pauling bond-order²³ that connect the six-membered central-ring to the 18-membered perimeter in each of 16, 17 and 18. Both Balaban et al.,⁷ by means of their ab initio ipso-centric calculations,^5,6 and we,⁹ by means of our HLPM ‘topological’ approach,^16–18 agree that 16 and 17 conform to the AWA, but that 18 does not. (Application of Randić's ‘conjugated-circuit’ formalism,^36b however, gives rise to the conclusion^9,36c,d that the entire trio of 16, 17, and 18 obeys the AWA rule); (b) M. Randić, Chem. Phys. Lett., 2010, 500, 123–127; (c) M. Randić, M. Nović, M. Vračko, D. Vukičević and D. Plavšić, Int. J. Quantum Chem., 2012, 112, 972–985; (d) M. Randić, D. Vukičević, A. T. Balaban and D. Plavšić, J. Comput. Chem., 2012, 33, 1111–1122.
37. (a) I. J. Maddox and R. McWeeny, J. Chem. Phys., 1962, 36, 2353–2354; (b) N. Jonathan, S. Gordon and B. P. Dailey, J. Chem. Phys., 1962, 36, 2443–2448.
38. (a) C. A. Coulson, Rev. Mod. Phys., 1960, 32, 170–177; (b) Commenting on the fact that the simple HLPM approach^16–18 shows that the ring-current intensity in the central ring of Peropyrene (structure (I) of ref. 18) is fully six times^38c that in the ostensibly similar central ring of Perylene (structure (II) in ref. 18), the late Professor Coulson remarked (in a letter to one of us [RBM] that is now amongst the Coulson Papers in the Bodleian Library, University of Oxford^38d): ‘I think your conclusions^38c about these “ring currents” are very exciting and clear cut…. This seems to me to be one of those rare cases where a simple theory predicts a very profound difference in two kinds of situations and where even a rough measurement should be enough to show that the theory is either right or wrong.’ That is the sort of philosophy that we are trying to invoke by means of this paper; (c) R. B. Mallion, J. Med. Chem., 1971, 14, 824–826; (d) C. A. Coulson, Letter to R. B. Mallion, December 1st, 1970, The Papers of Charles Alfred Coulson FRS 1910-1974 (Collection Reference CSAC 60.4.78), MS. Coulson, Box 175, Item No. 46, Department of Special Collections and Western Manuscripts, Bodleian Library, University of Oxford. We are very grateful to Mr Michael Hughes (Senor Archivist, Department of Special Collections and Western Manuscripts) and Mr Colin Harris (Superintendent, Special Collections Reading Rooms) for their kind help in locating the reference to this letter in the Coulson Papers at the Bodleian Library.

---