 Open Access Article
Open Access ArticleStudy of contact angle hysteresis using the Cellular Potts Model
Vahid
Mortazavi
,
Roshan M.
D'Souza
and
Michael
Nosonovsky
*
College of Engineering & Applied Science, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: nosonovs@uwm.edu; Fax: +1-414-229-6958; Tel: +1-414-229-4987
First published on 20th December 2012
Abstract
We use the Cellular Potts Model (CPM) to study the contact angle (CA) hysteresis in multiphase (solid–liquid–vapour) systems. We simulate a droplet over the tilted patterned surface, and a bubble placed under the surface immersed in liquid. The difference between bubbles and droplets was discussed through their CA hysteresis. Dependency of CA hysteresis on the surface structure and other parameters was also investigated. This analysis allows decoupling of the 1D (pinning of the triple line) and 2D (adhesion hysteresis in the contact area) effects and provides new insight into the nature of CA hysteresis.
1 Introduction
Superhydrophobicity has drawn attention from researchers in recent years because of the need to design non-wetting, non-sticky, antifouling, ice-phobic, and self-cleaning surfaces.1–17 Significant progress has been made in design, synthesis and characterization of functional superhydrophobic surfaces.18–21Besides experimental studies, analytical models of wetting of rough surfaces have been developed. The concept of the water contact angle (CA) was introduced by Young22 along with the concept of the surface tensions of the solid–vapor (γSV), solid–liquid (γSL), and liquid–vapor (γLV) interfaces. Wenzel23 and Cassie and Baxter24 proposed two classical models to modify the Young equation for rough or heterogeneous surfaces in the case of the solid–water and composite solid–air–water interface. Their models have been expanded for various cases of patterned and random surfaces. In general, these models can be called macroscopic, since they treat both fluid and solid as continuum media, which satisfy the equations of hydrodynamics and elasticity, and deal with the macroscale thermodynamic parameters such as the contact angle (CA). However, many interactions related to wetting of rough surfaces occur at the nanoscale (molecular scale) and the microscale (mesoscale). In order to study these interactions, numerical simulations are typically used.
In addition to static wetting and equilibrium CA, CA hysteresis has been a subject of many investigations (e.g., ref. 8, 25–27). Even in the quasi-static case of low velocity, the value of the CA is not unique due to CA hysteresis, and it depends on whether water is added (the advancing CA) or recedes (the receding CA). This is because solid surfaces are often rough or chemically heterogeneous and because it may take too much time to attain the true equilibrium state which corresponds to the equilibrium CA. Furthermore, due to molecular reorientation,5,7 surface deformation, dissolving, chemical and other interactions, water advancing is not reversible, and there is asymmetry between wetting and dewetting. In particular, due to this asymmetry, wetting of water droplets and air bubbles is different. In addition, adhesion hysteresis exists making the energy of bringing surfaces together different from the energy needed to separate them. As a result, many interactions, at the liquid volume, solid–liquid surface, and solid–liquid–air triple line are responsible for CA hysteresis and it is difficult to separate them and to tell which effect is dominant. To get a better understanding of the role of these effects, numerical simulation can be helpful.
So far different analytical and numerical models have been suggested to explain wetting and estimate the CA. Among those are the models based on the molecular-kinetic theory (MKT).28,29 This theory neglects hydrodynamic aspects of flow and the viscous dissipation, and links macroscopic behavior of the triple line, and the CA, with microscopic quantities like the frequency (k) and displacement (λ) of movement of individual molecules in the vicinity of the triple line.30 While a good agreement was obtained with experiment for the MKT models,31 they used some phenomenological parameters, which could be obtained only by curve fitting.30
Hydrodynamic (HD) models based on lubrication theory (e.g.ref. 32) are another significant approach for studying wetting dynamics. The HD models, unlike MKT, describe dynamics of wetting from a continuum viewpoint by considering the balance between capillary and viscous forces.33 Shikhmurzaev34 extended the approach by exploiting non-equilibrium thermodynamics to describe dissipation due to the interfacial creation and destruction processes occurring as the triple line moves along the solid surface. Phenomenological phase field (PF) models have also been used to study CA hysteresis.35
Molecular dynamics (MD) simulation was applied to explore the details of wetting at the molecular scale. Alder and Wainwright36 described the solution of the classical equations of motion (Newton's equations) for a set of molecules. While the first MD study of the static CA was done by Saville,37 it was after the studies of Koplik et al.38,39 and Thompson et al.40,41 that the approach has been used extensively for simulation of wetting. However, most practical MD simulations are still restricted to small systems of the order of tens of nanometers and short times of the order of a few nanoseconds. Scale-dependency of wetting parameters such as the CA, also, makes the practical application of the results of MD simulations questionable.
Usually it is very difficult to deduce macroscale parameters (such as the CA) directly from the molecular scale properties. This is because many important interactions occur at the mesoscale (with the typical length on the order of microns) involving surface roughness, heterogeneity, material domains and grains, etc. Therefore, the emphasis of the simulation activity should be on the mesoscale. The appropriate methods for mesoscale materials modelling include Monte Carlo (MC) simulation, Cellular Automata and others.42,43
In the present study we use the Cellular Potts Model (CPM) to investigate CA hysteresis and decouple 1D (triple line) and 2D (contact area) effects on that. The Cellular Potts Model44,45 is a lattice-based computational modelling method to simulate the behaviour of cellular structures, and has been applied to problems in which the dynamics is driven by energy minimization arising from interfacial tensions between different media. In recent years, the model has been used in different studies to simulate biological tissues,46 grain growth,47 foam structure,48 coarsening,49 and drainage,50 fluid flow and reaction–advection–diffusion systems.51 Messager et al.52 used the Potts model to study the wetting of the interface between two ordered phases by the disordered phase and established the validity of Antonov's rule. More recently, de Oliveira et al.53 suggested using the model for simulation of superhydrophobic behaviour of liquid droplets.
The strength of the CPM in the study of wetting is that, unlike MD, it does not require the detailed interaction potentials among the molecules. It can deal with the processes at the mesoscopic level, while at the same time simulating the macroscopic behaviour of the system as a whole. Thus, the CPM simulation can serve as a numerical experiment with a level of control that would be very difficult or even impossible to achieve in a physical experiment. This provides further insight into how different physical mechanisms and parameters influence CA hysteresis of droplets and bubbles.
2 Contact angle hysteresis
Since the concept of the CA was introduced, it was realized that this single parameter cannot completely characterize wetting. Furthermore, there is no unique value for the CA, but it can have a range of values θrec ≤ θ ≤ θadv, where θrec and θadv denote the receding and advancing CAs when liquid is removed or added, respectively. The difference between the advancing and receding CAs is called CA hysteresis. The phenomenon of CA hysteresis on chemically heterogeneous surfaces was apparently noticed for the first time by A. Pockels54 and then investigated by Ablett,55 Frenkel,56 Bartell and Shepard,57 Furmidge,58 Johnson and Dettre59 and others. However, much attention was paid to CA hysteresis after the discovery of the superhydrophobicity and the Lotus effect.Superhydrophobicity is the ability of some surfaces to have very high water CA (>150°) and low CA hysteresis. The Lotus effect is characterized by surface roughness induced superhydrophobicity and self-cleaning. The field of superhydrophobicity is relatively new, although the phenomenon has been discussed in the literature since the 1930s, by Adam and other surface scientists of that time.60 Wenzel23 was the first who investigated wetting of rough surfaces. Using simple arguments related to the surface tension force equilibrium, he derived an equation for the water contact angle (CA) with a rough surface. The same equation was derived, independently, by Derjaguin61 and Good,62 using thermodynamic arguments and a powerful concept of the “disjoining pressure”.63 Cassie and Baxter24 studied wetting of a surface composed of two fractions. The Wenzel and Cassie–Baxter equations correspond to two distinct wetting regimes. The Cassie wetting regime with air pockets trapped between the solid and liquid is desirable for superhydrophobicity. It is recognized that the Cassie regime is needed to attain small CA hysteresis and superhydrophobicity.
CA hysteresis can be measured also on a tilted surface, although it is recognized that the values measured in this way do not always provide true values of the advancing and receding angles.64,65 There are several theories explaining CA hysteresis. One theory attributes CA hysteresis to pinning of the triple line by sharp asperities at the surface.66 Two surfaces come together at a sharp edge, so the value of the CA is not unique at the edge, being in the range of values from the minimum value (corresponding to the slope on one side of the edge) to the maximum value (corresponding to the slope on the other of the edge). When liquid front advances, the triple line will be pinned at the edge until the CA reaches its maximum value. Similarly, when liquid recedes, the triple line is pinned until the CA reaches its minimum value. Therefore, varying surface slope results in CA hysteresis.25
In a similar manner, chemical heterogeneity or contamination leads to CA hysteresis. If a surface is composed of spots with different surface energies, water will cover the spots with higher energy first and leave them last, effectively resulting in CA hysteresis. It has been discussed25 that CA hysteresis is equal to dissipated energy during the motion of a droplet. This dissipation can occur either in the bulk of the liquid, at the solid–liquid interface or at the triple line. The bulk dissipation (3D) is mostly due to the viscosity and it can be eliminated in the quasi-static limit of low velocity, however, the interfacial (2D) and triple line (1D) dissipation cannot be eliminated completely and both contribute to CA hysteresis. Therefore, CA hysteresis involves a term proportional to the contact area and a term proportional to the length of the triple line. Despite all studies done so far on the subject, more advanced modelling is needed to separate these effects and investigate how different parameters such as surface roughness, heterogeneity and drop/bubble size affect CA hysteresis.
3 The Cellular Potts Model
The Cellular Potts Model (CPM) is a method to model the mesoscale phenomenon using statistical techniques. The simulation domain is discretized using a lattice, as shown in Fig. 1. Each lattice site has a spin. Contiguous simply-connected lattice sites with the same spin constitute a generalized cell. A generalized cell can be a bubble, a biological cell, or a metal grain. The configuration of the simulation domain evolves one lattice site at a time based on a set of probabilistic rules. This configuration evolution is done based on a Hamiltonian function that is used for calculating the probability of accepting changes.44 The CPM Hamiltonian is given by:| H = Ha + Hv + Hs + Hp | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) is a uniform potential field, and
is a uniform potential field, and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) (i) is the position of the lattice with respect to the reference frame.
(i) is the position of the lattice with respect to the reference frame.
 | ||
| Fig. 1 Schematic of a 2D lattice and a spin flipping attempt in CPM. | ||
Monte Carlo simulations of Potts models have traditionally used local algorithms such as that of Metropolis.44 A lattice site is chosen at random and a new trial spin is also chosen at random from one of its pre-defined neighbourhood lattice sites (usually the immediate Moore neighbourhood) to test local boundary energy minimization (Fig. 1). The probability (P(σ(i) → σ(j))) of accepting such a reassignment is:44
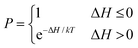 | (6) |
4 The Cellular Potts modelling of wetting
To study CA hysteresis with CPM, we simulate two different cases: first, a droplet over a tilted solid surface, second, a bubble placed under the solid surface immersed in liquid. Although, in principle, it is expected that the bubble and the droplet demonstrate the same CA hysteresis (dealing with the same solid–liquid–gas system), the experimental study shows that the values can be quite different.25 The asymmetry between the droplets and the bubbles is attributed to the compressibility of gas bubbles (as opposed to almost incompressible water droplets), interactions at the solid–water interface, and even to the fractal structure of the interface.67Consider the case of a small droplet on a plane surface in equilibrium with the gas phase, and where a spherical gas–liquid interface has a surface energy γ without gravity or line tension effects. The conditions for mechanical equilibrium can be determined by minimizing Gibbs free energy
| dE = −ΔPdV + γdAlg + (wls − wgs)dAls | (7) |
As it was pointed out, the CPM minimizes total energy and essentially solves the minimal surface equations for a lattice. Our model consists of a 2D lattice with the dimensions of L2 = 500 × 250 sites, and three different media: σ = 0 for vapour, σ = 1 for liquid and σ = 2 for solid. The adhesive term of Hamiltonian, Ha, as defined in eqn (2), is based on the interaction between neighboring cells, and involves interfacial energies. When neighbouring cells belong to the same medium, we have J(τ(σ(i)),τ(σ(j))) = 0; which means the Potts energy imposes that there is an interfacial energy only between cells of different media, i.e., between neighbouring liquid–vapour, liquid–solid, and vapour–solid cells.
The volume restriction term, Hv, in eqn (3) is responsible for the compressibility of the medium. When spin flip is attempted, one cell will increase its volume and another cell will decrease. Thus the overall energy of the system may change. Volume constraint essentially ensures that cells maintain the volume close to its target volume. In simulations, for the liquid medium, the value of λvolume = 1, and target volume for each cell was its initial volume. For λsurface in eqn (4), we also set the value to 1. Hs, as it was pointed out, is the pressure energy term.
Moreover, to include a gravity effect on the droplet (or on the bubble), eqn (5) was written in the following form:
 | (8) |
The range of interactions for each site in computing the adhesive term in the Hamiltonian was specified to be the fifth Moore neighbour. We observed that increasing this range to 6 or 7 neighbours did not affect the final results. Since all values in CPM are dimensionless, we were free to set different parameters as a means to fix the length scale and the time scale of the simulations in the order of micrometers and milliseconds, respectively. For example, we set 1 pixel to 20 μm and 1 MCS to 10 ms; then, other parameters like gravity, surface energy, etc. can be obtained based on their actual relative values. In this way, our choice of parameters is somewhat arbitrary, since after experiments, and comparison with simulation results, we can set their exact values.
The initial configuration for a droplet on the homogenous solid surface is shown in Fig. 2 for fSL = 1, where fSL (solid–liquid fraction) is defined as the ratio of solid–liquid length to whole contact (solid–liquid + solid–air) length. We changed the structure of the solid surface in further simulations to investigate the effect of solid–liquid fraction, slope of surface, and its material (surface energy) on CA hysteresis. Simulations were performed using the CompuCell3D software,68 which is an open source modelling environment, primarily used to study cellular behaviour, and was built with the C++ programming language.
 | ||
| Fig. 2 Initial configuration of simulation for a droplet along a tilted homogeneous (fSL = 1) solid surface. | ||
The surface energies of the vapour–liquid, liquid–solid and vapour–solid interfaces were considered to be equal to 80, 110, and 70, respectively (all values are dimensionless in the CPM), i.e., in eqn (2), we have J(v,l) = 80, J(l,s) = 110, and J(v,s) = 70. Note that, according to Young's equation, only the ratios of the surface energies matter for determining the CA, rather than their absolute dimensional values. Substituting the dimensionless values in Young's equation we will have
 | (9) |
Looking into eqn (1), we can say it is the gravity term in the Hamiltonian, which is responsible for the weight of the droplet (or buoyancy of a bubble) which results in the asymmetry between the advancing and receding angles. Physically, the system finds a compromise shape between the lowest possible position of its centre of mass and minimized surface area.
5 Results
The slope of the tilted surface (the tilt angle) was initially set to 10°, and the radius of the initial circular droplet (R) was set to 35, 50 and 60 lattice sites, in three different simulations. The simulation was performed for different values of fSL (0.1, 0.2, 0.4, 0.6, 0.8, and 1.0), and in each case we changed the initial configuration. Values of fSL and the slope were entered into the simulation just as a part of the initial configuration. The influence of the solid–liquid fraction on the CA hysteresis is presented in Fig. 3. The values of the CA and its hysteresis were obtained using DropSnake plug-in for ImageJ software.69 It can also be noted that while hysteresis usually has been defined as the value of the maximal advancing minus the minimal receding angles, when the two do not need to occur simultaneously, we estimated hysteresis for the given situation. For all the three different droplets, with decreasing fSL, the CA hysteresis decreased, and around fSL = 0.2, it reached very low values (3.28°, 2.13° and 1.5°, for R = 35, 50 and 60, respectively). For lower values (fSL = 0.1), an increase in CA hysteresis was observed. This is apparently because two different factors contribute to CA hysteresis. First, for large contact areas the droplet diverges from the spherical shape making asymmetry more pronounced and, thus, larger CA hysteresis, as observed visually from the modelling results. Second, for small solid–liquid fractions, small contact area corresponds to high roughness pinning the droplet and thus leading to hysteresis. The second effect fades out quickly with increasing 0 ≤ fSL ≤ 0.2, so the minimum CA hysteresis is at around fSL = 0.2. The same effect (with the minimum at fSL = 0.2) was also reported by De Oliveira et al.53 who attributed it to the possible Cassie–Wenzel wetting transition.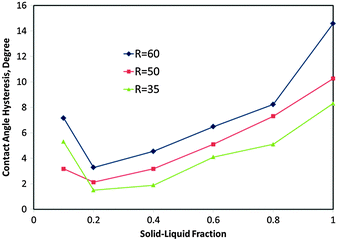 | ||
| Fig. 3 Contact angle hysteresis versus solid–liquid fraction for a droplet on the tilted surface; for three different drop diameters (R). | ||
The evolution of advancing and receding contact angles as a function of the surface energy of solid–liquid for a homogeneous interface (fSL = 1) is presented in Fig. 4. For this comparison, the initial droplet was set to 60 lattice sites and all other parameters were kept constant, and the same as the ones described for previous simulations. An increase in CA hysteresis (from 7.15° to 18.33°) is noticeable with increasing surface energy (from J(l,s) = 80 to J(l,s) = 140).
 | ||
| Fig. 4 Advancing and receding contact angles for different surface energies of solid–liquid. | ||
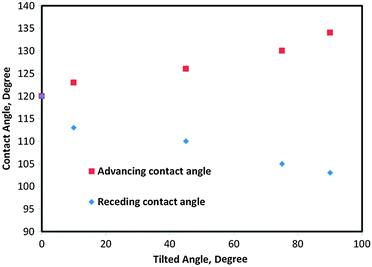
The effect of droplet size on the advancing and receding contact angles was investigated as well. Fig. 5 compares these two parameters for different radii of an initial circular droplet ranging from 35 to 60 lattice sites. While advancing CA increased (from 121.46° to 124.08°) with increasing droplet size, there was little decrease in receding CA (from 113.15° at R = 35 to 109.5° at R = 60 sites). This leads to increasing CA hysteresis with droplet size, which can be attributed to the gravity effect.
 | ||
| Fig. 5 Advancing and receding contact angles for different drop diameters. | ||
In order to investigate the effect of the compressibility and separate the triple line and the contact area effects on CA hysteresis, we compared CA hysteresis for droplets and bubbles on the same surface. We considered the surface energies of the gas–liquid, liquid–solid and gas–solid to be equal to 80, 110, and 70, respectively. Fig. 6 shows advancing and receding CAs of droplets for different tilt angles (TA), i.e., 0, 10, 45, 75 and 90 degrees after 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS. The results show that CA hysteresis increased with large tilt angles and reached its maximum value (31°) at the 90° tilt (a vertical surface). The similar results were obtained for bubbles and are shown in Fig. 7. In this case, for tilt angles greater than 40°, the bubble detached from the solid. The reason that the water droplet remained attached to the solid even at the tilt angle of 90° can be attributed to the fact that droplet–solid adhesion was stronger since the solid–water interface (2D contact area) component was present in addition to the triple line (1D) component, while an air bubble did not have contact area adhesion. Fig. 8 compares CA hysteresis in these two systems. It is observed that CA hysteresis for a bubble is larger than that for a droplet. The difference is attributed to the fact that the gas bubble is compressible and that no interaction occurs between the gas and the solid at the bubble–solid contact area.
000 MCS. The results show that CA hysteresis increased with large tilt angles and reached its maximum value (31°) at the 90° tilt (a vertical surface). The similar results were obtained for bubbles and are shown in Fig. 7. In this case, for tilt angles greater than 40°, the bubble detached from the solid. The reason that the water droplet remained attached to the solid even at the tilt angle of 90° can be attributed to the fact that droplet–solid adhesion was stronger since the solid–water interface (2D contact area) component was present in addition to the triple line (1D) component, while an air bubble did not have contact area adhesion. Fig. 8 compares CA hysteresis in these two systems. It is observed that CA hysteresis for a bubble is larger than that for a droplet. The difference is attributed to the fact that the gas bubble is compressible and that no interaction occurs between the gas and the solid at the bubble–solid contact area.
 | ||
| Fig. 6 Advancing and receding contact angles versus titled angle for a droplet on the tilted surface. | ||
 | ||
| Fig. 7 Advancing and receding contact angles versus titled angle for a bubble submerged in liquid. | ||
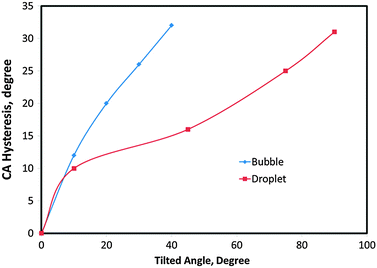 | ||
| Fig. 8 Comparison of CA hysteresis for bubbles and droplets of the same surface energies. | ||
In order to validate observations made from simulation results, we measured experimentally CA hysteresis for different size of droplets and bubbles. The experiments were done for droplets on concrete TiO2 coated tiles, and for bubbles on the Al sample. For each sample, we measured the value of roughness average, Ra, using a profilometer (Mitutoyo Surftest, 40) which was found to be 19.45 μm, and 0.763 μm for tiles and the Al sample, respectively. For all experiments, the droplets and bubbles of different volume were deposited on the solid surface, and the tilt angle was gradually increased. The advancing and receding CAs were measured using a standard ramé-hart goniometer/tensiometer, model 250, at different tilt angles. The results are presented in Fig. 9. Fig. 9a summarizes the effect of droplet size on CA hysteresis for three different tilt angles. Similar to the simulation results, for large droplets, a large value of CA hysteresis was observed, i.e., with increasing droplet volume from 8 μL to 60 μL, CA hysteresis increased from 4.09° to 15.76° for TA = 10°, from 6.80° to 27.89° for TA = 20° and from 9.86° to 34.13° for TA = 30°. The same phenomenon was also observed for air bubbles (Fig. 9b), i.e., with increasing bubble volume from 7 μL to 25 μL, CA hysteresis increased from 4.5° to 14.98° for TA = 10°, and from 6.95° to 20.08° for TA = 20°. In the latter case, for tilt angles larger than 20°, bubbles detached from the solid surface. It is also observed that upon increasing the size of the bubbles, this detachment occurred in smaller tilt angles. These experimental observations confirm that due to the stronger droplet–solid adhesion in the presence of both the solid–water interface (2D contact area) and the triple line (1D) components, CA hysteresis for droplets is smaller than for bubbles.
 | ||
| Fig. 9 CA hysteresis obtained by experiment for (a) droplets of different sizes on concrete TiO2 coated tiles, and (b) bubbles of different sizes on the Al sample, for different tilt angles (TA). | ||
6 Conclusions
We used the Cellular Potts Model (CPM) to study CA hysteresis for a droplet along a tilted solid surface, and a bubble placed on the solid surface immersed in liquid. CPM minimizes total surface energy of the solid–liquid–vapour system, and shows how the system reaches its single value of the contact angle. The dependency of CA hysteresis on surface structure was discussed based on the simulation results. We observed how CA hysteresis decreases at heterogeneous interfaces with a decrease in the solid–liquid fraction, and reaches its minimum value. The effects of solid–liquid surface energy and droplet size on advancing and receding contact angles were also discussed. We compared the dependency of CA hysteresis on the titled angle for bubbles and droplets. The value of hysteresis depends on the interactions in the solid–liquid contact area and at the triple line. Although the solid–liquid–vapour triple line is the same for bubbles and droplets, the adhesion of droplets was much stronger, which points to the role of the 2D interface and bubble compressibility.Acknowledgements
This work was partially funded by grants CNS-0968519 and CCF-1013278 from the National Science Foundation (NSF). The authors thank Dr Maciej Swat and Ivan Komarov for their helpful notes and advice.References
- M. Nosonovsky and P. K. Rohatgi, Biomimetics in Materials Science: Self-Healing, Self-Lubricating, and Self-Cleaning Materials, Springer, 2011 Search PubMed.
- N. Shirtcliffe, G. McHale, S. Atherton and M. I. Newton, An introduction to superhydrophobicity, Adv. Colloid Interface Sci., 2010, 161(1–2), 124–138 CrossRef CAS.
- B. Bhushan and M. Nosonovsky, The rose petal effect and the modes of superhydrophobicity, Philos. Trans. R. Soc., A, 2010, 368(1929), 4713–4728 CrossRef CAS.
- L. Boinovich and A. Emelyanenko, Principles of Design of Superhydrophobic Coatings by Deposition from Dispersions, Langmuir, 2009, 2907–2912 CrossRef CAS.
- R. Tadmor, P. Bahadur, A. Leh, H. E. N'guessan, R. Jaini and L. Dang, Measurement of Lateral Adhesion Forces at the Interface between a Liquid Drop and a Substrate, Phys. Rev. Lett., 2009, 103(26), 266101–266104 CrossRef.
- A.-M. Kietzig, S. G. Hatzikiriakos and P. Englezos, Patterned Superhydrophobic Metallic Surfaces, Langmuir, 2009, 25(8), 4821–4827 CrossRef CAS.
- R. Tadmor, Line energy, line tension and drop size, Surf. Sci., 2008, 602, L108–L111 CrossRef CAS.
- M. Bouteau, S. Cantin, F. Benhabib and F. Perrot, Sliding behavior of liquid droplets on tilted Langmuir–Blodgett surfaces, J. Colloid Interface Sci., 2008, 317(1), 247–254 CrossRef CAS.
- E. Bormashenko, Y. Bormashenko, T. Stein, G. Whyman and R. Pogreb, Environmental Scanning Electron Microscopy Study of the Fine Structure of the Triple Line and Cassie–Wenzel Wetting Transition for Sessile Drops Deposited on Rough Polymer Substrates, Langmuir, 2007, 23(8), 4378–4382 CrossRef CAS.
- E. Bormashenko, T. Stein, G. Whyman, Y. Bormashenko and R. Pogreb, Wetting Properties of the Multiscaled Nanostructured Polymer and Metallic Superhydrophobic Surfaces, Langmuir, 2006, 22(24), 9982–9985 CrossRef CAS.
- C.-H. Choi and C.-J. Kim, Large Slip of Aqueous Liquid Flow over a Nanoengineered Superhydrophobic Surface, Phys. Rev. Lett., 2006, 96(6), 066001–066004 CrossRef.
- M. M. Ma and R. Hill, Superhydrophobic Surfaces, Curr. Opin. Colloid Interface Sci., 2006, 11, 193–202 CrossRef CAS.
- W. Li and A. Amirfazli, A Thermodynamic Approach for Determining the Contact Angle Hysteresis for Superhydrophobic Surfaces, J. Colloid Interface Sci., 2006, 292, 195–201 CrossRef.
- T. Krupenkin, J. Taylor, T. Schneider and S. Yang, From Rolling Ball to Complete Wetting: the Dynamic Tuning of Liquids on Nanostructured Surfaces, Langmuir, 2004, 20, 3824–3827 CrossRef CAS.
- R. Furstner, W. Barthlott, C. Neinhuis and P. Walzel, Wetting and Self-Cleaning Properties of Artificial Superhydrophobic Surfaces, Langmuir, 2005, 21, 956–961 CrossRef.
- N. A. Patankar, Transition Between Superhydrophobic States on Rough Surfaces, Langmuir, 2004, 20, 7097–7102 CrossRef CAS.
- S. Herminghaus, Roughness-Induced Non-Wetting, Europhys. Lett., 2000, 52, 165–170 CrossRef.
- L. Huang, S. P. Lau, H. Y. Yang, E. S. P. Leong and S. F. Yu, Stable Superhydrophobic Surface via Carbon Nanotubes Coated with a ZnO Thin Film, J. Phys. Chem. B, 2005, 109(16), 7746–7748 CrossRef CAS.
- X. Feng and L. Jiang, Adv. Mater., 2006, 18(23), 3063–3078 CrossRef CAS.
- V. Hejazi and M. Nosonovsky, Langmuir, 2012, 28(4), 2173–2180 CrossRef CAS.
- M. Nosonovsky, V. Hejazi, A. E. Nyong and P. K. Rohatgi, Langmuir, 2011, 27(23), 14419–14424 CrossRef CAS.
- T. Young, An Essay on the Cohesion of Fluids, Philos. Trans. R. Soc. London, 1805, 95, 65–87 CrossRef.
- R. N. Wenzel, Resistance of Solid Surfaces to Wetting by Water, Ind. Eng. Chem. Res., 1936, 28, 988–994 CrossRef CAS.
- A. Cassie and S. Baxter, Wettability of Porous Surfaces, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- V. Hejazi and M. Nosonovsky, Contact angle hysteresis in multiphase systems, Colloid Polym. Sci., 2012 DOI:10.1007/s00396-012-2838-0.
- T. Biben and L. Joly, Phys. Rev. Lett., 2008, 100, 186103 CrossRef CAS.
- E. Pierce, F. J. Carmona and A. Amirfazli, Understanding of sliding and contact angle results in tilted plate experiments, Colloids Surf., A, 2008, 323, 73–82 CrossRef CAS.
- T. D. Blake and J. Haynes, J. Colloid Interface Sci., 1969, 30, 421 CrossRef CAS.
- T. D. Blake, in Wettability, ed. J. C. Berg, Marcel Dekker, New York, 1993, pp. 251–309 Search PubMed.
- T. D. Blake, A. Clarke, J. De Coninck and M. J. de Ruijter, Contact angle relaxation during droplet, Langmuir, 1997, 13, 2164–2166 CrossRef CAS.
- R. A. Hayes and J. Ralston, Langmuir, 1994, 10, 340 CrossRef CAS.
- R. G. Cox, J. Fluid Mech., 1986, 16, 169–194 CrossRef.
- E. Dussan, E. Rame and S. Garoff, J. Fluid Mech., 1991, 230, 97 CrossRef.
- Y. Shikhmurzaev, J. Fluid Mech., 1997, 334, 211 CrossRef CAS.
- S. Vedantam and M. Panchagnula, Phase Field Modeling of Hysteresis in Sessile Drops, Phys. Rev. Lett., 2007, 99, 176102 CrossRef.
- B. J. Alder and T. E. Wainwright, Phase transition for a hard sphere system, J. Chem. Phys., 1957, 27, 1208–1209 CrossRef CAS.
- G. Saville, Computer simulation of the liquid–solid–vapour contact angle, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 1122–1132 RSC.
- J. Koplik, J. R. Banavar and J. F. Willemsen, Molecular dynamics of Poiseuille flow and moving contact lines, Phys. Rev. Lett., 1988, 60, 1282–1285 CrossRef.
- J. Koplik, J. R. Banavar and J. F. Willemsen, Molecular dynamics of fluid flow at solid surfaces, Phys. Fluids A, 1989, 1, 781–794 CrossRef CAS.
- P. A. Thompson, W. B. Brinckerhoff and M. O. Robbins, Microscopic studies of static and dynamic contact angles, J. Adhes. Sci. Technol., 1993, 7, 535–541 CrossRef CAS.
- P. A. Thompson and M. O. Robbins, Simulations of contact-line motion: slip and the dynamic contact angle, Phys. Rev. Lett., 1989, 63, 766–769 CrossRef CAS.
- M. Nosonovsky and S. Esche, Multiscale Effects in Crystal Grain Growth and Physical properties of metals, Phys. Chem. Chem. Phys., 2008, 10, 5192–5195 RSC.
- M. Nosonovsky, X. Zhang and S. Esche, Scaling of Monte Carlo simulations of grain growth in metals, Model. Simul. Mater. Sci. Eng., 2009, 17, 025004 CrossRef.
- F. Graner and J. A. Glazier, Phys. Rev. Lett., 1992, 69, 2013–2016 CrossRef CAS.
- J. A. Glazier and F. Graner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 2128–2154 CrossRef.
- J. A. Glazier, M. P. Anderson and G. S. Grest, Philos. Mag. B, 1990, 62, 615 CrossRef CAS.
- J. A. Glazier, G. S. Grest and M. L. P. Anderson, Ideal Two-Dimensional Grain Growth, Simul. Theory Evol. Microstruct., Proc. Symp., 1990, 41–54 Search PubMed.
- Y. Jiang, P. J. Swart, A. Saxena, M. Asipauskas and J. A. Glazier, Hysteresis and Avalanches in Two-Dimensional Foam Rheology Simulations, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5819–5832 CrossRef CAS.
- J. A. Glazier, M. P. Anderson and G. S. Grest, Coarsening in the Two-Dimensional Soap Froth and the Large-Q Potts Model: A Detailed Comparison, Philos. Mag. B, 1990, 62, 615 CAS.
- Y. Jiang and J. A. Glazier, Extended Large-Q Potts Model Simulation of Foam Drainage, Philos. Mag. Lett., 1996, 74, 119–128 CrossRef CAS.
- D. Dan, C. Mueller, K. Chen and J. A. Glazier, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2005, 72, 041909 CrossRef.
- A. Messager, S. Miracle-Sole and S. Shlosman, Interfaces in the Potts model II: Antonov's rule and rigidity of the order disorder interface, Commun. Math. Phys, 1991, 140, 275–290 CrossRef.
- L. de Oliveira, D. M. Lopes, S. M. M. Ramosb and J. C. M. Mombach, Two-dimensional modeling of the superhydrophobic behavior of a liquid droplet sliding down a ramp of pillars, Soft Matter, 2011, 7, 3763 RSC.
- A. Pockels, Surface tension, Nature, 1891, 43, 437–439 Search PubMed.
- R. Ablett, An investigation of the angle of contact between paraffin wax and water, Philos. Mag., 1923, 46, 224 Search PubMed.
- Y. I. Frenkel, On the Behavior of Liquid Drops on a Solid Surface. 1. The Sliding of Drops on an Inclined Surface, J. Exp. Theor. Phys., 1948, 18, 659 CAS.
- F. Bartell and J. Shepard, Surface Roughness as Related to Hysteresis of Contact Angles, J. Phys. Chem., 1953, 57, 455–458 CrossRef CAS.
- C. G. L. Furmidge, Studies at Phase Interfaces. I. The Sliding of Liquid Drops on Solid Surfaces and a Theory for Spray Retention, J. Colloid Sci., 1962, 17, 309–324 CrossRef CAS.
- R. Johnson and R. H. Dettre, Contact Angle Hysteresis, in Contact Angle, Wettability, and Adhesion, ed. F. M. Fowke, 1964 Search PubMed.
- N. K. Adam and G. Jessop, Angles of contact and polarity of solid surfaces, J. Chem. Soc., 1925, 1863 RSC.
- B. V. Derjaguin, On the dependence of the contact angle on the microrelief or roughness of a wetted solid surface, C. R. (Dokl.) Acad. Sci. URSS, 1946, 51, 361–364 Search PubMed.
- R. J. Good, J. Am. Chem. Soc., 1953, 79, 5041 Search PubMed.
- L. Boinovich and A. Emelyanenko, Wetting and surface forces, Adv. Colloid Interface Sci., 2011, 165, 60–69 CrossRef CAS.
- B. Krasovitski. and A. Marmur, Drops Down the Hill: Theoretical Study of Limiting Contact Angles and the Hysteresis Range on a Tilted Plane, Langmuir, 2004, 21, 3881–3885 CrossRef.
- G. Whyman, E. Bormashenko and T. Stein, The rigorous derivation of Young, Cassie–Baxter and Wenzel equations and the analysis of the contact angle hysteresis phenomenon, Chem. Phys. Lett., 2008, 450(4–6), 355–359 CrossRef CAS.
- M. Nosonovsky, Model for Solid–Liquid and Solid–Solid Friction for Rough Surfaces with Adhesion Hysteresis, J. Chem. Phys., 2007, 126, 224701 CrossRef.
- P. Letellier, A. Mayaffre and M. Turmine, Drop size effect on contact angle explained by nonextensive thermodynamics. Young's equation revisited, J. Colloid Interface Sci., 2007, 314, 604–614 CrossRef CAS.
- T. M. Cickovski, C. Huang, R. Chaturvedi, T. Glimm, H. G. E. Hentschel, M. S. Alber, J. A. Glazier, S. A. Newman and J. A. Izaguirre, A framework for three-dimensional simulation of morphogenesis, IEEE/ACM Trans. Comput. Biol. Bioinf., 2005, 2, 3 CrossRef.
- A. F. Stalder, G. Kulik, D. Sage, L. Barbieri and P. Hoffmann, A Snake-Based Approach to Accurate Determination of Both Contact Points and Contact Angles, Colloids Surf., A, 2006, 286(1–3), 92–103 CrossRef CAS.
| This journal is © the Owner Societies 2013 |
