 Open Access Article
Open Access ArticleDynamics of silver nanoparticle formation and agglomeration inside the cavitation bubble after pulsed laser ablation in liquid
Philipp
Wagener
a,
Shyjumon
Ibrahimkutty
b,
Andreas
Menzel
c,
Anton
Plech
*b and
Stephan
Barcikowski
*a
aTechnical Chemistry I and Center for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen, Universitaetsstrasse 7, D-45141 Essen, Germany. E-mail: stephan.barcikowski@uni-due.de; Fax: +49 201-1833049; Tel: +49 201-1833150
bInstitute for Synchrotron Radiation, Karlsruhe Institute of Technology, Postfach 3640, D-76021 Karlsruhe, Germany. E-mail: anton.plech@kit.edu; Tel: +49 (0)721-608 28665
cPaul Scherrer Institut, CH-5232 Villigen PSI, Switzerland
First published on 8th November 2012
Abstract
The formation of nanoparticles within the laser-induced cavitation bubble is studied in situ using small angle X-ray scattering with high spatiotemporal resolution. Directly after laser ablation, two different particle fractions consisting of compact primary particles of 8–10 nm size and agglomerates of 40–60 nm size are formed. The abundance of these species is strongly influenced by the dynamics of the oscillating cavitation bubble. Primary particle mass is most abundant during maximal expansion of the first bubble and reappears a little weaker in the rebound. In contrast to this, the mass abundance of agglomerates is relatively low in the first bubble but strongly increases during first bubble collapse and following rebound. Although most of the ablated material is trapped inside the bubble and follows its oscillation, a minor fraction of both species could be detected outside the cavitation bubble even before its final collapse.
1 Introduction
In recent years, pulsed laser ablation in liquid has been established as a versatile technique to fabricate a manifold of colloidal nanoparticles.1–3 To date there is continuously growing interest accompanied by an increasing shift from fundamentals to applications.4 Meanwhile, some fundamental questions including the detailed formation mechanism are still vividly debated in the literature.The challenge in clarifying the nanoparticle formation mechanism is based on different aspects. First, the time scale of nanoparticle formation is very broad: it includes ultrafast physical processes like laser pulse absorption and relaxation of excited electrons by electron–phonon coupling,5,6 energy dissipation and target ablation7,8 and cavitation bubble formation.9,10 Finally, slow diffusion-controlled chemical processes like ligand adsorption and particle growth due to coalescence, agglomeration and ripening contribute.11–13 Due to this complexity, post-mortem analysis of fabricated nanoparticles is not capable of providing precise information about single reaction steps. Second, in a conventional batch set-up used for pulsed laser ablation in liquid, all those steps take part in parallel and lead to additional secondary processes like post-irradiation of nanoparticles formed by previous pulses.14–16 Consequently, it is necessary to separate the different formation steps and analyse them in detail by sophisticated techniques. The usefulness of spatial separation of primary nanoparticle formation and subsequent slow processes like growth and ligand adsorption was recently shown by Sajti et al. using a flow reactor instead of a stationary batch chamber.17
The fast processes of nanoparticle formation are still unclear. It is generally accepted that the laser-induced cavitation bubble plays a significant role and acts as a kind of nanoparticle reactor in which the nanoparticles are formed.18,19 After laser pulse absorption, a shock wave is emitted from the target after about 50 ns20 followed by formation of an expanding bubble within 1 μs, which starts oscillating and finally collapses after hundreds of microseconds.21,22 Material ejection from the target starts after dissipation of absorbed pulse energy and again during bubble collapse due to plasma etching.23 Significant contributions in elucidating the role of the cavitation bubble during nanoparticle formation were done by the group of Sasaki who characterized the laser-induced cavitation bubble and its dynamics by shadowgraphy,22 laser scattering24 and Rayleigh–Plesset-calculations.25 The reaction conditions inside the bubble are strongly time-dependent and cover a broad temperature range during expansion and shrink phases including temperature and pressure peaks up to 104 K and 104 bar during bubble collapse.19 Although these reaction conditions within the cavitation bubble are quite well known, a direct observation of particle formation inside the cavitation bubble is not trivial. In established optical methods like shadowgraphy or laser light scattering, the optical dense bubble–liquid-interface scatters the incident light and prohibits imaging of the species inside the bubble. Furthermore, the involved species during nanoparticle formation can be expected to be much smaller than the wavelength of the incident laser resulting in a low sensitivity. As a consequence, optical methods bear limitations for time-resolved observation of nanoparticle formation inside the cavitation bubble.
A more promising approach to look inside the cavitation bubble during nanoparticle formation is the use of X-rays which can penetrate the bubble interface and are capable of analysing even nanometer-sized particle distributions and intermediate structures by scattering.26,27 Lavisse et al. investigated laser ablation of titanium in ambient air using small-angle X-ray scattering (SAXS)28 and identified two distinguishable species of around 20 and 180 nm diameter within the ablation plume. We recently investigated laser ablation of gold in water by SAXS29 by adding spatial and temporal resolution. Therein two different species could also be identified within the cavitation bubble at its maximum elongation: small particles of about 10 nm diameter and secondary particles in the range of 45 nm. While the small particles are distributed all over the bubble and can even penetrate the liquid–bubble interface, a few percent of the ablated mass nucleate as 45 nm-sized secondary particles presumably formed in the upper part but strictly confined by the bubble. The identification of species involved in the nanoparticle formation inside the bubble is only the first part of the puzzle. Since the laser-induced cavitation bubble is highly dynamic, the temporal evolution of involved species during bubble expansion, collapse and rebound is of high interest for a deeper understanding of their formation mechanism. For this purpose, we performed time-resolved SAXS of laser ablation in liquid flow to investigate the dynamics of species formed inside the cavitation bubble during its entire lifetime. Besides gold, silver is one of the most studied materials using laser ablation in liquid due to its unique optical and antibacterial properties and was chosen as a model system.
2 Materials and methods
2.1 Experimental set-up
Small angle X-ray scattering (SAXS) is usually accompanied by low scattering cross section and acquires long data accumulation times. Since pulsed laser ablation in a liquid batch chamber is not a stationary process but highly dynamic due to the changing concentration of nanoparticles, unequal flow conditions, progressing target ablation and post-irradiation of nanoparticles by subsequent pulses,16 a stationary and reproducible process has to be secured for sufficient time.The ablation from a silver target (ribbon) immersed in water has been induced by a nanosecond laser with 10 mJ pulse energy (1064 nm, 6 ns, 200 Hz, EdgeWave HD-40I-E). It was focused onto a spot size of about 100 μm by means of a plano-convex lens. A chamber, which is schematically depicted in Fig. 1 (left), has been built that allows for a continuous refreshing of the target and water column. The metal ribbon is moved with a speed of about 10 cm s−1 while the water is refreshed in a stream above the target with 25 l h−1. An X-ray beam probes transmission through the liquid (on a photo diode) and SAXS (on a 2D detector) perpendicular to the moving direction of the ribbon by entering the chamber through thin Kapton (DuPont) windows. The experiment was performed at the Swiss Light Source (PSI Villigen, CH) at the cSAXS beamline. The monochromatic X-ray beam (photon energy = 13.6 keV) is focused onto a spot size of 6 by 23 μm (vert. by horiz.). A hybrid pixel detector (Pilatus 2M)30 at a distance of 2.53 m was used to record the SAXS pattern. Its pixels possess independent counters that can be gated to be active within a given time period. We have used gates of 40 and 80 μs. A beam stop that prevents the direct beam from hitting the detector is equipped with a photo diode for simultaneous measurement of the transmitted X-ray intensity. This temporal response is recorded on an oscilloscope (LeCroy). Laser, detector and oscilloscope are triggered from a delay generator with the mutual delays being freely movable. This scheme is illustrated in Fig. 1 (right). For the 80 μs gate, typically a total number of 1.5 × 104 shots are accumulated before reading out the detector. This number is doubled for the 40 μs gate because of the lower duty cycle.
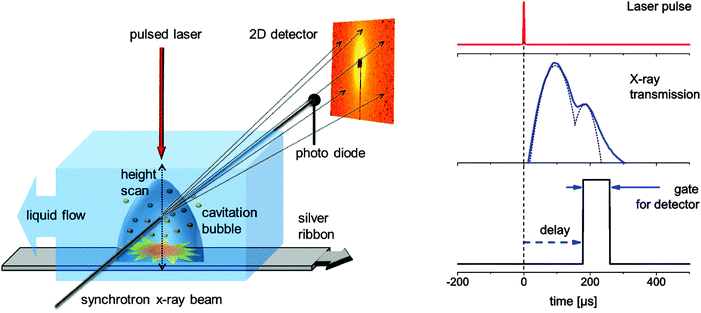 | ||
| Fig. 1 Left: experimental setup displaying the X-ray scattering experiment, liquid flow conditions and moving target to provide reproducible experimental conditions for every laser pulse during time-gated data accumulation. Right: scheme of the stroboscopic data acquisition with the detector being gated active for a fixed interval with delay with respect to the laser impact. The oscilloscope traces of the transmission change are recorded at the same time. | ||
The 2D scattering patterns have been converted into one-dimensional scattering curves I(q) with q = 4π/λsin(2θ/2) with X-ray wavelength λ and scattering angle 2θ after standard space angle corrections.
The X-ray transmission changes temporally due to the formation of a vapor bubble in the liquid and was used to reconstruct the bubble size and duration. A silver ribbon of 3 mm width and 0.2 mm thickness (Allgemeine, Germany) and deionized water were used.
2.2 Small angle X-ray scattering
Small angle X-ray scattering probes (electron) density modulations on a scale from sub-nanometer sizes to hundreds of nanometers.31–33 The atomic ordering can be neglected for given objects with density contrast Δρ(r) in an otherwise homogeneous matrix. The scattering distribution I(q) can be written as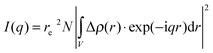 | (1) |
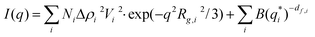 | (2) |
In our case, one can consider ablated nanoparticles of different size and agglomeration state that are the origin of the scattering distribution. A real model-independent quantity is the scalar Porod invariant P:34,35
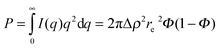 | (3) |
3 Results and discussion
3.1 Cavitation bubble dynamics
Cavitation bubble dynamics were measured using the time-dependent X-ray transmission changes. The laser-induced vapor bubble causes less absorption. Therefore the amplitude of change is directly proportional to the change in water thickness and also to the bubble size.Recording this change as a function of both height above the target and time delay allows us to reconstruct the bubble size and duration. Such a map of spatiotemporal transmission change is depicted in Fig. 2. The bubble expands to a maximum height of slightly more than 1 mm at about 80 μs. The total duration of the cavitation is about 350 μs. A closer inspection reveals that the bubble recedes quickly after 150 μs, but then the collapse seems to stop, displaying a peak shoulder in the transmission diagram (Fig. 2). We interpret this behavior as a second rebound of the bubble after collapse due to oscillation described by the Rayleigh–Plesset equation. It is not fully resolved in time due to the averaging over the number of shots per measurement. The rebound expands to about 0.7 mm at 220 μs. A single transmission curve at 0.17 mm is also seen in Fig. 1 (right) with a guide-to-the-eye for the bubble dynamics.
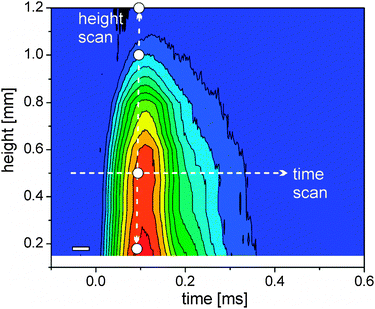 | ||
| Fig. 2 Colour scale plot of the change in X-ray transmission as a function of delay and height above the target (blue – no change, red – strong change). The arrows mark exemplary scans in delay (horizontal) and space (vertical). Used height positions for time-resolved scans are marked as white dots; the time resolution element is given by the white rectangle (left bottom). | ||
Since cavitation bubble dynamics are known, the discriminable bubble phases of maximal expansion during the first cycle, first collapse, maximal expansion during the second cycle and final collapse can be identified and assigned to spatiotemporal-resolved measurements of laser-generated particles.
3.2 Spatiotemporal particle distribution in the cavitation bubble
The spatiotemporal distribution of species formed after laser ablation was calculated using the methods described in the Experimental section. Fig. 3 displays the I(q)q2 curves for different heights above the target both within the first bubble and the rebound. Fits with eqn (3) are added. The data allow us to distinguish between size fractions around 8–10 nm and a second fraction of up to 60 nm diameter. This finding is similar to the ablation from gold.29 At 1 mm and 1.2 mm height scattering is very weak and fitting is not unique. The noise there is high due to subtracting the background at negative delay. In particular the high q region is affected by a varying baseline due to the (small) transmission change. As both heights are above the maximal bubble extension, a low particle mass is found in the liquid phase.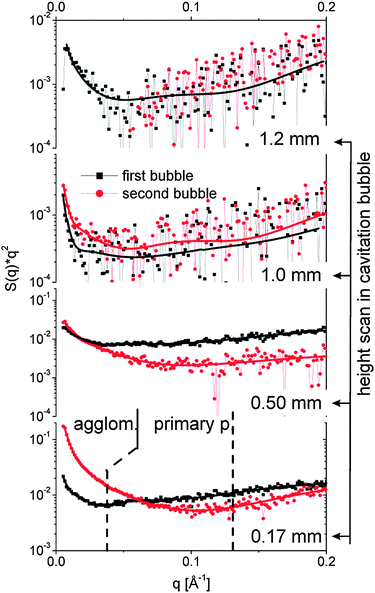 | ||
| Fig. 3 SAXS curves I(q)q2 for different heights above the target both during the first bubble (80 μs, black squares) and the rebound (220 μs, red bullets). The lines are fits with the unified equation. The dotted lines separate the q range for derivation of the partial invariants shown in Fig. 4. | ||
The fits reveal particle size, mass scaling factor and the power law exponent df. The larger size fraction needs to be described by a small exponent at or below 2. This is in agreement with the findings of Lavisse et al.28 who ascribed this exponent to a fractal structure of chain-like particle assemblies. This is an indication that the large size fraction is composed of agglomerates or aggregates of smaller entities. These smaller particles in the range of 8–10 nm are best fitted with high exponents close to 4. An exponent of 4 is expected for compact particles.
The partial invariants are plotted in Fig. 4 for both size fractions of agglomerates and primary particles. Inside the bubble, primary particles and agglomerates in principle follow the cavitation bubble dynamics (0.17 and 0.5 mm). Nevertheless, it is clear that the behavior of the two populations is very different. The primary particle mass is most abundant during maximal expansion of the first bubble and reappears during the rebound. The agglomerations are relatively weak in the first bubble but the mass increases strongly within the rebound. One should keep in mind that the particle mass is displayed rather than numbers. The particle number of the agglomerates would be lower by their volume ratio to the primary particles.
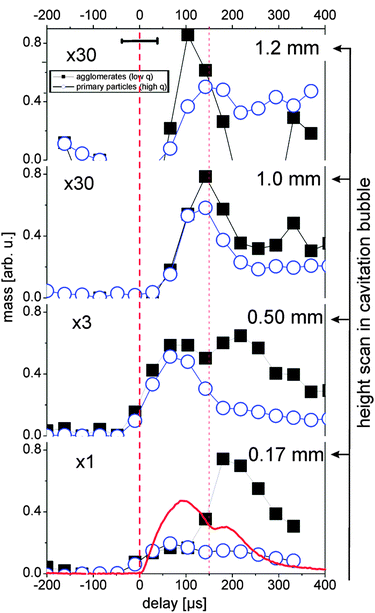 | ||
| Fig. 4 Partial invariants 0.01 < q < 0.037 (black squares, agglomerates) and 0.037 < q < 0.13 Å−1 (blue circles, primary particles) as a measure for the total particle mass in the illuminated X-ray path for several heights. The red line displays the X-ray transmission change during the bubble oscillation. The horizontal error bar marks the time resolution. The error of the values is approximately represented by the symbol size. First vertical dashed line marks the laser impact, the second line first bubble collapse. | ||
Agglomerates are not necessarily globular neither are they compact, as seen above through the exponent df of the fit function. Therefore it is difficult to estimate number ratios. The fit suggests a ratio of 20–100 between primary particle and agglomerate number.
As previously observed for gold, the abundance of agglomerates in the first bubble close to the target is low and increases with height. Outside the bubble a very low mass of agglomerates is detected. Note that the curves in Fig. 4 are scaled by the factors given in the plot. During the rebound, however, this changes strongly. A much higher fraction of the mass is incorporated in the agglomerates inside the bubble. We conclude that the collapse of the bubble retracts the ablated material towards the target, which leads to an increased rate of agglomeration. Agglomerates can finally be released after the rebound has decayed. An interesting behavior is seen right above (or at) the bubble apex (1 mm height). Here, as expected the particle mass at the first bubble is low, but a mass maximum is seen during the collapse phase of the first bubble.
This could be explained by the penetration of particles into the liquid during the backward movement of the bubble wall. Another explanation would be the formation of a jet at the bubble collapse that has been observed earlier for cavitation bubbles in vicinity to a boundary.36 At present we cannot distinguish between both scenarios. Anyway, it is clear that most of the detected particle mass is trapped inside the first bubble as primary particles with a small extent of agglomeration. The bubble collapse reconcentrates the particles, but also allows releasing a part through the receding bubble front. In the bubble rebound a strong agglomeration occurs, which can be released into the surrounding liquid upon complete collapse.
Furthermore, it is important to note that there is an experimental indication of small sub-nm-sized clusters or ionic species which are below the resolution of our experimental set-up. Sajti et al. showed that gold nanoparticles continuously grow outside the cavitation bubble on a multisecond time scale until achieving their final size and postulated the existence of small, non-plasmonresonant species that feed the primary particles to induce growth.17 Thus, a third species of very small particles (<2 nm) may be generated during laser ablation in liquid. Those are to present below the detection limit of our experiment.
3.3 Temporal evolution of particle size
The high and low q-fractions can be assigned to two clearly distinguishable particle fractions (primary particles and agglomerates), the particle size of each fraction slightly changes as a function of time and place. The spatiotemporal primary particle and agglomerate diameters are shown in Fig. 5. Only values with stable fit parameters are shown.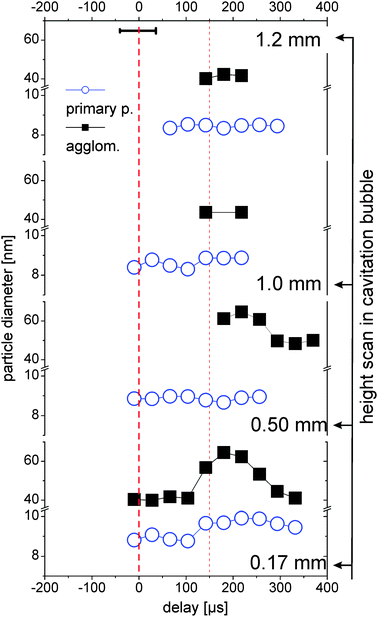 | ||
| Fig. 5 Diameters of the two size fractions measured at different heights above the target as a function of delay. For details of the description see Fig. 4. | ||
The primary particle size is almost constant with a small trend towards smaller particles at larger height, which is in good agreement with recent measurements on laser ablation of gold.29 The primary particles are emitted from the target with a distinct distribution in nascence and/or drift velocity. Under the assumption that expansion of the bubble front is faster than particle drift velocity, the fastest and subsequent smallest particles accumulate in the upper part of the bubble after its formation.
Close to the target (0.17 mm) there is a trend of increase in the primary particle size during the bubble rebound, probably by growth or coalescence due to high temperatures at the bubble collapse.25 Agglomerates are also seen to grow in the rebound at 0.17 and 0.5 mm. Above the bubble (1.0 and 1.2 mm), no temporal trend of particle size change can be seen. This might also be due to the low counting statistics there (30 times less abundance, see Fig. 4).
The variability of agglomerate size within the first bubble, the rebound and after bubble collapse supports the notion that these agglomerates are rather loose networks than compact objects. This is in agreement with the modelling of the SAXS data as explained in Section 3.2. The parameter df for the large entities is considerably smaller than the one for the primary particles. The values of 3.6–4 for the primary particles are indicative of compact objects. This also may explain why the formation of aggregates can be efficiently prevented by addition of a surfactant or a stabilizing ligand,11 since it is still unknown, when this size-quenching takes part during the formation mechanism.
The comparison of the observed transient particle size with electron microscopy reveals some significant differences. Silver nanoparticles fabricated in pure water using similar laser parameters show an average particle diameter of about 18 nm37 which is almost twice the diameter of primary particles identified within the cavitation bubble. Thus, ripening processes take part after final collapse of the cavitation bubble and release of primary particles. This tendency of the primary particles to grow during the life time of the cavitation bubble is also shown in Fig. 5. Nevertheless, all comparisons of transient particle size with post-mortem analysis by electron microscopy have to be done with great care since it is known that unstabilized silver nanoparticles slowly dissolve in water38 or even can ripen at a surface like a TEM grid39. Further, electron micrographs always reflect the situation after a drying process and not within the liquid.
3.4 Correlation of cavitation bubble dynamics and particle formation
The dynamics of the nanoparticle formation inside the cavitation bubble can be summarized in the following way: primary particle mass is predominantly formed directly after laser ablation and diluted during bubble expansion over the bubble volume. In contrast to this, the abundance of agglomerates is much more influenced by the cavitation bubble dynamics. The mass of the secondary particles is relatively low in the first bubble but strongly increases close to the target probably due to agglomeration of primary particles captured during first collapse. The bubble represents a confinement, which upon collapse gathers the primary particles into agglomerates and increases the size of those agglomerates.To complete the picture of the particle formation even at long delays after final collapse of the bubble, we performed a long time scan at a position of 0.17 mm above the target up to a delay time of 0.8 ms. For this experiment, the time resolution was improved by using a shorter gate of 40 μs. Fig. 6 shows a comparison between the development of mass of the agglomerates and primary particles versus the bubble expansion. It can be resolved clearly that the particle mass development is closely connected to the bubble dynamics. The increase in the agglomerate abundance during the rebound is significant. Additionally, a strong release of agglomerates is seen at later times beyond 400 μs where no macroscopic bubbles were detected by the X-ray beam down to 170 μm above the target. This also points towards a slow (diffusional) release of part of the ablated material after collapse-driven redeposition onto or close to the target. Such back-deposition of ablated materials during bubble collapse could also be visualized using optical spectroscopy by De Giacomo et al.40
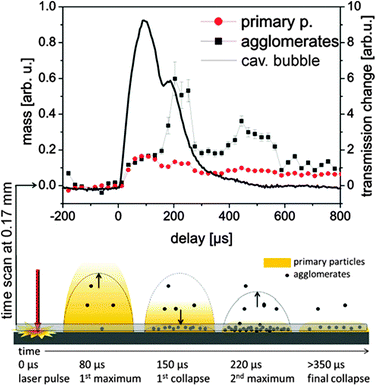 | ||
| Fig. 6 Upper: partial invariants as a function of delay with a 40 μs gate of the detector. The line displays the X-ray transmission at a height of 0.17 mm. Lower: sketch of the particle distribution for several characteristic delays. | ||
4 Conclusions
Time-resolved SAXS of laser ablation in liquid reveals that after laser absorption a vapor-filled cavitation bubble is formed at the target surface which undergoes oscillation including a rebound and final collapses after 220 μs. Inside the cavitation bubble two individual species can be identified: compact primary particles of 8–10 nm size and bigger agglomerates of 40–60 nm size. The presence of clusters or very small particles (<2 nm) is possible but cannot be proven due to the detection limit of the experiment.The particle abundance is strongly linked to cavitation bubble dynamics: during maximum elongation of the cavitation bubble, the primary particle mass goes through a maximum and reappears in the rebound, probably then contained in agglomerates. Vice versa, the total mass of agglomerates is relatively weak in the first bubble but it increases strongly within the rebound. Although most of the ablated material is trapped inside the bubble and follows its oscillation, there is a certain fraction of primary particles and agglomerates which can be localized outside the bubble. This indicates that bubble–liquid interface is penetrable by the ablated matter. Primary particles may enter the liquid already during the bubble expansion phase possibly due to high ejection velocities. Agglomerates stay inside the bubble with highest concentration close to the target surface and are released by the bubble only after its collapse.
The size of primary particles and agglomerates does not strongly depend on time and position, the average size of primary particles slightly decreases with higher distance to the target. Furthermore, there is a slight tendency for growth of primary particles and agglomerates during the first rebound. A picture is finally established that implies that most of the mass release happens after recompaction onto the surface during bubble collapse.
Acknowledgements
This work was funded by the German Research Foundation (DFG) by the priority programme 1327. AP would like to acknowledge support from KIT and the Heisenberg Fellowship of the DFG. Beamtime at the SLS and funding from the European Community's Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 226716 are gratefully acknowledged, with special thanks to the excellent support by C. Kramer, M. Caspar, B. Henrich and H. Billich. We thank R. Rosenfeld for his support in construction of the ablation chamber.Notes and references
- H. Zeng, X. W. Du, S. C. Singh, S. A. Kulinich, S. Yang, J. He and W. Cai, Adv. Funct. Mater., 2012, 22, 1333–1353 CrossRef CAS.
- V. Amendola and M. Meneghetti, Phys. Chem. Chem. Phys., 2009, 11(20), 3805–3821 RSC.
- S. Barcikowski, F. Devesa and K. Moldenhauer, J. Nanopart. Res., 2009, 11, 1883–1893 CrossRef.
- S. Barcikowski and F. Mafune, J. Phys. Chem. C, 2011, 115, 4985 CAS.
- C. Momma, B. N. Chichkov, S. Nolte, F. von Alvensleben, A. Tünnermann, H. Welling and B. Wellegehausen, Opt. Commun., 1996, 129, 134–142 CrossRef CAS.
- S. Nolte, C. Momma, H. Jacobs and A. Tünnermann, J. Opt. Soc. Am. B, 1997, 14(10), 2716–2722 CrossRef CAS.
- L. V. Zhigilei, Z. Lin and D. S. Ivanov, J. Phys. Chem. C, 2009, 113, 11892–11906 CAS.
- P. Lorazo, L. J. Lewis and M. Meunier, Phys. Rev. B, 2006, 73, 134108 CrossRef.
- W. Hentschel and W. Lauterborn, Appl. Sci. Res., 1982, 38, 225–230 CrossRef.
- A. Vogel, J. Noack, K. Nahen, D. Theisen, S. Busch, U. Parlitz, D. Hammer, G. Noojin, B. Rockwell and R. Birngruber, Appl. Phys. B: Lasers Opt., 1999, 68, 271–280 CrossRef CAS.
- F. Mafune, J. Y. Kohno, Y. Takeda, T. Kondow and H. Sawabe, J. Phys. Chem. B, 2000, 104(39), 9111–9117 CrossRef CAS.
- J. P. Sylvestre, A. V. Kabashin, E. Sacher, M. Meunier and J. H. T. Luong, J. Am. Chem. Soc., 2004, 126, 7176–7177 CrossRef CAS.
- H. H. Liu, S. Surawanvijit, R. Rallo, G. Orkoulas and Y. Cohen, Environ. Sci. Technol., 2011, 45, 9284–9292 CrossRef CAS.
- V. Kotaidis and A. Plech, Appl. Phys. Lett., 2005, 87, 213102 CrossRef.
- A. Plech, V. Kotaidis, M. Lorenc and M. Wulff, Chem. Phys. Lett., 2005, 401, 565 CrossRef CAS.
- A. Schwenke, P. Wagener, S. Nolte and S. Barcikowski, Appl. Phys. A: Solid surf., 2011, 104, 77–82 CrossRef CAS.
- C. Sajti, A. Barchanski, P. Wagener, S. Klein and S. Barcikowski, J. Phys. Chem. C, 2011, 115, 5094–5101 CAS.
- T. Tsuji, Y. Okazaki, Y. Tsuboi and M. Tsuji, Jpn. J. Appl. Phys., 2007, 46, 1533–1535 CrossRef CAS.
- K. Sasaki and N. Takada, Pure Appl. Chem., 2010, 82, 1317–1327 CrossRef CAS.
- T. Tsuji, D.-H. Thang, Y. Okazaki, M. Nakanishi, Y. Tsuboi and M. Tsuji, Appl. Surf. Sci., 2008, 254, 5224–5230 CrossRef CAS.
- A. Vogel, W. Lauterborn and R. Timm, J. Fluid Mech., 1989, 206, 299–338 CrossRef.
- K. Sasaki, T. Nakano, W. Soliman and N. Takada, Appl. Phys. Express, 2009, 2, 046501 CrossRef.
- A. V. Kabashin, M. Meunier, C. Kingston and J. H. Luong, J. Phys. Chem. B, 2003, 107(19), 4527–4531 CrossRef CAS.
- W. Soliman, N. Takada and K. Sasaki, Appl. Phys. Express, 2010, 3, 035201 CrossRef.
- W. Soliman, T. Nakano, N. Takada and K. Sasaki, Jpn. J. Appl. Phys., 2010, 49, 116202 CrossRef.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
- M. Sztucki, T. Narayanan and G. Beaucage, J. Appl. Phys., 2007, 101, 114304 CrossRef.
- L. Lavisse, J. L. Le Garrec, L. Hallo, J. M. Jouvard, S. Carles, J. Perez, J. B. A. Mitchell, J. Decloux, M. Girault, V. Potin, H. Andrzejewski, M. C. Marco de Lucas and S. Bourgeois, Appl. Phys. Lett., 2012, 100, 164103 CrossRef.
- S. Ibrahimkutty, P. Wagener, A. Plech, A. Menzel and S. Barcikowski, Appl. Phys. Lett., 2012, 101, 103104 CrossRef.
- B. Henrich, A. Bergamaschi, C. Broennimann, R. Dinapoli, E. F. Eikenberry, I. Johnson, M. Kobas, P. Kraft, A. Mozzanica and B. Schmitt, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 607, 247–249 CrossRef CAS.
- A. Guinier and G. Fournet, Small-angle scattering of X-rays, John Wiley & Sons, New York, 1955 Search PubMed.
- B. E. Warren, X-ray Diffraction, Dover Publications, New York, 1990 Search PubMed.
- N. Dingenouts, J. Bolze, D. Poetschke and M. Ballauff, Adv. Polym. Sci., 1999, 144, 1 CrossRef CAS.
- G. Porod, Kolloidn. Zh., 1952, 125, 109 Search PubMed.
- A. Plech, A. Siems, V. Kotaidis and M. Sztucki, Phys. Chem. Chem. Phys., 2008, 10, 3888 RSC.
- W. Lauterborn and T. Kurz, Rep. Prog. Phys., 2010, 73, 106501 CrossRef.
- P. Wagener, A. Schwenke and S. Barcikowski, Langmuir, 2012, 28, 6132 CrossRef CAS.
- S. Kittler, C. Greulich, J. Diendorf, M. Koller and M. Epple, Chem. Mater., 2010, 22, 4548 CrossRef CAS.
- R. D. Glover, J. M. Miller and J. E. Hutchison, ACS Nano, 2011, 5, 8950 CrossRef CAS.
- A. De Giacomo, R. G. Audiuso, M. Dell'Aglio, A. Santagata, O. De Pascale, S. Barcikowski, P. Wagener, G. C. Messina and G. Compagnini, Phys. Chem. Chem. Phys. 10.1039/C2CP42649H.
| This journal is © the Owner Societies 2013 |
