 Open Access Article
Open Access ArticleSynthesis, crystal structure and phase transitions of a series of imidazolium iodides†
Magdalena
Węcławik
a,
Anna
Gągor
b,
Anna
Piecha
*a,
Ryszard
Jakubas
a and
Wojciech
Medycki
c
aFaculty of Chemistry, University of Wrocław, F. Joliot-Curie 14, 50-383 Wrocław, Poland. E-mail: anna.piecha@chem.uni.wroc.pl; Fax: +48713757270; Tel: +48713757288
bW. Trzebiatowski Institute of Low Temperature and Structure Research PAS, P. O. Box 1410, 50-950 Wrocław, Poland
cInstitute of Molecular Physics, PAS, M. Smoluchowskiego 17, 60-179 Poznań, Poland
First published on 10th May 2013
Abstract
The reaction of imidazole with hydroiodic acid leads to three products crystallizing as ionic salts; [C3N2H5+][I−], [C3N2H5+]2[I42−] and [C3N2H3I2+][I−]. All the analogs were characterized by single-crystal X-ray diffraction, while the first two were additionally studied by calorimetric, dilatometric, dielectric and proton magnetic resonance methods. At room temperature (RT), [C3N2H5+][I−] adopts the centrosymmetric, trigonal space group (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ). The crystal structure consists of disordered imidazolium cations and discrete I− ions. [C3N2H5+][I−] undergoes two discontinuous phase transitions (PTs) at 180/185 K and 113/123 K (cooling–heating), both of them governed by the imidazolium cation dynamics. [C3N2H5+]2[I42−] consists of disordered imidazolium cations and quite rare and exotic [I4]2− tetraiodide counterion. It undergoes continuous PT at 204 K of the ferroelastic type with a symmetry change from orthorhombic Fddd to monoclinic C2/c. The mechanism of PT is complex and consists of ‘order–disorder’ and ‘displacive’ contributions that are assigned to the dynamics of cations and to the distortion of the [I42−] rods, respectively. [C3N2H3I2+][I−] is built up of discrete 4,5-diiodoimidazolium cations and isolated I− ions. A characteristic feature of this compound is the presence of a layered structure in which moieties are held together by strong I⋯I halogen interactions and N–H⋯I hydrogen bonds.
). The crystal structure consists of disordered imidazolium cations and discrete I− ions. [C3N2H5+][I−] undergoes two discontinuous phase transitions (PTs) at 180/185 K and 113/123 K (cooling–heating), both of them governed by the imidazolium cation dynamics. [C3N2H5+]2[I42−] consists of disordered imidazolium cations and quite rare and exotic [I4]2− tetraiodide counterion. It undergoes continuous PT at 204 K of the ferroelastic type with a symmetry change from orthorhombic Fddd to monoclinic C2/c. The mechanism of PT is complex and consists of ‘order–disorder’ and ‘displacive’ contributions that are assigned to the dynamics of cations and to the distortion of the [I42−] rods, respectively. [C3N2H3I2+][I−] is built up of discrete 4,5-diiodoimidazolium cations and isolated I− ions. A characteristic feature of this compound is the presence of a layered structure in which moieties are held together by strong I⋯I halogen interactions and N–H⋯I hydrogen bonds.
Introduction
Ionic liquids based on various substituted imidazolium salts are characterized by low melting points, many of them are liquid at room temperature. Extensive studies of ionic liquids have revealed a great number of useful properties such as extremely low volatility, high thermal stability and high ionic conductivity.1–4 Therefore, the above-mentioned ionic liquids have found application in solar cells, electrochemical devices and ion transport systems.5Bulky plane organic cations like non-substituted imidazolium are widely used in numerous organic–inorganic hybrids. Such organic molecules play a role of simple dielectric rotator units which have been used to obtain new ferroelectric materials. The known representatives of this group of ferroic compounds are based on haloantimonates(III) and halobismuthates(III) with the R5M2X11 chemical stoichiometry (where R = imidazolium cation (C3N2H5+), M = Sb, Bi and X = Cl, Br). Three imidazolium ferroelectrics with this composition have already been synthesized and characterized.6–8 The ‘order–disorder’ mechanism of ferroelectric transition in R5M2X11 type compounds was assigned to the dynamics of imidazolium cations. Very recently, bis(imidazolium) L-tartrate, a hydrogen-bonded ‘displacive’ type ferroelectric material was discovered.9 The simple (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) ionic complexes of imidazolium and tetrahedral anions were found to also exhibit ferroelectric properties at the room temperature phases; [C3N2H5+][ClO4−]10 and [C3N2H5+][BF4−].11
1) ionic complexes of imidazolium and tetrahedral anions were found to also exhibit ferroelectric properties at the room temperature phases; [C3N2H5+][ClO4−]10 and [C3N2H5+][BF4−].11
Imidazolium analogs in which the anionic network is formed by the halogen atoms appeared to be the simplest as regards the crystal structure; however, they have been studied only fragmentarily. Recently, we have characterized the molecular-ionic compound, [C3N2H5+][Br−] (ImBr), which shows very interesting structural and dynamic properties.12 The crystal structure of the RT phase is described by the polar, R3 space group and consists of a highly disordered imidazolium cations and discrete Br− anions. ImBr reveals a first order phase transition at 199/201 K (cooling–heating cycle) which leads to the monoclinic centrosymmetric space group P21/m. The mechanism of the phase transition is mixed; related to the freezing of cation motions (‘order–disorder’ (‘o–d’) contribution) and to a significant rebuilding of the anionic substructure (‘displacive’ (‘d’)-type mechanism).
The aim of this paper is to present details of physicochemical properties of a series of imidazolium salts; [C3N2H5+][I−] (1) and [C3N2H5+]2[I42−] (3) including preparation, crystal structures in various phases, thermal and dielectric properties. Structural characterization is presented also for a new substituted imidazolium compound; [C3N2H3I2+][I−] (2). The molecular motions in (1) and (3) are studied by means of proton magnetic resonance measurements (1H NMR) (for more information, see ESI†). The molecular mechanism of the phase transitions in the crystals under investigation is also proposed.
Experimental section
Materials and instrument
(1) crystals were prepared at ambient temperature by dissolving imidazole in the 20% HI solution. Single crystals were grown by slow evaporation from the solution. The crystalline product was twice recrystallized. Single transparent crystals were grown by slow evaporation from an aqueous solution and characterized by an elemental analysis: C: 18.37% (theor. 18.39%), N: 14.25% (theor. 14.29%), H 2.49% (theor. 2.57%).
(2) crystals were prepared by dissolving imidazole in the 20% HI solution. Subsequently, the mixture was stirred (at 320 K for about 30 min). After a few days, tiny minuscule transparent solids were formed by a slow evaporation from the colorless solution. Nevertheless, due to small amounts of obtained material (only X-ray diffraction measurements were undertaken) we were not able to make the physicochemical characterization of this material. We obtained successfully the 4,5-diiodoimidazolium iodide crystals only during the first crystallization. The following crystallization produced exclusively the (1) crystals.
(3) crystals were prepared at ambient temperature by dissolving imidazole in concentrated (57%) HI. Single crystals were grown by slow evaporation from the solution. The dark, navy blue, needle like crystals were characterized by an elemental analysis: C: 11.18% (theor. 11.16%), N: 8.55% (theor. 8.68%), H 1.59% (theor. 1.56%).
General details
All the solvents and starting materials for the synthesis were purchased commercially and were used as received.DSC traces were obtained using a Perkin Elmer model 8500 differential scanning calorimeter calibrated using n-heptane and indium. Hermetically sealed Al pans with the polycrystalline material were prepared in a controlled-atmosphere N2 glovebox. The measurements were performed between 100 and 470 K. The thermal hysteresis was estimated from the scans performed at various rates (20, 10 and 5 K min−1) extrapolated to a scanning rate of 0 K min−1. Simultaneous Thermogravimetric Analysis (TGA) and Differential Thermal Analysis (DTA) were performed on a Setaram SETSYS 16/18 instrument in the temperature range 300–700 K with a ramp rate 2 K min−1 the scans was performed in flowing nitrogen (flow rate: 1 dm3 h−1).
The complex electric permittivity, ε* = ε′ − iε′′ was measured between 100 and 290 K by the Agilent E4980A Precision LCR Meter in the frequency range between 135 Hz and 2 MHz. The overall error was less than 5%. The single crystal samples had dimensions ca. 2 × 2 × 0.5 mm3. Silver electrodes were printed on opposite faces. The dielectric measurements were carried in a controlled atmosphere (N2).
Single crystal X-ray diffraction crystallographic data were collected on a KM4 diffractometer with CCD detector and graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). Low temperature was maintained using an open flow unit (Oxford Cryosystem). The CrysAlis software version 1.171.32 was used for data processing.13 An empirical absorption correction was applied using spherical harmonics implemented in SCALE3 ABSPACK scaling algorithm. The structure was solved by direct methods and refined against F2 by means of SHELX-97 program package.14 All non-hydrogen atoms were refined anisotropically. H atoms were included in geometric positions and treated as riding atoms. The Uiso(H) were constrained to be xUeq (carrier atom), where x = 1.2.
Structural phase transitions observed with temperature lowering led to twinning of the (1) and (3) crystals. In (3) symmetry changed from orthorhombic to monoclinic which resulted in crystal twinning with two dominating domains, with partially overlapped diffraction peaks. Refinement of the structure was performed using the data from both domains and HKLF 5 instruction.
In the case of (1) two structural transformations were encountered. During the cooling cycle the crystal symmetry changed from trigonal to triclinic (at 180 K) and with further cooling to a monoclinic one (113/123 K cooling–heating). Lowering of the crystal class led to non-merohedral twinning of the sample. Six triclinic crystal domains were encountered at 150 K from the splitting of diffraction peaks. Partial overlapping of the peaks together with weak intensities did not allow satisfactory indexing, thus the crystal structure of this intermediate phase has not been determined. Below 113 K the symmetry of (1) increased to monoclinic and the number of domains was reduced to three. The structure refinement was based on the diffraction intensities from one dominating crystal domain, indexing 60% of the measured diffraction peaks. All peaks were completely separated. Table 1 contains crystal data and structure refinement results of measured crystals.
| Crystal data | (1) | (2) | (3) | ||
|---|---|---|---|---|---|
| Chemical formula | C3H5IN2 | C3H5IN2 | C3H3I3N2 | C6H10I4N4 | C6H10I4N4 |
| Temperature (K) | 295, Phase I | 110, Phase III | 295 | 295, Phase I | 115, Phase II |
| M r | 195.99 | 195.99 | 447.77 | 645.98 | 645.98 |
| Crystal system, space group | Trigonal, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
Monoclinic, P21/n | Orthorhombic, Pmmn | Orthorhombic, Fddd | Monoclinic, C2/c |
| Lattice parameters (Å) | a = 7.8956(9), c = 8.077(2), γ = 120° | a = 7.8732(5), b = 15.4592(7), c = 9.6771(6), β = 106.64(1)° | a = 7.2366(3), b = 8.4314(3), c = 7.2292(3) | a = 14.154(1), b = 15.736(1), c = 27.108(2) | a = 13.963(2), b = 15.660(1), c = 14.940(1), β = 116.778(7) |
| V (Å3) | 436.1(1) | 1128.5(1) | 441.09(3) | 6037.7(7) | 2916.4(5) |
| Z (Z for primitive cell) | 3(1) | 8 | 2 | 16(4) | 8(4) |
| Data collection | |||||
| Radiation type | Mo Kα | ||||
| μ (mm−1) | 5.37 | 5.53 | 10.55 | 8.24 | 8.52 |
| Crystal size (mm) | 0.25 × 0.20 × 0.20 | 0.25 × 0.22 × 0.19 | 0.25 × 0.21 × 0.01 | ||
| T min, Tmax | 0.777, 1.000 | 0.552, 1.000 | 0.860, 1.000 | ||
| No. of measured, independent and observed [I > 2σ(I)] reflections | 1677, 118, 118 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112, 2126, 1881 112, 2126, 1881 |
1414, 489, 432 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210, 2088, 894 210, 2088, 894 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335, 17 335, 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 352, 14 352, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
| R int | 0.022 | 0.092 | 0.021 | 0.051 | 0.061 |
| Refinement | |||||
| R[F2 > 2σ(F2)], wR(F2), S | 0.025, 0.074, 1.20 | 0.063, 0.138, 1.31 | 0.023, 0.051, 1.06 | 0.034, 0.106, 0.83 | 0.046, 0.129, 1.20 |
| No. of reflections | 118 | 2126 | 489 | 2088 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 352 352 |
| No. of parameters | 5 | 109 | 29 | 49 | 115 |
| No. of restraints | 0 | 0 | 1 | 13 | 0 |
| Δ > max, Δ > min (e Å−3) | 0.35, −0.22 | 4.82, −1.60 | 0.47, −0.99 | 0.97, −0.94 | 1.29, −2.26 |
| H-atom treatment | H atoms treated by a mixture of independent and constrained refinement | ||||
Results and discussion
Thermal properties
The DSC runs of (1) (Fig. 1(a)) revealed two PTs at 180/185 K and 113/123 K (cooling–heating) of the first order type. The PTs are reversible, however, the enthalpy effects differ on cooling and heating significantly. The entropy values were estimated to be ca. 7 J mol−1 K−1 for the I ↔ II PT and 2 J mol−1 K−1 for the II ↔ III one (the heating cycle) and are characteristic of the ‘o–d’ mechanism of phase transition. | ||
| Fig. 1 DSC curves for (a) (1) (b) (3) upon cooling and heating runs (2 K min−1, (a) m = 20.8 mg, (b) m = 21.2 mg). | ||
A complex sequence of PTs is also encountered in (3) (Fig. 1(b)). For the cooling cycle only one heat anomaly characteristic of the second order transition is revealed at ca. 204 K, whereas on heating two thermal anomalies are seen; at 136 K typical of the first order type and another one at higher temperature corresponding to the PT detected on cooling at 204 K. The presence of a lower temperature heat anomaly may suggest the possibility of existence of a metastable phase below 204 K.
The sequence of the PTs observed in the calorimetric measurements (DSC) for (1) and (3) is in a good agreement with the linear thermal expansion measurements. Both compounds are stable up to ca. 500 K, however, above this temperature a continuous decomposition takes place (see Fig. S1(a) and S1(b) in ESI†).
Structure discussion
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. I− ions occupy all corners of the unit cell as well as two positions on the [−111] diagonal whereas imidazolium cations are located in the middle of the line connecting two adjacent anions in the c direction. The packing is similar to those reported for ImBr (ref. 12) although these two simple structures are not isomorphic. (1) adopts higher symmetry compared to Br− analog (R
space group. I− ions occupy all corners of the unit cell as well as two positions on the [−111] diagonal whereas imidazolium cations are located in the middle of the line connecting two adjacent anions in the c direction. The packing is similar to those reported for ImBr (ref. 12) although these two simple structures are not isomorphic. (1) adopts higher symmetry compared to Br− analog (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) vs. R3) and reveals a much more complicated disorder of the counterions.
vs. R3) and reveals a much more complicated disorder of the counterions.
[C3N2H5+] are disordered over a three-fold axis adopting 6 possible orientations. High values of displacement parameters of anions together with an unstable position of imidazolium cations indicate a low stability of the trigonal structure. Thermal motions dominate over possible directional bonding down to 180 K. Below this point, a drastic symmetry lowering occurs and the crystal structure transforms to triclinic in the first order phase transition. All cell parameters show discrete changes that are much pronounced for the angles and the bmono direction (Fig. S2, ESI†). The transition from Phase I to II is accompanied by a crystal expansion in the bmono direction by about 2.3% and a slight contraction of amono and cmono axes; the most pronounced changes are observed for all unit cell angles that deviate greatly from 90° indicating a triclinic symmetry of Phase II.
The lack of any anomalies of pyroelectric current in the vicinity of the 180 K temperature points to the centrosymmetric space group, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , for Phase II. The intermediate, triclinic phase is preserved down to 113 K. Then, the crystal symmetry increases to the monoclinic one, P21/n (Phase III). Both phase transitions have a clear first-order character, there is no group–subgroup relation between the phases and translation symmetry also changes distinctively.
, for Phase II. The intermediate, triclinic phase is preserved down to 113 K. Then, the crystal symmetry increases to the monoclinic one, P21/n (Phase III). Both phase transitions have a clear first-order character, there is no group–subgroup relation between the phases and translation symmetry also changes distinctively.
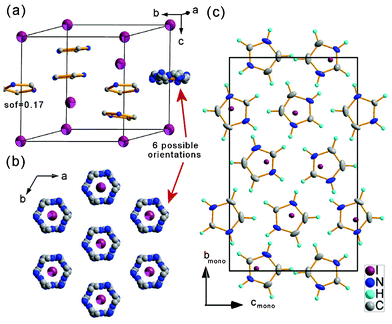 | ||
Fig. 2 Crystal structure of (1) (a) and (b) trigonal Phase I with disordered imidazolium counterions, six possible orientations of imidazolium are possible in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry, selected positions with the site occupation factor equal to 0.17 are presented as well as the averaged picture, T = 295 K, (c) Phase III with ordered, pseudo-hexagonal arrangement of ions, T = 110 K. symmetry, selected positions with the site occupation factor equal to 0.17 are presented as well as the averaged picture, T = 295 K, (c) Phase III with ordered, pseudo-hexagonal arrangement of ions, T = 110 K. | ||
Phase transitions affect both the imidazolium cations that are stabilized in the low temperature structure and positions of the anions that shift from ‘trigonal’ sites distinctively. The phase transitions are thus of a mixed character possessing both ‘o–d’ and ‘d’ contributions. The local symmetry of the cation stays the same in all phases whereas the high ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry site of I− in Phase I lowers to 1 in Phase III. The reorientation motions of imidazolium cations are frozen in Phase III, the arrangement of the ions is established due to the weak N–H⋯I interactions. The low temperature phase is composed of two non-equivalent chains of I−–[C3N2H5+]–I− propagating perpendicular to each other within the adjacent planes.
m symmetry site of I− in Phase I lowers to 1 in Phase III. The reorientation motions of imidazolium cations are frozen in Phase III, the arrangement of the ions is established due to the weak N–H⋯I interactions. The low temperature phase is composed of two non-equivalent chains of I−–[C3N2H5+]–I− propagating perpendicular to each other within the adjacent planes.
Fig. 3 presents the hydrogen-bonded chains propagating in the b and c directions. The geometry of the hydrogen bonds is given in Table 2. The I− anions exhibit large shifts from their high temperature positions. The I–I distance shrinks in chex direction from 8.08(1) Å at 295 K to 7.87(2) Å at 110 K that results in contraction of the amono lattice parameter whereas shifts of anions in hexagonal (001) plane are at the origin of a pronounced increase of the bmono parameter.
![Hydrogen bonded chains of I−–[C3N2H5+]–I− in Phase III, T = 110 K.](/image/article/2013/CE/c3ce40559a/c3ce40559a-f3.gif) | ||
| Fig. 3 Hydrogen bonded chains of I−–[C3N2H5+]–I− in Phase III, T = 110 K. | ||
| D–H⋯A | D–H/Å | H⋯A/Å | D⋯A/Å | D–H⋯A (°) |
|---|---|---|---|---|
| a Symmetry code(s): (i) −x + 1/2, y − 1/2, −z + 3/2; (ii) x − 1/2, −y + 1/2, z − 1/2. | ||||
| N1–H1⋯I2 | 0.86 | 2.91 | 3.591(8) | 136.9 |
| N3–H3⋯I2i | 0.86 | 2.75 | 3.533(8) | 151.5 |
| N6–H6⋯I1 | 0.86 | 2.83 | 3.551(8) | 143.1 |
| N8–H8⋯I1ii | 0.86 | 2.83 | 3.525(8) | 139.6 |
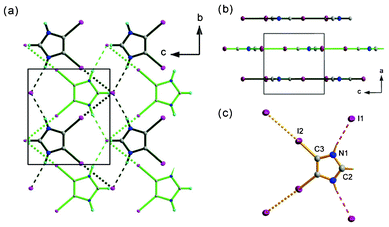 | ||
| Fig. 4 Crystal structure of (2) (a) view along a direction, the crystal is composed of layers with halogen and hydrogen bonds as motif-defining interactions, green bonds – top layer, black bonds – down layer, dense dashed lines stand for halogen I–I bonds, thicker ones represent N–H⋯I interactions. (b) View along the b direction, the interlayer spacing is equal to 3.62 Å (c) model of interactions between 4,5-diiodoimidazolium and iodide, the atoms from the asymmetric unit are labeled. | ||
The distance between the planes is equal to 3.618(1) Å. In the plane, each diiodoimidazolium is involved in two hydrogen and two halogen bonds. I− acts as an acceptor in these four interactions.
Both bonds are considerably strong although the geometrical parameters indicate that halogen bonds predominate hydrogen interactions. The I–I distance of 3.5410(1) Å is significantly shorter then the sum of the van der Waals radii (4.12 Å), and the angle θ1 that is equal to 177.6° gives almost a linear configuration. The I⋯N distance is equal to 3.505(5) Å in N(1)–H(1)⋯I(1) bond and donor-to-acceptor angle equals 170(7)°. The basic hydrogen and halogen bonded pattern is a ten membered ring. The asymmetric unit contains half of the diiodoimidazolium counter ion, laying on a m lattice plane and being intersected by a m mirror plane and 2 axis, and one I− anion adopting mm2 symmetry site. The exceptional feature of this simple salt is the layered crystal structure that has not been observed in other dihalogenoimidazolium salts and its derivatives. It is formed probably as a consequence of halogen–halogen interactions. These interactions are important packing forces in brominated hydroxyimidazoles.15
| Compound | I⋯I/[Å] | I–I/[Å] | I⋯I/[Å] | Ref. |
|---|---|---|---|---|
| a 1-Macrocyclic azocyclophane. b tHPMT – 2-mercapto-3,4,5,6-tetrahydropyrimidine analog. c PMTH – 2-mercaptopyrimidine analog. d BTMAH2+ – (CH3)3N+(CH2)6N+(CH3)3. | ||||
| Phenancetin·H2I4·2H2O | 3.403 | 2.773 | 3.403 | 19 |
| (C10H14N4Se2)(I3)(I4)0.5 | 3.405 | 2.819 | 3.405 | 20 |
| [Ni(OSMe2)6]I4 | 3.345 | 2.848 | 3.452 | 21 |
| [Co(OSMe2)6]I4 | 3.338 | 2.845 | 3.338 | 22 |
| [V(MeCN)6]I4 | 3.166 | 2.846 | 3.516 | 23 |
| α-(1)·3HI·I2 | 3.201 | 2.792 | 3.547 | 24 |
| 3.294 | 2.814 | 3.429 | ||
| β-(1)·3HI·I2 | 3.357 | 2.814 | 3.357 | 24 |
| 3.362 | 2.792 | 3.418 | ||
| (Pentafluorobenzyldibenzyl-ammonium)3·I3−·I42− | 3.363 | 2.762 | 3.363 | 17 |
| 1,3-Bis(diphenylpentafluoro-benzylphosphonium)propane I−·I42− | 3.403 | 2.826 | 3.403 | 17 |
| [2{tHPMT)22+}(2I−)·(I42−)]b | 3.360 | 2.825 | 3.360 | 25 |
| [2{PMTH)2+}·(I42−)]c | 3.346 | 2.761 | 3.346 | 25 |
| BTMAH2+·I42−d | 3.440 | 2.829 | 3.440 | 26 |
| (3) Phase I, orthorhombic | 3.415 | 2.811 | 3.415 | This work |
| (3) Phase III, monoclinic | 3.207 | 2.805 | 3.511 | This work |
The room temperature structure is disordered. The asymmetric unit comprises one-half of [I42−] dianion, one imidazolium with occupancy 0.5 and two one-half imidazolium cations with occupancy 0.5, see Fig. 5(a) and (b).
![Crystal structure of (3) in Phase I, T = 295 K (a) pseudo-hexagonal arrangement of ions along the a direction (b) model of disorder of imidazolium counterions together with the structure of [I42−] dianion, site occupation factor for each imidazolium position equals 0.5; atoms from asymmetric unit are labeled, double symmetry axis (.2.) are marked (c) arrangement of counterions in respect to [I42−] rods, hydrogen atoms are omitted for the clarity.](/image/article/2013/CE/c3ce40559a/c3ce40559a-f5.gif) | ||
| Fig. 5 Crystal structure of (3) in Phase I, T = 295 K (a) pseudo-hexagonal arrangement of ions along the a direction (b) model of disorder of imidazolium counterions together with the structure of [I42−] dianion, site occupation factor for each imidazolium position equals 0.5; atoms from asymmetric unit are labeled, double symmetry axis (.2.) are marked (c) arrangement of counterions in respect to [I42−] rods, hydrogen atoms are omitted for the clarity. | ||
The bonds I–Iterminal are equivalent and equal to 3.415 Å, the internal I–I bond is equal to 2.811 Å. The terminal iodides are weakly bonded to iodine molecule. Similar distances to terminal iodides in other crystals are shorter, e.g. 3.363 Å in 1,3-bis(diphenylpentafluorobenzylphosphonium)propane salts.17
[I42−] tetraiodide dianions and imidazolium counterions stack along one direction giving pseudo-hexagonal crystal packing. Fig. 5(c) shows the arrangement of ions at 295 K. Imidazolium cations, distributed in large channels, are able to perform thermally activated librations and rotations in and out of the plane of the rings.
The rings are almost perpendicular to the iodide rods. Despite the fact that two NH groups are in a bonding distance to [I42−] the H-bonds are not strong enough to overcome thermally activated motions. Thus the possible hydrogen bonds have a dynamical character. Below 204 K directional bonding starts dominating over thermal motions that stands at the origin of a second-order phase transition. Due to this transformation the symmetry changes from orthorhombic Fddd to monoclinic C2/c (C2/c is a maximal non-isomorphic subgroup of Fddd). The phase transition is group–subgroup related, the crystal class changes from mmm to 2/m. According to the Aizu classification (3) belongs to the ferroelastic species mmmF2/m.18 In both phases of (3) the size of the primitive cells coincides and the number of C6H10I4N4 formal molecules in primitive cells (Z) is equal to 4. Fig. S3, ESI,† presents the thermal evolution of the lattice parameters. Deformation of the crystal structure is much pronounced in the direction of the iodide rods and stacking imidazolium counter ions. Observed temperature changes have continuous character. Phase transition is associated with ordering of the cationic substructure and deformation of the [I42−] dianions that lose their symmetrical arrangement. The internal distance between iodides remains almost identical as in the high temperature phase whereas distances between I–Iterminal change significantly from 3.43 Å in Phase I to 3.51 Å and 3.21 Å in Phase II.
Independent content of the unit cell consists now of three, fully occupied imidazolium positions A, B and C and four iodides forming a highly asymmetric [I42−] dianion, see Fig. 6. In Phase II imidazolium rings are not perpendicular to the iodide rods, they bend aside approx. 12° from the initial positions. H-bond interactions stabilize three different spatial orientations of imidazolium ions in the crystal structure.
![Arrangement of counterions in respect to [I42−] rods in Phase II. Dashed lines represent hydrogen bond interactions. Hydrogen bonded motif is marked on red. Independent imidazolium ions are labeled with A, B and C.](/image/article/2013/CE/c3ce40559a/c3ce40559a-f6.gif) | ||
| Fig. 6 Arrangement of counterions in respect to [I42−] rods in Phase II. Dashed lines represent hydrogen bond interactions. Hydrogen bonded motif is marked on red. Independent imidazolium ions are labeled with A, B and C. | ||
A basic hydrogen bonded pattern consists of two iodide rods interconnected via a counterion by two symmetrical N(6)–H(6)⋯I(1) bonds with a donor-to-acceptor distance of 3.52 Å and two imidazolium cations type B interacting via N(1)–H(1)⋯I(2) with terminal iodides with the distance of 3.61 Å. Imidazolium C does not interact by hydrogen bonds with the rods. Fig. 6 shows the structure of hydrogen bonds in Phase II.
To the best of our knowledge there are only twelve crystal structures containing discrete polyiodide [I42−] moieties. The [I42−] species may be described as an I2 molecule bound to two I− ions through linear halogen bonding that is the intermolecular interaction involving the halogen atoms as electrophilic species with the central I–I bond length ranging from 2.76 and 2.85 Å and the external I–I⋯I− distances ranging from ca. 3.17 to 3.55 Å.
Despite the fact that the linear [I42−] ion has been found to be unstable, nine of twelve compounds possess symmetrical configuration at room temperature. The present work is a first report on the temperature stability of the [I42−] rods.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1 1] direction, in the temperature region covering the two low temperature PTs. Both PTs are dielectrically active. The low frequency dielectric response possesses interesting features which are encountered both in antiferroelectric compounds and crystals possessing high temperature plastic-like phases. When the temperature approaches 180 K ε′c increases linearly up to 16 units and below 180 K it suddenly drops to 8 units. A similar behavior of ε′(T) is observed in the vicinity of the II → III PT, however, the reduction of ε′ is smaller, ca. 25%.
1 1] direction, in the temperature region covering the two low temperature PTs. Both PTs are dielectrically active. The low frequency dielectric response possesses interesting features which are encountered both in antiferroelectric compounds and crystals possessing high temperature plastic-like phases. When the temperature approaches 180 K ε′c increases linearly up to 16 units and below 180 K it suddenly drops to 8 units. A similar behavior of ε′(T) is observed in the vicinity of the II → III PT, however, the reduction of ε′ is smaller, ca. 25%.
![Temperature dependence of the real part of the complex electric permittivity along the [1̄ 1 1] direction for (1) during the cooling cycle.](/image/article/2013/CE/c3ce40559a/c3ce40559a-f7.gif) | ||
Fig. 7 Temperature dependence of the real part of the complex electric permittivity along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1 1] direction for (1) during the cooling cycle. 1 1] direction for (1) during the cooling cycle. | ||
Dielectric dispersion is not observed both in the high and low temperature phase. It means that the possible motion of the dipolar groups should be relatively fast in the disordered Phase I and II.
It is interesting to compare dynamic properties of closely related halogen analogs: ImBr (ref. 12) and (1), taking into account their sequence of PTs presented in Fig. 8.
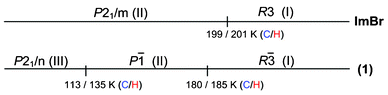 | ||
| Fig. 8 Sequence of PTs for ImBr and (1) (C-cooling, H-heating). | ||
The common feature of the RT Phases I of both compounds is a high dynamic disorder of the imidazolium cations. The low temperature PTs are governed by a change in the motions of dipoles of imidazole rings. The completely freezing of these motions in the case of ImBr takes place exactly at 199 K, whereas in (1) a two-stage freezing was observed at 180 and 113 K. The total entropy transition effect (ΔStr) for (1) corresponds to a three-site model describing the cations disorder in Phase I.
Compared compounds adopt different symmetries at the RT phase: ImBr has polar space group (R3) while (1) a centrosymmetric one (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ). In general, the electric response of both analogs in the vicinity of I → II PT reveals some similarities (e.g. the shape of ε vs. T), however, in the case of ImBr the εmax(Tc) is nearly three times larger than that in (1). As for ImBr the polar character of the Phase I results from two contributions; permanent electric dipole of organic cations (ΔP′) and dipoles arising from mutual positions of the centre of gravity of the C3N2H5+ cations and Br− anions along the c-axis (ΔP). In the case of (1) we deal only with the (ΔP′) contribution of the cations which justifies the lower ε′ value over the Phase I.
). In general, the electric response of both analogs in the vicinity of I → II PT reveals some similarities (e.g. the shape of ε vs. T), however, in the case of ImBr the εmax(Tc) is nearly three times larger than that in (1). As for ImBr the polar character of the Phase I results from two contributions; permanent electric dipole of organic cations (ΔP′) and dipoles arising from mutual positions of the centre of gravity of the C3N2H5+ cations and Br− anions along the c-axis (ΔP). In the case of (1) we deal only with the (ΔP′) contribution of the cations which justifies the lower ε′ value over the Phase I.
The temperature dependence of real (ε′) and imaginary (ε′′) parts of the complex electric permittivity for (3) along the [2 3 1] direction (on heating) is presented in Fig. 9(a) and (b), respectively. The expected PTs at 136 and 204 K are visible as a rapid increase in the ε′ value. In the low temperature region over the Phases II and III one can observe a relaxation process which is characteristic of the glass-like phases, where the value of ε′′max increases with the frequency of the measuring electric field.
![Temperature dependence of the (a) real and (b) imaginary part of the complex electric permittivity along the [231] direction for (3) during the heating cycle.](/image/article/2013/CE/c3ce40559a/c3ce40559a-f9.gif) | ||
| Fig. 9 Temperature dependence of the (a) real and (b) imaginary part of the complex electric permittivity along the [231] direction for (3) during the heating cycle. | ||
The activation energy for the temperature region 110–140 K was found to be ca. 17 kJ mol−1 (see Fig. S4 and S5, ESI†). Concluding, the dielectric relaxation process taking place below room temperature in (3) is due to a freezing and slowing down motion of dipolar units assigned to the imidazolium cations.
The molecular mechanism of PTs in (3) seems also to be complex and associated with an ordering of the cationic moieties and a significant deformation of the [I42−] dianions
Conclusion
The reaction between imidazole amine and hydroiodic acid in an aqueous solution results in simultaneous crystallization of three molecular-ionic compounds: [C3N2H5+][I−] (1), [C3N2H3I2+][I−] (2) and [C3N2H5+]2[I42−] (3). The crystal structure of all the compounds consisted of isolated discrete imidazolium cations and simple iodide anions, however, in the case of (3) we have a rarely encountered polyiodide form [I42−]. The characteristic feature of compounds under investigation is the presence of N⋯H–I hydrogen bonds and I⋯I halogen interactions. As a result a two-dimensional (2D) framework structure of (2) and (3) complexes is generated, whereas in (1) a 1D structure, as I−–[C3N2H5+]–I− chains, is observed. The structure of (2) appeared to be very rigid since the I− anion interacts with four atoms (via N–H⋯I and I⋯I). It is an exceptional feature because such a layered crystal structure is not observed in other dihalogenoimidazolium derivatives.Two complexes were found to undergo reversible PTs; (1) at ca. 180/185 K and 113/123 K (cooling–heating) and (3) at ca. 204 K and 136 K.
The X-ray, thermal, 1H NMR and dielectric studies used to study the molecular mechanism of the PTs in (1) and (3) indicated a mixed molecular mechanism (‘o–d’ and ‘d’ contributions). It should be emphasized that (3) is the first example of an ionic salt among all of the known compounds (12) containing polyiodide anions, [I42−], which undergo structural PTs. The most unexpected in this case is the fact that the instability of the crystal structure of (3) at 204 K is governed by the distortion of an unstable, symmetric [I42−] species.
The proton spin–lattice relaxation time (T1) measurements confirmed that a free in-plane reorientation of the imidazolium ring takes place over the high temperature phase of (1) and (3) whereas large-amplitude librations or small-angle reorientations of cations are permitted at low temperatures (Phases II and III).
Notes and references
- P. Wasserscheid and T. Welton, Ionic Liquids in Synthesis, Wiley-VCH, Weinheim, 2003 Search PubMed.
- J. Dupont, R. F. de Souza and P. A. Suarez, Chem. Rev., 2002, 102, 3667 CrossRef CAS.
- C. E. Song, Chem. Commun., 2004, 1033 RSC.
- H. Ohno, Electrochemical Aspect of Ionic Liquids, Wiley-Interscience, 2005 Search PubMed.
- H. Ohno, Electrochemical Aspect of Ionic Liquids, Wiley-Interscience, in particular Part V and VI, ch. 24–27, 2005 Search PubMed.
- R. Jakubas, A. Piecha, A. Pietraszko and G. Bator, Phys. Rev. B, 2005, B72, 104107 CrossRef.
- A. Piecha, A. Białońska and R. Jakubas, J. Phys.: Condens. Matter, 2008, 20, 325224 CrossRef.
- A. Piecha, A. Pietraszko, G. Bator and R. Jakubas, J. Solid State Chem., 2008, 181, 1155 CrossRef CAS.
- Z. Sun, T. Chen, J. Luo and M. Hong, Angew. Chem., Int. Ed., 2012, 51, 3871 CrossRef CAS.
- Z. Pająk, P. Czarnecki, B. Szafrańska, H. Małuszyńska and Z. Fojud, J. Chem. Phys., 2006, 124, 144502 CrossRef.
- Z. Pająk, P. Czarnecki, B. Szafrańska, H. Małuszyńska and Z. Fojud, Phys. Rev. B, 2004, B69, 132102 CrossRef.
- A. Gągor, A. Piecha, R. Jakubas and A. Miniewicz, Chem. Phys. Lett., 2011, 503, 134 CrossRef.
- Oxford Diffraction, CrysAlis CCD, Data Collection software, Oxford Diffraction Ltd., Wrocław, Poland, 2005 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, A64, 112–122 Search PubMed.
- G. Laus, K. Wurst, V. Kahlenberg and H. Schottenberger, Z. Naturforsch., B: J. Chem. Sci., 2012, 67, 354 CrossRef CAS.
- O. Hassel, Mol. Phys., 1958, 1, 241 CrossRef CAS.
- M. Muller, M. Albrecht, V. Gossen, T. Peters, A. Hoffmann, G. Raabe, A. Valkonen and K. Rissanen, Chem.–Eur. J., 2010, 16, 12446 CrossRef.
- K. Aizu, J. Phys. Soc. Jpn., 1969, 27, 387 CrossRef CAS.
- F. H. Herbstein, M. Kapon and W. Schwotzer, Helv. Chim. Acta, 1983, 66, 35 CrossRef CAS.
- F. Bigoli, F. Demartin, P. Deplano, F. A. Devillanova, F. Isaia, V. Lippolis, M. L. Mercuri, M. A. Pellinghelli and E. F. Trogu, Inorg. Chem., 1996, 3683 Search PubMed.
- D. L. Long, H. M. Hu, J. T. Chen and J. S. Huang, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 339 Search PubMed.
- V. V. Tkachev, E. A. Lavrenteva, O. S. Roshchupkina, I. P. Lavrentev and L. Y. Atovmyan, Koord. Khim., 1994, 20, 674 CAS.
- P. B. Hitchcock, D. L. Hughes, G. J. Leigh, J. R. Sanders, J. Desouza, C. J. McGarry and L. F. Larkworthy, J. Chem. Soc., Dalton Trans., 1994, 3683 RSC.
- C. A. Ilioudis and J. W. Steed, CrystEngComm, 2004, 6, 239–242 RSC.
- A. M. Owczarzak, M. Kubicki, N. Kourkoumelis and S. K. Hadjikakou, RSC Adv., 2012, 2, 2856 RSC.
- A. Abate, M. Brischetto, G. Cavallo, M. Lahtinen, P. Metrangolo, T. Pilati, S. Radice, G. Resnati, K. Rissanen and G. Terraneo, Chem. Commun., 2010, 46, 2724 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the thermal (TGA), X-ray diffraction and dielectric and 1H NMR measurements. CCDC 929449–929453. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3ce40559a |
| This journal is © The Royal Society of Chemistry 2013 |
