A mechanistic investigation of hydrodehalogenation using ESI-MS

Abstract

The rate of hydrodehalogenation of aryl iodides with a palladium catalyst in methanol exhibits a strong primary kinetic isotope effect from both CD₃OD and CH₃OD, suggesting that deprotonation plays a major role in the mechanism.

---

The replacement of a C–X (X = halide) bond with a C–H bond (hydrodehalogenation) is a frequent competing reaction in palladium-catalyzed cross-coupling reactions, and is responsible for diminished yields and unwanted byproducts. An early mechanism for catalytic hydrodehalogenation of aryl halides was proposed by Zask,¹ and then extended by Nolan² involving oxidative addition of aryl halide (Ar–X) to a Pd(0) complex, followed by displacement of the halide ligand by methoxide, β-elimination of formaldehyde and reductive elimination of Ar–H to regenerate the Pd(0) species (Scheme 1).

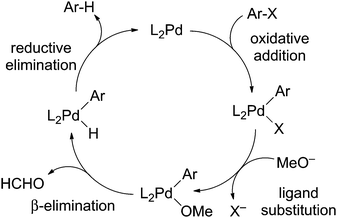Scheme 1 A possible mechanism of hydrodehalogenation of aryl halides.

The same mechanism also was reported using Ni(0)/imidazolium chloride³ and Ru(II)⁴ catalysts. Oxidation of the alcohol solvent has been reported by Zhang⁵ in homocoupling as well as hydrodehalogenation of aryl halides. Recently, another report⁶ on equivalent oxidation of solvent during hydrodehalogenation also supports the involvement of beta hydride elimination as a key step in the reaction. Our interest in the reaction stemmed from our observation that hydrodehalogenation was the major side reaction in the copper-free Sonogashira reaction/Heck alkynation when conducted in methanol,⁷ and we decided to study it in its own right by the simple expedient of leaving out the other coupling partner, the terminal alkyne. Hydrodehalogenation is slow in the presence of weak bases such as triethylamine, but is greatly accelerated by using the relatively strong base potassium tert-butoxide. Our approach to catalytic analysis is to use the continuous monitoring technique of pressurized sample infusion electrospray ionisation mass spectrometry (PSI-ESI-MS)⁸ in conjunction with substrates tagged on the periphery of the molecule with a charged functional group.⁹ The combination of charge-tagging and ESI-MS is an increasingly popular approach to establishing speciation in catalytic mixtures.¹⁰

Examination of the reaction of the charge-tagged aryl iodide [Ph₃PCH₂C₆H₄I][PF₆] (ArI) in methanol using Pd(PPh₃)₄ as the catalyst and ^tBuOK as the base allowed us to follow the abundance of starting material, product, byproduct (in this case the biphenyl product of homocoupling) and all intermediates containing the charged tag that are present in reasonable abundance. The reaction was repeated in CH₃OD and CD₃OD. The reaction takes about 100 minutes to go to completion in CH₃OH at a catalyst loading of 6 mol% under pseudo first-order kinetics (k = 0.0292 min⁻¹). In addition to the product (ArH), the homocoupling byproduct (ArAr) also forms in low yield (∼2%). The main palladium-containing species observed over the course of the reaction are PdP₂(Ar)(I), PdP₂(Ar)(H), and PdP₂(Ar)₂. Fig. 1 shows intensity vs. time traces for ArI, ArH, ArAr, PdP₂(Ar)(I) and PdP₂(Ar)(H) (the two Pd-containing species have been multiplied by 100 to get them on the same scale as the other species). Note that the behaviour of the PdP₂(Ar)₂ is discussed in ESI;† the low yield of this byproduct means we have neglected it as contributing significantly to the overall process.

Fig. 1 Plot is an average of three runs. Intermediates have been multiplied by 100 to get them on the same scale. Inset: plot of ln[X] vs. t, showing the overall first-order kinetics. Note: only the first 50 minutes is shown, because after that catalyst decomposition causes significant deviation from first-order behaviour.

Because two different plausible intermediates are observed, the reactions that consume these compounds are both relatively slow, and both reactions are likely to contribute to the overall rate of the reaction. Both of these species appear in the mechanism in Scheme 1, suggesting that it was reasonable. However, given the involvement of the solvent in the reaction, the opportunity for isotopic labelling promised to give us additional insight into the key elementary steps. Both the β-elimination and the reductive elimination involve breaking of a bond to H, so we can expect these steps to be slowed if CH₃ is replaced with CD₃, thanks to the primary kinetic isotope effect (KIE).¹¹ Accordingly, the reaction was repeated in CD₃OD, and it was, as expected, considerably slower. However, when the reaction was repeated in CH₃OD, the reaction was equally slow. The intermediate behaviour in all three cases was qualitatively similar: a steady state for PdP₂(Ar)(I), and a jump at the start for PdP₂(Ar)(H), then a slow tapering off. Fig. 2 compares the rate of appearance of product in the three experiments.

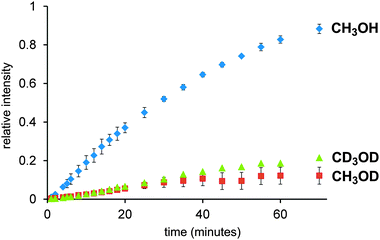Fig. 2 Overlay of product build up in CH₃OH (blue), CH₃OD (red) and CD₃OD (green). Error bars are generated from duplicates (green) and triplicates (red and blue).

The CH₃OD experiment was particularly informative. If the turnover-limiting step involved β-elimination or reductive elimination, we would expect the rate to be essentially unaffected when compared to CH₃OH. The monitoring of the reaction in CH₃OD revealed a 1 : 1 mixture of ArH and ArD products (see ESI†). If the reductive elimination is responsible for the slower rate in CH₃OD, we would expect this reaction to be faster than the reaction in CD₃OD but slower than that in CH₃OH.

The fact that the rate was just as slow for CH₃OD as for CD₃OD suggests instead that the key step was deprotonation. If the deprotonation happens off the metal to make RO⁻, the amount of RO⁻ will be determined by the position of the ROH + KO^tBu ↔ ROK + HO^tBu equilibrium in solution, this will be approximately the same for R = CD₃ as it is for R = CH₃. So we assume that the deprotonation instead occurs when the methanol is bound to the metal, and that it is methanol as opposed to methoxide that displaces the iodide ligand to make [PdP₂(Ar)(MeOH)]⁺. However, this intermediate is not observed, so how can the deprotonation therefore be turnover limiting? This possibility arises if an equilibrium PdP₂(Ar)(I) + MeOH ↔ [PdP₂(Ar)(MeOH)]⁺ + I⁻ exists and lies a long way to the left. This assumption is reasonable given that we detect only PdP₂(Ar)(I) in a methanol solution of this compound (see Fig. S6 in ESI†) and no [PdP₂(Ar)(MeOH)]⁺ + I⁻. If we run the catalytic reaction without a charged tag (i.e. with PhI or MeOC₆H₄I rather than ArI), we see roughly equal amounts of [PdP₂(Ar)(I) + K]⁺ and [PdP₂Ar]⁺. The potassium ion adduct appears because of the presence of the KO^tBu base, despite the fact that the interaction between the complex and K⁺ is typically a weak one. The [PdP₂Ar]⁺ ion is not a fragment of the potassium adduct (see ESI†), so represents an independent species, albeit present in very low concentration. The modified mechanism appears in Scheme 2. Assuming this mechanism is operative, it suggests a couple of avenues of further exploration. If dissociation of iodide is critical, its removal ought to accelerate the reaction and addition of iodide ought to slow it down. Both of these experiments were conducted, by adding AgNO₃ at the start of the reaction to precipitate out any iodide that is released, and by adding one equivalent to I⁻ to the reaction. The predicted effects indeed played out (Fig. 3).

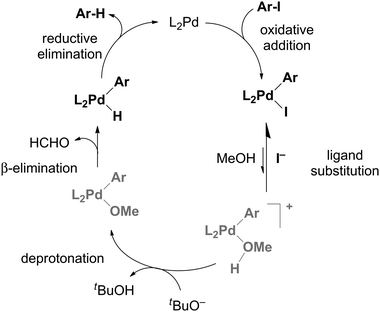Scheme 2 Catalytic cycle and rate constants used to simulate the reaction progress. Concentrations used were the same as employed experimentally.

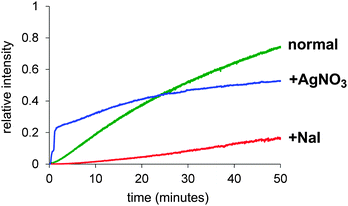Fig. 3 A comparison of the “normal” reaction (green) and after addition of one equivalent of AgNO₃ (blue) or I⁻ (red).

The AgNO₃ experiment was especially interesting because the reaction was initially very fast but after conversion of about 25% rapidly slowed to a crawl. We suspect this is due to removal of the catalyst somehow, perhaps a combination of oxidation of Pd(0) by Ag(I), and co-precipitation of remaining Pd(0) with the Ag(0) so formed. The solution discoloured substantially when the catalyst precursor was combined with AgNO₃. Whatever is going on to slow the reaction, the initial burst of productivity does not compensate for the later slow down, so AgNO₃ is not a helpful adulterant in the long run. The slow reaction in the presence of I⁻ is predictable given that we expect the iodide dissociation to be suppressed in the presence of high concentrations of I⁻. Addition of halide has been reported to decelerate the reaction of PdP₂ArBr with PhB(OH)₂ in Suzuki cross coupling reactions which suggest that PdP₂(Ar)Br is in equilibrium with more reactive species.¹² Using the modified mechanism in Scheme 2, a numerical model was constructed using Powersim¹³ and tested to see if there exists a combination of rate constants that allow us to approximate the experimental traces, including the qualitative behaviour of the intermediates. While ESI-MS has a high dynamic range, it is still quite plausible for intermediates to have a low enough abundance that they do not appear above the noise; nonetheless, their abundance in the numerical model should be lower than the other intermediates that are observed. In this case, the PdP₂(Ar)(OMe) intermediate is not observed, which suggests that the reaction that consumes it (β-elimination) is not turnover-limiting. The numerical model had substantial constraints: it needed to emulate the normal behaviour of the system, as well as predict how the reaction changes when the various perturbations (d1 and d4 deuteration, addition of iodide, addition of AgNO₃) are made. As a starting point it was assumed that the primary kinetic isotope effect would slow all reactions involving the breaking of a bond to hydrogen by a factor of 7, and that AgNO₃ would remove any iodide formed immediately. We also added an undefined catalyst decomposition process, but did not endeavour to model the homocoupling pathway explicitly, since it only involved approximately 2% of the final product. The KIE for the deprotonation step needs to be >7 to account for the dramatic change in reactivity, and the best fit is obtained if modelled at k_H/k_D = 16 for that particular transformation. This value is relatively high, and may indicate that tunnelling is occurring or that our estimates of the rate constants of other steps are not accurate. Such deviations are to be expected in such a complex system; our main hope is to generate a model that responds accurately to perturbations in the system, rather than as a means of accurately establishing all rate constants in the catalytic cycle. In this sense, the optimized model is a success; it closely matches the observed behaviour of the system (Fig. 4) under normal conditions, and the model responds appropriately to the tested changes in conditions (see ESI†).

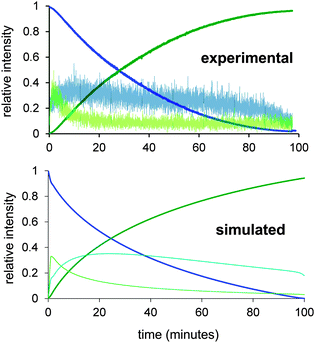Fig. 4 Experimental (top) and numerically modelled hydrodehalogenation (bottom). Intermediate intensity has been multiplied by 20 to get them on the same scale.

The combination of dense, real-time monitoring of the catalytic mixture under realistic conditions, measurement of the abundances of key species throughout (especially the intermediates), isotope studies and numerical modelling provide evidence for a mechanism that invokes deprotonation of the alcohol occurring on a cationic palladium complex. We plan to move on to examine the extent to which the observed pathway operates for other aryl halides (Br, Cl, F) and in other solvents (especially non-alcoholic solvents). We will also examine the details of the homocoupling reaction, as well as apply our approach to a variety of other cross-coupling reactions.

Notes and references

1. A. Zask and P. Helquist, J. Org. Chem., 1978, 43, 1619–1620.
2. (a) M. S. Viciu, G. A. Grasa and S. P. Nolan, Organometallics, 2001, 20, 3607–3612; (b) O. Navarro, H. Kaur, P. Mahjoor and S. P. Nolan, J. Org. Chem., 2004, 69, 3173–3180.
3. C. Desmarets, S. Kuhl, R. Schneider and Y. Fort, Organometallics, 2002, 21, 1554–1559.
4. M. E. Cucullu, S. P. Nolan, T. R. Belderrain and R. H. Grubbs, Organometallics, 1999, 18, 1299–1304.
5. M. Zeng, Y. Du, L. Shao, C. Qi and X.-M. Zhang, J. Org. Chem., 2010, 75, 2556–2563.
6. J. Moon and S. Lee, J. Organomet. Chem., 2009, 694, 473–477.
7. K. L. Vikse, Z. Ahmadi, C. C. Manning, D. A. Harrington and J. S. McIndoe, Angew. Chem., Int. Ed., 2011, 50, 8304–8306.
8. K. L. Vikse, M. P. Woods and J. S. McIndoe, Organometallics, 2010, 29, 6615–6618.
9. D. M. Chisholm, A. G. Oliver and J. S. McIndoe, Dalton Trans., 2010, 39, 364–373.
10. (a) D. Agrawal, D. Schröder and C. M. Frech, Organometallics, 2011, 30, 3579–3587; (b) M. A. Schade, J. E. Fleckenstein, P. Knochel and K. Koszinowski, J. Org. Chem., 2010, 75, 6848–6857; (c) K. Vikse, G. N. Khairallah, J. S. McIndoe and R. A. J. O'Hair, Dalton Trans., 2013, 42, 6440–6449; (d) H. Jansen, M. C. Samuels, E. P. A. Couzijn, J. C. Slootweg, A. W. Ehlers, P. Chen and K. Lammertsma, Chem.–Eur. J., 2010, 16, 1454–1458; (e) F. F. D. Oliveira, M. R. dos Santos, P. M. Lalli, E. M. Schmidt, P. Bakuzis, A. A. M. Lapis, A. L. Monteiro, M. N. Eberlin and B. A. D. Neto, J. Org. Chem., 2011, 76, 10140–10147; (f) L. S. Santos, Reactive Intermediates, Wiley-VCH Verlag GmbH & Co. KGaA, 2010, pp. 133–198; (g) Y. E. Corilo, F. M. Nachtigall, P. V. Abdelnur, G. Ebeling, J. Dupont and M. N. Eberlin, RSC Adv., 2011, 1, 73–78; (h) C. H. Beierlein, B. Breit, R. A. Paz Schmidt and D. A. Plattner, Organometallics, 2010, 29, 2521–2532.
11. (a) G. Parkin, J. Labelled Compd. Radiopharm., 2007, 50, 1088–1114; (b) W. D. Jones, Acc. Chem. Res., 2002, 36, 140–146; (c) E. Rosenberg, E. V. Anslyn, C. Barner-Thorsen, S. Aime, D. Osella, R. Gobetto and L. Milone, Organometallics, 1984, 3, 1790–1795; (d) O. Matsson and K. C. Westaway, in Adv. Phys. Org. Chem., ed. D. Bethell, Academic Press, 1999, pp. 143–248.
12. C. Amatore, A. Jutand and G. Le Duc, Chem.–Eur. J., 2011, 17, 2492–2503.
13. (a) C.-C. Chang, K. O. Siegenthaler and A. Studer, Helv. Chim. Acta, 2006, 89, 2200–2210; (b) C.-C. Chang and A. Studer, Macromolecules, 2006, 39, 4062–4068; (c) A. Studer, Chem. Soc. Rev., 2004, 033, 267–273.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, numerical modelling, additional mass spectra. See DOI: 10.1039/c3cc46271d

---