Angular dependence of the exchange interaction in fluoride-bridged Gd^III–Cr^III complexes

Abstract

The observed angular variation of the magnetic exchange coupling parameter in a series of fluoride-bridged chromium(III)–gadolinium(III) complexes is explained by DFT calculations.

---

The relatively new research field of magnetic refrigeration, by means of adiabatic demagnetisation, in paramagnetic, molecular, polynuclear, complexes¹ and MOFs² has reinvigorated the study of magnetically isotropic, polynuclear d- and f-metal ion compounds.³ As the magnetocaloric effect (MCE) delicately depends on the nature of the low-lying energy levels of such systems, it is necessary to develop methodologies for the prediction of the sign and magnitude of the magnetic exchange interactions between their constituent metal ions.⁴ Gd^III has a well-isolated, orbitally non-degenerate ⁸S_7/2 ground term and can be considered magnetically isotropic.⁵ Similarly, Cr^III has only weak magnetic anisotropy.⁶ Thus, a combination of these two metal-ions for the development of new molecular refrigerants seems promising. We have recently reported a penta-nuclear, trigonal bipyramidal {Gd₃Cr₂} complex displaying good refrigeration properties.⁷ We report here magneto-structural correlation studies on a simple dinuclear Cr^III–Gd^III model complex and three, previously described, polynuclear Gd^III–Cr^III complexes (Fig. 1).⁸ Characteristically, only very small differences in the Cr^III–F and Gd^III–F bond lengths are observed in the series 1–4 suggesting that the differences in exchange interactions are essentially governed by the Gd^III–F–Cr^III angle. The synthetic approach to the series is based on the kinetic robustness of Cr^III which prevents the precipitation of highly insoluble GdF₃.⁹ The intrinsic preference of the fluoride ion for linear bridging facilitates the prediction of the cluster topology, giving rods for trans-difluorido, squares for cis-difluorido and trigonal bipyramids for fac-trifluorido chromium(III) precursors.

Fig. 1 Molecular structures of 1–4 (see also Scheme S1, ESI†). Gd, purple; Cr, dark green; F, light green; O, red; N, blue. The auxiliary ligand sphere is shown as a wireframe and hydrogens are omitted for clarity.

The χT products of 1–4 are shown in Fig. 2 of which the magnetic properties of 2–4 have already been reported.^7,8b The high-temperature χT values are all in agreement with the values expected for the uncorrelated ions (S_Gd = 7/2, S_Cr = 3/2, g = 2.0 for both Cr^III and Gd^III). On cooling, all χT products decrease indicating the presence of intra-cluster antiferromagnetic interactions. All thermodynamic magnetometry data were fitted by use of the Levenberg–Marquardt algorithm¹⁰ and by numerical diagonalisation of the isotropic spin-Hamiltonian (1):

where the indices i and j run through the constitutive single-ions of each compound, g is the single-ion g-factor, Ŝ is a spin-operator and J is the isotropic exchange parameter. Note that a non-zero value for J_Gd–Gd is only employed in the case of 4. Independently fitting the χT product and low temperature magnetization data (Fig. S2, ESI†) of 1 affords J = 0.84(4) cm⁻¹ and J = 0.82(4) cm⁻¹, respectively, with the g factors fixed to g_Cr = 1.97 and g_Gd = 1.99. Determination of an isotropic exchange parameter of this small magnitude solely from magnetic measurements may be inaccurate as other small terms, such as zero-field splittings, may be non-negligible, especially at low temperatures. Inelastic neutron scattering (INS) is a well-suited method for the determination of the magnetic anisotropy and exchange parameters in paramagnetic complexes due to the selection rules ΔS = 0, ±1 and ΔM_S = 0, ±1. Despite the extremely large neutron absorption cross-section of ¹⁵⁷Gd (ca. 16% natural abundance), we managed to acquire INS spectra of 1 (Fig. 2 and Fig. S3, ESI†). Although noisy, the energy loss peaks A, at 2.2 cm⁻¹, and B, at 3.0 cm⁻¹, are clearly discernible in the spectrum at λ_i = 6.5 Å and assigned to magnetic excitations originating from the ground state, on the basis of their temperature dependence. Unfortunately, the poor quality of the observed Q-dependence, because of the presence of ¹⁵⁷Gd and large incoherent scattering from ¹H, does not allow affirming the magnetic nature of these excitations. The experimental spectra were interpreted by use of home-written software¹¹ invoking the anisotropic extension of spin-Hamiltonian (1) given in eqn (2):where D_Gd is neglected.⁵ For comparison, the broader, but more intense, spectrum at λ_i = 4.8 Å is shown in Fig. S3 (ESI†). In the T = 15 K spectrum (Fig. 2, right), a hot peak (C) arises at 3.3 cm⁻¹. For D_Cr = 0, the S = 3, 4 and 5 spin manifolds are separated from the S = 2 ground state by 3J, 7J and 12J (Fig. S4, ESI†), respectively, and only one prominent INS peak would be observed at low temperature from the S = 2 to S = 3 excitation (Fig. S5, ESI†). Introduction of D_Cr breaks the degeneracy of the M_S levels, and an optimized value of D_Cr = 0.5 cm⁻¹, together with J = 0.87 cm⁻¹, results in good agreement with the experiment (cf.Fig. 2, right).

Fig. 2 (left) χT (χ = M/H) data for 1–4 acquired with H_dc = 1000 Oe (circles) and best fits as described in the main text (solid lines). (right) INS spectra of 1 obtained with an incident neutron wavelength of λ_i = 6.5 Å at T = 1.5 K and 15 K. Solid black lines are simulations.

The obtained J parameters for 2–4, for which the INS spectra were not acquired, are shown together with that for 1 in Fig. 3 as a function of the Gd–F–Cr angle. All the extracted couplings are antiferromagnetic and their strength seems to correlate with the Gd–F–Cr angle. Magnetic interactions in {3d–Gd} dinuclear complexes are in general ferromagnetic with some notable exceptions, such as a cyanide-bridged {CrGd} complex.^12,13 A {GdCr₄} hydroxide bridged complex is also reported to be antiferromagnetic in nature.¹⁴ This fuelled our curiosity as to whether Cr^III in particular promotes antiferromagnetic interactions. Indeed, for 1–4, the exchange interaction is antiferromagnetic. Moreover, there is a structural correlation to this antiferromagnetic interaction as shown in Fig. 3, which presents J as a function of the Gd–F–Cr angle. To shed light on this issue, as well as on the angular dependence of J, we performed DFT (B3LYP/TZV) calculations on 1. All the calculations were performed with the Gaussian 09 program suite (cf. ESI† for computational details). The computed J value of 0.80 cm⁻¹ for 1 is in excellent agreement with the values extracted from experiments (see Table S2 for DFT computed energies, ESI†). The reproduction of both the sign and the magnitude of J provides confidence in the computed J values.

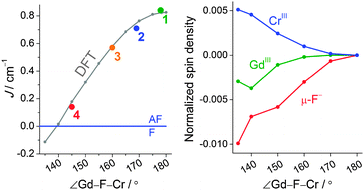Fig. 3 (left) Angular dependence on the J parameters for 1–4 (coloured circles) and DFT results (grey circles). (right) Normalized spin density plot for an angular distortion of 1.

Understanding the mechanism by which the coupling is operational in this {Cr–Gd} pair is important, as it is expected to provide clues about the nature of the exchange interaction and its angular dependence. The following generic mechanistic points emerge from our earlier studies.^15a–f In a general {3d–4f} pair, the overlap between the 4f orbitals and the 3d orbitals only partly determines the nature of the magnetic exchange interaction. Orthogonality between the 3d and 4f orbitals results in ferromagnetic, J_F, contributions, whereas, non-vanishing overlap of the same orbitals results in antiferromagnetic, J_AF, contributions to the magnetic exchange. Additionally, charge transfer excitations from a 3d orbital to an empty 5d orbital of the lanthanide contribute to J_F. Since the 4f orbitals are contracted, contributions to J_AF are generally weak and therefore most of the {3d–4f} pairs exhibit ferromagnetic behaviour. In complex 1, the unpaired electrons on Cr^III are located in the t_2g {d_xy, d_xz, d_yz} set of orbitals. Since these orbitals exhibit π character, an efficient σ-type charge transfer from 3d to 5d, observed for {Cu^II(t_2g⁶e_g³)–Gd} and {Ni(t_2g⁶e_g²)–Gd} complexes, is absent in 1 and thus, the J_F contribution is significantly reduced.^15a–c To estimate the J_AF contributions, the overlap integrals (S_ab) between the magnetic orbitals of Cr^III and Gd^III have been computed and significant S_ab values have been detected indicating a relatively strong 3d–4f overlap (Fig. S6, ESI†). Previously, we have shown that the number of bridges plays a vital role in the sign of magnetic coupling. In particular, when going from two alkoxo-bridges to one bridge in {3d–Gd} complexes, a strong antiferromagnetic interaction is predicted, essentially due to a larger direct 3d–4f orbital overlap and thus a large J_AF contribution.^15b This correlates well with the single fluoride bridge and the antiferromagnetic interaction observed in this series. Additional insight into the mechanism of the exchange interaction is provided by DFT-calculated spin densities. Spin densities of 3.09 on Cr^III and 7.03 Gd^III indicate predominant spin polarisation (Fig. 4, left; Table S3, ESI†). All the coordinated nitrogen and oxygen atoms have negative spin densities, however the fluoride ions, both the bridging and the terminal, have positive spin densities in the high spin state (cf. Table S4, ESI†). The bridging fluoride has negative spin density values in the broken symmetry state and this essentially indicates that delocalization from Cr^III predominates over the Gd^III. Comparing the magnitude and the sign of the spin densities at the fluoride bridge, it is apparent that a mixture of spin delocalization and polarization is operational on these atoms and this diminishes the charge transfer component and thus reduces the J_F part. This is also supported by our NBO analysis where an extremely weak Cr^III 3d_z²–Gd^III 5d_z² donor–acceptor interaction has been detected (Fig. 4, right). To gain insight into the angle dependency, the Cr–F–Gd angle was gradually varied from 135° to 180° in steps of 10°. The computed variation of J with the bridging angle is shown in Fig. 3 along with the experimental points.

Fig. 4 (left) Spin density plot for the parent Cr–Gd complex. (right) Representation of charge transfer donor(Cr^III 3d_z²)–acceptor(Gd^III 5d_z²) NBO plot from second order perturbation theory analysis.

As the angle increases the J becomes more antiferromagnetic, but shows a plateau at larger angles. On the other hand at an acute angle (at ca. 138°), a switch from antiferro- to ferromagnetic interaction is predicted. Mapping the experimental J's and structural parameters on the computed graph yields an excellent match. The plateau at higher angles and less antiferromagnetic J at lower angles was nicely reproduced. To analyse the factors behind the observed trend, we have computed the overlap integrals, which reveal that there is a significant decrease in the Cr–Gd orbital overlap as the angle decreases leading to a reduction in the J_AF contribution. (cf. Table S5, ESI†) This along with a moderate increase in the charge transfer (cf. 5d occupation in Table S6, ESI†) leads to a predicted ferromagnetic coupling at lower Cr–F–Gd angles. Our analysis reveals that at lower angles, the metal ion spin densities increase and, concomitantly, for μ-F⁻ the spin densities decrease proportionally indicating an increasing ferromagnetic contribution as evidenced from the computed J values (see Fig. 3, right; Table S4, ESI†).

In conclusion, the angular dependence of the exchange in a small family of fluoride-bridged {Gd^III_xCr^III_y} complexes has been analysed. The observed variation and magnitude of J is reproduced and rationalised by DFT calculations in terms of geometric variation of 3d–4f overlap and charge transfer. This insight paves the way for preparative control of magnetic exchange interactions in systems with small magnetic anisotropy and thereby for the development of new molecular, magnetic coolers.

K.S.P. and S.P. thank the Danish Ministry of Science, Innovation and Higher Education for an EliteForsk travel scholarship and a Sapere Aude Fellowship (10-081659), respectively. GR thanks DST (SR/S1/IC-41/2010; SR/NM/NS-1119/2011) for financial support and SKS thanks IITB for SRF fellowship. GR and SKS acknowledge the HPC facility at IITB.

Notes and references

1. (a) M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672–4676; (b) J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91–103.
2. (a) G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592–7594; (b) R. Sibille, T. Mazet, B. Malaman and M. François, Chem.–Eur. J., 2012, 18, 12970.
3. (a) R. E. P. Winpenny, Chem. Soc. Rev., 1998, 27, 447–452; (b) C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2388; (c) M. Andruh, J.-P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342–3359.
4. E. Cremades, S. Gómez-Coca, D. Aravena, S. Alvarez and E. Ruiz, J. Am. Chem. Soc., 2012, 134, 10532–10542.
5. O. Kahn, Molecular Magnetism, VCH, New York, 1993.
6. H. I. Karunadasa, K. D. Arquero, L. A. Berben and J. R. Long, Inorg. Chem., 2010, 49, 4738–4740.
7. T. Birk, K. S. Pedersen, C. Aa. Thuesen, T. Weyhermüller, M. Schau-Magnussen, S. Piligkos, H. Weihe, S. Mossin, M. Evangelisti and J. Bendix, Inorg. Chem., 2012, 51, 5435–5443.
8. (a) J. Dreiser, K. S. Pedersen, C. Piamonteze, S. Rusponi, Z. Salman, Md. E. Ali, M. Schau-Magnussen, C. Aa. Thuesen, S. Piligkos, H. Weihe, H. Mutka, O. Waldmann, P. Oppeneer, J. Bendix, F. Nolting and H. Brune, Chem. Sci., 2012, 3, 1024–1032; (b) C. Aa. Thuesen, K. S. Pedersen, M. Schau-Magnussen, M. Evangelisti, J. Vibenholt, S. Piligkos, H. Weihe and J. Bendix, Dalton Trans., 2012, 41, 11284–11292.
9. (a) A. McRobbie, A. R. Sarwar, S. Yeninas, H. Nowell, M. L. Baker, D. Allan, M. Luban, C. A. Muryn, R. G. Pritchard, R. Prozorov, G. Timco, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, Chem. Commun., 2011, 47, 6251–6253; (b) J. Dreiser, K. S. Pedersen, T. Birk, M. Schau-Magnussen, C. Piamonteze, S. Rusponi, T. Weyhermüller, H. Brune, F. Nolting and J. Bendix, J. Phys. Chem. A, 2012, 116, 7842–7847.
10. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, MA, 2nd edn, 1992.
11. P. L. W. Tregenna-Piggott, D. Sheptyakov, L. Keller, S. I. Klokishner, S. M. Ostrovsky, A. V. Palii, O. S. Reu, J. Bendix, T. Brock-Nannestad, K. Pedersen, H. Weihe and H. Mutka, Inorg. Chem., 2009, 48, 128–137.
12. (a) N. Georgopoulou, R. Adam, C. P. Raptopoulou, V. Psycharis, R. Ballesteros, B. Abarca and A. K. Boudalis, Dalton Trans., 2010, 39, 5020–5027; (b) M. Ferbinteanu, F. Cimpoesu, M. A. Gîrţu, C. Enachescu and S. Tanase, Inorg. Chem., 2012, 51, 40–50.
13. H.-Z. Kou, S. Gao, C.-H. Li, D.-Z. Liao, B.-C. Zhou, R.-J. Wang and Y. Li, Inorg. Chem., 2002, 41, 4756–4762.
14. D. J. Hodgson, K. Michelsen and E. J. Pedersen, J. Chem. Soc., Chem. Commun., 1988, 1558–1559.
15. (a) S. K. Singh, N. K. Tibrewal and G. Rajaraman, Dalton Trans., 2011, 40, 10897–10906; (b) S. K. Singh and G. Rajaraman, Dalton Trans., 2013, 42, 3623–3630; (c) G. Rajaraman, F. Totti, A. Bencini, A. Caneschi, R. Sessoli and D. Gatteschi, Dalton Trans., 2009, 3153–3161; (d) J. Paulovic, F. Cimpoesu, M. Ferbinteanu and K. Hirao, J. Am. Chem. Soc., 2004, 126, 3321–3331; (e) T. Rajeshkumar and G. Rajaraman, Chem. Commun., 2012, 48, 7856–7858; (f) S. K. Singh, T. Rajeshkumar, V. Chandrasekhar and G. Rajaraman, Polyhedron, 2013 DOI:10.1016/j.poly.2013.02.037.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedures, crystallographic details, spectroscopic results, reduced magnetization data, computational details. CCDC 921006. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3cc42552e

‡ These authors contributed equally to the work.

---