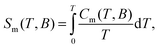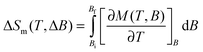A ferromagnetically coupled diphenoxo-bridged Gd³⁺–Mn²⁺ dinuclear complex with a large magneto-caloric effect

Abstract

A novel diphenoxo-bridged Gd³⁺–Mn²⁺ dimer is proposed as a good candidate for cryogenic magnetic refrigeration. The large MCE is enhanced by the ferromagnetic interaction between the two metal ions.

---

Heteropolynuclear 3d-Gd³⁺ complexes are attracting much attention because, amongst other things, they have potential application as low-temperature magnetic coolers.¹ These systems show an enhanced magneto-caloric effect (MCE), which is based on the change of magnetic entropy upon application of a magnetic field, that can be exploited for cooling applications via adiabatic demagnetisation.¹ The MCE is greatly enhanced in molecules containing isotropic magnetic ions with large total spin S.¹ Taking this into account, 3d/Gd³⁺ complexes are very good candidates for molecular refrigerants as the Gd³⁺ ion has an isotropic f⁷ configuration and the 3d-Gd³⁺ magnetic interactions are generally ferromagnetic in nature, leading to ground states with increased and large spin multiplicity.² Moreover, the 3d-Gd³⁺ magnetic exchange interactions are very weak, due to the very efficient shielding of the 4f orbitals of the Gd³⁺ by the fully occupied 5s and 5p orbitals,² and this generates multiple low-lying excited and field-accessible states, each of which can contribute to the magnetic entropy of the system. Another factor favouring a large MCE is the presence of a large metal/ligand mass ratio, in order to limit the amount of passive, non-magnetic elements and in small cluster molecules this is more easily accomplished than in larger ones. Therefore, small, lightweight 3d-Gd³⁺ complexes containing isotropic transition metal ions such as Mn²⁺, Fe³⁺, Cr³⁺, Cu²⁺, that exhibit weak ferromagnetic interactions between the metal ions, are appropriate candidates for constructing magnetic coolers.

Although a number of molecular 3d-Gd³⁺ complexes have been reported so far, those containing Mn²⁺ are limited to phosphonate-bridged Mn₄Gd₆ and Mn₉Gd₉ cages,³ one diphenoxo-bridged Mn₂Gd₂ tetranuclear complex,⁴ three triphenoxo-bridged Mn₂Gd trinuclear complexes,⁵ and one alkoxo-bridged MnGd dinuclear complex.⁶ We note that the two former compounds exhibit significant MCE and most exhibit ferromagnetic interactions.

In this communication we report the first example of a diphenoxo-bridged Gd³⁺–Mn²⁺ complex from the compartmental H₂L ligand shown in the inset of Fig. 1, which has an inner pentadentate N₃O₂ coordination pocket and an external O₂O₂ site that favours the formation of Mn²⁺–Ln³⁺. The new compound was predicted to exhibit a ferromagnetic interaction between the metal ions, leading to an enhanced MCE.

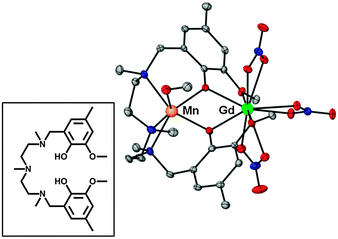Fig. 1 Perspective view of the molecular structure of 1. H-atoms are omitted for clarity. Colour code: N = blue, O = red, Mn = orange, Gd = green, C = grey. The inset shows the H₂L pro-ligand.

The molecular structure of [Mn(CH₃OH)(μ-L)Gd(NO₃)₃] (1, Fig. 1) consists of a dinuclear molecule in which the Gd³⁺ and Mn²⁺ ions are bridged by two phenoxo groups of the L²⁻ ligand. Within the dinuclear unit, the Mn²⁺ ion exhibits a [slightly] trigonally distorted MnN₃O₃ coordination polyhedron, where the three N-atoms from the amine groups, and consequently the three O-atoms belonging to the methanol molecule and phenoxo bridging groups, occupy fac positions. The Mn–O and Mn–N distances are found in the ranges 2.148(2) Å to 2.158(2) Å and 2.298(3) Å to 2.376(3) Å, respectively. The Gd³⁺ ion exhibits a GdO₁₀ coordination sphere, consisting of the two phenoxo bridging oxygen atoms, the two methoxy oxygen atoms and six oxygen atoms belonging to three bidentate nitrate anions. The GdO₁₀ coordination sphere is rather asymmetric, exhibiting short Gd–O_phenoxo bond distances of 2.342(2) Å and 2.322(2) Å, longer Gd–O_nitrate bond lengths in the range 2.492(2)–2.522(2) Å and weakly coordinated methoxy groups with Gd–O_methoxy distances of 2.608(2) Å and 2.564(2) Å. The Mn(μ-O₂)Gd bridging fragment is almost planar with a hinge angle of 4.1° and rather symmetric with similar pairs of Mn–O bond distances (2.148 Å and 2.158Å), Gd–O bond distances and Mn–O–Gd bridging angles (110.27° and 110.68°). The Mn⋯Gd separation is 3.686 Å. In the crystal, molecules are held in pairs by a couple of symmetrically related hydrogen bonds involving the non-coordinated O-atom of one of the bidentate nitrate anions and the methanol molecule, with O⋯O distances of 2.831 Å (Fig. S1, ESI§). The shortest intermolecular M⋯M distance is 7.707(1) Å (Mn⋯Gdⁱi = 2 − x, 1 − y, 2 − z).

The room temperature χ_MT value for 1 (12.90 cm³ K mol⁻¹) is slightly higher than the expected value for a pair of non-interacting Mn²⁺ (S = 5/2) and Gd³⁺ (S = 7/2) ions (12.25 cm³ K mol⁻¹) with g = 2. On lowering the temperature χ_MT slowly increases from room temperature to 50 K (13.70 cm³ K mol⁻¹) before rising more sharply to reach a quasi-plateau of 19.90 cm³ K mol⁻¹ below 3.5 K (see Fig. S2, ESI§). This behaviour is due to a ferromagnetic interaction between the Mn²⁺ and Gd³⁺ ions leading to a S_T = 6 spin ground state. The fact that χ_MT does not reach the expected value for a S = 6 ground state (21.0 cm³ K mol⁻¹ for g = 2) at 2 K is probably due to the combined result of intermolecular antiferromagnetic interactions, mediated by the hydrogen bonding interactions, and weak zero-field splitting effects from both metal ions. The magnetic properties have been modelled by using the following spin-Hamiltonian:

H = −Js_Gds_Mn − zJ′〈S_z〉S_z + gμ_Bs_GdB + gμ_Bs_MnB (1)

The first term accounts for the isotropic magnetic exchange coupling between the Mn²⁺ and Gd³⁺ ions, the second accounts for the intermolecular interactions by means of the molecular field approximation, and the last two are the Zeeman terms. The fit of the experimental susceptibility data to the theoretical equation derived from the above Hamiltonian by using the van Vleck equation afforded the following set of parameters: J = +0.99(2) cm⁻¹, g_Gd = 2.02(4), g_Mn = 2.01(7) and zJ′ = −0.008(1) cm⁻¹. The zJ′ parameter also includes the effects of the very weak local anisotropy of Gd³⁺ and Mn²⁺ ions.

Previous DFT calculations^7,8 and experimental^2,8 results have clearly shown that the J_MGd coupling in diphenoxo-bridged Gd³⁺–M²⁺ complexes (M²⁺ = Mn, Ni, Cu) increases when the planarity of the M–O₂–Gd bridging fragment and the M–O–Gd bridging angle increase. Both structural factors are correlated, so that the latter increases as the bridging fragment becomes more planar. In line with this, compound 1, with an almost planar Mn–(O)₂–Gd bridging fragment, presents the second largest J_MnGd value found for ferromagnetically coupled diphenoxo- and triphenoxo-bridged Gd³⁺–Mn²⁺ complexes. Fig. 2 shows the magnetic field dependence of the isothermal magnetization (M) for T ranging from 2 K to 10 K. The experimental data can be modelled using eqn (1) by neglecting in first instance anisotropies and intermolecular interactions. By using the same values obtained from fitting the susceptibility data, we calculate the magnetization curves (depicted as solid lines in Fig. 2) which nicely account for the experimental data.

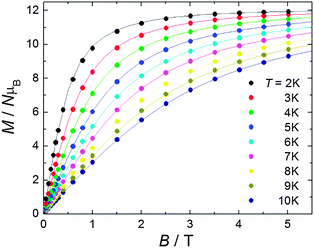Fig. 2 (Circles) Experimental isothermal magnetization curves for fields up to B = 5 T and taken at several T, as labelled. The solid lines are the calculated magnetization curves, see the main text for details.

The molar heat capacity, C/R, measured in the presence of several magnetic fields B is plotted in Fig. 3 against temperature. A non-magnetic heat capacity, which we associate to vibrational phonon modes of the lattice, is seen to develop at high temperatures. The fit to the Debye function (dotted line) gives a Debye temperature θ_D = 50.6 K, in agreement with values reported for this class of material.⁹ At low temperatures, the experimental magnetic heat capacity for B ≥ 1 T is well described by the calculated Schottky curves as obtained from eqn (1) using the set of eigenvalues found from the fitting of the magnetic data. Intriguingly, the zero-field experimental curve shows two broad Schottky-like features which are well-separated in temperature – being centred at T ≈ 0.3 K and 5.5 K, respectively. We tentatively explain the anomaly at higher temperatures as the result of the zero-field splitting between the S_T = 6 ground state and the first excited level S = 5 (dashed-dotted line; see Fig. S3, ESI§ for the energy-level diagram). For temperatures lower than ≈ 1 K, only the S_T = 6 ground state is populated. In the mean-field approach, the onset of intermolecular magnetic correlations can be interpreted in terms of an interaction field B_int, producing a Zeeman splitting of the (otherwise degenerate) S_T = 6 ground state leading to an anomaly, as indeed reported in Fig. 4 for such low temperatures. An excellent description of the experimental data is obtained for the interaction field B_int = 0.16 T (dashed line in Fig. 3). The solid lines in Fig. 3 are the sum of calculated magnetic and lattice contributions.

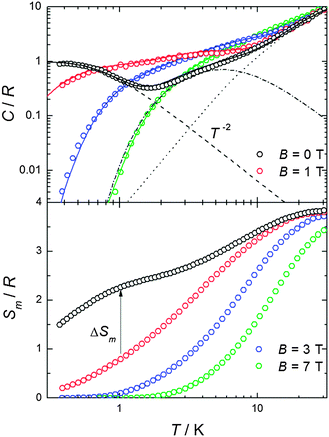Fig. 3 Top: temperature dependence of the heat capacity C normalized to the gas constant R and measured in the presence of several magnetic fields, as labelled. Fit of heat capacity (solid lines) is calculated as explained in the text. Lattice (dotted line) and magnetic (dot-dashed lines, dashed lines) contributions are shown. Bottom: experimental magnetic entropies as obtained from the corresponding C data.

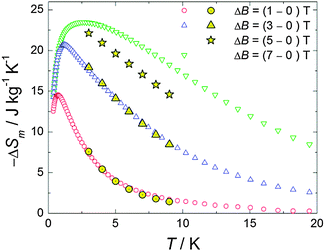Fig. 4 Temperature-dependencies of the magnetic entropy change ΔS_m, for the indicated applied-field changes ΔB, as obtained from heat capacity (empty markers) and magnetization (full markers) measurements.

An estimate of the magnetic exchange acting between the S_T = 6 molecular units can be obtained by comparing the experimental T⁻² term, CT²/R = 0.6 K² to the theoretical expression for the high-temperature tail of the magnetic heat capacity, i.e., CT²/R = 2nz[S(S + 1)|J′|/3k_B]², where z is the number of nearest magnetic neighbours between different S_T = 6 molecular units and n = 1, 2, and 3 for Ising, XY, and Heisenberg models, respectively.¹⁰ This comparison provides z^1/2|J′|/k_B = 1.5 × 10⁻² cm⁻¹, in satisfactory agreement with the previous estimate from magnetic data. We note that this value should be considered as an upper estimate for the magnetic exchange since our simple model does not take into account the magnetic dipolar interactions or the magnetic anisotropies. From the heat capacity data we derive the magnetic entropy by making use of the equation:

where C_m is the experimental magnetic heat capacity which we obtain after subtracting the lattice contribution from the total C. This integral is limited by the lowest experimental temperature T₀ ∼ 0.3 K. For B = 0 and 1 T, the lack of experimental data for T < T₀ has been accounted for by matching the limiting S_m/R at high T to the full entropy content ln(2s_Gd + 1) + ln(2s_Mn + 1) = 3.87. From the results depicted in the bottom panel of Fig. 3, it is straightforward to derive the change of magnetic entropy, ΔS_m(T, ΔB = B_f − B_i), which characterizes a material in terms of the MCE. Independently, ΔS_m is also obtained from the magnetization data by using the Maxwell relation, i.e.,

The results, reported in Fig. 4, show a perfect agreement between the two independent derivations. The MCE for ΔB = 7 T is maximum at T = 2.7 K reaching a value of 23.5 J kg⁻¹ K⁻¹.

To summarize, by diagonalizing spin Hamiltonian (1) we have fitted the susceptibility and magnetization data for complex 1 obtaining an intramolecular ferromagnetic exchange coupling between the metal centres. The value so-obtained for the exchange is amongst the largest so far reported for similar dinuclear and trinuclear Mn²⁺–Gd³⁺ compounds. This is attributed to the near planar Mn–(O)₂–Gd bridging fragment.^7,8 From heat capacity measurements, we found that the magnetic entropy change reaches significant values for 1–3 K, namely ΔS_m = 23.5 J kg⁻¹ K⁻¹ for ΔB = 7 T. Our results therefore suggest that the Gd³⁺–Mn²⁺ molecular dimer 1 is a very good candidate for a magnetic coolant for liquid-helium temperatures.

We are grateful to MINECO (contracts MAT2012-38318-C03 and CTQ2011-24478), EC for a Marie Curie-IEF (PIEF-GA-2011-299356 to GL). EKB thanks the EPSRC and Leverhulme Trust.

Notes and references

1. M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672.
2. M. Andruh, J. P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342.
3. Y.-Z. Zheng, E. M. Pineda, M. Helliwell and R. E. P. Winpenny, Chem.–Eur. J., 2012, 18, 4161.
4. Y. Bi, Y. Li, W. Liao, H. Zhang and D. Li, Inorg. Chem., 2008, 47, 9733.
5. (a) T. Yamaguchi, J. P. Costes, Y. Kishima, M. Kojima, Y. Sunatsuki, N. Brefuel, J. P. Tuchagues, L. Vendier and W. Wernsdorfer, Inorg. Chem., 2010, 49, 9125; (b) V. Chandrasekhar, B. M. Pandian, R. Boomishankar, A. Steiner and R. Clérac, Dalton Trans., 2008, 5143; (c) J. P. Costes, J. García-Tojal, J. P. Tuchagues and L. Vendier, Eur. J. Inorg. Chem., 2009, 3801.
6. A. N. Georgopoulou, R. Adam, C. P. Raptopoulou, V. Psycharis, R. Ballesteros, B. Abarca and A. K. Boudalis, Dalton Trans., 2010, 39, 5020.
7. E. Cremades, S. Gomez-Coca, D. Aravena, S. Alvarez and E. Ruiz, J. Am. Chem. Soc., 2012, 134, 10532.
8. E. Colacio, J. Ruiz, A. J. Mota, M. A. Palacios, E. Cremades, E. Ruiz, F. J. White and E. K. Brechin, Inorg. Chem., 2012, 51, 857.
9. See for example M. Evangelisti, F. Luis, L. J. de Jongh and M. Affronte, J. Mater. Chem., 2006, 16, 2534 and references therein.
10. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, England, 1970.

---

Footnotes

† Celebrating 300 years of Chemistry at The University of Edinburgh and 100 years at the University of Granada.

‡ This paper is dedicated to Dr. Jean Pierre Costes on the occasion of his retirement.

§ Electronic supplementary information (ESI) available: Experimental details, crystallographic data in CIF format for 1, selected bond distance and angles for 1, energy levels patterns. CCDC 926238. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3cc41483c

---