Linking gold nanoparticles with conductive 1,4-phenylene diisocyanide–gold oligomers

Abstract

It is demonstrated that 1,4-phenylene diisocyanide (PDI)–gold oligomers can spontaneously bridge between gold nanoparticles on mica, thereby providing a strategy for electrically interconnecting nanoelectrodes. The barrier height of the bridging oligomer is 0.10 ± 0.02 eV, within the range of previous single-molecule measurements of PDI.

---

A major challenge to fabricating molecular electronic circuits¹ is the difficulty of simultaneously chemically bonding molecular components to two metal electrodes. This can be accomplished by adjusting the electrode separation to match the molecular dimensions using break junctions^2–5 or by using a sharp tip to vary the electrode-surface spacing.⁶ Such approaches provide detailed information on molecular conduction, but are not easily extended to planar systems required for a realistic circuit.⁷ Molecularly linked nanoparticles have been synthesized in solution and deposited onto surfaces^7,8 but the location of the nanoparticles in the circuit is dictated by the cross-linking structure. Ordered assemblies have been formed from functionalized nanoparticles but they are often not covalently connected.⁹ Finally, the length of the molecular linker can be matched to the nanoparticle spacing but requires the molecular size to be tailored to the separation of the nanoparticles.¹⁰

An alternative strategy is proposed based on recent observations that molecules that bind strongly to metals with low cohesive energies such as gold or copper can oligomerize by extracting metal atoms from the substrate.^11–14 An example of this is the lateral self-assembly of 1,4-phenylene diisocyanide (PDI) on Au(111) that forms –(Au–PDI)_n– oligomers comprising long, one-dimensional chains by extracting low-coordination gold atoms from surface defect sites.^15–17 The relatively short (∼1.1 nm) repeat distance between gold atoms in the oligomer suggests the possibility of being able to chemically bond between gold nanoparticles with various separations by incorporating a number of repeat units until the gap is bridged. PDI has been previously proposed as a prototypical molecular electronic component,^4,6,18–21 and theory suggests that PDI is a suitable candidate for device applications.²²

This lateral self-assembly is explored by measuring the conductivity of a gold nanoparticle film on mica that has been exposed to PDI. Evaporating gold films on mica (and other insulating substrates)^23–28 provides a simple method for growing isolated nanoparticles with different spacings merely by ensuring that the gold film thickness remains below a critical value, above which a continuous film is formed. The success of this approach relies on the oligomers being sufficiently mobile to bridge between nanoparticles. This mobility is illustrated in Fig. 1, which displays a typical series of 15 consecutive STM images (taken 53 seconds apart) of a saturated layer of Au–PDI chains on Au(111) showing the repeated lateral motion of an entire chain, where a line is drawn to highlight the chain motion, showing nine hopping events corresponding to a maximum rate of 1 hop every 82 seconds. The motion is independent of tip bias indicating that it is thermally driven. It is proposed that chains can migrate between adjacent sites of different types as illustrated in Fig. S2 (ESI†).¹⁵ A maximum activation energy of ∼0.8 eV is estimated for this process by assuming that the partition functions in the initial and transition states are equal yielding an Arrhenius pre-exponential factor (kT/h) of ∼10¹³ s⁻¹. In fact, the hopping rate could be higher if more events had occurred that were not observed within the time resolution of our experiment.

Fig. 1 Time-dependent sequence of images of Au–PDI chains collected every 53 seconds scanning a 5.0 × 5.0 nm² region. A dotted line showing the chains has been included as a guide to the eye. V_t = 2.08 V, I_t = 86.2 pA. Scanning speed = 30.0 nm s⁻¹.

The ability of the mobile oligomers to bridge nanoparticles is illustrated by the series of STM images (Fig. 2) of a Au(111) surface containing nanoparticles (Labelled A, B and C). Clearly, the Au–PDI oligomers are capable of bridging between the gold nanoparticles (as depicted in the inset to Fig. 3) and the images show the same chain mobility as seen in Fig. 1. For greater clarity, a movie of the images in Fig. 2 is included in the ESI.†

Fig. 2 Sequence of images of Au–PDI oligomers linking between gold nanoparticles on a Au(111) surface where the location of the nanoparticles is indicated by A, B and C. V_t = −2.00 V, I_t = 198 pA.

Fig. 3 Plot of the change in conductivity of a gold film deposited onto mica exposed to PDI as a function dosing time. The inset shows a schematic depiction of the oligomer-linked nanoparticles.

In order to determine whether similar bridging occurs between gold nanoparticles on an insulating substrate, as required for device applications, and to measure the conductivity of the connecting oligomers, gold was evaporated onto cleaved mica. The number of particles on the surface was constant (3.3 ± 0.1 × 10¹⁵ m⁻²) for different initial gold film thicknesses (characterized by its sheet resistance, R_C) (Fig. S3, ESI†). The sample was then exposed to PDI in vacuo and Fig. 3 shows a typical plot of the film conductivity versus PDI dosing time (■), which increases with PDI exposure, reaching a constant value after ∼2000 s. As a control, clean mica was exposed to PDI (Fig. S4 (●), ESI†) and no conductivity change was found. The effect of exposing gold-covered mica surfaces to phenyl isocyanide (which contains a single isocyanide group) was also measured (Fig. S4A–C, ESI†) for several gold films where no change in conductivity was observed. This confirms that two isocyanide groups and the gold nanoparticles are required to obtain the conductivity change shown in Fig. 3. Fig. S5 (ESI†) demonstrates that dosing PDI does not significantly change the particle morphology by comparing STM images prior to (Fig. S5(a) ESI;† particle diameter = 8.3 ± 2.2 nm) and after (Fig. S5(b) ESI;† particle diameter = 7.2 ± 2.2 nm) PDI dosing and is in accord with recent scanning-electron microscope images of gold nanoparticles dosed with PDI.²⁹

The conductivities of all PDI-saturated gold films on mica showed Ohmic behaviour. Plots of ln(R), where R is the sheet resistance, versus 1/√T for various values of R_C, are shown in Fig. S6 (ESI†). The low expansion coefficient of mica and the linearity of the data in Fig. S6 (ESI†) indicate that artefacts due to substrate expansion are absent.⁸ These results also confirm that the conductivity increase is not due to particle restructuring since the resulting metallic films would have much weaker temperature dependences. Such temperature dependences (Fig. S6, ESI†) have been attributed to the form of the density of states near the Fermi level.^30,31 It is also predicted by the Abeles model for thermally assisted tunnelling through granular materials,^32,33 which also provides an explicit dependence of conductivity on the size and separation of the nanoparticles.^34,35 The low-field limit in the Abeles model, which applies since there are ∼10⁵ particles between the electrodes (Fig. S2, ESI†), predicts that ln(R) = α/√T + β, where α and β are constants, in agreement with experimental (Fig. S6, ESI†). As shown in the ESI,† and by assuming that the particle morphology does not change (Fig. S5, ESI†), the Abeles model predicts that α and ln(R_C) are linearly related as confirmed experimentally in Fig. 4, with a slope given by where , ϕ is the height of the tunnelling barrier, m is the electron mass, and ε_F is the dielectric constant. The subscripts F and C refer to PDI-covered and clean gold films, respectively. This behaviour confirms that the gold nanoparticles on mica are bridged by –(Au–PDI)– oligomers. The slope in Fig. 4 (3.7 ± 0.2) yields a barrier height ϕ_F = 0.10 ± 0.02 eV (see Fig. S7, ESI†).

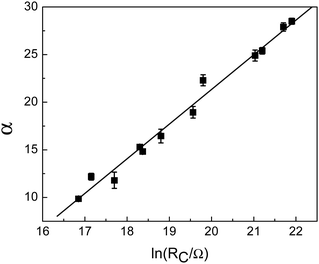Fig. 4 Plot of α, the slope of plots of ln(R/Ω) versus 1/√T (Fig. S3, ESI†), versus ln(R_C), where R_C is the initial resistance of the films.

It is instructive to compare the barrier height of the oligomer bridges with previous measurements for PDI. STM measurements of several phenyl-based isocyanides and diisocyanides attributed the barrier height to the energy difference between the Fermi level (E_F) of the metal (gold) contacts and the energy of the highest-occupied molecular orbital (HOMO), and was found to be 0.38 ± 0.1 eV for PDI bridging gold.⁶ Spectroscopic studies of Au–PDI oligomers on Au(111) show that the HOMO of the oligomer lies ∼0.88 eV below the Fermi level, with a LUMO ∼3.32 eV above it, consistent with a HOMO tunnelling barrier.¹⁷ More recent experiments found a barrier height of 0.19 ± 0.02 eV (ref. 36) where the difference from previous results was ascribed to different numbers of PDI molecules in the contact. Break-junction measurements suggested a thermionic barrier height of 0.22 eV for PDI between gold electrodes.⁴ These values are somewhat higher than, but within the same range as the value of ∼0.1 eV measured here. However, the tunnelling barrier height for extended Au–PDI oligomers bridging gold nanoparticles might be expected to be lower than for a single PDI linker. Nevertheless, the results are in accord with the idea that PDI self-assembles to effectively bridge between gold nanoparticles. Such a simple method of linking nano-electrodes will provide a viable strategy for forming large-scale molecular electronic devices having differing electrode separations. Successfully being able to make switching devices will rely on being able to modulate the current through the molecule. While this appears to be possible with analogous dithiol-linked nanoparticles⁵ it has been suggested that this is not possible with PDI.²¹

PDI on Au(111) self-assembles with gold to form oligomers that are sufficiently mobile to bridge between gold nanoparticles. The conductivity of gold nanoparticles on mica increases substantially when exposed to PDI and requires both the presence of the nanoparticles and two isocyanide groups. The temperature dependence of the conductivity is in accord with the particles being electrically linked with a tunnelling barrier height of ∼0.1 eV.

Notes and references

1. A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283.
2. S. Martín, I. Grace, M. R. Bryce, C. Wang, R. Jitchati, A. S. Batsanov, S. J. Higgins, C. J. Lambert and R. J. Nichols, J. Am. Chem. Soc., 2010, 132, 9157–9164.
3. M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254.
4. J. Chen, W. Wang, J. Klemic, M. A. Reed, B. W. Axelrod, D. M. Kaschak, A. M. Rawlett, D. W. Price, S. M. Dirk, J. M. Tour, D. S. Grubisha and D. W. Bennett, Ann. N. Y. Acad. Sci., 2002, 960, 69–99.
5. H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043.
6. B. Kim, J. M. Beebe, Y. Jun, X. Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2006, 128, 4970–4971.
7. A. Zabet-Khosousi and A.-A. Dhirani, Chem. Rev., 2008, 108, 4072–4124.
8. K. H. Müller, J. Herrmann, G. Wei, B. Raguse and L. Wieczorek, J. Phys. Chem. C, 2009, 113, 18027–18031.
9. L. Jianhui, A. M. Markus, G. Sergio, M. Marcel, S. Christian and C. Michel, New J. Phys., 2008, 10, 065019.
10. P. Banerjee, D. Conklin, S. Nanayakkara, T.-H. Park, M. J. Therien and D. A. Bonnell, ACS Nano, 2010, 4, 1019–1025.
11. M. Treier, N. V. Richardson and R. Fasel, J. Am. Chem. Soc., 2008, 130, 14054–14055.
12. S. L. Tait, A. Langner, N. Lin, S. Stepanow, C. Rajadurai, M. Ruben and K. Kern, J. Phys. Chem. C, 2007, 111, 10982–10987.
13. F. Klappenberger, A. Weber-Bargioni, W. Auwarter, M. Marschall, A. Schiffrin and J. V. Barth, J. Chem. Phys., 2008, 129, 214702–214710.
14. G. Pawin, K. L. Wong, D. Kim, D. Sun, L. Bartels, S. Hong, T. S. Rahman, R. Carp and M. Marsella, Angew. Chem., Int. Ed., 2008, 47, 8442–8445.
15. J. Boscoboinik, J. Kestell, M. Garvey, M. Weinert and W. Tysoe, Top. Catal., 2011, 54, 20–25.
16. J. A. Boscoboinik, F. C. Calaza, Z. Habeeb, D. W. Bennett, D. J. Stacchiola, M. A. Purino and W. T. Tysoe, Phys. Chem. Chem. Phys., 2010, 12, 11624–11629.
17. J. Zhou, D. Acharya, N. Camillone, P. Sutter and M. G. White, J. Phys. Chem. C, 2011, 115, 21151–21160.
18. Y. Kim, T. Pietsch, A. Erbe, W. Belzig and E. Scheer, Nano Lett., 2011, 11, 3734–3738.
19. S. Hong, R. Reifenberger, W. Tian, S. Datta, J. I. Henderson and C. P. Kubiak, Superlattices Microstruct., 2000, 28, 289–303.
20. C. J. F. Dupraz, U. Beierlein and J. P. Kotthaus, ChemPhysChem, 2003, 4, 1247–1252.
21. J.-O. Lee, G. Lientschnig, F. Wiertz, M. Struijk, R. A. J. Janssen, R. Egberink, D. N. Reinhoudt, P. Hadley and C. Dekker, Nano Lett., 2003, 3, 113–117.
22. N. D. Lang and P. Avouris, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125323.
23. T. Andersson, J. Phys. D: Appl. Phys., 1976, 9, 973.
24. M. Adamov, B. Perović and T. Nenadović, Thin Solid Films, 1974, 24, 89–100.
25. D. Hecht and D. Stark, Thin Solid Films, 1994, 238, 258–265.
26. S. Norrman, T. Andersson, C. G. Granqvist and O. Hunderi, Phys. Rev. B: Solid State, 1978, 18, 674–695.
27. M. James E, Vacuum, 1998, 50, 107–113.
28. G. Grimvall and T. G. Andersson, J. Phys. D: Appl. Phys., 1983, 16, 1985.
29. Y. Sohn, D. Pradhan, L. Zhao and K. T. Leung, Electrochem. Solid-State Lett., 2012, 15, K35–K39.
30. A. L. Efros and B. I. Shklovskii, J. Phys. C: Solid State Phys., 1975, 8, L49.
31. P. Sheng and J. Klafter, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2583–2586.
32. B. Abeles, P. Sheng, M. D. Coutts and Y. Arie, Adv. Phys., 1975, 24, 407–461.
33. P. Sheng, B. Abeles and Y. Arie, Phys. Rev. Lett., 1973, 31, 44–47.
34. G. R. Wang, L. Wang, Q. Rendeng, J. Wang, J. Luo and C.-J. Zhong, J. Mater. Chem., 2007, 17, 457–462.
35. J. Herrmann, D. J. Bray, K. H. Müller, G. Wei and L. F. Lindoy, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 212201.
36. E. Lörtscher, C. J. Cho, M. Mayor, M. Tschudy, C. Rettner and H. Riel, ChemPhysChem, 2011, 12, 1677–1682.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, supporting figures, Abeles model for the relationship between α and ln(R_C), video of the sequence of images shown in Fig. 4. See DOI: 10.1039/c2cc38389f

---