How to optimize binding of coated nanoparticles: coupling of physical interactions, molecular organization and chemical state

Abstract

One of the key challenges in the development of nano carriers for drug delivery and imaging is the design of a system that selectively binds to target cells. A common strategy is to coat the delivery device with specific ligands that bind strongly to overexpressed receptors. However such devices are usually unable to discriminate between receptors found on benign and malignant cells. We demonstrate, theoretically, how one can achieve enhanced binding to target cells by using multiple physical and chemical interactions. We study the effective interactions between a polymer decorated nano micelle or nanoparticle with three types of model lipid membranes that differ in the composition of their outer leaflet. They are: (i) lipid membranes with overexpressed receptors, (ii) membranes with a given fraction of negatively charged lipids and (iii) membranes with both overexpressed receptors and negatively charged lipids. The coating contains a mixture of two short polymers, one neutral for protection and the other a polybase with a functional end-group to optimize specific binding with the overexpressed receptors and electrostatic interactions with charged lipid head-groups. The strength of the binding for the combined system is much larger than the sum of the independent electrostatic or specific interactions binding. We find a range of distances where the addition of two effective repulsive interactions become an attraction in the combined case. The changes in the strength and shape of the effective interaction are due to the coupling that exists between molecular organization, physical interactions and chemical state, e.g., protonation. The predictions provide guidelines for the design of carrier devices for targeted drug and nanoparticle delivery and give insight in the competing and highly non-additive nature of the different effective interactions in nanoscale systems in constrained environments that are ubiquitous in synthetic and biological systems.

---

1. Introduction

Biological systems have the ability to respond to cues by changing the environment. For example binding of hormones to signaling proteins may lead to dimerization and change in the local lipid composition that is the first step in a signaling cascade.¹ The combination of specific chemical cues with molecular reorganization provide an exquisite tool to optimize function. Can we learn from biology to optimize interaction through molecular rearrangements at the nanoscale with potential applications in tissue engineering or drug delivery? Targeted drug delivery presents a challenging design problem where the carrier needs to recognize sick cells over a large population of healthy ones.^2–5 Consider, for example, the case of cancer. The typical approach used for cellular delivery is based on taking advantage of overexpressed receptors in the plasma membrane of pathogenic cells, which are ubiquitous in many different types of cancer.² The idea is then to cover the carrier with ligands that specifically interact with those receptors.⁶ The problem is that, in general, the specific binding of the ligand–receptor pair is very strong and therefore when the carrier finds a receptor on a healthy cell it binds to it. The question is whether one can design a drug carrier that will exclusively bind to malignant cells without interacting with healthy ones. A possible approach in the case of cancer may be to use ligands on the carrier that only bind weakly to some of the overexpressed receptors and that in addition take advantage of other changes in the plasma membrane of the cancer cells.⁷ The design of specific drug delivery systems together with the understanding of combined interactions to optimize function found in biological systems serve as the motivation of the work presented here. Our findings however, have a potential wide range of applications for coatings of nanoparticles for e.g., nano-sensor applications or fabrication of nanostructured materials.

We design systems that bind to cell membranes through specific ligand–receptor interactions with overexpressed receptors and electrostatic interactions taking advantage of the fact that in a few types of cancer there is evidence of negatively charged lipids in the outer leaflet of the plasma membrane.^8–10 We explicitly show how the effective interactions between a polymer coated nanomicelle/nanoparticle and a lipid layer presents very large synergetic effects between ligand–receptor binding, molecular reorganization, protonation state and electrostatic interactions that include regions of interactions where the addition of two repulsions leads to an attraction. Furthermore, we find that the effective distance dependence of the different contributions to the interaction change their nature depending upon the environment. Explicitly we demonstrate that the binding of a polymer coated nanomicelle to a lipid layer having both overexpressed receptors and charged lipids is much stronger than to a lipid membrane having only overexpressed receptors or only negatively charged lipids. The way that enhanced and selective binding is achieved here is different from previous approaches where differences in receptor densities on the cell surface were used to increase the binding.^11–15 There only one type of interaction is used. Here on the other hand, the synergy between multiple different (weak) chemical and physical interactions are used to enhance binding. Furthermore, the molecular organization and the resulting effective interactions are not the outcome of optimizing each contribution separately but rather the total free energy of the system. Many of the results presented here may seem non-intuitive, but they provide a platform for developing novel understanding of the interactions in complex molecular environments with applications ranging from nanoparticles to molecular cell biology.

Most of our intuitive understanding of interactions in soft matter is based upon the application of additivity ideas. Consider, for example, colloidal stabilization and DLVO theory, where the addition of van der Waals attractions with electrostatic repulsions works remarkably well. The use of polymer brushes for steric repulsions in addition to the surface (or particles) van der Waals attractions provides direct ways of determining the optimal conditions for polymer coatings.¹⁶ Interactions between lipid layers have been modeled using combinations of solvation forces, protrusion interactions, van der Waals attractions, and electrostatic interactions providing insightful explanations, and sometimes quantitative predictions, for the forces that are measured experimentally.¹⁷ Formally, the effective interactions are potentials of mean-force that result from averaging over different degrees of freedom. This leads to a temperature dependence of the effective interactions as for example in depletion forces.¹⁸ These interactions are purely entropic and they are certainly not pairwise additive, even though their use as additive potentials is common and in many cases this approach works remarkably well. The question that arises is under what conditions does the additivity of the effective interactions break down in a such a way that it provides qualitatively the wrong result. What are the molecular driving forces for this non-additive behavior and how are we to build up a framework for the understanding in these complex cases?

The lack of additivity of effective interactions is very important for the fundamental understanding of physical processes in molecular and cell biology where it is clear that the efficiency and selectivity of many processes are not only due to the specific molecules involved, but rather to the coupling that exist between molecular organization, physical interactions (VdW, electrostatic, etc.) and the possibility of chemical changes (acid–base equilibrium or ligand receptor binding) within nanoscale environment. Two examples of this behavior are: (1) the role of macromolecular crowding in processes such as protein folding and chromatin compaction^19,20 and (2) the local changes in composition in cell membranes associated with specific function such as the triggering of a signal cascade.¹ More generally, systems in which the length scale of the interactions competes with that of nano confinement results in non-trivial molecular organization that lead to novel and emergent behavior.²¹

2. Model and theoretical approach

In this work we present theoretical predictions for the interactions between a micellar drug carrier and model cell membranes (lipid layers). We shall consider so called lipid-core (nano) micelles. Lipid-core micelles are micellar assemblies formed by lipids conjugated with short hydrophilic polymers. The lipid–polymer conjugate self-assemble into micelles where the lipid tails form the core and the polymer chains form the corona of the micelles.⁴ The lipid-core micelles we treat are formed by a mixture of lipid molecules with head-groups that have been functionalized with two types of different low molecular weight polymers as well as unfunctionalized lipids (see Fig. 1). One of the polymers is polyethylene glycol, for stability of the micelle against aggregation and for biocompatibility to prevent clearance by the immune system (“stealth” protection²²), and the second is a polybase whose end-group is functionalized with a ligand that selectively binds to the overexpressed receptor in the cell membrane. The polybase is chosen so as to have positive charges in the carrier in order to favorably interact with negatively charged lipids, e.g., phosphatidylserine (PS), that may be present on cell membranes.⁹ The composition of the corona of the micelle is defined and controlled by the ratios between the PEG and polybase conjugated lipids and unfunctionalized lipids. In the calculations we choose to have a composition having 1–1 ratio between the PEG and polybase functionalized lipids. The total amount of lipid–polymer conjugated molecules has a surface coverage of σ = 0.40 chains per nm². This amount of polymer chains in the corona is sufficient to prevent aggregation between different micelles.²³

Fig. 1 Schematic depiction of a polymer nanomicelle interacting with a lipid membrane. The polybases with their functional ligand-end group are black while the PEG chains are in red. The lipids of the membrane are shown to have uncharged head-groups (purple) overexpressed receptors (red) and negatively charged head-groups (green). D is the distance from the center of the micelle to the plane defined by the membrane lipids’ head-groups and R is the micellar radius.

The idea is to look at how the effective interactions between the micelle and the membrane change depending upon the presence in the membrane of overexpressed receptors, anionic lipids or both. We will consider the micelle to be in an aqueous solution containing salt at physiological concentration and the lipid layer to be in the liquid disordered phase under three different scenarios. One is when there are overexpressed receptors on the lipid layers, the second is when a certain percentage of the lipids is negatively charged and there are no overexpressed receptors and the third case is when there are both overexpressed receptors and negatively charged lipids on the membrane. Most of the results will be for physiological pH conditions, however, due to the interesting interplay between molecular organization and chemical equilibrium coupling, we will also consider different pH's.

The theoretical approach used in this work is based on a molecular theory that for each molecular species treats the size, shape, charge distribution, acid–base equilibrium of each acid and base group and the polymer conformations explicitly.^24,25 The predictions of the molecular theory have been shown to be in excellent quantitative agreement with experimental observations for a large variety of systems;^26–29 therefore we believe that the predictions presented here are reliable.

The basic idea of the molecular theory is to write the free energy of the system as a functional of the probability of the conformations of the different molecules and the spatial distribution of them. The minimization of the free energy determines what is the probability of each of the different conformers depending upon the value of the controlled variables, e.g., temperature, pH, salt concentration, etc. The total free energy is given by

F = −TS_conf − TS_mix,poly − TS_mix + E_elec + E_rep + F_chem + G_bind + F_surf (1)

where T is the temperature; S_conf is the conformational entropy of the polymers chains; S_mix,poly represents the mixing (translation) entropy of the PEG and polybases, which is due to the lateral mobility of the polymer chains attached the lipid-core micelle. This term accounts for the lateral mobility of the lipids compromising the core of the micelle. For solid nanoparticles the tethered polymers are lateral immobile and hence this term will be constant. The next free energy contribution, S_mix, is the mixing (translational) entropy of the cations, anions, water, protons, and hydroxyl ions; E_elec corresponds to the total electrostatic energy; E_rep represents the steric repulsions between all molecular species; F_chem is the free energy of the acid–base chemical equilibrium, i.e., the enthalpic and entropic cost associated with charging and uncharging of the basic groups on the polybase; G_bind is the free energy associated with the ligand–receptor binding of the end-functionalized polybase with receptors found on the membrane surface. Here we considered only the case of overexpressed receptors, i.e., the density of receptors is much larger than the number of ligands under all conditions, consequently the ligand–receptor binding can be modeled as a potential. The contact of any ligand of the end-functional polymer chain with the cell surface results in binding to a receptor due to the fact that they are found in large excess. Therefore size exclusion effects related to the receptor density do not need to be considered. On the other hand, the size of the ligand was included. Similarly the size and thus the exclude volume of all the other molecular species was included explicitly. F_surf represents the free energy arising from the cell surface's lipids and includes contributions from the local mixing (translational) entropy of the mobile lipids and the protonation free energy of the PS head-groups.

Each of the terms is written as functionals of the density distribution of their molecular components and the probability distribution function for the polymeric species. The distribution profiles, the probability of the different conformers, the electrostatic and repulsive position dependent potentials and the state of protonation of each species is determined by the minimization of the total free energy. The input to the theory includes a very large number of unbiased polymer conformations, the pK_a of the isolated base in solution (and that of the isolated PS lipid head-group) the type of lipids in the cell membrane, the bulk salt concentration and pH and the distance between the micelle and the membrane. The minimized free energy for each condition provides for the probability of each polymer conformation, the state of protonation of each basic and PS group, the number of ligand–receptor pairs, as well as the local densities of each of the different components. Thus, we obtain detailed thermodynamic and structural information for each micelle–membrane distance. The coupling between the molecular organization, the physical interactions and the chemical equilibrium, that leads to the non-additivity shown below, arises because the probability for the chain conformations, the protonation state, the densities and interactions fields appearing in the different free energy contributions are coupled. Thus, their optimal value originates from the minimum of the global free energy, and not from each separate contribution. A detailed description of the functional form of the free energy functional and each of its terms, as well as how we generate the chain conformations and numerically perform the minimization is presented in the ESI.†

3. Results and discussion

Fig. 2 presents the predictions for the effective interactions between the micelle and the lipid layer. The effective interaction is defined as the minimal free energy of the micelle–membrane system for a fixed separation. Thus, the effective interactions as a function of separation represent the minimal free energy at each of the different separations. We first discuss the case of pH = 7.5, i.e., physiological conditions (Fig. 2B). The red curve shows the free energy for the case in which the membrane is composed by 6.5% of negatively charged lipids. The free energy profile shows that the micelle does not feel the presence of the lipid layer until the distance between the head groups of the lipids in the membrane and those of the lipids in the micelle, D − R, is about 5 nm. For shorter distances there is a relatively weak attraction followed by a repulsion. The minimal free energy is found at D − R = 2.7 nm with a strength of −3.7k_BT, a relatively weak attraction corresponding to a dissociation constant of 18 mM. In this case the only driving force for the attraction are the electrostatic interactions (both charge–charge attractions and counterion release) and it is clear that with the relatively small amount of charged lipids present only weak binding can be achieved. The repulsions at short distances are mainly due to the confinement of the polymers between the micelle and the lipid surface with the resulting increase in osmotic pressure and loss of conformational entropy of the polymer chains. The osmotic pressure represents the largest repulsion at short distance and the conformational entropy loss arises exclusively from the polybases due to the segregation of the polybase to the region between the micelle and the lipid membrane. A more detailed discussion of the segregation is presented below.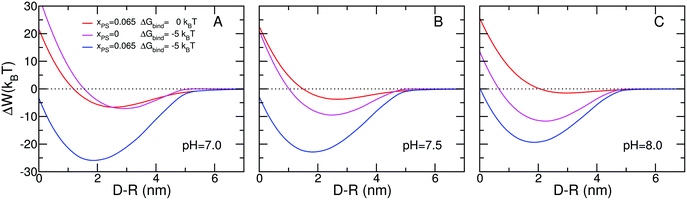

Fig. 2 Free energy versus separation distance between charged micelle and surface for: (A) pH = 7.0, (B) pH = 7.5, and (C) pH = 8.0. The micelle has a radius of R = 2.5 nm and the surface coverage of both PEG and polybase is σ = 0.20 nm⁻² and their chain length is n = 20. The polybase has a pK_a = 7.5. The salt concentration is c_s = 0.10 M. The red curves correspond to membranes with no overexpressed receptors and a concentration of 6.5% charged lipids. The magenta curves correspond to lipid membranes with overexpressed receptors and no charged lipids. The blue curves correspond to membranes with both overexpressed receptors and charged lipids.

The magenta curve in Fig. 2B corresponds to a model cell membrane with overexpressed receptors and no charged lipids. The shape of the free energy curve is similar to the case of a membrane with only charged lipids, the red curve in Fig. 2B. The minimal free energy, however, corresponds to a distance of 2.5 nm and strength of −9.5k_BT. The source of the attractions is the direct binding between the specific ligands at the end of the polybases and the receptors on the lipid surfaces.

Because the strength of one ligand–receptor pair or binding event equals −5k_BT, one might expect that the minimal free energy correspond to two binding events. However, at the optimal free energy of binding we find that the contribution of the ligand–receptor to the total free energy is around −25k_BT, as can seen from Fig. 3B which shows the different contributions to the free energy. Therefore at the optimal binding distance there are five binding events instead of two. This indicates that the formation of the ligand–receptor pairs is accompanied by large repulsions arising from confinement of the polymer tethered to the micelle. The reason is that for the ligand to properly bind to the receptor the end of the polybase has to be in contact with the lipid head-groups; limiting the possible number of polymer conformations that are accessible, in particular at large micelle–membrane separations.³⁰ It is only at very short distances that the repulsions arising from the osmotic pressure are larger than the conformational entropy loss. The shape of the free energy for both cases, charged lipids and overexpressed receptors, is very similar with only quantitative differences, however the source for the contributions is very different as shown in Fig. 3.

Fig. 3 Individual free energy contributions versus separation distance between of charged micelle and lipid surface. The conditions correspond to the situation shown in Fig. 2B; pH = 7.5. Panel A correspond to membranes with no overexpressed receptors and a concentration of 6.5% charged lipids. Panel B correspond to lipid membranes with overexpressed receptors and no charged lipids. Panel C correspond to membranes with both overexpressed receptors and charged lipids. Panel A also shows the legend for the various free energy contributions.

The question that arises next is how would the free energy of binding between the micelle and the lipid layer change if both overexpressed receptors and charged lipids are present on the membrane. The results are shown in the blue curve of Fig. 2B. The free energy behavior is qualitatively different than in the other two cases discussed. There is a dramatic synergetic effect leading to binding that is much more than the sum of the two optimal free energies. Furthermore, an interesting novel feature appears where the minimum of free energy obtained by the combined presence of charged lipids and overexpressed receptors is found at a distance from the membrane that is lower than that of each of the individual cases. The minimum occurs at D − R = 1.8 nm and the strength of the attraction is −22.8k_BT. This implies that in the region between 2.5 nm and 1.8 nm the addition of two effective repulsions leads to an attraction! This effect, that has a truly nanoscopic origin, is general and not specific to the particular choice of parameters or conditions as discussed below. The nanoscopic nature of the effect arises from the ability of the molecules to reorganize around the nanoparticle. This effect disappears when the interactions are between a lipid layer and a planar surface with the same mixture of polymers, see free energy curves of Fig. S2 of the ESI.† Interestingly, the synergetic effect, while not as pronounced, is still there since its source is mainly from the osmotic contribution, as discussed above.

To understand the results of Fig. 2B we need to look at the different contributions to the free energy and how they change for each of the three systems studied. There are thirteen different contributions to the free energy and they are shown for the three different types of membranes in Fig. 3. There are three main observations from the comparison. First, the osmotic pressure contribution (solvent) is very similar in the three cases (red lines). The reason is that this contribution only depends on the volume fraction distribution of water in the confined region, which does not change significantly regardless of the type of lipid layer. This is the main source for the synergetic effect. Second, the attractions arise from counterion release in the case where charged lipids are present and specific binding when receptors are present. Interestingly, the purely electrostatic contribution, i.e., that arising from charge–charge interactions, is repulsive when charged lipids are present, but they contribute a small attraction when there are no charged lipids. The charge–charge interactions include all the charges, namely those on the polybase, on the lipid layer as well as the co- and counterions free in the aqueous solution. Clearly, the gain in free energy by counterion release, for the charged lipids case, is more than the charge–charge repulsion resulting in an overall attraction. Third, there is a qualitative change in the shape of the repulsions arising from the conformational entropy of the polybases. This is due to the fact that when receptors are present the polymer molecules need to have one end on the micelle surface and the other on the lipid layer. Many of the polymers stretch laterally in order to reach receptors that are not exactly in the micellar axis. Interestingly, the shape of the conformational entropy loss is very similar for both cases in which overexpressed receptors are present. However, in the membranes with both receptors and negatively charged lipids the entropy loss is significantly larger. This is due to the larger amount of ligand–receptor pairs as can be seen from the binding contribution.

What are the factors responsible for the change in the position of the minimal free energy? To this end it is important to emphasize that while we are looking at all thirteen different contributions to the free energy they are not independent of each other but rather are very strongly coupled. As a result, the distance dependence of each contribution is not the same in the different cases as clearly exemplified by the conformational entropy loss of the polybases. Therefore, one cannot analyze just the different contributions as independent entities but rather what is the result of how the molecular organization results from the overall optimization of the combined contributions. The source of this behavior is even more transparent when one considers the electrostatic contribution to the free energy. The total contribution to the free energy from electrostatics arises from the combination of the charge–charge interactions and the counterion confinement (release). However, the charge on the polymers is not fixed; rather, there is the possibility of charge regulation through the acid–base equilibrium that is strongly dependent on the local environment. Therefore, the total electrostatic contribution is coupled to the chemical equilibrium. To get a better understanding of the large changes in charge regulation we consider next the molecular organization and local state of charge for different micelle–membrane separations.

Fig. 4 display volume fraction maps for both the polybase and the PEG for two different distances of the micelle from the membrane for the case in which the membrane includes overexpressed receptors and charged lipids. The volume fraction of a molecule of type i at position (r, z) correspond to the volume occupied by that species in the element of volume defined in the range (r, z; r + dr, z + dz) divided by the volume of the element. When the micelle is at a distance beyond the range of interactions the distribution of both polymers is symmetric and the polybase is slightly more stretched than the PEG, since the polybase carries some charge. For a short distance between the membrane and the micelle the polymers are segregated in a very dramatic way with most of the PEG on the side of the micelle facing the solvent while the polybase is found mostly on the side of the micelle facing the lipid layer. This surface induced ‘Janus’ like structure is the result of the optimization of the combined ligand–receptor binding of the functional end-group of the polybases and the overexpressed receptors together with the electrostatic attractions arising from the polybases and the charged lipids. Interestingly, at this distance the charged lipids strongly segregate, by a factor larger than 2, to the region where the micelle is found, i.e., in a circle in the xy-plane of radius 5 nm (see Fig. S3, showing the distribution of the charged lipids on the membrane, in the ESI†).

Fig. 4 Contour maps of the polymer segment volume fractions for both polybase and PEG for a micelle far and close to the lipid membrane. The left column correspond to the segment volume fraction of PEG polymer chains, while the right column corresponds to segment volume fraction of the polybase. The conditions correspond to the blue curve in Fig. 2B. The black sphere denotes the core of the micelle.

The very large molecular reorganization induced by the presence of the lipid layer is accompanied by a change in the state of charge of the polybase. This is quantified in Fig. 5 where the fraction of charged groups of the polybases is shown for the same two separations shown in Fig. 4. When the micelle does not feel the presence of the membrane the fraction of charge groups (f) has spherical symmetry but it is a strongly varying function of the distance from the head groups of the micellar lipids. At the given pH the fraction of charged isolated bases in bulk solution would be f = 0.5, since the pH is equal to the pK_a. However, in the micelle corona region where the density of polybase is large the fraction of charged groups is reduced to around f = 0.25 and it increases as the density of polybase decreases, with no region with f = 0.5. The regulation of the charge by shifting the acid–base equilibrium towards the unprotonated state of the base is the result of the system paying in chemical free energy in order to reduce the electrostatic repulsions. Namely, in the micellar corona the local density of chargeable groups is large since the molecules cannot leave that region. From the chemical free energy the optimal fraction of charged groups would be 0.5. However, the system has the option to reduce the charge by shifting the local chemical equilibrium in order to reduce the number of locally confined charges, thus reducing the electrostatic repulsions. This effect is very strong and the fraction of charged bases in the micelle corona is much lower than what it would be for individual bases in bulk solution. This interplay between state of charge and environment is even more pronounced when the micelle is close to the lipid membrane. In that case, and with the polybase more concentrated in the region between the micelle and the membrane, we can see a large enhancement of the fraction of charge in a region close to the lipid layer. This region has a width of around 1 nm, which is the Debye length under the conditions studied. The reason for the large enhancement of the charge there is the presence of the negatively charged lipids and the ability to then release both the positive and negative counterions from the confined environment. Interestingly, beyond that region the fraction of charged groups is even smaller than in the symmetric case due to the higher concentration of polybases, as seen in Fig. 4. In Fig. S3 in the ESI† we show also that the presence of the micelle close to the lipid layer results in a very large segregation of the charged lipids to the region of contact. In this way there is an overall optimization of the electrostatic attractions between the micelle and the lipids with a relatively low cost associated with the loss off entropy of mixing by the membrane lipids. Similar charged lipid segregation has been predicted by May et al.³¹ in the case of charged protein adsorption.

Fig. 5 Contour maps of the fraction of charged groups in the polybases for a micelle far (left map) and close (right map) to the lipid membrane. The distance Z is measured from the lipids surface. The conditions correspond to the blue curve in Fig. 2B.

The local charge regulation can now be used to explain the large synergetic effect observed when both charged lipids and overexpressed receptors are present. The presence of ligand–receptor binding can be achieved only if there are enough polybases in the close vicinity of the lipid surface. In the absence of negatively charged lipids this leads to a large shift on the polybases towards the unprotonated state (uncharged) in order to reduce the electrostatic repulsions, but at the cost of chemical free energy. When charged lipids are also present, the polybases can now become even more charged, still at a chemical free energy cost but now of overprotonation, and in this way optimize the electrostatic attraction between the polybase and the charged lipids. All these effects result in non-trivial molecular reorganizations, as clearly seen in Fig. 4 and 5, which in turn result in a variation of the distance dependence of each contribution to the free energy, as presented in Fig. 3.

The non-trivial coupling between molecular organization, charge regulation and ligand–receptor binding is found under all different conditions. An interesting case is shown in Fig. 2C where the pH is 8 and all other conditions are identical to the case shown in Fig. 2B. For the case of the micelle interacting with a model membrane with charged lipids the attractions are very weak, smaller than k_BT at the optimal separation. The reason for this very weak attraction is that at this pH the polybase is very weakly charged. Under the same conditions but now with no charged lipids but overexpressed receptors the minimal free energy is −12k_BT. Comparing the two cases one may be tempted to conclude that in the combined membrane, overexpressed receptors and negatively charged lipids, the ligand–receptor binding should be completely dominant since it is more than one order of magnitude larger (in absolute value) than the electrostatic driven attraction. However, the results in the combined system demonstrate that such a conclusion would be qualitatively and quantitatively wrong since the combined lipid layer has an attraction of −19k_BT! Note also that the position of the minimum in the combined system is at smaller distances than when only one of the attractive components is present, demonstrating again the dramatic changes in molecular organization when the optimization is global.

It should be noted that in the context of targeted drug delivery, synergetic or selective binding of nanoparticles has been observed experimentally and predicted theoretically using multivalent ligand–receptor interactions.^{7,11–15,32,33} In these cases the increased binding arises from multiple ligand–receptor binding events, i.e., only one type of interaction. The synergetic effects discussed here on the other hand, arise from the optimization of multiple interactions and are a general feature of systems in which there is a coupling between molecular organization, physical interactions, and chemical equilibrium. We have performed calculations under many different conditions. For example, in Fig. 2A we show the case of pH = 7 where the system is more charged than in the other two cases finding again a very large synergetic effect and shift in the minimal free energy. We have further studied polymer coated solid nanoparticles (see Fig. S4, ESI†), where the polymers have no lateral mobility since they are chemically bound to the surface of the solid nanoparticle. The synergetic effect and the shift of the minimal free energy, i.e., the addition of two effective repulsions leading to an attraction, are still present. The optimal free energy values are slightly smaller in magnitude and the repulsions at short distances are steeper than in the micellar case, due to the inability of the polymers to segregate completely out of the nanoparticle-membrane confined region.³⁴

To show the large changes in binding that can be achieved by controlling pH, the type of phase of the membrane lipids and the role that charge regulation plays even in the lipid head-groups, Fig. 6 show the strength of the free energy minima (the free energy that corresponds to the optimal separation between the micelle and the cell membrane) as a function of the bulk pH for two types of membranes. Fig. 6A corresponds to gel phase like lipids, i.e., the lipids do not have lateral mobility, whereas Fig. 6B shows the case where the lipids have lateral mobility and are in a liquid disordered phase. Also shown on the second y-axis is the value of the dissociation constants defined as K_d = e^{−ΔG_dis/k_BT} = e^ΔG_min/k_BT. For both the gel phase and liquid disordered phase 6.5% of the lipids have an acidic head-group. For each of the lipid membrane phases considered there are two different scenarios, one in which the acidic lipids have a pK_a = 3.6,^35,36 the experimentally determined value for PS³⁶ and the other assumes that the PS lipids are charged regardless of the pH, i.e., no charge regulation on the membrane's lipid head-groups. For pH > 8.5 all the cases are very similar and they represent the binding arising mostly from the specific ligand–receptor binding. It is interesting to note that pK_a = 7.5 for the segments of the polybase but already at pH around 10 there is an increase in the binding strength due to the ability of the charges on the lipid layer to induce a slight charging of the polybase.

Fig. 6 Binding energy of charged micelle with lipid membrane versus pH for different ‘types’ of lipid membranes. The left y-axis shows the binding free energy, while the right y-axis shows the corresponding dissociation constant. Panel A correspond to a gel like membrane (charges cannot move), whereas panel B correspond to a liquid like membrane (charges are mobile). The blue lines correspond to membranes where the amount of charge is determined by an acid–base equilibrium, whereas as the red lines correspond to membranes where the amount of charge on the lipids is fixed. The inset shows the binding energy for a gel like membrane (dotted lines) as well as for a liquid like membrane (solid lines). The conditions see Fig. 2.

For the gel lipids, i.e., no lateral mobility, we find that the strongest binding is around pH = 7.5, whether or not the PS head groups are assumed to allow for charge regulation. The presence of the minima is due to the balance between the charging of the polymers close to the interface to optimize the attractions with the charged lipid head-groups while at the same time having a relative lower charge further away (within a Debye length) from the interface to reduce the electrostatic repulsions due to the crowding of the polybase in the contact region. At pH > 7.5 the charge on the polymers is weak but enough to result in a strong synergy between ligand–receptor, electrostatic binding and molecular reorganization. For 6 < pH < 7.5 the charge on the polybase induces repulsions that are enough to slightly decrease the strength of binding as the pH is reduced. For the systems in which the lipids have fixed charge, there is a saturation effect at pH = 6 and at lower pH's the strength of binding is constant. However, when the proper pK_a of the PS head-groups is taken into account we see that lowering the pH below pH < 6 there is a sharp decrease in the binding strength. The reason for this effect is that as the pH is lowered the charge on the lipid head-group is reduced and even the charge on the micelles is not enough to induce enough deprotonation of the lipid head-groups.

When the membrane lipids are in the liquid phase we see that above pH = 6.5 there is no difference between the case where we assume fixed charges on the PS head-groups and that where charge regulation is allowed. There is a very sharp decrease in the strength of binding as a function of increasing pH that is very different from that when the lipids are in the gel phase. The reason is that the lateral mobility of the lipids enables the increase of the charge that interacts with the polybases in the micelles in the region of micelle–lipid contact (see Fig. S3, ESI†) and the coupling between the electrostatic and the specific binding can be maximized to lead to more than 15k_BT gain as compared to the gel phase lipids where the maximal charge is given by the fraction of PS lipids. Interestingly, this results in a dissociation constant that is 4 orders of magnitude lower for the liquid phase lipids as compared to the gel phase case. For pH < 6 there is a dramatic difference between the systems in which the ability of the PS to be protonated is accounted for versus the case of constant charge. We predict a change of 9 orders of magnitude in the dissociation constant between pH 3 and 6 for the case in which protonation/deprotonation of the PS is allowed as compared to the case where it is not. The reason for the change in minimal free energy is that the PS gets protonated as the pH is lowered while the charge on the polybase is increased. Even with the molecular reorganization at very low pH the cost of protonating the PS is so large that the interactions with the lipid layer arise only from the specific ligand–receptor binding. Interestingly the polybases continue to be charged leading to a large free energy cost associated with lowering the pH.

The main points that arise from the presented results are: first, pH changes can lead to orders of magnitude differences in the optimal binding, depending on the details of the system. Note that the optimal conditions are not at a pH that is intermediate between the pK_a of the acid and the base, but it rather depends on the molecular details of the system and the ability to couple the molecular organization to the interactions and the chemical equilibrium. In the specific example shown, just changing one degree of freedom (the mobility of the lipids by looking at different phases) the optimal pH changes 1.5 units and the strength of the apparent dissociation constant changes by many orders of magnitude. Second, for pH ∼ 7.5 relevant for blood or most tissues, we find that explicitly considering the pK_a or assuming constant charge of the PS head-groups makes no difference in the results. However, under different pH-conditions, e.g., the acidic environment in the gut or the acidic extracellular environment in tumors,³⁷ the proper treatment is required or one can obtain quantitatively and qualitatively wrong predictions. Interestingly, for the polybase the ability to regulate the charge depending on the environment needs to be taken into account in all the regimes of pH studied, otherwise the predictions would be simply wrong. Third, it is important to emphasize that the calculations shown here are for a particular choice of the parameters and conditions. Complete treatment of the coupling between chemical equilibrium, molecular organization and physical interactions is needed for the proper description of the system. The phenomena shown above are qualitatively correct under all conditions, but the quantitative details depend on the conditions. In the ESI, Fig. S5 and S6,† we show how changing the mole fraction of PS lipids in the membrane can result in many orders of magnitude changes in the dissociation constants under otherwise identical conditions. The results provide for guidelines on the design of optimal coating conditions for different types of surfaces.

There are several experimental methods that can be used to test the predictions presented above. One is the direct measurement of the binding constants of fluorescent labeled polymer modified nanoparticles/micelles as a function of pH to different formulations of lipid layers.³⁸ Another is the use of AFM tips in which the proposed mixtures of polymers are used to functionalize nanometric tips.^39,40 Measurements of the force profiles for different conditions can be directly compared with the predictions from the theory. Alternatively the surface force apparatus can be used in which one surface is coated with a lipid layer while the other contains the polymer mixture.⁴¹ These experiments, coupled with the AFM ones, can be used to test our assertion that the addition of two effective repulsions leads to an attraction is a nano metric effect.

4. Conclusions

To summarize we have shown that the interactions between polymer coated nanoparticles (micelles and solid NP) and lipid layers depend in a non-trivial way on the coupling that exists between molecular organization, chemical equilibrium and physical interactions. The complexity of the combined interactions results from the ability of the system to optimize the molecular organization so as to minimize the free energy. Our predictions demonstrate that one cannot predict the behavior in systems with different types of interactions by adding them without consideration of how the effective interactions change due to the coupling between them. The important degrees of freedom that enable the synergetic effect are the changes in local composition and in molecular organization. The non-trivial interactions in multicomponent liquid systems are an important tool that biological systems use to optimize their interactions. Moreover, it is clear that the variety of local environments found at sub-cellular levels may enable the switch of interactions from attractive to repulsive as we have shown when combining charged lipids with overexpressed receptors. These ideas need to be incorporated in the molecular design of delivery systems (drugs and nanoparticles) and scaffolds for tissue engineering where more that one optimal interaction, e.g., a particular ligand–receptor binding pair, may lead to better optimization than current available systems. Furthermore, we can use our findings for the design of novel materials with switchable properties that can be tuned by changes in the environment. The molecular theory used here can be used as a tool in the design of these complex non-additive systems. In all the cases that we have studied the total is not only more than the sum of the parts, it is actually qualitatively different from the addition of the components. Therefore, for these complex systems we need to develop new intuition to be built on top of the physical insights that already exists for simpler systems.

Acknowledgements

The authors thank Dr Mario Tagliazucchi and Dr Greg Putzel for a critical reading of the manuscript. This work was supported by the National Science Foundation under grant CBET-0828046, and the National Institutes of Health grant No. NIH GM087016.

References

1. B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, New York, 5th edn, 2008.
2. V. P. Torchilin, Nat. Rev. Drug Discovery, 2005, 4, 145–160.
3. V. P. Torchilin, Adv. Drug Delivery Rev., 2006, 58, 1532–1555.
4. O. M. Koo, I. Rubinstein and H. Onyuksel, Nanomedicine, 2005, 1, 193–212.
5. J. Shi, A. R. Votruba, O. C. Farokhzad and R. Langer, Nano Lett., 2010, 10, 3223–3230.
6. S. Bamrungsap, T. Chen, M. I. Shukoor, Z. Chen, K. Sefah, Y. Chen and W. Tan, ACS Nano, 2012, 6, 3974–3981.
7. C. B. Carlson, P. Mowery, R. M. Owen, E. C. Dykhuizen and L. L. Kiessling, ACS Chem. Biol., 2007, 2, 119–127.
8. H. Woehlecke, A. Pohl, N. Alder-Baerens, H. Lage and A. Herrmann, Biochem. J., 2003, 376, 480–496.
9. P. A. Leventis and S. Grinstein, Annu. Rev Biophys., 2010, 39, 407–427.
10. T. Utsugi, A. J. Schroit, J. Connor, C. D. Bucana and I. J. Fidler, Cancer Res., 1991, 51, 3062–3066.
11. F. J. Martinez-Veracoechea and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10963–10968.
12. S. Wang and E. E. Dormidontova, Soft Matter, 2011, 7, 4435–4445.
13. S. Wang and E. E. Dormidontova, Phys. Rev. Lett., 2012, 109, 238102.
14. N. A. Licata and A. V. Tkachenko, Phys. Rev. Lett., 2008, 100, 158102.
15. M. Caplan and E. Rosca, Ann. Biomed. Eng., 2005, 33, 1113–1124.
16. I. Szleifer and R. Yerusalmi-Rozen, Polymer, 2005, 46, 7803–7818.
17. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 3rd edn, 2011.
18. J.-L. Barrat and J.-P. Hansen, Basic Concepts for Simple and Complex Liquids, Cambridge University Press, New York, 2003.
19. K. Richter, M. Nessling and P. Lichter, J. Cell Sci., 2007, 120, 1673–1680.
20. J. S. Kim, V. Backman and I. Szleifer, Phys. Rev. Lett., 2011, 106, 168102.
21. M. Tagliazucchi and I. Szleifer, Soft Matter, 2012, 8, 3292–3305.
22. M. L. Immordino, F. Dosio and L. Cattel, Int. J. Nanomed, 2006, 1, 297–315.
23. Y. Park, R. D. Whitaker, R. J. Nap, J. L. Paulsen, V. Mathiyazhagan, L. H. Doerrer, Y.-Q. Song, M. D. Hürlimann, I. Szleifer and J. Y. Wong, Langmuir, 2012, 28, 6246–6255.
24. I. Szleifer and M. A. Carignano, Macromol. Rapid Commun., 2000, 21, 423–448.
25. R. Nap, P. Gong and I. Szleifer, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2638–2662.
26. G. S. Longo, D. H. Thompson and I. Szleifer, Langmuir, 2008, 24, 10324–10333.
27. D. Wang, R. J. Nap, I. Lagzi, B. Kowalczyk, S. Han, B. A. Grzybowski and I. Szleifer, J. Am. Chem. Soc., 2011, 133, 2192–2197.
28. C. Ren, D. Carvajal, K. R. Shull and I. Szleifer, Langmuir, 2009, 25, 12283–12292.
29. M. Tagliazucchi, O. Azzaroni and I. Szleifer, J. Am. Chem. Soc., 2010, 132, 12404–12411.
30. S. Wang and E. E. Dormidontova, Biomacromolecules, 2010, 11, 1785–1795.
31. S. May, D. Harries and A. Ben-Shaul, Biophys. J., 2000, 79, 1747–1760.
32. M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794.
33. P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271–16284.
34. R. J. Nap, Y.-Y. Won and I. Szleifer, Soft Matter, 2012, 8, 1688–1700.
35. C. Fleck, R. Netz and H. H. von Grünberg, Biophys. J., 2002, 82, 76–92.
36. F. C. Tsui, D. M. Ojcius and W. L. Hubbell, Biophys. J., 1986, 49, 459–468.
37. X. Zhang, Y. Lin and R. J. Gillies, J. Nucl. Med., 2010, 51, 1167–1170.
38. J. R. Silvius and F. l'Heureux, Biochemistry, 1994, 33, 3014–3022.
39. Y. F. Dufrêne, W. R. Barger, J.-B. D. Green and G. U. Lee, Langmuir, 1997, 13, 4779–4784.
40. H. Schönherr, Z. Hruska and G. J. Vancso, Macromolecules, 2000, 33, 4532–4537.
41. U. Raviv, S. Giasson, N. Kampf, J.-F. Gohy, R. Jérôme and J. Klein, Nature, 2003, 425, 163–165.

---

Footnote

† Electronic supplementary information (ESI) available: Full description of the free energy functional and numerical methods used to solve the molecular theory are presented. Also additional theoretical results, namely the individual free energy contributions, free energy curves for solid nanoparticles, and the dissociation constant versus pH and amount of surface charge, are presented. See DOI: 10.1039/c3bm00181d

---