 Open Access Article
Open Access ArticleThe protonation state and binding mode in a metal coordination complex from the charge measured in solution by electrophoretic NMR†
Marianne
Giesecke
a,
Zoltán
Szabó
b and
István
Furó
*a
aDivision of Applied Physical Chemistry, Department of Chemistry, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden. E-mail: furo@kth.se; Fax: +46-8-790-8207; Tel: +46-8-790-8592
bDivision of Organic Chemistry, Department of Chemistry, KTH Royal Institute of Technology, SE-10044 Stockholm, Sweden
First published on 22nd February 2013
Abstract
We measured with high accuracy the effective charge of a uranium(VI)–AMP complex by electrophoretic NMR (eNMR). Using the same method, the degree of counterion association is also assessed which leads to a quantitative determination of the nominal charge which then provides the degree of ligand deprotonation in the complex. This demonstrates a new application of eNMR for resolving structural details of supramolecular complexes.
Metal-coordinated supramolecular complexes display an enormous diversity and are of paramount significance. Nucleotides and nucleic acids are important ligands, not least because of their biological role. They are polydentate with various potential binding sites, including nitrogens in the purine base, hydroxyls in the ribose sugar, and negatively charged oxygens in the phosphate group. Depending on conditions (e.g. pH) either monodentate or multidentate coordination to these donor atoms or groups is possible. NMR spectroscopy has been shown to be a powerful tool to identify the stoichiometry and the mode of metal binding in nucleotide complexes.1
If, as often, the binding sites can be deprotonated such as hydroxyl and amine groups of nucleotides, the structure of formed complexes attains a new source of uncertainty which can be resolved by firmly establishing the deprotonation state of those groups. Conventionally, potentiometric pH measurements have been applied for this purpose. However, this indirect technique has significant drawbacks; it requires a quite complex experimental setup involving reliable electrodes, stable temperature, the presence of a suitable ionic medium and inert atmosphere. At high pH, glass electrodes may not be reliable while using hydrogen electrodes is tedious. Low ionic strength can also be a problem (junction potentials).
As we exemplify below in a uranium(VI)–AMP complex, electrophoretic NMR (eNMR) spectroscopy2 is a tool, new in this context, that can be used to assess directly the deprotonation state of ligands and thereby the structure of supramolecular metal coordination complexes. The water-soluble uranyl ion (UO22+) has two strongly bound oxygens (called “yl”-oxygens) that are chemically inert under most circumstances. Binding sites of exchangeable ligands are all arranged in a plane perpendicular to the linear UO22+-unit; therefore, steric requirements in ligand substitution reactions and in template and catalytic reactions are strict. The UO22+-unit may enhance the nucleophilicity of coordinating OH groups. Hence, it has been recently reported that uranium(VI) can form oxo-bridged complexes with α-hydroxycarboxylic acids.3 Formed by proton dissociation from the α-hydroxy group already around pH 3, they indicate a dramatic increase, by at least a factor of 1013, of the dissociation constant upon coordination to uranium(VI).
By coordinating and activating sugar moieties, uranyl may promote the formation of internucleotide bonds and can be an effective catalyst in oligonucleotide synthesis.4 Conversely, it can also induce DNA damage, a subject of considerable recent interest.5 Nucleotide-like ligands are also promising for metal extraction.6 We recently characterized a uranium(VI)–AMP (adenosine monophosphate) complex with a metal-to-ligand ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (hereafter called Complex 3
3 (hereafter called Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, see Scheme 1) in the alkaline pH range by using a combinatorial NMR approach7 supplemented by X-ray diffraction and molecular modelling.
3, see Scheme 1) in the alkaline pH range by using a combinatorial NMR approach7 supplemented by X-ray diffraction and molecular modelling.
 | ||
| Scheme 1 The structure of the uranium(VI)–AMP complex7 investigated here. The monodentate 2-OH oxygens with unresolved state of protonation are shown in red. | ||
Similarly to complexes formed with α-hydroxycarboxylic acids, we observed an increase of the dissociation constant of the sugar OH groups and subsequent deprotonation upon chelate formation with uranyl. Nevertheless, it remained unclear whether or not both hydroxyl groups of the coordinating AMPs are deprotonated. As is clear from Scheme 1, the degree of deprotonation of AMP is a remaining key issue when deciding about the fine structure of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. In an attempt to resolve this issue we measure here the charge of the complex by an NMR method.
3. In an attempt to resolve this issue we measure here the charge of the complex by an NMR method.
eNMR can be used to measure the effective charge z of charged species in solution via the well-known Nernst–Einstein relationship. Hence,
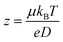 | (1) |
The samples (see Table 1, further details in the ESI†) were prepared in two steps. First, an appropriate amount of AMP monohydrate was added to 10 ml of D2O that was then neutralized to pD = 6.5 (calculated using pD = pH + 0.4 (ref. 11)) by adding a concentrated solution of TBA-OH (tetrabutylammonium hydroxide) in order to facilitate full dissolution of the AMP. Then, uranyl nitrate UO2(NO3)2·6H2O was added and the pD was increased to the desired value by adding TBA-OH. The solutions contained mainly Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and a small amount of free AMP (ca. 30% of the total). As has already been established, Complex 3
3 and a small amount of free AMP (ca. 30% of the total). As has already been established, Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 was long lived.7 TBA-OH was used to adjust the pD since it has been shown that quaternary ammonium cations are, in contrast to other possible ions like Na+, relatively inert to association with the phosphate group of nucleotides12 like AMP. In addition, the effective charge of the TBA+ cation can be determined directly by the same 1H eNMR experiment that is used for measuring the effective charge of Complex 3
3 was long lived.7 TBA-OH was used to adjust the pD since it has been shown that quaternary ammonium cations are, in contrast to other possible ions like Na+, relatively inert to association with the phosphate group of nucleotides12 like AMP. In addition, the effective charge of the TBA+ cation can be determined directly by the same 1H eNMR experiment that is used for measuring the effective charge of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. To quantify the ion-pairing behavior of the pure TBA+, experiments were also performed on a TBA-OH solution with no uranyl.
3. To quantify the ion-pairing behavior of the pure TBA+, experiments were also performed on a TBA-OH solution with no uranyl.
The self-diffusion coefficients were obtained by stimulated echo experiments while the electrophoretic mobilities were measured by recording with the double stimulated echo eNMR pulse sequence2d the variation of spectral phases with the electric field strength. Due to the high pD in the studied solutions, HDO was not used as a supposedly uncharged reference to correct for bulk flow effects2d in eNMR experiments. Instead, a small amount of DMSO (dimethylsulfoxide) was added to the studied solutions and its phase shift was monitored parallel to that of the target components Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and TBA+ (see Fig. 1). The results obtained from the diffusion and eNMR experiments are summarized in Table 2. As can be seen, for the TBA ions with smaller average charge the error in effective charge is dominated by the error in the electrophoretic mobility; for the complex, the error is contributed rather evenly by the diffusion and electrophoretic results obtained on the complex-bound AMP lines. Note that the errors for effective charges are calculated under the assumption of uncorrelated errors for D and μ; possibly, this leads to some overestimate. However, the random errors given in Table 2 do not account for the systematic errors, such as those arising from gradient miscalibration. Note, however, that z is derived as a ratio of D and μ, which reduces calibration errors in z, presumably to a value far below that of random error.
3 and TBA+ (see Fig. 1). The results obtained from the diffusion and eNMR experiments are summarized in Table 2. As can be seen, for the TBA ions with smaller average charge the error in effective charge is dominated by the error in the electrophoretic mobility; for the complex, the error is contributed rather evenly by the diffusion and electrophoretic results obtained on the complex-bound AMP lines. Note that the errors for effective charges are calculated under the assumption of uncorrelated errors for D and μ; possibly, this leads to some overestimate. However, the random errors given in Table 2 do not account for the systematic errors, such as those arising from gradient miscalibration. Note, however, that z is derived as a ratio of D and μ, which reduces calibration errors in z, presumably to a value far below that of random error.
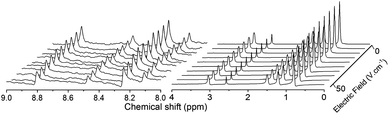 | ||
Fig. 1
1H eNMR spectral portions with an increasing electric field for Sample 2. The spectra on the left present the peaks of AMP and their phase shifts, either in Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (larger peaks) or free in solution (smaller peaks). The spectra on the right exhibit the phase shifts of TBA+ peaks with the exception of the peak at ca. 2.6 ppm that arises from uncharged DMSO. Notice the opposite sign of phase shifts for AMP (negatively charged entities, both the free AMP− ions and the complexed AMP) and TBA+ (positively charged). For the full spectrum, the detailed assignment and details of data evaluation, see ESI.† 3 (larger peaks) or free in solution (smaller peaks). The spectra on the right exhibit the phase shifts of TBA+ peaks with the exception of the peak at ca. 2.6 ppm that arises from uncharged DMSO. Notice the opposite sign of phase shifts for AMP (negatively charged entities, both the free AMP− ions and the complexed AMP) and TBA+ (positively charged). For the full spectrum, the detailed assignment and details of data evaluation, see ESI.† | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and TBA+ in the studied samples. The precision is given as ±σ, as obtained by repeated NMR experiments, at least 3 (and at most 5) for each sample; precision is calculated as average standard deviation for Samples 1 and 2 on one hand and Samples 3–5 on the other hand. The precision of the effective charge is calculated under the assumption of uncorrelated errors in D and μ
3 and TBA+ in the studied samples. The precision is given as ±σ, as obtained by repeated NMR experiments, at least 3 (and at most 5) for each sample; precision is calculated as average standard deviation for Samples 1 and 2 on one hand and Samples 3–5 on the other hand. The precision of the effective charge is calculated under the assumption of uncorrelated errors in D and μ
In Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the central oxygen has a charge of −2, the three uranyl groups have a total charge of +6 and the three phosphate groups have a total charge of −6. The charge of Complex 3
3, the central oxygen has a charge of −2, the three uranyl groups have a total charge of +6 and the three phosphate groups have a total charge of −6. The charge of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 is then −2 which becomes −5 if the bidentate 3-OH oxygens in the bridge position are deprotonated. If the monodentate 2-OH oxygens were also deprotonated, the total charge would be −8. However, positive ions can associate with the complex, changing the charge from its nominal to its detected effective value. As the only ones around, those ions must be TBA+.
3 is then −2 which becomes −5 if the bidentate 3-OH oxygens in the bridge position are deprotonated. If the monodentate 2-OH oxygens were also deprotonated, the total charge would be −8. However, positive ions can associate with the complex, changing the charge from its nominal to its detected effective value. As the only ones around, those ions must be TBA+.
Indeed, association of TBA+ with Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 is indicated by detecting a higher effective charge of TBA+ in Sample 3 (see Table 2) that lacks both uranyl or AMP. Experiments with additional samples with both AMP and TBA-OH but without uranyl (see ESI†) provided the same effective charge for TBA+ as that in Sample 3; in other words, TBA+ does not associate with AMP alone. As indicated by the single-component spectral appearance and the single-component behavior of the TBA+ signal in both the diffusion NMR and the eNMR experiments, the cation is in fast exchange between the states free and associated with Complex 3
3 is indicated by detecting a higher effective charge of TBA+ in Sample 3 (see Table 2) that lacks both uranyl or AMP. Experiments with additional samples with both AMP and TBA-OH but without uranyl (see ESI†) provided the same effective charge for TBA+ as that in Sample 3; in other words, TBA+ does not associate with AMP alone. As indicated by the single-component spectral appearance and the single-component behavior of the TBA+ signal in both the diffusion NMR and the eNMR experiments, the cation is in fast exchange between the states free and associated with Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. On the other hand, we stress that Complex 3
3. On the other hand, we stress that Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 was long lived7 with the AMP in slow exchange between its bound and free states (see Fig. 1).
3 was long lived7 with the AMP in slow exchange between its bound and free states (see Fig. 1).
The degree of TBA+ association can be estimated from either the measured self-diffusion coefficients or from the electrophoretic mobilities, both of which are rendered average quantities by fast exchange as
| DTBA = (1 − p)Dfree + pDC | (2a) |
| μTBA = (1 − p)μfree + pμC | (2b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, with all other data defined and given in Table 2. (One should note that Dfree and μfree are themselves fast-exchange averages over properties of TBA+ ions un-associated and associated with OH−.) Hence, p can be obtained either from the diffusion or from the eNMR data as
3, with all other data defined and given in Table 2. (One should note that Dfree and μfree are themselves fast-exchange averages over properties of TBA+ ions un-associated and associated with OH−.) Hence, p can be obtained either from the diffusion or from the eNMR data as | (3a) |
 | (3b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and the nominal charge znominal of Complex 3
3 and the nominal charge znominal of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 calculated viaeqn (4)
3 calculated viaeqn (4)
When a TBA+ ion associates with Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, it is plausible to assume that the association is electrostatic. Hence, it should involve TBA+ ions not neutralized by association with their OH− counterions. Therefore, we can assume that TBA+ contributes +1 charge to the complex (see also ESI†) and the effective charge of Complex 3
3, it is plausible to assume that the association is electrostatic. Hence, it should involve TBA+ ions not neutralized by association with their OH− counterions. Therefore, we can assume that TBA+ contributes +1 charge to the complex (see also ESI†) and the effective charge of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 becomes
3 becomes
 | (4) |
For those two cases, the calculated nominal charges znominal of Complex 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (with concentrations from Table 1) are summarized in Table 3. One can conclude that the nominal charge of −5 with the 2-OH groups protonated is consistent with our data at pH = 11.9. Upon increasing the pH to 13, znominal increases toward −8 which indicates the 2-OH groups becoming (at least fractionally) deprotonated.
3 (with concentrations from Table 1) are summarized in Table 3. One can conclude that the nominal charge of −5 with the 2-OH groups protonated is consistent with our data at pH = 11.9. Upon increasing the pH to 13, znominal increases toward −8 which indicates the 2-OH groups becoming (at least fractionally) deprotonated.
In summary, we have shown that in this particular uranium(VI)–AMP complex the binding involves deprotonated 3-OH but the protonation state of 2-OH sugars of AMP changes with pH while leaving the structure of the formed complex apparently intact. Such information is difficult to be obtained by any other method. Thus, a new application of electrophoretic NMR is demonstrated.
Acknowledgements
Support from the Swedish Research Council VR (I.F.) is gratefully acknowledged.Notes and references
- Z. Szabó, Coord. Chem. Rev., 2008, 252, 2362 CrossRef.
- (a) M. Holz, Chem. Soc. Rev., 1994, 35, 165 RSC; (b) U. Scheler, in Encyclopedia of Magnetic Resonance, ed. R. K. Harris and R. Wasylishen, Wiley, 2012, DOI:10.1002/9780470034590.emrstm0154; (c) P. C. Griffiths, in Annual Reports on NMR Spectroscopy, ed. A. W. Graham, Academic Press, 2009, vol. 65, p. 139 Search PubMed; (d) F. Hallberg, I. Furó, P. V. Yushmanov and P. Stilbs, J. Magn. Reson., 2008, 192, 69 CrossRef CAS.
- Z. Szabó and I. Grenthe, Inorg. Chem., 2000, 39, 5036 CrossRef.
- (a) H. Sawai, K. Kuroda and T. Hojo, Bull. Chem. Soc. Jpn., 1989, 62, 2018 CrossRef CAS; (b) M. Shimazu, K. Shinozuka and H. Sawai, Angew. Chem., Int. Ed. Engl., 1993, 32, 870 CrossRef; (c) H. Sawai, T. Ito, K. Kokaji, M. Shimazu, K. Shinozuka and H. Taira, Bioorg. Med. Chem. Lett., 1996, 6, 1785 CrossRef CAS; (d) H. Sawai, A. Hirano, H. Mori, K. Shinozuka, B. Dong and R. H. Silverman, J. Med. Chem., 2003, 46, 4926 CrossRef CAS.
- (a) W. J. Hartsock, J. D. Cohen and D. J. Segal, Chem. Res. Toxicol., 2007, 20, 784 CrossRef CAS; (b) D. M. Stearns, M. Yazzie, A. S. Bradley, V. H. Coryell, J. T. Shelley, A. Ashby, C. S. Asplund and R. C. Lantz, Mutagenesis, 2005, 20, 417 CrossRef CAS; (c) S. S. Wise, D. W. Thompson, A. Aboueissa, M. D. Mason and J. P. S. Wise, Chem. Res. Toxicol., 2007, 20, 815 CrossRef CAS.
- J. Kim, M. Y. Kim, H. S. Kim and S. S. Hah, Bioorg. Med. Chem. Lett., 2011, 21, 4020 CrossRef CAS.
- Z. Szabó, I. Furó and I. Csöregh, J. Am. Chem. Soc., 2005, 127, 15236 CrossRef.
- (a) F. Hallberg, I. Furó and P. Stilbs, J. Am. Chem. Soc., 2009, 131, 13900 CrossRef CAS; (b) F. Hallberg, C. F. Weise, P. V. Yushmanov, E. T. Pettersson, P. Stilbs and I. Furó, J. Am. Chem. Soc., 2008, 130, 7550 CrossRef CAS.
- (a) U. Böhme and U. Scheler, J. Colloid Interface Sci., 2007, 309, 231 CrossRef; (b) U. Böhme and U. Scheler, J. Phys. Chem. B, 2007, 111, 8348 CrossRef; (c) U. Böhme, C. Vogel, J. Meier-Haack and U. Scheler, J. Phys. Chem. B, 2007, 111, 8344 CrossRef.
- U. Böhme and U. Scheler, Chem. Phys. Lett., 2007, 435, 342 CrossRef.
- P. K. Glasoe and F. A. Long, J. Phys. Chem., 1960, 64, 188 CrossRef CAS.
- (a) R. M. Smith and R. A. Alberty, J. Phys. Chem., 1956, 60, 180 CrossRef CAS; (b) P. Haake and R. V. Prigodich, Inorg. Chem., 1984, 23, 457 CrossRef CAS; (c) R. M. Smith, A. E. Martell and A. E. Chen, Pure Appl. Chem., 1991, 63, 1015 CrossRef CAS; (d) E. Stellwagen and N. C. Stellwagen, Electrophoresis, 2007, 28, 1053 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, NMR spectra, additional eNMR data, diffusion coefficients and electrophoretic mobilities. See DOI: 10.1039/c3ay00023k |
| This journal is © The Royal Society of Chemistry 2013 |
